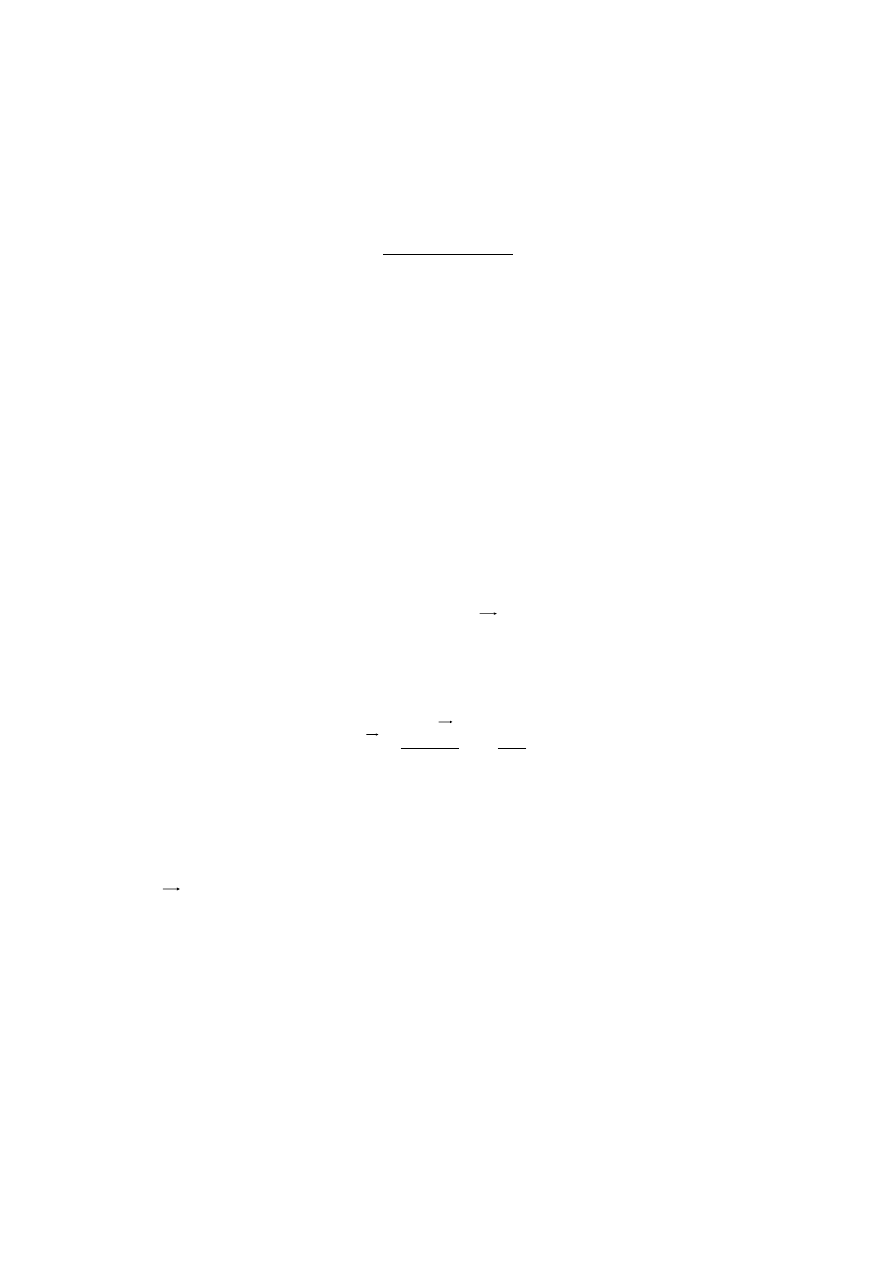
141

T e c h n i k i b a d a w c z e s t o s o w a n e w a e r o d y n a m i c e

dr inż. Tadeusz Tarnowski

Ć w i c z e n i e 8

Temat:

Określanie oddziaływania strugi powietrza na opływane modele ciał

1. Cel ćwiczenia:

Celem ćwiczenia jest określenie związku między siłą oddziaływania aerodyna-

micznego przepływającego płynu a kształtem modelu „zanurzonego” w przepływie .

2. Wprowadzenie

Zjawiska oporu ośrodka tworzą bardzo ważny dział mechaniki płynów, związany

z ruchem ciał w środowisku płynnym; gazie lub cieczy.

Siłę z jaką strumień płynu (cieczy lub gazu) działa na obiekt wystawiony na jego

działanie nazywamy reakcją hydrodynamiczną lub aerodynamiczną.

Z zasady zachowania ilości ruchu

(

)

dt

P

U

m

d

=

⋅

i z zasady stałości masy

const

m

=

wynika, że szybkość zmiany ilości ruchu, wyodrębnionej w myśli masy

strumienia płynu jest równa naporowi, jaki ta masa wywiera na opływane ciało [1].

( )

dt

U

d

m

dt

U

m

d

P

r

=

=

gdzie:

→

P

- reakcja dynamiczna (hydrodynamiczna lub aerodynamiczna),

m

- wyodrębniona masa strumienia płynu,

U

- prędkość poruszającego się płynu,

t

- czas.

Z

powyższego wzoru wynika, że napór dynamiczny jest wywołany zmianą prędko-

ści płynu w analizowanej objętości.
Jeżeli skorzystamy z prawa względności ruchu zgodnie z którą reakcja wywierana
przez płyn na ciało zależy tylko od prędkości względnej ciała stałego i płynu to wiel-
kość reakcji ciała na płyn będzie taka sama dla ciała nieruchomego, opływanego pły-
nem, jak i ciała poruszającego się w płynnym ośrodku nieruchomym.

142

Tak więc opór ośrodka – jest zjawiskiem makroskopowym zachodzącym

w płynnym medium, najczęściej w powietrzu lub w wodzie natomiast opory ruchu –
powstają zarówno przy przepływach ośrodka płynnego dookoła nieruchomego ciała
stałego, jak i przy ruchu ciał stałych w ośrodku płynnym. Ruchy względne ośrodka
płynnego dookoła ciał stałych całkowicie w nim „zanurzonych” nazywamy opływami.

Wszystkie ciała stałe poruszające się w otaczającym je ośrodku płynnym są podda-

ne działaniu sił wywieranych przez ten ośrodek na ich powierzchnię, które nazywamy
siłami lub reakcjami aerodynamicznymi.

Jeżeli ciało pozostaje w położeniu niezmiennym w poruszającym się ośrodku

płynnym, wówczas siły działające na nie nazywane są siłami aerodynamicznymi.

Siły aerodynamiczne działające na poszczególne elementy powierzchniowe opły-

wanego ciała można zastąpić jedną wypadkową siłą aerodynamiczną

P

, przedstawia-

jącej sobą całkowity opór aerodynamiczny ciała.

Wypadkową siłę aerodynamiczną

P

rozkłada się na opór aerodynamiczny

P

x

działający w kierunku ruchu oraz na siłę nośną

P

z

prostopadłą do kierunku ruchu.

W oporze aerodynamicznym możemy wyróżnić dwie składowe: opór ciśnieniowy

P

xc

i opór tarcia powierzchniowego

P

xt

. Suma tych oporów jest całkowitym oporem

aerodynamicznym ciała.

P

x

= P

xp

+P

xt

(1)

Rys.1. Rozkład siły aerodynamicznej na opór profilowy i siłę nośną

143

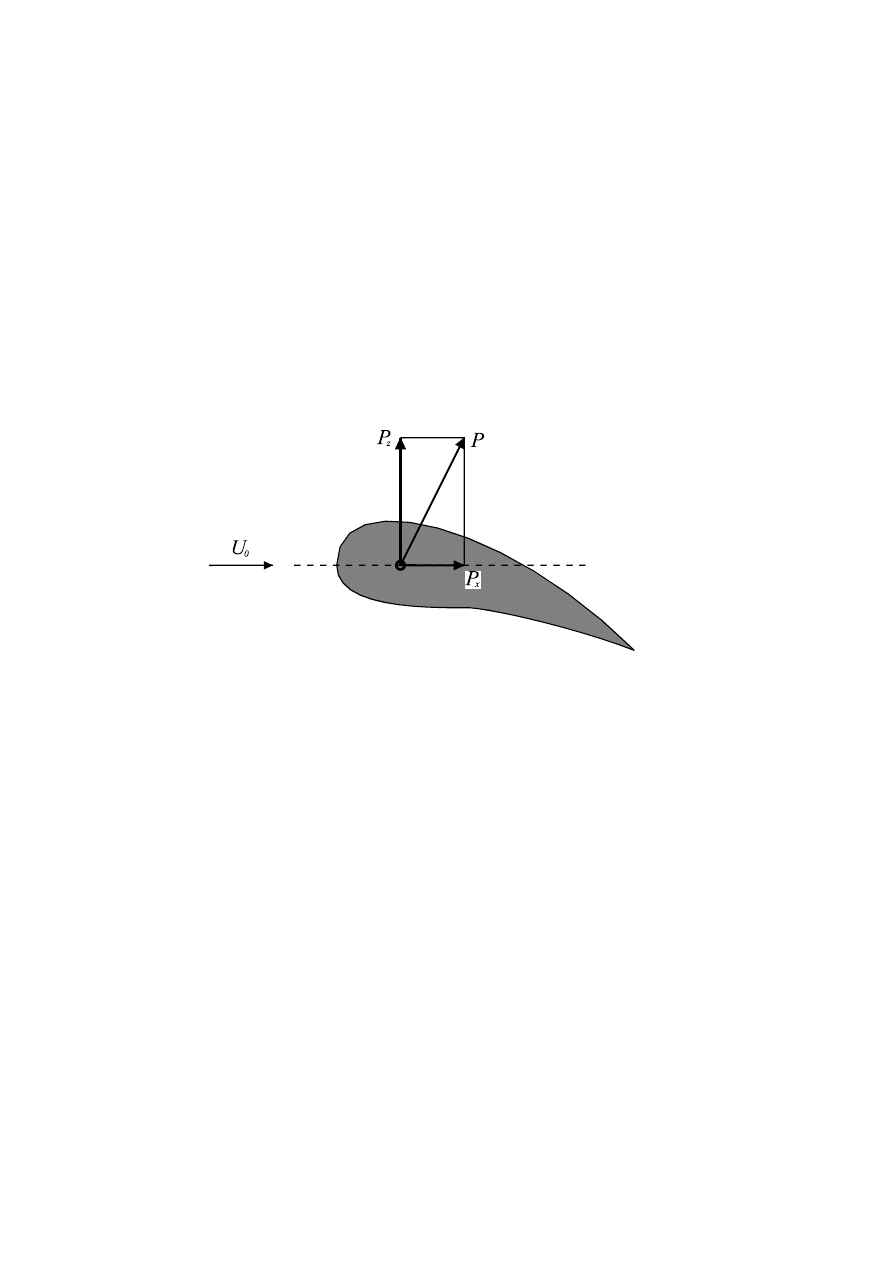
Opór aerodynamiczny

P

x

jest funkcją następujących wielkości: gęstości ośrodka

ρ,

względnej prędkości ruchu

U

, charakterystycznego wymiaru poprzecznego

l

i lepkości płynu

ν

,

co można zapisać następująco:

P

x

= f (

ρ,

U

,

l

, ν

)

(2)

Zależność określająca opór aerodynamiczny może być określona poprzez tzw.

analizę wymiarową, co pozwala zapisać ją następująco:

÷

ø

ö

ç

è

æ

=

ν

ρ

l

U

f

l

U

P

2

2

(3)

We wzorze tym funkcję

f

nazywamy współczynnikiem oporu aerodynamicznego

C

x

a wyrażenie w nawiasie (zmienna niezależna funkcji

f

) liczbą

R

EYNOLDSA

którą

oznaczamy jako

(Re).

Liczba ta może być uważana za bezwymiarową prędkość gdyż

przy stałym wymiarze poprzecznym i stałej lepkości, zmienia się ona

w sposób identyczny jak prędkość.

Wzór (3) może być zapisany w nieco innej postaci

F

2

U

c

P

2

x

x

ρ

=

(3a)

w której:

F

- tzw. przekrój czołowy opływanego ciała, będący największym przekrojem

tego ciała płaszczyzną prostopadłą do kierunku przepływu (ruchu),

2

U

2

ρ

- ciśnienie dynamiczne,

c

x

-

współczynnik oporu całkowitego.

Opór aerodynamiczny

P

x

(rys. 2) wyrażamy zatem iloczynem bezwymiarowego

współczynnika

c

x

ciśnienia dynamicznego

0,5

ρ

U

2

i przekroju czołowego

F

. Dla

ustalonej prędkości

U

i przekroju czołowego

F

siła oporu jest zatem zależna od war-

tości

c

x

, który często uważany jest za miarę doskonałości aerodynamicznej (nie doty-

czy to lotnictwa, gdzie doskonałością aerodynamiczną jest stosunek siły nośnej do siły
oporu). Wartość współczynnika oporu całkowitego

c

x

w określonym przedziale war-

tości

Re

zależy wyłącznie od kształtu ciała i jego ustawienia względem kierunku

przepływu.

144

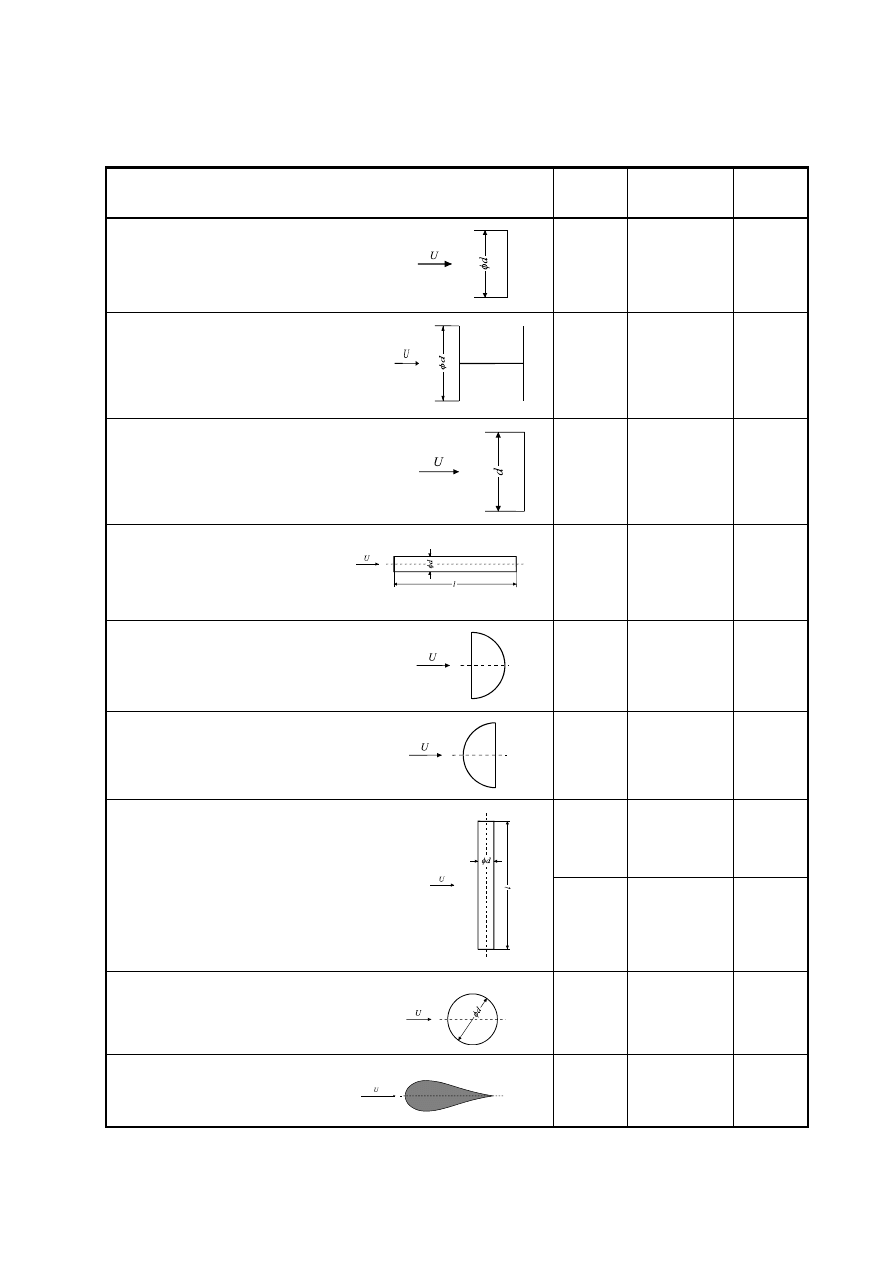
Przykładowe zestawienie wartości współczynników oporu

c

x

dla wybranych

kształtów ciał podano w Tabeli 1 w funkcji liczby Reynoldsa.

3. Metodyka badań modelowych zjawisk oporu aerodynamicznego

Przypomnijmy zasadę względności ruchów płynów i ciał stałych. Zgodnie z tą za-

sadą wszystkie zjawiska hydroaerodynamiczne można podzielić na trzy grupy:

1. ruch

ciała w nieruchomym środowisku,

2. opływ ciała nieruchomego poruszającym się płynem,
3.

ruch zarówno płynu jak i ciała względem nieruchomego układu odniesienia.

Do grupy pierwszej można zaliczyć np.: lot samolotu w atmosferze, łodzi podwod-

nej w morzu, do drugiej opływ budynków wiatrem, strumień wody lub gazu
w rurociągu, a do trzeciej przepływ powietrza wokół śmigieł wiatraka czy ruch pary
wodnej w układach przepływowych turbin ale również ruch samochodu przy wieją-
cym wietrze.

Rys.2. Ilustracja wielkości decydujących o oporze

aerodynamicznym

145

Tablica 1 Wartości liczbowe współczynnika oporu niektórych wybranych ciał

Kształt ciała

l/d Re

c

x

Tarcza kołowa
(

⊥

do kierunku prądu)

-

> 10

3

1,12

Układ posobny tarcz kołowych
(

⊥

do kierunku prądu)

0
1
2
3

> 10

3

1,12
0,93
1,04
1,52

Płyta prostokątna
(

⊥

do kierunku prądu)

(l - długość płyty)

1
5

20

∞

> 10

3

1,16
1,20
1,50
2,00

Walec kołowy
o osi ║ do kierunku prądu

0
1
2
4
7

> 10

3

1,12
0,91
0,85
0.87
0,99

Półkula wydrążona zwrócona
wklęsłością przeciw prądowi

-

> 10

3

1,33

Półkula wydrążona zwrócona
wklęsłością w kierunku prądu

-

> 10

3

0,34

1
5

20

∞

10

3

÷

10

5

0,63
0,74
0,90
1,20

Walec kołowy o osi

⊥

do kierunku prądu

5

∞

> 5

•

10

5

0,35
0,33

Kula

-

10

3

÷

10

5

> 3

•

10

5

0,47
0,20

Osiowo-symetryczne ciało
opływowe

-

> 2

•

10

5

0.04

146

W aerodynamice eksperymentalnej wykorzystuje się zasadę odwracalności opisa-

nych powyżej względnych ruchów ciał stałych i płynów co oznacza, że możliwe jest
np.: badanie zjawiska opływu nieruchomego płata samolotu przy jego omywaniu po-
ruszającym się powietrzem, jeżeli ruch powietrza jest wywołany w sposób sztuczny.

W podobny sposób możemy badać zjawiska opływu najrozmaitszych ciał np.:

opływu budowli a także aerację (przewietrzanie) osiedli mieszkaniowych, rozprze-
strzenianie się zanieczyszczeń w środowisku naturalnym itp..

W czasie badań zjawisk zachodzących w różnego typu maszynach przepływowych

a także zachodzących na zewnątrz budowli inżynierskich lub środków transportu czy
też wewnątrz urządzeń i rurociągów, wykorzystuje się w bardzo szerokim zakresie
modelowanie tych zjawisk w warunkach laboratoryjnych. Ma to szczególne znacze-
nie w przypadkach dużych prędkości względnych płynów i ciał stałych oraz gdy bada-
ne obiekty charakteryzują się dużymi wymiarami geometrycznymi a także wówczas
gdy zależy nam na bardzo szczegółowym poznaniu mechanizmów zjawisk zachodzą-
cych w przepływach.

Spektakularnymi osiągnięciami aerodynamiki doświadczalnej ostatnich lat są wy-

niki sportowe. Dążenie do coraz lepszych rezultatów w kolarstwie, narciarstwie zjaz-
dowym, wyścigach samochodowych, a więc w tych sportach, w których liczy się naj-
krótszy czas pokonania dystansu, doprowadziło sportowców do tuneli aerodynamicz-
nych i udoskonalenia ich sylwetek, ubioru, techniki poruszania się i kształtów sprzętu
sportowego, poprawiło również bezpieczeństwo sportowców w trakcie zawodów. Ba-
dania te sprowadzają się do prób zmniejszenia wartości oporu aerodynamicznego
a więc współczynnika

c

x

.

3.1. Tunele aerodynamiczne i eksperymentalne określenie oporu aerodynamicz-
nego

Do badań modelowych maszyn i urządzeń służą najczęściej tunele aerodynamicz-

ne różnych typów, różniące się budową wynikającą z ich przeznaczenia.

Pierwsze tunele aerodynamiczne powstały ponad sto lat temu i służyły do badań

mało skomplikowanych przepływów. W miarę rosnących potrzeb budowano tunele
o coraz to nowocześniejszych konstrukcjach i przeważnie większe dochodząc do tak
dużych konstrukcji, które pozwalały badać wybrane obiekty w skali 1:1, czego przy-
kład pokazano na rys 3.

Konstrukcje tuneli obecnie służących do badań zależą od ich przeznaczenia, do-

kładniej od rodzaju obiektu, który ma zostać w tunelu poddany badaniom – inne są

147

bowiem stawiane wymagania przy badaniach modeli np.: mostów wiszących a inne
przy badaniach samochodów, nie wspominając o całej następnej grupie tuneli prze-
znaczonych do badań wymiany ciepła lub masy. Wyposażenie tunelu zależy również
od jego przeznaczenia a dokładniej od typu przepływu jaki ma być w tunelu modelo-
wany albowiem modelowaniu podlegają nie tylko obiekty ale i sama organizacja prze-
pływu w przestrzenia pomiarowej (jego turbulencja, gradient prędkości itp.)

W trakcie badań przepływów w tunelach aerodynamicznych określane są różne

wielkości fizyczne dotyczące zjawisk występujących bądź na powierzchni „styku”
badanych obiektów z omywającym je płynem, bądź też w samym przepływie. Do tych
wielkości zaliczyć można: ciśnienia (całkowite, statyczne i dynamiczne), prędkości,
kierunki przepływu, temperatury, wydatki, parametry dyfuzji, wymiany ciepła. Mie-
rzone mogą być także siły i momenty związane z oddziaływaniami aerodynamicznymi
na opływane strumieniem płynu obiekty. Pomiary tych wielkości mogą być prowa-
dzone zarówno w warunkach przepływu stacjonarnego – bez zmiany w czasie parame-
trów przepływu – jak i w przepływach niestacjonarnych do których zaliczyć należy
przepływy turbulentne.

Jednym z obiektów poddawanych szczegółowym badaniom w tunelach aerodyna-

micznych są pojazdy samochodowe zarówno osobowe jak i ciężarowe. Celem takich

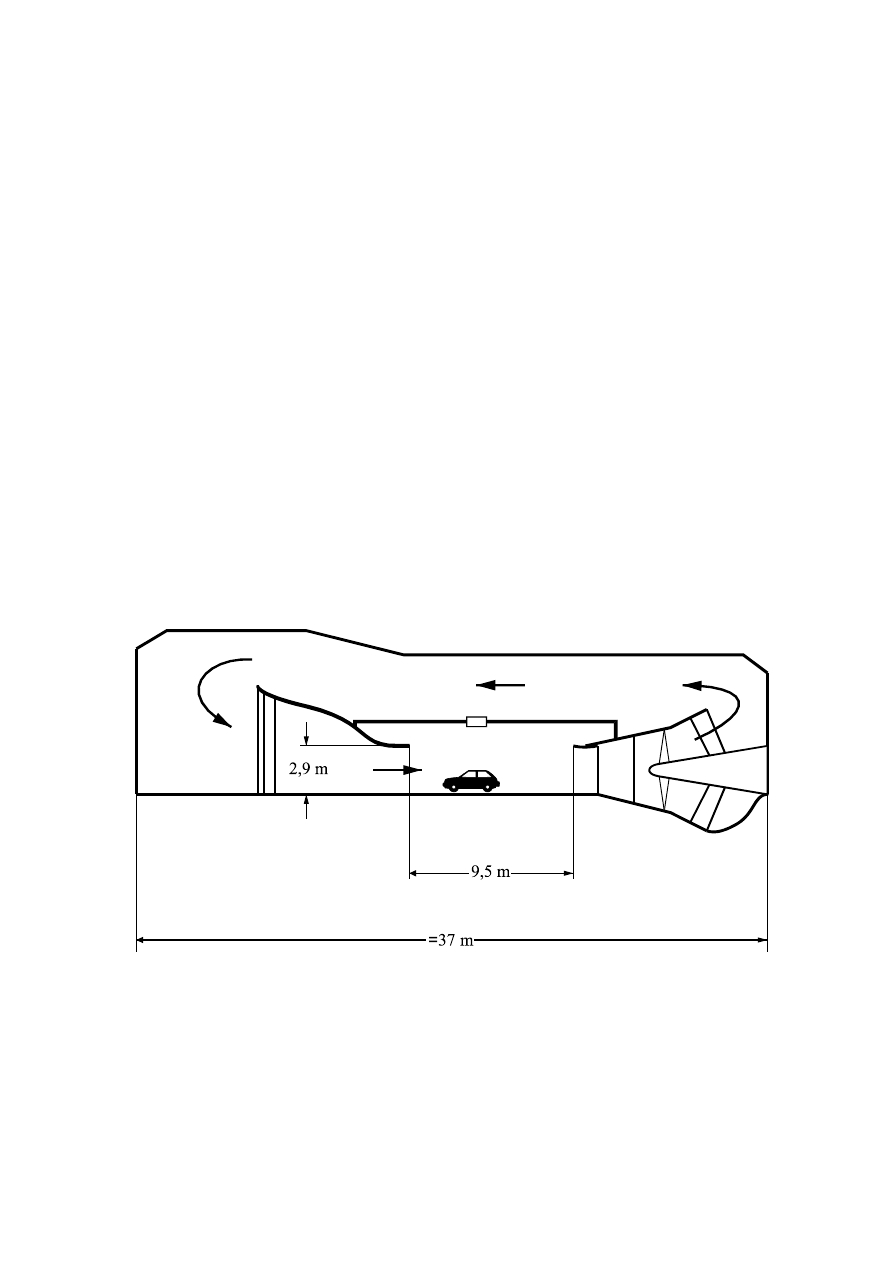
Rys.3. Tunel aerodynamiczny do badań samochodów w podziałce 1:1 (Włochy), pole

przekroju części pomiarowej F = 11,75m

2

; prędkość powietrza U = 40 m/s; moc

napędu N = 625 kW.[5]

148

badań jest uzyskanie takiej sylwetki pojazdu by opory opływu były jak najniższe, co
przyczynia się do zmniejszenia zużycia paliwa a przez to zmniejsza szkodliwe oddzia-
ływanie spalin na środowisko naturalne.

Przy milionach produkowanych pojazdów zmniejszenie ilości spalin emitowanych

do atmosfery jest jednym ze sposobów znacznego ograniczenia zatruwania powietrza
(33% ogólnej emisji CO

2

to efekt spalania paliw w silnikach napędowych środków

transportu) a także zmniejszenia wraz z gazami spalinowymi emisji ciepła.
Dodatkowym efektem, wcale niebagatelnym jest często podniesienie warunków
bezpieczeństwa kierowcy i pasażerów przez np. odpowiednie ukierunkowanie strug
deszczu na szybach, zapobieganie osadzaniu błota i innych zanieczyszczeń na reflek-
torach i światłach pozycyjnych itp.
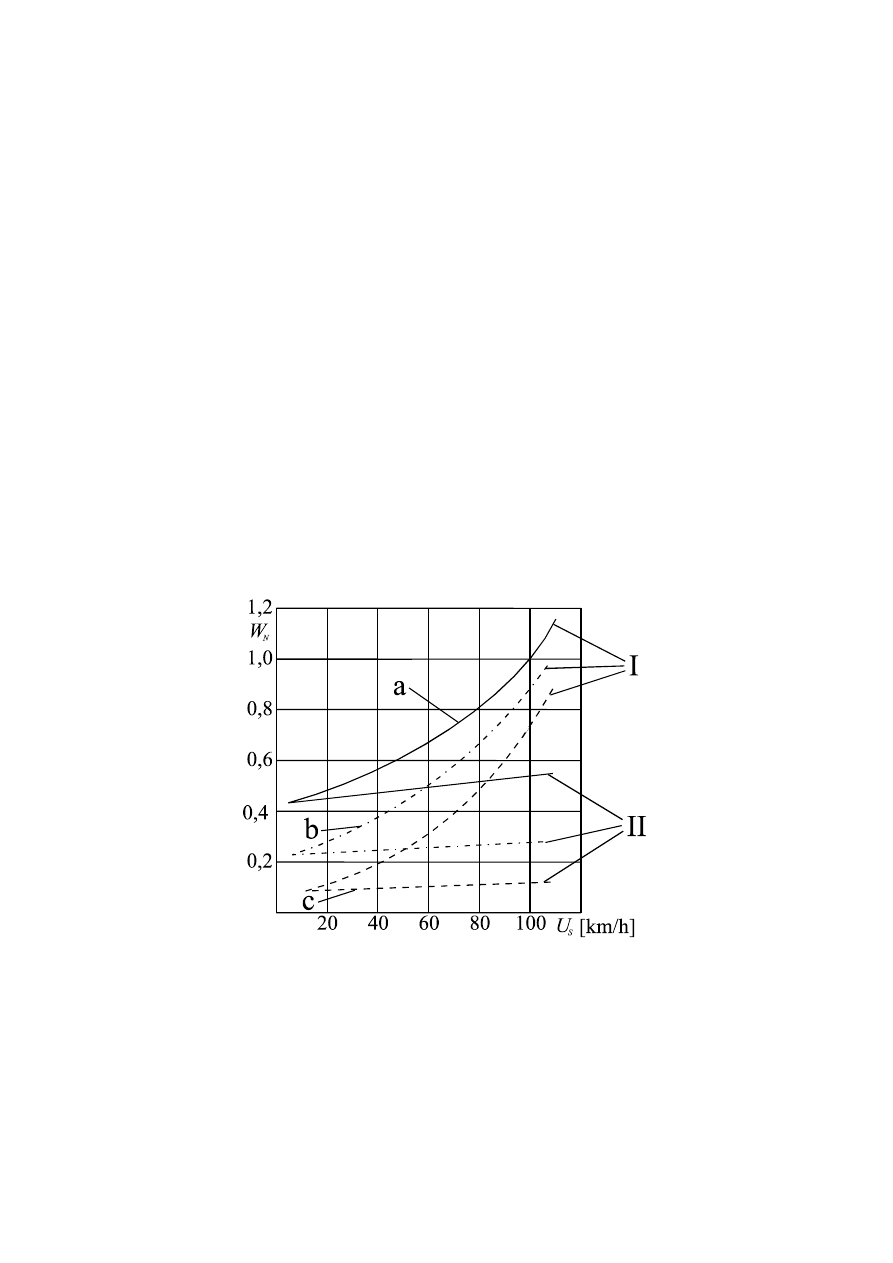
Na rysunku 4 przedstawiono za [5] opory ruchu i energię niezbędną do ich poko-
nania dla trzech grup pojazdów. Z rysunku widać, że dla samochodów wszystkich ty-
pów analizowanych tu samochodów opory powietrza są większe od oporów toczenia
nawet przy niewielkich prędkościach ruchu.

Rys.4. Rozkład poszczególnych sił oporu ruchu działających na samochody [5]

a – ciągnik siodłowy z kontenerem, b – samochód ciężarowy o średniej ładow-
ności bez przyczepy, c – szybki samochód dostawczy, I – opór toczenia i powie-
trza, II – opór toczenia, W

N

– opór jednostkowy jazdy (odniesiony do mocy sil-

nika N

N

), V

S

– średnia prędkość jazdy

149

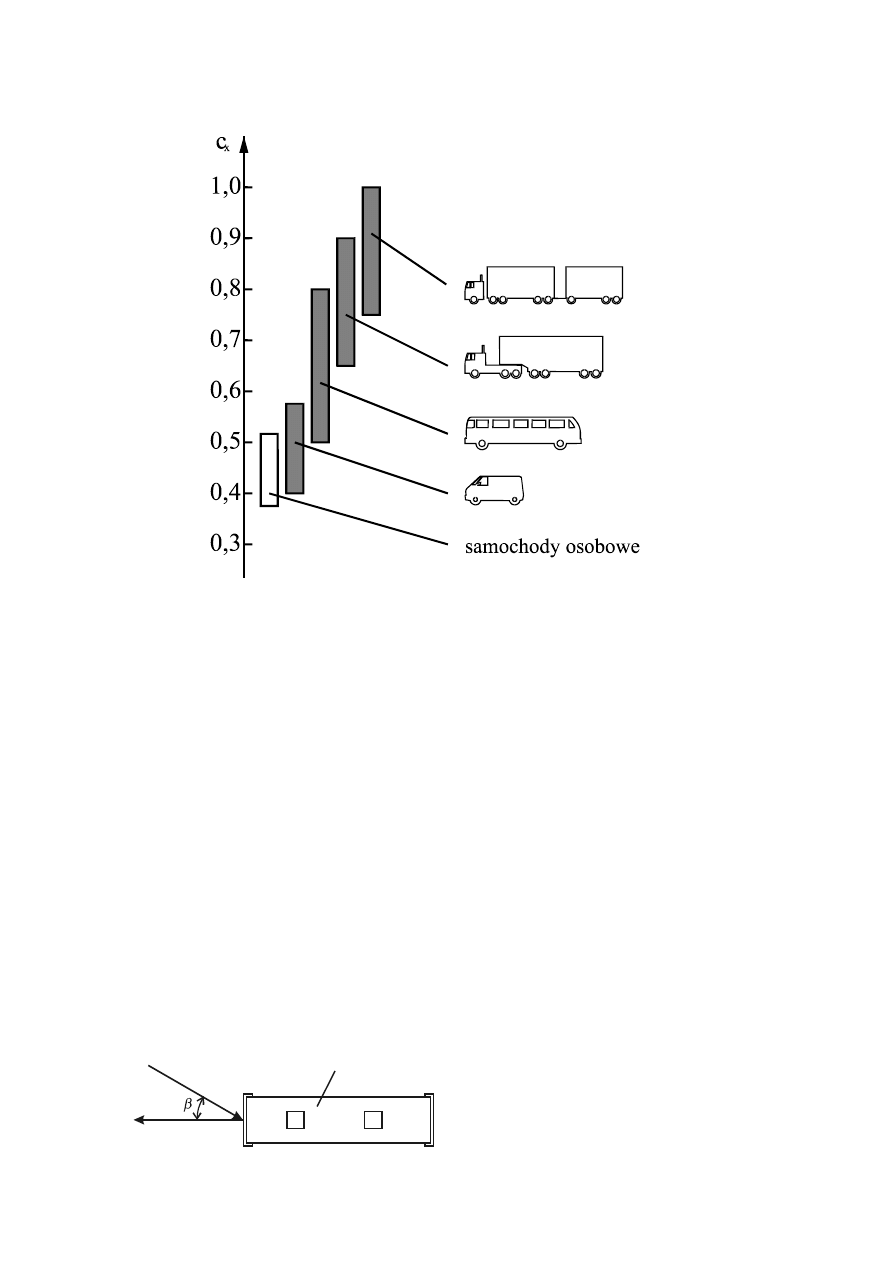
Na kolejnym rysunku (rys. 5) przedstawiono porównanie wartości współczynni-
ków

c

x

dla różnych typów samochodów.

Autobusy, jak to widać z rysunku osiągają 1,5 krotną wartość

c

x

w porównaniu

z samochodami osobowymi a zespoły pojazdów i ciągniki siodłowe około dwukrotną
wartość

c

x

. Świadczy to o dość dużym rozrzucie wartości współczynnika oporów po-

wietrza, odpowiednio do różnorodności kształtów tych pojazdów.
Pełniejszą ocenę własności aerodynamicznych pojazdów uzyskuje się przez ocenę
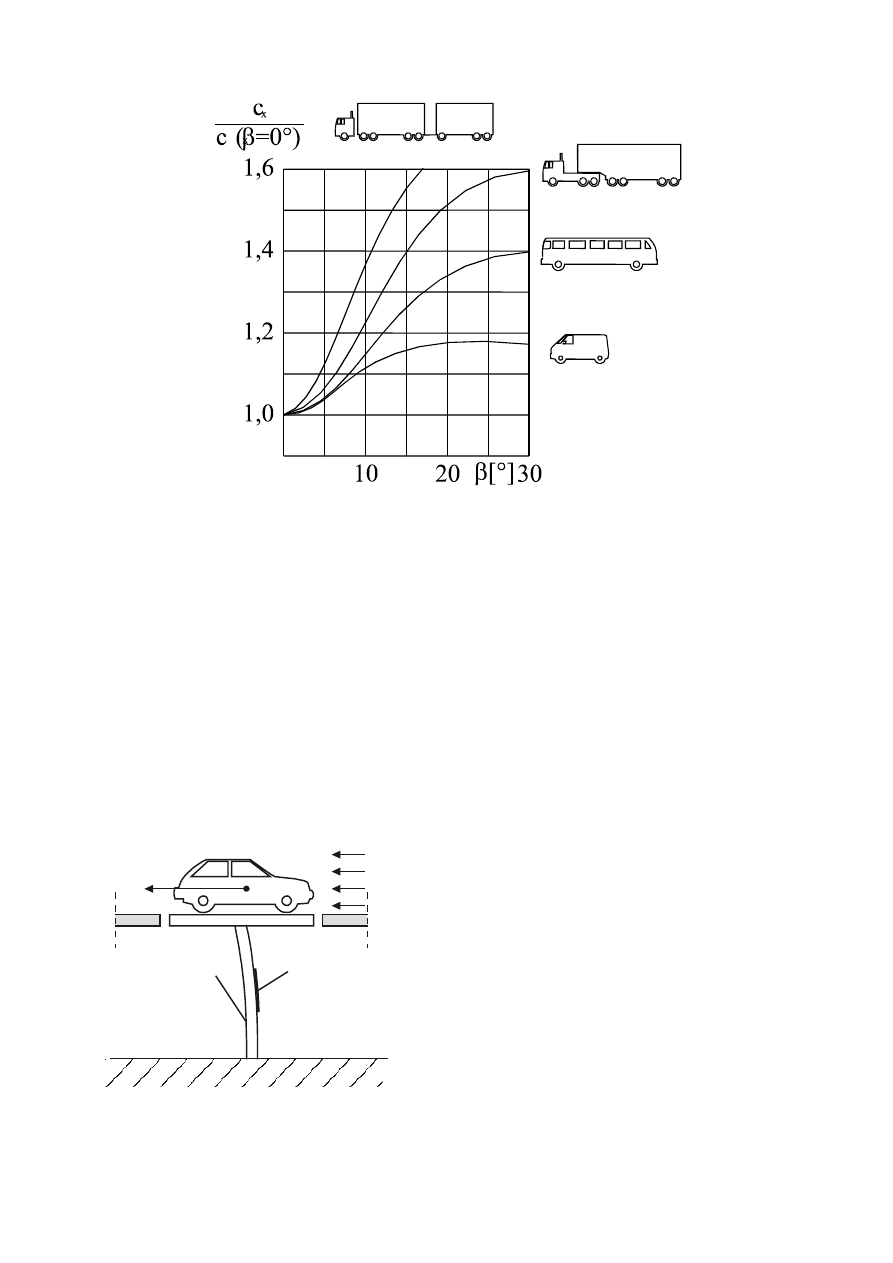
współczynnika oporu przy różnych od osiowego (równoległego do kierunku jazdy)
kierunkach napływu wiatru. Okazuje się, że współczynnik oporu w funkcji kąta

β

wy-

raźnie rośnie i wzrost ten jest tym większy im mniej opływowy jest kształt pojazdu.

Rys.5. Aerodynamiczna jakość kształtu różnych samochodów użytkowych

przy opływie symetrycznym c

x

– współczynnik oporu powietrza [5]

badany model

kierunek ruchu

kieru

nek

napły

wu

Rys.6. Definicja kąta napływu skośnego

na obiekt usytuowany w strudze
powietrza

150

3.2. Wyznaczanie reakcji płynu z użyciem wag aerodynamicznych

Dla wyznaczenia oporu aerodynamicznego koniecznym jest wyznaczenie siły dzia-

łającej na model w kierunku ruchu.
Najbardziej

dokładną metodą wyznaczenia tej wielkości jest zastosowanie wagi

aerodynamicznej i sposób ten jest stosowany najczęściej w praktyce. Wagą aerody-
namiczną nazywamy urządzenie, które w sposób bezpośredni wyznacza jedną lub
więcej składowych reakcji aerodynamicznych. Przykład takiej wagi z rys (8), pokazuje
opływ badanego modelu jednorodną strugą powietrza o prędkości

U

. Siła oporu ae-

rodynamicznego

P

x

działającego na model

przenoszona jest na wagę wywołując de-
formację sprężystej podpory. Jeżeli znać
będziemy zależność między deformacją
a siłą oporu, wówczas z wykresu wzorco-
wania (rys.12) będziemy mogli określić
siłę oporu

P

x

działającą na model. Pomiar

z pomocą wagi jest zatem przykładem po-
średniej metody pomiaru, w której poszu-
kiwana wielkość wyznaczana jest z uży-
ciem charakterystyki czy też krzywej

Rys.7. Opór powietrza przy napływie ukośnym

Rys.8. Zasada pomiaru siły aerodynamicznej

działającej na model obiektu

U

P

x

czujnik

tensometryczny

podpora

sprężysta

151

wzorcowania przyrządu. Krzywą wzorcowania sporządzamy przykładając do wagi
znaną siłę i mierząc deformację elementu sprężystego wagi w wyniku czego uzysku-
jemy związek między siłą a wskazaniem przyrządu.

Przykładowa charakterystyka wagi aerodynamicznej przedstawiona została na rys.

12. Deformacje elementu sprężystego wagi są rzecz jasna niewielkie i do ich pomiaru
koniecznym jest zastosowanie specjalnych technik.
Jedną z częściej stosowanych technik pomiaru deformacji jest stosowanie tzw.
czujników tensometrycznych naklejanych z pomocą nierozciągliwych klejów na ele-
ment sprężysty ( w tym przypadku belkę ) w sposób pokazany na rys. 9.
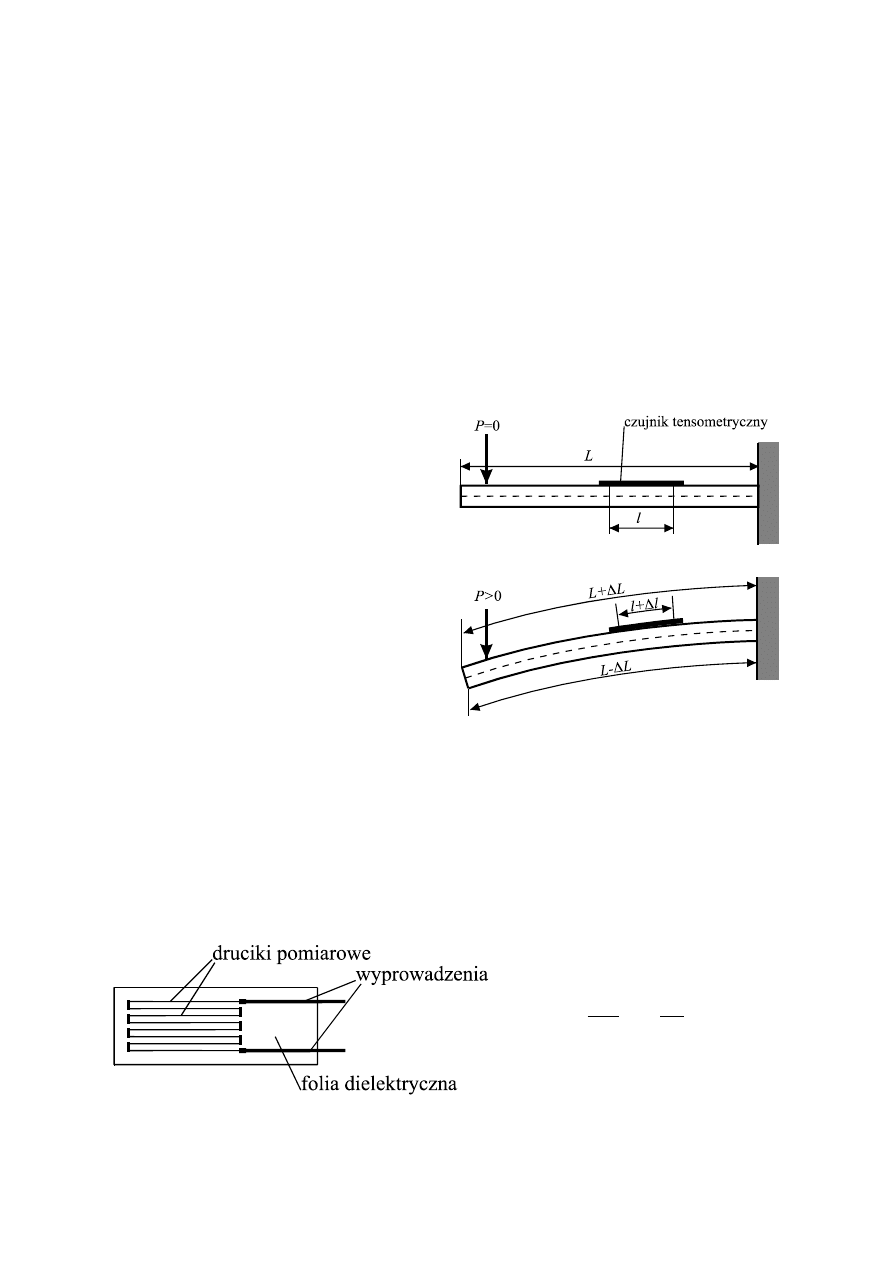
Jeżeli element sprężysty pozostaje w
stanie nieodkształconym (bez działania
sił) wówczas jego długość wynosi

L

.

Po obciążeniu elementu sprężystego siłą

P

.górne jego włókna wydłużą się

o

∆

L

a wraz z nimi przyklejony czuj-

nik tensometryczny. Odkształcenie belki
jest wprost proporcjonalne (w zakresie
obowiązywania prawa Hooka) do warto-
ści działającej nań siły.

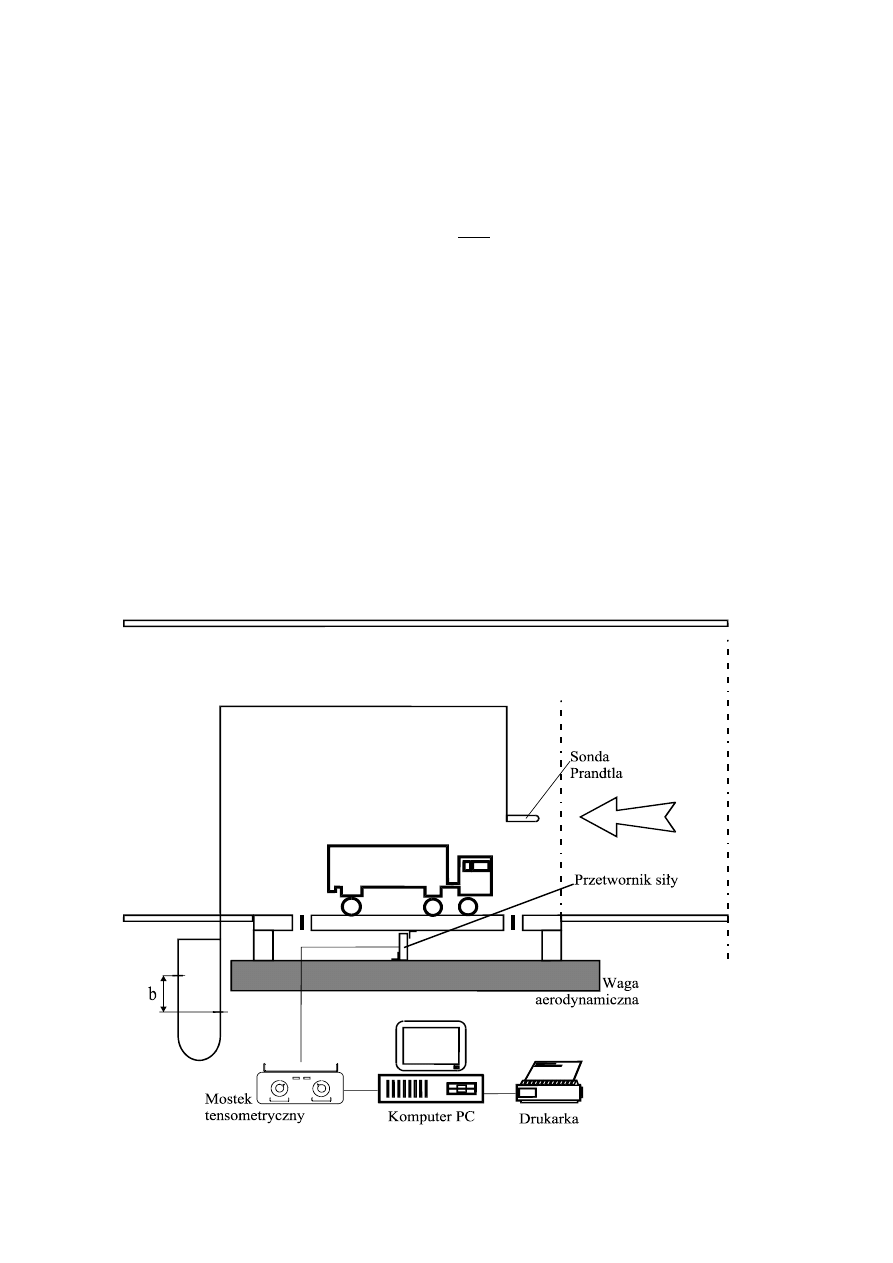
Zasadniczym elementem czujnika

tensometrycznego (tensometru) jest bar-
dzo cienki drucik (manganin, konstan-
tan) o średnicy, 0,02-0,04 mm ułożony
w zygzak i przyklejony do cienkiej die-
lektrycznej folii.

Wydłużenie pojedyńczego drucika czujnika wynosi

l

′

∆

natomiast sumaryczne

wszystkich drucików

l

n

l

′

⋅

=

∆

∆

. Zmiana wymiarów (długości i grubości) drucików

tensometru wystarcza by zmianie
uległ ich opór elektryczny:

ε

∆

∆

k

l

l

k

R

R

=

=

przy czym

k

jest wielkością stałą

dla danego tensometru, i zwana jest
jego czułością.

Rys.10. Drucikowy tensometr oporowy

Rys.9. Wydłużenie tensometru na ugiętej

sprężystej belce

152

Zmiana spadku napięcia prądu stałego w obwodzie jest wprost proporcjonalna do

zmiany wartości oporu elektrycznego i odwrotnie proporcjonalna do natężenia prądu
w tym obwodzie zgodnie z prawem Ohma (tu przedstawionym po przekształceniu)

I

R

E

∆

∆

=

Przy stałym prądzie

I

płynącym w obwodzie elektrycznym, zmiany oporu

∆

R

wynikłe ze zmiany geometrii opornika powodują zmiany napięcia

∆

E,

będące miarą

odkształcenia opornika. Odkształcenie to jest oczywiście proporcjonalne do siły przy-
łożonej do elementu na który naklejony jest tensometr. Ponieważ naprężenia w spręży-
stej podporze i związane z tym zmiany oporności są bardzo małe, dlatego tensometr
przyłączany jest do specjalnego przyrządu zwanego mostkiem tensometrycznym, któ-
rego zadaniem jest odpowiednie zwiększenie sygnału pomiarowego.

4. Część praktyczna ćwiczenia
4.1. Opis stanowiska pomiarowego:

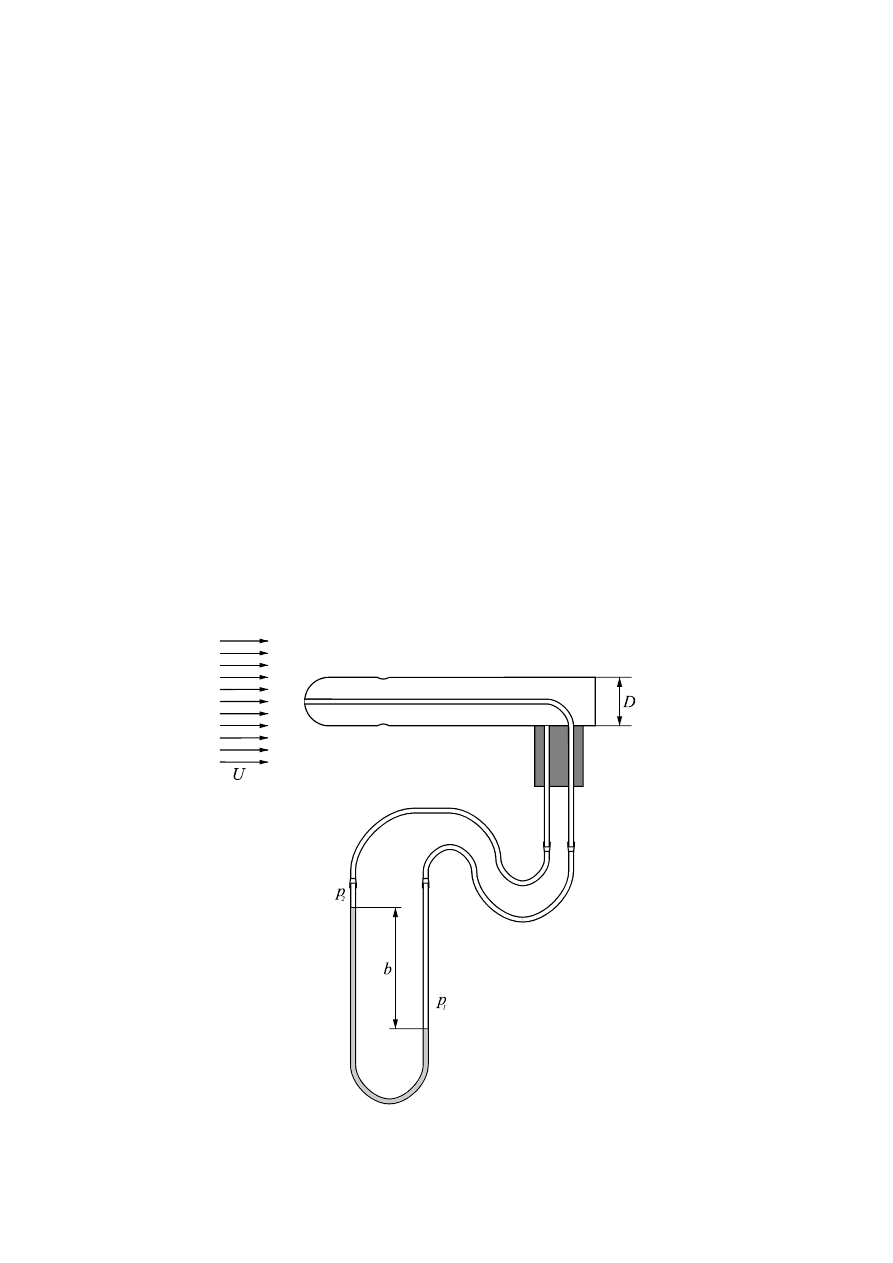
Rys.11. Schemat stanowiska pomiarowego

153

Stanowisko eksperymentalne służące do pomiaru siły oporu aerodynamicznego
zlokalizowane jest w tunelu aerodynamicznym Laboratorium aerodynamiki środowi-
ska. Stanowisko (rys. 11) składa się z jednoskładnikowej wagi aerodynamicznej
z przetwornikiem tensometrycznym, na której umieszcza się badany model. W skład
oprzyrządowania pomiarowego wchodzą ponadto:

- sonda Prandtla do pomiaru ciśnień panujących w przestrzeni pomiarowej.

Wykorzystując wskazania sondy jesteśmy w stanie określić i kontrolować
prędkość napływu czynnika na badany model

- mostek tensometryczny, którego wskazania posłużą do kalibracji wagi

i określenia siły aerodynamicznej działającej na model

- mikrokomputer do rejestracji danych wzorcowania i pomiarowych i pro-

gramowego przygotowania wykresów z wynikami badań,

- drukarka do przedstawienia wyników pomiarów,
- oprogramowanie do wykonania obliczeń i prezentacji wyników pomiarów.

4.2. Pomiar ciśnień i prędkości z pomocą sondy Prandtla i mikromanometru
Recknagla

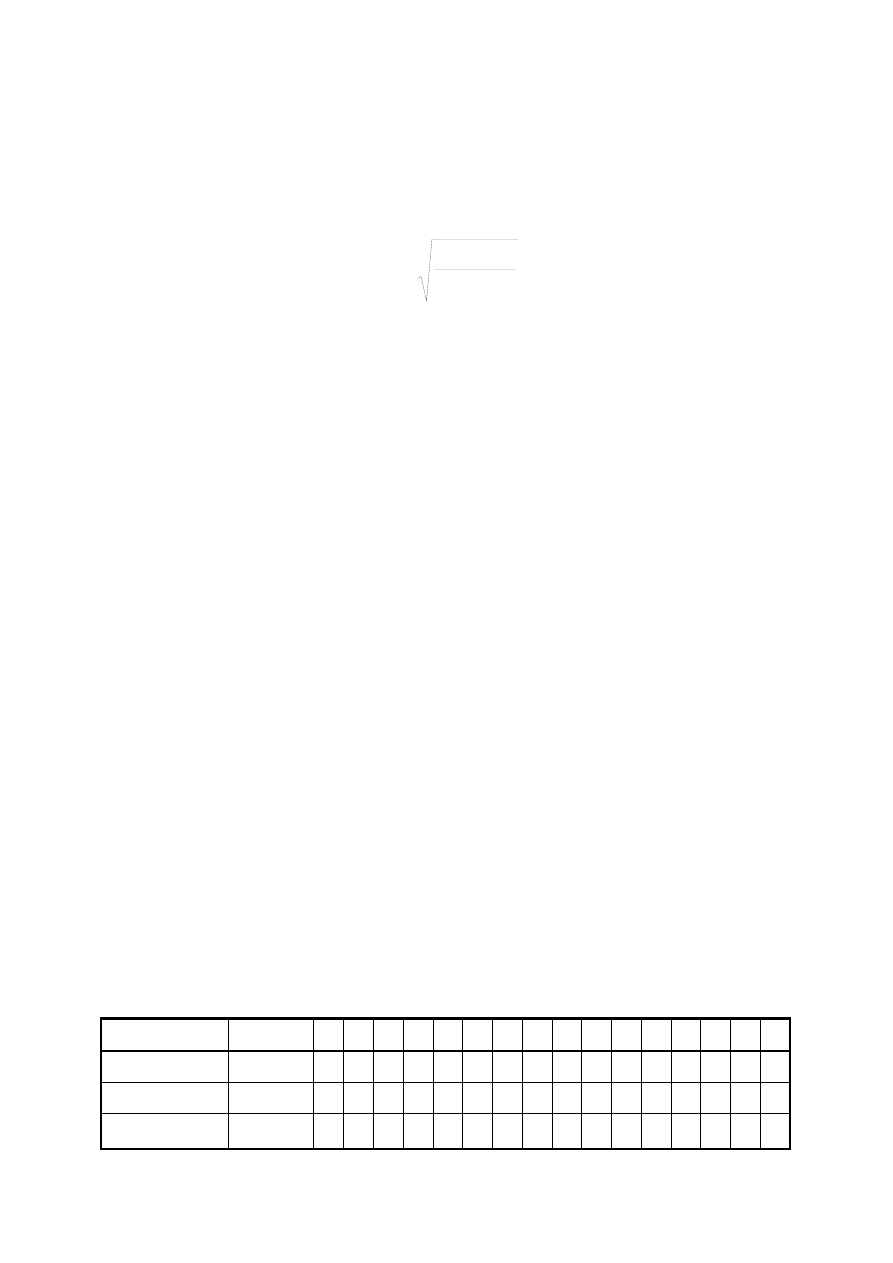
Rys.12. Sonda Prandtla do pomiaru prędkości przepływu

154

Pokazana na rys. 12 sonda Prandtla służy do wyznaczania prędkości napływające-
go powietrza. Do sondy tej podłączony jest różnicowy mikromanometr, który dla
zwiększenia czułości może być pochylony o znany kąt. Prędkość powietrza napływa-
jącego na sondę wyliczamy wówczas ze wzoru:

ρ

ρ

i

g

b

2

U

m

=

gdzie:

ρ

m

– gęstość cieczy manometrycznej,

g

– przyśpieszenie ziemskie,

b

– wskazania manometru w [m],

i

– przełożenie manometru,

ρ

- gęstość powietrza.

Dla alkoholu jako cieczy manometrycznej

ρ

m

,

gęstość powietrza

ρ

zależy od

temperatury i ciśnienia barometrycznego a przełożenia

i

można odczytać z odpowied-

niej skali mikromanometru.

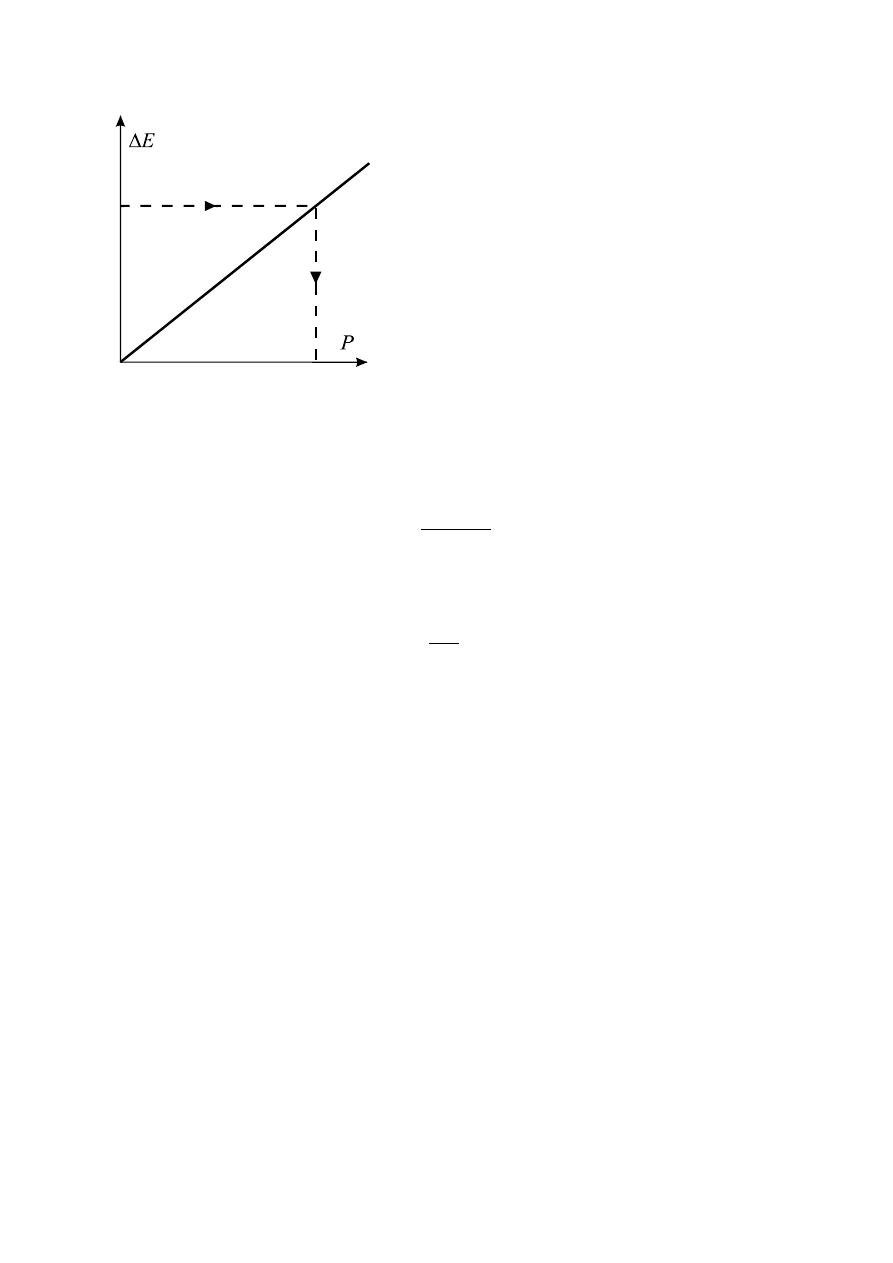
Krzywa wzorcowania wagi aerodynamicznej
Określenie sił działającej na model za wskazań bezpośrednich jest bardzo trudne i
obarczone znacznymi błędami stąd też przyjmuje się metodę porównawczą z wyko-
rzystaniem wzorcowania (tensometru) wagi. Wagę obciąża się siłami próbnymi po-
chodzącymi od mas zawieszanych na jedwabnej nici w ziemskim polu grawitacyjnym.
Notowane dla kolejnych mas odpowiedzi układu pomiarowego (woltomierza) pozwa-
lają na wykreślenie charakterystyki wagi w postaci wykresu wiążącego bezpośrednio
zmianę napięcia na tensometrze

∆

E

z siłą działającą na wagę.

Wykres ten umożliwia odczytanie wartości siły działającej na model dla znanej

zmiany napięcia na tensometrze. Wyniki wzorcowania dla wagi aerodynamicznej
używanej w trakcie ćwiczenia podano w tabeli 2 i na wykresie 13.

Tabela 2 Wzorcowanie wagi aerodynamicznej

Nr

pomiaru Jednostki 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

Masa

próbna

[g]

Siła

[N]

Napięcie na wyj-

ściu z mostka

[mV]

155

4.3. Obliczenia krzywych względnego oporu aerodynamicznego

Do obliczenia względnego oporu aerodynamicznego wykorzystujemy prostą for-

mułę o postaci:

100

P

P

P

RWOA

od

od

⋅

−

=

%

lub

100

P

P

WOA

od

⋅

=

%

gdzie:

RWOA

– różnica względnego oporu aerodynamicznego,

WOA

– względny opór aerodynamiczny,

P

od

– siła oporu przy konfiguracji odniesienia,

P

–

bieżące wartości siły oporu aerodynamicznego odczyta-

ne z charakterystyki wzorcowania wagi aerodynamicznej.

Kolejność wykonania czynności pomiarowych:
1. Odczytujemy temperaturę otoczenia i ciśnienie barometryczne i z pomocą odpo-

wiedniego programu wyliczamy gęstość powietrza

ρ

2. Na wadze umieszczamy model pojazdu samochodowego i uruchamiamy tunel
3. Z manometru odczytujemy różnicę poziomów cieczy manometrycznej i zapisuje-

my w stosownej tabeli widocznej na ekranie komputera

4. Dokonujemy odczytu spadku napięcia z mostka tensometrycznego i z krzywej

wzorcowania wagi aerodynamicznej odczytujemy wartość siły oporu i zapisujemy
ją w tabeli widocznej na ekranie komputera,

Rys. 13 Wykres charakterystyki wagi aero-

dynamicznej

156

5. Wyłączamy tunel aerodynamiczny (napływ czynnika),
6. Zmieniamy położenie modelu na wadze aerodynamicznej przez jego obrót o 10

stopni,

7. Powtarzamy czynności 1-3 przy czym ustalamy prędkość napływu na poprzednim

poziomie (różnica poziomów cieczy manometrycznej winna być identyczna w sto-
sunku do poprzedniego pomiaru). Pomiarów dokonujemy dla 5-u różnych wartości
kąta napływu czynnika na model,

8. Wykonujemy wydruk tabel pomiarowych i wykresów z wynikami badania.

5. Forma zaliczenia:

Samodzielne wykonanie sprawozdania, w którym studentka/student powinni za-

mieścić:
- stronę tytułową,
- cel

ćwiczenia,

- wstęp teoretyczny zawierający krótki opis stosowanej techniki pomiarowej, szkic

wagi aerodynamicznej oraz schemat stanowiska pomiarowego,

- metodykę obliczeń wyników pomiarów
- prezentacja wyników (w tabeli) oraz wykres zależności siły oddziaływania aero-

dynamicznego od kierunku napływu czynnika na model (prędkości wiatru, i/lub
innych parametrów)

- wnioski:

w jaki sposób zmienia się siła oporu aerodynamicznego w funkcji:

•

zmiany kształtu modelu

•

zmiany kierunku napływu strugi na model

•

zmiany prędkości napływu medium

Wnioski dodatkowe wynikające z samodzielnej lektury:

-

sposoby zmniejszania oporu aerodynamicznego (gdzie i po co?)

- sposoby

zwiększania oporu aerodynamicznego (gdzie i dlaczego?)

- porównanie

sił oporu aerodynamicznego i hydraulicznego

•

przykłady wykorzystania naporu

•

przykłady sposobów zmniejszania sił oporu

157

Literatura podstawowa:
1. Troskolański A. T: Hydromechanika, WNT, Warszawa 1967
2. Elsner J.W.: „Turbulencja przepływów”, 1987
3. Elsner J.W., Drobniak J.W.: „Metrologia przepływów turbulentnych”, 1995
4. Praca zbiorowa pod. red. S. Drobniaka: „Laboratorium mechaniki płynów”, 1989
5. Tłum. z niemieckiego K. Wituszyński: Aerodynamika samochodu. Od mechaniki

przepływu do budowy pojazdu WKiŁ Warszawa 1988

Literatura uzupełniająca:
6. Praca zbiorowa: Poradnik inżyniera Mechanika WNT Warszawa 1968