luty 1998

POLSKI

KOMITET

NORMALIZACYJNY

POLSKA NORMA

PN-EN ISO 10211-1

Mostki cieplne w budynkach

Strumień cieplny i

temperatura powierzchni

Ogólne metody obliczania

Zamiast:

Grupa katalogowa

ICS 91.120.10

EN ISO 10211-1:1995, IDT

This national document is identical with EN ISO 10211-1:1995 and is published with
the permission of CEN; rue de Stassart 36; B-1050 Bruxelles, Belgium

Niniejsza Polska Norma jest identyczna z EN-ISO 1211-1:1995 i jest opublikowana
za zgodą CEN; rue de Stassart 36; B-1050 Bruksela; Belgia

PRZEDMOWA KRAJOWA

Niniejsza norma jest oficjalnym tłumaczeniem angielskiej wersji normy europejskiej EN ISO 10211-1:1995 i jest wydana
jako norma identyczna z wprowadzoną normą europejską.
W normie są stosowane odsyłacze krajowe od

N1)

do

N6)

.

Niniejsza norma jest przeznaczona dla osób opracowujących programy komputerowe do obliczania pól temperatury w
przegrodach budowlanych, z uwzględnieniem mostków cieplnych, lub dla osób wykonujących obliczenia komputerowe
z użyciem takich programów.
Norma zawiera załączniki A,B,C (normatywne) oraz załączniki D,E,F,G (informacyjne).

NORMA EUROPEJSKA
EUROPEAN STANDARD
NORME EUROPÉENNE
EUROPÄISCHE NORM

EN ISO 10211-1

sierpień 1995

ICS 91.120

Deskryptory: budynki, izolacja cieplna, straty ciepła, wymiana ciepła, temperatura, zasady obliczeń

Wersja polska

Mostki cieplne w budynkach - Strumień cieplny i temperatura powierzchni - Ogólne metody obliczania

(ISO 10211-1:1995)

Thermal bridges in building
construction - Heat flows and surface
temperatures - Part I: General
calculation methods (ISO
10211-1:1995)

Ponts thermiques - Calcul des
témperatures superficielles et des flux
thermiques - Partie 1: Méthodes
générales de calcul (ISO
10211-1:1995) -

Wärmebrücken im Hochbau -
Wärmeströme und
Oberflächentempetemperaturen -
Teil 11: Allgemeine
Berechnungsverflachen (ISO
10211-1:1995)

PN-EN ISO 10211-1:1998 Mostki cieplne w budynkach Strumień cieplny i temperatura powierzchni Ogólne metody obliczania

Powielanie dokumentu zabronione. Wszelkie prawa zastrzeżone.

INTEGRAM BUDOWNICTWO

Strona 1

Niniejsza norma jest polską wersją normy europejskiej EN ISO 10211-1:1995. Została ona przetłumaczona przez Polski
Komitet Normalizacyjny i ma ten sam status co wersje oficjalne.
Norma europejska została przyjęta przez CEN 1995.03.13. Zgodnie z wewnętrznymi przepisami CEN/CENELEC,
członkowie CEN są zobowiązani do nadania normie europejskiej statusu normy krajowej bez wprowadzania
jakichkolwiek zmian.
Aktualne wykazy norm krajowych (powstałych w wyniku nadania normie europejskiej statusu normy krajowej), łącznie z
ich danymi bibliograficznymi, można otrzymać w Sekretariacie Centralnym CEN lub w krajowych jednostkach
normalizacyjnych będących członkami CEN.
Norma europejska została opracowana w trzech oficjalnych wersjach językowych (angielskiej, francuskiej i niemieckiej).
Wersja w każdym innym języku, przetłumaczona na odpowiedzialność danego członka CEN i zarejestrowana w
Sekretariacie Centralnym CEN, ma ten sam status co wersje oficjalne.
Członkami CEN są krajowe jednostki normalizacyjne następujących państw: Austrii, Belgii, Danii, Finlandii, Francji,
Grecji, Hiszpanii, Holandii, Irlandii, Islandii, Luksemburga, Niemiec, Norwegii, Portugalii, Szwajcarii, Szwecji, Włoch i
Zjednoczonego Królestwa.

CEN

Europejski Komitet Normalizacyjny

European Committee for Standardization

Comité Européen de Normalisation

Europäisches Komitee für Normung

SPIS TREŚCI

Przedmowa
Wprowadzenie
1 Zakres normy
2 Normy powołane
3 Definicje i symbole
4 Zasady
5 Modelowanie konstrukcji
5.1 Zasady modelowania
5.2 Warunki upraszczania modelu geometrycznego
6 Wartości obliczeniowe
6.1 Dane wartości obliczeniowe
6.2 Metody określania wartości obliczeniowych
7 Metoda obliczeń
7.1 Zasady obliczeń
7.2 Określanie współczynnika sprzężenia cieplnego i strumieni ciepła
7.3 Określanie temperatury na powierzchni wewnętrznej
8 Dane wejściowe i wyjściowe
8.1 Dane wejściowe
8.2 Dane wyjściowe
Załącznik A (normatywny) Uprawomocnianie metod obliczeniowych
Załącznik B (normatywny) Równoważna przewodność cieplna pustek powietrznych
Załącznik C (normatywny) Ustalanie liniowych i punktowych współczynników przenikania ciepła
Załącznik D (informacyjny) Przykłady zastosowania warstw quasi jednorodnych
Załącznik E (informacyjny) Opory przejmowania ciepła na powierzchni wewnętrznej
Załącznik F (informacyjny) Określanie wartości L oraz g w przypadku więcej niż dwóch wartości temperatury
brzegowej
Załącznik G (informacyjny) Ocena możliwości występowania kondensacji powierzchniowej

Przedmowa
Tekst normy EN ISO 10211-1:1995 został opracowany przez Komitet Techniczny CEN/TC 89 "Właściwości cieplne
budynków i komponentów budowlanych"

N1)

we współpracy z ISO/TC 163 "Izolacja cieplna"

N2)

.

Niniejsza norma europejska powinna uzyskać status normy krajowej przez opublikowanie identycznego tekstu lub
uznanie najpóźniej do lutego 1996 r., a normy krajowe sprzeczne z daną normą powinny być wycofane najpóźniej do
lutego 1996 r.
Zgodnie z przepisami wewnętrznymi CEN/CENELEC do wprowadzenia niniejszej normy europejskiej są zobowiązane
następujące kraje członkowskie: Austria, Belgia, Dania, Finlandia, Francja, Grecja, Hiszpania, Holandia, Irlandia,
Islandia, Luksemburg, Niemcy, Norwegia, Portugalia, Szwajcaria, Szwecja, Włochy i Zjednoczone Królestwo.

PN-EN ISO 10211-1:1998 Mostki cieplne w budynkach Strumień cieplny i temperatura powierzchni Ogólne metody obliczania

Powielanie dokumentu zabronione. Wszelkie prawa zastrzeżone.

INTEGRAM BUDOWNICTWO

Strona 2

Wprowadzenie
Mostki cieplne, które na ogół występują w każdym połączeniu między komponentami budynku lub wtedy, gdy zmienia
się układ struktury przegród, mają dwojakiego rodzaju konsekwencje:

a) zmiana wartości strumienia cieplnego
i
b) zmiana wartości temperatury wewnętrznej powierzchni przegrody
w porównaniu z wartościami temperatury dla konstrukcji bez mostka cieplnego.

Chociaż stosuje się podobne procedury obliczeniowe, nie są one identyczne przy obliczaniu strumieni cieplnych i
temperatury wewnętrznych powierzchni przegród.
Zazwyczaj mostek cieplny powoduje powstanie 3-wymiarowych

N3)

lub 2-wymiarowych

N4)

strumieni cieplnych, które

mogą być dokładnie określone specjalnymi metodami numerycznymi, opisanymi w tej normie. Są one określane jako
metody "Klasy A", a w części 1 niniejszej normy określono kryteria, które powinny być spełnione, aby metoda mogła
być zaliczona do "Klasy A".
W wielu zastosowaniach obliczenia oparte na 2-wymiarowym przedstawieniu strumieni cieplnych, są wystarczająco
dokładne. Są one określane jako metody "Klasy B". W części 2 niniejszej normy określono kryteria, które powinny być
spełnione, aby metoda mogła być zaliczona do "Klasy B".
Inne, mniej dokładne, lecz dużo prostsze metody, które nie są oparte na obliczeniach komputerowych, mogą
zapewniać wystarczająco dokładną ocenę dodatkowych strat ciepła z powodu mostków cieplnych. Te uproszczone
metody są podane w prEN 14683 Mostki cieplne w budynkach - Liniowe współczynniki przenikania ciepła - Metody
uproszczone i wartości obliczeniowe (ISO/DIS 14683:1995).

1 Zakres normy
W arkuszu 1 niniejszej normy ustalono wykaz modeli geometrycznych 3-D i 2-D mostka cieplnego do obliczeń
komputerowych:

- strumieni ciepła do oceny całkowitych strat ciepła budynku;
- minimalnych wartości temperatury wewnętrznej powierzchni przegród do oceny ryzyka wystąpienia na nich
kondensacji.

Te wykazy zawierają ograniczenia geometryczne i dalsze podziały modelu, warunki brzegowe oraz wartości cieplne i
wykorzystywane zależności.
Norma jest oparta na następujących założeniach:

- przyjęto warunki stanu ustalonego,
- wszystkie właściwości fizyczne są niezależne od temperatury,
- wewnątrz elementów budynku nie występują źródła ciepła.

Norma może być również stosowana do określania liniowych i punktowych współczynników przenikania ciepła oraz
współczynników temperatury powierzchni.

2 Normy powołane

N5)

Do niniejszej normy europejskiej wprowadzono, drogą datowanego lub niedatowanego powołania się, wymagania
zawarte w innych publikacjach. Powołania te znajdują się w odpowiednich miejscach w tekście normy, a wykaz
publikacji podano poniżej. W przypadku powołań datowanych późniejsze zmiany lub nowelizacja którejkolwiek z
wymienionych publikacji mają zastosowanie do niniejszej normy europejskiej tylko wówczas, jeżeli zostaną
wprowadzone do tej normy przez zmianę lub nowelizację. W przypadku powołań niedatowanych stosuje się ostatnie
wydanie powołanej publikacji.

ISO 7345

Thermal insulation - Physical quantities and definitions

prEN 673

Thermal insulation of glazing - Calculation rules for determining the steady state thermal
transmittance of glazing

prEN ISO 6946-1

Building components and building elements - Thermal resistance and thermal transmittance
- Calculation method

prEN ISO 10456

Thermal insulation - Building materials and products - Determination of declared and design
values

prEN ISO 13789

Thermal performance of buildings - Specific transmission heat loss - Calculation method

3 Definicje i symbole

3.1 Definicje

PN-EN ISO 10211-1:1998 Mostki cieplne w budynkach Strumień cieplny i temperatura powierzchni Ogólne metody obliczania

Powielanie dokumentu zabronione. Wszelkie prawa zastrzeżone.

INTEGRAM BUDOWNICTWO

Strona 3

Dla potrzeb niniejszej normy mają zastosowanie definicje podane w ISO 7345 oraz następujące definicje:

3.1.1 mostek cieplny: Część obudowy budynku, w której skądinąd jednolity opór cieplny jest znacznie zmieniony przez:

a) całkowite lub częściowe przebicie obudowy budynku przez materiały o innej przewodności cieplnej
i/lub
a) zmianę grubości warstw materiałów
i/lub
c) różnicę między wewnętrznymi i zewnętrznymi powierzchniami przegród, jak to ma miejsce w przypadku
połączeń: ściana/podłoga/sufit.

3.1.2 model geometryczny 3-D: Model geometryczny opracowany na podstawie rysunków budowlanych, w którym w
odniesieniu do każdej z ortogonalnych osi, przekrój prostopadły do tej osi zmienia się wewnątrz granic modelu (patrz
rysunek 1).

3.1.3 boczny element 3-D: Część geometrycznego modelu 3-D, która rozpatrywana oddzielnie może być
przedstawiona jako model geometryczny 2-D (patrz rysunki 1 i 2).

3.1.4 centralny element 3-D: Część geometrycznego modelu 3-D, która nie jest bocznym elementem 3-D (patrz
rysunek 1).

3.1.5 model geometryczny 2-D: Model geometryczny opracowany na podstawie rysunków budowlanych, taki że dla
jednej z ortogonalnych osi przekrój prostopadły do tej osi nie zmienia się wewnątrz granic modelu (patrz rysunek 2).

UWAGA: Model geometryczny 2-D jest używany do obliczeń dwuwymiarowych.

3.1.6 płaszczyzny konstrukcyjne: Płaszczyzny w modelach 3-D lub 2-D, które oddzielają:

- różne materiały,
- model geometryczny od reszty konstrukcji,
- boczne elementy od elementu centralnego (patrz rysunek 3).

3.1.7. płaszczyzny przekrojów: Płaszczyzny konstrukcyjne, które stanowią granice modelu 3-D lub 2-D, oddzielając
model od pozostałej części konstrukcji (patrz rysunek 3).

PN-EN ISO 10211-1:1998 Mostki cieplne w budynkach Strumień cieplny i temperatura powierzchni Ogólne metody obliczania

Powielanie dokumentu zabronione. Wszelkie prawa zastrzeżone.

INTEGRAM BUDOWNICTWO

Strona 4

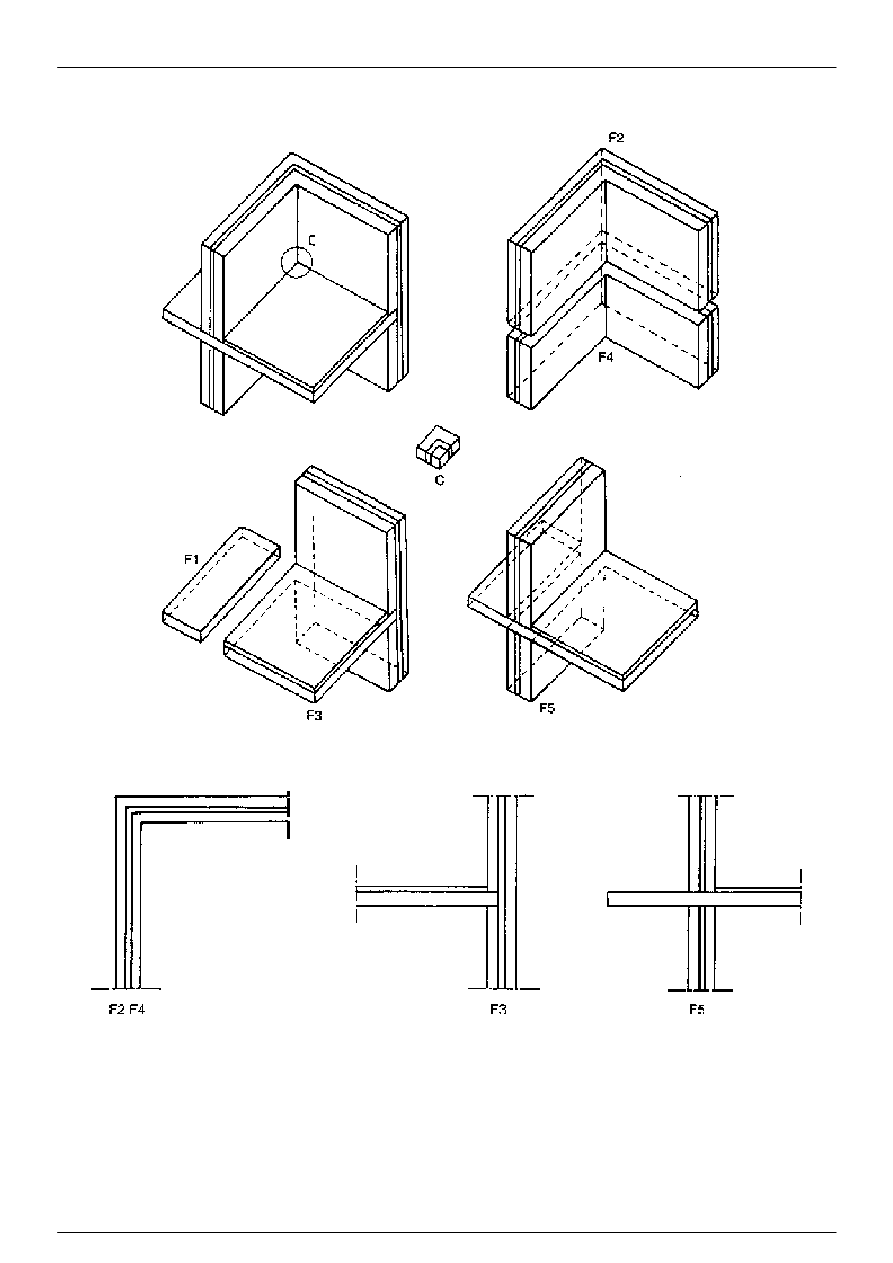
Rysunek 1: Model 3-D z pięcioma 3-D elementami bocznymi i jednym 3-D elementem centralnym. F1 do F5 mają

stałe przekroje poprzeczne prostopadłe co najmniej do jednej osi. C jest częścią pozostałą

Rysunek 2: Przekroje poprzeczne elementów bocznych w modelu 3-D mogą być traktowane jako modele 2-D.

F2 do F5 odnoszą się do rysunku 1

PN-EN ISO 10211-1:1998 Mostki cieplne w budynkach Strumień cieplny i temperatura powierzchni Ogólne metody obliczania

Powielanie dokumentu zabronione. Wszelkie prawa zastrzeżone.

INTEGRAM BUDOWNICTWO

Strona 5

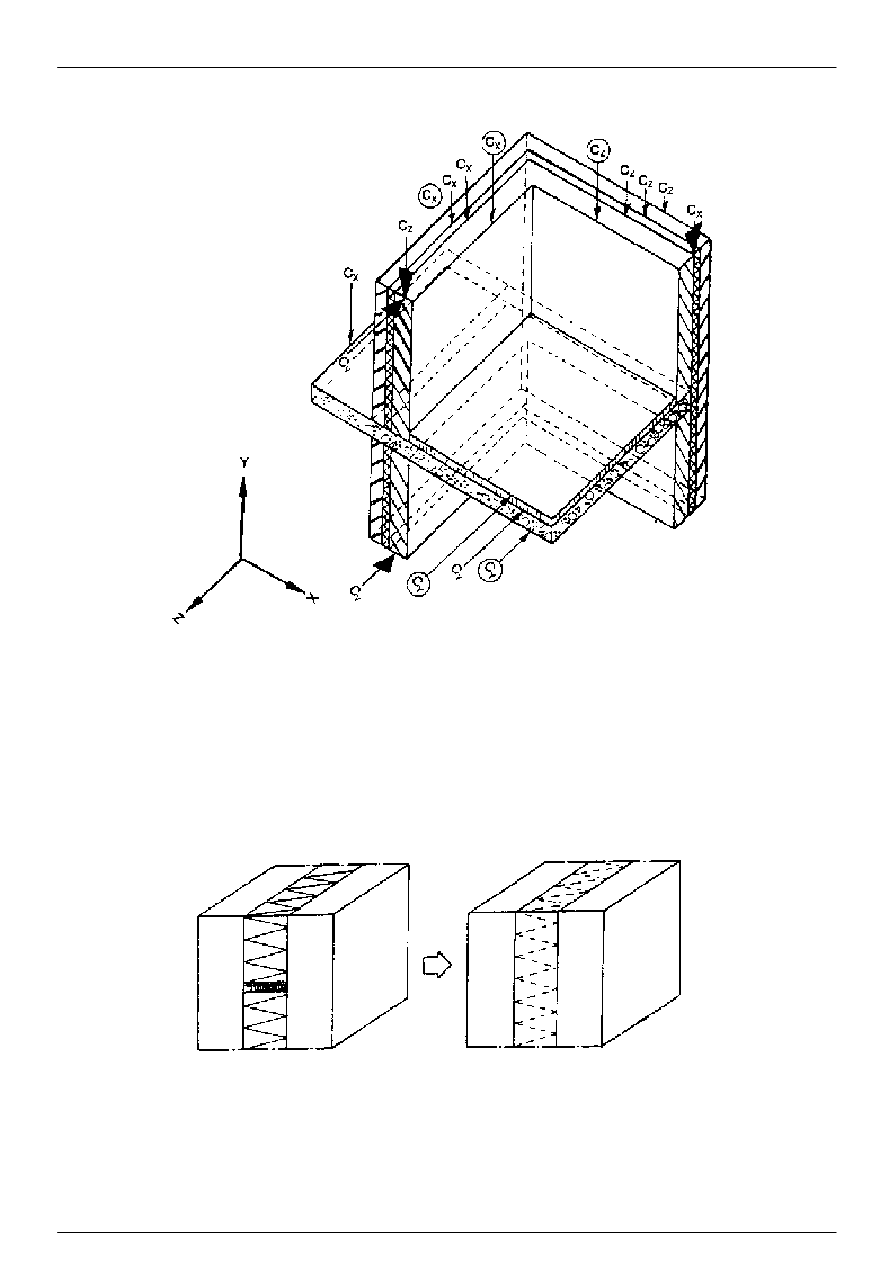
Rysunek 3: Przykład modelu 3-D, na którym pokazano płaszczyzny konstrukcyjne.

C

x

są płaszczyznami konstrukcyjnymi prostopadłymi do osi x

C

y

są płaszczyznami konstrukcyjnymi prostopadłymi do osi y

C

z

są płaszczyznami konstrukcyjnymi prostopadłymi do osi z

Rysunki przekrojów są zaznaczone powiększoną strzałką. Oznaczenia płaszczyzn, oddzielających boczne

elementy od elementu środkowego, są wzięte w kółka.

3.1.8 płaszczyzny pomocnicze: Płaszczyzny dodatkowe w stosunku do płaszczyzn konstrukcyjnych, które dzielą
model geometryczny na komórki.

3.1.9 warstwy quasi-jednorodne: Warstwy składające się z dwu lub więcej materiałów o różnej przewodności cieplnej,
które mogą być traktowane jako warstwa jednorodna o równoważnej przewodności cieplnej (patrz rysunek 4).

Rysunek 4: Przykład małego punktowego mostka cieplnego, wywołującego trójwymiarowy strumień ciepła,

zawartego w quasi-jednorodnej warstwie.

PN-EN ISO 10211-1:1998 Mostki cieplne w budynkach Strumień cieplny i temperatura powierzchni Ogólne metody obliczania

Powielanie dokumentu zabronione. Wszelkie prawa zastrzeżone.

INTEGRAM BUDOWNICTWO

Strona 6

3.1.10 stosunek różnicy temperatury, ζ

Rsi

: Różnica wartości temperatury powietrza wewnętrznego i wewnętrznej

powierzchni, podzielona przez różnicę wartości temperatury powietrza wewnętrznego i zewnętrznego, obliczona z
uwzględnieniem oporu przejmowania ciepła R

Si

na wewnętrznej powierzchni.

3.1.11 współczynnik temperaturowy na wewnętrznej powierzchni, f

Rsi

: Różnica wartości temperatury wewnętrznej

powierzchni i powietrza zewnętrznego podzielona przez różnicę wartości temperatury powietrza wewnętrznego i
zewnętrznego, obliczona z uwzględnieniem oporu przejmowania ciepła R

si

na wewnętrznej powierzchni.

UWAGA: f

Rsi

= 1 - ζ

RSi

3.1.12 wagowy współczynnik temperaturowy, g: Współczynnik, który określa względny wpływ temperatury powietrza
środowiska cieplnego na temperaturę powierzchni w rozważanym punkcie.

3.1.13 zewnętrzna temperatura odniesienia : Temperatura powietrza zewnętrznego przy założeniu, że niebo jest
całkowicie zachmurzone.

3.1.14 wewnętrzna temperatura odniesienia:

(a) Temperatura wynikowa powietrza w rozważanym pomieszczeniu, mierzona termometrem suchym.
(b) Średnia wartość temperatury powietrza wewnętrznego w rozważanym pomieszczeniu.
UWAGA 1: (a) stosuje się w przypadku określania strumieni ciepła w obliczeniach całkowitych strat ciepła, (b)
jest używane w przypadku określania temperatury powierzchni przy ocenie ryzyka kondensacji powierzchniowej.

UWAGA 2: Na potrzeby obliczeń przyjmuje się jednakową temperaturę odniesienia w całym środowisku
wewnętrznym.

3.1.15 temperatura wynikowa suchego termometru : Wartość średnia arytmetyczna z temperatury powietrza
wewnętrznego i średniej temperatury promieniowania wszystkich powierzchni otaczających środowisko wewnętrzne.

3.1.16 współczynnik sprzężenia cieplnego, L

i,j

: Strumień ciepła na jednostkę różnicy temperatur pomiędzy dwoma

środowiskami, które są połączone cieplnie przez rozpatrywaną przegrodę.

3.1.17 liniowy współczynnik przenikania ciepła, ψ

ψ

ψ

ψ : Element korekcyjny uwzględniający liniowy wpływ mostka

cieplnego w przypadku, kiedy współczynnik sprzężenia cieplnego L jest wyznaczany z 1-D obliczeń.

3.1.18 punktowy współczynnik przenikania ciepła, X: Element korekcyjny uwzględniający punktowy wpływ mostka
cieplnego w przypadku, kiedy współczynnik sprzężenia cieplnego L jest wyznaczany z 1-D obliczeń.

3.2 Symbole i jednostki

PN-EN ISO 10211-1:1998 Mostki cieplne w budynkach Strumień cieplny i temperatura powierzchni Ogólne metody obliczania

Powielanie dokumentu zabronione. Wszelkie prawa zastrzeżone.

INTEGRAM BUDOWNICTWO

Strona 7

Symbol

Wielkość fizyczna

Jednostka miary

A

powierzchnia

m

2

H

wysokość

m

L

długość

m

R

opór cieplny

m

2

⋅ K/W

R

se

opór przejmowania ciepła na powierzchni zewnętrznej

m

2

⋅ K/W

R

si

opór przejmowania ciepła na powierzchni wewnętrznej

m

2

⋅ K/W

T

temperatura termodynamiczna

K

U

współczynnik przenikania ciepła

W/(m

2

⋅ K)

V

objętość (kubatura)

m

3

b

szerokość

m

d

grubość

m

f

RSi

współczynnik temperaturowy na wewnętrznej powierzchni -

g

wagowy współczynnik temperaturowy

-

h

współczynnik przenikania ciepła

W/(m

2

⋅ K)

l

długość

m

q

gęstość strumienia cieplnego

W/m

2

Θ

Θ

Θ

Θ

temperatura w stopniach Celsjusza

°C

∆

∆

∆

∆ Θ

Θ

Θ

Θ

różnica temperatury

K

λ

λ

λ

λ

współczynnik przewodzenia ciepła

W/(m ⋅ K)

ζ

ζ

ζ

ζ

RSi

stosunek różnicy temperatur

-

Φ

Φ

Φ

Φ

strumień cieplny

W

X

punktowy współczynnik przenikania ciepła

W/K

ψ

ψ

ψ

ψ

liniowy współczynnik przenikania ciepła

W/(m ⋅ K)

Wykaz indeksów

cav

wnęka

dp

punkt rosy

e

zewnętrzny

i

wewnętrzny

l

liniowy

min

minimalny

s

powierzchnia

4 Zasady
Rozkład temperatury i strumień ciepła przepływający przez konstrukcję można obliczyć, jeżeli znane są warunki
brzegowe i detale konstrukcyjne. W tym celu model geometryczny dzieli się na pewną liczbę przylegających do siebie
komórek, o jednorodnej przewodności cieplnej. Kryteria, które powinny być spełnione przy konstruowaniu modelu,
podano w rozdziale 5.
W rozdziale 6 podano instrukcje ustalania wartości przewodności cieplnej i warunków brzegowych.

PN-EN ISO 10211-1:1998 Mostki cieplne w budynkach Strumień cieplny i temperatura powierzchni Ogólne metody obliczania

Powielanie dokumentu zabronione. Wszelkie prawa zastrzeżone.

INTEGRAM BUDOWNICTWO

Strona 8

Rozkład temperatury określa się przeprowadzając obliczenia iteracyjne albo stosując rozwiązania wprost, po czym
rozkład temperatury w komórkach materiału określa się przez interpolację.
Zasady obliczeń i metodę określania rozkładu temperatury opisano w rozdziale 7.

UWAGA: Niektóre z poniższych rozdziałów zawierają różnice między obliczeniami temperatury powierzchni i
obliczeniami strumieni ciepła; różnice te podano w tablicach 1, 3 i 4.

5 Modelowanie konstrukcji

5. 1 Zasady modelowania
Zwykle nie można modelować całego budynku, używając prostego modelu geometrycznego. W większości przypadków
budynek należy podzielić na kilka części (wliczając podłoże gruntowe w miarę potrzeby), używając płaszczyzn
przekrojów. Ten podział należy przeprowadzić w taki sposób, aby nie wystąpiły żadne różnice między budynkiem
podzielonym na części i traktowanym jako całość. Podział na kilka modeli geometrycznych osiąga się przez wybór
odpowiednich płaszczyzn przekrojów.

5.1.1 Płaszczyzny przekrojów modelu geometrycznego
Model geometryczny zawiera element centralny lub elementy centralne, elementy boczne i, w miarę potrzeby, podłoże
gruntowe. Model geometryczny jest ograniczony przez płaszczyzny przekrojów.
Płaszczyzny przekrojów powinny być usytuowane w następujący sposób:

- jako płaszczyzna symetrii, jeśli jest ona oddalona mniej niż 1 m od elementu centralnego (patrz rysunek 5);
- co najmniej 1 m od elementu centralnego, jeśli nie ma bliższej płaszczyzny symetrii;
- w podłożu gruntowym według tablicy 1.
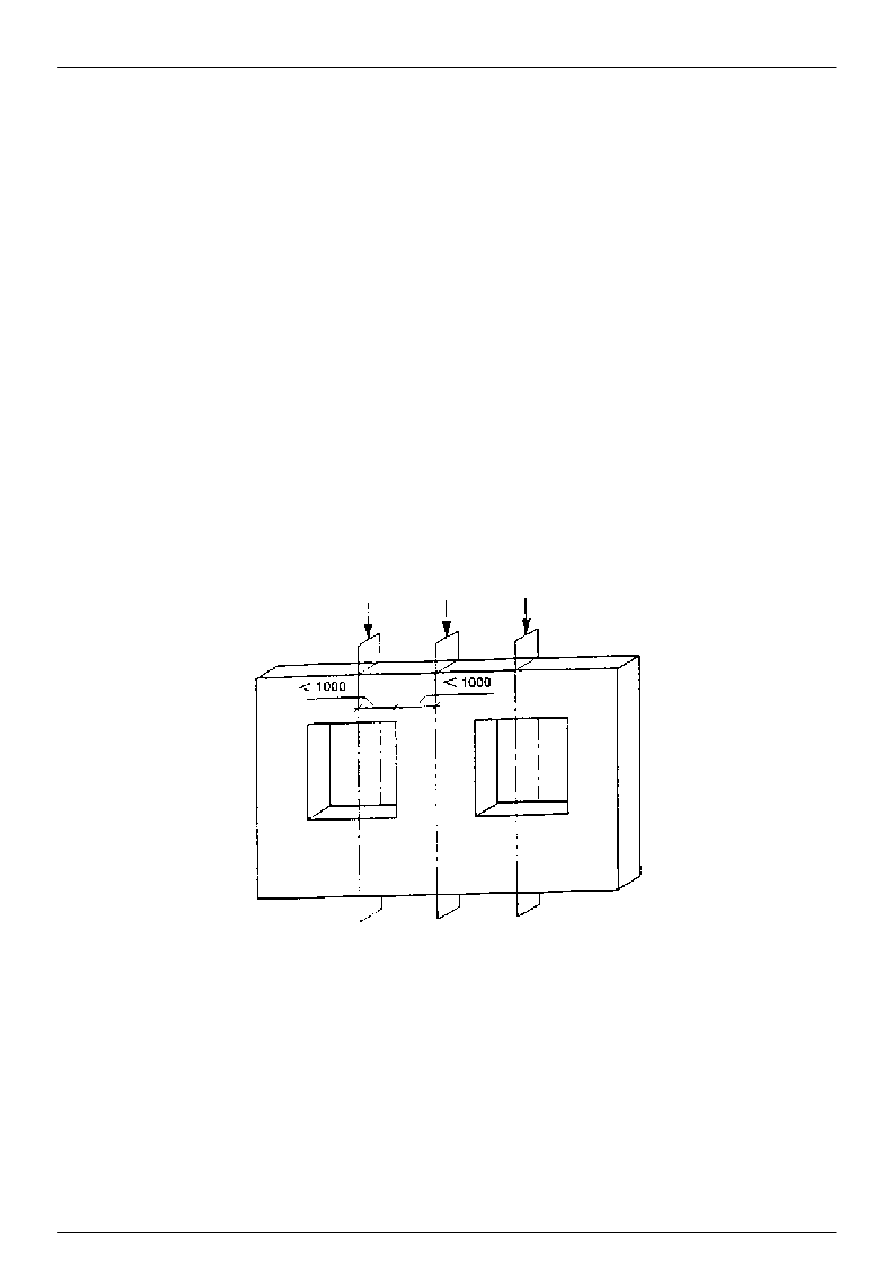
UWAGA: Jeśli w modelu geometrycznym występuje więcej niż jeden mostek cieplny, obliczeniowe pole
temperatury w centralnym elemencie drugiego mostka cieplnego jest tylko wtedy prawidłowe, gdy drugi mostek
cieplny jest oddalony co najmniej o 1 m od najbliższej płaszczyzny przekroju, z wyjątkiem przypadku gdy
płaszczyzna przekroju jest płaszczyzną symetrii.

Wymiary w mm

Rysunek 5: Płaszczyzny symetrii jako płaszczyzny przekroju

Wymiary w mm

PN-EN ISO 10211-1:1998 Mostki cieplne w budynkach Strumień cieplny i temperatura powierzchni Ogólne metody obliczania

Powielanie dokumentu zabronione. Wszelkie prawa zastrzeżone.

INTEGRAM BUDOWNICTWO

Strona 9

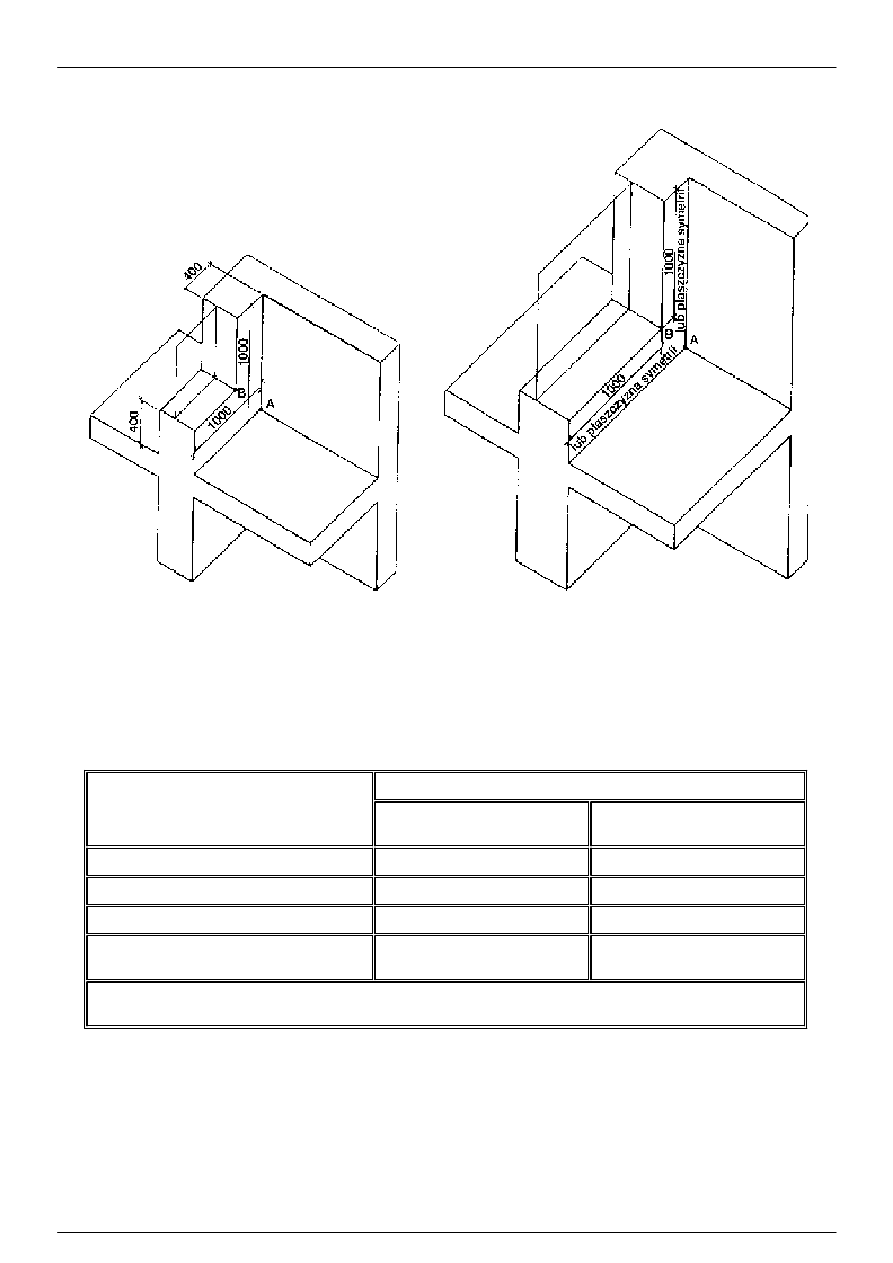
Rysunek 6: Dwa mostki A i B w tym samym modelu. Mostek bliższy płaszczyźnie przekroju nie spełnia

wymagań odległości 1 m od płaszczyzny przekroju (rysunek lewy). Można tego uniknąć przez powiększenie

modelu w dwu kierunkach (rysunek prawy)

Tablica 1: Rozmieszczenie płaszczyzn przekrojów w podłożu gruntowym (fundamenty, partery, piwnice)

Odległość do elementu centralnego w metrach

Kierunek

Cel obliczeń

Temperatura powierzchni, patrz

rysunek 7a

Strumień ciepła, patrz rysunek 7b

Poziomy wewnątrz budynku

co najmniej 1 m

0,5 b

Poziomy na zewnątrz budynku

jak wewnątrz budynku

2,5 b

Pionowy poniżej poziomu terenu

3 m

2,5 b

Pionowy poniżej poziomu podłogi
(patrz Uwaga)

1 m

-

gdzie:
b jest szerokością (mniejszym wymiarem) podłogi na gruncie w metrach

UWAGA: Tę wartość stosuje się jedynie w przypadku, gdy poziom rozpatrywanej podłogi znajduje się więcej niż
2 m poniżej poziomu gruntu.

Wymiary w mm

PN-EN ISO 10211-1:1998 Mostki cieplne w budynkach Strumień cieplny i temperatura powierzchni Ogólne metody obliczania

Powielanie dokumentu zabronione. Wszelkie prawa zastrzeżone.

INTEGRAM BUDOWNICTWO

Strona 10

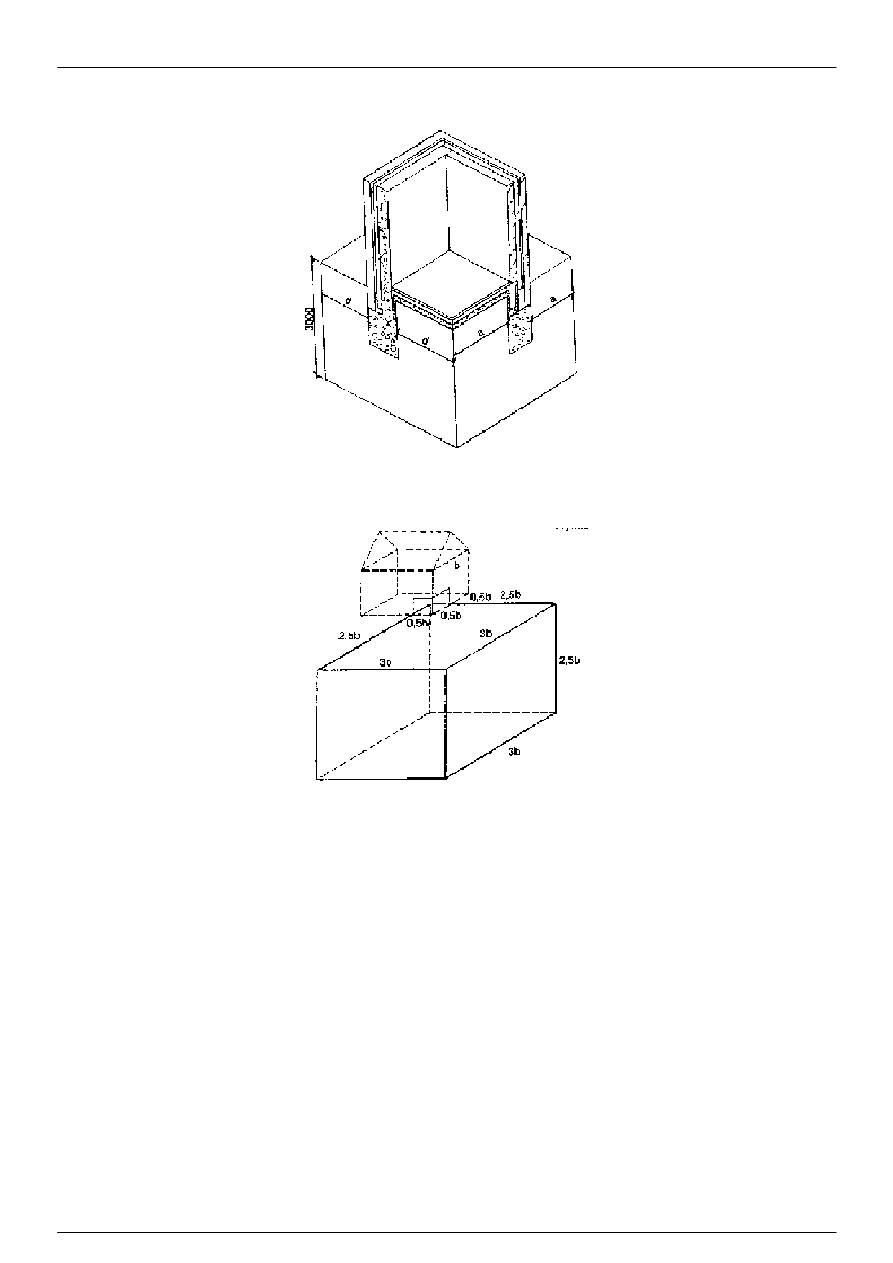
Rysunek 7a: Wymiary gruntu - Obliczenia temperatur powierzchni

Wymiary w mm

Rysunek 7b: Wymiary gruntu - Obliczenia strumienia ciepła

5.1.2 Korekta wymiarów
Korekta wymiarowa modelu geometrycznego w stosunku do wartości rzeczywistych jest dozwolona, jeśli nie ma
znaczącego wpływu na wynik obliczeń; można to założyć, jeśli są spełnione warunki podane w punkcie 5.2.1.

5.1.3 Płaszczyzny pomocnicze
Liczba pomocniczych płaszczyzn w modelu powinna być taka, że dodanie większej ich liczby nie zmienia wartości
stosunku różnicy temperatury ζ

RSi

więcej niż o 0,005 (patrz także załącznik 2).

UWAGA: Wskazówką do spełnienia tego wymagania w wielu przypadkach jest (patrz rysunek 8a):
Zaleca się, aby odległość między sąsiednimi równoległymi płaszczyznami nie przekraczała następujących
wartości:
- wewnątrz elementu centralnego: 25 mm,
- wewnątrz bocznych elementów, mierzona od płaszczyzn konstrukcyjnych oddzielających element centralny od
elementów bocznych: 25, 25, 50, 50, 100, 200, 500, 1000, 2000 i 4000 mm.

W przypadku konstrukcji z wcięciami o małych wymiarach (np. profili okiennych) będzie potrzebny gęstszy podział
(patrz rysunek 8b)

Wymiary w mm

PN-EN ISO 10211-1:1998 Mostki cieplne w budynkach Strumień cieplny i temperatura powierzchni Ogólne metody obliczania

Powielanie dokumentu zabronione. Wszelkie prawa zastrzeżone.

INTEGRAM BUDOWNICTWO

Strona 11

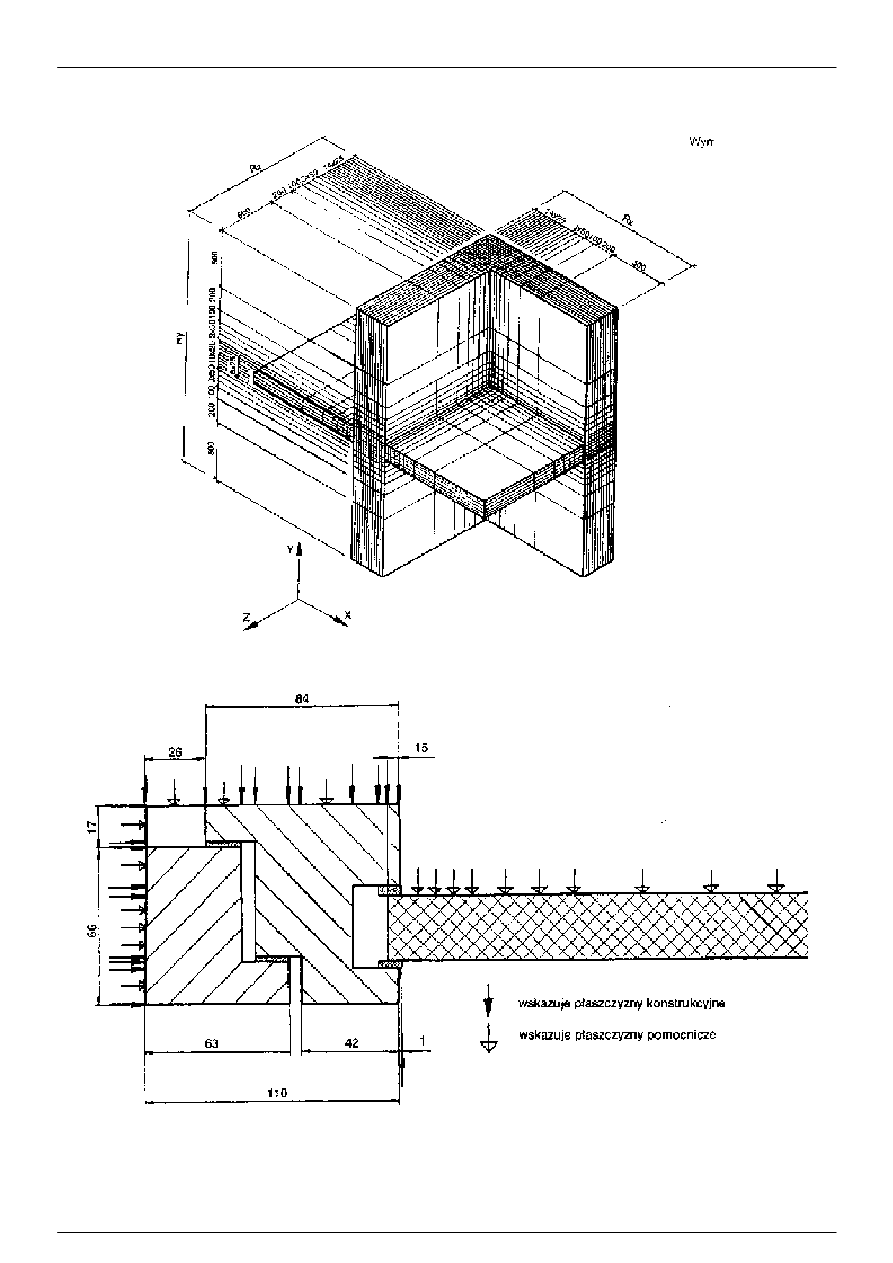
Rysunek 8a: Przykład płaszczyzn konstrukcyjnych uzupełnionych płaszczyznami pomocniczymi

PN-EN ISO 10211-1:1998 Mostki cieplne w budynkach Strumień cieplny i temperatura powierzchni Ogólne metody obliczania

Powielanie dokumentu zabronione. Wszelkie prawa zastrzeżone.

INTEGRAM BUDOWNICTWO

Strona 12

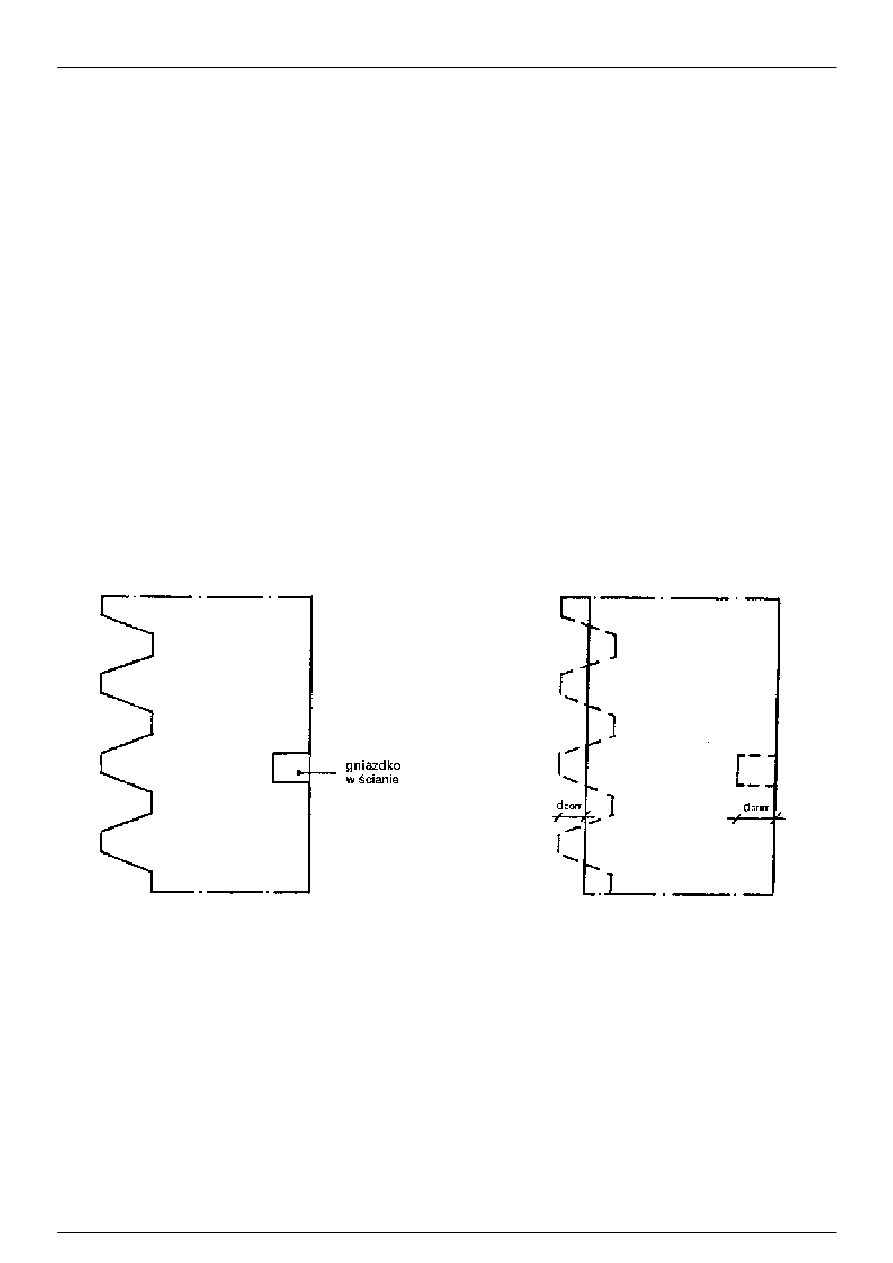
Rysunek 8b: Przykład płaszczyzn konstrukcyjnych i pomocniczych w 2-D modelu geometrycznym profilu

okiennego

5.1.4 Quasi-jednorodne warstwy i materiały
W modelu geometrycznym materiały o różnej przewodności cieplnej można zastąpić materiałem o jednakowej
przewodności cieplnej, jeśli spełnione są warunki podane w punkcie 5.2.2.

UWAGA: Przykładem są spoiny w murach, kotwie w murach szczelinowych, śruby w drewnianych listwach,
dachówki i związane z nimi szczelina powietrzna i łaty.

5.2 Warunki upraszczania modeli geometrycznych
Wyniki obliczeń, otrzymane z modelu geometrycznego bez uproszczeń, mają pierwszeństwo przed wynikami
otrzymanymi z modelu geometrycznego uproszczonego.
Można wykonać poniższe korekty.

UWAGA: Jest to ważne, kiedy wyniki obliczeń są zbliżone do wartości żądanej.

5.2.1 Warunki korekty wymiarów w celu uproszczenia modelu geometrycznego
Korektę wymiarów można przeprowadzać tylko w odniesieniu do materiałów o przewodności cieplnej mniejszej niż
3 W/(m ⋅ K).
a) Zmiana usytuowania powierzchni bloku materiału sąsiedniego do wewnętrznej lub zewnętrznej powierzchni
modelu geometrycznego (patrz rysunek 9): miejscowa korekta d

corr

usytuowania powierzchni niepłaskich, odniesiona

do usytuowania średniego powierzchni, nie może przekraczać:
d

corr

= R

corr

λ

gdzie:
d

corr

jest miejscową korektą prostopadłą do średniej pozycji wewnętrznej lub zewnętrznej płaszczyzny;

R

corr

? jest równe 0,03 m

2

⋅ K/W;

λ

λ

λ

λ jest współczynnikiem przewodności cieplnej rozpatrywanego materiału.
UWAGA: Przykładami są powierzchnie pochyłe, zaokrąglone kąty i profilowe powierzchnie, takie jak dachówki.

Rysunek 9: Zmiana położenia powierzchni wewnętrznej lub zewnętrznej

b) Zmiana powierzchni rozdziału dwóch obszarów z różnych materiałów:
- przemieszczenie powierzchni rozdziału powinno nastąpić w kierunku prostopadłym do powierzchni wewnętrznej;
- przemieszczenie powierzchni rozdziału powinno być przeprowadzone w ten sposób, aby materiał o niższej
przewodności cieplnej był zastępowany materiałem o wyższej przewodności cieplnej (patrz rysunek 10).
UWAGA: Przykładami są wyżłobienia na taśmy uszczelniające, spoiny, bloki wyrównawcze, puszki elektryczne,
powierzchnie pochylone i inne szczegóły połączeniowe.

PN-EN ISO 10211-1:1998 Mostki cieplne w budynkach Strumień cieplny i temperatura powierzchni Ogólne metody obliczania

Powielanie dokumentu zabronione. Wszelkie prawa zastrzeżone.

INTEGRAM BUDOWNICTWO

Strona 13

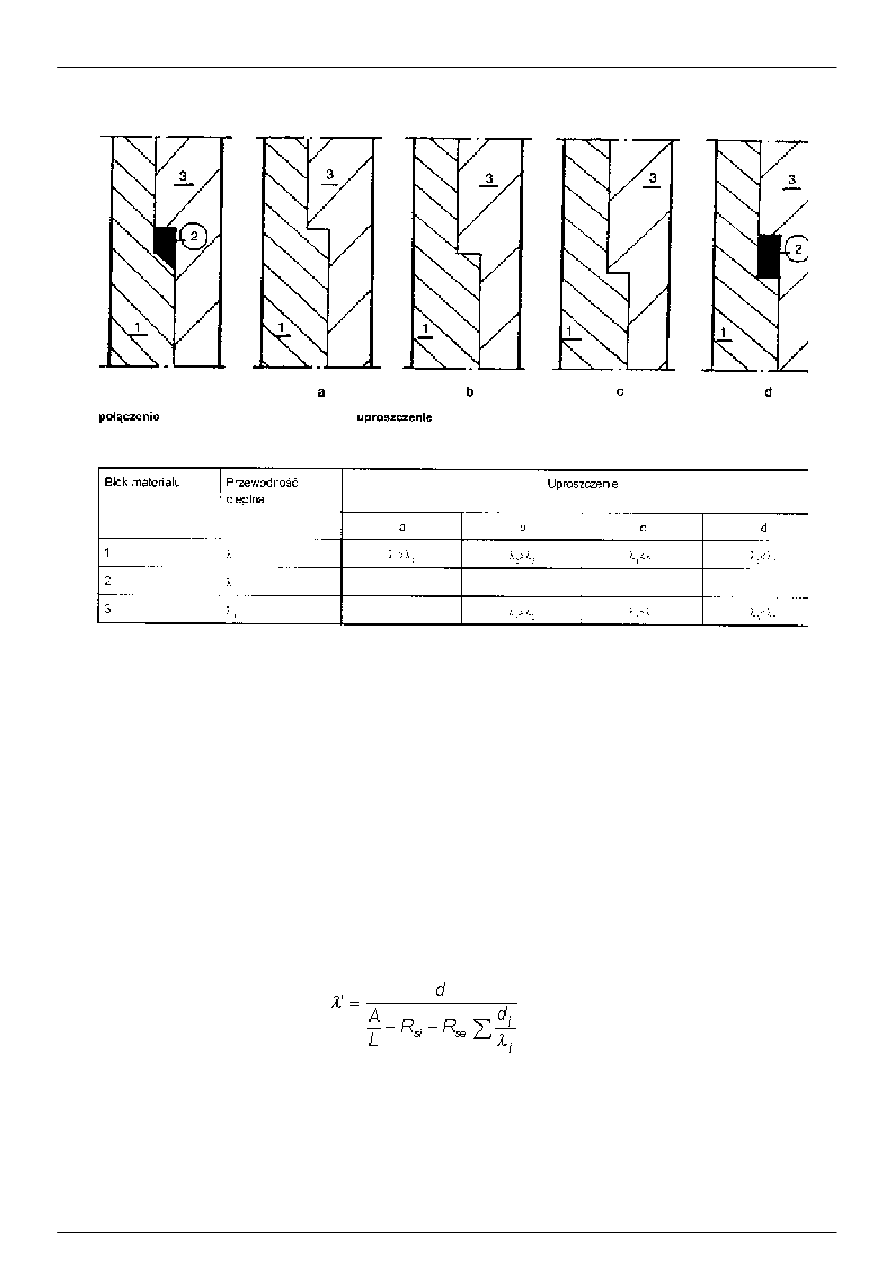
Rysunek 10: Cztery możliwości przemieszczania powierzchni rozdziału między trzema blokami materiałowymi

w zależności od stosunku ich przewodności cieplnej

c) Zaniedbywanie cienkich warstw:
- można pomijać warstwy o grubości nie większej niż 1 mm;
UWAGA: Przykładami są niemetalowe powłoki izolacji paroszczelnej.
d) Zaniedbywanie elementów wystających przyległych do powierzchni zewnętrznej:
- komponenty budynku, które przylegają do powierzchni zewnętrznej (tzn. przymocowane punktowo).

UWAGA: Przykładami są rynny i rury spustowe.

5.2.2 Warunki używania quasi-jednorodnych warstw materiałów w celu uproszczenia modelu geometrycznego
Aby małe liniowe i punktowe mostki cieplne mogły być włączone do warstw quasi-jednorodnych, we wszystkich
przypadkach powinny być spełnione następujące warunki:
- rozpatrywane warstwy materiału są umiejscowione w części konstrukcji, która po uproszczeniu staje się elementem
bocznym;
- przewodność cieplna warstw quasi-jednorodnych po uproszczeniu jest nie większa niż 1,5-krotność najniższej
przewodności cieplnej materiałów występujących w warstwie przed uproszczeniem.
a) Obliczanie współczynnika sprzężenia cieplnego L
Przewodność cieplną warstwy quasi-jednorodnej oblicza się z wzoru (1):

(1)

w którym:
λ' jest równoważną przewodnością cieplną warstwy quasi-jednorodnej;
d jest grubością warstwy niejednorodnej termicznie;

PN-EN ISO 10211-1:1998 Mostki cieplne w budynkach Strumień cieplny i temperatura powierzchni Ogólne metody obliczania

Powielanie dokumentu zabronione. Wszelkie prawa zastrzeżone.

INTEGRAM BUDOWNICTWO

Strona 14

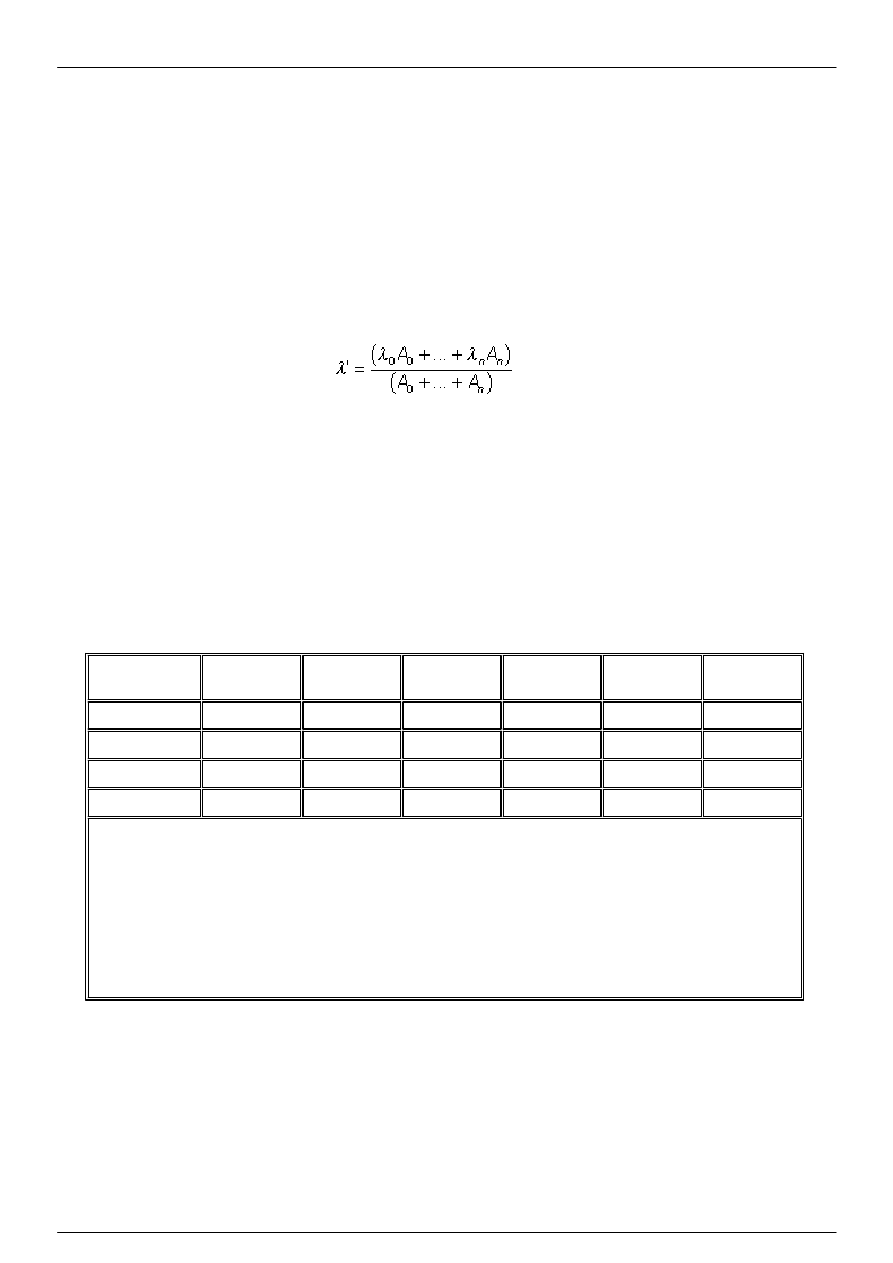
A jest powierzchnią komponentu budynku;
L jest współczynnikiem sprzężenia cieplnego komponentu budynku określanego według obliczeń dwuwymiarowych lub
trójwymiarowych;
d

j

są grubościami jednorodnych warstw, które stanowią część konstrukcji;

λ

j

są przewodnościami cieplnymi tych jednorodnych warstw.

UWAGA: Stosowanie wzoru (1) jest uzasadnione, jeśli występuje duża liczba jednakowych małych mostków
termicznych (kotwi w murach szczelinowych, spoin, pustaków itd.). Obliczenie wielkości L może być ograniczone do
podstawowej powierzchni, reprezentatywnej dla warstwy niejednorodnej. Na przykład mur szczelinowy z 4 kotwiami na
metr kwadratowy może być reprezentowany przez podstawową powierzchnię 0,25 m

2

z jedną kotwią.

b) Obliczenie temperatury wewnętrznej powierzchni i liniowego współczynnika przenikania ciepła ψ lub
punktowego współczynnika przenikania ciepła X (patrz załącznik C)
Współczynnik przewodzenia ciepła warstwy quasi-jednorodnej może być przyjęty według wzoru:

(2)

w którym:
λ' jest równoważnym współczynnikiem przewodzenia ciepła warstwy quasi-jednorodnej;
λ

0...

λ

0

są współczynnikami przewodzenia ciepła materiałów składowych;

A

0...

A

n

są powierzchniami materiałów składowych mierzonymi w przekroju warstwy;

pod warunkiem że:
- mostki cieplne w rozpatrywanej warstwie są prostopadłe lub prawie prostopadłe do wewnętrznej lub zewnętrznej
powierzchni konstrukcji i przenikają warstwę na całej jej grubości;
- opór cieplny (między powierzchniami) konstrukcji po uproszczeniu jest równy przynajmniej 1,5 (m

2

.

K)/W;

- są spełnione warunki co najmniej jednej z grup podanych w tablicy 2 (patrz rysunek 11).

Tablica 2: Szczególne warunki do włączania liniowych i punktowych mostków cieplnych do warstw

quasi-jednorodnych

Grupa (patrz

rysunek 11)

λ

tb

W/(m ⋅ K)

A

tb

m

2

R

0

m

2

⋅ K/W

R

t,i

m

2

⋅ K/W

λ

i

W/(m ⋅ K)

d

i

m

1

≤ 1,5

≤ 0,05 I

tb

≤ 0,5

-

-

-

2

> 3

≤ 30 ⋅ 10

-6

≤ 0,5

-

-

-

3

> 3

≤ 30 ⋅ 10

-6

> 0,5

≥ 0,5

-

-

4

> 3

≤ 30 ⋅ 10

-6

> 0,5

< 0,5

≥ 0,5

≥ 0,1

gdzie:
λ

tb

jest powierzchnią cieplną mostka cieplnego podlegającego włączeniu do warstwy quasi-jednorodnej;

A

tb

jest powierzchnią przekroju poprzecznego mostka cieplnego;

I

tb

jest długością mostka cieplnego;

R

0

jest oporem cieplnym warstwy bez występowania mostka cieplnego;

R

ti

jest całkowitym oporem cieplnym warstwy materiału między między rozpatrywaną warstwą quasi-jednorodną i

powierzchnią wewnętrzną;
λ

i

jest przewodnością cieplną warstwy materiału między rozpatrywaną warstwą quasi-jednorodną i powierzchnią

wewnętrzną z największą wartością λ

i

razy d

i

;

d

i

jest grubością tej samej warstwy.

UWAGA: Grupa pierwsza zawiera liniowe mostki cieplne. Przykładem są spoiny w murach, listwy drewniane w
szczelinach powietrznych lub wypełnionych izolacją o małej grubości.
Grupa 2 zawiera takie elementy jak kotwie ścienne, jeśli są one osadzone w murze lub betonie lub umieszczone
w szczelinach powietrznych, jak również gwoździe i śruby w warstwach materiału lub pasy o określonym
maksymalnym oporze cieplnym.
Grupy 3 i 4 zawierają takie elementy jak kotwie w szczelinach, jeśli one przenikają warstwę izolacyjną o

PN-EN ISO 10211-1:1998 Mostki cieplne w budynkach Strumień cieplny i temperatura powierzchni Ogólne metody obliczania

Powielanie dokumentu zabronione. Wszelkie prawa zastrzeżone.

INTEGRAM BUDOWNICTWO

Strona 15

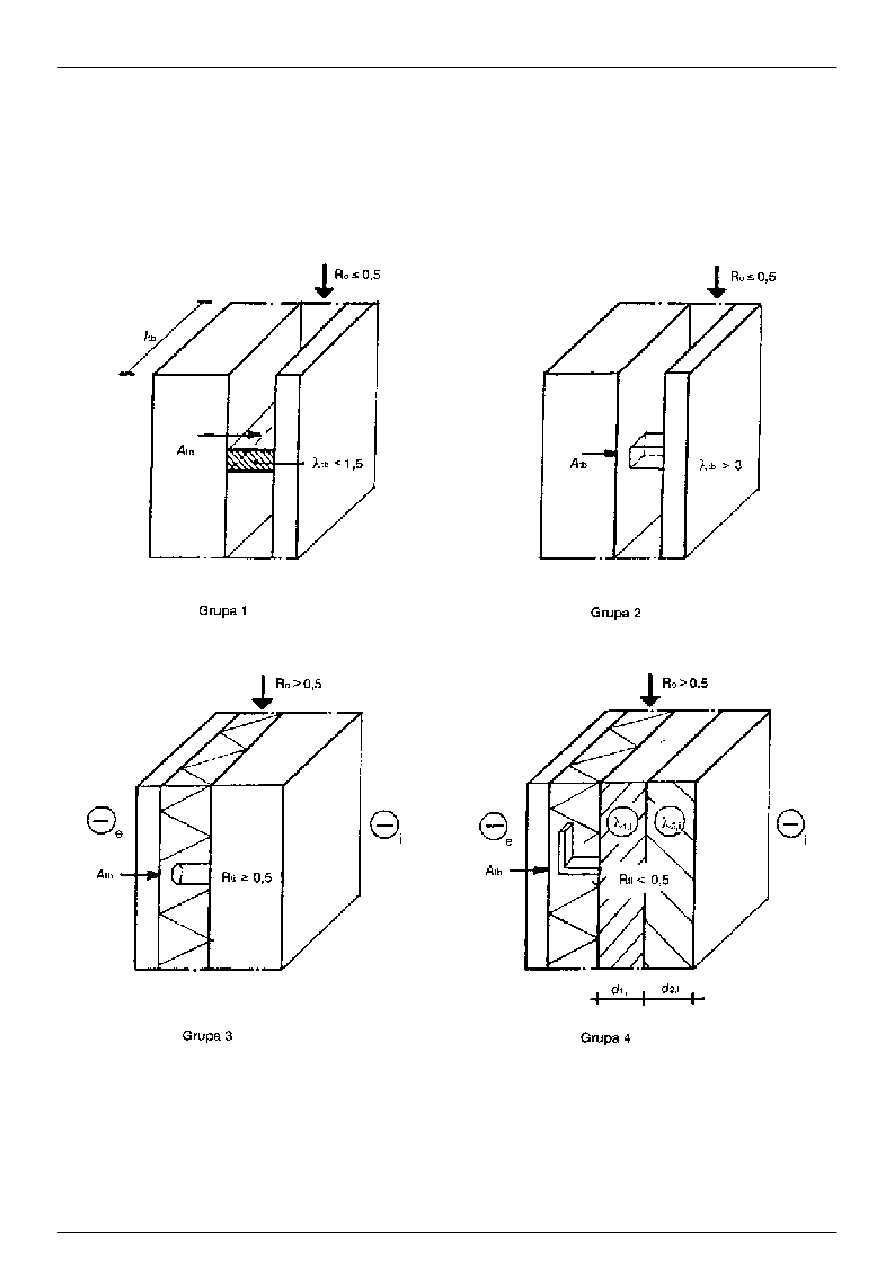
większym oporze cieplnym, niż wskazano odnośnie do grupy 2. Warstwa wewnętrzna powinna więc
charakteryzować się właściwościami cieplnymi, które wystarczająco ograniczają wpływ mostka cieplnego na
temperaturę na wewnętrznej powierzchni. Może być to przypadek warstwy wewnętrznej o wystarczającym oporze
cieplnym (grupa 3) lub takiej przewodności cieplnej warstwy wewnętrznej, że strumień cieplny przez kotwie w
szczelinach jest równo rozłożony na wewnętrznej powierzchni; większość warstw wewnętrznych z muru lub
betonu stanowi przykłady grupy 4.
Przykłady obliczeń podano w załączniku D.

Rysunek 11: Właściwe warunki włączania liniowych i punktowych mostków cieplnych do warstw

quasi-jednorodnych w przypadku grup wyróżnionych w tablicy 2

6 Wartości obliczeniowe

PN-EN ISO 10211-1:1998 Mostki cieplne w budynkach Strumień cieplny i temperatura powierzchni Ogólne metody obliczania

Powielanie dokumentu zabronione. Wszelkie prawa zastrzeżone.

INTEGRAM BUDOWNICTWO

Strona 16

6.1 Dane wartości obliczeniowe
Jeśli w szczególnych przypadkach jest uzasadnione stosowanie wartości nie znormalizowanych, stosuje się wartości
podane w tym punkcie.

UWAGA: Wartości nie znormalizowane mogą być uzasadnione w przypadku warunków miejscowych (np.
ustalenia rozkładu temperatury w gruncie) lub w przypadku specyficznych właściwości materiału (np. wpływu
pokrycia o niskiej emisyjności na opór przejmowania ciepła).

6.1.1 Przewodność cieplna materiałów
Wartości obliczeniowe przewodności cieplnej materiałów i wyrobów budowlanych należy obliczać według prEN 10456
lub przyjmować z tablic.
Wartość przewodności cieplnej gruntu należy przyjmować 2,0 W/(m ⋅ K)

UWAGA: Można przyjąć inne wartości przewodności cieplnej gruntu, jeżeli dostępne są informacje o gruncie pod
dany budynek. Patrz prEN 1190.

6.1.2 Opory przejmowania ciepła
Należy stosować wartości podane w tablicy 3.
Do obliczeń wartości strumienia cieplnego wartość R

si

odnosi się do średniej wewnętrznej temperatury wynikowej

suchego termometru.
Do obliczeń temperatur powierzchni wartość R

si

odnosi się do średniej temperatury powietrza wewnętrznego, ale

powinna uwzględniać nierównomierny rozkład temperatury powietrza na skutek uwarstwienia cieplnego i niejednakowej
temperatury promieniowania, co występuje przy krawędziach i w rogach.

UWAGA: Do obliczania temperatury powierzchni zaleca się następujące wartości oporów przejmowania ciepła
na powierzchniach wewnętrznych:
Oszklenie: 0,13 m

2

⋅ K/W

Górna część pomieszczenia: 0,25 m

2

⋅ K/W

Dolna część pomieszczenia: 0,35 m

2

⋅ K/W

Zaleca się wartość R

Si

= 0,50 m

2

⋅ K/W, jeśli występuje znaczne ekranowanie powierzchni przez przedmioty,

takie jak meble. Patrz załącznik E.

Tablica 3: Opory przejmowania ciepła na powierzchni (m

2

⋅ K/W)

Cel obliczenia

Temperatura powierzchni

Strumień ciepła

Na zewnętrznej powierzchni R

se

0,04

0,04

Na wewnętrznej powierzchni R

si

1)

0,13

1)

Patrz załącznik E

6.1.3 Temperatura brzegowa
W tablicy 4 podano wartości temperatury brzegowej, które należy stosować.

Tablica 4: Temperatura brzegowa

PN-EN ISO 10211-1:1998 Mostki cieplne w budynkach Strumień cieplny i temperatura powierzchni Ogólne metody obliczania

Powielanie dokumentu zabronione. Wszelkie prawa zastrzeżone.

INTEGRAM BUDOWNICTWO

Strona 17

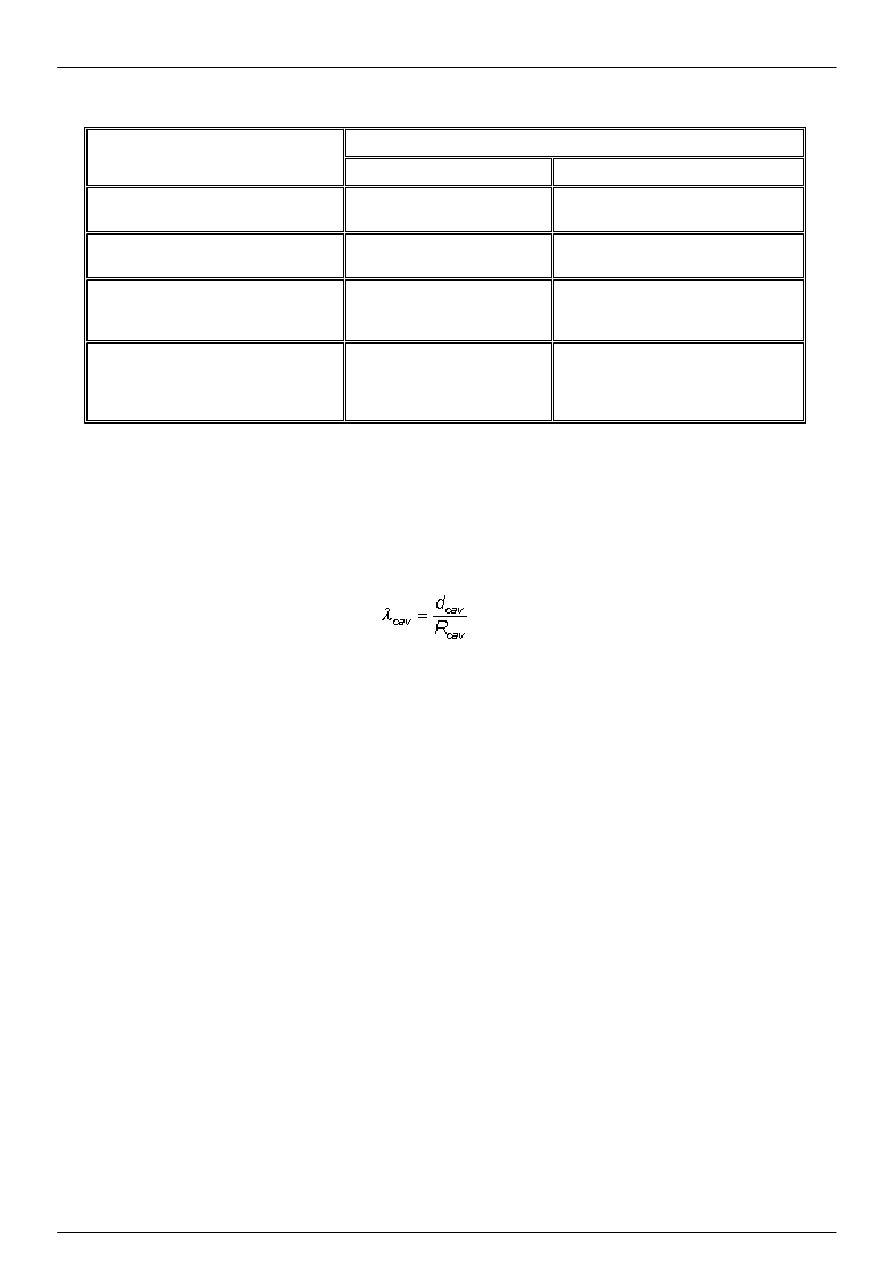
Cel obliczenia

Temperatura powierzchni

Strumień ciepła

Wewnętrzna

temperatura powietrza

temperatura wynikowa suchego
termometru

Wewnętrzna w pomieszczeniach
nieogrzewanych

patrz 6.2.3

patrz 6.2.3

Zewnętrzna

temperatura powietrza przy
założeniu, że niebo jest
całkowicie zasłonięte

temperatura powietrza przy założeniu,
że niebo jest całkowicie zasłonięte

Grunt (płaszczyzna przekroju
poziomego)

dla odległości poniżej poziomu
gruntu dane w tablicy 1: średnia
roczna temperatura powietrza
zewnętrznego

dla odległości poniżej poziomu gruntu
dane w tablicy 1: warunki graniczne
adiabatyczne

6.2 Metody określania wartości obliczeniowych

6.2.1 Przewodność cieplna warstw quasi-jednorodnych
Przewodność cieplną warstw quasi-jednorodnych należy obliczać z równań (1) i (2).

6.2.2 Równoważna przewodność cieplna warstw powietrznych
Warstwę powietrzną należy traktować jako materiał jednorodny z przewodnością cieplną λ

λ

λ

λ

cav

.

Jeśli opór cieplny warstwy lub przestrzeni powietrznej jest znany, przewodność cieplną oblicza się ze wzoru:

(3)

w którym:
λ

λ

λ

λ

cav

jest przewodnością cieplną warstwy lub przestrzeni powietrznej;

d

cav

jest grubością warstwy powietrza;

R

cav

jest oporem cieplnym w głównym kierunku strumienia cieplnego.

Opory i przewodności cieplne warstw i przestrzeni powietrznych, ograniczonych przez nieprzezroczyste materiały,
podano w załączniku B.
Opory cieplne warstw powietrza w wielowarstwowych szybach - patrz prEN 673.

UWAGA: Przestrzenie powietrzne, których wymiary są większe niż 0,5 m wzdłuż każdej z ortogonalnych osi,
należy traktować jako pomieszczenia (patrz 6.2.3).

6.2.3 Określanie temperatury w przyległym nieogrzewanym pomieszczeniu
Jeżeli są dostępne wystarczające informacje, temperaturę w przyległym nieogrzewanym pomieszczeniu można
obliczać według prEN 33789.
Jeżeli temperatura w przyległym nieogrzewanym pomieszczeniu nie jest znana i nie można jej obliczyć według
prEN 33789 z braku dostępnych informacji, strumieni ciepła i temperatury wewnętrznych powierzchni nie można
obliczyć. Jednakże wszystkie wymagane współczynniki sprzężenia i współczynniki wagowe temperatury można
obliczyć i przedstawić według załącznika F.

UWAGA: Do oceny mostków cieplnych dostępne informacje są zwykle ograniczone do właściwej części
konstrukcji (np. połączeń) i jest bardzo mało lub nie ma wcale informacji o wymiarach lub całkowitych
współczynnikach sprzężenia pomieszczenia przyległego.

7 Metoda obliczeń
Model geometryczny dzieli się na pewną liczbę komórek, każda z punktem charakterystycznym (nazywanym węzłem).
Stosując prawa zachowania energii (div q = 0) i Fouriera (q = λ

λ

λ

λ ⋅ grad Θ

Θ

Θ

Θ) oraz uwzględniając warunki brzegowe,

otrzymuje się układ równań, który jest funkcją wartości temperatury w węzłach. Rozwiązując ten układ albo metodą
bezpośrednią, albo iteracyjną, otrzymuje się temperatury w węzłach, z których można określić pole temperatury. Z
rozkładu temperatury, stosując prawo Fouriera, można obliczyć strumień ciepła.

PN-EN ISO 10211-1:1998 Mostki cieplne w budynkach Strumień cieplny i temperatura powierzchni Ogólne metody obliczania

Powielanie dokumentu zabronione. Wszelkie prawa zastrzeżone.

INTEGRAM BUDOWNICTWO

Strona 18

Programy obliczeniowe powinny być zweryfikowane zgodnie z wymaganiami załącznika A.

7.1 Zasady obliczeń

7.1.1 Strumień ciepła między komórkami materiału i przyległym środowiskiem
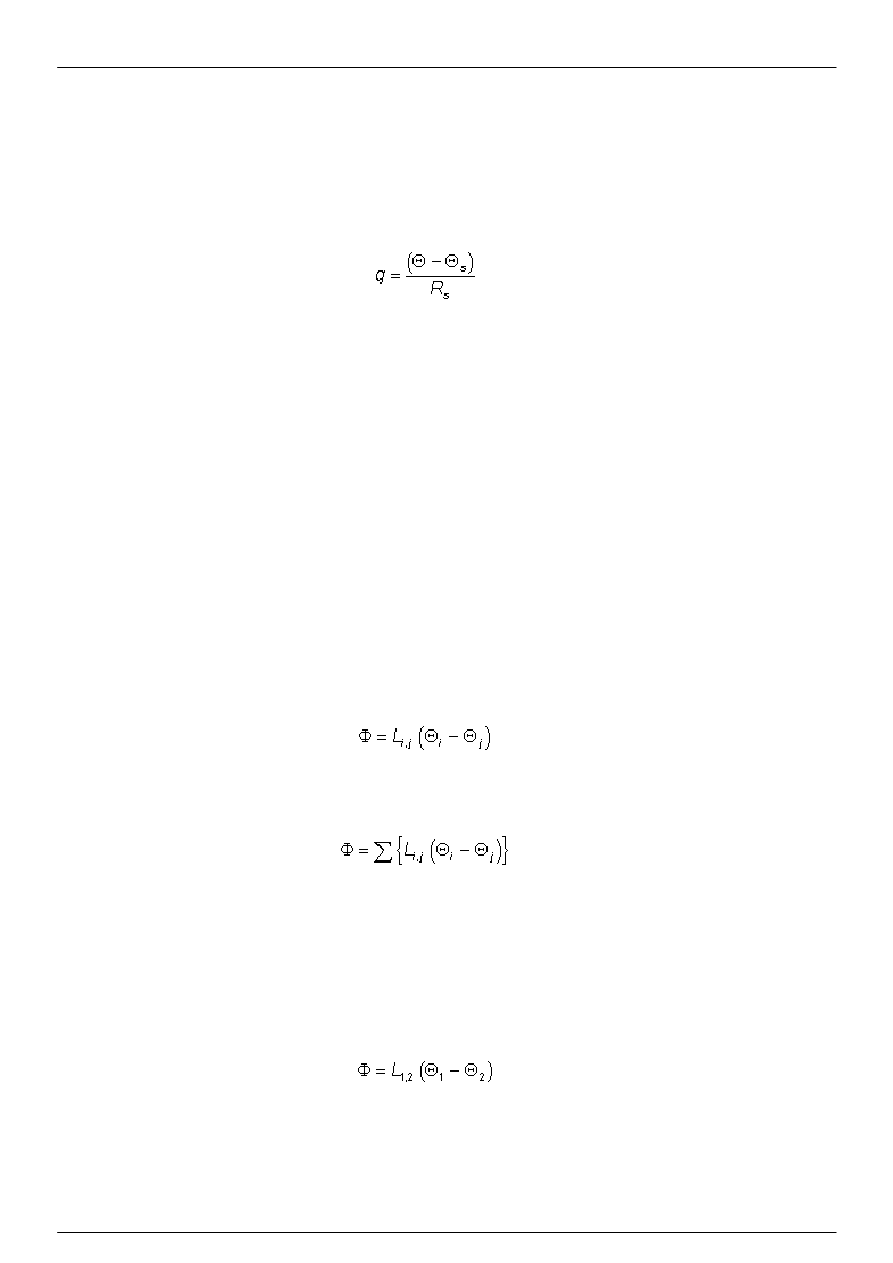
Gęstość strumienia cieplnego, prostopadłego do powierzchni między komórką materiału i przyległym środowiskiem
powinna spełniać równanie:

(4)

w którym:
q jest gęstością strumienia cieplnego;
Θ

Θ

Θ

Θ jest wewnętrzną lub zewnętrzną temperaturą odniesienia;
Θ

Θ

Θ

Θ

s

jest temperaturą wewnętrznej lub zewnętrznej powierzchni;

R

s

jest oporem przejmowania ciepła na powierzchni wewnętrznej lub zewnętrznej.

7.1.2 Strumienie ciepła i płaszczyzny przekrojów
Płaszczyzny przekrojów powinny być adiabatyczne (tzn. z zerowym strumieniem cieplnym), z wyjątkiem podanym w
6.1.3.

UWAGA: W przypadku obliczeń temperatury powierzchni pozioma płaszczyzna przekroju w gruncie nie jest
adiabatyczna, ale ma ustaloną temperaturę.

7.1.3 Rozwiązania równań
Równania należy rozwiązywać według wymagań podanych w załączniku A.2.

7.1 .4 Obliczenia rozkładu temperatury
Rozkład temperatury w każdej komórce materiału należy obliczać przez interpolację między temperaturami w węzłach.

UWAGA: Wystarcza interpolacja liniowa.

7.2 Określanie współczynnika sprzężenia cieplnego i strumieni ciepła

7.2.1 Więcej niż dwie wartości temperatury brzegowej
Strumień cieplny Φ

Φ

Φ

Φ

i,j

ze środowiska i do cieplnie połączonego środowiska j określa zależność:

(5)

Całkowity strumień cieplny z pomieszczenia lub budynku można obliczyć, stosując zasady podane w rozdziale 4. W
przypadku więcej niż dwu ośrodków z różnymi wartościami temperatury (tzn. różnymi wartościami temperatury
wewnętrznej lub zewnętrznej), całkowity strumień cieplny Φ

Φ

Φ

Φ z pomieszczenia lub budynku można obliczyć z zależności:

(6)

w której:
L

i,j

są całkowitymi współczynnikami sprzężenia cieplnego między każdą parą środowisk.

UWAGA: Metodę obliczania współczynników sprzężenia cieplnego podano w załączniku F.1.

7.2.2 Dwie wartości temperatury brzegowej, model niepodzielony
Jeśli występują tylko dwa środowiska o dwu różnych wartościach temperatury (tzn. jedna temperatura wewnętrzna i
jedna zewnętrzna) i jeśli wszystkie obliczenia dotyczące całego pomieszczenia lub budynku wykonuje się, używając
pojedynczego modelu 3-wymiarowego, wtedy całkowity współczynnik sprzężenia cieplnego L

1,2

można obliczać z

całkowitego strumienia cieplnego Φ

Φ

Φ

Φ pomieszczenia lub budynku:

(7)

7.2.3 Dwie wartości temperatury brzegowej, model podzielony

PN-EN ISO 10211-1:1998 Mostki cieplne w budynkach Strumień cieplny i temperatura powierzchni Ogólne metody obliczania

Powielanie dokumentu zabronione. Wszelkie prawa zastrzeżone.

INTEGRAM BUDOWNICTWO

Strona 19

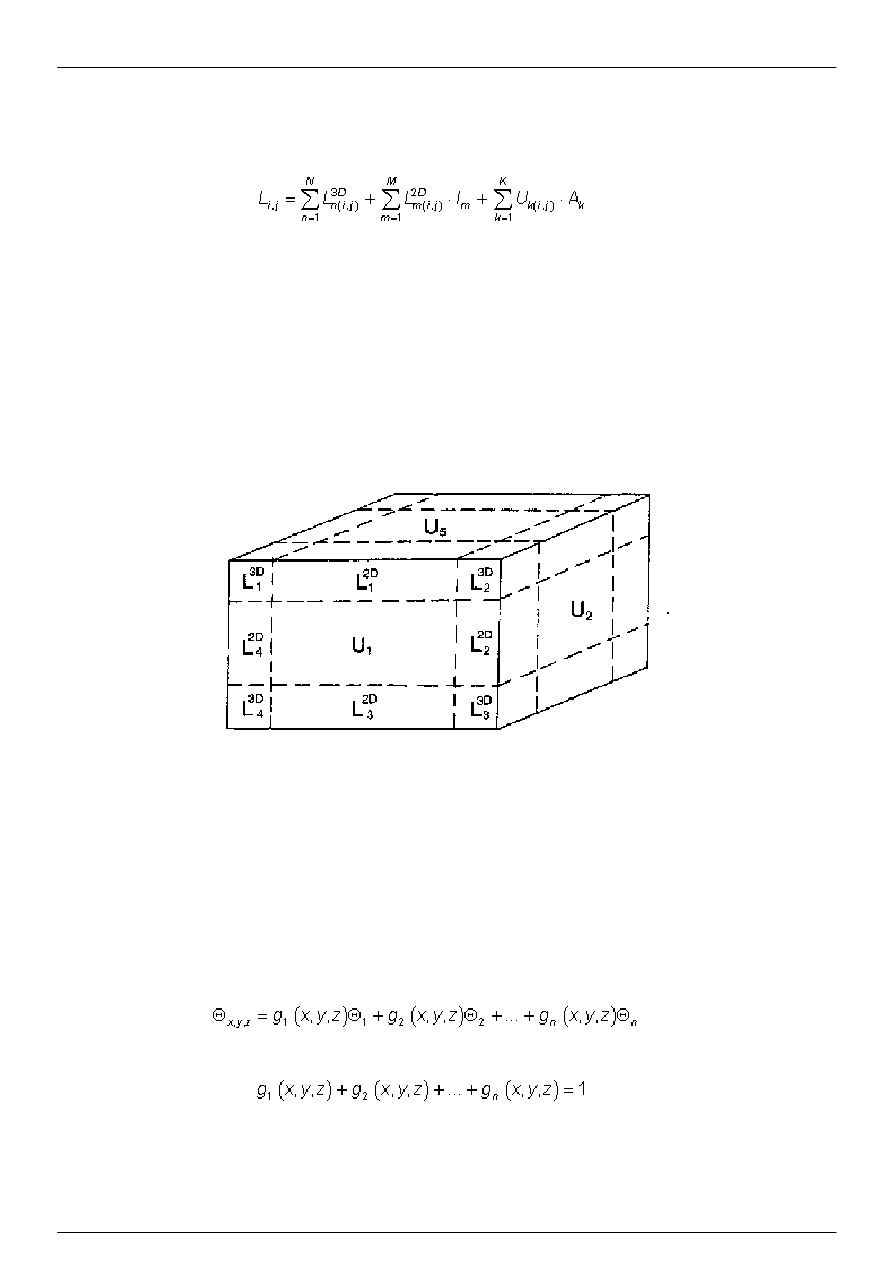
Jeżeli pomieszczenie lub budynek zostały podzielone (patrz rys. 12), całkowitą wartość L

i,j

oblicza się z następującej

zależności:

(8)

w której:
L

3D

n(i,j)

jest współczynnikiem sprzężenia cieplnego otrzymanym z obliczeń trójwymiarowych dla n-tej części

pomieszczenia lub budynku;
L

2D

n(i,j)

jest liniowym współczynnikiem sprzężenia cieplnego otrzymanym z obliczeń dwuwymiarowych dla m-tej części

pomieszczenia lub budynku;
I

m

jest długością, dla której stosuje się wartość L

2D

m(i,j)

U

k(i,j)

jest współczynnikiem przenikania ciepła, otrzymanym z obliczeń jednowymiarowych dla części k-tej

pomieszczenia lub budynku;
A

k

jest powierzchnią, dla której stosuje się wartość U

k

;

N jest liczbą wszystkich części trójwymiarowych;
M jest liczbą wszystkich części dwuwymiarowych;
K jest liczbą wszystkich części jednowymiarowych.

UWAGA: We wzorze (8) Σ

Σ

Σ

ΣA

k

jest mniejsza niż całkowita powierzchnia obudowy.

Rysunek 12: Obudowa budynku podzielona na modele geometryczne 3-D, 2-D i 1-D

7.3 Określanie temperatury na powierzchni wewnętrznej

7.3.1 Więcej niż dwie wartości temperatury brzegowej
Jeżeli występują więcej niż dwie wartości temperatury brzegowej, należy zastosować wagowy współczynnik
temperatury g. Wagowe współczynniki temperatury umożliwiają obliczenie temperatury w każdym punkcie powierzchni
wewnętrznej w układzie współrzędnych (x, y, z), jako funkcje liniowe dowolnej kombinacji wartości temperatury
brzegowej.

UWAGA 1: Co najmniej trzy wartości temperatury brzegowej występują, jeżeli model geometryczny zawiera
ośrodki wewnętrzne o różnych wartościach temperatury, a także jeżeli podłoże gruntowe stanowi część modelu
geometrycznego (patrz 6.1.3).

Stosując wagowe współczynniki temperatury, temperaturę powierzchni w punkcie (x, y, z) określa się z zależności:

(9)

przy czym:

(10)

PN-EN ISO 10211-1:1998 Mostki cieplne w budynkach Strumień cieplny i temperatura powierzchni Ogólne metody obliczania

Powielanie dokumentu zabronione. Wszelkie prawa zastrzeżone.

INTEGRAM BUDOWNICTWO

Strona 20

UWAGA 2: Metodę obliczania współczynników wagowych podano w załączniku F.3.

Temperaturę wewnętrznej powierzchni Θ

Θ

Θ

Θ

si

w interesującym punkcie oblicza się, wstawiając obliczone wartości

współczynników g

i

i rzeczywiste temperatury brzegowe Θ

Θ

Θ

Θ

i

do wzoru (9).

UWAGA 3: Zwykle punktem interesującym jest punkt o najniższej temperaturze na powierzchni. Jego położenie
może ulec zmianie, jeśli zmienią się wartości temperatury brzegowej.

7.3.2 Dwie wartości temperatury brzegowej
Jeżeli występują tylko dwa środowiska, a grunt nie jest częścią modelu geometrycznego, temperaturę powierzchni
można wyrazić w formie bezwymiarowej według wzorów (11) lub (12):

(11)

lub:

(12)

w których:
ζ

ζ

ζ

ζ

Rsi

(x,y,z) jest stosunkiem różnicy temperatury wewnętrznej powierzchni w punkcie (x, y, z);

f

Rsi

(x,y,z) jest współczynnikiem temperaturowym na wewnętrznej powierzchni w punkcie (x, y, z);

Θ

Θ

Θ

Θ

si

(x,y,z) jest temperaturą wewnętrznej powierzchni w punkcie (x, y, z);

Θ

Θ

Θ

Θ

i

jest temperaturą powietrza wewnętrznego;

Θ

Θ

Θ

Θ

e

jest temperaturą powietrza zewnętrznego.

Stosunek różnicy temperatury lub współczynnik temperatury należy obliczać z błędem mniejszym niż 0,005.

8 Dane wejściowe i wyjściowe

8.1 Dane wejściowe
Raport z obliczeń powinien zawierać następujące informacje:

a) Opis konstrukcji:
- plany budowlane, zawierające wymiary i materiały;
- w przypadku wykonanego budynku, wszelkie znane zmiany w konstrukcji i/lub pomiary fizyczne i szczegóły z
wizji lokalnej;
- inne istotne uwagi.
b) Opis modelu geometrycznego:
- model 3-D z wymiarami;
- dane wejściowe, pokazujące położenie płaszczyzn konstrukcyjnych i płaszczyzn pomocniczych, a także
współczynnik przewodzenia ciepła różnych materiałów;
- przyjęte wartości temperatury brzegowej;
- obliczenie wartości temperatury brzegowej, w miarę potrzeby;
- opory przejmowania ciepła i obszary, w których mają one zastosowanie;
- wszelkie korekty wymiarów, zgodne z p.5.2.1;
- wszelkie warstwy quasi-jednorodne i współczynniki przewodzenia ciepła, obliczone zgodnie z p.5.2.2;
- wszelkie stosowane wartości nienormowe, z uzasadnieniem odchyleń od wartości normowych.

UWAGA: Patrz p. 6.1.

8.2 Dane wyjściowe
W raporcie powinny być podane, jako wielkości niezależne od wartości temperatury brzegowej, następujące wyniki
obliczeń:
- współczynnik sprzężenia cieplnego L między sąsiednimi pomieszczeniami, uczestniczącymi w wymianie ciepła przez
komponenty budowlane;

UWAGA 1: Przykład podano w tablicy F.2.

- współczynnik temperaturowy f

Rsi

lub stosunek różnicy temperatury ζ

ζ

ζ

ζ

Rsi

dla punktów o najniższej temperaturze

powierzchni w każdym pomieszczeniu (wraz z położeniem tych punktów); jeżeli występują więcej niż dwie wartości

PN-EN ISO 10211-1:1998 Mostki cieplne w budynkach Strumień cieplny i temperatura powierzchni Ogólne metody obliczania

Powielanie dokumentu zabronione. Wszelkie prawa zastrzeżone.

INTEGRAM BUDOWNICTWO

Strona 21

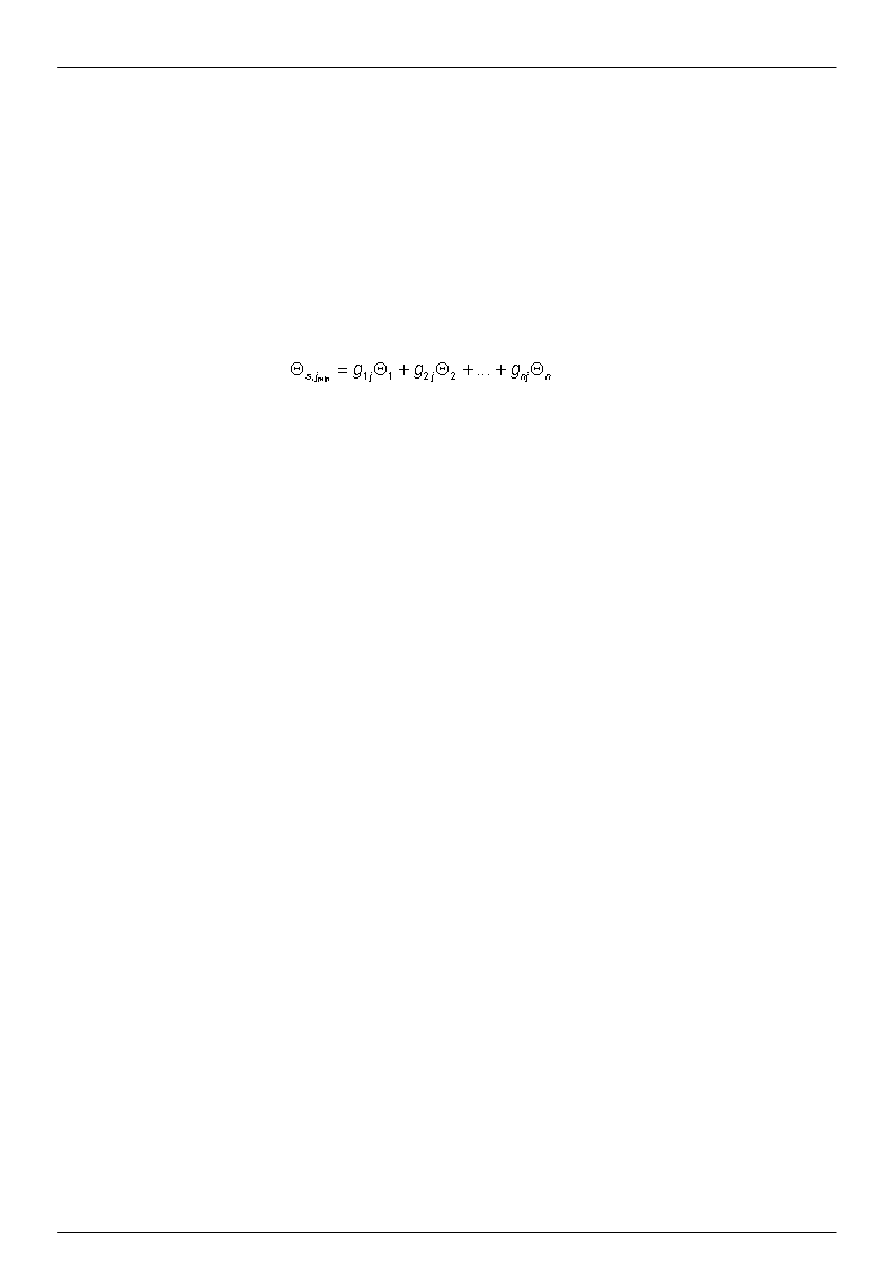
temperatury brzegowej, należy podać wagowe współczynniki temperaturowe.

UWAGA 2: Przykład sposobu prezentacji wagowych współczynników temperaturowych podano w tablicy F.4.

Wartości wszystkich wyników powinny być podawane z dokładnością co najmniej do trzech cyfr znaczących.

8.2.1 Obliczanie przepływu ciepła przy użyciu współczynnika sprzężenia cieplnego
Przepływ ciepła ze środowiska i-tego do środowiska j-tego wyrażony jest równaniem (5) wtedy, gdy występują więcej
niż dwie wartości temperatury brzegowej, natomiast równaniem (6) - gdy występują dwie wartości temperatury
brzegowej (patrz p. 7.2).

8.2.2 Obliczanie temperatur powierzchni przy użyciu współczynników wagowych
Najniższa temperatura powierzchni wewnętrznej, odniesiona do pomieszczenia j-tego, określona jest równaniem (9)
(patrz p. 7.3):

(13)

8.2.3 Dodatkowe dane wyjściowe
W przypadku specyficznego układu temperatury na brzegach należy podawać następujące dodatkowe wielkości:
- strumień cieplny, w watach na metr kwadratowy (w przypadku dwuwymiarowym) lub w watach (w przypadku
trójwymiarowym), dla każdej pary rozpatrywanych pomieszczeń;
- minimalne temperatury powierzchni, w stopniach Celsjusza, i położenie punktów o minimalnej temperaturze
powierzchni w każdym z rozpatrywanych pomieszczeń.

8.2.4 Szacowanie błędu
Procedury numeryczne dają rozwiązania przybliżone, które są zbieżne do rozwiązań analitycznych, jeżeli takie istnieją.
W celu oceny wiarygodności wyników należy oszacować residuum.
- W celu oszacowania błędów spowodowanych niedostateczną liczbą komórek należy wykonać dodatkowe
obliczenie(a), zgodnie z A.2. Należy określić różnicę wyników obu obliczeń.
- W celu oszacowania błędów numerycznego rozwiązania układu równań, należy podać stosunek sumy strumieni
cieplnych (dodatnich i ujemnych) przez wszystkie przegrody ograniczające budynek do całkowitego strumienia
cieplnego.

UWAGA: W A.2 sprecyzowano, że wartość tego stosunku powinna być mniejsza niż 0,001.

Załącznik A (normatywny)

Uprawomocnianie metod obliczeniowych
Niniejszy załącznik podaje procedurę uprawomocniania metod obliczeniowych o wysokiej dokładności w odniesieniu do
mostków cieplnych.

A.1 Przypadki testu odniesienia
W celu uznania danej metody za trójwymiarową metodę stanu ustalonego o wysokiej dokładności, należy stwierdzić
zgodność jej wyników z wynikami testu odniesienia, przypadek 1, 2 i 3, przedstawionego, odpowiednio, na rysunkach
A.1, A.2 i A.3.
W celu uznania danej metody za dwuwymiarową metodę stanu ustalonego o wysokiej dokładności, należy stwierdzić
zgodność jej wyników z wynikami testu odniesienia, przypadek 1 i 2, przedstawionego, odpowiednio, na rysunkach A.1 i
A.2.
Przypadek 1 (rysunek A.1):
Strumień cieplny przez połowę kwadratowej kolumny, przy znanych wartościach temperatury powierzchni (patrz
rysunek A.1 ), można obliczyć analitycznie. Analityczne rozwiązanie w 28 węzłach równomiernej siatki pokazano na tym
samym rysunku. Różnica między wartościami temperatury, obliczonymi metodą podlegającą uprawomocnieniu i
metodą analityczną, nie powinna przekraczać 0,1 K.

PN-EN ISO 10211-1:1998 Mostki cieplne w budynkach Strumień cieplny i temperatura powierzchni Ogólne metody obliczania

Powielanie dokumentu zabronione. Wszelkie prawa zastrzeżone.

INTEGRAM BUDOWNICTWO

Strona 22

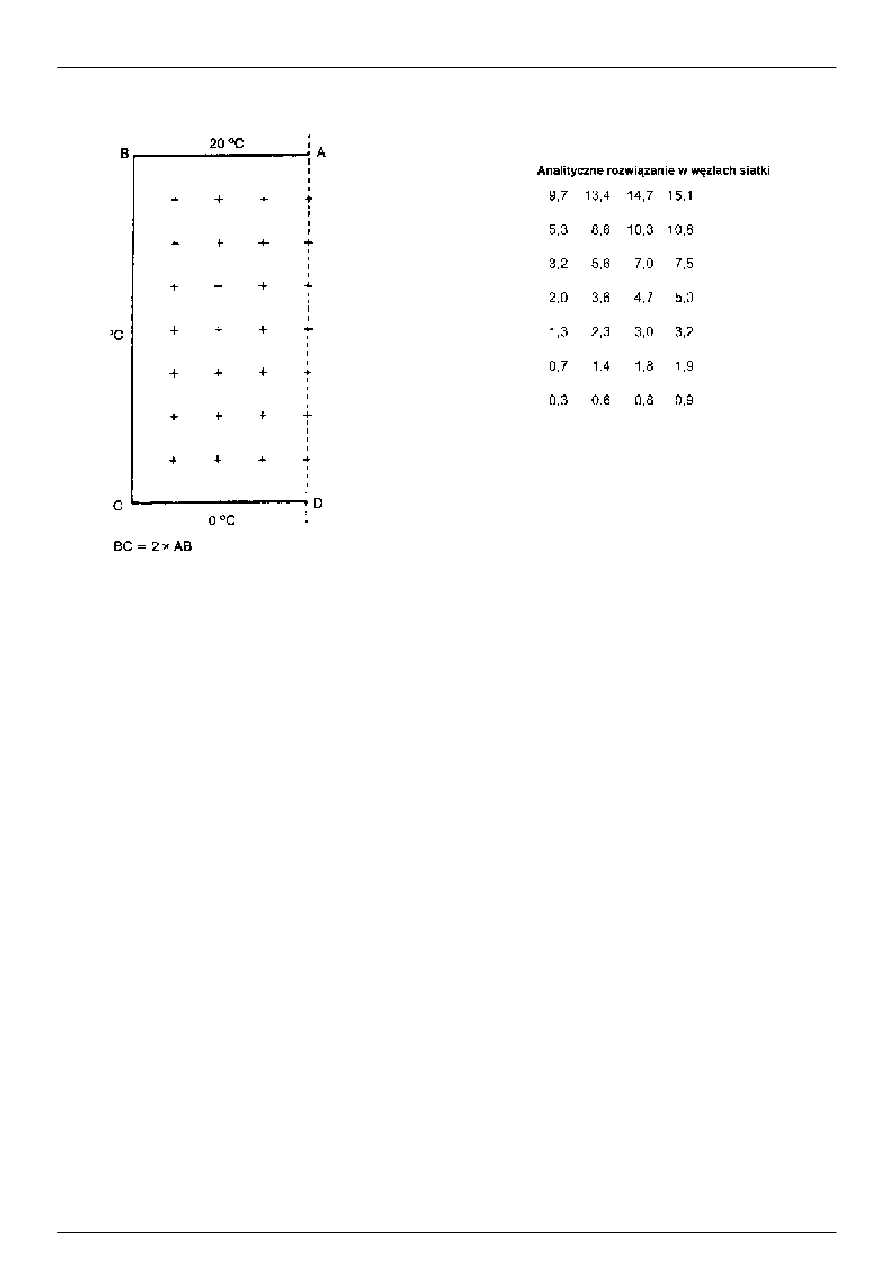
Rysunek A.1 : Test odniesienia, przypadek 1 : porównanie z rozwiązaniem analitycznym

Przypadek 2 (rysunek A.2):
Przykład dwuwymiarowego transportu ciepła podano na rysunku A.2. Na tym samym rysunku podano wartości
temperatury w pewnych szczególnych punktach i całkowity strumień ciepła przez cały obiekt (którego wymiar
prostopadły do płaszczyzny rysunku wynosi 1 m). Różnica między wartościami temperatury, obliczonymi metodą
podlegającą uprawomocnieniu i podanymi na rysunku, nie powinna przekraczać 0,1 K. Różnica między wartością
strumienia cieplnego, obliczonego metodą podlegającą uprawomocnieniu i wartością podaną na rysunku, nie powinna
przekraczać 0,1 W/m.

PN-EN ISO 10211-1:1998 Mostki cieplne w budynkach Strumień cieplny i temperatura powierzchni Ogólne metody obliczania

Powielanie dokumentu zabronione. Wszelkie prawa zastrzeżone.

INTEGRAM BUDOWNICTWO

Strona 23

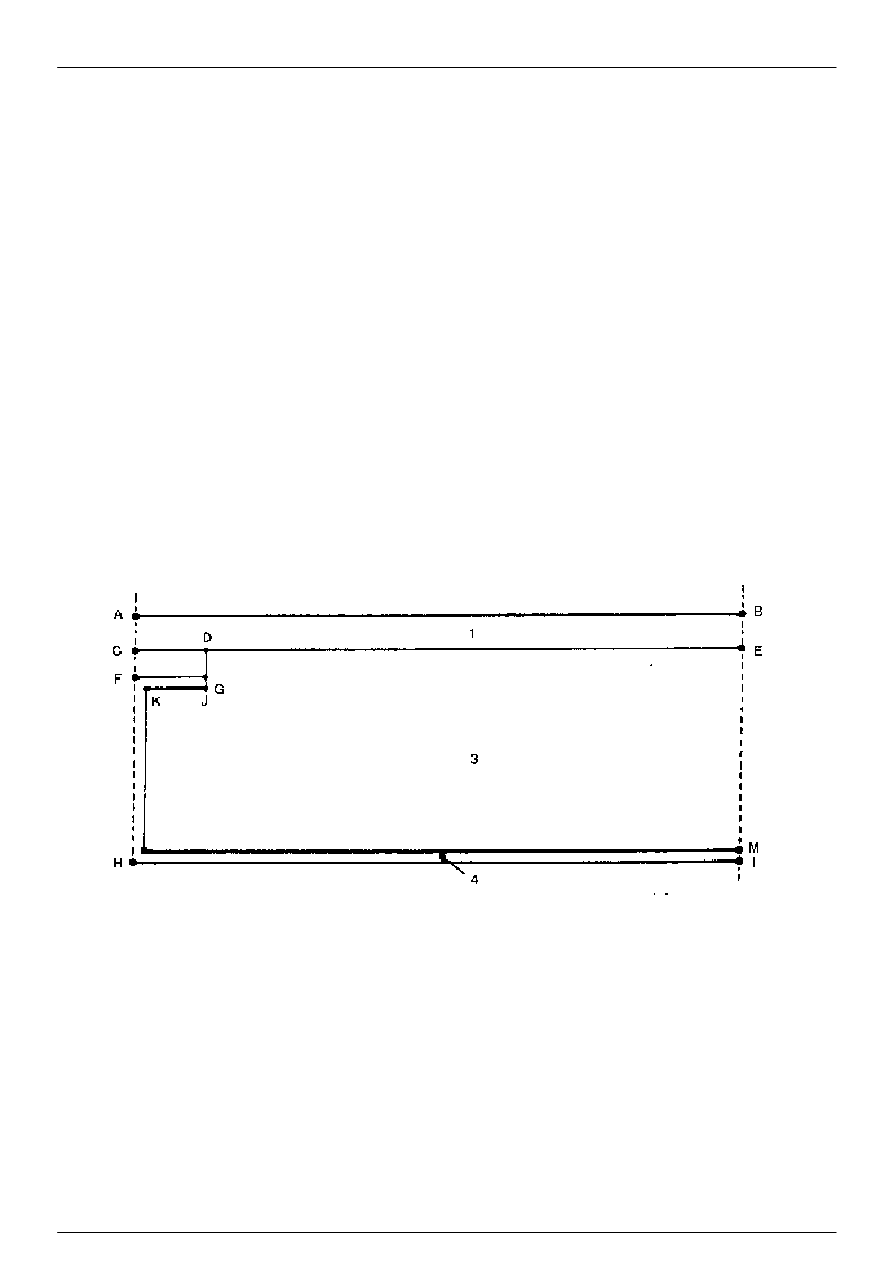
Opis modelu

Geometria
(mm)

Współczynnik przewodzenia ciepła
W/(m ⋅⋅⋅⋅ K)

Warunki brzegowe

AB = 500

1: 1,15

AB: 0°C,
R

se

= 0,06 m

2

⋅⋅⋅⋅ K/W

AC = 6

2: 0,12

HI: 20°C,
R

si

= 0,11 m

2

⋅⋅⋅⋅ K/W

CD = 15

3: 0,029

CF = 5

4: 230

EM = 40
GJ = 1,5
IM = 1,5
GF-KJ = 1,5

Temperatura, °C,

wyznaczona numerycznie:

Całkowity strumień cieplny:
9,5 W/m

A: 7,1

B: 0,8

C: 7,9

D: 6,3

E: 0,8

F: 16,4

G: 16,3

H: 16,8

I: 18,3

Rysunek A.2: Test odniesienia, przypadek 2: porównanie z obliczeniem 2-D

Przypadek 3 (rysunek A.3):
Przykład trójwymiarowego przepływu ciepła podano na rysunku 3. Na tym samym rysunku podano wartości
temperatury w pewnych szczególnych punktach i strumienie ciepła do lub z trzech rozpatrywanych środowisk. Różnica
wartości temperatury, obliczonych metodą podlegającą uprawomocnieniu i podanych na rysunku, nie powinna
przekraczać 0,1 K. Różnica wartości strumienia cieplnego, obliczonych tą metodą i podanych na rysunku, nie powinna
przekraczać 2 % wartości podanych.

PN-EN ISO 10211-1:1998 Mostki cieplne w budynkach Strumień cieplny i temperatura powierzchni Ogólne metody obliczania

Powielanie dokumentu zabronione. Wszelkie prawa zastrzeżone.

INTEGRAM BUDOWNICTWO

Strona 24

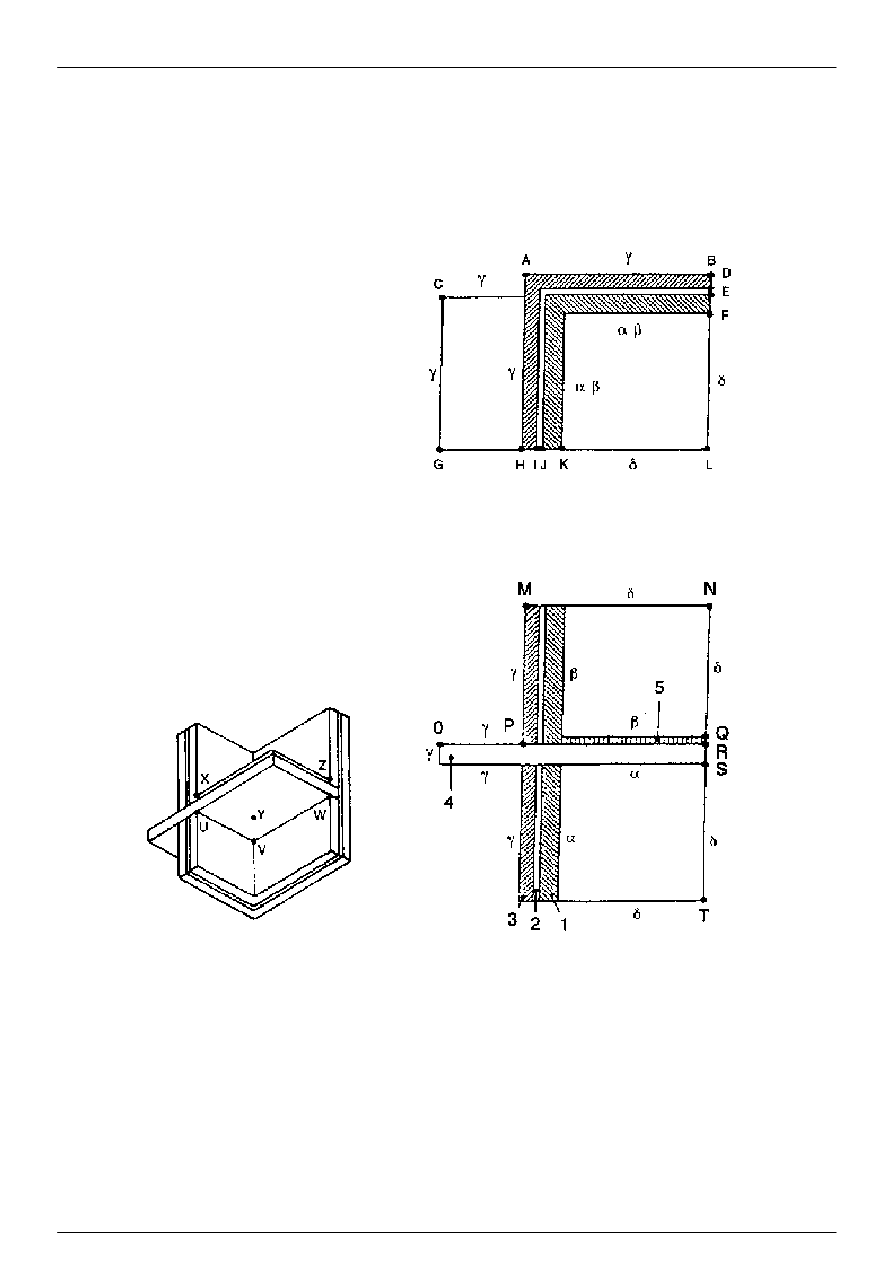
Opis modelu

Geometria,
mm

Współczynnik
przewodzenia ciepła,
W/(m ⋅⋅⋅⋅ K)

Przekrój poziomy

AB = 1300

1: 0,7

BD = HI = 100

2: 0,04

DE = IJ = 50

3: 1,0

EF = JK = 150

4: 2,5

FL = KL = 1000

5: 1,0

CG = 1150

GH = 600

Warunki brzegowe:

MP = ST = 1000

α: 20°C 0,20 m

2

⋅⋅⋅⋅ K/W

QR = 50

β: 15°C 0,20 m

2

⋅⋅⋅⋅ K/W

RS = 150

y: 0°C 0,05 m

2

⋅⋅⋅⋅ K/W

NQ = 950

δ: adiabata

OP = 600

Rozwiązanie numeryczne

Temperatura, °C: Strumienie cieplne, W:

Przekrój pionowy

U: 12,9 X: 12,6

α: straty = 46,3

V: 11,3 Y: 11,1

β: straty = 14,0

W: 16,4 Z: 15,3

y: zyski = 60,3

Perspektywa

Rysunek A.3: Test odniesienia, przypadek 3: porównanie z obliczeniem 3-D

A.2 Rozważania ogólne i wymagania w odniesieniu do metod obliczeń
Metody obliczeń o wysokiej dokładności znane są jako metody numeryczne (metoda elementów skończonych, metoda
różnic skończonych, metoda bilansu cieplnego, ....). Te metody numeryczne wymagają podpodziału rozważanego
obiektu. Metodę stanowi zespół reguł tworzenia układu równań, których liczba jest proporcjonalna do liczby
podpodziałów. Układ jest rozwiązywany metodą bezpośrednią lub metodą iteracyjną. Z rozwiązania układu równań
można wyznaczyć temperatury w szczególnych punktach, temperatury w dowolnym punkcie rozważanego obiektu
(przez interpolację), jak również strumienie ciepła przez wybrane powierzchnie.

PN-EN ISO 10211-1:1998 Mostki cieplne w budynkach Strumień cieplny i temperatura powierzchni Ogólne metody obliczania

Powielanie dokumentu zabronione. Wszelkie prawa zastrzeżone.

INTEGRAM BUDOWNICTWO

Strona 25

Metoda numeryczna podlegająca uprawomocnieniu powinna spełniać następujące wymagania:

a) Metoda powinna prowadzić do wyznaczenia temperatury i strumienie ciepła.
b) Stopień podpodziału obiektu (tzn. liczba komórek, węzłów) nie jest określony przez metodę, ale przez jej
użytkownika, chociaż w praktyce jest on ograniczony możliwościami maszyny (komputera). Zatem, w
przypadkach testów odniesienia metoda powinna dawać możliwość obliczenia temperatury i strumieni cieplnych
również winnych miejscach niż wymienione na rysunkach.
c) Przy zwiększaniu liczby podpodziałów, wyniki, uzyskane metodą podlegającą uprawomocnieniu, powinny
dążyć do rozwiązania analitycznego, o ile takie istnieje (np. w przypadku testu odniesienia 1).

UWAGA: Przy zwiększaniu liczby podpodziałów rozwiązania są zbieżne do pewnej wartości. Liczba
podpodziałów, wymagana do uzyskania dobrej dokładności, zależy od rozpatrywanego problemu.

d) Właściwa liczba podpodziałów powinna być ustalona w następujący sposób: sumę wartości bezwzględnych
wszystkich strumieni cieplnych, wpływających do obiektu, obliczyć dwukrotnie: dla n i dla 2n podpodziałów.
Różnica między dwoma uzyskanymi wynikami nie powinna przekraczać 2%. Jeżeli jest większa, należy
przeprowadzać dalsze podpodziały aż do spełnienia powyższego kryterium.
e) Jeżeli zastosowano metodę iteracyjną, iteracje należy kontynuować do chwili, gdy suma strumieni cieplnych
(dodatnich i ujemnych), wpływających do obiektu, podzielona przez połowę sumy wartości bezwzględnych tych
strumieni, będzie mniejsza niż 0,001.

Druga część

PN-EN ISO 10211-1:1998 Mostki cieplne w budynkach Strumień cieplny i temperatura powierzchni Ogólne metody obliczania

Powielanie dokumentu zabronione. Wszelkie prawa zastrzeżone.

INTEGRAM BUDOWNICTWO

Strona 26