A

A

R

R

K

K

U

U

S

S

Z

Z

M

M

A

A

T

T

U

U

R

R

A

A

L

L

N

N

Y

Y

N

N

R

R

2

2

Z

Z

A

A

K

K

R

R

E

E

S

S

P

P

O

O

D

D

S

S

T

T

A

A

W

W

O

O

W

W

Y

Y

1. a) Rozwiąż równanie

.

b) Oblicz wartość wyrażenia

, gdzie a jest rozwiązaniem równania podanego

w podpunkcie a).

2.

Dla jakiej wartości parametru m punkty A, B, C są współliniowe, jeśli

,

,

?

3.

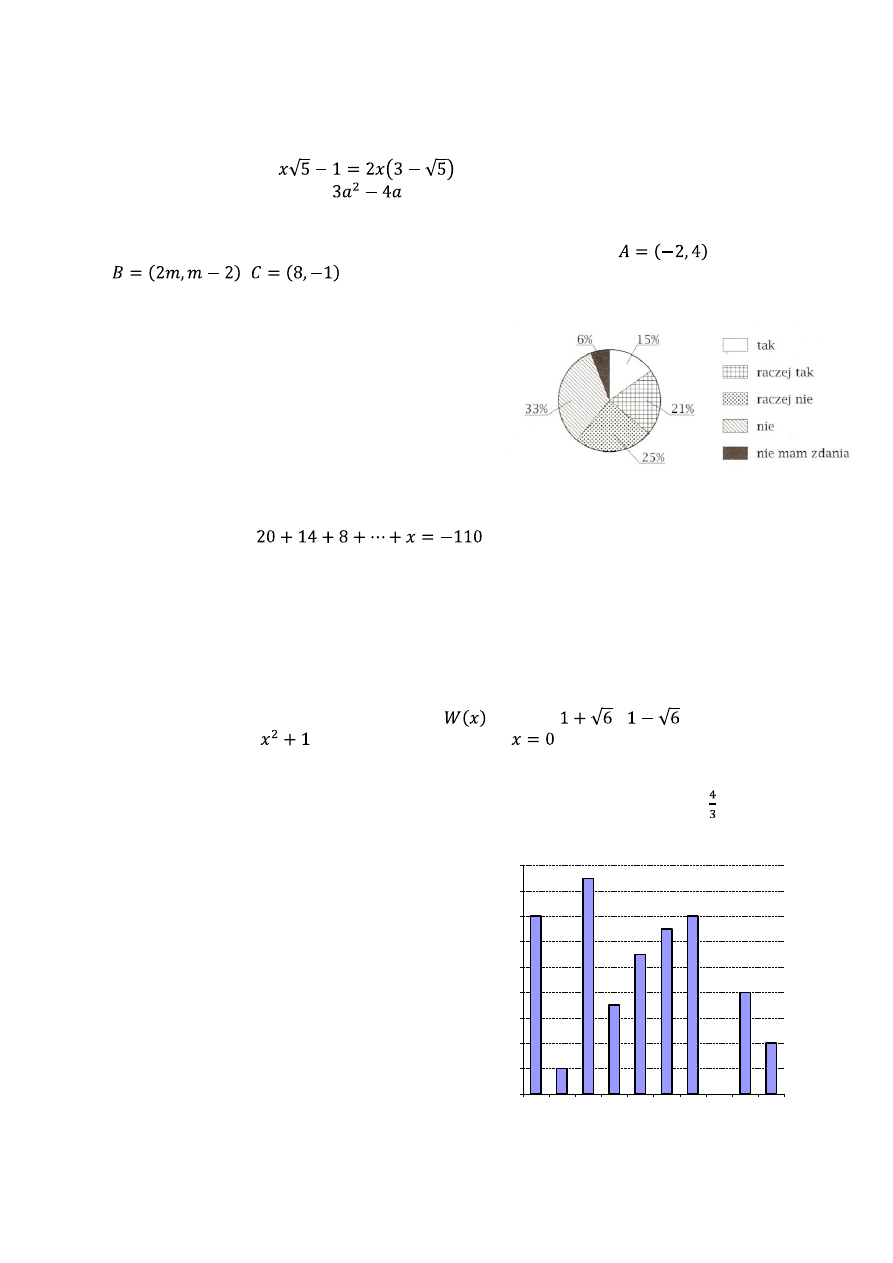
W dwóch miastach A i B, liczących odpowiednio 25
i 110 tys. mieszkańców przeprowadzono badanie
opinii publicznej. Rozkład odpowiedzi w mniej-
szym mieście przedstawia diagram kołowy. W in-
formacji opublikowanej po zakończeniu badania
podano: „Na nasze pytanie 58% osób odpowiedzia-
ło twierdząco (tzn. «tak» lub «raczej tak»)”. W mie-
ście B odpowiedzi „tak” udzieliło 31% osób. Jaki
był procent odpowiedzi „raczej tak” w tym mie-
ście?

4.

Rozwiąż równanie:

.

5.

W trójkąt prostokątny wpisujemy prostokąt w taki sposób, że dwa jego boki są zawarte w przy-
prostokątnych, a jeden wierzchołek leży na przeciwprostokątnej. Długości przyprostokątnych są
równe 5 cm i 12 cm. Jakie muszą być wymiary prostokąta, aby jego pole było największe?

6.

Trapez prostokątny, w którym różnica długości podstaw wynosi 3, opisany jest na okręgu
o promieniu 2. Oblicz odległości środka okręgu od wierzchołków trapezu.

7. Pierwiastkami wielomianu czwartego stopnia

są liczby

i

. Wielomian ten

jest podzielny przez

i przyjmuje wartość 10 dla

. Wyznacz wielomian, uporządkuj

go i podaj wszystkie liczby całkowite, dla których przyjmuje on wartości dodatnie.

8. Bok trójkąta ma długość 5, tangensy kątów przylegających do tego boku są równe i 2. Oblicz

pole i obwód tego trójkąta.

9. Wykonujemy rzut dwiema kostkami i notujemy

ostatnią cyfrę iloczynu oczek. Jeśli np. na kost-
kach otrzymamy 3 i 6, wynikiem doświadczenia
będzie „8”, a jeśli 2 i 3, wynikiem będzie „6”.
Doświadczenie takie powtórzono wielokrotnie i wy-
niki przedstawiono za pomocą diagramu. Oblicz
częstość występowania wyniku „0”. O ile procent
częstość ta różni się od prawdopodobieństwa tego
wyniku?

10.

Aby usmażyć naleśnik, lejemy ciasto na patelnię łyżką wazową w kształcie półkuli o pro-

0

2

4

6

8

10

12

14

16

18

0

1

2

3

4

5

6

7

8

9

lic

zb

a

rz

ut

ów

otrzymana cyfra

mieniu 3,2 cm. Porcja ciasta przeznaczona na wykonanie jednego naleśnika stanowi 90% po-
jemności łyżki. Mamy do dyspozycji patelnie o średnicach: 17 cm, 20 cm i 22 cm. Której z nich
należy użyć, jeśli chcemy otrzymać naleśnik o grubości nie większej niż l,5 mm? (Przyjmujemy,
że podczas smażenia ciasto zachowuje swoją objętość).

O

O

D

D

P

P

O

O

W

W

I

I

E

E

D

D

Z

Z

I

I

:

:

1. a)

, b) . 2. Dla

. 3. 32%. 4.

. 5. 2,5 cm 6 cm. 6.

,

,

,

. 7.

; -1, 0, 1, 2, 3. 8.

; Obwód

.

9.

; częstość jest o 6,7% niższa od prawdopodobieństwa równego . 10. Należy użyć

największej patelni.