1 Wyznaczenie współczynnika filtracji

Przeprowadzone do´swiadczenie polegało na wyznaczenie współczynnika filtracji, dla modelu
schematu wału przeciwpowodziowego. Współczynnik filtracji w literaturze oznaczany jest k,
ma wymiar pr˛edko´sci i oznacza ruch wody w jakim´s o´srodku, który odbywa si˛e pod wpły-
wem sił ci˛e˙zko´sci, przykładem w szczególno´sci jest ruch wody gruntowej.Zale˙zy on od rodzaju
gruntu (dokładniej jego wła´sciwo´sci filtracyjnych) i od lepko´sci filtruj ˛

acej wody (s ˛

a to parame-

try filtracji).
Dla przeprowadzonego do´swiadczenia, ruch wody jest ruchem laminarnym (za wzgl˛edu na mał ˛

a

pr˛edko´s´c przepływu)oraz woda ta wypełnia całkowicie pory gruntu, dlatego w tym przypadku
mozemy mowi´c o filtracji, b o w przypadku kiedy woda nie wypełnia całkowicie por gruntu,
mówimy wtedy o infiltracji.
Mo˙zna podzieli´c o´srodki gruntowe z punktu widzenia warunków filtracji, na:
1) o´srodek jednorodny, czyli taki który charakteryzuje si˛e jednakowymi parametrami filtracji
we wszystkich punktach rozpatrywanego o´srodka i o´srodek niejednorodny, czyli taki który nie
spełnia tego warunku;
2) o´srodek izotropowy, w którym parametry filtracji s ˛

a jednakowe we wszystkich kierunkach

oraz anizotropowy, czyli taki w którym te parametry s ˛

a zale˙zne od kierunku przepływu wody.

Prawa ruchu wody gruntowej przedstawione poni˙zej dotycz ˛

a o´srodka jednorodnego i izotropowego.

Zalezno´s´c pr˛edko´sci od współczynnika filtracji, okre´sla prawo Darcy:

v = k I

(1)

v - pr˛edko´s´c filtracji strugi wody
I - spadek zwierciadła wody gruntowej przy przepłuwach o swobodnym zwierciadle

i spadek linii ci´snie´n przy przwpływach pod ci´snieniem,

k - współczynnik filtracji.
Zasady ruchu mo˙zna zobrazowa´c na ponizszym schemacie:

gdzie:

tgα = I (x)

(2)

I (x)-spadek zwierciadła, tgα oznacza pochodn ˛

a funkcji w punkcie, zatem:

I (x) =

dz

dx

(3)

1

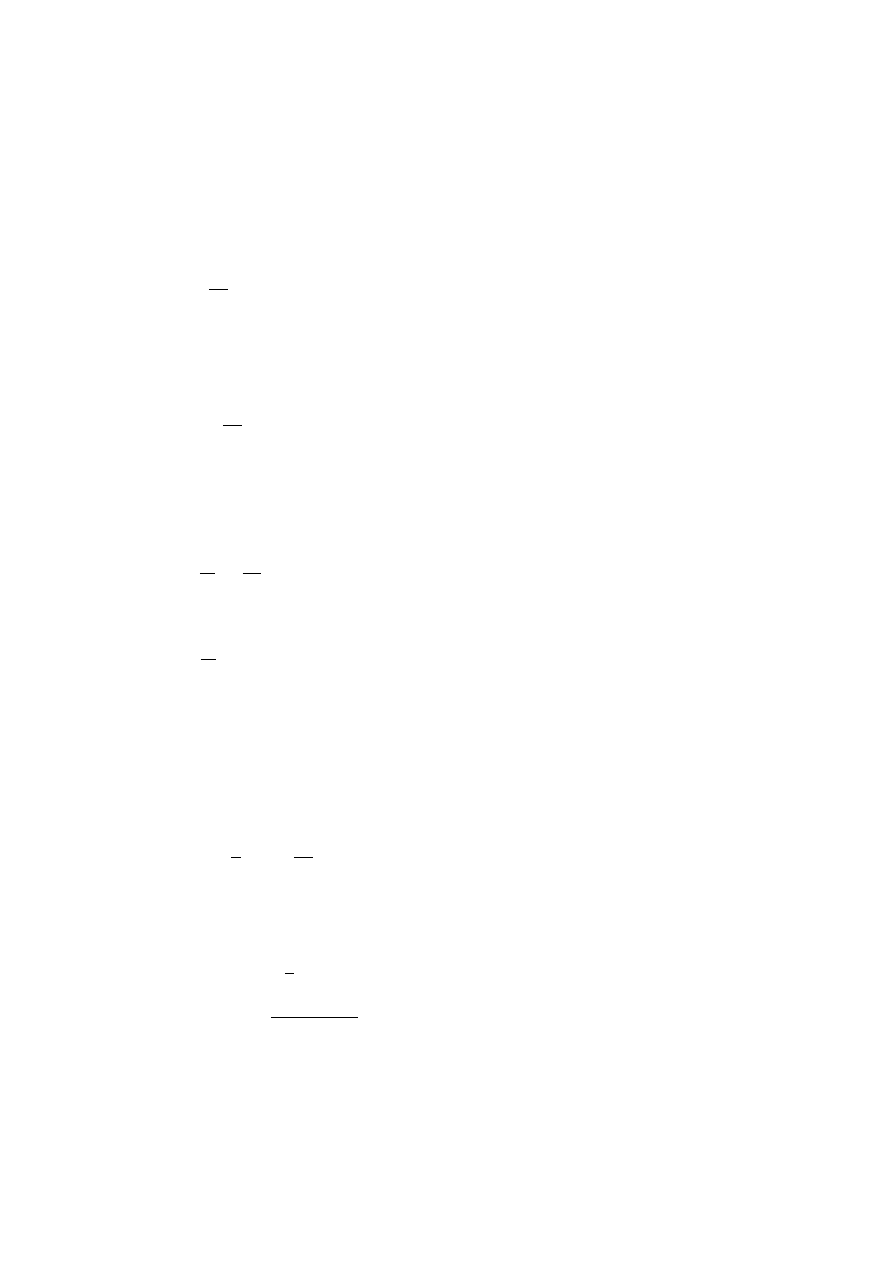
Uzmienniaj ˛

ac stała I ze wzoru (1) wzgl˛edem x i podstawiaj ˛

ac (1) do (3), otrzymujemy wzór

Dupnit’a:

v = k

dz

dx

(4)

W odró˙znieniu od prawa Darcy wzór Dupnit dotyczy strumienia a nie strugi oraz okre´sla pr˛ed-
ko´s´c ´sredni ˛

a w pionie badanego przekroju W naszym przypadku mamy do czynienia z gradien-

tem funkcji malej ˛

acej,czyli krzyw ˛

a depresji, dlatego wzór przyjmie posta´c:

v = −k

dz

dx

(5)

2 Sposób przeprowadzenia oblicze ´n

Wiedz ˛

ac, ˙ze

v =

Q

A

=

Q

dz

(6)

oraz

q =

Q

d

(7)

gdzie:
Q - wydatek przepływu, obliczony z ilorazu obj˛eto´sci cieczy, przez czas jej napełniania, wyra˙zony

w [m

3

/s];

d - szeroko´s´c wału, mierzona mi˛edzy piezometrami 8-18, wyra˙zona w [m];
z - wysoko´s´c słupa wody w piezometrze, wyra˙zona w [m];
q - wydatek jednostkowy, wyra˙zony w [m

2

/s] Podstawiaj ˛

ac (6) do (7):

q

z

= −k

dz

dx

qdx = −zdz

q

Z

x

2

x

1

dx = −k

Z

z

2

z

1

zdz

q(x

2

− x

1

) = −

1
2

k(z

2

1

− z

2

2

)

k =

2q(x

2

− x

1

)

z

2

1

− z

2

2

(8)

x

2

− x

1

- odległo´s´c miedzy kolejnymi piezometrami, wyrazona w [m]

2