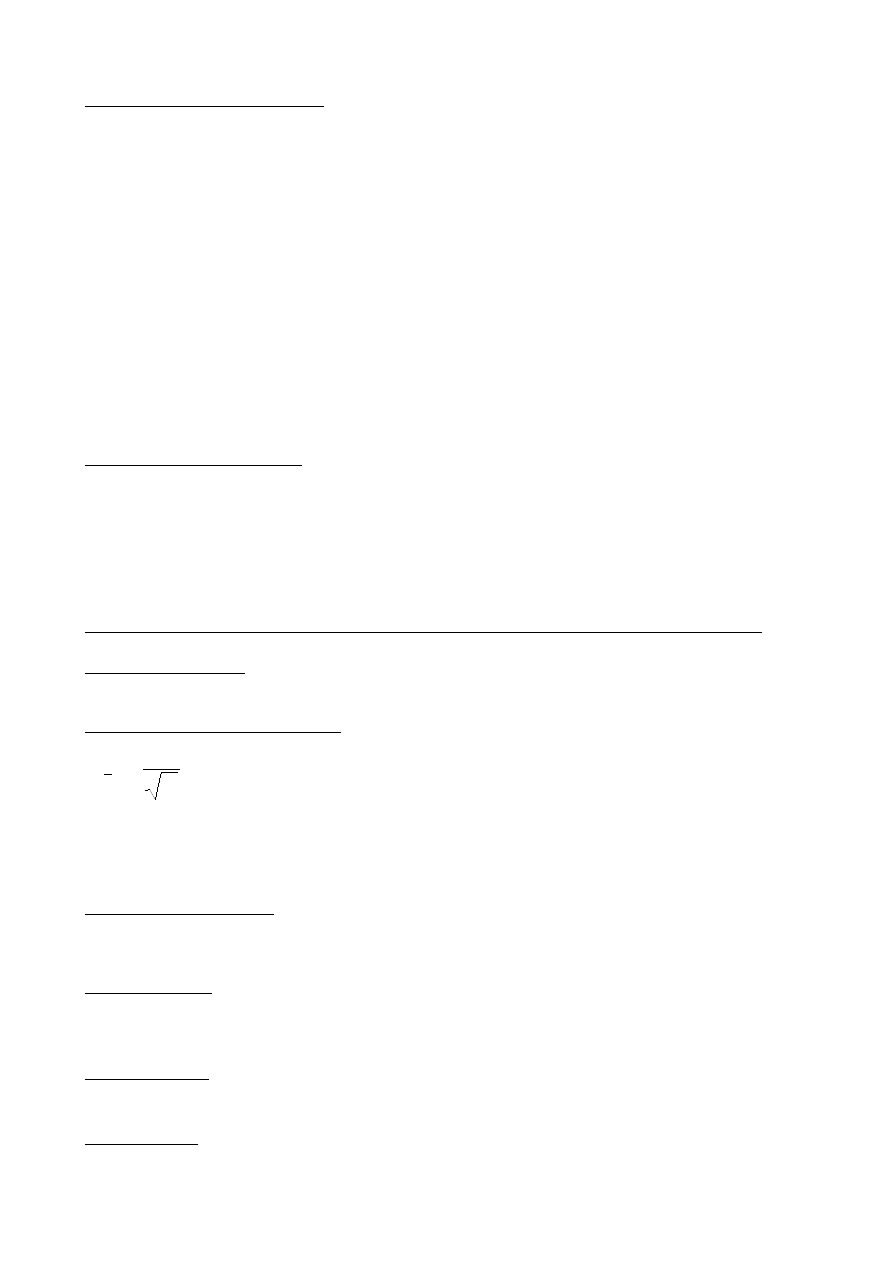
Metody statystyczne w naukach biologicznych
2006-03-12
Wykład: Teoria estymacji.
Estymacja to postępowanie statystyczne zmierzające do oszacowania parametrów populacji
generalnej (
µ
,
σ
) na podstawie statystyk uzyskanych z populacji próbnej.
Estymator (T
n
)- statystyka z próby służąca do oszacowania parametru (
θ
). Może nim być średnia
arytmetyczna, odchylenie standardowe, mediana, współczynniki zmienności. Estymator, podobnie
jak sama zmienna losowa, posiada własny rozkład. Nie zawsze jednak wymienione wcześniej
statystyki będą uznawane za najlepsze estymatory. Powinny spełniać one określone własności.
Ocenę estymatora można przeprowadzić na podstawie jego błędu (d). Załóżmy, że różnica między
wartością estymatora oraz parametru jest równa d, tj,:T
n
-
θ
=d. W związku z powyższym miarą błędu
estymatora będzie wartość oczekiwana kwadratu różnicy pomiędzy estymatorem a szacowanym
parametrem, czyli
∆
=E(T
n
-
θ
)
2
. W sytuacji, gdy wartość oczekiwana estymatora równa jest wartości
parametru populacji generalnej (
θ
), to
∆
możemy potraktować jako wariancję estymatora, tzn.
∆
=D
2
(T
n
), tym samym D(T
n
) należy traktować jako błąd standardowy estymatora.
Cechy dobrego estymatora to:
1.
Nieobciążoność. Estymator nazywamy nieobciążonym, gdy jego wartość oczekiwana jest
równa parametrowi populacji generalnej, czyli E(T
n
)=
θ
.
2.
Efektywność. Estymator efektywny, to taki, którego wariancja jest najmniejsza.
3.
Zgodność. Estymator nazywamy zgodnym, jeżeli wraz ze wzrostem liczebności próby jego
wartość zbliża się do szacowanego parametru.
Metody estymacji parametrycznej (szacowane są wartości parametrów rozkładu cechy):
Estymacja punktowa – polega na uznaniu estymatora z próby losowej, jako wartości parametru.
Powyższemu stwierdzeniu towarzyszy dodatkowo podanie błędu oszacowania.
Średni błąd średniej arytmetycznej:
n
S
S
x
x
=
Jeżeli względny błąd estymatora D(T
n
) nie przekracza 7,5%, to można uznać, iż wynik estymacji jest wysoce
precyzyjny. Jeśli przyjmuje wartości z przedziału 7,5%-15%, to dopuszczalny, a powyżej- nie jest do
przyjęcia.
Estymacja przedziałowa – polega na wyznaczeniu przedziału liczbowego, który z określonym
prawdopodobieństwem zawiera szacowany parametr. Końce przedziału zależą od wartości
estymatora.
Przedział ufności - losowy przedział, który z określonym prawdopodobieństwem określa wartość
parametru. To inaczej przedział liczbowy, w którym znajduje się prawdziwa, lecz nieznana wartość
parametru
θ
.
Przedział (g1,g2) jest przedziałem ufności parametru
θ
, określonym na poziomie ufności 1-
α
, jeżeli
prawdopodobieństwo, że
θ
leży w tym przedziale jest równe 1-
α
.
Poziom ufności -1-
α
jest prawdopodobieństwem, że
θ
leży w przedziale (g1,g2). Przedział (g1,g2),
którym g1 i g2 przyjmują skończone wartości nazywa się dwustronnym przedziałem ufności.
Autor: Dariusz Piwczyński
1
Metody statystyczne w naukach biologicznych
2006-03-12
Jeżeli
α
=0,05, to 1-
α
=0,95 oznacza to, że średnio na każde 100 przedziałów ustalonych na 100
prób losowych, w 95 przypadkach prawdziwa wartość parametru
θ
znajduje się wewnątrz
przedziału, natomiast w 5 przypadkach znajduje się poza przedziałem.
Im niższy przyjmiemy poziom ufności, tym mniejsze będzie prawdopodobieństwo błędnego
określenia przedziału, jednak jednocześnie wydłużony będzie przedział ufności.
Rozkład t-Studenta
(pseudonim angielskiego statystyka William Gosset 1876-1937)
Stosowany głównie do testowania małych próbek. Rozkład ten zależy od
ν
(liczba stopni swobody),
nie zależy natomiast od odchylenia standardowego.
Próba duża n
≥
100 (Łomnicki); n
≥
50 [n
≥
30] (Żuk)
Liczba
stopni swobody
(degrees of freedom) (N-1). Jeżeli znana jest średnia z N pomiarów, to
pomiar ostatni zdeterminowany jest przez wartość średniej. Jest to nieco inny sposób opisania
wielkości próby. Liczba stopni swobody służy do otrzymania nieobciążonego estymatora. Należy
go zatem (wariancję, odchylenie standardowe) podzielić nie przez N, lecz przez N-1.
Krzywa gęstości rozkładu t-Studenta zbliżona kształtem do krzywej rozkładu normalnego N(0,1).
Jest to krzywa symetryczna (z osią symetrii t=0) i tylko bardziej spłaszczona. Dla dużej liczby
stopni swobody (N>120) rozkład t jest praktycznie nierozróżnialny od standaryzowanego rozkładu
normalnego.
Autor: Dariusz Piwczyński
2
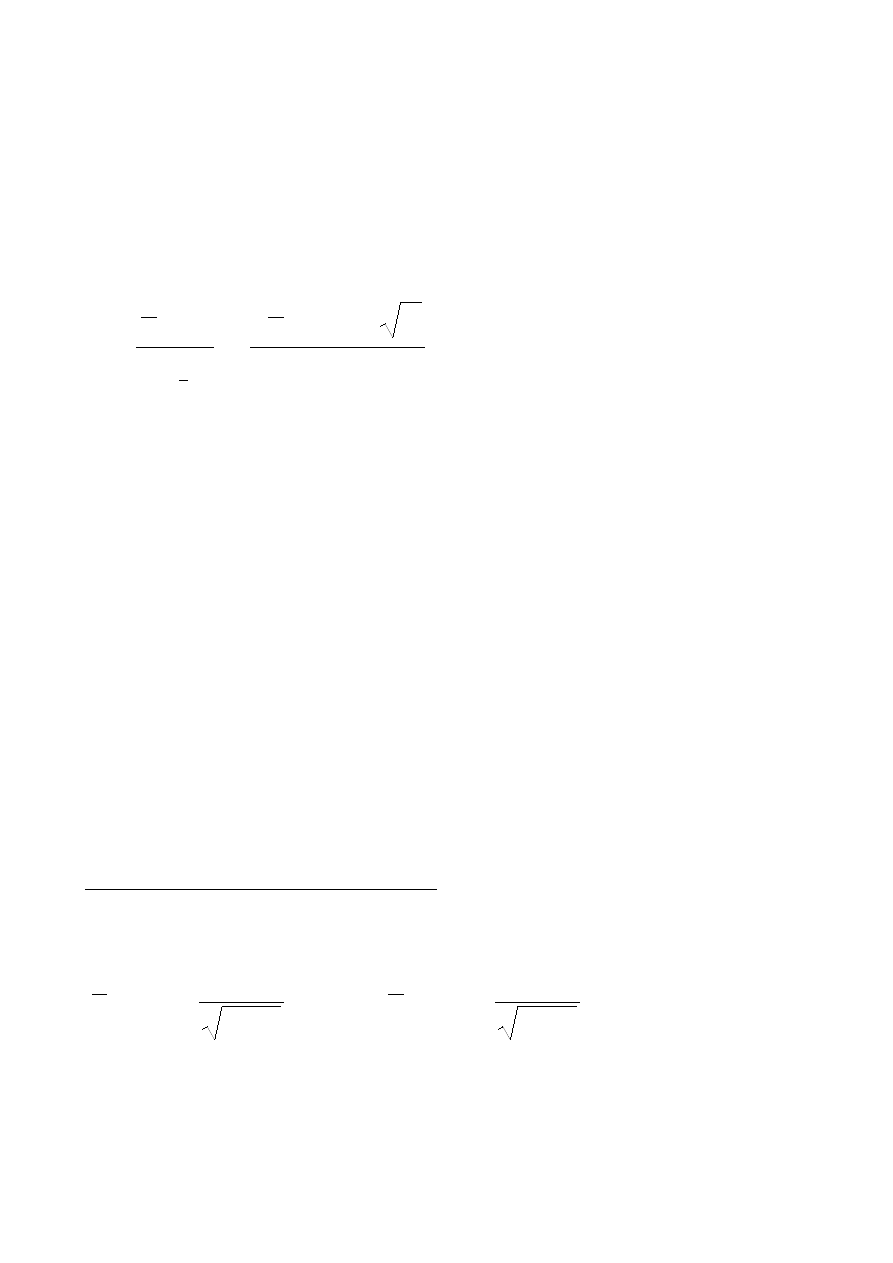
Metody statystyczne w naukach biologicznych
2006-03-12
Załóżmy, że jeżeli z populacji o jakimkolwiek rozkładzie ze średnią
µ
i odchyleniem standardowym
σ
pobieramy próby o dużej liczebności N, to rozkład średnich z tych prób będzie rozkładem
normalnym o średniej
µ
i odchyleniu
σ
/
√
N.
Z powyższą sytuacją raczej się zbyt często nie spotykamy, ponieważ nie znamy zwykle odchylenia
standardowego populacji, średniej dla całej populacji, próby są małe.
Jeżeli z populacji o rozkładzie normalnym pobieramy próby N - elementowe, to dla każdej próby
możemy obliczyć statystykę t.
Błąd standardowy (SE; S
x
) opisuje on odchylenie średnich z prób N - elementowych od średniej dla
całej populacji, a nie odchylenie poszczególnych pomiarów od średniej. Jest to teoretycznie
wyliczone odchylenie standardowe średnich z pomiarów dla wielu prób.
S
x
– statystyka obliczona na podstawie prób.
σ
x
– jeśli jest parametrem
Obszar krytyczny – zbiór tych wartości funkcji testowej, dla których hipotezę H
0
odrzucamy.
Wyróżniamy obszary krytyczne jednostronne i dwustronne.
Obszar krytyczny złożony z dwu rozłącznych podzbiorów przestrzeni próby, wyznaczany jest
najczęściej symetrycznie w rozkładzie statystyki. Test dwustronny używa się z reguły, gdy hipoteza
alternatywna jest w postaci nierówności.
Wartości krytyczne są to takie wartości t
α
, że prawdopodobieństwo, iż zmienna losowa t przyjmie
wartość większą od t
α
lub mniejszą od -t
α
, wynosi
α
. Wartości krytyczne – punkty oddzielające
obszar krytyczny od obszaru (zbioru) tych wartości, dla których nie ma podstaw do odrzucenia
hipotezy H
0.
Prawdopodobieństwo, iż zmienna losowa przyjmie wartość z przedziału (-t
α
,-t
α
) jest równe
1-
α
.
Przedział ufności dla średniej arytmetycznej:
Stosowany wtedy, gdy mamy do czynienia z rozkładem normalnym, ale nie znamy
σ
i próbie
małej, tj. poniżej 30 elementów.
)
1
*
(
)
1
(
−
+
<
Θ
<
−
∗
−
n
S
t
x
n
S
t
x
x
x
α
α
t - odczytujemy z tabeli testu t-Studenta dla liczby stopni swobody równej n-1 i odpowiedniego
poziomu ufności.
Autor: Dariusz Piwczyński
3
S
n
x
S
x
t
x
×
−
=
−
=
)
(
µ
µ
Metody statystyczne w naukach biologicznych
2006-03-12
Przedział ufności dla średniej arytmetycznej:
Stosowany wtedy, gdy mamy do czynienia z rozkładem normalnym, znane
σ
.
)
*
(
)
(
n
u
x
n
u
x
σ
σ
α
α
+
<
Θ
<
∗
−
u
α
- dystrybuanta rozkładu normalnego
Przedział ufności dla średniej arytmetycznej:
Stosowany wtedy, gdy mamy do czynienia z rozkładem normalnym lub innym,
σ
jest nieznane,
próba duża > 30.
)
*
(
)
(
n
S
u
x
n
S
u
x
x
x
α
α
+
<
Θ
<
∗
−
u
α
- dystrybuanta rozkładu normalnego
SAS
Title 'Obliczamy przedział ufności 95%';
proc means clm alpha=0.05 data=stat.krowy;
var mlkg;
run;
Analysis Variable : mlkg
Dolna 95% Górna 95%
Gr. ufn. dla ¶redniej Gr. ufn. dla ¶redniej
4509.8
5267.44
Oszacowany przedział ufności przy poziomie istotności
α
=0.05, pozwala stwierdzić, iż średnia wydajność
mleka (parametr) w populacji generalnej zawiera się w przedziale liczbowym [4509.08;5267.44].
Autor: Dariusz Piwczyński
4