B÷¾

edy studentów

na egzaminach z matematyki

W opracowaniu omówi÷

em typowe b÷¾

edy pope÷

niane przez studentów na kolokwiach

i egzaminach z algebry oraz analizy. Ponadto podaj ¾

e b÷¾

edy rzadziej spotykane, które

zaskoczy÷

y mnie pomys÷

owo´sci ¾

a zdaj ¾

acych. Mam nadziej ¾

e, ·

ze dzi ¾

eki opracowaniu stu-

denci nie pope÷

ni ¾

a ju·

z tego rodzaju b÷¾

edów.

I. Fa÷

szywe wzory algebraiczne, trygonometryczne i inne

Studenci b÷¾

ednie przyjmuj ¾

a, ·

ze funkcje elementarne s ¾

a liniowe i dlatego stosuj ¾

a wzory a), b).

a) (

a + b)

2

= a

2

+ b

2

;

p

x + y =

p

x +

p

y;

1

x + y

=

1

x

+

1

y

;

b) sin 2 = 2 sin

;

tg (x + y) = tg x + tg y;

c)

p

x

2

= x;

ln a

ln b

= ln (a

b) ;

a

n

a

m

= a

n m

;

d)

a

x

+

b

y

=

a + b

x + y

;

a + b

x

=

a

x

+ b:

II. B÷¾

edne metody obliczania granic ci ¾

agów i funkcji

Jednym z najcz ¾

e´sciej pope÷

nianych b÷¾

edów przy wyznaczaniu granic ci ¾

agów i funkcji jest obliczenie

granicy w dwóch etapach. Studenci najpierw przechodz ¾

a do granicy z cz ¾

e´sci ¾

a zmiennych i dopiero po

uproszczeniu wyra·

zenia, przechodz ¾

a do granicy z pozosta÷

ymi zmiennymi.

a) lim

n

!1

1 +

1

2n

n

= lim

n

!1

(1 + 0)

n

[ ! ] = lim

n

!1

1 = 1:

Prawid÷

owy wynik

p

e:

b) lim

n

!1

1

p

n

2

+ 1

+

1

p

n

2

+ 2

+ : : : +

1

p

n

2

+ n

= lim

n

!1

(0 + 0 + : : : + 0) [ ! ] = lim

n

!1

0 = 0: Prawid÷

owy wynik 1:

c) lim

x

!1

p

x

2

+ 5x

p

x

2

+ 2x = lim

x

!1

x

r

1 +

5

x

x

r

1 +

2

x

!

lim

x

!1

x

p

1 + 0

x

p

1 + 0 [ ! ] = lim

x

!1

(x 1

x 1) = lim

x

!1

0 = 0:

Prawid÷

owy wynik

3
2

:

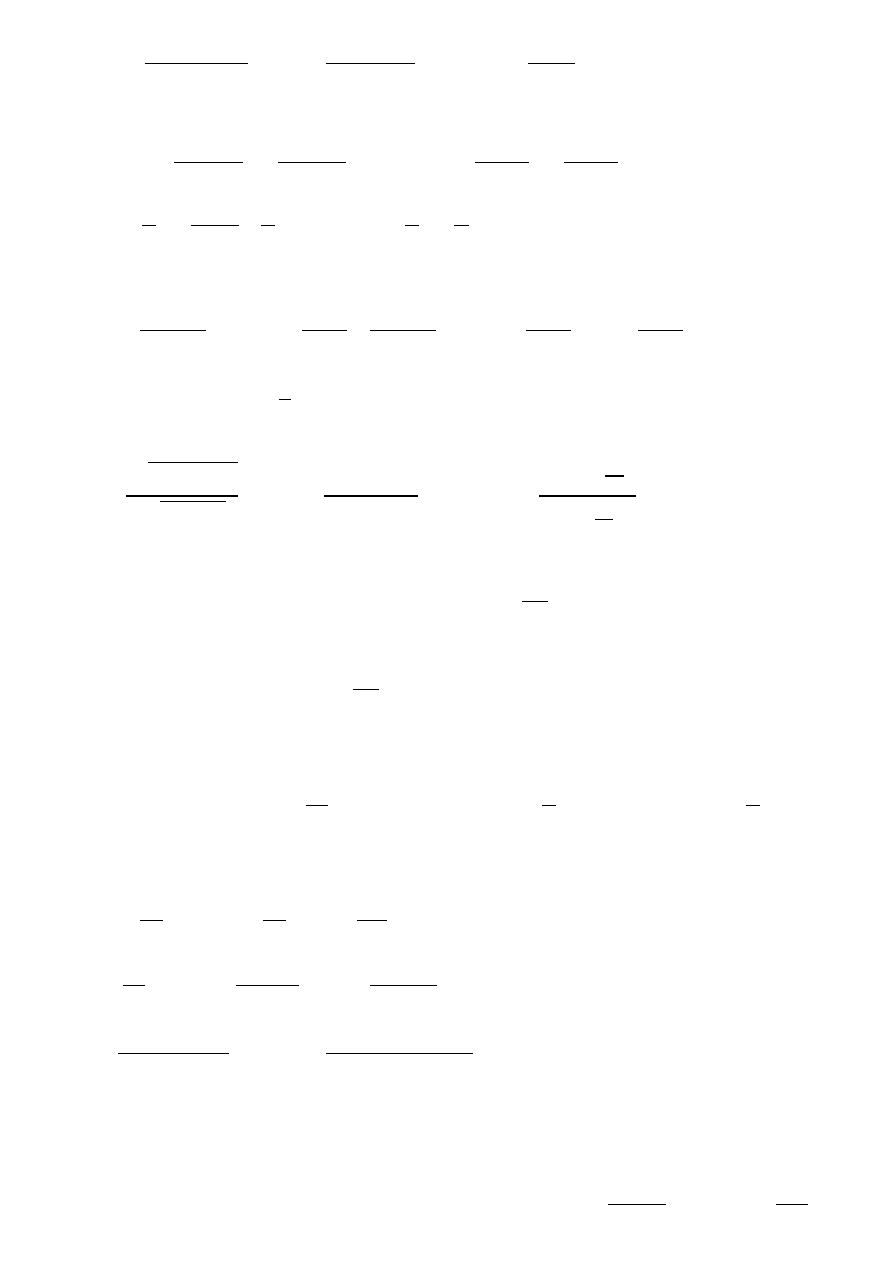
d) lim

x

!0

3x + sin x

x

= lim

x

!0

0 + sin x

x

[ ! ] = lim

x

!0

sin x

x

= 1:

Prawid÷

owy wynik 4:

e) lim

x

!0+

1 + 8x

x

1 + 3x

sin x

= lim

x

!0+

1 + 0

x

1 + 0

sin x

[ ! ] =

lim

x

!0+

1

x

x

sin x

1

x

= lim

x

!0+

1

x

1

x

1 [ ! ] = lim

x

!0+

0 = 0:

Prawid÷

owy wynik 5:

f ) lim

x

!0

e

x

1

sin 2x

= lim

x

!0

1

sin 2

e

x

1

x

[ ! ] =

1

sin 2

1 =

1

sin 2

:

Prawid÷

owy wynik

1
2

:

g)

Po podniesieniu wyra·

zenia za limesem do czwartej pot ¾

egi otrzymam:

lim

x

!1

4

p

16x

4

+ 1

p

x

2

+ 3

= lim

x

!1

16x

4

+ 1

(x

2

+ 3)

2

[ ! ] = lim

x

!1

16 +

1

x

4

1 +

3

x

2

2

= 16:

Prawid÷

owy wynik 2:

h)

Dla wielu studentów wyra·

zenia 1 1;

1
1

; 0

1; 1

1

s ¾

a tylko pozornie

nieoznaczone, gdy·

z ich zdaniem zachodz ¾

a wzory:

1

1 = 0;

1
1

= 1;

0 1 = 0;

1

1

= 1:

Z poni·

zszych równo´sci wynika, ·

ze stwierdzenia te s ¾

a fa÷

szywe:

lim

x

!1

x

2

x =

1; lim

x

!1

e

x

x

= 1; lim

x

!0+

sin x

2

x

= 2; lim

x

!1

1 +

1

x

x

= e:

i)

Studenci stosuj ¾

a regu÷¾

e de L’Hospitala bez sprawdzenia za÷

o·

ze´n:

lim

x

! 1

x

e

x

H

= lim

x

! 1

1

e

x

[ ! ] =

1

0+

= 1; prawid÷owy wynik 1;

lim

x

!0+

2

x

x

H

= lim

x

!0+

2

x

ln 2

1

[ ! ] =

1 ln 2

1

= ln 2; prawid÷

owy wynik 1;

lim

x

!1

x

2

+ sin x

2

x

2

H

= lim

x

!1

2x + 2x cos x

2

2x

= lim

x

!1

1 + cos x

2

;

a poniewa·

z

ostatnia granica nie istnieje, wi ¾

ec nie istnieje tak·

ze granica pocz ¾

atkowa[ ! ] :

Prawid÷

owy wynik 1: Ponadto stosuj ¾

a fa÷

szyw ¾

a "regu÷¾

e de L’Hospitala" do

obliczania warto´sci wyra·

zenia nieoznaczonego 0 1 : lim

x

!x

0

[p (x) q (x)] =

lim

x

!x

0

[p

0

(x) q

0

(x)] ; np. lim

x

!0+

(x

ctg x) = lim

x

!0+

1

1

sin

2

x

[ ! ] = 1

1

0+

=

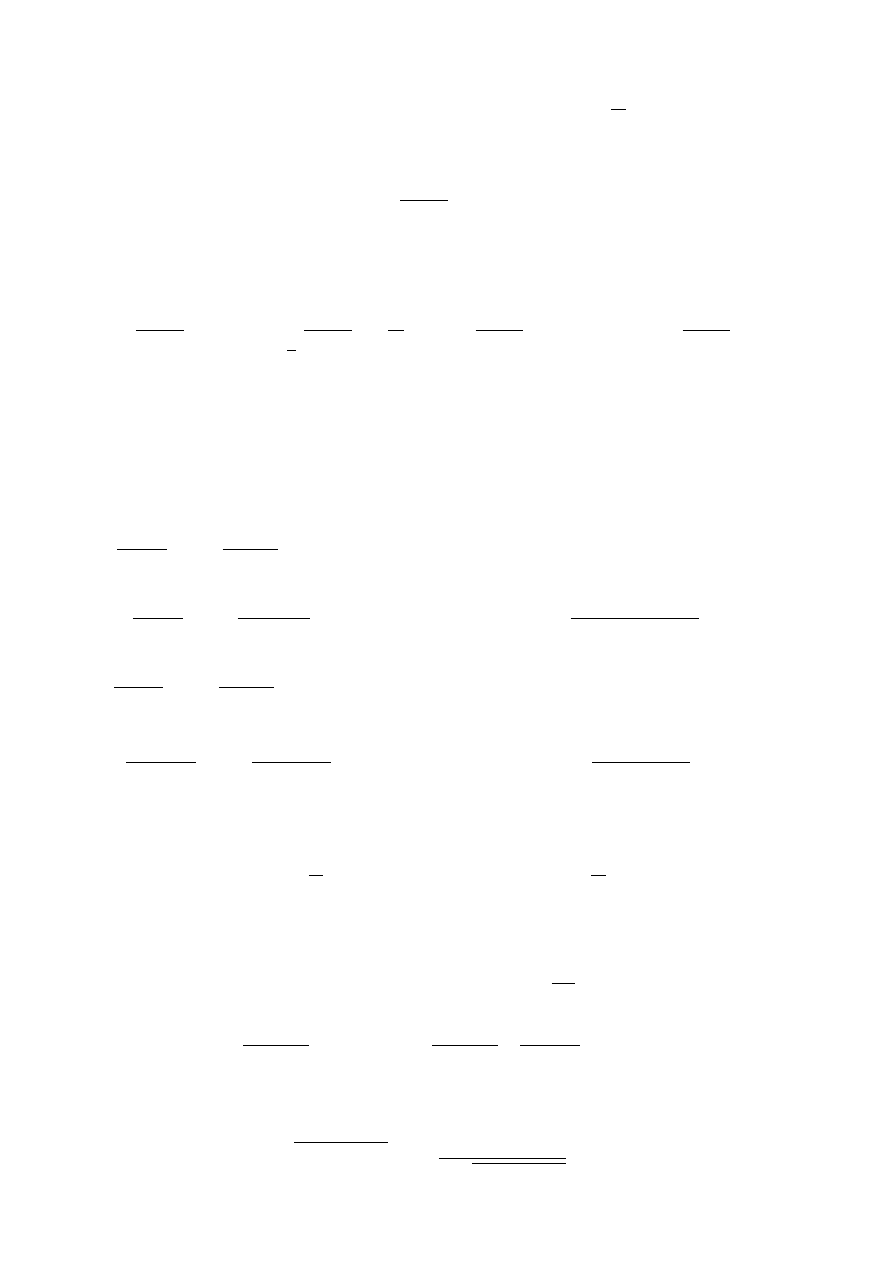
1 - poprawna warto´s´c 1 oraz do wyra·

zenia 1 1: lim

x

!x

0

[p (x)

q (x)] =

lim

x

!x

0

[p

0

(x)

q

0

(x)] ; np. lim

x

!1

(x

ln x) = lim

x

!1

1

1

x

[ ! ] = 1

0 = 1 -

poprawna warto´s´c 1:

j)

Dla studentów granica lim

x

!

sin x

x

zawsze równa si ¾

e 1; niezale·

znie od

symbolu wpisanego w ramk¾

e. W rzeczywisto´sci ta granica w punktach

ró·

znych od 0 ma inne warto´sci, np.

lim

x

!

sin x

x

= 0;

lim

x

!

2

sin x

x

=

2

; lim

x

!1

sin x

x

= sin 1;

lim

x

!1

sin x

x

= 0:

III. B÷¾

edne wzory do obliczania pochodnych

a) [

p (x) q (x)]

0

= p

0

(x) q

0

(x) ;

np. x

3

sin x

0

= 3x

2

cos x [ ! ] ; poprawny wynik 3x

2

sin x + x

3

cos x;

b)

p (x)
q (x)

0

=

p

0

(x)

q

0

(x)

;

np.

hcos x

e

x

i

0

=

sin x
e

x

[ ! ] ; poprawny wynik

sin x + cos x

e

x

;

c)

1

q (x)

0

=

1

q

0

(x)

;

np.

1

x

4

x

0

=

1

4x

3

1

[ ! ] ; poprawny wynik

4x

3

1

(x

4

x)

2

;

d)

ff [g (x)]g

0

= f

0

[g

0

(x)] ;

np. [sin (ln x)]

0

= cos

1

x

[ ! ] ; poprawny wynik

1

x

cos (ln x) ;

e) (9

x

)

0

= x 9

x 1

;

(arcsin x)

0

= arccos x;

(tg x)

0

= ctg x;

f ) (

x

x

)

0

= x

x

ln x;

e

7 0

= e

7

;

(ln 44)

0

=

1

44

;

5 0

= 5

4

;

g) (

arc tg x)

0

=

1

1 + x

2

(tg x)

0

=

1

1 + x

2

1

cos

2

x

;

h

jxj

3

i

0

= 3 jxj

2

:

h)

Studenci potra… ¾

a ró·

zniczkowa´c nie istniej ¾

ace funkcje, np. :

p

cos x

3

0

=

sin x

2

p

cos x

3

[ ! ] ;

arcsin 2 + x

2

0

=

2x

q

1

(2 + x

2

)

2

[ ! ] ;

h

ln 1

e

x

2

i

0

=

1

1

e

x

2

e

x

2

(2x) [ ! ] :

i)

Zadanie: dla f (x; y) =

p

x

4

+ y

4

zbada´c, czy istnieje

@f

@x

(0; 0) : Roz

-

wi ¾

azanie studenta:

@f

@x

(0; 0) =

"

4x

3

2

p

x

4

+ y

4

#

(0;0)

=

0
0

:

Otrzyma÷

em wyra

-

·

zenie nieoznaczone, wi ¾

ec

@f

@x

(0; 0) nie istnieje [ ! ] : Odp.

@f

@x

(0; 0) = 0:

IV. B÷¾

edne sposoby obliczania ca÷

ek nieoznaczonych

a)

Z

[f (x) g (x)] dx =

Z

f (x) dx

Z

g (x) dx;

np.

Z

x cos xdx =

x

2

2

sin x + C; poprawny wynik cos x + x sin x + C;

b)

Z

f (x)

g (x)

dx =

R

f (x) dx

R

g (x) dx

;

np.

Z

x

e

x

dx =

1
2

x

2

e

x

+ C [ ! ] ; poprawny wynik

(x + 1)

e

x

+ C;

c)

Z

p

n

(x) dx =

p

n+1

(x)

n + 1

+ C (n 2 N) ;

np.

Z

cos

3

xdx =

cos

4

x

4

+ C [ ! ] ; poprawny wynik x

sin

3

x

3

+ C;

d)

Z

dx

p (x)

= ln jp (x)j + C;

np.

Z

dx

e

x

+ 1

= ln je

x

+ 1j + C [ ! ] ; poprawny wynik x

ln (e

x

+ 1) + C;

e)

Z

e

p(x)

dx = e

p(x)

+ C;

np.

Z

e

p

x

dx = e

p

x

+ C [ ! ] ; poprawny wynik 2

p

x

1 e

p

x

+ C;

f )

Z

dx

1 + p

2

(x)

= arctg p (x) + C;

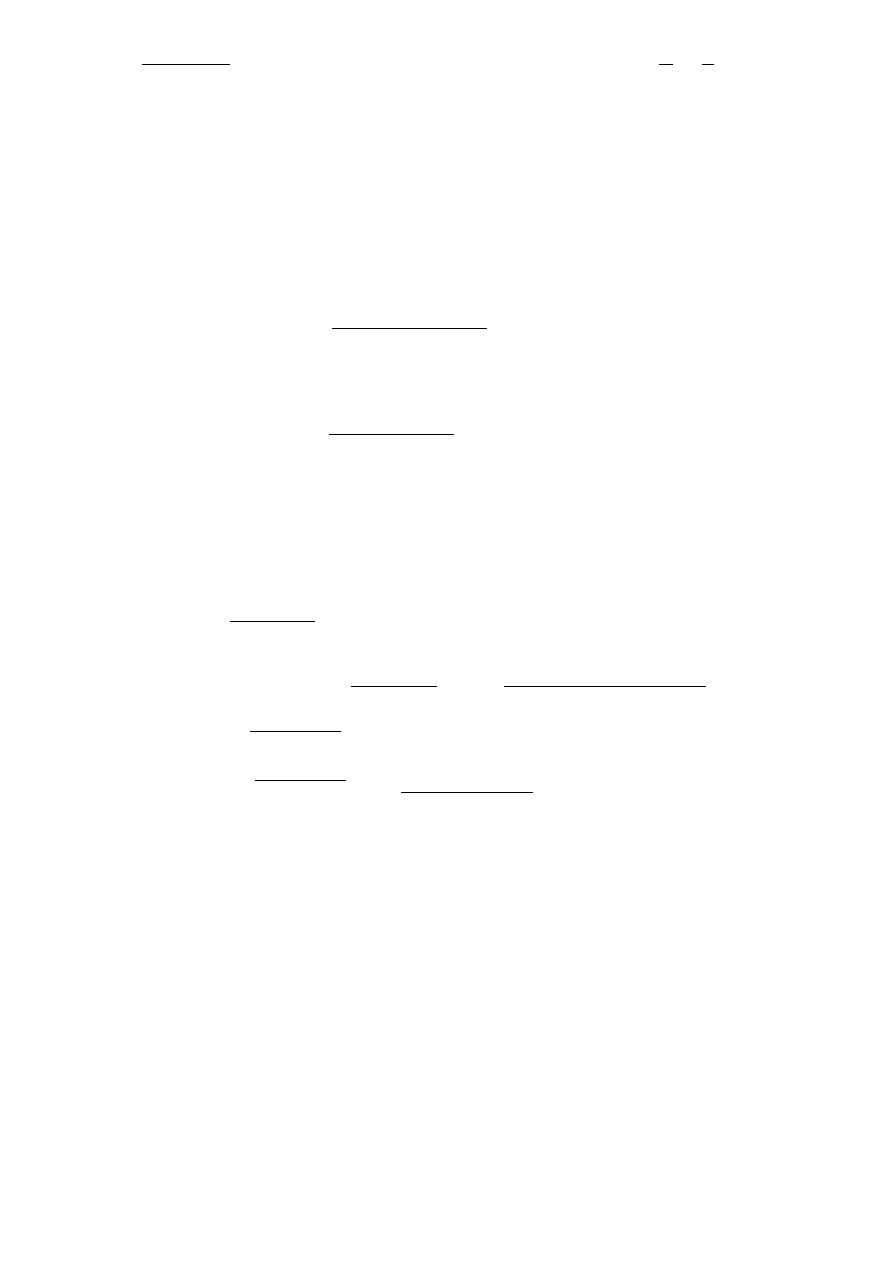
np.

Z

dx

1 + tg

2

x

= arctg (tg x) + C [ ! ] ; poprawny wynik

x

2

1
4

sin 2x + C:

V. Je·

zeli student mo·

ze utrudni´c sobie ·

zycie, to tak zrobi

a)

Rozwi ¾

aza´c równanie (x

1) (x

2) (x

3) (x

4) = 0: Metoda stu-

denta: po wymno·

zeniu czynników po lewej stronie równania otrzymam

x

4

10x

3

+ 35x

2

50x + 24 = 0 [ ! ] :

b)

Rozwi ¾

aza´c nierówno´s´c

(x

2) (x + 4)

(x + 1) (x

3)

< 0:

Rozwi ¾

azanie studenta: po

wyznaczeniu iloczynów w liczniku i mianowniku otrzymam nierówno´s´c

x

2

+ 2x

8

x

2

2x

3

< 0 [ ! ] :

c)

Obliczy´c

h

x

2

+ 3

4

i

0

:

Rozwi ¾

azanie studenta: po obliczeniu pot¾

egi

otrzymam

h

x

2

+ 3

4

i

0

= x

8

+ 12x

6

+ 54x

4

+ 108x

2

+ 81

0

[ ! ] :

d)

Obliczy´c

Z

dx

(x

2)

3

:

Rozwi ¾

azanie studenta: po podniesieniu mianow-

nika do sze´scianu dostan¾

e

Z

dx

(x

2)

3

=

Z

dx

x

3

6x

2

+ 12x

8

[ ! ] :

e)

Wyznaczy´c

4

q

(3

2i)

4

:

Rozwi ¾

azanie studenta: po obliczeniu czwartej

pot¾

egi otrzymam

4

q

(3

2i)

4

=

4

p

119

120i [ ! ] :

f )

Obliczy´c det

0

B

@

2

4

1 2 3
2 5 4
1 3 2

3

5

1

1

C

A : Rozwi ¾

azanie studenta: po wyznacze-

niu macierzy odwrotnej otrzymam

det

0

B

@

2

4

1 2 3
2 5 4
1 3 2

3

5

1

1

C

A = det

0

@

2

4

2

5

7

0

1

2

1

1

1

3

5 [ ! ]

1

A = 1:

g)

Obliczy´c det

2 3
1 2

5

!

:

Rozwi ¾

azanie studenta: po obliczeniu pi ¾

atej

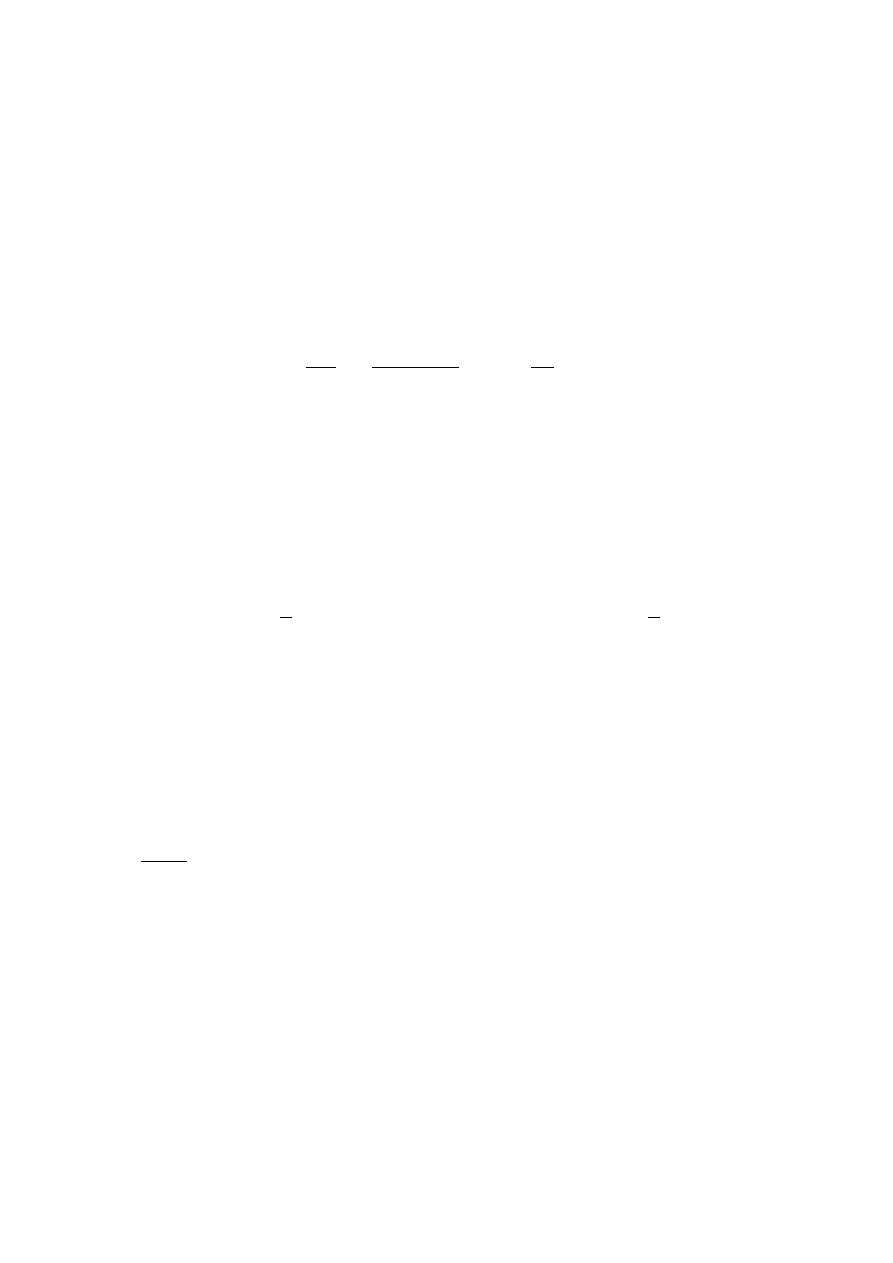
pot¾

egi macierzy otrzymam

det

2 3
1 2

5

!

= det

362 627
209 362

[ ! ]

= 1:

h)

Znale´z´c wszystkie rozwi ¾

azania równania (z + 2i)

6

+ (z

1)

6

= 0: Roz-

wi ¾

azanie studenta: po wykonaniu dzia÷

a´n otrzymam równanie równowa·

zne

2z

6

(6

12i) z

5

45z

4

(20 + 160i) z

3

+ 255z

2

(6

192i) z

63 = 0 [ ! ] :

i)

Student napisa÷

: po obliczeniu silni otrzymam:

8!

10!

=

40 320

3628 800

[ ! ] =

1

90

:

VI. B÷¾

edne de…nicje, fa÷

szywe twierdzenia, ciekawe sformu÷

owa-

nia, dziwne rozumowania oraz zaskakuj ¾

ace wnioski

a)

Fragment rozwi ¾

azania zadania z rachunku prawdopodobie´nstwa o

wyst ¾

epowaniu daltonizmu w´sród m¾

e·

zczyzn i kobiet: wyznacz¾

e liczb ¾

e m¾

e·

z-

czyzn, którzy nie rozró·

zniaj ¾

a

kobiet.

b)

Poniewa·

z ca÷

y okr ¾

ag ma równanie x

2

+y

2

= r

2

;

wi ¾

ec jego dolna po÷

owa

jest opisana wzorem

1
2

x

2

+ y

2

= r

2

;

a górna wzorem

1
2

x

2

+ y

2

= r

2

:

c)

Je·

zeli twierdzenie T

n

okre´slone dla n liczb naturalnych jest prawdziwe

dla n + 1 liczb i zachodzi implikacja T

n

=) T

n+1

;

to mamy do czynienia z

zasad ¾

a indukcji matematycznej.

d)

Granica lim

x

!0

f (x)

nie istnieje. Zatem w punkcie x = 0 funkcja f nie

mo·

ze by´c ju·

z nigdy ci ¾

ag÷

a i dobrze jej tak!

e)

Ci ¾

ag ( 1)

n

raz d ¾

a·

zy do +1; a raz do

1; wobec tego zachodzi

stosunek

+1

1

:

f )

Móg÷

bym policzy´c pochodn ¾

a, ale nie ka·

z ¾

a.

g)

Funkcja f jest monotoniczna w przedziale (a; b); gdy wszystkie punkty

z tego przedzia÷

u daj ¾

a si ¾

e po÷¾

aczy´c prost ¾

a lub krzyw ¾

a.

h)

Bez linijki i gumki nie potra…¾

e narysowa´c wykresu tej funkcji.

i)

Monotoniczno´s´c funkcji f okre´sl ¾

e na podstawie znaku ró·

znicy

f (x + 1)

f (x) :

j)

Z powodu braku czasu dalsz ¾

a cz¾

e´s´c rozwi ¾

azania przeprowadz¾

e w formie

kontemplacji.

k)

Granica ci ¾

agu jest to ostatnia liczba ze zbioru liczb nale·

z ¾

acych do tego

ci ¾

agu.

l)

Zachodzi wzór lim

n

!1

(a

n

b

n

) = lim

n

!1

a

n

+ lim

n

!1

b

n

;

bo logarytm iloczynu

równa si ¾

e sumie logarytmów.

m)

Po pomno·

zeniu obu stron równania przez x otrzymam:

1

sin x

+

1

cos x

= 1 ()

1

sin

+

1

cos

= x:

n)

Prawdziwa jest równowa·

zno´s´c tg x < 1 () x <

4

+ k

(k 2 Z) :

o)

Nierówno´s´c wyk÷

adnicza jest ró·

zniczkowalna, wi ¾

ec mo·

zemy opu´sci´c

podstawy.

p)

Po podzieleniu obu stron równania ctg x = 3 tg x przez tg x otrzy-

mamy, ·

ze sta÷

a c równa si ¾

e 3:

q)

Dla ka·

zdego x > 0 funkcje f; g; h spe÷

niaj ¾

a nierówno´sci

f (x)

6 g (x) 6 h (x) ; ale lim

x

!1

f (x)

6= lim

x

!1

h (x) :

Zatem granica lim

x

!1

g (x)

nie istnieje.

r)

Zak÷

adam, ·

ze to·

zsamo´s´c jest prawdziwa dla ka·

zdego n = 1:

s)

Zadanie rozwi ¾

a·

z¾

e metod ¾

a spekulacji.

t)

Wyobra´zmy sobie sze´scian, który ma sze´s´c tysi ¾

ecy ´scian.

u)

Granic ¾

a ci ¾

agu nazywamy warto´s´c, jak ¾

a osi ¾

aga funkcja przy d ¾

a·

zeniu do

ko´nca przedzia÷

u.

v)

Z niemo·

zliwo´sci matematycznego rozwi ¾

azania pos÷

u·

zy÷

am si ¾

e logik ¾

a.

w)

Niech zdarzenie A oznacza, ·

ze czerwony tramwaj jedzie z prawej

strony. Wtedy zdarzenie przeciwne do A oznacza, ·

ze niebieski tramwaj

jedzie z przeciwnej strony.

x)

Prawie wszystkie oznacza wszystkie, oprócz tych co nie nale·

z ¾

a.

y)

W ten sposób pokaza÷

em rodzicom, ·

ze nie nadaj ¾

e si ¾

e na studia.

z)

Zachodzi tutaj zjawisko indukcji matematycznej.

A)

Sam si ¾

e dziwi ¾

e, jak zda÷

em matur¾

e.

B)

Istnieje twierdzenie, niepotrzebne w zadaniu, które brzmi ... .

C)

Prawdopodobie´nstwo zdarzenia wynosi 1000! 999! 998! : : : 1!:

D)

Rozumowania w rozwi ¾

azaniach zadania dotycz ¾

acego wieku trzech

braci. „W celu skorzystania z ostatniej informacji w zadaniu dodatkowo
wprowadzam czwartego brata”. Inny zadaj ¾

acy otrzyma÷ujemny wiek braci,

jednak nie straci÷g÷

owy i napisa÷

: „Najstarszy brat urodzi si ¾

e za 6 lat, ´sredni

za 9 lat, a najm÷

odszy za 12 lat”.

E)

Uk÷

ad równa´n jest nie do rozwi ¾

azania.

F)

Pochodn ¾

a nazywamy granic¾

e okresów ilorazowych.

G)

W trójk ¾

acie jeden k ¾

at ma 135

0

;

drugi ma tak·

ze 135

0

;

a trzeci - 90

0

:

Poniewa·

z suma k ¾

atów w tym trójk ¾

acie równa si ¾

e 360

0

;

wi ¾

ec taki trójk ¾

at nie

istnieje.

H)

Go÷

ym okiem wida´c, ·

ze funkcja f (x) =

p

2x

1 jest ´sci´sle rosn ¾

aca.

I)

Zadanie jest tak proste, ·

ze nie ma co rozwi ¾

azywa´c.

J)

Oczywi´scie w praktyce wybiera si ¾

e du·

zo mniejsze " ni·

z na rysunku.

K)

Zak÷

adamy, ·

ze nierówno´s´c jest prawdziwa dla dowolnej liczby natu-

ralnej n: Poka·

zemy, ·

ze jest ona prawdziwa tak·

ze dla liczby n + 1:

L)

Proste l

1

i l

2

s ¾

a prostopad÷

e, gdy s ¾

a w stosunku.

Z prac egzaminacyjnych wybra÷

: Zbigniew Skoczylas