1.

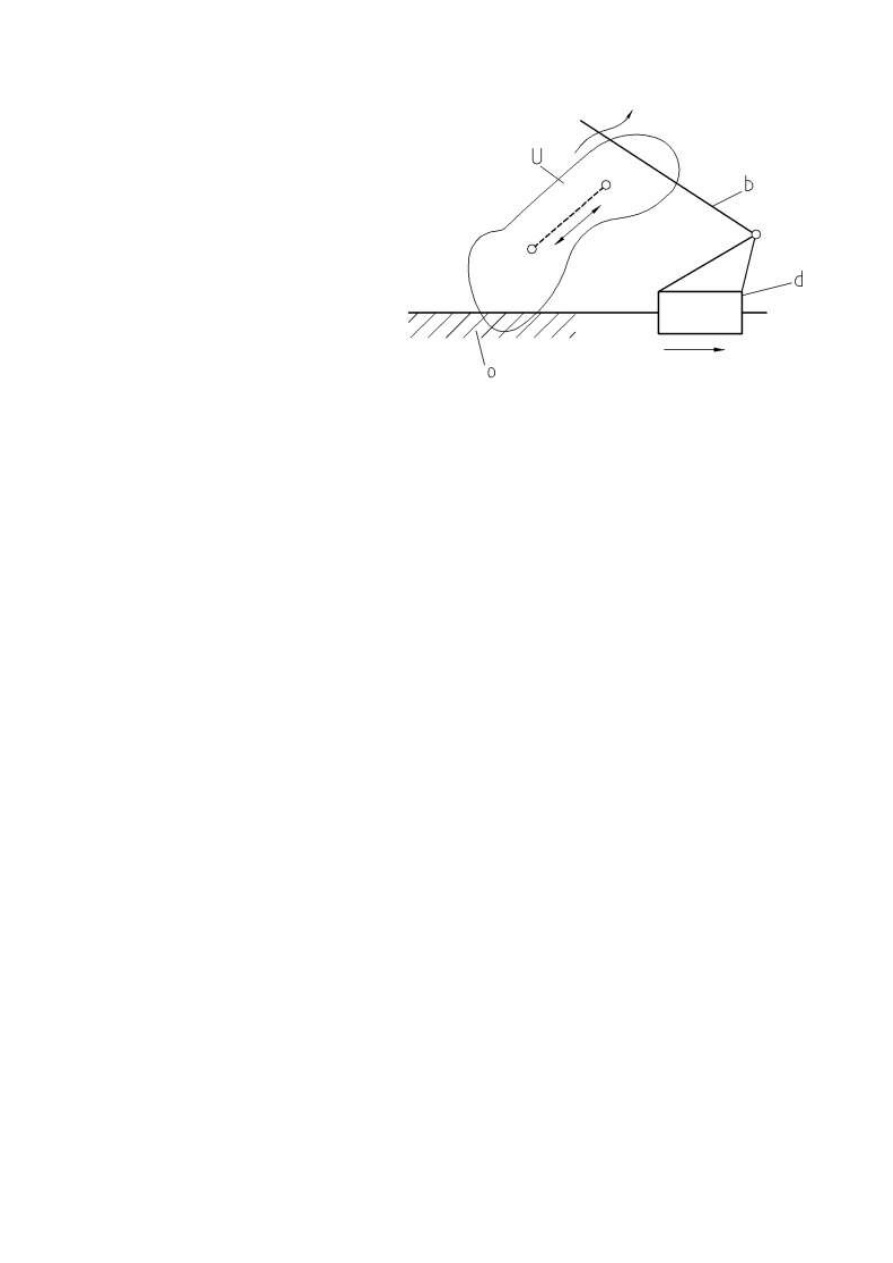
Treść zadania

Zmiana długości

siłownika powinna

wywoływać jednoznaczny ruch członu
biernego

przy

wykorzystaniu

odpowiedniego łańcucha pośredniczącego.
Należy:
•

wyprowadzić równanie strukturalne

łańcucha dla p

2

< 2, 1 < k ≤ 3,

•

sporządzić

tabelę

struktur

mechanizmu,
•

jedną strukturę (z parą II klasy)

przedstawić

w

postaci

schematów

kinematycznych

1.

Równanie strukturalne łańcucha pośredniczącego

Ruchliwość teoretyczna układu pośredniczącego wynosi:

W

t

= W

c

+ W

b

+ W

U

gdzie:
W

t

– ruchliwość teoretyczna; ustalonej długości siłownika układ ma być w jednoznacznym

położeniu, zatem W

t

= 0,

W

c

– ruchliwość członów czynnych; ze względu na brak członów czynnych poza łańcuchem

pośredniczącym W

c

= 0,

W

b

– ruchliwość członu biernego, z rysunku można zauważyć że może on wykonywać dwa

rodzaje ruchu (posuw w jednym kierunku oraz obrót), zatem W

b

= 2

W

U

– ruchliwość łańcucha pośredniczącego U,

W

U

= W

t

– W

c

– W

b

W

U

= 0 – 0 – 2 = –2

Jednocześnie:

W

U

= 3(n-1) – 2p

1

– 1p

2

gdzie:
n – liczba członów łańcucha U,
p

1

– liczba par pierwszej klasy,

p

2

– liczba par drugiej klasy,

k = n-1

W

U

= 3k – 2p

1

– 1p

2

Otrzymujemy zatem równanie łańcucha:

3k – W

U

= 2p

1

+ 1p

2

2.

Tabela struktur łańcucha pośredniczącego

Tabelę z możliwymi strukturami wyznaczamy na podstawie równania strukturalnego, które dla
naszego łańcucha przyjmuje postać:

3k + 2 = 2p

1

+ 1p

2

Z treści zadania wynikają również ograniczenia:

p

2

< 2

1 < k ≤ 3

oraz w łańcuchu występuje siłownik, który jest połączony parami pierwszej klasy, zatem:

p

1

≥ 2

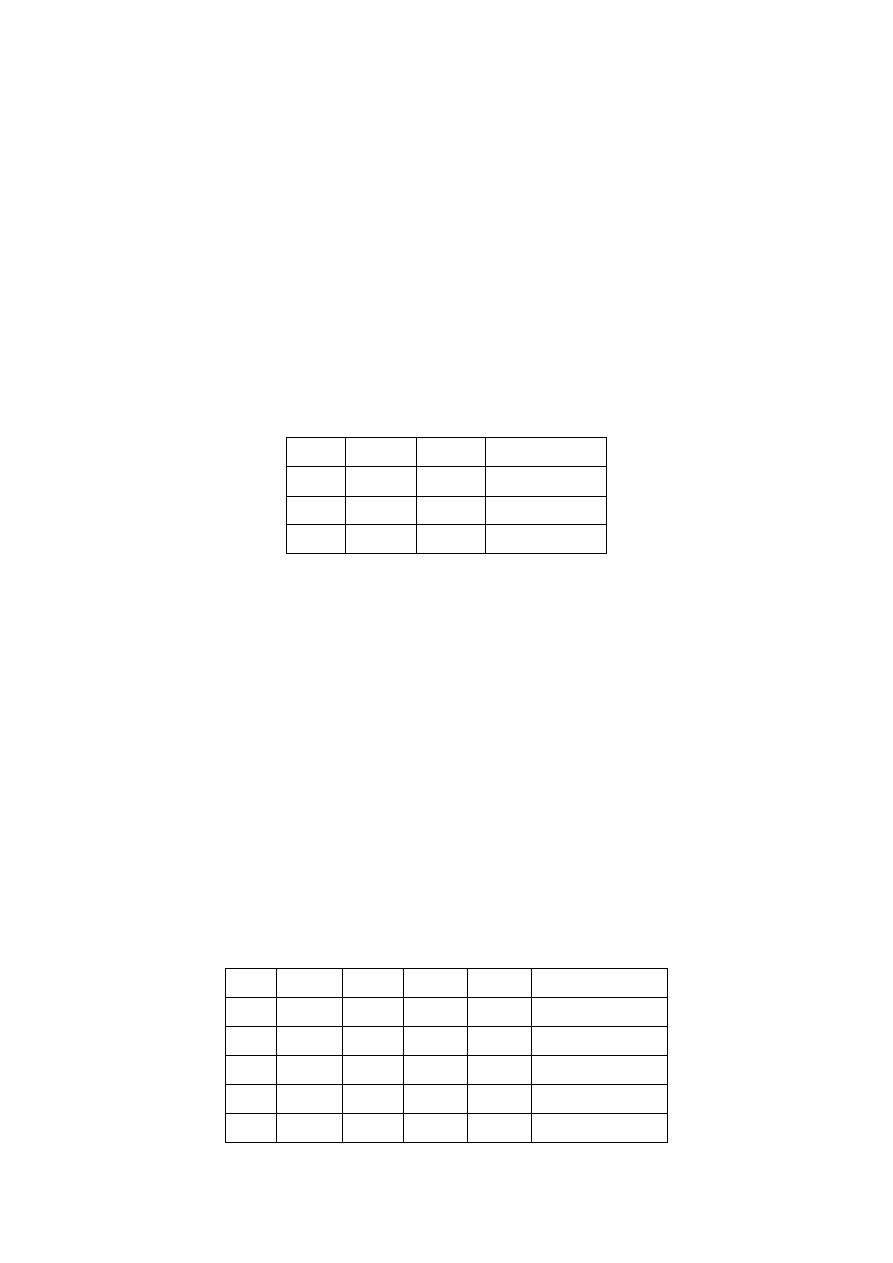
Tabela struktur łańcucha wygląda zatem następująco:

k

p

1

p

2

k.p

1

.p

2

1

2

1

1.2.1

2

4

0

2.4.0

3

5

1

3.5.1

3.

Struktury zamkniętego łańcucha

Założono, że w łańcuchu w członie mogą być maksymalnie 4 węzły. W łańcuchu muszą zachodzić
następujące równości:

k + 1 = n

2

+ n

3

+ n

4

2(p

1

+ p

2

) = 2n

2

+ 3n

3

+4n

4

gdzie:
n

2

– ilość członów dwuwęzłowych,

n

3

– ilość członów trójwęzłowych,

n

4

– ilość członów czterowęzłowych,

Na rozwiązanie nałożono ograniczenie ze względu na występujący w łańcuchu siłownik:

n

2

≥ 1

Tabela rozwiązań układu wygląda zatem następująco:

Lp.

k+1

n

2

n

3

n

4

k.p

1

.p

2

-n

2

.n

3

.n

4

1

1+1

1

0

1

1.2.1-1.0.1

2

2+1

1

2

0

2.4.0-1.2.0

3

2+1

2

0

1

2.4.0-2.0.1

4

3+1

1

2

1

3.5.1-1.2.1

5

3+1

2

0

2

3.5.1-2.0.2

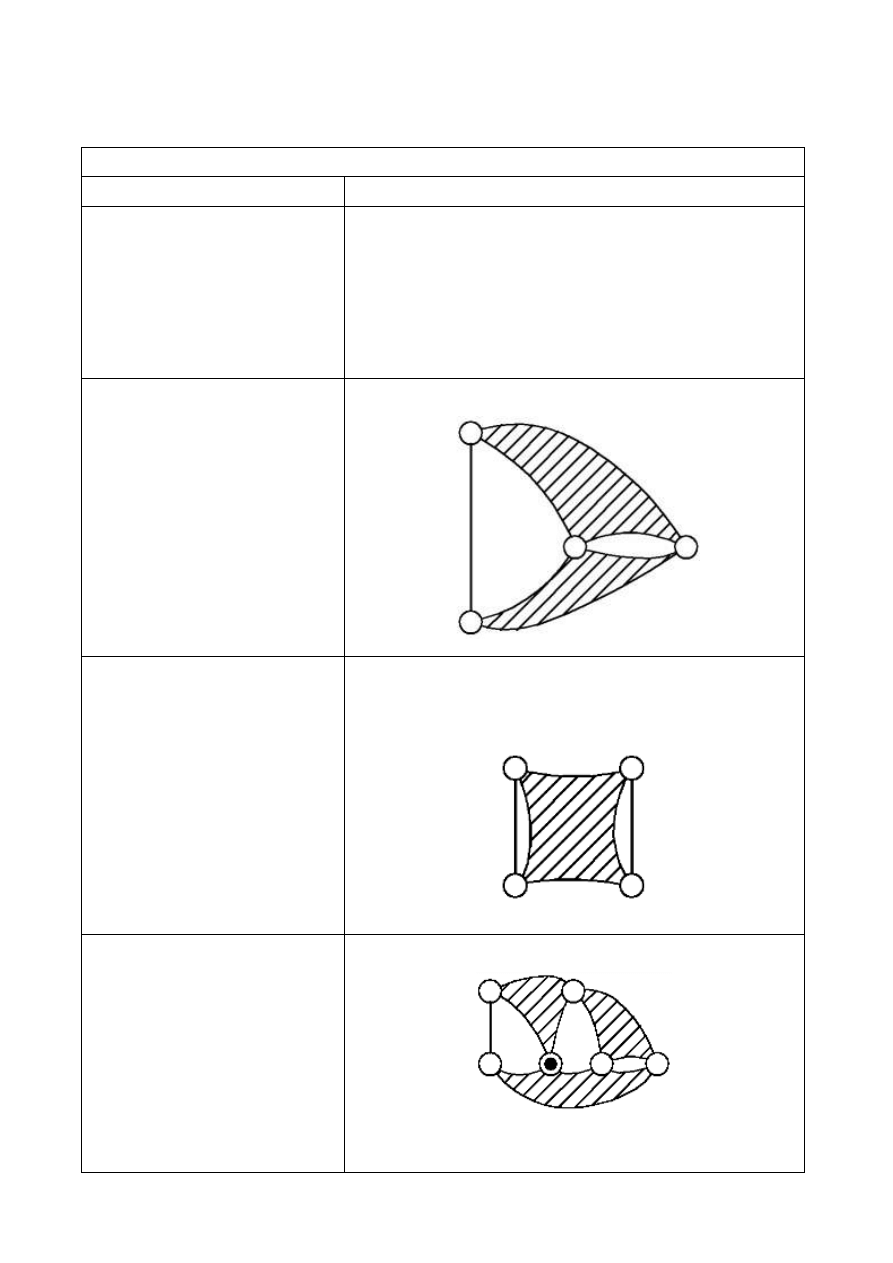
Tabela macierzy połączeń i schematów strukturalnych zamkniętych łańcuchów:

Łańcuchy zamknięte

Symbol i macierz połączeń

Schemat strukturalny łańcucha

1.2.1-1.0.1

𝑁

2

𝑁

4

𝐴

1

= [

0

𝑥

1

𝑥

1

0 ]

𝑁

2

𝑁

4

x

1

= 2

x

1

= 4

Sprzeczność

2.4.0-1.2.0

𝑁

2

𝑁

3

(1)

𝑁

3

(2)

𝐴

2

= [

0

𝑥

1

𝑥

2

𝑥

1

0

𝑥

3

𝑥

2

𝑥

3

0

]

𝑁

2

𝑁

3

(1)

𝑁

3

(2)

x

1

+ x

2

= 2

x

1

+ x

3

= 3

x

2

+ x

3

= 3

x

1

= 1, x

2

= 1, x

3

= 2

2.4.0-1.2.0

2.4.0-2.0.1

𝑁

2

(1)

𝑁

2

(2)

𝑁

4

𝐴

3

= [

0

𝑥

1

𝑥

2

𝑥

1

0

𝑥

3

𝑥

2

𝑥

3

0

]

𝑁

2

(1)

𝑁

2

(2)

𝑁

4

x

1

+ x

2

= 2

x

1

+ x

3

= 2

x

2

+ x

3

= 4

x

1

= 0, x

2

= 2, x

3

= 2

2.4.0-2.0.1

3.5.1-1.2.1

𝑁

2

𝑁

3

(1)

𝑁

3

(2)

𝑁

4

𝐴

4

= [

0

𝑥

1

𝑥

2

𝑥

3

𝑥

1

0

𝑥

4

𝑥

5

𝑥

2

𝑥

4

0

𝑥

6

𝑥

3

𝑥

5

𝑥

6

0

]

𝑁

2

𝑁

3

(1)

𝑁

3

(2)

𝑁

4

x

1

+ x

2

+ x

3

= 2

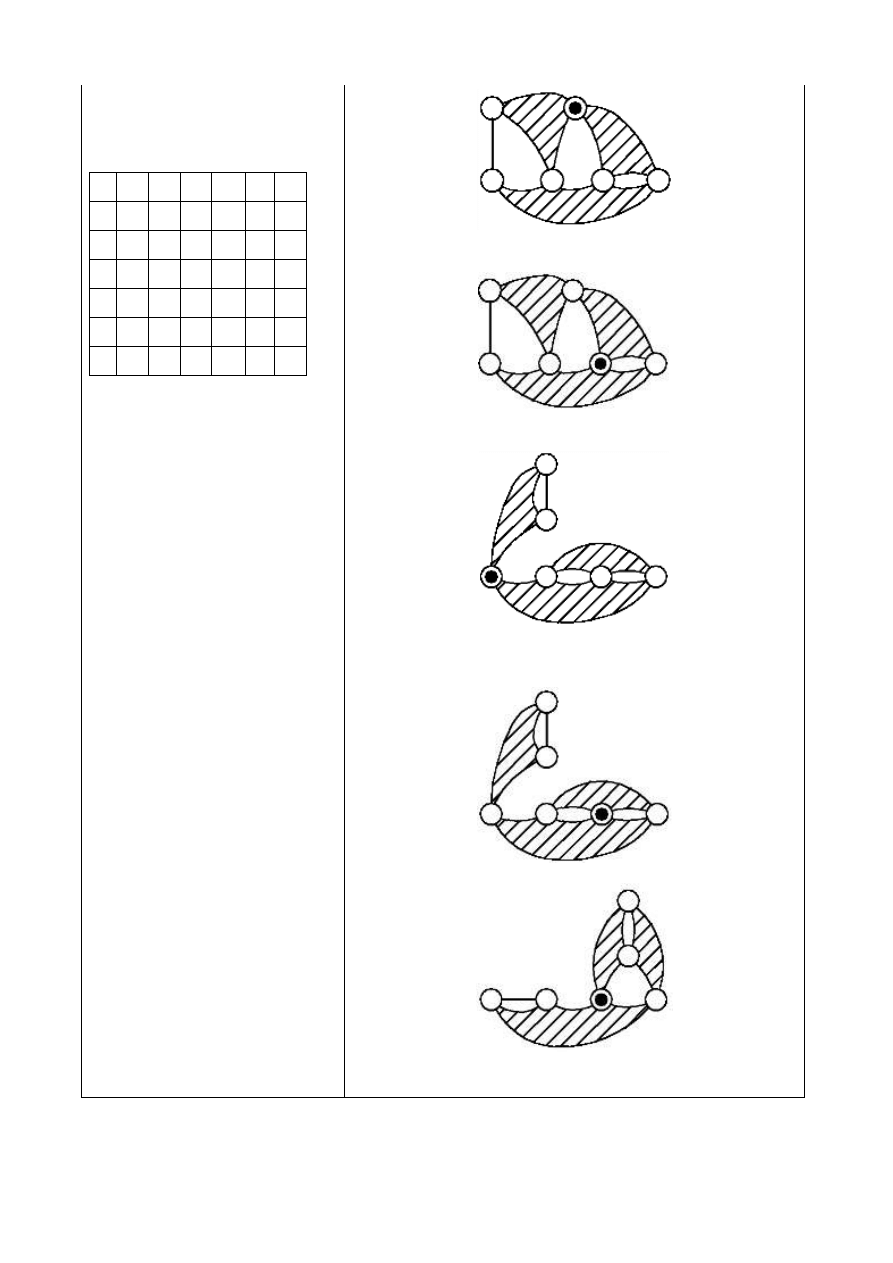
3.5.1-1.2.1-A1

3.5.1-1.2.1-A2

x

1

+ x

4

+ x

5

= 3

x

2

+ x

4

+ x

6

= 3

x

3

+ x

5

+ x

6

= 4

A B C D E F

x

1

0

0

0

1

1

2

x

2

1

2

0

1

0

0

x

3

1

0

2

0

1

0

x

4

1

0

2

0

1

0

x

5

2

3

1

2

1

1

x

6

1

1

1

2

2

3

Wyniki A i E oraz B i F dają

identyczne schematy strukturalne

3.5.1-1.2.1-A3

3.5.1-1.2.1-B1

3.5.1-1.2.1-B2

3.5.1-1.2.1-C1

3.5.1-1.2.1-C2

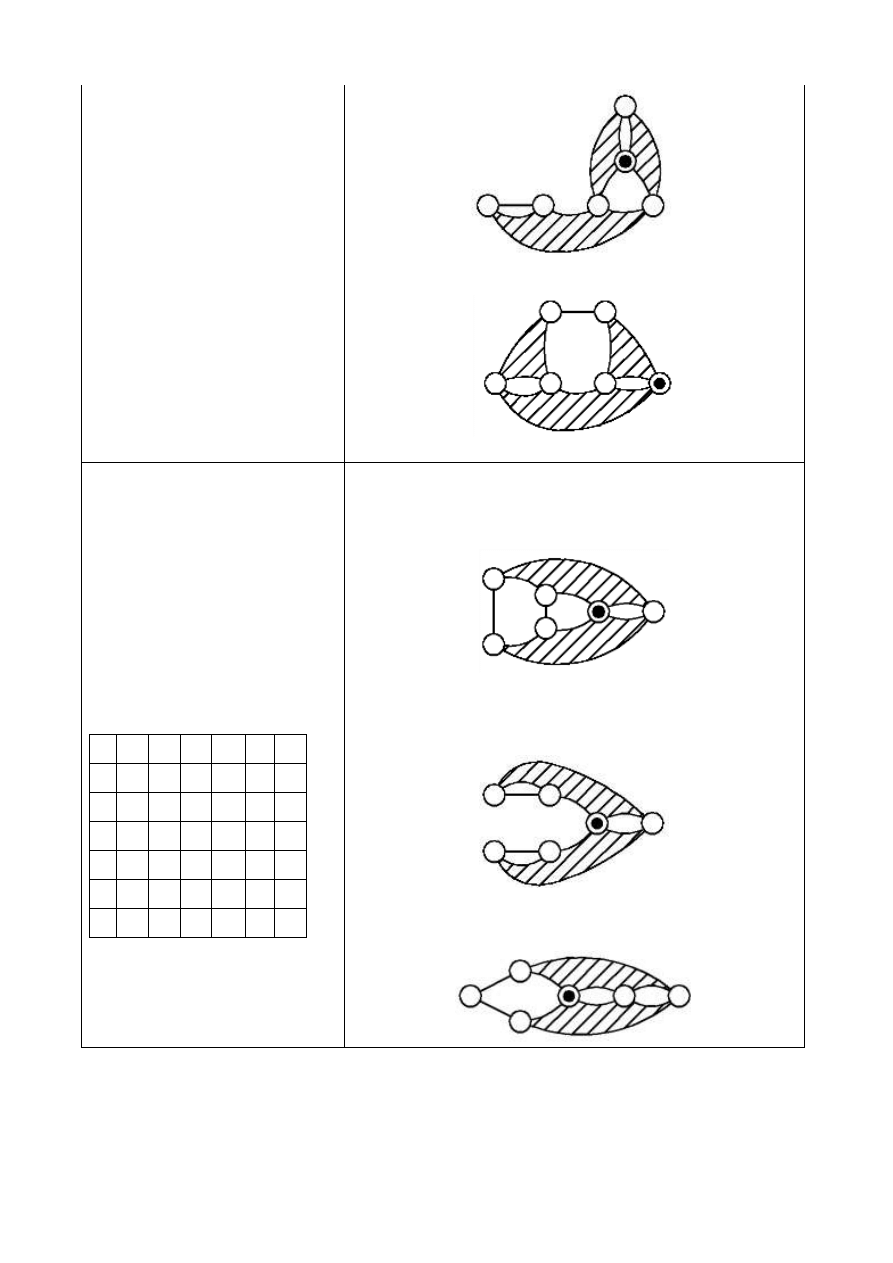
3.5.1-1.2.1-D

.5.1-2.0.2

𝑁

2

(1)

𝑁

2

(2)

𝑁

4

(1)

𝑁

4

(2)

𝐴

5

= [

0

𝑥

1

𝑥

2

𝑥

3

𝑥

1

0

𝑥

4

𝑥

5

𝑥

2

𝑥

4

0

𝑥

6

𝑥

3

𝑥

5

𝑥

6

0

]

𝑁

2

(1)

𝑁

2

(2)

𝑁

4

(1)

𝑁

4

(2)

x

1

+ x

2

+ x

3

= 2

x

1

+ x

4

+ x

5

= 2

x

2

+ x

4

+ x

6

= 4

x

3

+ x

5

+ x

6

= 4

A B C D E F

x

1

0

0

0

1

1

2

x

2

1

2

0

1

0

0

x

3

1

0

2

0

1

0

x

4

1

0

2

0

1

0

x

5

1

2

0

1

0

0

x

6

2

2

2

3

3

4

Wyniki B i C oraz D i E dają

identyczne schematy strukturalne.

Wynik F daje dwa łańcuchy, zatem

go odrzucamy

3.5.1-2.0.2-A

3.5.1-2.0.2-B

3.5.1-2.0.2-D

4.

Struktury otwartego łańcucha

Otwieramy łańcuchy zamknięte poprzez usunięcie jednego z członów w taki sposób aby wszystkie

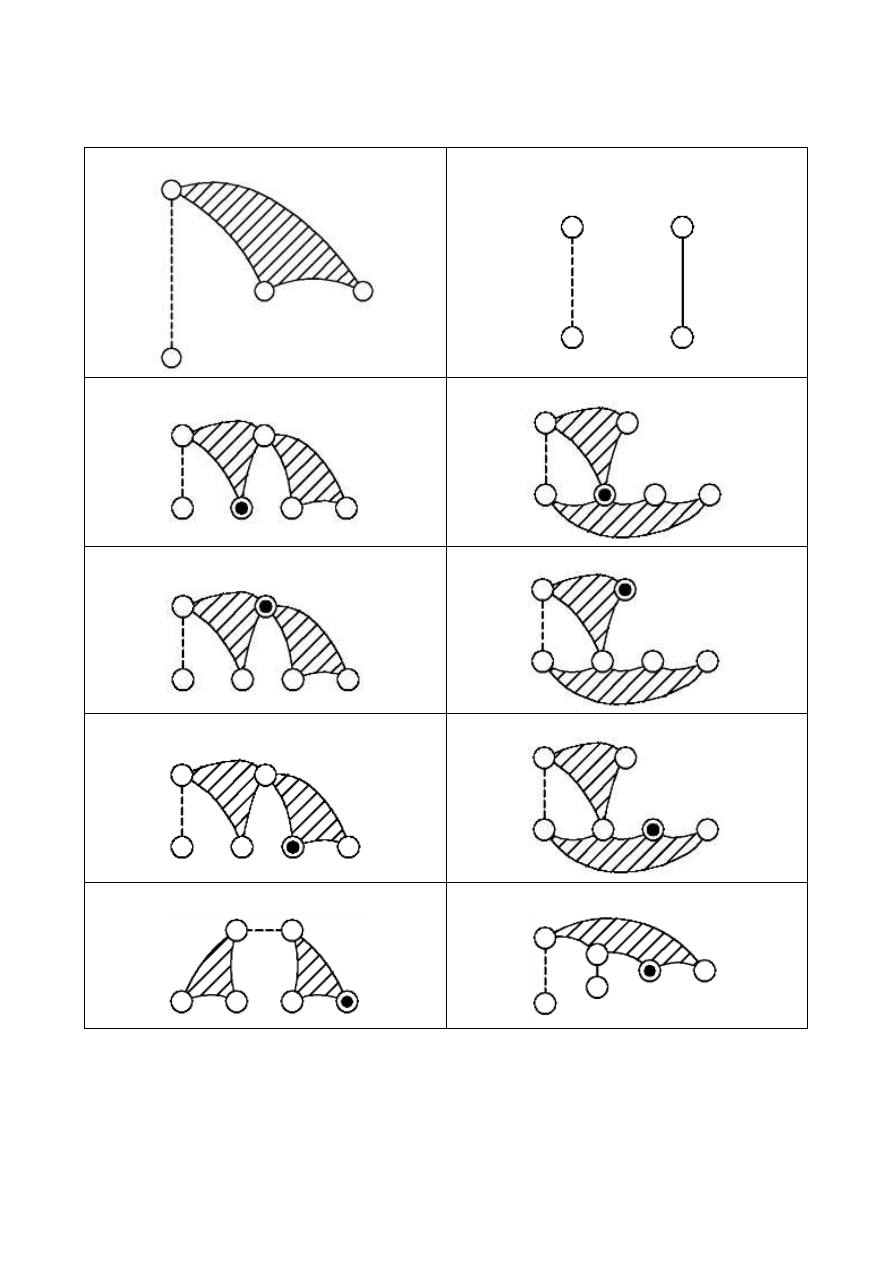
kontury o ruchliwości nie większej od zera zostały otwarte oraz łańcuch musi posiadać jeden człon
dwuwęzłowy, który zastąpimy siłownikiem.

2.4.0-1.2.0

2.4.0-2.0.1

3.5.1-1.2.1-A1-1

3.5.1-1.2.1-A1-2

3.5.1-1.2.1-A2-1

3.5.1-1.2.1-A2-2

3.5.1-1.2.1-A3-1

3.5.1-1.2.1-A3-2

3.5.1-1.2.1-D

3.5.1-2.0.2-A

5.

Tabela schematów podstawowych

Łańcuchy zostały podłączone do układu z zadania:

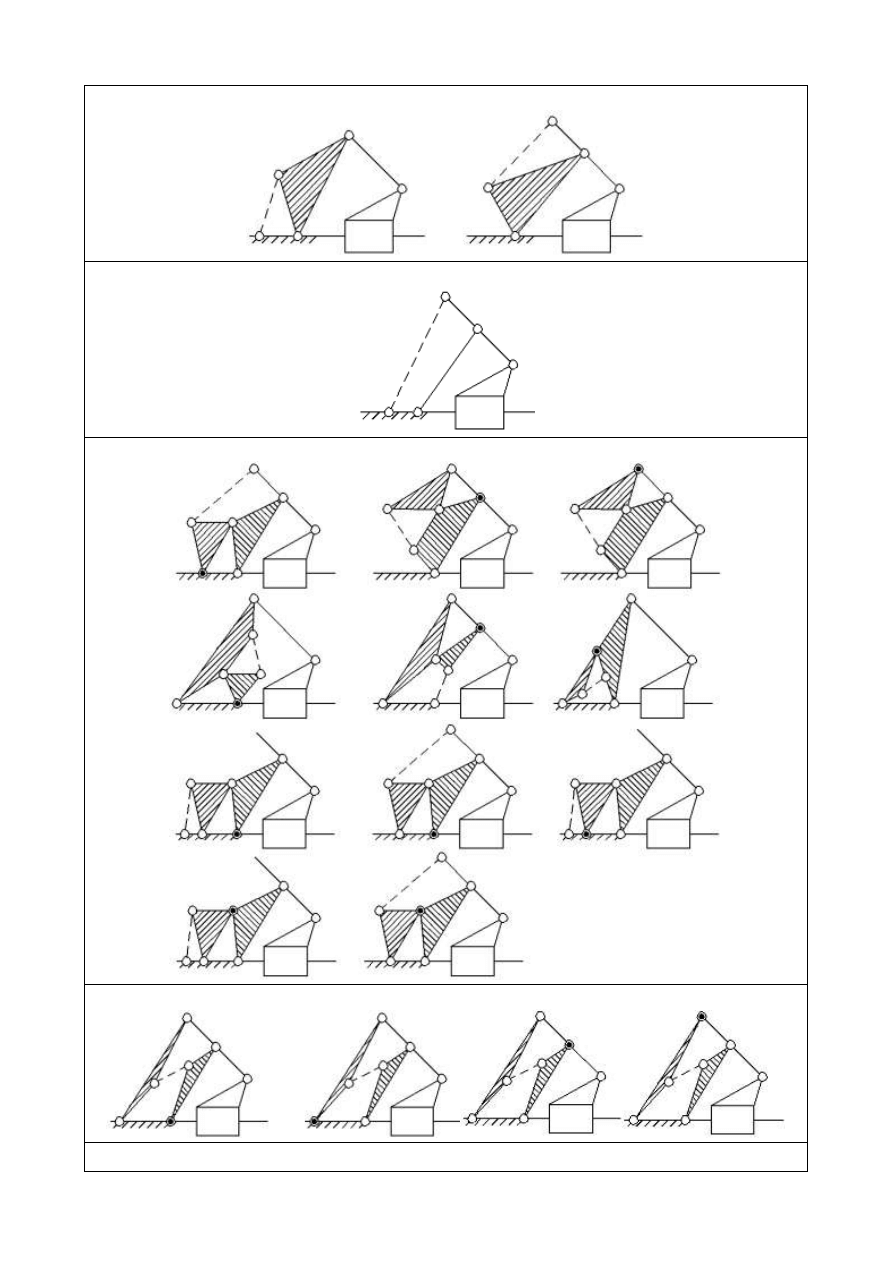
2.4.0-1.2.0

2.4.0-2.0.1

3.5.1-1.2.1-A

3.5.1-1.2.1-D

3.5.1-2.0.2-A

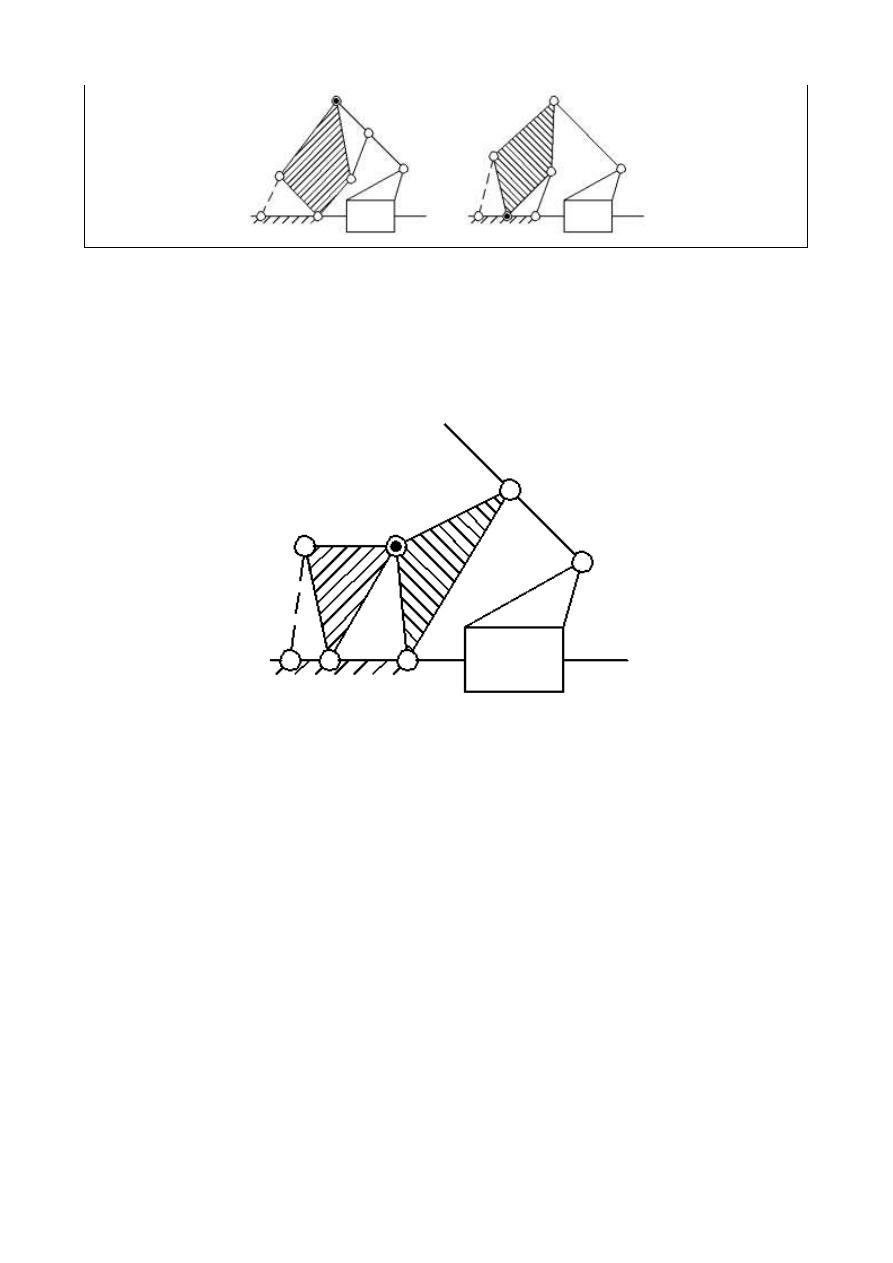
6.

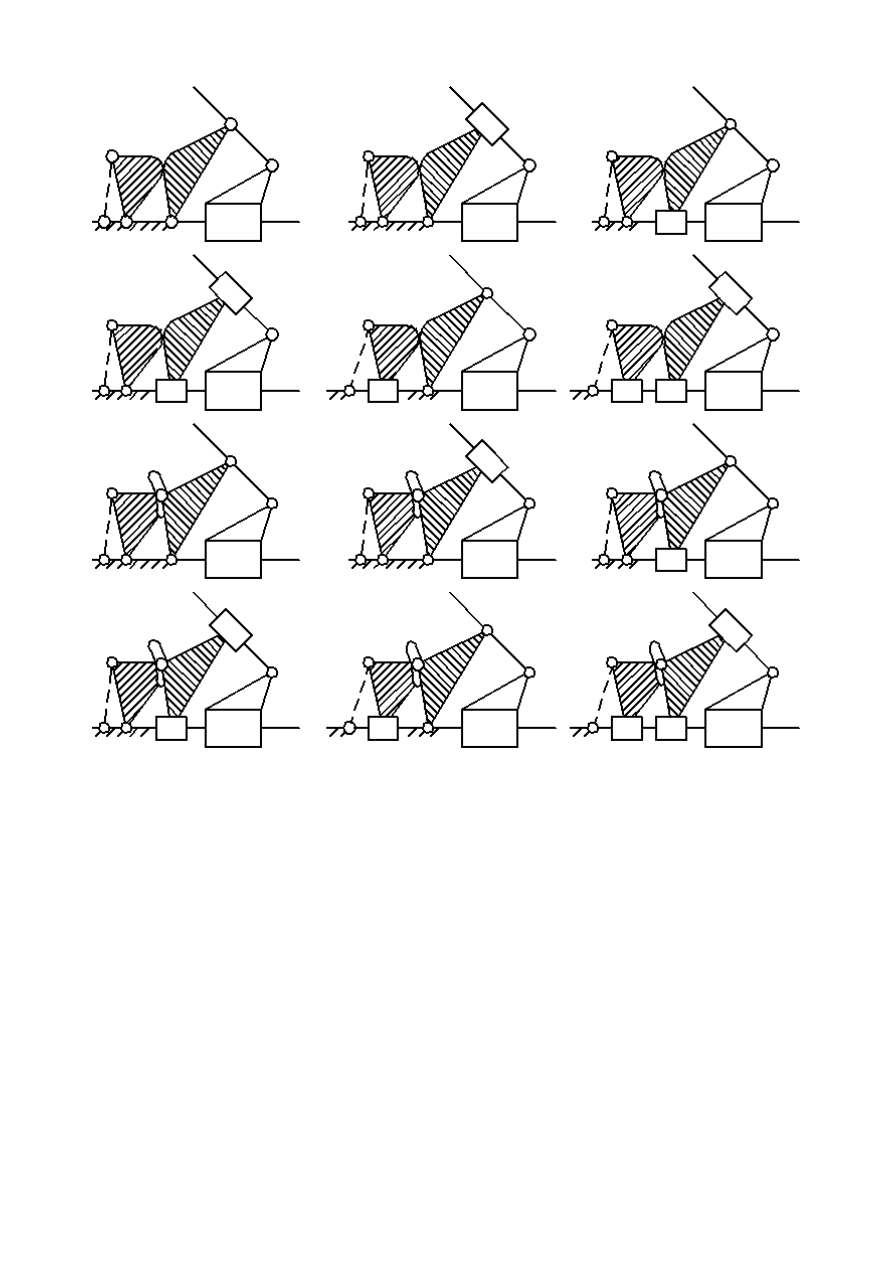
Schematy kinematyczne

Wybrany schemat podstawowy:

Przykładowe schematy kinematyczne dla wybranej struktury podstawowej: