1 

 

1. Niech 

Ω = [0, 1], 𝑃 = 𝜇

𝐿

, 

ℱ = ℬ([0, 1]). Połóżmy 𝑋

𝑛

(𝜔) = {

𝑒

𝑛

, 0 ≤ 𝜔 ≤

1

𝑛

,

0,

1

𝑛

< 𝜔 ≤ 1.

 

a) Czy 

𝑋

𝑛

  𝑃  

→  0, gdy 𝑛 → ∞? 

b) Czy 

𝑋

𝑛

𝑝.𝑝.

→  0, gdy 𝑛 → ∞? 

c) Czy 

𝑋

𝑛

 𝐿

𝑝

 

→  0, gdy 𝑛 → ∞? 

d) Czy 

𝑋

𝑛

⟹ 0, gdy 𝑛 → ∞? 

Rozwiązanie: 

(a) Sprawdzimy, czy 

𝑋

𝑛

  𝑃  

→  0, gdy 𝑛 → ∞? 

Przypomnijmy, że 

𝑋

𝑛

  𝑃  

→  𝑋 ⇔ ⋀ lim

𝑛→∞

𝑃(|𝑋

𝑛

− 𝑋| >  𝜀) = 0.

𝜀>0

 

Zauważmy, że 

⋀ lim

𝑛→∞

𝑃(|𝑋

𝑛

− 0| >  𝜀) =

𝜀>0

lim

𝑛→∞

𝑃(𝑋

𝑛

>  𝜀) ≤   lim

𝑛→∞

𝑃(𝑋

𝑛

= 𝑒

𝑛

) = lim

𝑛→∞

1

𝑛

= 0. 

Stąd 𝑋

𝑛

  𝑃  

→  0, gdy 𝑛 → ∞. 

(b) Sprawdzimy, czy 

𝑋

𝑛

𝑝.𝑝.

→  0, gdy 𝑛 → ∞? 

Skorzystamy z warunku, że 

𝑋

𝑛

𝑝.𝑝.

→  𝑋 ⇔ ⋀ lim

𝑁→∞

𝑃 (⋂{|𝑋

𝑛

− 𝑋| ≤  𝜀}

∞

𝑛=𝑁

)

𝜀>0

= 1 

Zauważmy, że dla 𝜀 > 0 i dostatecznie dużych 𝑁 mamy 

𝑃 (⋂{|𝑋

𝑛

− 0| ≤  𝜀}

∞

𝑛=𝑁

) = 𝑃 (⋂{𝑋

𝑛

= 0}

∞

𝑛=𝑁

) = 𝑃 (⋂ [

1

𝑛

, 1]

∞

𝑛=𝑁

) = 𝑃 ([

1

𝑁

, 1]) = 1 −

1

𝑁

. 

Zatem 

lim

𝑛→∞

𝑃 (⋂{|𝑋

𝑛

− 0| ≤  𝜀}

∞

𝑛=𝑁

) = lim

𝑛→∞

(1 −

1

𝑁

) = 1, 

co oznacza, że 𝑋

𝑛

𝑝.𝑝.

→  0, gdy 𝑛 → ∞. 

(c) Sprawdzimy, czy 

𝑋

𝑛

 𝐿

𝑝

 

→  0, gdy 𝑛 → ∞? 

Zauważmy, że dla 

𝑝 ∈ (0, +∞), 𝐸|𝑋

𝑛

|

𝑝

=

𝑒

𝑛𝑝

𝑛

< ∞ oraz 

lim

𝑛→∞

𝐸|𝑋

𝑛

− 0|

𝑝

= lim

𝑛→∞

𝐸|𝑋

𝑛

|

𝑝

= lim

𝑛→∞

[(𝑒

𝑛

)

𝑝

∙ 𝑃(𝑋

𝑛

= 𝑒

𝑛

) + 0

𝑝

∙ 𝑃(𝑋

𝑛

= 0)] = lim

𝑛→∞

𝑒

𝑛𝑝

𝑛

= +∞ . 

2 

 

Zatem nie jest prawdą, że 𝑋

𝑛

 𝐿

𝑝

 

→  0, gdy 𝑛 → ∞. 

(d) Sprawdzimy, czy 

𝑋

𝑛

⟹ 0, gdy 𝑛 → ∞? 

Zauważmy, że 

𝐹

𝑋

𝑛

(𝑥) = 𝑃(𝑋

𝑛

≤ 𝑥) = {

0, 𝑥 < 0,

1 −

1

𝑛

,

1, 𝑥 ≥ 𝑒

𝑛

.

𝑥 ∈ [0, 𝑒

𝑛

), 

Ponadto 

lim

𝑛→∞

𝐹

𝑋

𝑛

(𝑥) = {

0, 𝑥 < 0
1, 𝑥 ≥ 0

= 𝐹

𝑋

0

(𝑥), gdzie 𝑋

0

≡ 0, 

czyli 

𝑋

𝑛

⟹ 0, gdy 𝑛 → ∞. 

 

2.  Wiadomo,  że  prawdopodobieństwo  urodzenia  się  chłopca  wynosi  ok.  0,515. 

Oszacować prawdopodobieństwo (z twierdzenia de Moivre'a-Laplace'a), że wśród 10 

tysięcy noworodków liczba chłopców nie przewyższy liczby dziewcząt. 

Rozwiązanie: 

 

Niech  zmienna  losowa 

𝑋  określa  liczbę  urodzonych  chłopców  wśród  10  tysięcy 

noworodków. Oczywiście zmienna losowa 𝑋 ma rozkład dwumianowy z parametrami 𝑛 =

10 000  oraz  𝑝 = 0,515.  Z  centralnego  twierdzenia  granicznego  de  Moivre'a-Laplace'a 

mamy, że  

𝑋 − 𝐸𝑋

𝜎𝑋

=

𝑋 − 𝑛𝑝

√𝑛𝑝𝑞

=

𝑋 − 5150

49,9775

~𝑁(0,1). 

Zatem szukane prawdopodobieństwo wynosi 

𝑃(𝑋 ≤ 5000) = 𝑃 (

𝑋 − 5150

49,9775

≤

5000 − 5150

49,9775

) = 𝑃 (

𝑋 − 5150

49,9775

≤ −3,0014) ≈ 

≈ Φ(−3,0014) = 1 − Φ(3,0014) = 1 − 0,9987 = 0,0013, 

gdzie 

Φ(𝑥) jest dystrybuanta rozkładu normalnego 𝑁(0,1). 

 

 

3 

 

3.  Wiadomo,  że  średnia  waga  dorosłego  człowieka  wynosi  75  kg  i  odchylenie 

standardowe wagi wynosi 3 kg (ale nie wiemy dokładnie jaki jest to rozkład). Samolot 

zabiera  81  pasażerów.  Obliczyć  prawdopodobieństwo,  że  łączna  waga  pasażerów 

przekroczy 6 ton. 

Rozwiązanie: 

Zauważmy, że z centralnego twierdzenia granicznego Lindeberga-Levy'ego wynika, 

że  dla  ciągu  𝑋

1

, 𝑋

2

, … , 𝑋

𝑛

  niezależnych  zmiennych  losowych  o  jednakowym  rozkładzie, 

takim, że 

𝜇 = 𝐸𝑋

1

= 𝐸𝑋

2

=. . . = 𝐸𝑋

𝑛

 oraz 

𝜎

2

= 𝑉𝑎𝑟𝑋

1

= 𝑉𝑎𝑟𝑋

2

=. . . = 𝑉𝑎𝑟𝑋

𝑛

< ∞ 

wynika, że dla dostatecznie dużych 𝑛 

𝑆

𝑛

− 𝐸𝑆

𝑛

√𝑉𝑎𝑟𝑆

𝑛

~𝑁(0, 1),  

gdzie 

𝑆

𝑛

= 𝑋

1

+ 𝑋

2

+. . . +𝑋

𝑛

, 

𝐸𝑆

𝑛

= 𝐸𝑋

1

+ 𝐸𝑋

2

+ ⋯ + 𝐸𝑋

𝑛

= 𝑛𝜇, 

𝑉𝑎𝑟𝑆

𝑛

= 𝑉𝑎𝑟𝑋

1

+ 𝑉𝑎𝑟𝑋

2

+. . . +𝑉𝑎𝑟𝑋

𝑛

= 𝑛𝜎

2

. 

Zatem  niech  zmienna  losowa 

𝑋

𝑖

  określa  wagę  (w  kg) 

𝑖 −tego  pasażera,  gdzie  𝑖 =

1, 2, … ,81. Natomiast zmienna losowa 𝑆

81

= 𝑋

1

+ 𝑋

2

+. . . +𝑋

81

 określa łączną wagę tych 

pasażerów.  

Zamieniając tony na kg otrzymujemy, że szukane prawdopodobieństwo wynosi 

𝑃(𝑆

81

> 6000) = 1 − 𝑃(𝑆

81

≤ 6000) = 1 − 𝑃 (

𝑆

81

− 𝐸𝑆

81

√𝑉𝑎𝑟𝑆

81

≤

6000 − 𝐸𝑆

81

√𝑉𝑎𝑟𝑆

81

) = 

= 1 − 𝑃 (

𝑆

81

− 81 ∙ 75

√81 ∙ 3

2

≤

6000 − 81 ∙ 75

√81 ∙ 3

2

) = 1 − 𝑃 (

𝑆

81

− 81 ∙ 75

√81 ∙ 3

2

≤

6000 − 81 ∙ 75

√81 ∙ 3

2

) = 

= 1 − 𝑃 (

𝑆

81

− 6075

27

≤

6000 − 6075

27

) ≈ 1 − Φ(−2,7778) = 

= 1 − (1 − Φ(2,7778)) = Φ(2,7778) = 0,9973. 

 

4 

 

4.  Zmienne  losowe 

𝑋  i  𝑌  są  niezależne  i  mają  jednakowe  rozkłady  wykładnicze  z 

parametrem 

𝜆 = 1. Określmy następujące zmienne losowe 𝑈 = 𝑋 + 𝑌 oraz 𝑉 = 𝑋 − 𝑌. 

Wyznaczyć  gęstość  rozkładu  łącznego  wektora  (dwuwymiarowej  zmiennej  losowej) 

(𝑋, 𝑌), a następnie gęstość wektora (𝑈, 𝑉) oraz gęstości brzegowe zmiennych 𝑈 i V. Czy 

zmienne losowe 

𝑈 i V są niezależne? 

Rozwiązanie: 

Niech 

𝑓

𝑋

(𝑥)  będzie  gęstością  zmiennej  losowej  𝑋,  a  𝑓

𝑌

(𝑦)  gęstością  zmiennej 

losowej 

𝑌. Wówczas 

𝑓

𝑋

(𝑥) = {

𝑒

−𝑥

, 𝑥 > 0

0, 𝑥 ≤ 0

 oraz 

𝑓

𝑌

(𝑦) = {

𝑒

−𝑦

, 𝑦 > 0

0, 𝑦 ≤ 0

. 

Korzystając z niezależności zmiennych losowych 𝑋 i 𝑌 możemy wyznaczyć gęstość 

dwuwymiarowej zmiennej losowej (

𝑋, 𝑌): 

𝑓

(𝑋,𝑌)

(𝑥, 𝑦) = 𝑓

𝑋

(𝑥) ∙ 𝑓

𝑌

(𝑦) = {

𝑒

−𝑥

∙ 𝑒

−𝑦

, 𝑥 > 0  i 𝑦 > 0

0,

𝑥 ≤ 0  lub 𝑦 ≤ 0

= {

𝑒

−(𝑥+𝑦)

, 𝑥 > 0  i 𝑦 > 0

0,

𝑥 ≤ 0  lub 𝑦 ≤ 0

. 

Aby  wyznaczyć  gęstość  dwuwymiarowej  zmiennej  losowej  (𝑈, 𝑉)  musimy 

skorzystać z odpowiedniego wzoru na zmianę zmiennych. 

Niech 

ℎ: 𝑅

+

2

→ 𝑅

2

 będzie przekształceniem danym wzorem ℎ(𝑥, 𝑦) = (𝑥 + 𝑦, 𝑥 − 𝑦). 

Wyznaczymy teraz odwzorowanie odwrotne 

ℎ

−1

. W tym celu niech 

ℎ: {

𝑢 = 𝑥 + 𝑦
𝑣 = 𝑥 − 𝑦

 dla 

𝑥 > 0  i 𝑦 > 0. 

Stąd dodając i odejmując powyższe równania stronami otrzymujemy, że 

ℎ

−1

: {

𝑥 =

𝑢+𝑣

2

𝑦 =

𝑢−𝑣

2

  dla  

𝑢+𝑣

2

> 0  i 

𝑢−𝑣

2

> 0. 

Rozwiązując układ równań 

{

𝑢 + 𝑣

2

> 0  

𝑢 − 𝑣

2

> 0

 

dostajemy, że 

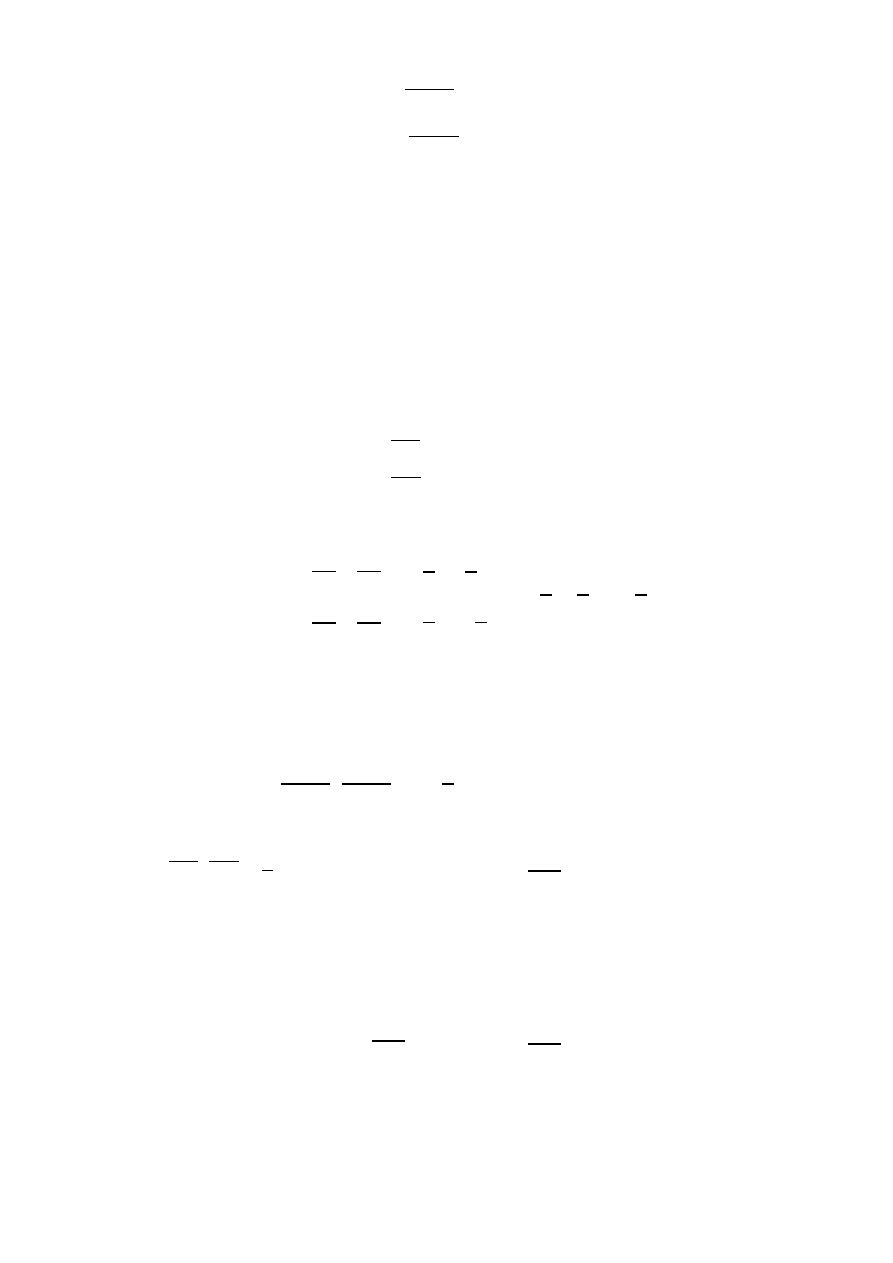
5 

 

{

𝑢 + 𝑣

2

> 0  

𝑢 − 𝑣

2

> 0

 

{

𝑢 + 𝑣 > 0  

𝑢 − 𝑣 > 0

 

Dodając stronami otrzymujemy, że 𝑢 > 0. Ponadto z powyższego układu nierówności 

dostajemy, że 

{

𝑣 > −𝑢  

𝑣 < 𝑢

, 

czyli 

𝑣 ∈ (−𝑢, 𝑢) lub |𝑣| < 𝑢. 

 

Stąd ostatecznie 

ℎ

−1

: {

𝑥 =

𝑢+𝑣

2

𝑦 =

𝑢−𝑣

2

  dla  𝑢 > 0  i 𝑣 ∈ (−𝑢, 𝑢). 

Obliczmy teraz jakobian przekształcenia odwrotnego ℎ

−1

: 

𝐽

ℎ

−1

= |

𝜕𝑥
𝜕𝑢

𝜕𝑥
𝜕𝑣

𝜕𝑦
𝜕𝑢

𝜕𝑦
𝜕𝑣

| = |

1
2

1
2

1
2

−

1
2

| = −

1
4

−

1
4

= −

1
2

. 

Zatem gęstość dwuwymiarowej zmiennej losowej (𝑈, 𝑉) wyraża się wzorem: 

𝑓

(𝑈,𝑉)

(𝑢, 𝑣) = {

𝑓

(𝑋,𝑌)

(ℎ

−1

(𝑢, 𝑣)) ∙ |𝐽

ℎ

−1

|, dla 𝑢 > 0  i 𝑣 ∈ (−𝑢, 𝑢)

0,          poza

= 

= {

𝑓

(𝑋,𝑌)

(

𝑢 + 𝑣

2

,

𝑢 − 𝑣

2

) ∙ |−

1
2

| , dla 𝑢 > 0  i 𝑣 ∈ (−𝑢, 𝑢)

0,          poza

= 

= {𝑒

−(

𝑢+𝑣

2 +

𝑢−𝑣

2 )

∙

1
2

, dla 𝑢 > 0  i 𝑣 ∈ (−𝑢, 𝑢)

0,          poza

= {

𝑒

−𝑢

2

, dla 𝑢 > 0  i 𝑣 ∈ (−𝑢, 𝑢)

0,          poza

. 

Wyznaczymy teraz gęstości rozkładów brzegowych, czyli gęstości zmiennych 𝑈 =

𝑋 + 𝑌 oraz 𝑉 = 𝑋 − 𝑌. 

𝑓

𝑈

(𝑢) = ∫ 𝑓

(𝑈,𝑉)

(𝑢, 𝑣)

+∞

−∞

𝑑𝑣 = {

∫

𝑒

−𝑢

2

𝑑𝑣, 𝑢 > 0

𝑢

−𝑢

0,

𝑢 ≤ 0 

= {

𝑒

−𝑢

2

[𝑣]

−𝑢

𝑢

, 𝑢 > 0

0,

𝑢 ≤ 0 

= {

𝑢𝑒

−𝑢

, 𝑢 > 0

0,

𝑢 ≤ 0 

. 

6 

 

𝑓

𝑉

(𝑣) = ∫ 𝑓

(𝑈,𝑉)

(𝑢, 𝑣)

+∞

−∞

𝑑𝑢 = ∫

𝑒

−𝑢

2

𝑑𝑢 =

1
2

∙ [−𝑒

−𝑢

]

|𝑣|

+∞

=

+∞

|𝑣|

1
2

∙ (0 + 𝑒

−|𝑣|

)

=

𝑒

−|𝑣|

2

, dla 𝑣 ∈ 𝑅. 

Zauważmy, że np. 

𝑓

(𝑈,𝑉)

(1,2) = 0 

oraz 

𝑓

𝑈

(1) ∙ 𝑓

𝑉

(2) = 𝑒

−1

∙

𝑒

−2

2

=

1

2𝑒

3

≠ 0, 

czyli zmienne losowe 

𝑈 i V nie są niezależne. 

 

5.  Zmienne losowe 

𝑋

1

, 𝑋

2

, … , 𝑋

𝑛

 są niezależne i mają dystrybuanty 

𝐹

1

(𝑥),  𝐹

2

(𝑥), … , 𝐹

𝑛

(𝑥).  

Wyznaczyć  dystrybuanty  zmiennych  losowych  𝑀

𝑛

= max(𝑋

1

, 𝑋

2

, … , 𝑋

𝑛

)  oraz  

𝑚

𝑛

= min(𝑋

1

, 𝑋

2

, … , 𝑋

𝑛

)

. Ponadto wyznaczyć dystrybuanty zmiennych losowych 𝑀

𝑛

 i 

𝑚

𝑛

 przy dodatkowym założeniu, że zmienne losowe 

𝑋

1

, 𝑋

2

, … , 𝑋

𝑛

 mają taki sam rozkład, 

czyli 

𝐹

1

(𝑥) = 𝐹

2

(𝑥) =   … = 𝐹

𝑛

(𝑥) = 𝐹(𝑥). 

Rozwiązanie: 

Korzystając z niezależności zmiennych losowych 𝑋

1

, 𝑋

2

, … , 𝑋

𝑛

 otrzymujemy, że 

𝐹

𝑀

𝑛

(𝑥) = 𝑃(𝑀

𝑛

≤ 𝑥) = 𝑃(max(𝑋

1

, 𝑋

2

, … , 𝑋

𝑛

) ≤ 𝑥) = 𝑃(𝑋

1

≤ 𝑥, … , 𝑋

𝑛

≤ 𝑥) = 

= 𝑃(𝑋

1

≤ 𝑥) ∙ … ∙  𝑃(𝑋

𝑛

≤ 𝑥) = 𝐹

𝑋

1

(𝑥) ∙ … ∙ 𝐹

𝑋

𝑛

(𝑥) 

oraz  

𝐹

𝑚

𝑛

(𝑥) = 𝑃(𝑚

𝑛

≤ 𝑥) = 𝑃(min(𝑋

1

, 𝑋

2

, … , 𝑋

𝑛

) ≤ 𝑥) = 1 − 𝑃(min(𝑋

1

, 𝑋

2

, … , 𝑋

𝑛

) > 𝑥) = 

= 1 − 𝑃(𝑋

1

> 𝑥, … , 𝑋

𝑛

> 𝑥) = 1 − 𝑃(𝑋

1

> 𝑥) ∙ … ∙  𝑃(𝑋

𝑛

> 𝑥) = 

= 1 − (1 − 𝑃(𝑋

1

≤ 𝑥)) ∙ … ∙ (1 − 𝑃(𝑋

𝑛

≤ 𝑥)) =  1 − (1 − 𝐹

𝑋

1

(𝑥)) ∙ … ∙ (1 − 𝐹

𝑋

𝑛

(𝑥)). 

Ponadto, gdy dodatkowo zmienne losowe 

𝑋

1

, 𝑋

2

, … , 𝑋

𝑛

 mają taki sam rozkład, czyli 

𝐹

1

(𝑥) = 𝐹

2

(𝑥) =   … = 𝐹

𝑛

(𝑥) = 𝐹(𝑥) 

to  

𝐹

𝑀

𝑛

(𝑥) = 𝐹

𝑛

(𝑥) 

oraz  

7 

 

𝐹

𝑚

𝑛

(𝑥) = 1 − (1 − 𝐹(𝑥))

𝑛

. 

Jeżeli dodatkowo założymy, że zmienne losowe 𝑋

1

, 𝑋

2

, … , 𝑋

𝑛

 mają (tę samą ) funkcję 

gęstości 𝑓(𝑥), czyli  

𝑓(𝑥) = 𝐹

′

(𝑥), 

to wówczas funkcje gęstości zmiennych 𝑀

𝑛

 i 

𝑚

𝑛

 mają postać 

𝑓

𝑀

𝑛

(𝑥) = 𝑛𝐹

𝑛−1

(𝑥)𝑓(𝑥) 

oraz  

𝑓

𝑚

𝑛

(𝑥) = 𝑛(1 − 𝐹(𝑥))

𝑛−1

𝑓(𝑥). 

6.  Niech {

𝑋

𝑛

, 𝑛 ≥ 1} będzie ciągiem zmiennych losowych takim, że 𝑃(𝑋

𝑛

= 1) = 1 −

1

𝑛

  

i 

𝑃(𝑋

𝑛

= 0) =

1

𝑛

. Wyznaczyć słabą granicę ciągu {𝑋

𝑛

, 𝑛 ≥ 1}. 

Rozwiązanie: 

Na początku wyznaczmy dystrybuantę zmiennej losowej 𝑋

𝑛

:  

𝐹

𝑋

𝑛

(𝑥) = 𝑃(𝑋

𝑛

≤ 𝑥) = {

0,   𝑥 < 0 

1

𝑛

, 0 ≤ 𝑥 < 1

1,   𝑥 ≥ 1

. 

Obliczmy teraz do czego dąży dystrybuanta 𝐹

𝑋

𝑛

(𝑥), gdy 𝑛 → ∞: 

lim

𝑛→∞

𝐹

𝑋

𝑛

(𝑥) = lim

𝑛→∞

{

0,

𝑥 < 0 

1
𝑛

, 0 ≤ 𝑥 < 1

1,

𝑥 ≥ 1

= {

0, 𝑥 < 1 

1, 𝑥 ≥ 1

. 

Zauważmy, że funkcja graniczna jest dystrybuantą zmiennej losowej 𝑋

0

: 

𝐹

𝑋

0

(𝑥) = {

0, 𝑥 < 1 

1, 𝑥 ≥ 1

, 

zatem zmienna losowa 

𝑋

0

 taka, że 

𝑃(𝑋

0

= 1) = 1 jest słabą granicą ciągu {𝑋

𝑛

, 𝑛 ≥ 1}, co 

zapisujemy jako 

𝑋

𝑛

⇒ 𝑋

0

 lub 

𝑋

𝑛

⇒ 1. 

Zauważmy, że zbieżność 

lim

𝑛→∞

𝐹

𝑋

𝑛

(𝑥) = 𝐹

𝑋

0

(𝑥) 

8 

 

ma  miejsce  dla  wszystkich 

𝑥 ∈ 𝑅,  a  wystarczyłoby,  aby  zbieżność  ta  miała  miejsce  dla 

wszystkich punktów ciągłości dystrybuanty granicznej 𝐹

𝑋

0

, czyli dla 𝑥 ∈ 𝑅\{1} ( u nas dla 

𝑥

0

= 1 zbieżność ta też ma miejsce). 

7.  Niech {

𝑋

𝑛

, 𝑛 ≥ 1} będzie ciągiem niezależnych zmiennych losowych o jednakowym 

rozkładzie jednostajnym 𝑈(0, 1). Wyznaczyć rozkład graniczny dla 𝑌

𝑛

= 𝑛(1 − 𝑀

𝑛

). 

Rozwiązanie: 

Ponieważ {𝑋

𝑛

, 𝑛 ≥ 1} jest ciągiem niezależnych zmiennych losowych o jednakowym 

rozkładzie jednostajnym 𝑈(0, 1), to  

𝑓

𝑋

𝑛

(𝑥) = 𝑓(𝑥) = {

1, 𝑥 ∈ (0,1)
0, 𝑥 ∉ (0,1)

, dla 

𝑛 ≥ 1 

oraz  

𝐹

𝑋

𝑛

(𝑥) = 𝐹(𝑥) = {

0, 𝑥 < 0 

𝑥, 0 ≤ 𝑥 < 1

1, 𝑥 ≥ 1

, dla 

𝑛 ≥ 1. 

Ponadto, 

przy 

naszych 

założeniach, 

dystrybuanta 

zmiennej 

losowej 

 

𝑀

𝑛

= 𝑚𝑎𝑥(𝑋

1

, 𝑋

2

, … , 𝑋

𝑛

) ma postać (na mocy zadania 1): 

𝐹

𝑀

𝑛

(𝑥) = 𝐹

𝑛

(𝑥) = {

0,   𝑥 < 0 

𝑥

𝑛

, 0 ≤ 𝑥 < 1

1,    𝑥 ≥ 1

. 

Wyznaczymy  teraz  dystrybuantę  zmiennej  losowej  𝑌

𝑛

  w  oparciu  o  dystrybuantę 

zmiennej losowej 

𝑀

𝑛

 

𝐹

𝑌

𝑛

(𝑥) = 𝑃(𝑌

𝑛

≤ 𝑥) = 𝑃(𝑛(1 − 𝑀

𝑛

) ≤ 𝑥) = 𝑃 (1 − 𝑀

𝑛

≤

𝑥
𝑛

) = 𝑃 (𝑀

𝑛

≥ 1 −

𝑥
𝑛

) = 

= 1 − 𝑃 (𝑀

𝑛

< 1 −

𝑥
𝑛

) = 1 − 𝑃 (𝑀

𝑛

≤ 1 −

𝑥
𝑛

) = 1 − 𝐹

𝑀

𝑛

(1 −

𝑥
𝑛

)

= 1 −

{

 

 

 

 

0,

1 −

𝑥
𝑛

< 0 

(1 −

𝑥
𝑛

)

𝑛

, 0 ≤ 1 −

𝑥
𝑛

< 1

1,

1 −

𝑥
𝑛

≥ 1

= 

9 

 

= {

1,      𝑥 > 𝑛 

1 − (1 −

𝑥

𝑛

)

𝑛

, 0 < 𝑥 ≤ 𝑛

0,     𝑥 ≤ 0

= {

0,     𝑥 ≤ 0

1 − (1 −

𝑥

𝑛

)

𝑛

, 0 < 𝑥 ≤ 𝑛

1,      𝑥 > 𝑛 

. 

 

Mając  dystrybuantę  zmiennej  losowej  𝑌

𝑛

  możemy  już  wyznaczyć  jej  rozkład 

graniczny: 

lim

𝑛→∞

𝐹

𝑌

𝑛

(𝑥) = lim

𝑛→∞

{

0,

𝑥 ≤ 0

1 − (1 −

𝑥
𝑛

)

𝑛

, 0 < 𝑥 ≤ 𝑛

1,

𝑥 > 𝑛 

= {

0,

𝑥 ≤ 0 

1 − 𝑒

−𝑥

, 𝑥 > 0

= {

0,

𝑥 < 0 

1 − 𝑒

−𝑥

, 𝑥 ≥ 0

. 

Zauważmy, że  otrzymana w granicy funkcja jest dystrybuantą zmiennej  losowej o 

rozkładzie  wykładniczym  z    parametrem  𝜆 = 1  (czyli  zmiennej  losowej  𝐸𝑥𝑝(1)). 

Oczywiście powyższa zbieżność ma miejsce dla wszystkich punktów ciągłości granicznej 

dystrybuanty (czyli dla wszystkich 

𝑥 ∈ 𝑅).  

Zatem 

𝑌

𝑛

⇒ 𝐸𝑥𝑝(1), 

czyli granicznym rozkładem zmiennej losowej 𝑌

𝑛

= 𝑛(1 − 𝑀

𝑛

) jest rozkład wykładniczy z 

parametrem 

𝜆 = 1. 

8. Niech  {

𝑋

𝑛

, 𝑛 ≥ 1}  będzie  ciągiem  niezależnych  zmiennych  losowych  o  jednakowym 

rozkładzie  wykładniczym  𝐸𝑥𝑝(1).  Wyznaczyć  rozkłady  graniczne  dla  𝑌

𝑛

=

1

𝑛

𝑒

𝑀

𝑛

, 

 𝑍

𝑛

= 𝑀

𝑛

− ln 𝑛.  

Rozwiązanie: 

 

Skoro  {

𝑋

𝑛

, 𝑛 ≥ 1}  jest  ciągiem  niezależnych  zmiennych  losowych  o  jednakowym 

rozkładzie wykładniczym 𝐸𝑥𝑝(1), to 

𝑓

𝑋

𝑛

(𝑥) = 𝑓(𝑥) = {

𝑒

−𝑥

, 𝑥 > 0

0,    𝑥 ≤ 0

, dla 

𝑛 ≥ 1 

oraz  

𝐹

𝑋

𝑛

(𝑥) = 𝐹(𝑥) = {

0,      𝑥 < 0 

1 − 𝑒

−𝑥

, 𝑥 ≥ 0

, dla 

𝑛 ≥ 1. 

Wyznaczmy najpierw dystrybuantę zmiennej losowej 𝑀

𝑛

 

𝐹

𝑀

𝑛

(𝑥) = 𝐹

𝑛

(𝑥) = {

0,        𝑥 < 0

(1 − 𝑒

−𝑥

)

𝑛

,    𝑥 ≥ 0

. 

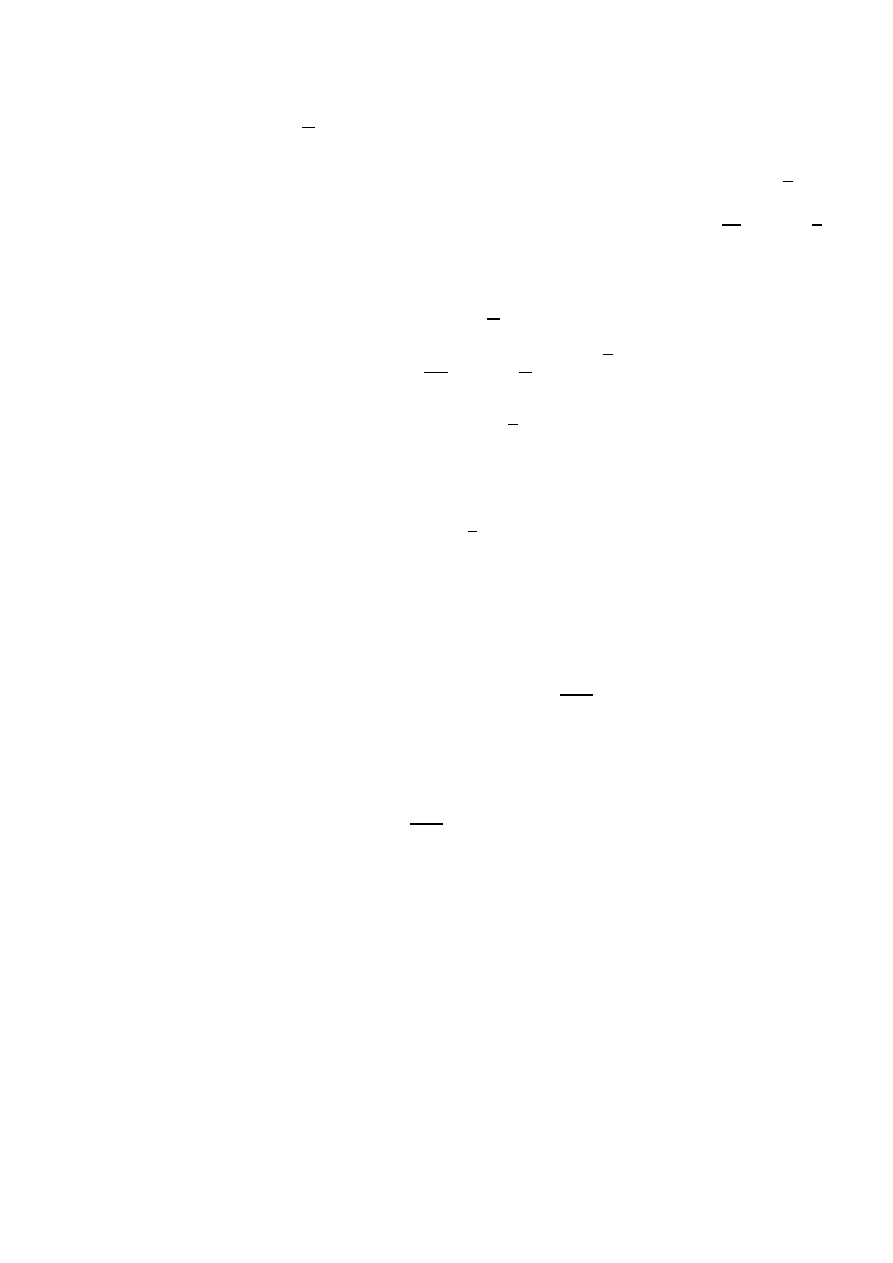
10 

 

Wyznaczymy teraz dystrybuantę zmiennej losowej 𝑌

𝑛

 

𝐹

𝑌

𝑛

(𝑥) = 𝑃(𝑌

𝑛

≤ 𝑥) = 𝑃 (

1
𝑛

𝑒

𝑀

𝑛

≤ 𝑥) = 𝑃(𝑒

𝑀

𝑛

≤ 𝑛𝑥) = {

0,        𝑥 ≤ 0

𝑃(𝑀

𝑛

≤ ln(𝑛𝑥)),    𝑥 > 0

= 

= {

0,        𝑥 ≤ 0

𝐹

𝑀

𝑛

(ln(𝑛𝑥)),    𝑥 > 0 = {

0,              𝑥 ≤ 0

0,    ln(𝑛𝑥) < 0 

(1 − 𝑒

− ln(𝑛𝑥)

)

𝑛

,    ln(𝑛𝑥) ≥ 0

= {

0,      𝑥 <

1

𝑛

 

(1 −

1

𝑛𝑥

)

𝑛

, 𝑥 ≥

1

𝑛

. 

Zatem 

lim

𝑛→∞

𝐹

𝑌

𝑛

(𝑥) = lim

𝑛→∞

{

0,      𝑥 <

1
𝑛

 

(1 −

1

𝑛𝑥

)

𝑛

, 𝑥 ≥

1
𝑛

= {

0,

𝑥 ≤ 0 

𝑒

−

1
𝑥

, 𝑥 > 0

, 

czyli rozkładem granicznym zmiennej losowej 𝑌

𝑛

=

1

𝑛

𝑒

𝑀

𝑛

 jest rozkład zmiennej losowej 

𝑌

0

 

(𝑌

𝑛

⇒ 𝑌

0

 ) o dystrybuancie 

𝐹

𝑌

0

(𝑥) = {

0,

𝑥 ≤ 0 

𝑒

−

1
𝑥

, 𝑥 > 0

. 

Wyznaczymy teraz dystrybuantę zmiennej losowej 𝑍

𝑛

 

𝐹

𝑍

𝑛

(𝑥) = 𝑃(𝑍

𝑛

≤ 𝑥) = 𝑃(𝑀

𝑛

− ln 𝑛 ≤ 𝑥) = 𝑃(𝑀

𝑛

≤ 𝑥 + ln 𝑛) = 𝐹

𝑀

𝑛

(𝑥 + ln 𝑛) = 

= {

0,        𝑥 + ln 𝑛 < 0

(1 − 𝑒

−(𝑥+ln 𝑛)

)

𝑛

,    𝑥 + ln 𝑛 ≥ 0

= {

0,        𝑥 < − ln 𝑛

(1 −

𝑒

−𝑥

𝑛

)

𝑛

,    𝑥 ≥ −ln 𝑛

. 

Zatem 

lim

𝑛→∞

𝐹

𝑍

𝑛

(𝑥) = lim

𝑛→∞

{

0,        𝑥 < − ln 𝑛

(1 −

𝑒

−𝑥

𝑛

)

𝑛

,    𝑥 ≥ ln 𝑛

= 𝑒

−𝑒

−𝑥

, 𝑥 ∈ 𝑅, 

czyli  rozkładem  granicznym  zmiennej  losowej   𝑍

𝑛

= 𝑀

𝑛

− ln 𝑛  jest  rozkład  zmiennej 

losowej 

𝑍

0

 (

𝑍

𝑛

⇒ 𝑍

0

 ) o dystrybuancie 

𝐹

𝑍

0

(𝑥) = 𝑒

−𝑒

−𝑥

, 𝑥 ∈ 𝑅.