
1
- PODSTAWY EKONOMETRII -
→YKŁAD ń
18.02.2011r.
Punktualno ć bardzo wa na Ą
Żaworyzuje studentów, którzy pracuj na ćwiczeniach. Ocena 5 z ćwicze dopuszcza do egzaminu zerowego (dla
najlepszych studentów).
Termin zerówkiŚ Ńγ.Ń6.βŃńńr. 9Ś4Ń Aula
Egzamin
Ś wykłady + literatura + zagadnienia z ćwicze --- PISEMNY
PRZEDMIOT EKONOMETRII
Ekonometria
zrodziła si w latach γŃ-tych. Powstała w reakcji na wielki kryzys przełomu lat βŃ-tych i 30-tych
(1929-
ń9γγ). Kryzys ten spowodował potrzeb znalezienia pewnych narz dzi wspomagania gospodarki, aby
zmniejszyć amplitud waha koniunkturalnych.
W latach 30-
tych rz d ameryka ski powołał grup ekonomistów - Komisj COWLES.
→ komisji tej byli najwybitniejsi ekonomi ci głównie o zaci ciu ekonomiczno-statystycznym. Szefem tego zespołu
był Cowles. Znalazł si w niej tak e polski ekonomista – geniusz ekonomii (chocia słabego charakteru) – Oskar
Lange
, który zajmował si teori ekonomii, statystyk . Jego student napisał genialne dzieło. Drugim gigantem
nauk ekonomicznych był Kalecki.
Poj cie ekonometria istniało ju w czasie kryzysu. → ń9β6 roku Ragnar FRISCH utworzył Towarzystwo
Ekonometryczne
, które rozpocz ło wydawanie czasopisma naukowego pt.Ś „
ECONOMETRICA
” – st d wzi ło si
poj cie ekonometrii. To czasopismo do dzi jest najwa niejszym czasopismem ekonometrycznym. wiat uwa a, e
rok ń9β6 jest rokiem, w którym pojawiła si ekonometria w sensie instytucjonalnym. Frisch był Norwegiem, przy
czym całe ycie naukowe sp dził w Stanach Zjednoczonych.
W latach 80-
tych uczeni z Krakowa odnale li w bibliotece Akademii źkonomicznej prac prof. Pawła CIOMPA,
wydan w żalicji w ń9ńŃ roku, pt.Ś „Zarys ekonometrii i teoria buchalterii”.
Słowo „ekonometria” pojawiło si po raz pierwszy w Polsce w ń9ńŃr.
Zesp
ół COWLES stworzył pierwsze narz dzia ekonometryczne – barametry koniunktury – narz dzi słu ce do
opisu waha koniunkturalnych i wykorzystywania ich do prognozowania koniunktury oraz podejmowania decyzji
w skali pa stwa powoduj cych zmniejszenie amplitudy waha koniunkturalnych.
Pierwszy okres dynamicznego rozwoju ekonometrii to lata 30-te. Drugi okres
to okres II wojny wiatowej, przy
czym w tym czasie powstały zwłaszcza narz dzia bada operacyjnych, które s cz ci ekonometrii rozumianej
szeroko, np. n
arz dzia optymalizacji szlaków / dróg transportowych. źkonometria nie rozwijała si w okresie II
wojny wiatowej w tzw. bloku wschodnim ZSRR poniewa Stalin napisał, e ekonometria jest pseudonauk
wykorzystywan przez bur uazj .
Pó niej ekonometria w ZSRR była wykładana jako cybernetyka.
→ II połowie lat 8Ń-tych powstały pierwsze komputery, co przyspieszyło rozwój gospodarczy.
Spowodowało to ogromne mo liwo ci rozwoju ekonometrii empirycznej.
Leonid Kantorowicz
– znakomity Rosjanin, specjalista bada operacyjnych, opracował metody optymalizacji
przemieszczania floty / konwoju.
→ okresie po II wojnie wiatowej rozwijała si teoria estymacji i testowania statystycznego.
Prace ekonometryków pojawiły si w czasopismach w latach 50-tych.
W latach 80-
tych nie mo na było oficjalnie u ywać słowa „ekonometria”. Jedynym pa stwem, w którym mo na
było oficjalnie u ywać tego słowa była Polska, dzi ki Oskarowi Lange, który wydał podr cznik pt.Ś „Wst p do
ekonometrii
”(ń957). Podr cznik ten wydany został w latach 6Ń-tych i był on ksi k tłumaczon na γŃ j zyków –
była to ksi ka najbardziej znana na wiecie. Hindusi byli pierwszymi, którzy przetłumaczyli t ksi k na swój
j zyk.
2
Za ycia Lange nie wykładano ekonometrii na uczelniach polskich. źkonometri zacz to wykładać dopiero w
drugiej połowie lat 6Ń-tych. źkonometria bardzo intensywnie rozwijała si w Katowicach, dzi ki Zbigniewowi
Pawłowskiemu. Pawłowski pisał ksi ki w sposób zrozumiały, co nie jest łatwe. Zwłaszcza w Poznaniu nie był on
lubiany ze wzgl du na pisanie j zykiem zrozumiałym.
EKONOMETRIA
powstała w styku trzech dyscyplinŚ
1. Matematyki
SM
– statystyka matematyczna
2. Statystyki
SE
– statystyka ekonomiczna (GUS – żł. ←rz d Statystyczny)
3. Ekonomii
W Polsce is
tnieje obowi zek statystycznyś
składania sprawozda do ż←S
EM
– ekonomia matematyczna
EKONOMETRIA
źKONOMźTRI dzielimy naŚ
1) źkonometri klasyczn – głównie oparta na analizie regresji
2) Badania operacyjne zwane tak e oprogramowaniem matematycznym – podczas wojny słu yły gł. w
obszarze optymalizacji transportu morskiego
→ ekonometrii klasycznej wyró nić mo emyŚ
I.
Teori ekonometrii – ta cz ć, w której tworzy si metody estymacji parametrów oraz metody
programowania
II.
Ekonometria stosowana :
1. Makroekonomia, która zajmuje si badaniem gospodarek narodowych i ich cz ci za pomoc
stosowanych przez teorie ich cz ciś w historii była pierwsz ekonometri stosowan ś powstała w
okresie wojennym tu po komisji Cowles.
Powstały pierwsze modele, czyli modele gospodarek narodowych.
2. Mikroekonometria – wykorzystywanie narz dzi ekonometrii do mikro danych.
ROLA EKONOMTERII W WARUNKACH EKONOMICZNYCH
Laureatami Nagrody NOBLA w dziedzinie ekonomii byli:
- Frisch,
- Jan Tinbergen.
(Podz
ielili oni mln dolarów na pół)
→i kszo ć noblistów w dziedzinie ekonomii to Amerykanie. Poza nimi to Rosjanin Leonid Kantorowicz –
specjalista teorii optymalistycznej (nie był nigdy w Ameryce). Kantorowicz nie odebrał tej nagrody, poniewa nie
został on tam puszczony. Był jeszcze jeden ekonomista rosyjskiego pochodzenia Leontiew, który stworzył teori
„in put, out put” (tzw. „Teoria Leontiewa”), która daje precyzyjne rozwi zania w kalkulacji kosztów. T teori
mo na wykorzystywać w obliczaniu kosztów po rednich.
→ ród laureatów Nagrody NOBLA w dziedzinie ekonomii ponad ⅔ to ekonometrycy.
Pozycja ekonometryków w wiecie ekonomii jest bardzo wa na.
Jan Tinbergen
otrzymał Nagrod NOBLA za budow modeli gospodarki ameryka skiej. Znany jest on z funkcji
produkcji nazywanej
funkcją Tinbergena.
SM
Matematyka
M
Ekonomia
E
Statystyka
S
EM
SE
EKONOMETRIA jest
nauk ekonomiczn , która
wykorzystuje i tworzy
wyspecjalizowane
narz dzia badawcze
pochodz ce głównie z
obszaru statystyki
matematycznej do badania
zjawisk i procesów
ekonomicznych.

3
Ekonometria
nale y do sfery nauk ekonomicznych. Najpierw zacz ła rozwijać si w Polsce, ale równie jeszcze w
dwóch miejscachŚ
a)
→ gry – → grzy uzyskali status wa nego pa stwa bada ekonometrycznychś w ń986 roku w Budapeszcie
odbył si wiatowy kongres ekonometryczny,
b)
Słowacja – w Bratysławie prowadzono badania ekonometryczne za spraw ONZ, która ulokowała tam O rodek
Bada źkonometrycznych.
Dwa znane nazwiska: Szujan,
Kołek.
- PODSTAWY EKONOMETRII -
→YKŁAD β
25.02.2011r.
MODEL EKONOMETRYCZNY
Ekonometria
jest dyscyplin nauk ekonomicznych, która tworzy narz dzia analizy współzale no ci
ekonomicznych pocz wszy od skali mikro, czyli od przedsi biorstwa a sko czywszy na skali makro, czyli
gospodarki narodowej. Te narz dzia wykorzystywane s doŚ
- szacowania prognoz zmiennych ekonomicznych,
- symulacji,
-
podejmowania bie cych decyzji.
Podstawowym narz dziem ekonometrii jest model ekonometryczny, który w najprostszej postaci mo na zapisać
nast puj co:
przy czym mamy do czynienia z obserwacjami statystycznymi od 1 do n, gdzie:
n - liczba obserwacji statystycznych,
t
– indeks oznacza numer obserwacji statystycznej t=ń,β,…,n
y
t
– obserwacje na zmiennej y, któr nazywamy zmienn obja nian o obserwacjach y
n
Y
– zmienna obja niana ( stosujemy konwencje statystyki – zmienne zaznaczamy du ymi literami)
Zmienna y
zale y od zbioru zmiennych obja niaj cychŚ
x
1
... x
j
... x
k
o Zmienna obja niaj ca x
1
jest reprezentowana przez obserwacj x
t1
o Zmienna obja niaj ca x
j
jest reprezentowana przez obserwacj x
tj
o Zmienna obja niaj ca x
k
jest reprezentowana przez obserwacj x
tk
η
t
– oznacza składnik losowy, zawsze wyst puj cy w modelu, nadaje mu charakter stochastyczny inaczej losowy.
Powoduje, e zmienna y jest zmienn losow .
Model w ko cowej fazie b dzie tym lepszy im mniejsz mas waha losowych b dzie zawierała zmienn
obja niaj ca.
[Doczytać z ksi ki – Pięć powodów pojawiania się zmiennej losowej (składnika losowego w modelu)]
Istot modelu ekonometrycznego jest to, e zmienna obja niana jest zmienn o charakterze ekonomicznym, a wi c
przynale no ć zmiennej obja nianej rozstrzyga o typie modelu, np.
je li zmienn obja nian jest zmienna demograficzna to model b dzie demograficzny,
je li zmienn obja nian jest zmienna psychologiczna to model b dzie psychometryczny,
je li zmienn obja nian jest zmienna biologiczna to model b dzie biometryczny.
Charakter zmiennej obja nianej decyduje o tym, jak nazw ma model.
Zmienne obja niaj ce powinny reprezentować przyczyny zmienno ci zmiennej obja nianej.
Lange nie miał poj cia o teorii pomiaru. Teoria pomiaru pojawiła si w latach 4Ń-tych, której tez jest, e
wszystko jest mierzalne.
W 1946
roku Stevens ogłosił teori pomiaru, któr opublikował w czasopi mie „SCIźNCź”. Stevens udowodnił,
e wszystko da si zmierzyć, przy czym liczby mog oznaczać ró ne cechy.
t
t
t
t
t
k
j
X
X
X
f
Y
;
;...;
;
1

4
y
t
=
Stevens wyró nił cztery skale pomiarowe (poziomy pomiaru) – dwie s słabe ,a dwie mocneŚ
1. skala nominalna – najsłabsza,
2. skala porz dkowa (rangowa) – słaba,
3. skala przedziałowa (interwałowa) – mocna,
4. skala stosunkowa (ilorazowa) – najmocniejsza.
SKALA NOMINALNA
Najcz ciej spotykamy liczby nale ce do skali nominalnej. → tej skali liczby pełni role identyfikatorów,
pewnych symboli, a wi c słu one do odró niania obiektów b d ich cech. O liczbach nale cych do tej skali
mo emy powiedzieć tylko tyle, e para licz jest równa a=b lub ro na b≠c – dwie liczby s równe lub dwie liczby s
ró ne. Na liczbach tej skali nie wolno wykonywać adnych operacji arytmetycznych (nie wolno ich dodawać,
odejmować, mno yć i dzielić)ś wolno je zliczać, np. student opisany numerem albumu, przeznaczony PESEL,
numer telefonu. Liczby te słu do identyfikacji, aby ułatwić nam ycie.
Zmienna zerojedynkowa
nale y do pomiaru nominalnegoŚ
Za pomoc zerojedynkowej mo na zmierzyć wszystko, np. mo na zmierzyć grup przypisuj c wariantom Ń to
piłkarze a ń to s dziowie, a nast pnie wykonać operacj zliczan , czyli zliczamy „Ń” i „ń”, które mo na dodać, np.
płać – uzyskujemy liczb kobiet i liczb m czyzn.
Do wyniku pomiaru nominalnego mog być stosowane narz dzia analizy statystycznej w do ć ograniczonym
zakresie, tzn. dopuszczalne s techniki analizy frakcji, co nale y do sfery analizy struktury. Cała sfera rachunku
prawdopodobie stwa i empirycznej analizy cz sto ci.
Je li mamy pomiar zerojedynkowy to dopuszczalne s narz dzia analizy asocjacji cech, inaczej skojarzenia cech
nie tylko za pomoc narz dzi Czuprowa, tymczasem dopuszczalny jest współczynnik kojarzenia z przekształcenia
współczynnika korelacji Pearsona, który mie ci si w przedziale od –1 do 1.
→spółczynnik asocjacji posiada te same cechy, co współczynnik Pearsona, czyli –1 do 1.
Mo liwe jest stosowanie analizy regresji do zmiennej zerojedynkowej, oznacza to, eŚ
1, ...
0, ...
Zmienna obja niana mo e być zmienn zerojedynkow , w takim przypadku mówimy o liniowej funkcji
prawdopodobieństwa, która bywa nazywana te Modelem GOLDBERGERA.
SKALA RANGOWA, PORZ DKOWA
Liczby posiadaj now cech , now własno ć. Liczby s nie tylko albo równe, albo ró ne, ale mo emy ustalić ich
kolejno ć (porz dek), np.
a < b < c < ... <
a ≥ b ≥ c ≥ … ≥
Wiemy, co
jest mniejsze a co wi ksze.
Istnieje wiele struktur, które s uporz dkowane rangowo, np. struktura przedsi biorstwa, słu by mundurowe,
wojsko, armia
– s uporz dkowane hierarchicznie.
Nie wiemy, jakie
s ró nice pomi dzy liczbamiŚ
1) Ró nice s nieznane
2) Ró nice te s odmienne (niejednakowe) – odległo ć mi dzy a i b jest inna ni mi dzy b i c.
�
�
�
=
=
ń gdy spełnione s warunki V
j
Ń gdy nie s spełnione warunki
V
j

5
Znany jest porz dek, ale nie jest znana odległo ć mi dzy liczbami, oznacza to, e liczby w skali porz dkowej nie
podlegaj operacjom arytmetycznym. Nie wolno wykonywać operacji arytmetycznych na rangach z powodu
nieznajomo ci odległo ci mi dzy rangami oraz ró nych odległo ci mi dzy s siednimi rangami.
Odległo ci pomi dzy rangami s ró ne i nie s znane: 5 – 4 ≠ ńŃ – 9
Na liczbach tej skali nie mo na wykonywać adnych operacji arytmetycznych a to oznacza, e współczynnik
korelacji
rang Spirmana to współczynnik korelacji licz naturalnych.
Przykład γ.
Odległo ć pomi dzy pułkownikiem, a generałem to jest ń punkt, a odległo ć mi dzy szeregowym a starszym
szeregowym to te ń punkt – ale te odległo ci s ró ne.
→spółczynnik korelacji rang jest niedopuszczalny. W przypadku rang dopuszczalna jest analiza frakcji. Rangi
mo na przekształcić metod zerojedynkow i stosować narz dzia dopuszczalne dla zerojedynkowej.
Kierownicy bardzo lubi stosować podział rangowy. Huragany w Ameryce s opisywane w skali rangowej.
SKALA PRZEDZIAŁOWA
→ skali przedziałowej dochodzi nowa własno ć, tzn. znane s odległo ci mi dzy liczbami a ponadto odległo ci
mi dzy s siednimi liczbami s jednakowe i identyczne
5
– 4 = 10 – 9
Natomiast w skali przedziałowej nie jest znane zero naturalne, a to uniemo liwia dzielenie liczb.
Przykładem pomiaru przedziałowego jest pomiar temperatury w skali C°.
Pomiar przedziałowy stosowany jest w statystyce.
→yró niamy dwa zapisy stosowane w statystyce prowadz ce do pomiaru przedziałowegoŚ
a) normujemy zmienne losowe – polega to na takim przekształceniu zmiennej losowe, e nowa zmienna
charakteryzuje si ...................... odchyleniem od redniej arytmetycznej. Suma obserwacji zmiennych
unormowanych wynosi Ń i ta rednia arytmetyczna zmiennej unormowanej wynosi te Ń.
Zmienna umiarkowana jest wynikiem pomiaru przedziałowego.
b) zmienna losowa standaryzowana
– tablice rozkładu s dla zmiennych standaryzowanych. Standaryzacja polega
na tym,
e zmienn unormowan przekształcamy dziel c j przez odchylenie standardowe. Jak podzielimy zmienn
unormowan przez odchylenie standardowe to otrzymamy zmienn standaryzowan .
Zmienna standaryzowana posiada dwie cechy:
-
warto ć rednia wynosi Ń,
- wariancja jednostkowa wynosi ń, a tym samym odchylenie standardowe te wynosi ń.
N (0,1)
– oznacza, e jest to standaryzowany rozkład unormowany.
Operacja niedopuszczalna na liczbach skali przedziałowej to dzielenie, nie wolno przeprowadzać proporcji.
SKALA STOSUNKOWA
Dochodzi kolejny element
– zero naturalneś Mo na stosować operacje arytmetyczne.
Liczby maj wszelkie cechy liczb pomiaru przedziałowego, a ponadto znane jest zero naturalne.
Je li zmienna jest wyra ona w jednostkach pieni nych to jest to zmienna ekonomiczna.
Zmiennymi ekonomicznymi wyra onymi w jednostkach niepieni nych s jednostki naturalneŚ kg, litry.
→zgl dne miary ekonomiczneŚ stopa inflacji (wyra ona w punktach procentowych – zamienna ekonomiczna).
Stopa bezrobocia to zmienna mierza
lna, jest po cz ci zmienn ekonomiczn , a po cz ci zmienn społeczn .
6
parametry elementarne
n x 1 n x (k+1)(k+1) x 1 n x 1
n x 1
- PODSTAWY EKONOMETRII -
→YKŁAD γ
04.03.2011r.
TEMAT: LINIOWY MODEL EKONOMETRYCZNY.
Liniowy model ekonometryczny
→ liniowym modelu ekonometrycznym mamy dwie grupy elementówŚ
1) zmienne:
- zmienna obja niana – składnik losowy,
- zmienne obja niaj ce – powinny być nielosowe,
2) parametry modelu:
- parametry strukturalne,
- parametry struktury stochastycznej modelu.
Parametrami strukturalnymi
s wszystkie α. One informuj o strukturze powi za w modelu.
Parametry struktury stochastycznej modelu
dotycz pewnej cz ci modelu, musz one dotyczyć parametrów
rozkładu składnika losowego.
Parametry opisuj ce rozkład zmiennej losowejŚ
a)
nadzieja matematyczna (warto ć oczekiwana),
b) wariancje.
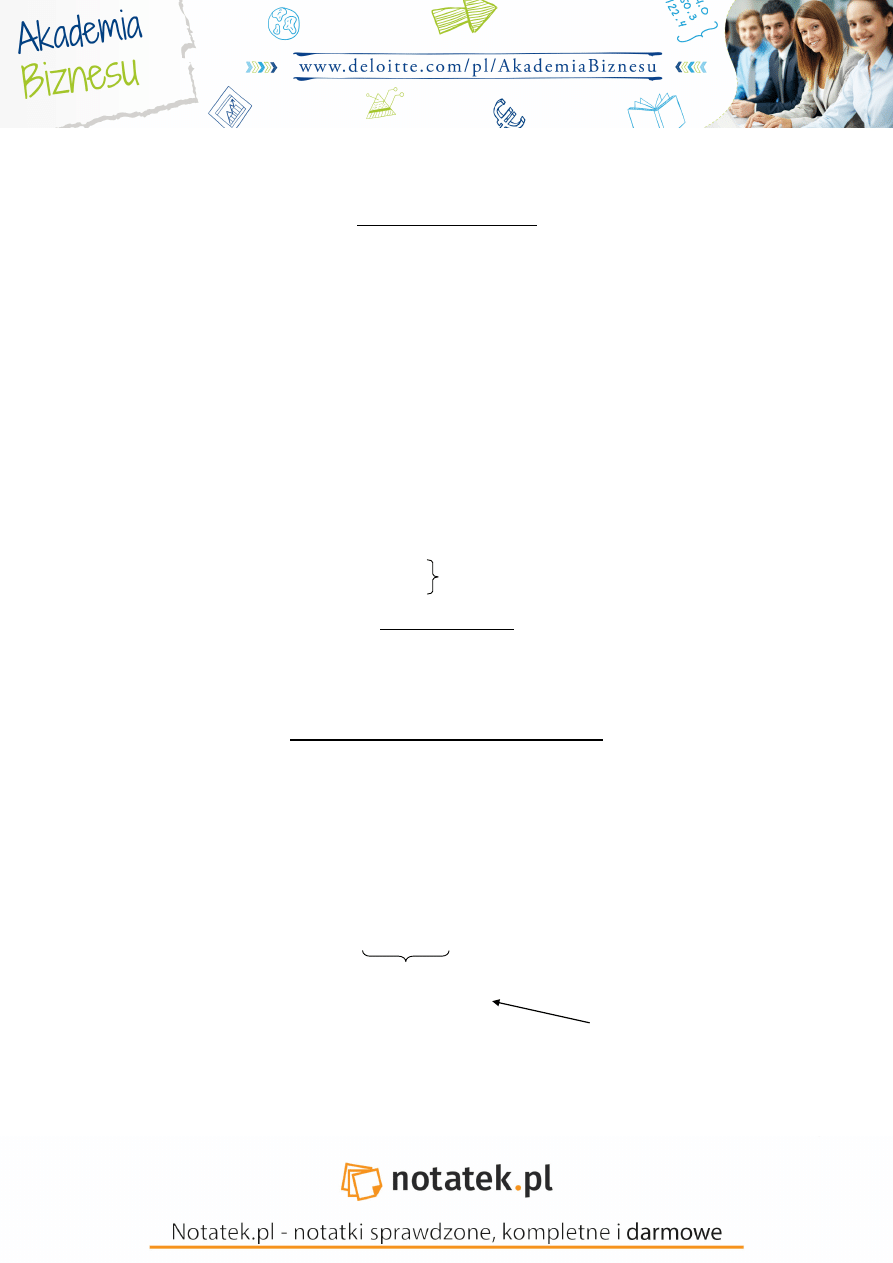
Macierzowy zapis modelu
Zapis macierzowy, który uwzględnia obserwacje statystyczne
W tym modelu Y jest wektorem n x 1
Model liniowy dla obserwacji statystycznej na zmiennej obja nianej
X
– jest macierz obserwacji dla zmiennych obja niaj cych, ma ona n-wierszy oraz k+1 kolumn
α – to wektor parametrów strukturalnych (to wektor kolumnowy o k+1 wierszy) k+1 x 1
η – jest wektorem składników losowych.
lewa strona = prawa strona
zapis jest równoznaczny
X
· α – taki iloczyn jest dopuszczalny
α · X – taki iloczyn nie jest dopuszczalny
t
tk
k
tj
j
t
t
x
x
x
y
...
...
1
1
0
t
tk
tj
t
x
x
x
f
y
,...,
,...,
1
X
Y
X
Y
k
j
t
tj
j
t
x
y
0

7
n x (k+1)
obserwacje na
zmiennych obja niaj cych
x
t1
x
tj
x
tk
(k+1)x1
n x 1
Dwie macierze s macierzami obserwacji statystycznej (m·y i m·x zawieraj obserwacje statystyczne)
Natomiast wektory
α i η s wektorami elementów nieobserwowalnych, które b dziemy szacować (α i η podlegaj
szacowaniu
– estymacji)
zmienna obja niana – cena ropy naftowej
zmienna obja niaj ca – czynniki, które wpływaj na cen ropy naftowej (np. popyt na rop , technologia
wydobywania)
Z
mienne s obserwowalne
Parametry s nieobserwowalne (α
0
, α
1
, … , α
k
) -
szacuje si je lub estymuje
Dowolny parametr strukturalny z wyj tkiem α
0
informuje o tym jak zmienia si ( o ile si zmieni ) wielko ć
zmiennej
obja nianej, je li warto ć zmiennej obja niaj cej x
j
wzro nie o jednostk przy zało eniu, e wielko ć
pozostałych zmiennych obja niaj cych nie ulega zmianie ( przy zasadzie ceteris paribus). Parametry strukturalne s
nieznane mo emy je oszacować (przyj ć w przybli eniu).
Składnik losowy – wyst puje w modelu strukturalnym (zawsze opisujemy z dokładno ci do składnika losowego,
który jest nieobserwowany i podlega estymacji).
Oszacowane wielko ci losowych nosz nazw modelu.
ETAPY BUDOWY MODELU EKONOMETRYCZNEGO
→ zale no ci od stopnia koncentracji zagadnie mo emy wyró nić od 5 do ńŃ etapów budowy modelu.
Najbardziej skoncentrowany sposób post powania pozwala wyró nić 5 etapów budowy modelu ekonometrycznego:
ETAP I
– Specyfikacja modelu
ETAP II
– Identyfikacja modelu
ETAP III
– źstymacja parametrów modelu
ETAP IV
– Weryfikacja modelu]
ETAP V
– Eksploatacja modelu (wyzysk modelu)
n
t
y
y
y
Y
1
n k
n j
n
tk
tj
t
k
j
x
x
x
x
x
x
x
x
x
X
1
1
1
1
1 1
1
1
1
k
j
1
0
n
t
1
Obserwacje na zmiennej X
zaczynamy od x
t0,
np.
(x
t0
– zmienna „ lepej”)

8
E
ETAP I
– Specyfikacja modelu
Jak w ka dym badaniu nale y po pierwsze zdefiniować jego cel, okre lić zakres badania zarówno czasowy jak te
przestrzenny oraz wybrać metody bada .
→ specyfikacji wyró niamy dwie fazyŚ
Faza 1
– specyfikacja zmiennych modelu – w tej fazie rozwi zuje si problem celu, zakresu i metody,
Faza 2
– specyfikacja równa modelu.
Faza 1 - Specyfikacja zmiennych modelu -
→adliwo ć specyfikacji modelu skutkuje wadliwym modelem. Specyfikacje
modelu ekonometrycznego mo na dokonać tylko ekonomista, jest ona bardzo wa na.
→ fazie specyfikacji po pierwszeŚ musimy wskazać przedmiot badania, np. inflacja, popyt na sprz t elektroniczny
gospodarstwa domowego, mechanizm ks
ztałtowania si płac.
→skazujemy czynniki, które wpływać mog na to, co badamy, np., gdy badamy inflacj to zmienn obja nian b dzie
stopa inflacji; zastanawiamy
si , od czego zale y inflacja, co mo e na ni wpływać, np. dynamika płac, stopy
procentowe, kursy walut.
WARTO Ć NETTO = warto ć pocz tkowa – umorzenie
Definiujemy zmienne obja niaj ce (ekwiwalentne) w stosunku do czynników.
Musimy zgromadzić dane statystyczne, je li tego nie zrobimy to o modelu mo na zapomnieć. Bez informacji model nic
nie zna
czy. Te dane statystyczne musz być rzetelne, kompletne, porównywalne, tzn. jednolite definicyjnie i w
jednolitych cenach.
Kompletne
– nie mo e być uszczerbku w szeregu jakichkolwiek braków.
Mo na uzupełnić szereg statystyczny metod interpolacji.
Mo na te szacować technik ekstrapolacji szeregu statystycznego.
Żaza specyfikacji zmiennych ko czy si , gdy posiadamy kompletne informacje statystyczne o zmiennej obja nianej i
zmiennych obja niaj cych.
To pozwala przej ć do fazy specyfikacji równa .
Faza 2 -
Specyfikacja równań modelu – Je li jest to model składaj cy si z jednego równania to musimy wskazać
hipotetyczn jego postać analityczn . To mo e być wariant modelu liniowego lub modelu nieliniowego, najcz ciej
bywa to model iloczynowy.
ETAP II
– Identyfikacja modelu – Identyfikacja wyst puje tylko w przypadku modelu wielorównaniowym. →
modelach jednorównaniowych nie ma etapu II.
ETAP III
– Estymacja parametrów modelu – źstymacja modelu odbywa si w dwóch fazachŚ
Faza 1
– dokonujemy wyboru estymatora, czyli funkcji pewnego narz dzia do szacowania parametrów modelu.
Jak dokonać wyboru?
Dokonujemy wyboru estymatora kieruj c si pewnymi kryteriami (stosuje si trzy kryteria czasami doł cza si czwarte
kryterium):
1. estymator zgodny –estymator powinien być zgodny,
2. estymator nieobci żony – estymator pozbawiony bł du systematycznego
Estymator nieobci żony
3. estymator efektywny
– poszukujemy estymatora najbardziej efektywnego w danej klasie. Miar efektywno ci
estymatora jest wariancja.
źstymator bardziej efektywny jest estymatorem bardziej precyzyjnym, a wynika to z poj cia precyzji w statystyce.
Miar niedokładno ci estymatora jest odchylenie standardowe. Im wi ksze b dzie odchylenie standardowe estymatora
tym jest on mniej dokładny.
9
1
Y
Odwrotno ć odchylenia standardowego nosi nazw precyzji.
Precyzja
Im wi ksze odchylenie standardowe tym precyzja mniejsza. źstymator bardziej precyzyjny tym jest lepszy i jest bardziej
efektywny.
4.
dostateczno ć estymatora
Faza 2
– Faza obliczeń numerycznych - Dysponuj c estymatorem wykorzystujemy go do oblicze numerycznych
maj c do dyspozycji zapisane w macierzach ↓ oraz Y dane statystyczne.
→ wyniku oblicze numerycznych uzyskujemy szacunki albo oceny parametrów modelu (zarówno parametrów
składników losowych oraz oceny parametrów stochastycznej struktury modelu).
Mo emy przej ć do weryfikacji modelu.
- PODSTAWY EKONOMETRII -
→YKŁAD 4
11.03.2011r.
ETAP IV
– Weryfikacja modelu – Weryfikacja modelu dzieli si na dwie fazyŚ
Faza 1
– Weryfikacja statystyczna – polega na wykorzystaniu statystycznych miar ogólnej dobroci modelu lub
ogólnych dokładno ci modelu oraz szczegółowych miar dobroci modelu.
Ogólne (globalne) dobroci pozwalaj na ocen roli składnika losowego w modelu.
Model b dzie tym lepszy im mniejsz rol b dzie odgrywał składnik losowy.
[Szczegółowe miary dobroci (s to miary statystyczne) pozwol ocenić pewne charakterystyki składnika losowego pod
k tem tego, czy jest on, tzw. czystym składnikiem losowym, bo takim być powinien i wreszcie dokonuje si oceny
znaczenia ka dej ze zmiennych obja niaj cych w tym sensie, e model empiryczny powinien zawierać wył cznie
wa ne, czyli istotne statystycznie zmienne obja niaj ce, czyli takie, których parametr strukturalny jest ró ny od zera.
Je li b d zmienne nieistotne to narz dziami statystyki mo na to ustalić i zmienne nieistotne powinny zostać usuni te.
Je li model jest dobry i jego własno ci oraz zawiera wył cznie wa ne zmienne obja niaj ce to mo na przej ć do jego
weryfikacji ekonomicznej.]
←mywamy testów statystycznych – sprawdzamy hipotezyś Składnik losowy powinien odgrywać niewielk rol i być
tzw.
czystym składnikiem losowym, zmienne obja niaj ce modelu empirycznego winny być istotne statystycznie, czyli
takie, których parametr strukturalny jest ró ny od zera.
Je eli w trakcie weryfikacji oka e si , e model spełnia wszystkie cechy jako ciowe modelu ekonometrycznego i mamy
akceptowalny model empiryczny i mo emy przej ć do jego eksploatacji pod warunkiem, e jest on logiczny
ekonomicznie. Je li model jest wadliwy statystycznie to nale y go poprawić, czyli powrócić do jego specyfikacji,
mówimy wówczas o respecyfikacji modelu.
Respecyfikacja
mo e polegać na usuni ciu zmiennej obja niaj cej, dodania nowej zmiennej obja niaj cej albo zmianie
postaci analitycznej równania.
Empiryczny model akceptowany statystycznie poddajemy weryfikacji ekonomicznej, czyli sprawdzamy jego
ekonomiczn logik . Je eli potrafimy wyja nić ekonomiczn logik modelu empirycznego to uznajemy, e jest on w
pełni akceptowany i kwalifikuje si do eksploatacji.
Faza 2 - Weryfikacja ekonomiczna modelu
pozytywnie zweryfikowana pod wzgl dem statystycznym polega na
ocenie ekonomicznej jego logiki zwłaszcza zgodno ci z teori .
Przykład 6.
Jak działa cena na popyt na dobro podstawowe?
Ze wzrostem ceny popyt spada. → naszym badaniu okazuje si , e cena nie wpływa na popyty (popyt jest sztywny,
poniewa cena nie działa). Mo e si zdarzyć tak, e ze wzrostem ceny popyt ro nie.
10
y
t
x
t
y
t
= α
0
+ α
1
x
t
+ u
t
ŷ
t
= α
0
+ α
1
x
t
x
x
x
x
x
x
x
x
x
x
x
x
x
→eryfikacja ekonomiczna polega na wła nie takiej interpretacji logicznej w oparciu o literatur i do wiadczenia. Je li
uznamy, e model jest ekonomicznie logiczny. Ko czy si weryfikacj modelu i mo emy przej ć do eksploatacji
ETAP V
– Eksploatacja modelu - Najcz ciej model ekonometryczny wykorzystywany jest do szacowania prognoz (do
przewidywania tego, co
stanie si w przyszło ci).
Od Sylwii: {Eksploatacja
– praktyczne wykorzystanie modelu:
mo na go wykorzystać wielorako – mo e być narz dziem szacowania prognoz zmiennych ekonomicznych –
przyszłe warto ci rozpatrywanych zmiennych ekonomicznych.
Bud et składa si z cz ciŚ
-
dochodowej, czyli prognoz wpływu bud etowego
- wydatkowej
Wykorzystanie modelu ekonometrycznego: (obszary eksploatacji)
szacowanie prognoz
symulacja – rozwi zywanie rozmaitych wariantów decyzyjnych – najbardziej korzystnych; racjonalnych
rozwi za
podejmowanie bie cych decyzji zarz dczych – np. wybór sprawnego pracownika.}
Prognozy ekonometryczne stanowi grup najdoskonalszych, najlepszych, najbardziej precyzyjnych, najmniej
uzale nionych od woluntaryzmu prognoz.
→szelkie prognozy makroekonomiczne konstruowane s za pomoc modeli ekonometrycznych.
Prognozy stóp procentowych, prognozy kurów walutowych, prognozy ż←S-u s prognozami ekonometrycznymi
opartymi na modelach, wi c najcz stszym kierunkiem wykorzystania modelu jest budowa prognoz.
Drugi kierunek
– model mo e być narz dziem symulacji ekonomicznej. Symulacja ekonomiczna polega na
wariantowaniu mo liwo ci decyzyjnej.
- PODSTAWY EKONOMETRII - W
YKŁAD 4 c.d.
11.03.2011r.
ESTYMULACJA PARAMETRÓW MODELU
KLASYCZNA METODA NAJWI KSZYCH KWADRATÓW (KMNK)
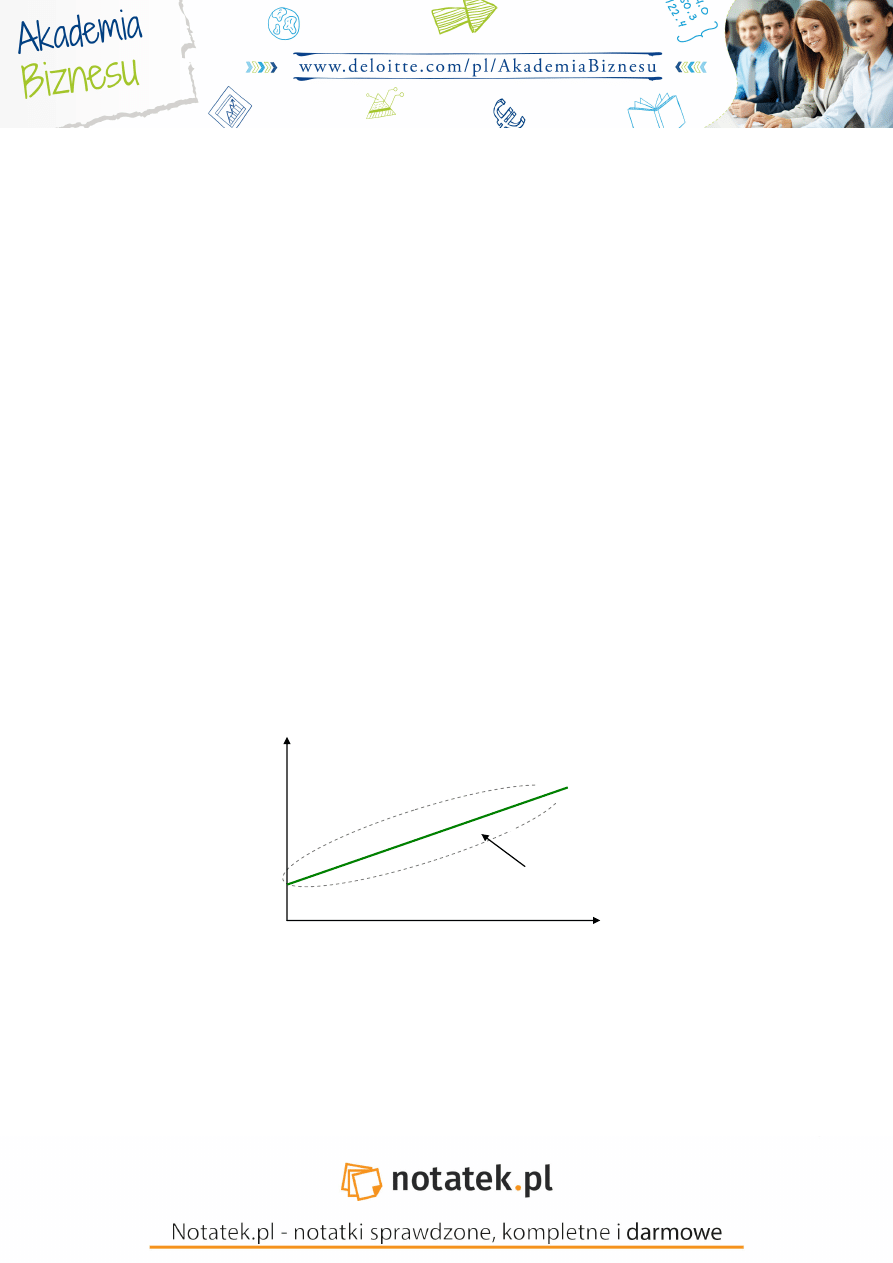
x
– punkty empiryczne – obserwacje statystyczne
Im wy sze działania marketingowe tym wy sze przychody ze sprzeda y. Jest to pewna smuga, nale y dopasować
przebieg prostej do y-
tych rozrzutów.
Aprokrymanta
– to prosta wyrównuj ca
Jak dopasowujemy prostą wyrównującą?
Kierujemy si tym, eby składnik losowy empirycznych reszt grał jak najmniejsz rol .
Hiperpłaszczyzna, – gdy wyst puje wiele zmiennych obja niaj cych.
Musimy znale ć prost , dla której suma reszt b dzie zerowa.
α
1
=tgγ
dane rzeczywiste
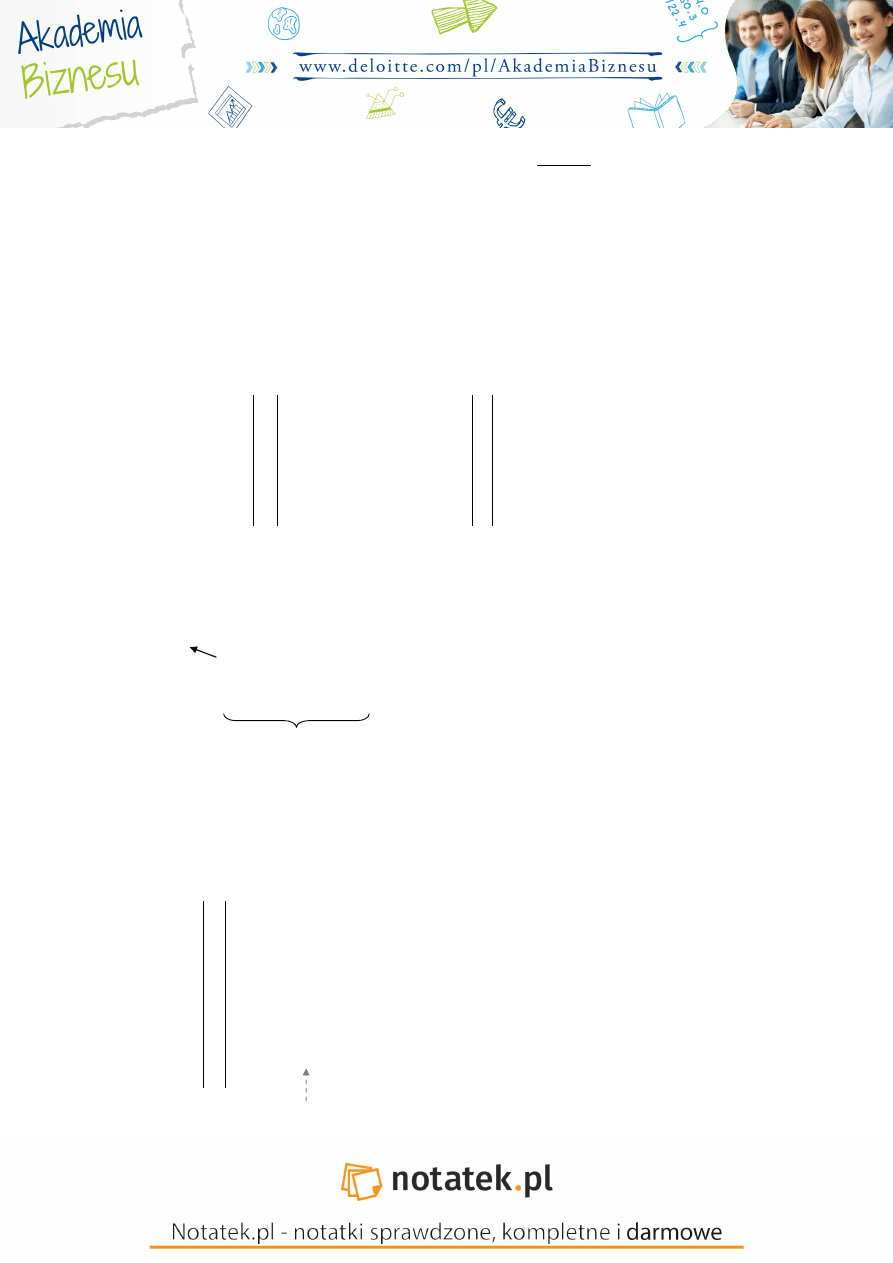
11
n
t
U
U
U
U
1
n
t
y
y
y
Y
1
Y
Y
U
)
(
)
(
Y
Y
T
Y
Y
U
T
U
S
Y
X
X
X
T
T
1
)
(
t
t
t
y
y
U
ˆ
k
j
1
0
żauss wpadł na pomysł, aby interpretować sum kwadratów reszt, e jest ona minimalna.
=
−
2
=
2
=1
Suma
kwadratów reszt jest parabol , charakteryzuj ca si tym, e posiada extremum (max lub min.).
szukamy funkcj posiadaj c minimumŚ
-
warunek konieczno ci
- warunek dostateczny
Powstaj ró nice U
t
mi dzy warto ciami rzeczywistymi y
t
a warto ciami teoretycznymi ŷ
t.
B
dziemy chcieli zminimalizować sum kwadratów reszt, przy czym u jest wektorem reszt n x1, który powstaje
Ze znalezienia wektora
ŷ
i wektora warto ci teoretycznej zmiennej obja nianej.
Minimalizujemy funkcj S
=
estymator
=
=
− − =
−
−
+
=
=
− 2
+
Estymator KMNK (
ά
) równa si Ś
Je li dokonamy przekształce macierzy X i Y to otrzymamy ά, w którym b d szacunki modelu liniowego i otrzymamy
wektor takich składowychŚ
Estymator Gaussa
Ten iloczyn jest dozwolony, poniewa wewn trzne parametry s takie same.
-
jest to suma kwadratów reszt
←, Ŷ – wg warto ci
z linii prostej
n x 1
n x 1
(k+1) x n n x (k+1)
X
X
T
(k+1) x (k+1)
- to macierz HESSA, zwana hesjanem
iloczyn wielomianu
1x1
1x1
1x1
1x1
Y
X
X
X
T
T
1
)
(

12
(k+1) x n n x 1
(k+1) x (k+1)
(k+1) x 1
(k+1) x 1
α
1
α
j
α
k
x
t1
x
tj
α
tk
A) Jest to macierz kwadratowa, stopnia k+1. Tego typu konstrukcja generuje macierz o jeszcze jednej charakterystyce.
B) Macierz symetryczna
– charakteryzuje si tym, e istniej pary identycznych elementów, np.
macierz jest systematyczna, je li istniej takie paryŚ
a
25
= a
52
i ≠ j
Macierz Hessa
nale y do klasy pewnych form. Jest form kwadratow , a to oznacza, e jej wyznacznik nie mo e być
ujemny.
źstymator powinien dać wynik o postaci wektora (k+1) x 1, a wi c powinien dać wynik o postaci parametrów
strukturalnych.
Macierz nie mo e być osobliwaś mo e być okre lona dodatnio wtedy istnieje macierz odwrotna. Powstaje macierz
jednostkowa, stopnia k+1
- PODSTAWY EKONOMETRII -
→YKŁAD 5
18.03.2011r.
Warunki stosowania KMNK
Warunek 1.
Model musi być liniowy, mo liwe jest jednak stosowanie KMNK do modeli nieliniowych, które daje
si zlinearyzować, czyli sprowadzić do postaci liniowej.
Je eli model nieliniowy mo na zlinealizować to do tej wersji niezlinearyzowanej wolno stosować metod KMNK.
Istnieje wiele modeli
nieliniowych, które daj si zlinearyzować. Model iloczynowy (in. model multiplikatywny)
mo e wyst pować w postaci pot gowej.
Pierwsz gr. takich modeli s modele iloczynoweŚ
pot gowe
Model
iloczynowy pot gowy
e
– podstawa logarytmu naturalnego
η – składnik losowy
wykładnicze
Model iloczynowy wykładniczy
Model pot gowy ma zastosowanie do zmiennych ci głych, których obserwacje osi gaj wył cznie warto ci
dodatnie. Zmienna obja niana w ka dym z tych modeli musi osi gać wył cznie warto ci dodatnie, nie wolno np.
unormować zmiennej obja nianej.
ij
a
A
n x n
ji
ij
a
a
X
X
T
Y
X
T
t
e
x
x
x
y
tk
tj
t
t
1
0
t
e
y
k
j
t
1
0

13
za podstawiamy
0
)
(
T
X
E
Modele wykładnicze mo na stosować zarówno dla zmiennych ci głych jak i dla zmiennych skokowych,
dyskretnych.
Oba te modele mo na zlinealizować traktuj c je obustronnie.
Model linowy:
Dokonujemy podstawie Ś
Po podstawieniach otrzymujemy model:
-
Model pot gowyŚ
Model wykładniczyŚ
Model hiperboliczny
– jest modelem nieliniowym, ale je li istnieje mo liwo ć nale y sprowadzić go do postaci
linowej.
Model logistyczny -
…(spr. w ksi ce)
Warunek 2.
By estymator KMNK był nieobci ony zmienne obja niaj ce modelu powinny być nielosowe. Losowo ć
zmiennych obja niaj cych powoduje, e estymator KMNK jest obci ony.
Warunek 3.
Zmienne obja niaj ce modelu nie powinny być skorelowane ze składnikiem losowym modelu, co
zapisujemy w nast puj cy sposóbŚ
(→szelkie kowariancje obja niaj ce ze składnikiem losowym powinny być zerowe.)
Je li ten warunek nie jest spełniony to estymator KMNK nie jest zgodny.
Warunek 4.
Rz d macierzy dla zmiennych obja niaj cych musi być równy liczbie parametrów strukturalnych modelu.
rz(x) = k+1
t
tk
e
tj
j
t
t
x
x
x
y
ln
ln
ln
ln
ln
1
1
0
t
tk
k
tj
j
t
t
y
*
*
*
1
1
*
0
*
t
t
x
t
t
t
t
e
x
x
y
t
4
0
3
3
2
2
1
1
*
*
0
0
*
ln
ln
ln
tj
tj
t
t
x
x
y
y
)
,
,
1
(
k
j
t
tk
k
tj
j
t
t
x
x
x
y
*
*
*
1
1
*
0
*
-
model pot gowo – wykładniczy
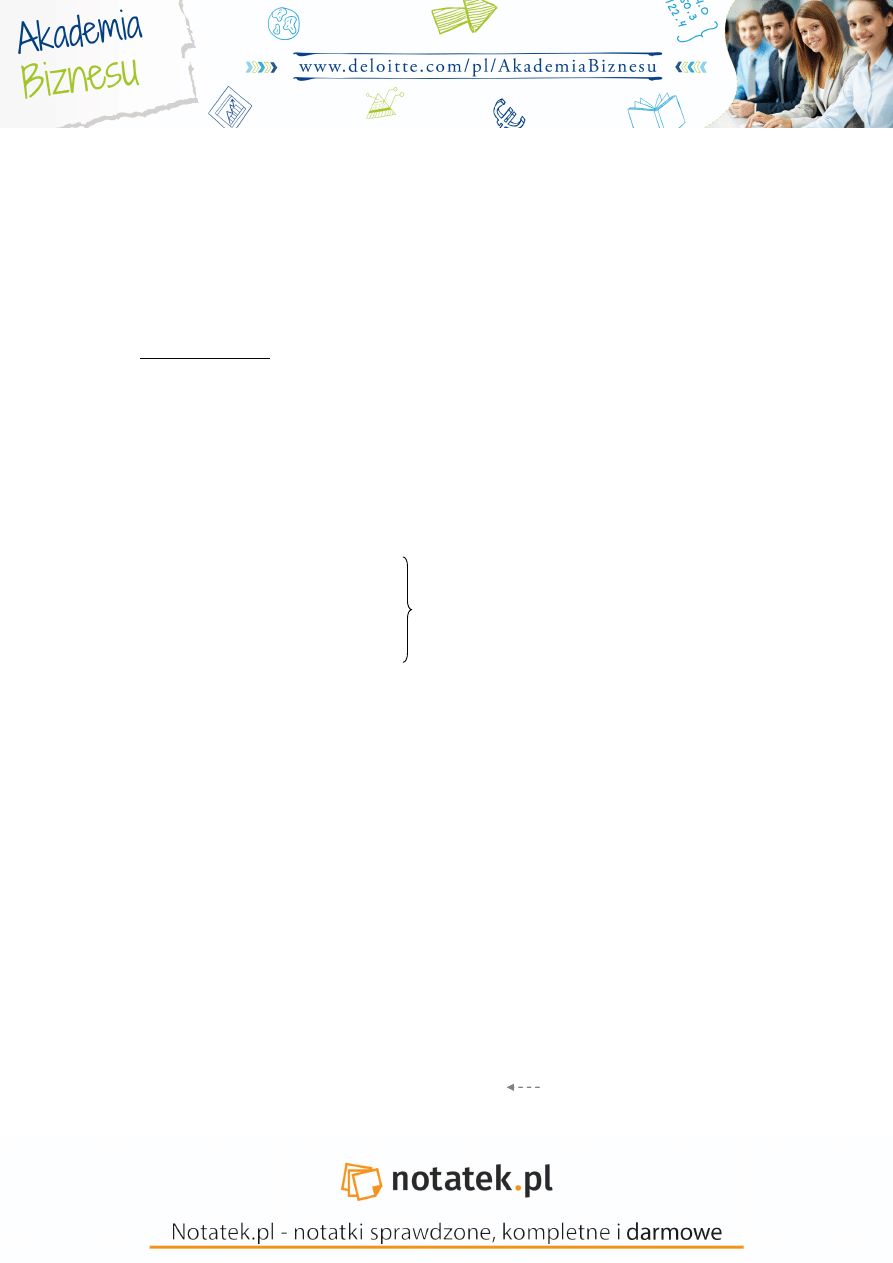
14
`
'
1
0
tj
j
j
tj
x
x
2
2
n
t
n
t
t
t
n
t
→arunek ten nie jest spełniony Ś
-
je li w modelu pojawi si współliniowo ć determistyczna zmiennych obja niaj cych to rz d macierzy ↓ b dzie
mniejszy ni k+ń.
-
je eli rz(x)< k+ń to jest ona osobliwa, a je eli macierz Hessa jest osobliwa to nie istnieje macierz odwrotna.
Rz d macierzy Hessa w tym przypadku b dzie
rz(x
T
x) < k+1
Bł d specyfikacji modelu - dopuszczono współliniowo ć deterministyczn .
Współliniowo ć deterministyczna – jest elementarnym bł dem specyfikacji modelu, oznacza ona, e w modelu
istnieje, co
najmniej jedna para zmiennych obja niaj cych w postaci kombinacji liniowej, czyli
dla wszystkich j, j
’
= 0,1,2,...,k
j ≠ j
’
Nale y przebudować model – usuni cie jednej zmiennej z modelu, bo jest zb dna …(jak na zaj ciach)
=
ść �
− ł ć
=
1
0
ęż
ź
− ł ć
=
1
ęż
ź
0
Warunek 5.
Składnik losowy powinien być tzw. czystym składnikiem losowym ( lub sferycznym).
ń) Powinien być jednorodny (homostetastyczny)
2) Bez autokorelacji
Struktura macierzy:
=
2
�
diagonalne elementy to wariancje
, natomiast pozostałe s to kowariancje.
1) →AR←NźK JźDNORODNO CIŚ
Oznacza to, e wszystkie wariancje dla wszystkich obserwacji s sobie równe i s równe jednej obserwacji składnika
losowego.
Jest to niedopuszczalne
2
2
1
2
2
1
2
2
2
2
1
2
1
1
2
1
2
1
)
cov(
)
cov(
)
cov(
)
cov(
)
cov(
)
cov(
)
cov(
)
cov(
)
cov(
)
cov(
)
cov(
)
cov(
n
t
n
n
n
n
t
t
t
t
n
t
n
t
równo ć wariancji
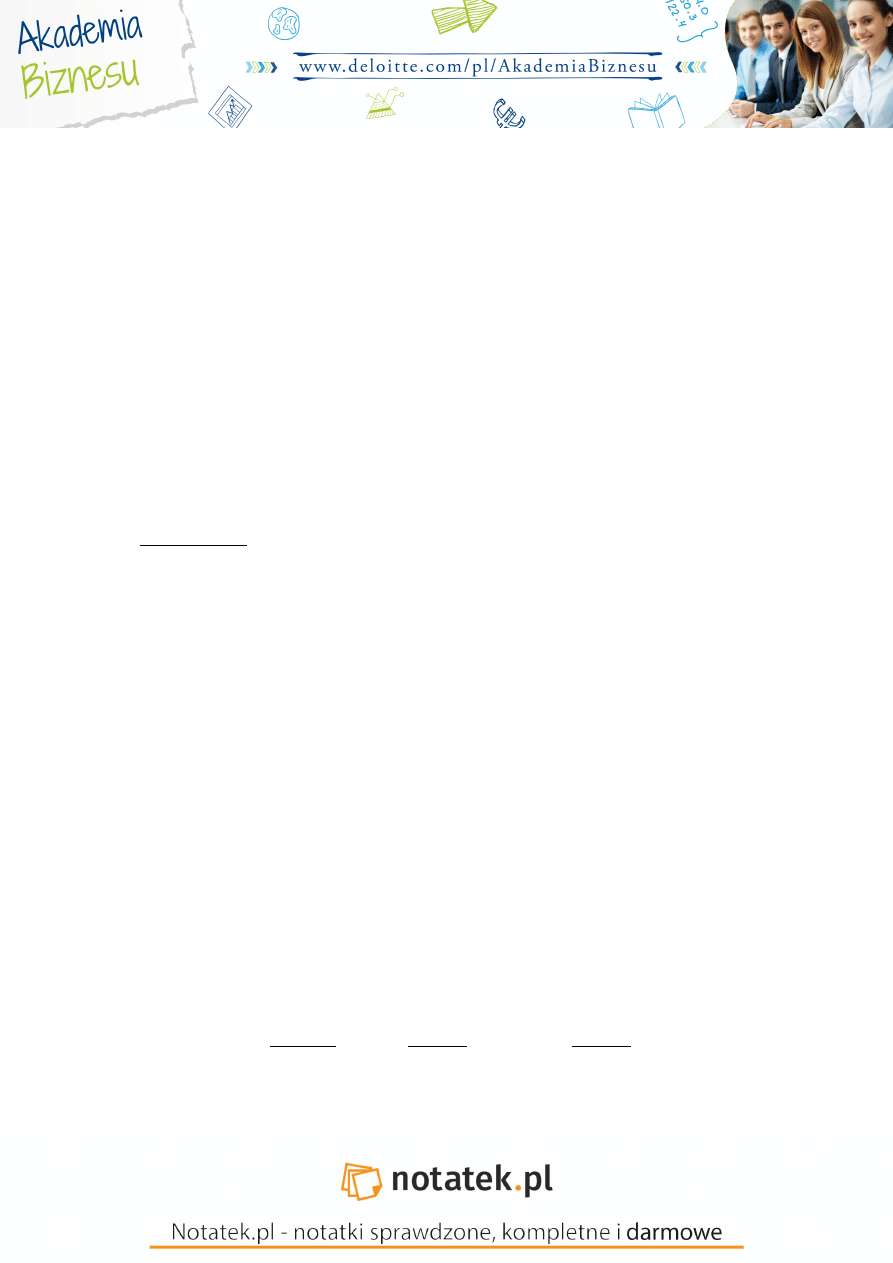
15
0
)
cov(
`
t
t
Je li ten warunek jednorodno ci wariancji nie jest spełniony, pogarsza si efektywno ć estymatora KMNK. Pogarszanie
efektywno ci estymatora mo e prowadzić do bł du poznawczego, który przejawia si tzw. pozorn nieistotno ci
zmiennej obja niaj cej (jednej lub wielu).
2) BRAK AUTOKORELACJI
Je li ka da z kowariancji b dzie równa zero, bo to oznacza brak autokorelacji składnika losowego.
t, t‘ = 1, ... , n ś t
t‘
Kowariancja wyst puje zawsze w liczniku współczynnika korelacji (statystyka).
Autokorelacja nie powinna si pojawić w modelu składnika losowego.
Wystąpienia autokorelacji:
Pogorszenie efektywno ci estymatora KMNK
Warunek 6.
→ modelu nie powinna wyst pić współliniowo ć stochastyczna zmiennych obja niajacych
r (x
ej
, x
ej’
) = Ń (j j’ = Ń,ń, … , t
ij
, t
ij’
)
Zbiór zmiennych ortogonalnych (nie istnieje)
Sprawdzenie korelacji
Aby sprawdzić czy jest korelacja czy nie ma nale y si posłu yć narz dziem – testem statystycznym
t- Studenta na poziomie
istotno ci, czyli bł dy pierwszego rodzaju.
Brak współliniowo ci stochastycznej oznacza, e wszystkie współczynniki korelacji dla ka dej z par zmiennych
obja niaj cych s statystycznie nieistotne na rozs dnym poziomie istotno ci przy zastosowaniu, np. testu t- Studenta
Je li w modelu wyst puje współliniowo ć stochastyczna to pogarsza si efektywno ć estymatora KMNK, co mo e prowadzić
do bł du poznawczego. Zasadniczo w przypadku współliniowo ci stochastycznej eliminuje si jedn z pary zmiennych
obja niaj cych wzajemnie skorelowanych. Liniowo ć schochastyczna jest trudna do unikni cia istniej takie modele
ekonometryczne, w których współliniowo ć stochastyczna jest nieunikniona przykładem mo e być model produkcji znany od
blisko 100 lat
– model Coma Daglasa
Pt =
α0 Lt + Kt
P
t
=
α
0
L
t
α
1
+ K
t
α
t
+ e
ηt
P
– produkcja
L-
nakłady pracy ywej
K
– nadkłady kapitalne, przy czym Kt najcz ciej reprezentowane jest przez maj tek fabryki
Zwi zek mi dzy kapitałem a prac Ś
-
komplementarno ć
-
substytucja pracy, kapitału
Wariancja składnika losowego za pomoc wariancji resztowej
2
=
1
− − 1
2
=1
=
1
− − 1
−
2
=
1
− − 1
wariancja resztowa nieobci ony estymator składnika losowego

16
n
t
t
u
u
k
n
S
1
2
2
)
1
(
1
n
t
t
n
t
t
y
y
y
y
1
2
1
2
)
(
)
(
n
t
t
n
t
t
y
y
U
1
2
1
2
)
(
n
t
t
n
t
t
y
y
y
y
R
1
2
1
2
2
)
(
)
(
n
t
t
n
t
t
y
y
U
Y
1
2
1
2
2
)
(
%
100
y
S
V
u
- PODSTAWY EKONOMETRII -
→YKŁAD 6
25.03.2011r.
1) →ariancja resztowa (z poprzedniego wykładu)
→ariancja powinna być mała – im mniejsza tym lepiej
→ariancji si nie interpretuje.
2) Interpretujemy BŁ D STANDARDO→Y RźSZTŚ
=
1
− −1
2
=1
Interpretacja S
u
S
U
informuje o tym, o ile rednio rzecz bior c teoretyczne warto ci zmiennej obja nianej (ŷ
t
) obliczone na podstawie
modelu empirycznego ró ni si od empirycznych (rzeczywistych) warto ci zmiennej obja nianej, yt.
Su nie daje mo liwo ci porównywania, jako ci dwóch ró nych modeli ĄĄĄ
3)
Wsp
ółczynnik zmienno ci losowej – mierzy udział bł du standardowego reszt w redniej …………..
←dział zmienno ci losowej powinien być mały.
Buduj c model staramy si stworzyć taki model empiryczny, w którym udział zmiennej zmienno ci losowej b dzie
mały. (?)
( − )
2
=
( − )
2
+
( − )
2
=1
=1
=1
całkowita masa zmienno ci
+
=
1
4) Dwie miary:
Bł d standardowy reszt jest estymatorem odchylenia
standardowego składnika losowego.
Su jest liczb mianowan ś Su jest w takich samych
jednostkach jak zmienna obja niana
R
2
– udział zmienno ci
powodowany przez zmienne
obja niaj ce w modelu
całkowitej zmienno ci
zmiennej obja nianej
�
2
-
współczynnik
zmienno ci oznacza udział
zmienno ci losowej zmiennej
obja nianej
R
2
– współczynnik
determinacji
Interpretacja:
Informuje o tym jak cz ć
całkowitej zmienno ci
zmiennej obja nianej
wyja niaj zmienne
obja niaj ce uwzgl dniane
w modelu empirycznym
(w%)
�
2
-
współczynnik zbie no ci
Interpretacja:
Informuje o tym jaka cz ć
całkowitej zmiennej
obja nianej modelu
empirycznego ma charakter
losowy (w%)
1
2
2
Y
R

17
1
2
3
4
k
S
2
)
(
2
D
PrzykładŚ
�
2
=0,042
R
2
=1-0,042=0,958
4,β % całkowitej zmienno ci zmiennej ze sprzeda y ma charakter losowy
95,8% całkowitej zmienno ci zmiennej ze sprzeda y wyja niaj zmienne obja niaj ce w modelu empiryczny.
Im wi ksze R
2
tym model jest lepszy/
REGUŁAŚ
Jeżeli �
�
jest poniżej 0,1 a R
2
powyżej 0,9 to uznajemy, że model jest dobry. – Ta reguła dot. tylko
makrodanych o rocznym okresie obserwacji.
Je eli mamy mikromodel opisuj cy np. model obliczaj cy w przedsi biorstwie oparty na danych miesi cznych to -
zyskanie R
2
na poziomie 0,75
– Ń,8Ń mo na uznać za du y sukces.
Nie widać waha sezonowych, okresowych w modelu rocznym te wahania s zatarte natomiast w danych
miesi cznych pojawiaj si wahania okresowe (sezonowe).
Na podstawie R
2
mo emy porównywać ró ne modele, ale o takich samych okresach obserwacji np. dla danych
rocznych b
d miesi cznych, ale w obu modelach musz być takie same dane.
5) Miary szczegółowe dobroci
Model empiryczny
=
0
+
1
1
+
… +
+
… +
+
(Sa
0
) (Sa
1
) (Sa
j
)
(Sa
k
)
„a” – oceny parametrów strukturalnych
Sa
1
porównujemy z a
1
- Sa
1
powinno być małe.
„Bł d oceny z oceny”
Pod ka d empiryczn znajdzie si redni bł d szacunku.
Bł dy w stosunku do oceny powinny być małe. Im mniejszy bł d tym wi ksza precyzja szacunku.
Bł dy powstaj z wariancji. Bł d jest pierwiastkiem kwadratowym wariancji. Najpierw musimy ustalić wariancj ocen
parametrów strukturalnych, a potem ich bł dów. Konieczne jest oszacowanie macierzy wariancji i kowariancji ocen
parametru strukturalnego
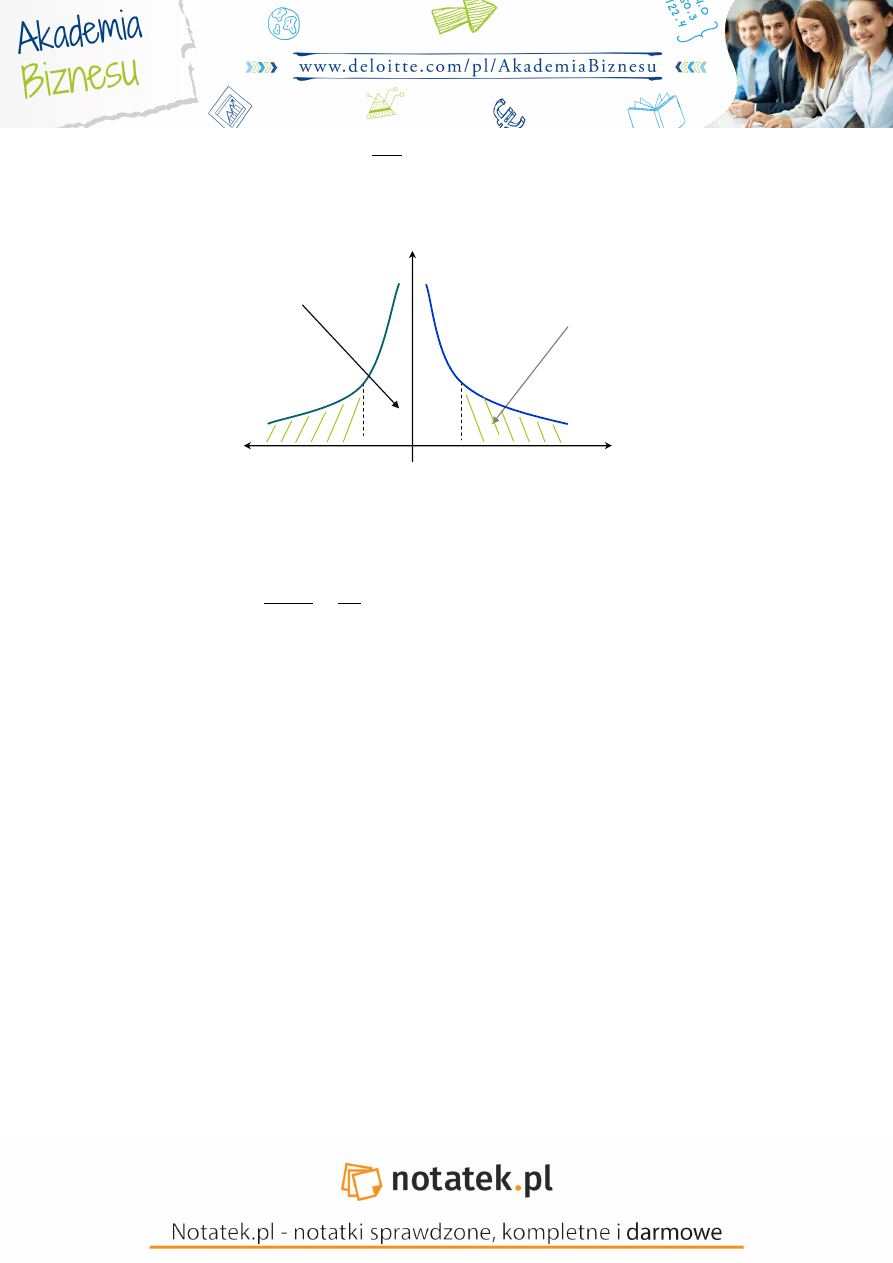
. Macierz oznaczać b dziemy symbolem Ś
2
=
2
(
)
−1
Macierz wariancji
– kowariancji = odwrotno ć macierzy Hessa
wariancja macierzy
Jest to macierz
symetryczneś diagonalne elementy s wariancjami a pozostałe kowariancjami
Struktura tej macierzy:
Interesuj nas elementy diagonalne macierzyŚ
1
,
2
,
3
i
4
.
Model z ocenami parametrów
Wszystko co
szacujemy, dokonujemy z jakim bł dem Ą
2
1
0
2
1
0
1
1
2
0
1
0
0
1
0
2
2
)
cov(
)
cov(
)
cov(
)
cov(
)
cov(
)
cov(
)
cov(
)
cov(
)
cov(
)
cov(
)
cov(
)
cov(
)
(
1
0
k
j
a
t
k
k
k
k
j
a
j
j
k
j
a
k
j
a
S
a
a
a
a
a
a
a
a
S
a
a
a
a
a
a
a
a
S
a
a
a
a
a
a
a
a
S
a
D
18
(j=0,1,...,k)
2
0
− łą
�
0
Stosunek oceny parametru strukturalnego do bł du redniego ma rozkład t-studenta.
6) Testowanie istotno ci zmiennych obja niaj cych w model
tγ – w statystyce nosi nazw warto ci krytycznej, przy czym γ w statystyce jest poziomem istotno ci.
Poziom istotno ci w statystyce oznacza ryzyko / prawdopodobie stwo popełnienia bł du pierwszego rodzaju, czyli
przyj cia fałszywej hipotezy zerowej. →ybieraj c ryzyko bł du pierwszego rodzaju wybieramy małe ryzyko. żama γ
powinna być liczb mał . Nie ma mo liwo ci wyboru z ryzykiem zerowym.
H
0:
α
j
= 0
=
−
=
H
1:
α
j
≠ Ń
Co mo emy zrobić z hipotez zerow ?
1) Powiedzieć, e nie ma podstaw do odrzucenia H
0
, odrzucamy H
0
na rzecz hipotezy alternatywnej.
Ń,Ńń ≤ γ ≤ Ń,Ń5
Na ogół staramy si , aby gamma tyle wynosiła.
1. t
j
≤ t ś n- k -ń nie ma podstaw do odrzucenia H
0
; j-
ta zmienna obja niaj ca jest nieistotna
2. t
j
˃ t ś n- k -1 odrzucamy H
0
na rzecz hipotezy alternatywnej i
wnioskujemy, e j-ta zmienna
obja niaj ca jest statystycznie istotna.
Testowanie zmiennych obja niaj cych t-studenta stawiamy hipotez zerow (hipotezy dotycz parametrów), e warto ć
parametrów j jest równa zero (j=Ń)
Przypadek 1.
→ hipotezie zakładamy, e zmienna x
5
nie wpływa na zmienn obja nian , natomiast w alternatywie wpływa.
Przypadek 2.
→ przypadku ń mówimy, e interesuje nas pewien typ obszaru krytycznego. Po takim rozkładzie hipotez mówimy o
dwustronnym obszarze krytycznym.
żdyby hipoteza alternatywna była „przypadkiem β” to byłby obszar prawostronny krytyczny.
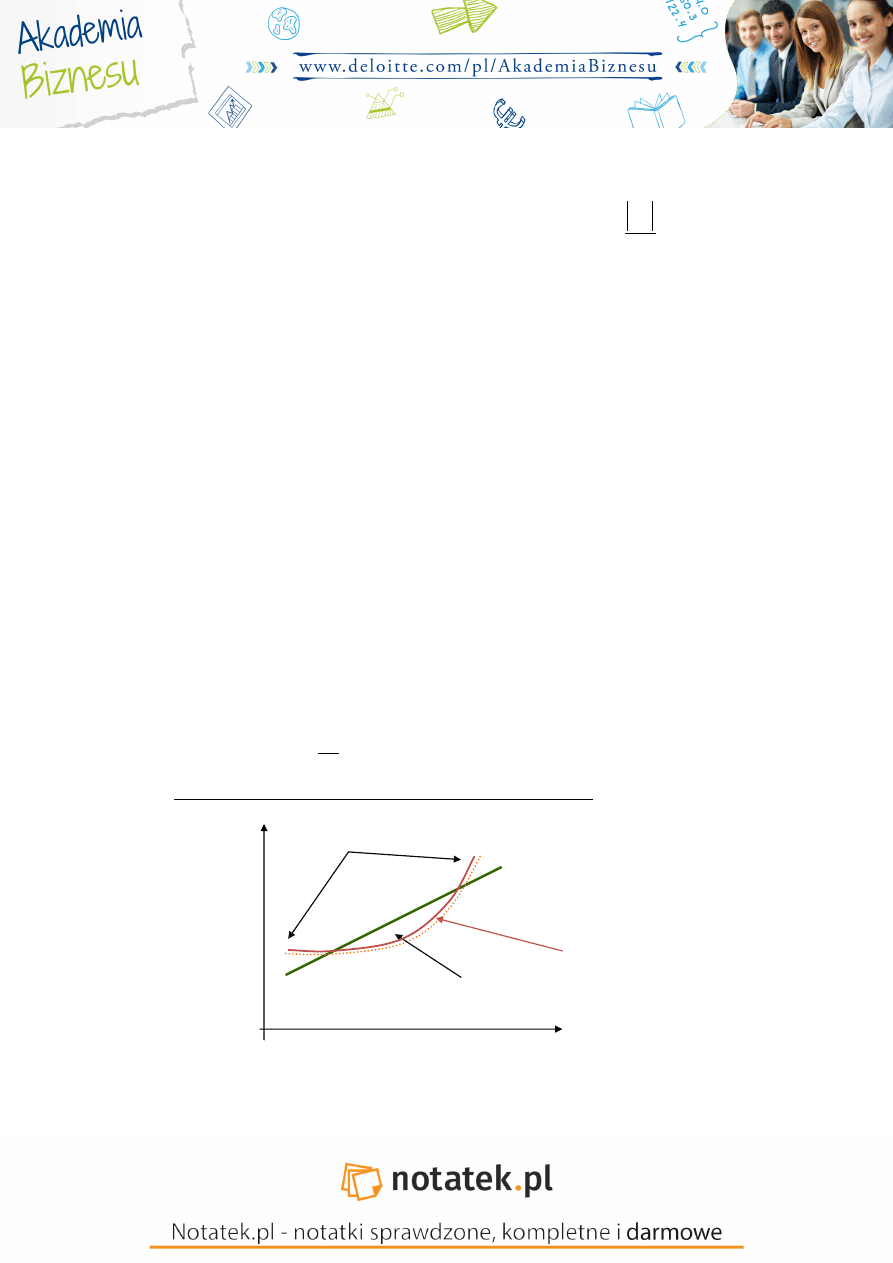
obszar krytyczny
- t 0 t t
obszar zera
statystycznego
(to co bli ej zera)
-
ryzyko bł du pierwszego
rodzaju (gama)
(powinno być małe ryzyko)
0
:
0
:
0
0
j
j
H
H
0
:
0
:
0
0
j
j
H
H
19
)
,...,
,
(
2
1
t
t
t
t
f
)
,...,
,
(
2
1
t
t
t
t
f
y
t
x
t
ŷ
t
= α
0
+ α
1
x
t
model liniowy
)
,
(
1
t
t
t
f
Je li obszar krytyczny jest dwustronny to w liczniku posługujemy si modułem, tzn. kasujemy znak ujemny (musi być
znak dodatni).
Przy weryfikacji hipotez statystycznych z hipotez zerow mo emyŚ
1. M
o na wykorzystać dwa rodzaje wniosków statystycznych,
a) mo emy hipotez zerow odrzucić na rzecz hipotezy alternatywnej,
b) nie ma podstaw do odrzucenia hipotezy zerowej – (wniosek kategoryczny), ale zawsze nale y wskazać, z jakim
ryzykiem pierwszego rodzaju.
- PODSTAWY EKONOMETRII -
→YKŁAD 7
na
EGZAM
01.04.2011r.
BADANIź A←TOKORźLACJI SKŁADNIKA LOSOWEGO
Zerowe kowariancje składników losowych z ró nych okresów oznaczaj brak autokorelacji składnika losowego.
Składnik losowy charakteryzuje autokorelacj , je li składnik losowy z okresu t zale y od składnika losowego z okresy
t-1.
Mówimy, e w tym przypadku składnik losowy tworzy proces autoregresyjny, to oznacza, e model jest wadliwy, czyli
składnik losowy nie powinien tworzyć procesu autoregresyjnego, tzn. nie ma autokorelacji składnika losowego.
Sytuacja poprawna to:
Miar autokorelacji składnika losowego jest współczynnik autokorelacji składnika losowego ρ (ro).
→ modelu bada si autokorelacj I rz du.
Je eli współczynnik jest równy zero to nie ma autokorelacji.
Przyczyny autokorelacji składnika losowegoŚ
a) Wadliwa postać modelu powoduje dodatni autokorelacj składnika losowego (+).
Autokorelacja składnika losowego powoduje pogorszenie efektywno ci estymatora KMNK
j
S
t
j
j
reszty ujemne
reszty dodatnie
=
0
∙
1
Model wykładniczy b dzie bardzo
dobrze opisywał rozrzut empiryczny
(linia ró owa ma nachodzić na
kropki)
aproksymacja
Mniej jest reszt dodatnich, wi cej jest
reszt ujemnych.

20
Powy szy model jest modelem liniowym katastroficznym, wadliwym ze wzgl du na postać autonomiczn z dodatni
autokorelacj składnika losowego.
b) Niedobór wa nych zmiennych obja niaj cych w modelu , czyli statystycznie istotnej zmiennej obja niaj cej.
→ sytuacji gdzie brakuje informacji statystycznych o zmiennej obja niaj cej warto zastosować rozwi zanie w postaci
modelu symptomatycznego i zamiast zmiennej
obja niaj cej, o której brakuje nam informacji wprowadzić zmienn
symptomatyczn , o której wiemy, e jest silnie skorygowana z pomini t wa n zmienn obja niaj c . źfektem b dzie
usuni cie modelu autokorelacji składnika losowego. Model ten b dzie poznawczo – gorszy od modelu przyczynowo –
skutkowego w sensie poznawczym. Natomiast jego walory decyzyjne b d znacznie wi ksze ni tego modelu bez
wa nej zmiennej obja niaj cej z autokorelacji składnika losowego.
Tylko wtedy (jedyny przypadek, kiedy
mo na budować model asymptomatyczny)
c) Nadmiar zmiennych statystycznie nieistotnych w modelu
źfektem tego mo e być ujemna autokorelacja składnika losowego wówczas bardzo cz sto wyst puje zmiana znaków
reszt. Model taki jest wadliwy, bo
s zmiennej nieistotne i na dodatek mo e wyst pić w modelu autokorelacja ujemna.
Nale y pojedynczo pozbyć si zmiennych nieistotnych statystycznie – eliminuje to ujemna autokorelacja składników
losowych.
[B d γ pyt. na egzaminie z tego tematu ĄĄĄ]
Jak si bada autokorelacj ?
Stosowanie testu DW Darwina
– Watsona
Ten test słu y do badania autokorelacji I rz du. Mo na, bowiem wykazać, e je eli nie ma autokorelacji I rz du to nie
ma autokorelacji rz dów wy szych. Natomiast, je eli jest autokorelacja I rz du to mo e wyst pić autokorelacja
powy szych rz dów, ale my nie mo emy si na to zgodzić, nale y usun ć przyczyn autokorelacji.
TEST DW
Zakładamy, e nie ma autokorelacji składnika losowego.
Jest to test z prawostronnym obszarem krytycznym.
DW =
u
t
−u
t
−1
2
n
t =
u
t
2
n
t =1
DW
≈ 2( 1 − �
1
)
t
u
t
u
t-1
1
u
1
-
2
u
2
u
1
3
u
3
u
2
⋮
⋮
⋮
n-1
u
n-1
u
n-2
n
u
n
u
n-1
0
:
0
:
0
0
j
j
H
H
współczynnik autokorelacji reszt
Przypadek 1.
�
1
= 0
≫
≈ 0 dodatnia autokorelacja
składnika losowego
Przypadek 2.
�
1
= 0
≫
≈ 2 nie ma autokorelacji składnika
losowego
Przypadek 3.
�
1
=
−1 ≫
≈ 4 ujemna autokorelacja
składnika losowego
21
1
odrzucamy H
0
na rzecz hipotezy alternatywnej H
1
wnioskujemy, e wyst puje dodatnia autokorelacja składnika losowego DW < d
L
2
nie ma autokorelacji składnika losowego. Model jest dobryś nie ma podstaw do odrzucenia H
0
DW > d
U
przypadek po dany
3 d
L
≤ D→ ≤ d
L
test nie daje odpowiedzi na pytanie o autokorelacje
Ń ≤ D→ ≤ β
statystyka D→ znalazła si w obszarze nieczuło ci testu
1
skoro mamy autokorelacj dodatni (+) to musimy ustalić, co jest jej przyczyn i j wyeliminować.
Po usuni ciu przyczyny autokorelacja znika.
2 DW > 2 w przypadku, gdy DW > 2 zmieniamy h
ipotez alternatywn na
DW* = 4
– DW
Ka da tablica ma inny poziom istotno ci, najcz ciej korzystamy z
= 0,05
Liczba zmiennych obja niajacych – k
Najni sza warto ć w tablicy to 15
3
nale y zastosować inny test – test na wsp. autokorelacji t - Studenta
Je eli model jest poprawny to nie wyst puje w nim autokorelacja
Najlepiej jak zmienne obja niaj ce w modelu s ba poziomie istotno ci 0,01 i aby były odpowiednie warto ci R
2
.
Je eli jest autokorelacja to pogorsza si efektywno ć estymatora KMNK.
Je li DW > d
u
- dobrze,
Je li DW < d
l
- niedobrze.
Współliniowo ć zmiennych obja niaj cych w modelu i ich wpływ na efektywno ć estymatora, KMNK.
→spółlioniowo ć deterministyczna
=
�
0
+
�
′
∙
′
0
<
+ 1
j, j‘=Ń,ń, …, k, j ≠ j
det( X
T
X) = 0 macierz Hessa jest nieosobliwa
→spółliniowo ć stochastyczna
r(x
tj
, x
tj‘
) ≠Ń
(jj‘ = Ń,ń,β,…,kśj≠j)
Gdy skorelowane model
ro nie, współliniowo ć korelacji i
r
j,j
‘
ro nie to wyznacznik macierzy Hessa maleje.
det(X
T
X)
-1
↓
Ze spadkiem wyznacznika b d rosły elementy macierzy diagonalnej. diagD
2
(a)
↑
Wariancja ocen parametru w skutek
……. b d rosły S
2
a
j
(j = Ń,ń,…,k) ↑
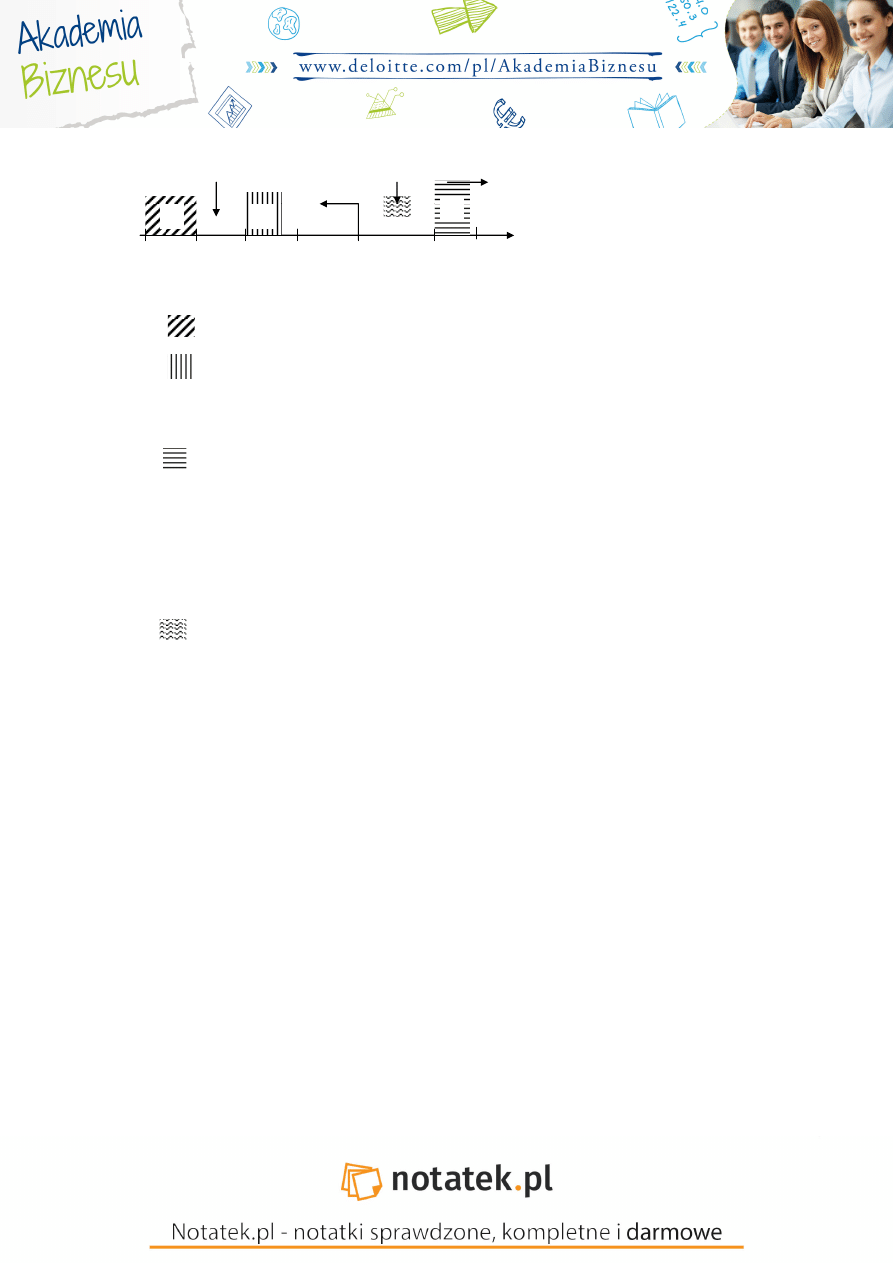
0
d
L
1
2
d
U
2
4-d
U
4-d
L
4
1
3
3
2
warto ć
krytyczna
górna
warto ć
krytyczna
dolna
d
U
< d
L
0
:
0
:
0
0
j
j
H
H
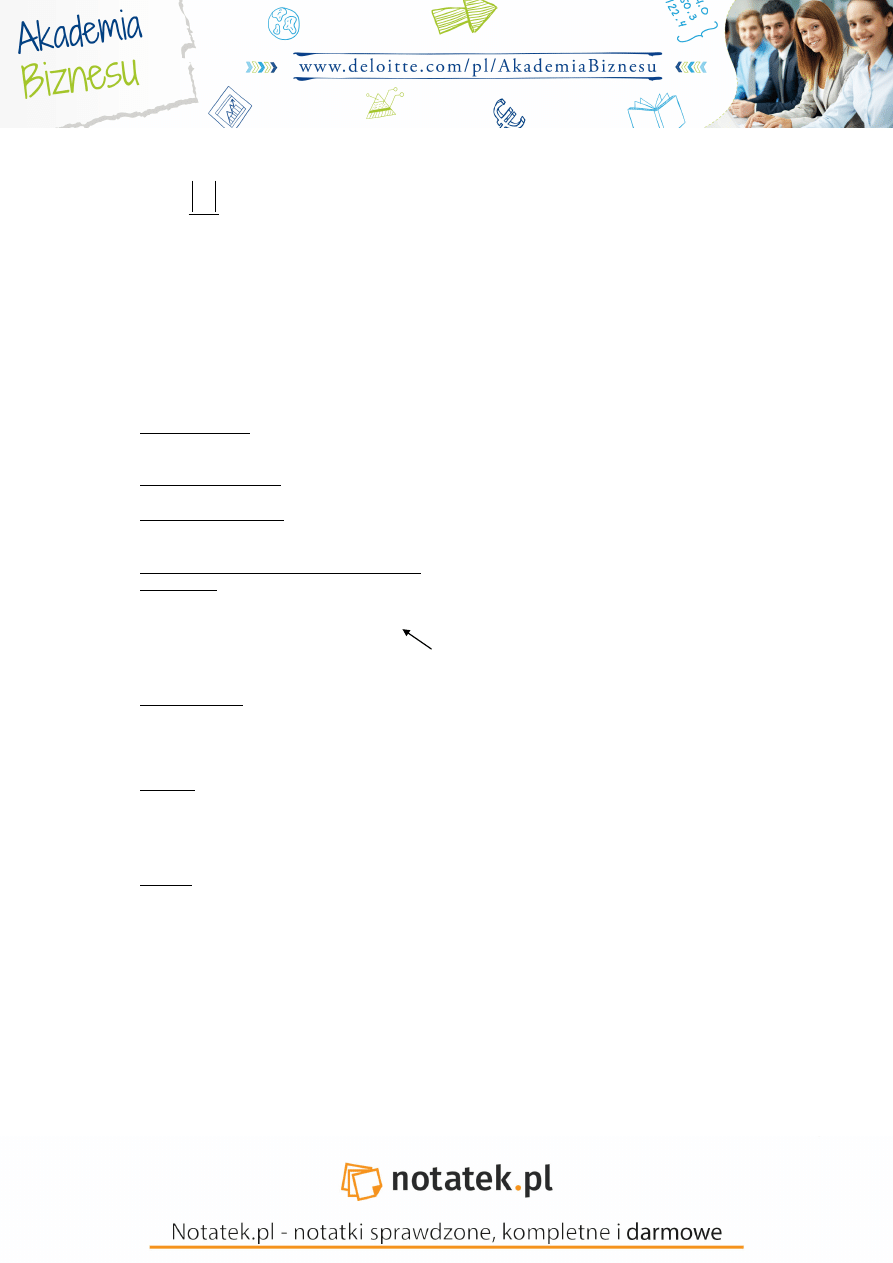
22
Statystyki t-
Studenta, gdy b d rosły bł dy statystyczne to wtedy b d spadały warto ci
statystyczne t
– Studenta.
Ulubione pyt. egzam:
Psuje si efektywno ć szacunków w skutek skorelowania zmiennych obja niaj cych , owe skorelowane mo e
spowodować, e zmienna tj mo e być nieistotna w sferze testu t – Studenta. Ta nieistotno ć mo e być pozorna
spowodowana współliniowo ci stochastyczn .
- PODSTAWY EKONOMETRII -
→YKŁAD 8
08.04.2011r.
T: PREDYKCJA EKONOMETRYCZNA
Szacowanie prognoz
– przez prognozy b dziemy rozumieć naukowo uzasadniony s d o przyszłej warto ci
zmiennej prognozowanej albo o prawdopodobie stwie wyst pienia zdefiniowanego zdarzenia ekonometrycznego.
Prognoza ekonometryczna
– jest wynikiem predykcji ekonometrycznej.
Predykcja ekonometryczna
– jest zbiorem czynno ci polegaj cych na wykorzystaniu empirycznego modelu
ekonometrycznego, którego rezultatem jest prognoza.
Na
jbardziej precyzyjne s prognozy ekonometryczne, które maj charakter obiektywny, powinny być wolne od
wolontaryzmu, czyli od tego, kto te prognozy buduje.
Okres prognozowania (T) T = n+ń, n+β, …, n+
�
(tał)
obserwacje
statystyczne t = ń, …, n
Horyzont predykcji
– jest to najdalej wysuni ty w przyszło ć okres prognozowany, dla którego mo liwe jest
oszacowanie prognozy dopuszczalnej, czyli wystarczaj co dokładnej z punktu widzenia u ytkownika.
gdy
�
=0
– to nie ma adnej prognozy wystarczaj co dokładnej
Realizacja jest
znana w wyniku upływu czasu. realizacja w momencie oszacowania jest nieznana.
y
Tp
– prognoza
y
T
– realizacja zmiennych w prognozie
=
− ą � �
Predyktor
– jest narz dziem szacowania prognoz opartych na empirycznym modelu ekonometrycznym.
=
0
+
1
1
+
… +
+
… +
x
Tj
( j=ń, …, k)
a
0
, a
1
– oceny parametrów strukturalnych
x
Tj
– warto ci zmiennych obja niaj cej w okresie prognozowanym (T)
Czy ka dy model empiryczny mo e być predykcj ? - Nie
Podstawowe założenia teorii predykcji ekonometrycznej
1) Znany musi być akceptowalny empiryczny model ekonometryczny, zmienne obja niaj ce musz być
statystycznie istotne na wystarczaj co niskim poziomie istotno ci Ń,Ńń.
→a na jest warto ć Su i Su
2
, bo one wa na dokładno ci prognozy.
j
a
j
j
S
a
t
horyzont predykcji

23
2) Parametry strukturalne modelu powinny być stabilne w czasie
α
j
= const (j = 0,1,
… , k)
Dopuszczalne s zmiany parametrów strukturalnego modelu pod warunkiem, e znany jest mechanizm takich
zmian.
α
3
≠ const − predykcja jest wtedy niedopuszczalna
3
=
30
+
31
−
3
zmienia si liniowoś predykcja jest wtedy dopuszczalna
=
0
+
1
1
+
2
2
+
30
+
31
3
+
… +
3) Stabilna powinna by struktura stochastyczna modelu.
Zakładamy i typ rozkładu składnika losowego si nie zmienia (rozkład normalny)
N(Ń, ń) rozkład normalny, standaryzowany
zero
– nadzieja matematyczna
jeden
– jednostkowa wariancja
N ( 0,
2
) -
rozkład normalny
0
– zerowej nadziei
2
- wariancja sigma kwadrat
(je li warto ć składnika losowego si zmienia to predykcja jest niedopuszczalna)
4) Znane powinny być warto ci zmiennych obja niaj cych w okresach (T)
y
Tp
= X
T
-a
X
T
= [ 1 x
T1
… x
Tj
… x
Tk
]
=
0
1
⋮
⋮
- PODSTAWY EKONOMETRII -
→YKŁAD 9
15.04.2011r.
5) Dopuszczalno ć ekstrapolacji poza prób statystyczn
Ekstrapolacja
– przedłu enie szeregu czasowego.
Nie mo na adnej decyzji podj ć (wybrać funkcji) bo mamy za mało obserwacji.
1x(k+1) (k+1)x1
Zmienna obja niaj ca to zmienna czasowa
???
Metody:
1.
2.
γ. Znane s prognozy demograficzneś mo emy zakładać okre lone daneś
prognoza symulacyjna
4. wykorzystanie statystycznych narz dzi ekstrapolacyjnych np. mo emy
zbudować model trendu liniowego lub nieliniowego i ekstrapolować trendy
uzysk
uj c informacje o zmiennej obja niaj cej w okresie prognozowania jako
ekstrapolant trendu
y
t
x
t
Trzy odmienne funkcje:
1. (orange)
=
0
+
1
+
�
2. (ziel)
=
0
+
1
+
�
3. (blue)
=
0
+
1
1
+
�
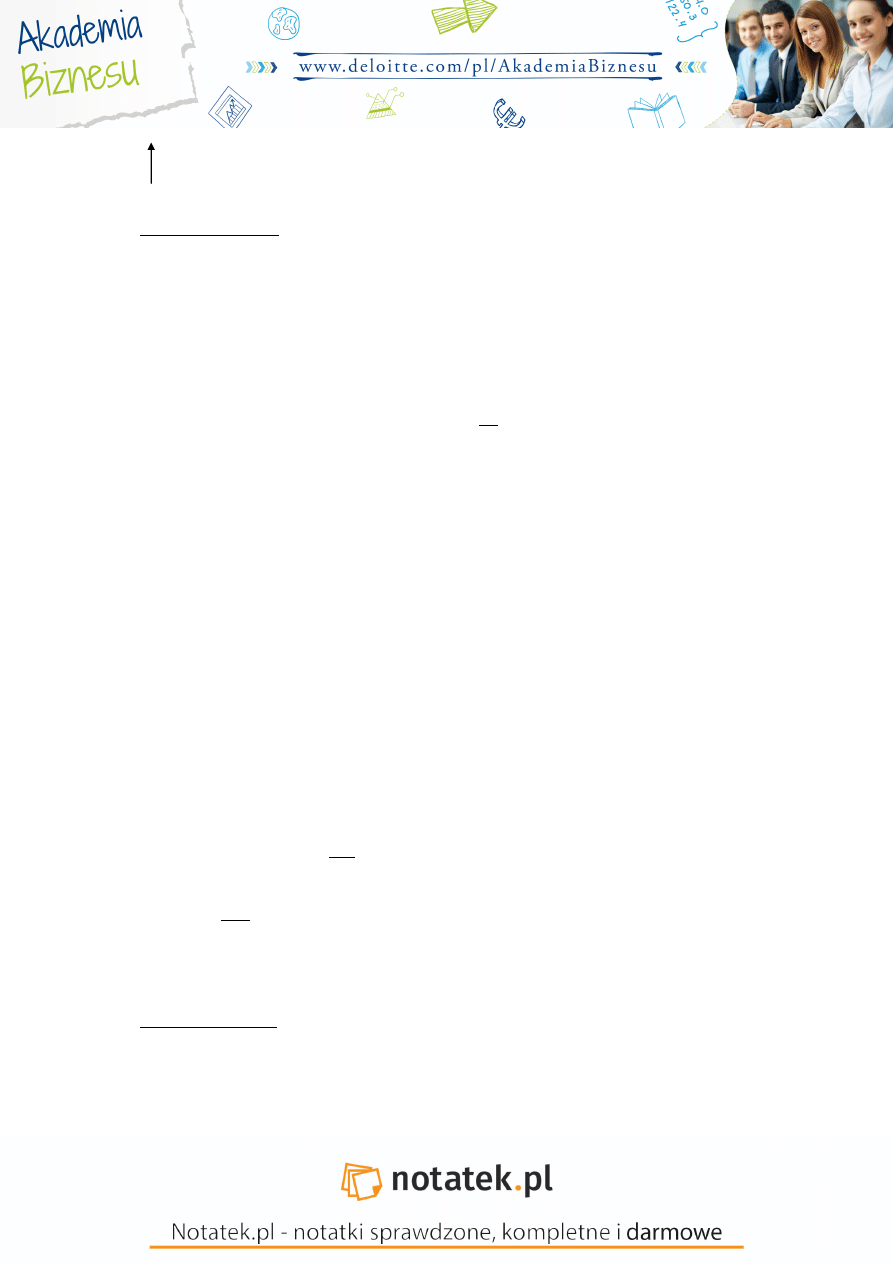
24
→ tym przypadku nie mo emy wyró nić modelu trafnego (jest za mało obserwacji istotnych, musi być
przynajmniej n>10
– dane roczne) ; n>20 – dane kwartalne czyli z 5 lat; dla danych miesi cznych z 4 lat
dane
Dopuszczalno ć prognozy
y
Tp
= X
T
a X
T
= [ 1 x
T1
… x
Tj
… x
Tk
]
Od czego zale y ↑
T
:
- wiel
ko ci bł du standardowego reszt czyli od Su
V
2
T
– wariancja predykcji – zale y od wariancji i kowariancji ocen parametrów strukturalnych i wariancji resztowej
2
=
2
[ 1 +
(
)
−1
=
2
2
- wariancja resztowa
(
)
−1
-
odwrotno ć macierzy Hessa
- wektor transponowany X
T
- wektor wierszowy
(
)
−1
– jest to forma kwadratowa (jest liczb nieujemn )
2
2
z tego wynika, e prognoza nie mo e być nigdy bardziej dokładna ni empiryczny model
ekonometryczny. Buduj c model korzystamy z predykcji nale y d yć do małej wariancji resztowej.
2
=
2
+
2
=
[ 1
−1
]
V
T
– bł d prognozy ex – ante (dopasowanie)
Im mniejszy V
T
tym lepiej i prognoza bardziej dokładna. → zwi zku z tym mo emy mówić o dopuszczalno ci
prognozy.
Prognoza jest dopuszczalna je li jest wystarczaj co precyzyjna z punktu widzenia u ytkownika.
← ytkownik ustala granice dopuszczalno ci prognozy.
← ytkownik wprowadza bł d graniczny predykcji ( ↑
G
)
1. V
T
≤ ↑
G
prognoza dopuszczalna
– spełnia wymogi u ytkownika
2. V
T
> V
G
prognoza niedopuszczalna poniewa nie spełnia warunków jakie zało ył u ytkownik
V
G
jest w jednostkach zmiennych prognozowanych
– tak samo jak V
T
→zgl dny bł d predykcji
∗
=
�
100 [%]
jest to udział redniego bł du predykcji w warto ci prognozy.
V
G
-
ustala si przed szacowaniem prognoz !!!
∗
�
-
graniczny wzgl dny bł d predykcji
1.
∗
∗
�
prognoza dopuszczalna
2.
∗
>
∗
�
prognoza niedopuszczalna
Analiza trafno ci prognoz
y
T
– realizacja zmiennej prognozowanej
=
�
−
-
bł d analizy ax – poste (trafno ć)
Trafno ć prognozy oceniamy dopiero gdy znamy realizacj
Prognoza musi być opatrzona pewn miar dokładno ci
V
T
– bł d redni predykcji
=
0
1
⋮
⋮
25
1.
> 0
Prognoza osi gn ła wi ksz warto ć ni realizacja - prognoza przeszacowana
2.
< 0 Prognoza osi
gn ła mniejsz warto ć ni realizacja np. w przypadku inflacji na koniec roku
− prognoza niedoszacowania
Kiedy prognoza b dzie trafna?
-
Trzeba ustalić wzgl dny bł d prognozy
∗
=
100 [%]
←znamy, e prognoza była trafna wówczas gdy |
∗
|
∗
�
∗
| >
∗
�
prognoza jest chybiona, nietrafna
Systematyczny bł d predykatora – wymaga poprawienia gdy ci g prognoz przeszacowanych lub nieoszacowanych
wymagaj korekty predykatora poniewa generuje on bł d systematyczny polegaj cy na niedoszacowaniu prognoz
albo na ich przeszacowaniu.
Prognozy jako ciowe - s to prognozy prawdopodobie stwa o ograniczonych zmiennych endogenicznych
Ń ≤ � < 1
0
– zdarzenie niemo liwe
1 - zdarzenie pewne
y
min
≤ y
t
≤ y
max
Transformacja logikowa
( )
= ln
(
�)
=
(
−
min
)
(
− )
- PODSTAWY EKONOMETRII -
→YKŁAD ńŃ
26.04.2011r.
TźMATŚ MODźLź →IźLORÓ→NANIO→ź
MODźL →IźLORÓ→NANIO→Y składa si z wielu równa stochastycznych. Najogólniej w modelu
wielorównaniowym wyst puje ż zmiennych endogenicznych. Najmniejsza ż wynosi co najmniej β.
B dziemy posługiwali si obserwacjami oznaczonymiŚ
y
1t,
y
2t,
..., y
t,
..., y
Gt
Model
wielorównaniowy opisuje system ekonomiczny albo jego cz ć nazywan subsystemem lub
podsystemem. Dla potrzeb tego modelu wprowadzimy nowe poj cieŚ
ń) zmienna ł czniewspółzale na modelu to ka da zmienna endogeniczna nieopó niona w czasie,
β) zmienne z góry ustalone to wszystkie zmienne egzogeniczne oraz zmienne endogeniczne opó nione w
czasie.
=
0
+
0
y
min
y
max
x
t
y
t
→ska nik struktury jest udziałem procentowym
(
�)
=
−
−
( )
(
�)
+
min
2

26
Opisuje on system ekonometryczny lub jego cz ć zwan podsystemem lub subsystemem.
zmienne endogeniczne – w jednym z równa wyst puje w roli zmiennej obja nianej, mo e być te zmienna
obja niaj caś zmienne wewn trzne
zmienne egzogeniczne – s to zewn trzne systemu, w modelu pełni wył cznie rol zmiennych obja niaj cych.
Modele wielorównaniowe - jest to konstrukcja przynajmniej dwóch równa .
Modele Kleina
– 6 równa
Pierwszy model w Polsce składał si z ń7 równa z połowie lat 6Ń- tych
KLASYŻIKACJA modeli wielorównaniowych
żłównym kryterium klasyfikacyjnym modeli wielorównaniowych jest sposób powi za zmiennych
ł czniewspółzale nych. To kryterium pozwala wyró nićŚ
- modele proste,
- modele rekurencyjne,
-
układy równa współzale nych.
MODELE PROSTE
→ modelach prostych nie ma adnych powi za pomi dzy zmiennymi ł czniewspółzale nymi. Oznacza to,
e w ka dym z równa takiego modelu zmiennymi obja niaj cymi s wył cznie zmienne z góry ustalone.
MODELE REKURENCYJNE
→ modelu rekurencyjnym zmienne ł czniewspółzale ne s powi zane ła cuchowo czyli rekurencyjnie.
Oznacza to tzw. jednokierunkowy mechanizm powi za zmiennych ł czniewspółzale nych, którego
specyfik jest mo liwo ć wskazania pocz tku i ko ca ła cucha.
←KŁADY RÓ→NA →SPÓŁZALź NYCH
→ układach równa współzale nych wyst puj dwa mechanizmy powi za Ś
-
sprz enie zwrotne nazywane niekiedy sprz eniem zwrotnym bezpo rednim,
-
zamkni ty cykl powi za zmiennych ł czniewspółzale nych nazywany niekiedy sprz eniem zwrotnym
po rednim.
O przynale no ci modelu do danej klasy decyduje mechanizm powi za zmiennych ł cznie współzale nych.
Ad. 1
Nie ma wzajemnych zwi zków pomi dzy zmiennymi ł cznie współzale nymi.
y
1
, y
2
, …, y
g
, …, y
G
1
,
2
, … ,
�
, … ,
�
- obserwacje
1
2
3
jest to zbiór autonomicznych równa – brak zwi zków.
4
Ad. 2
Pojawiaj si powi zania jednokierunkowe
1
2
3
4
Ad. γ Dwa mechanizmy powi za Ś
sprz enie zwrotne bezpo rednie
y
gt
y
g’t
(g, g’=ń , … , ż , g ≠ g’)
zamkni ty cykl powi za tzw. sprz enie zwrotne po rednie
y
1t
y
2t
y
3t
y
4t
-
nie jest to model rekurencyjny bo nie ma pocz tku i ko ca
1
2
3
4
równanie opisuj ce
4
jest równaniem pocz tkowym
modelu rekurencyjnego.
Jest to max liczba poł cze dla modelu o czterech równaniach
Przynajmniej jedno powi zanie, aby model był rekurencyjny
Model
o ła cuchowym mechanizmie powi za .

27
Zamkni ty cykl powi za w obr bie małego przedsi biorstwa Ą
MODEL PROSTY
1
=
10
+
11
1
+
14 3
−1
+
�
1
2
=
20
+
22
+
23 2
−1
+
�
2
3
=
30
+
33
3
+
34 3
−1
+
�
3
– parametry przy zmiennych ł cznie współzale nych
I indeks
– nr równania
II indeks
– nr zaj ty ł cznie współzale ny
α – parametry strukturalne przy zmiennych z góry ustalonych ( maj dwa indeksy)
I indeks
– nr równania
II indeks
– zmiennej z góry ustalonej
* w β i γ równaniu wyst puje autoagresja
Model prosty w zapisie macierzowym:
Forma strukturalna modelu
1
−
10
+
11
1
+
14 3
−1
=
�
1
2
−
20
+
22
+
23 2
−1
=
�
2
3
−
30
+
33
3
+
34 3
−1
=
�
3
=
1
⋮
�
⋮
�
Ma
cierz B jest trójk tna co oznacza, e model jest rekurencyjny. Je li w modelu rekurencyjnym równania s
uporz dkowane zgodnie z ła cuchem powi za zmiennych ł cznie współzale nych to macierz B jest trójk tna,
brak takiego uporz dkowania powoduje, e macierz B mo e nie być trójk tna, a mimo to model b dzie
rekurencyjny.
W przypadku modelu PROSTEGO macierz B
b dzie diagonalna JźDNOSTKO→A. Je li macierz B wyjdzie
nam jednostkowa to model jest na pewno PROSTY !!!!
- PODSTAWY EKONOMETRII -
→YKŁAD ńń
20.05.2011r.
←kład równa współzale nych
1
=
10
+
12 2
+
11
−1
+
12
+
�
1
- sprz enie zwrotne
2
=
20
+
21 1
+
23 3
+
22
2
+
�
2
3
=
30
+
34 4
+
33 4
+
33
3
+
�
3
4
=
40
+
42 2
+
45 3
−1
+
�
4
BY + AZ = ƞ
(GxG)(Gx1) (Gxk+1)(k+1) (Gx1)
Gx1 Gx1 Gx1
=
0
1
⋮
⋮
� =
�
1
⋮
�
�
⋮
�
�
=
1
−
1
…
−
2
1
…
…
−
�
…
−
. . .
…
−
1
�
−
�
. . .
1
…
…
…
…
−
1
�
−
�
…
−
�
=
−
10
−
11
…
−
20
−
21
…
…
−
�0
…
−
�0
…
−
�1
…
−
�1
…
…
…
…
−
1
… −
1
−
2
… −
2
…
−
�
…
−
�
…
…
…
…
…
−
�
…
−
�
1
2
3
1
−
12
0
0
1
−
23
0
0
1
1
2
3
+
−
10
−
11
0
−
20
0
−
22
−
30
0
0
0
0
−
15
−
23
−
24
0
0
−
34
0
0
0
−
36
0
1
2
−1
2
−1
3
−1
1
2
3
0
1
2
−1
2
−1 3 −1

28
y
1t
y
2t
y
2t
y
3t
y
4t
=
1
−
12
0
0
−
21
1
−
23
0
0
0
0
−
42
1
−
34
0
1
IDENTYFIKACJA MODELU
Model identyfikowany to model poprawnie skonstruowany z matematycznego punktu widzenia. Przedmiotem
dalszych rozwa a mog być wył cznie modele identyfikowalne, czyli poprawnie skonstruowane.
B
-1
/ BY+AZ = ƞ
zapis macierzowy w formie strukturalnej
Zał: zakładamy, e macierz B jest nieosobliwa.
Jak macierz jest nieosobliwa to macierz odwrotna nie istnieje.
B
-1
– mo emy pomno yć TYLKO lewostronnie
B
– jest macierz nieosobliw czyli istnieje odwrotno ć macierzy B, wówczas mo emy pomno yć równanie
strukturalne przez B odwrotne tylko lewostronnie:
B
-1
/BY +
AZ = η
otrzymamy
B
-1
BY + B
-1
AZ = B
-1
η
J
w efekcie otrzymamy iloczyn jednostkowy (J)
Po lewej stronie mamy Y
Y = - B
-1
AZ + B
-1
η
Żorm zredukowan upro cimy podstawiaj c pod - B
-1
A jakie C, a za B
-1
η jakie ε.
C = - B
-1
A
B
-1
η = ε
→ówczas otrzymujemy form zredukowan o postaciŚ
Y = CZ + ε
Y
– wektor zmiennych ł czniewspółzale nych,
Z
– wektor zmiennych z góry ustalonych,
ε – wektor składników losowych w formie zredukowanej,
C
– macierz parametrów strukturalnych równa formy zredukowanej modelu.
→ formie zredukowanej równa jest tyle ile zmiennych ł cznych współzale nych czyli 5.
ε
1t
C
10
C
11 ...
C
1j ...
C
1K
ε
=
ε
gt
C
=
C
g0
Cg
1 ...
C
gj ...
C
gK
ε
Gt
C
G0
C
G1 ...
C
Gj ...
C
GK
macierz C zawiera parametry strukturalne równa w formie zredukowanej
=
1
⋮
�
⋮
�
1
2
3
4
żdy
12
i
21
s nie
zerowe to jest sprz enie
zwrotne
Gdy model jest
rekurencyjny to macierz
jest trójk tna
Gx(k+1)
Gx1
=
0
1
⋮
⋮
wektor zmiennych ustalonych całego modelu

29
- B
-1
A = C
równanie identyfikacyjne
Równanie identyfikacyjne jest równanie zwi zku pomi dzy parametrami formy strukturalnej modelu i parametrami
jego formy zredukowanej.
B / -B
-1
A = C
- B
-1
BA = BC
macierz jednostkowa
-A=BC
proste równanie identyfikacyjne
Mamy wprost opisane zale no ci pomi dzy parametrami formy strukturalnej z parametrami formy zredukowanej.
Macierz C jest zawsze znanaś natomiast nieznane s macierz A i B
Problem identyfikacyjny polega na ustaleniu czy korzystaj c z równania identyfikacyjnego przyznanych
składowych macierzy C mo liwe jest jego rozwi zanie ze wzgl du na składowe macierzy B oraz A. Jest to zatem
problem rozwi zania układu równa liniowych ze wzgl du na parametry α oraz .
(α
Gj
,
żż’
)
Mo e istnieć jedno rozwi zanie – jednoznaczne równanie
1) Jednoznaczne rozwi zanie układu równa
Je li tak jest to model jest identyfikowalny jednoznacznie. Jest to przypadek niej bardziej po dany ale
rzadko spotykany.
2) Mo e istnieć wiele rozwi za modelu – niejednoznacznym
Mówimy wówczas o modelu identyfikacyjnym niejednoznacznieś najcz stszy przypadek.
Model identyfikacyjny inaczej nazywany jest modelem przeidentyfikowalnym.
3) Model, w którym jest brak rozwi zania układu, czyli sprzeczny model. Jest to model nieidentyfikowany
czyli wadliwie skonstruowany. Je li model jest nieidentyfikowany. Nale y ustalić przyczyn braku
identyfikalno ci i przebudować go. Przebudować sprowadza si do usuni cia jakiej zmiennej z której z
równa lub znalezienie nowej wa nej zmiennej pomini tej w jednym z równa – wi c model nale y
respecyfikować.
1
=
10
+
12 2
+
11
1
+
�
1
2
=
20
+
23 3
+
22
+
24
−1
+
�
2
3
=
30
+
31 1
+
33 3
+
33
+
�
3
Jest to układ równa współzale nych, bo jest tu sprz enie zwrotne. Zamkni ty ła cuch
Musimy wyspecyfikować zmienne ustalone z góry.
=
0
1
3
−1
y
1t
= C
10
+ C
11
x
t1
+ C
12
t + C
13
x
t3
+ C
14
y
t-1
+ ε
1t
y
2t
= C
20
+ C
21
x
t1
+ C
22
t + C
23
x
t3
+ C
24
y
t-1
+ ε
2t
y
3t
= C
30
+ C
31
x
t1
+ C
32
t + C
33
x
t3
+ C
34
y
t-1
+ ε
3t
Ka de równanie formy zredukowanej zawiera ten sam zestaw zmiennych obja niaj cych, w którym s zmienne z
góry ustalone.

30
źSTYMACJA PARAMźTRÓ→ MODźLI →IźLORÓ→NANIO→YCH
1) MODEL PROSTY
Parametry
równa prostych mo na szacować za pomoc metody KMNK, traktuj c ka de z równa modelu
prostego jak model
jednorównaniowy. Je li składniki losowe ró nych równa modelu prostego s mi dzy sob
skorygowane to bardziej efektywnym estymatorem jest estymator
ZźLLNźR’a nale cy do klasy metod ł cznej
estymacji parametrów modeli wielorównaniowych. Tym samym metody estymacji parametrów modeli o wielu
równaniach mo emy podzielić na dwie kategoriaŚ
Po pierwsze metody estymacji pojedynczej, których istota jest szacowanie parametrów ka dego równania
oddzielnie np. KMNK dla poszczególnych równa modelu prostego.
Po drugie metody estymacji ł cznej, których istot jest szacowanie parametrów strukturalnych wszystkich
równa jednocze nieś przykładem takiej metody jest metoda ZźLLNźR’a.
Metody estymacji
ł cznej znalazły zastosowanie stosunkowo niedawno poniewa wymagaj znacznej mocy
obliczeniowej komputera. → praktyce pojawiły si w latach 8Ń- tych. Metoda ZźLLNźR’a nie mo e być
stosowana np. do parametru równa formy zredukowanej.
Forma zredukowana jest m
odelem prostym, a tu metoda ZźLLNźR’a nie ma zastosowania.
Idea metody ZźLLNźR’a opiera si na koncepcji uogólnionej metody najmniejszych kwadratów, której twórc był
AITKEN.
Metoda ZźLLNźR’a jest bardziej efektywna od metody KMNK, ale wymaga rozmaitych zmiennych
obja niaj cych w ró nych równaniach modelu prostego.
2) MODELE ZREDUKOWANE
Dopuszcza
si stosowanie metody KMNK do estymacji parametrów ka dego z równa modelu rekurencyjnego
oddzielnie.
3) ←KŁAD RÓ→NA →SPÓŁZALź NYCH
Je li ukł d ten jest identyfikowalny jednoznacznie to stosuje si posredni metod najmniejszych kwadratów
(PMNK). Metoda ta przebiega
w dwóch stepachŚ
I.
Stosuje si KMNK do estymacji równa formy zredukowanej
1
∗
=
10
+
11
1
+
12
+
13
3
+
14
−1
2
∗
=
20
+
21
1
+
22
+
23
3
+
24
−1
3
∗
=
30
+
31
1
+
32
+
33
3
+
34
−1
=
10
11
12
13
14
20
21
22
23
24
30
31
32
33
34
II.
Rozwi zanie empirycznego równiania identyfikacyjnego.
A
10
11
0
0
0
20
0
22
0
24
30
0
32
33
0
=
1
−
12
0
0
1
−
23
−
31
0
1
10
11
12
13
14
20
21
22
23
24
30
31
32
33
34
DANE
PMNK nie daje macierzy wariancji
– kowariancji ocen parametrów strukturalnych zatem nie nadaje si do
predykcji czyli do prognozowania.
→szystkie C z daszkiem s ocenami
parametrów formy zredukowanej uzyskanej za
pomoc KMNK.

31
Równania nieidentyfikowane niejednoznaczne
KMNK jest niedopuszczalna ze
wzgl du na skorelowanie ł cznie współzale nych zmiennych obja niajacych ze
składnikami losowymi.
Stosuje
si podwójn metod najmniejszych kwadratów (2MNK) polega ona na dwukrotnym zastosowaniu metody
najmniejszych
kwadratów.
Pierwszym krokiem do równa formy zredukowanej przy czy celem jest uzyskanie teoretycznych współzale nych
z formy zredukowanej, które s pozbawione losowo ci.
→ drugim kroku obja niaj ce ł cznie współzale ne zast pujemy ich teoretycznymi warto ciami uzyskanymi z
empirycznej formy zredukowanej. Do tak przekształconych równa formy zredukowanej wolno zastosować
KMNK poniewa obja niaj ce zmienne ł cznie współzale ne po takim zabiegu s nielosowe praz nieskorelowane
ze składnikiem losowym.
- PODSTAWY EKONOMETRII -
→YKŁAD ńβ
27.05.2011r.
PRźDYKCJA MODźLI →IźLORÓ→NANIO→YCH
1. Modele proste
Ka de równanie modelu prostego mo na traktować identycznie jak model jednorównaniowy. Predykcja z takiego
równania odbywa si identycznie jak w modelu jednorównaniowym. Odmienno ć predykcji z równania modelu
prostego pojawia si wówczas, gdy w zbiorze zmiennych z góry ustalonych wyst puje przynajmniej jedna zmienna
endogeniczna opó niona w czasie.
1
=
10
+
11
1
+
12
+
14 3
−1
+
�
1
2
=
20
+
23
3
+
25 1
+
�
2
3
=
30
+
31
1
+
33
3
+
�
3
→ówczas konieczna jest predykcja sekwencyjna, która powoduje konieczno ć post powania w okre lonej
kolejno ci jaka wynika z opó nie zmiennych endogenicznych.
1
∗
=
10
+
11
1
+
12
+
14 3
−1
+
�
1
2
∗
=
20
+
23
3
+
25 1
+
�
2
3
∗
=
30
+
31
1
+
33
3
+
�
3
Z modelu empirycznego mo emy przej ć do predyktora.
Predyktor:
1
�
=
10
+
11
1
+
12
+
14 3
−1
T
– ozn. e jeste my w obszarze predykcji
2
�
=
20
+
23
3
+
25 1
3
�
=
30
+
31
1
+
33
3
Trzecie równanie zawiera tylko zmienne egzogeniczne, mo na wi c przesuwać prognoz w czasie bez ogranicze Ą
Prognoza dla okresu:
T=n+1
3
+ 1 − 1 =
3
=
+ 2
3
+ 2 − 1 =
3
1
=
3
+ 1
Aby oszacowaćŚ y
2
, n+1p
Trzeba mieć toŚ y
1n
y
2
, n+2p
y
1n
+ 1p
32
2. Modele rekurencyjne
W przypadku modelu rekurencyjnego obo
wi zuje przeprowadzenie predykcji tzw. ła cuchowej, oznacza to
konieczno ć predykcji z poszczegóolnych równa zgodnie z ła cuchem powi za zmiennych ł cznie
współzale nych.
1
�
-
równanie oderwane od modelu ( traktujemy jak równanie modelu prostego)
2
�
3
�
4
�
je li w modelu rekurencyjnym pojawi si opó nione w czasie zmienne endogeniczne, wówczas przeprowadza si
predykcj ła cuchowo – sekwencyjn .
(przykład w mikroekonometrii)
3. Modele równa ł czniewspółzale nych.
1
�
=
10
+
11
1
+
15 4
−1
2
�
=
20
+
24 4
�
+
22
2
3
�
=
30
+
32 2
�
+
33
3
4
�
=
40
+
43 3
�
+
44
→ przypadku układu równa współzale nych przeprowadza si predykcj z empirycznej formy zredukowanej przy
czym mo na pomin ć równanie oderwane.
1
�
=
10
+
11
1
+
15
∗
4,
−1
∗
2
�
=
20
+
21
1
+
22
2
+
23
3
+
24
+
25
∗
4,
−1,
∗
3
�
=
30
+
31
1
+
32
2
+
33
3
+
34
+
35
∗
4,
−1,
∗
4
�
=
40
+
41
1
+
42
2
+
43
3
+
44
+
24
∗
4,
−1,
Forma zredukowana ma charakter modelu prostego, czyli predykcja dekwencyjna.
Równania formy zredukowanej charakteryzuj si wystepowaniem wielu zmiennych statystycznie nieistotnych co
oznacza, e oceny parametrów empirycznych równa w formie zredukowanej posiadaj du e bł dy Konsekwencj
tefo faktu jest w przypadku predykcji -
du y bł d redni predykcji dla prognoz z układu równa współzaleznych,
nale y szacować w oparciu o równania formy strukturalnejŚ
1
�
= 2,1 + 0,85
1
+ 1,21
3
−1
(ksi ka mikroekonomia – przykłdyĄ)
2
�
= 0,6 + 1,84
3
�
− 0,97
2
3
�
= 3,6 + 1,2
2
�
+ 2,44
3
Predyktor:
1
�
= 2,1 + 0,85
1
+ 1,21
∗
3,
−1,
np. na E
– zapisać predyktor dla empirycznego ukł równa
2
�
=
20
+
22
1
+
23
2
3
�
=
30
+
32
2
+
33
3

33
B
Y
A
X
1
−1,84
−1,2
1
2
�
3
�
+ −
0,6
0,97
0
−3,6
0
−2,44
0
2
3
=
0
0
0
C = B
-1
A
BC = -A
1
−1,84
−1,2
1
−
0,6
0,97
0
−3,6
0
−2,4
=
20
22
23
30
32
33
EGZAMIN:
przynie ć legitymacje ś kalkulator
2 pytania z literatury
ń pytanie z wykładu
+ zadanie
„Mikroekonomtria” – ograniczone zmienne niezale ne (zalezne) Ą transkrypcje ś wykresyĄ
Najbardziej rozdział β i 7 (chyba) – co o funkcji produkcji, krzywej jednakowego produktuś ostatni b d
przedostatni rozdział
„źlementy ekonometrii” – Rozdział ń,β i ostatni
Tematy, które cz sto pojawiaj si na egzaminieŚ
1.
Przyczyny i skutki autokorelacji składnika losowego
β. Równanie oderwane w ekonometrycznym modelu małego przedsi biorstwa
3. Decyzyjne walory modelu ekonometrycznego
4. Miary dokładno ci predykcji
5. Ekonometryczne modele zmiennych ograniczonych
6. ekonometryczna analiza cen
7. Identyfikacja modelu ekonometrycznego
8. Ekonometryczna analiza popytu
9. Sprz enie zwrotne w ekonometrycznym modelu małego przedsi biorstwa
ńŃ. Metody estymacji parametrów modeli wielorównaniowych
ńń. źstymacja parametrów modeli prostych i rekurencyjnych
12. Walory zreduko
wanej formy modelu małej firmy
ńγ. źkonometryczna analiza sprzeda y
ń4. Predykcja z modeli wielorównaniowych
ń5. źkonometryczna analiza kosztów
ń6. Przyczyny i skutki współliniowo ci zmiennych w modelu ekonometrycznym
ń7. Charakterystyka powi za w modelu małej firmy
18. Model ekonometryczny w wyborze efektywnego robotnika\
ń9. Modele dochodów
βŃ. Analiza prognoz wygasłych
βń. Istota modelu du ego przedsi biorstwa
ββ. Bł dy specyfikacji modelu
23. Model ekonometryczny w podejmowaniu decyzji kadrowych
24. Etapy budowy modelu ekonometrycznego
25. Teoria predykcji ekonomicznej
β6. Przyczyny wyst powania składnika losowego
27. KMNK
28. Test t-studenta
Wyszukiwarka
Podobne podstrony:
notatek pl podstawowe zagadnienia wyklady
pyt+odp-Notatek.pl, UEK EKONOMIA, Semestr 4, Rynki finansowe, cuda-wianki
polityka spoleczna- opracowane kwestie-Notatek.pl, UEK - Ekonomia, Polityka społeczna
notatek pl Kowalski,ekonomia menedzerska, test
notatek pl rynki finansowe wyklady
notatek pl podstawy zarzadzania pytania i odpowiedzi cz 3
notatek pl podstawy zarzadzania zagadnienia cz 1
notatek pl podstawy zarzadzania pytania
notatek pl teoria polityki wyklady
notatek pl krajobraz kulturowy wyklady 1 5
notatek pl podstawy zarzadzania pytania odpowiedzi cz 1
notatek pl finanse przedsiebiorstwa wyklad
notatek pl rynki finansowe wyklady
notatek pl socjologia organizacji wyklady dr slawomir pilipiec
notatek pl podstawy zarzadzania 30 godzin
więcej podobnych podstron