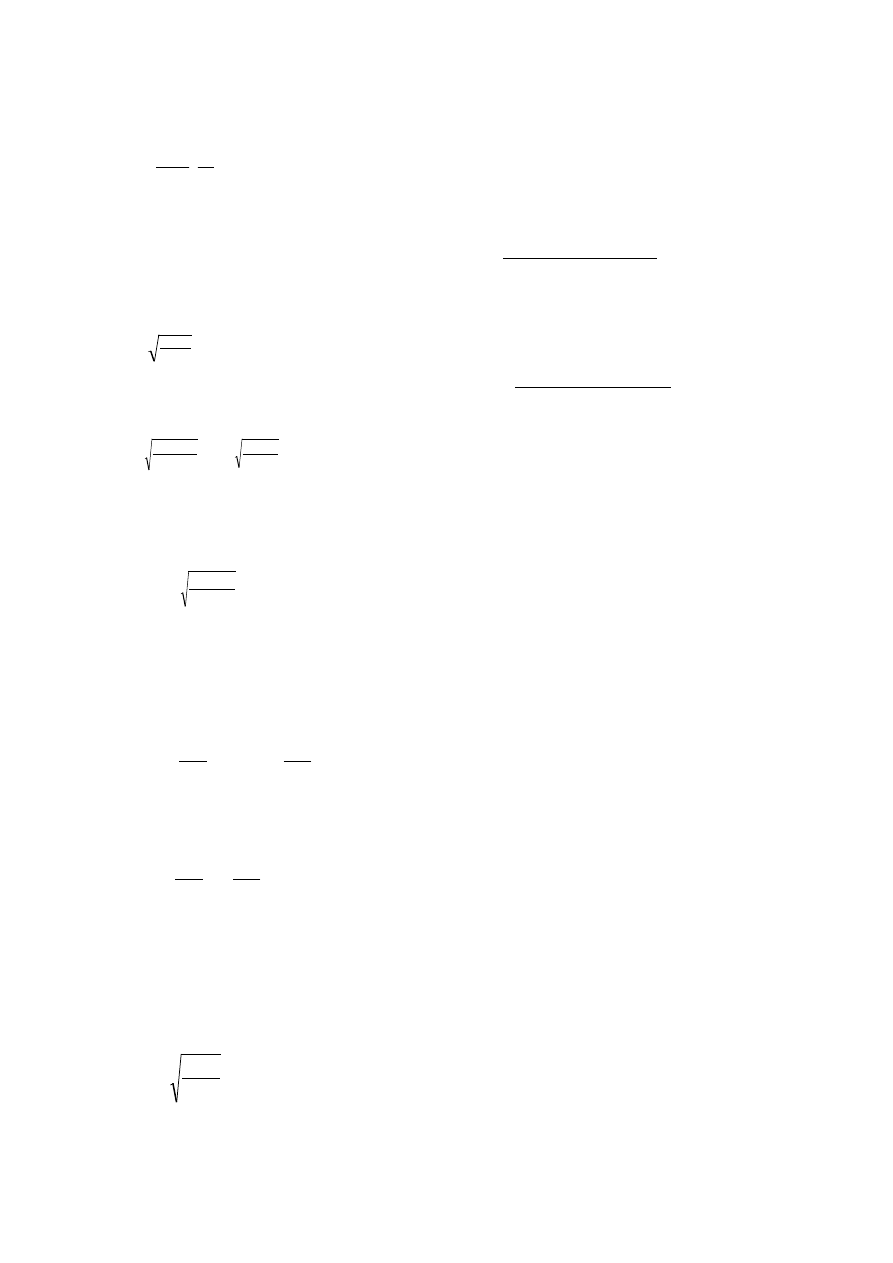
Ekonomiczna wielkość zamówienia (EOQ)

Kz – koszty zapasów (bez kosztów wyczerpania zapasów)

Ku – koszty utrzymania zapasów

Kd – koszty składania zamówień

Wz – wielkość zamówienia

Kj – koszt jednostki zapasów

i –stopa określająca koszty utrzymania zapasów (%)

P – wielkość popytu na dany produkt (szt/rok)

s – koszty stałe złożenia zamówień (zł/zamówienie)

Minimalizacja całkowitych rocznych kosztów

zapasów – Formuła Wilsona

Ekonomiczna wielkość zamówienia w

warunkach inflacji

I.

Ciągła zmiana cen

d – stopa rocznej inflacji

i – stopa rocznego kosztu utrzymania zapasów

II.

Skokowa zmiana cen, gdy marża jest

stała

f – marża w stosunku do kosztów zakupu

III.

Gdy uwzględnimy rabaty ilościowe

Jeżeli Kj’ = Kj(1 – u) i Wz graniczne > EOQ to

należy przeprowadzić porównawczy rachunek

ekonomiczny kosztów zapasów i ich wartości dla

obliczenia EOQ i granicznej wielkość zamówienia.

Kj’ – jednostkowy koszt zakupu z uwzgl. rabatu.

Wz graniczne – min. wielkość zamówienia dla

uzyskania rabatu cenowego.

Dla EOQ < Wzg

Dla EOQ = Wzg

Prawo pierwiastka kwadratowego

Eliminacja liczby magazynów umożliwia

zredukowanie zapasów przy utrzymaniu

dotychczasowego poziomu obsługi

klienta, co można obliczyć za pomocą

wzoru:

Rz – wielkość zredukowanych zapasów

LMz – liczba zredukowanych zapasów

LMp – pierwotna liczba magazynów

Obliczanie centrum grawitacji

x,y – nieznane zmienne punktu ciążenia

xi,yi,xj,yj – współ. Istniejących punktów

zaopatrzenia i zbytu

n,m. – liczba punktów zaopatrzenia (n) i

zbytu (m)

zi – wolumeny wagowe produktów

pochodzących z punktów zaopatrzenia

dla i=1...n

sj - wolumeny wagowe produktów

pochodzących z punktów zbytu dla

j=1...m

ti – stawki taryfowe za przewóz produktu

z punktów zaopatrzenia dla i=1...n

Tj - stawki taryfowe za przewóz produktu

z punktów zbytu dla j=1...m

min

*

2

*

*

⇒

+

=

+

=

Wz

P

s

i

Kj

Wz

kd

ku

Kz

Kji

sP

Wz

2

=

i

d

EOQ

d

i

Kj

Ps

EOQ

/

1

1

)

(

2

−

=

−

=

i

fd

EOQ

EOQ

/

1

1

"

+

=

Pkj

EOQ

Ps

Kji

EOQ

EOQ

KW

+

+

=

2

)

(

)

1

(

*

)

1

(

2

)

(

u

Pkj

s

Wzg

P

i

u

Kj

Wzg

Wzg

KW

−

+

+

−

=

LMp

LMz

Rz

−

= 1

∑

∑

∑

∑

=

=

=

=

+

+

=

n

i

m

j

j

j

i

i

n

i

m

j

j

j

j

i

i

i

s

T

z

t

s

x

T

z

x

t

x

1

1

1

1

∑

∑

∑

∑

=

=

=

=

+

+

=

n

i

m

j

j

j

i

i

n

i

m

j

j

j

j

i

i

i

s

T

z

t

s

y

T

z

y

t

y

1

1

1

1