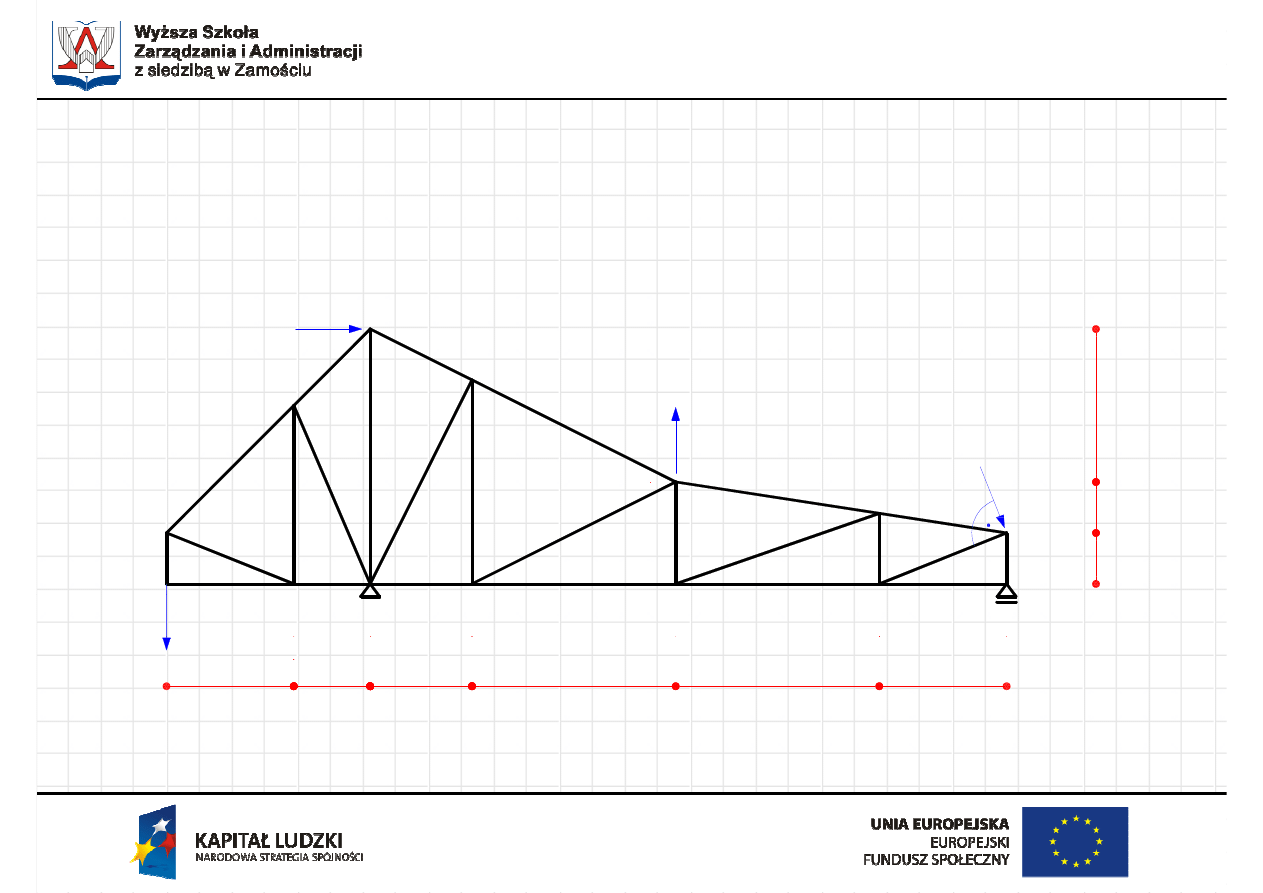
Aleksander Robak, Ewa Błazik-Borowa

Katedra Mechaniki Budowli, Politechnika Lubelska

Wy

ż

sza Szkoła Zarz

ą

dzania i Administracji

Analiza statyczna kratownic statycznie wyznaczalnych

2kN

2kN

5kN

3kN

7kN

1

m

1

m

3

m

Projekt współfinansowany przez Unię Europejską

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

w ramach Europejskiego Funduszu Społecznego

2.5m

1.5m

2m

4m

4m

2.5m

5kN

1.5m

2m

1.5m

2m

1.5m

2m

Opis problemu

Kratownica jest schematem statycznym konstrukcji pr

ę

towych, w których pr

ę

ty s

ą

poł

ą

czone przegubami. W praktyce in

ż

ynierskiej cz

ę

sto stosuje si

ę

takie rozwi

ą

zania,

poniewa

ż

elementy konstrukcji s

ą

poddane jedynie takim działaniom jak rozci

ą

ganie i

ś

ciskanie a w zwi

ą

zku z tym mo

ż

na uzyska

ć

znacznie wi

ę

ksz

ą

no

ś

no

ść

konstrukcji ni

ż

przy innych rozwi

ą

zaniach przy takim samym zu

ż

yciu materiału.

W ramach wykładu zostan

ą

przedstawione podstawowe informacje o kratownicach oraz

zostanie omówiony przykład wyznaczania reakcji i sił wewn

ę

trznych w pr

ę

tach kraty

płaskiej, które s

ą

potrzebne przy projektowaniu tego rodzaju układów.

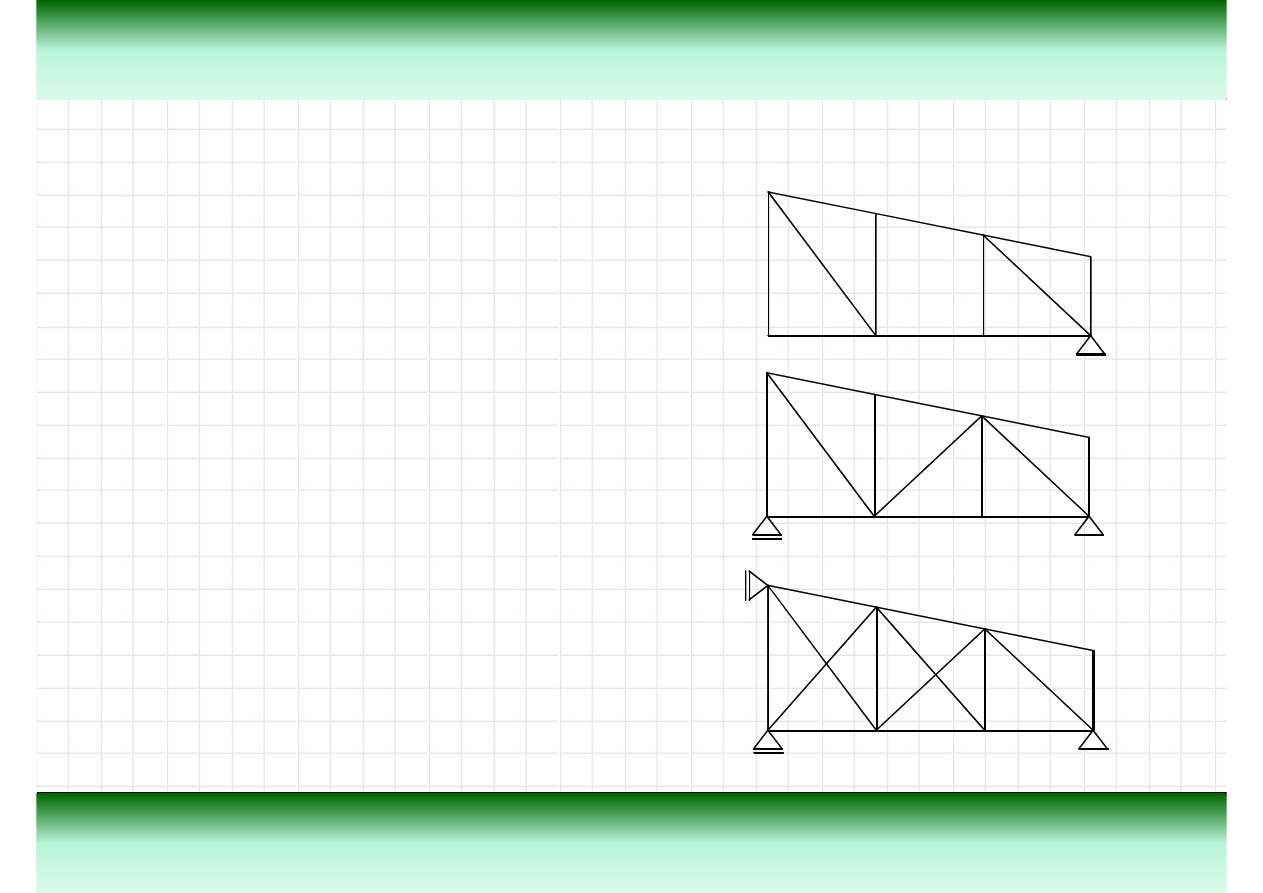
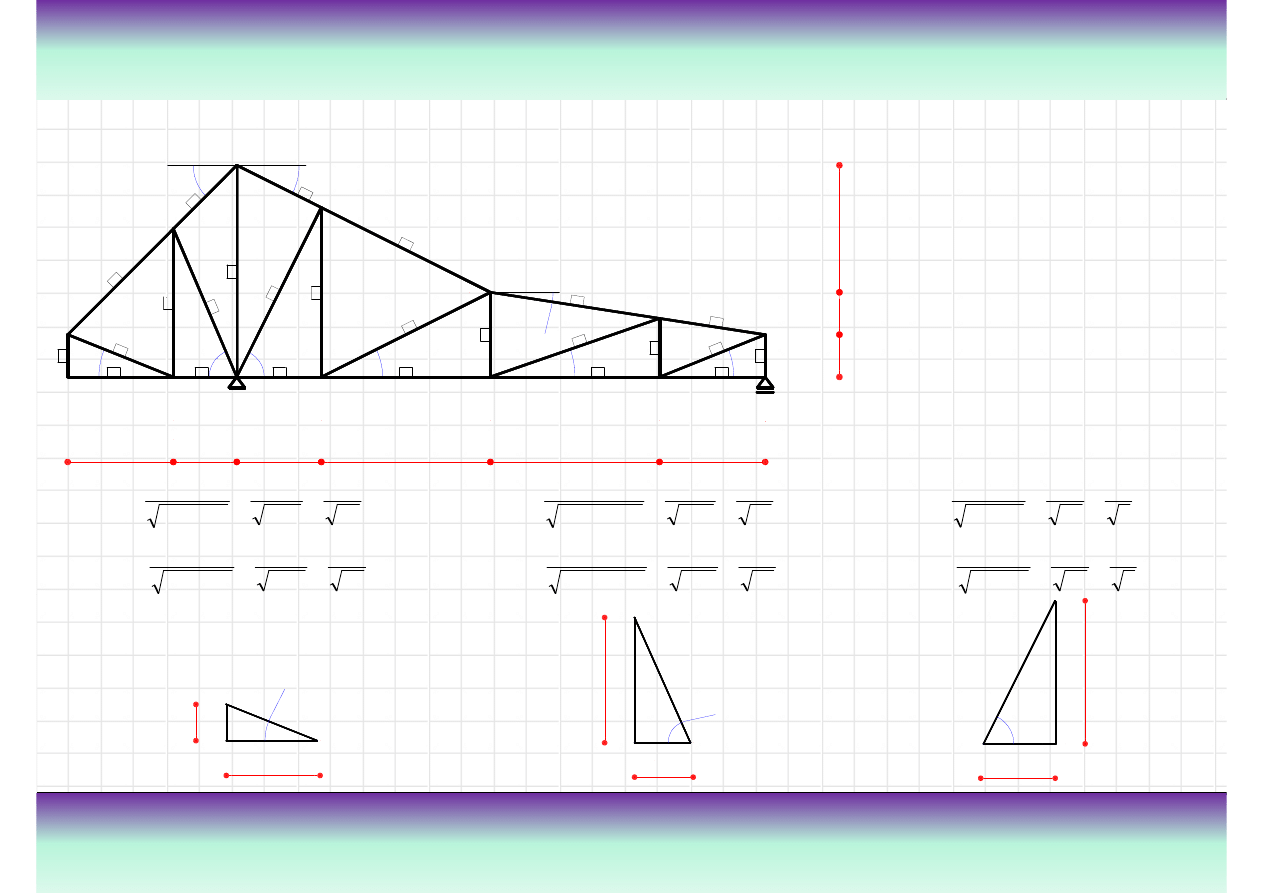
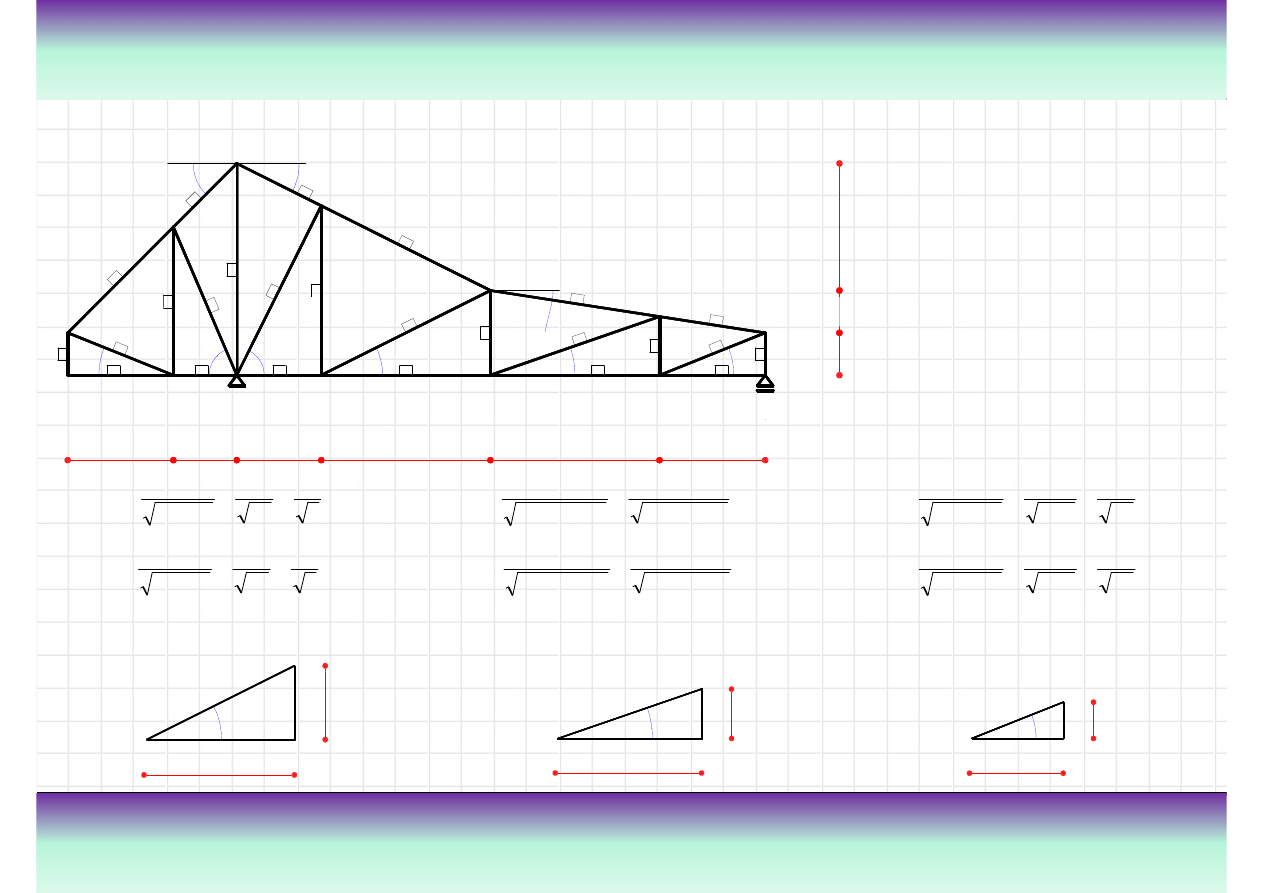
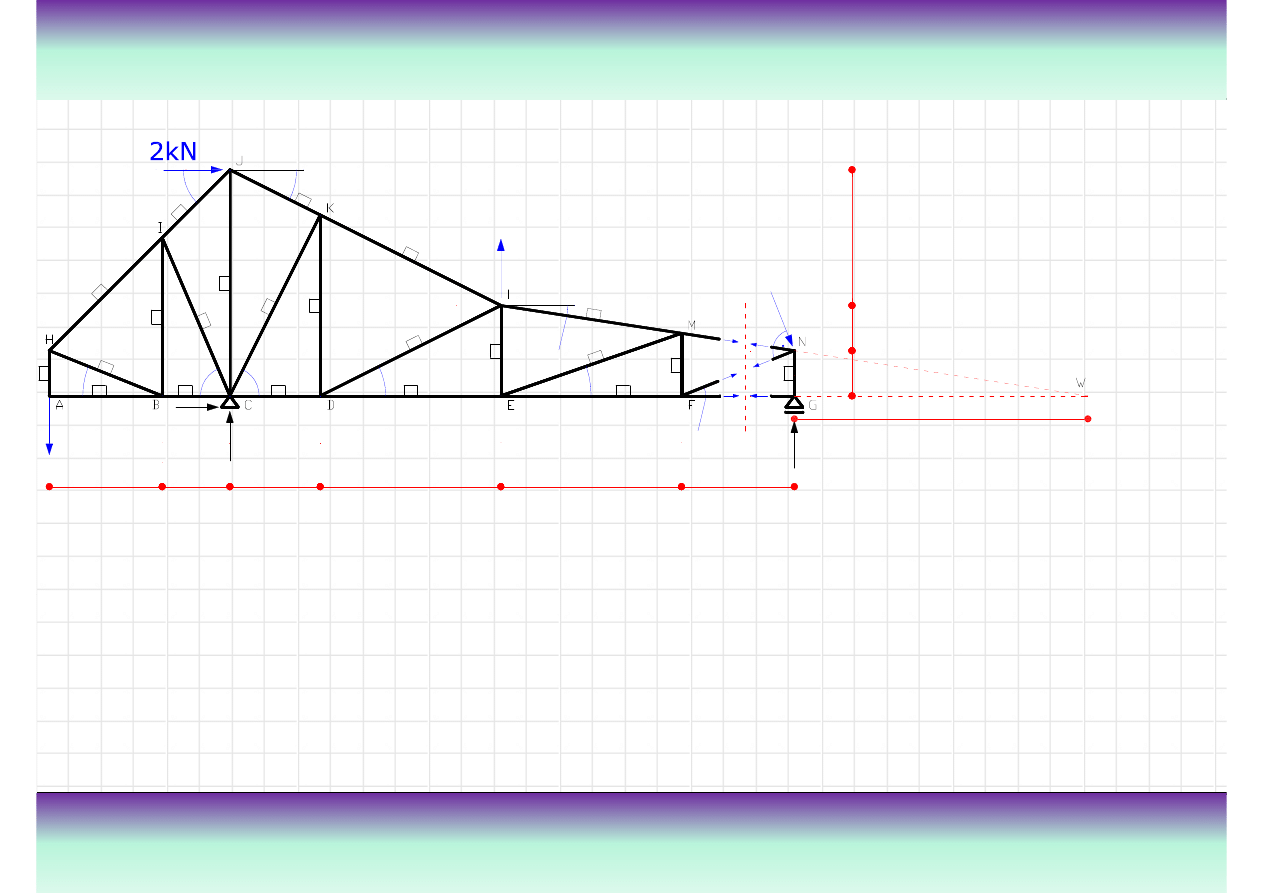
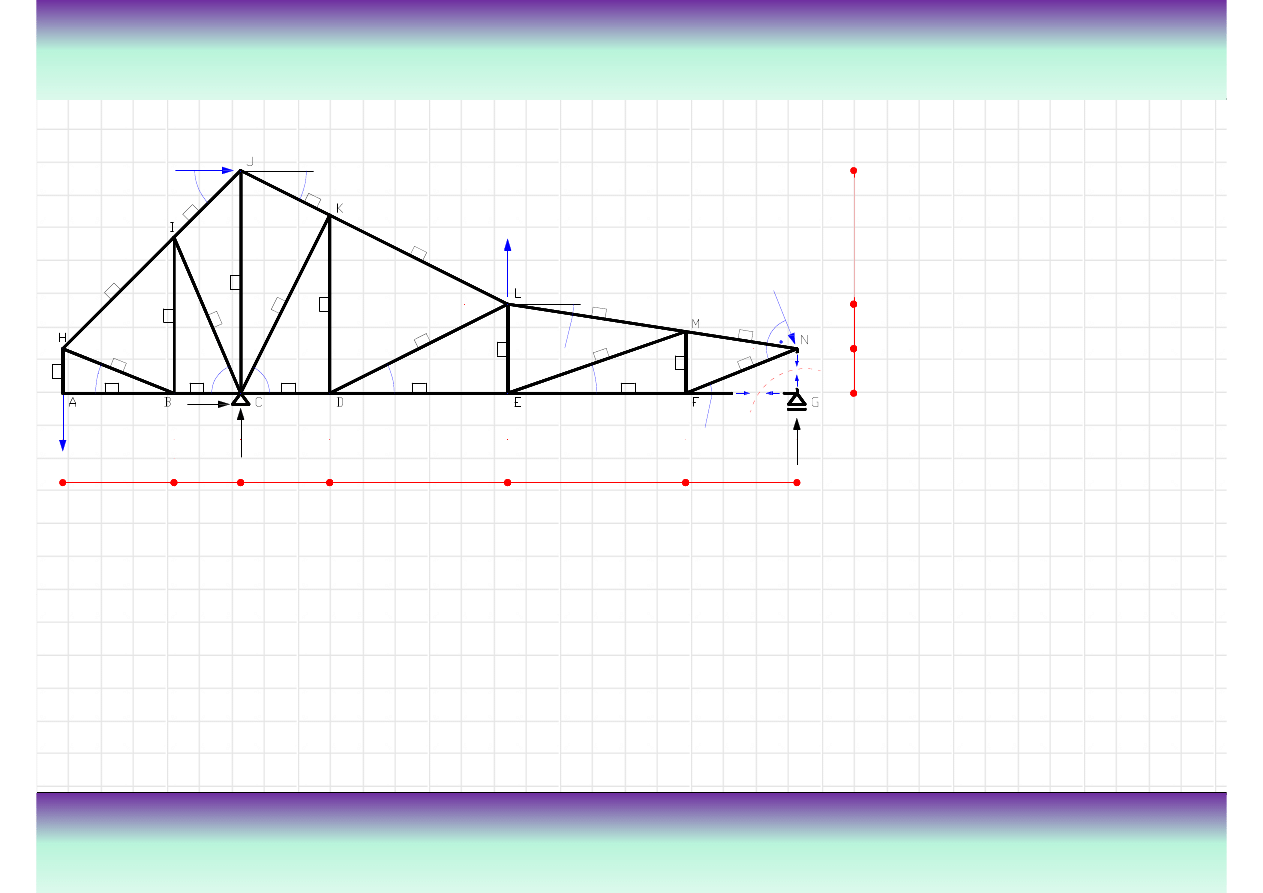
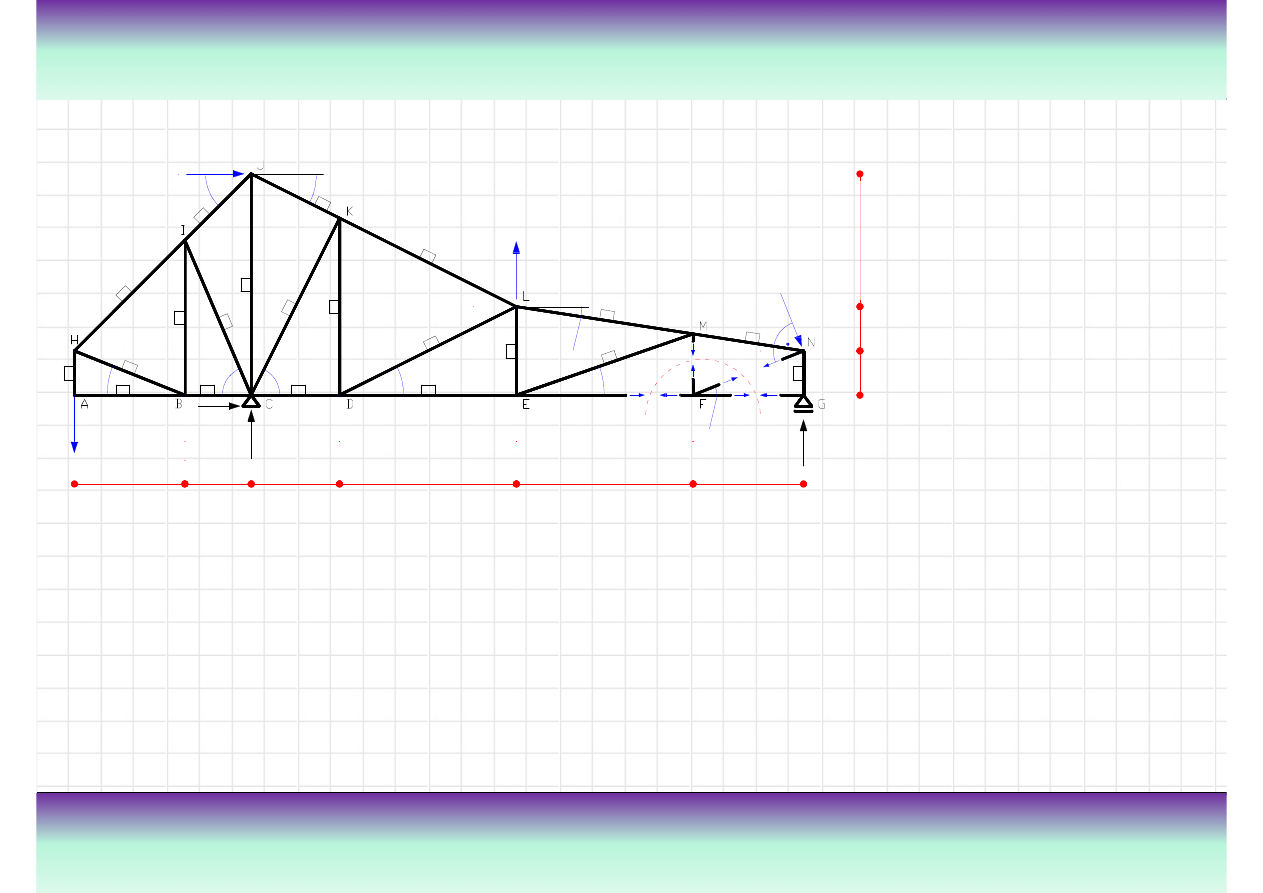
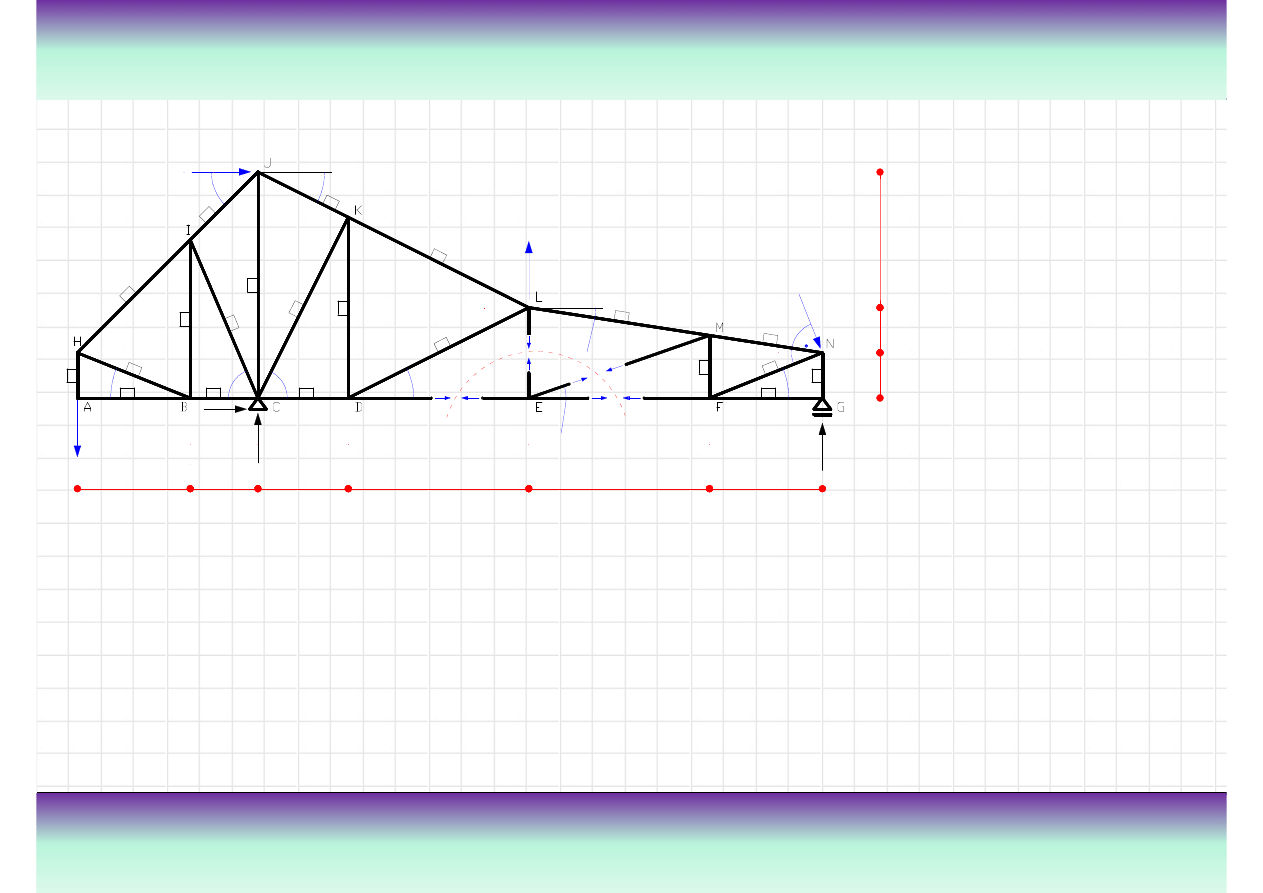
Przykład kratownicy „K”

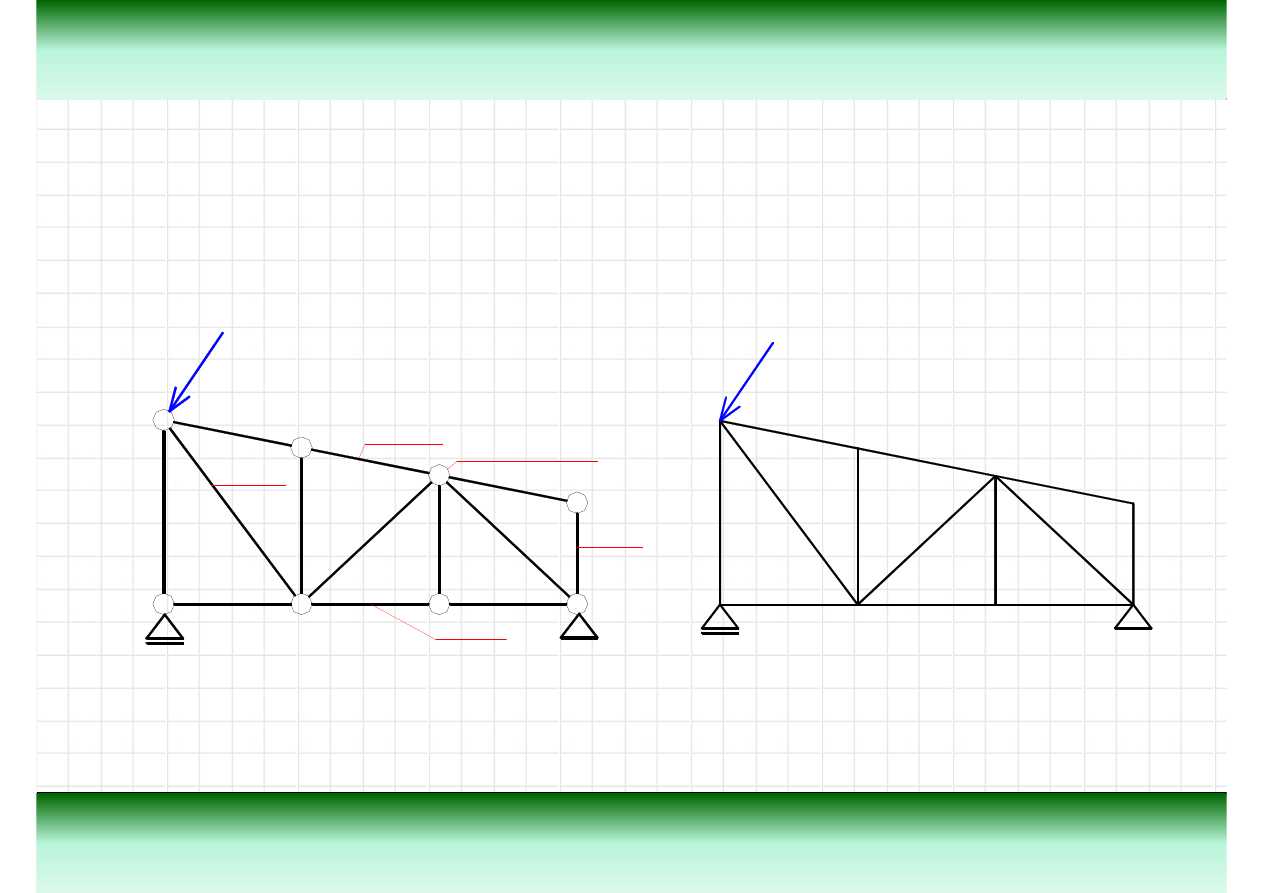
Teoria

Kratownica jest szczególnym przypadkiem ramy. Układ taki stanowi zestaw pr

ę

tów

poł

ą

czonych przegubowo z obci

ąż

eniami przyło

ż

onymi w formie sił skupionych,

ustawionych w w

ę

złach. Na rysunku z lewej strony pokazana jest kratownica z

zaznaczonymi przegubami oraz nazwami elementów.

Definicja kratownicy

zaznaczonymi przegubami oraz nazwami elementów.

pas górny

słupek

krzyżulec

połączenie przegubowe

Poniewa

ż

z definicji pr

ę

ty kratownicy s

ą

poł

ą

czone przegubowo, to tych poł

ą

cze

ń

si

ę

zwykle nie rysuje a schemat statyczny wygl

ą

da w sposób pokazany na rysunku z prawej

strony.

pas dolny

Teoria

Ró

ż

nice pomi

ę

dzy ram

ą

i krata

Kratownica (krata)
- poł

ą

czenia przegubowe,

- obci

ąż

enie w formie sił skupionych

Rama
- dowolny rodzaj poł

ą

cze

ń

: przegubowe i

sztywne,
- dowolne obci

ąż

enie przyło

ż

one do w

ę

złów lub

- obci

ąż

enie w formie sił skupionych

przyło

ż

one do w

ę

złów, nie mo

ż

na do

w

ę

złów przyło

ż

y

ć

momentów skupionych,

- podpory blokuj

ą

ce przesuw,

- ze wzgl

ę

du na poł

ą

czenia przegubowe

oraz przyło

ż

enie sił do w

ę

złów w pr

ę

tach

wyst

ę

puje tylko siła normalna.

- dowolne obci

ąż

enie przyło

ż

one do w

ę

złów lub

do elementów,
- podpory blokuj

ą

ce przesuwy i obroty,

- elementy ramy płaskiej poddane s

ą

trzem

siłom wewn

ę

trznym: sile normalnej, tn

ą

cej

(poprzecznej) i momentowi zginaj

ą

cemu.

P

q

P

Q

q

P

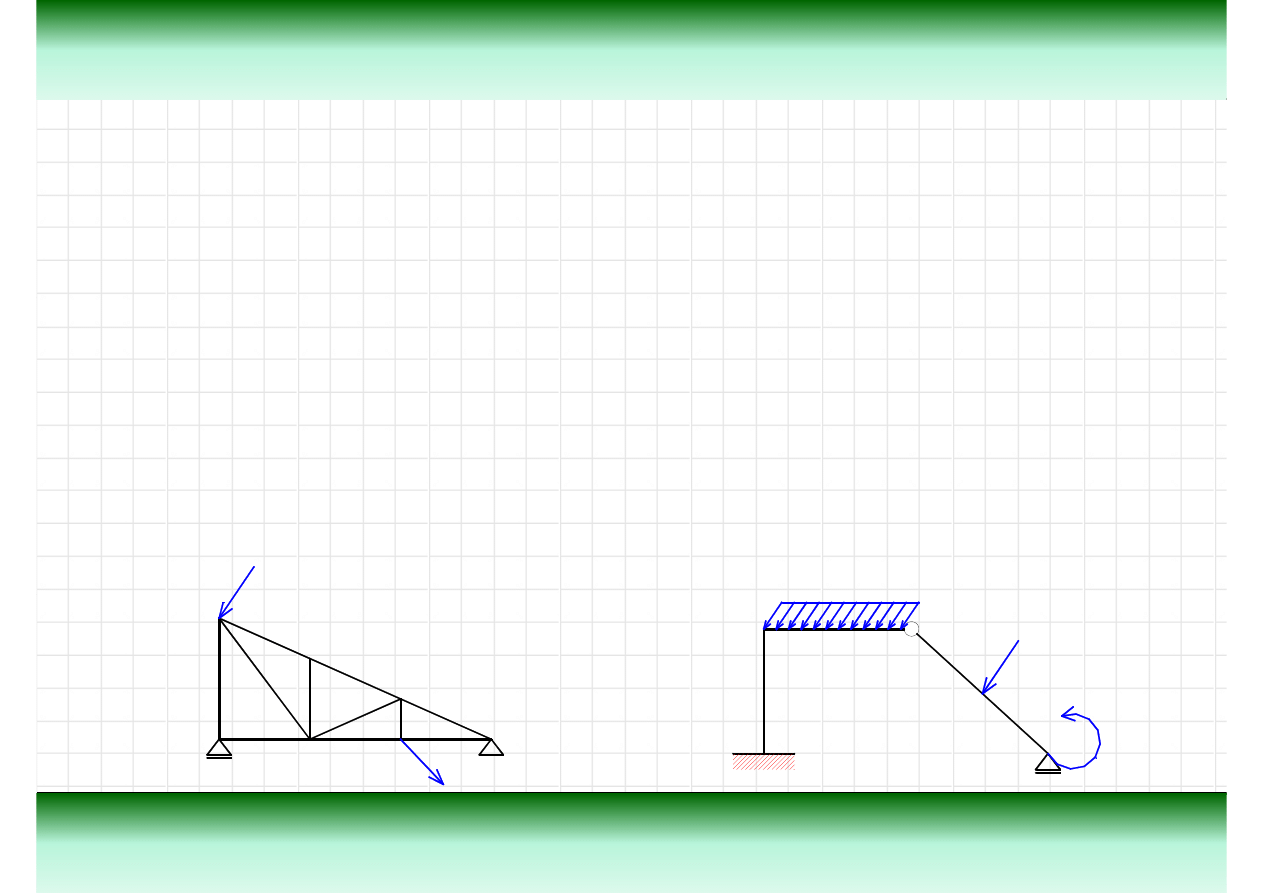
Teoria

Statyczna wyznaczalno

ść

kratownic - przykłady

Kratownica geometrycznie zmienna – układ, który
nie mo

ż

e znale

źć

si

ę

w stanie równowagi

statycznej.

Kratownica statycznie wyznaczalna – wyznaczenie
reakcji i sił wewn

ę

trznych mo

ż

liwe za pomoc

ą

równa

ń

równowagi.

Kratownica statycznie niewyznaczalna –

Kratownica statycznie niewyznaczalna –
wyznaczenie reakcji i sił wewn

ę

trznych nie jest

mo

ż

liwe za pomoc

ą

równa

ń

równowagi.

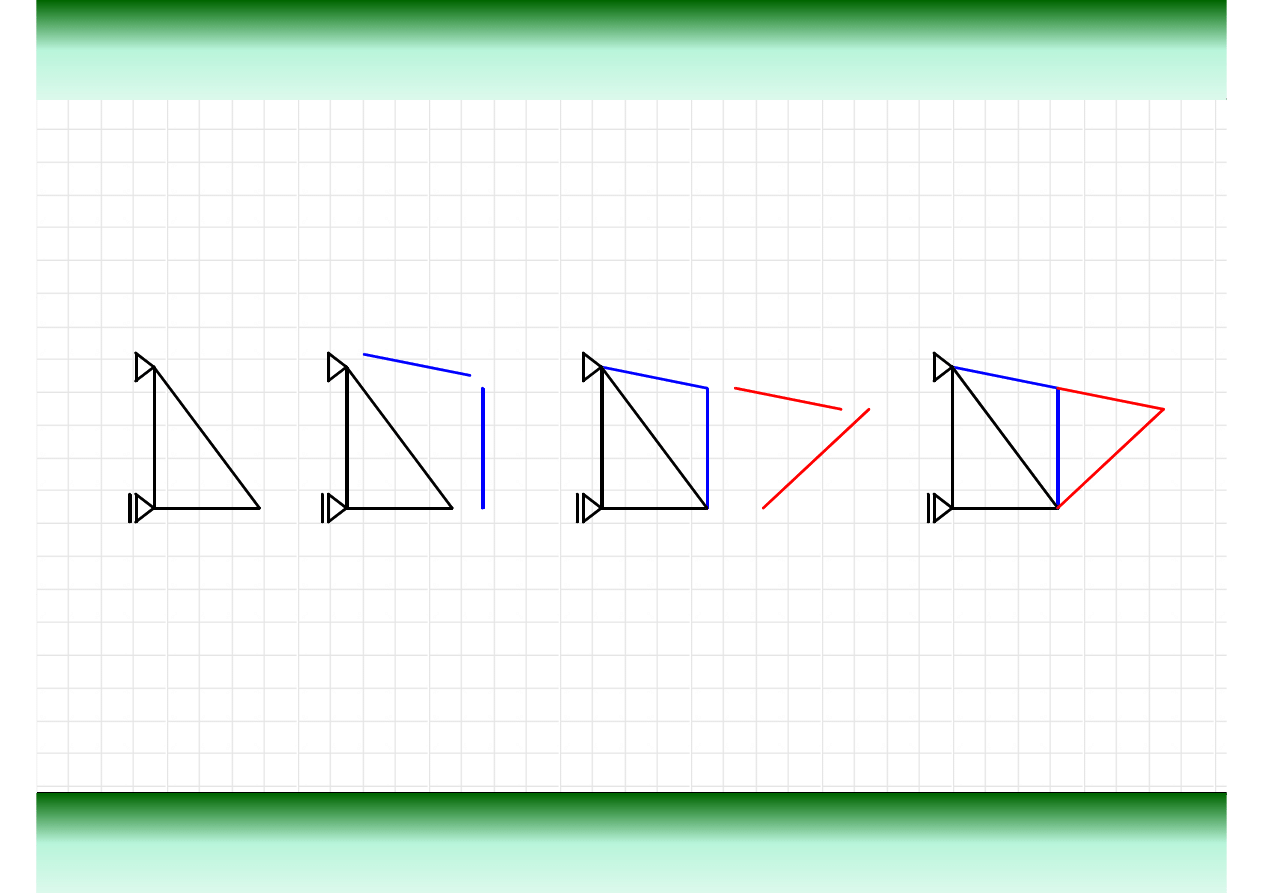
Teoria

Statyczna wyznaczalno

ść

kratownic

Najprostsza kratownica zło

ż

ona z trzech pr

ę

tów poł

ą

czonych przegubowo tworzy tarcz

ę

sztywn

ą

i jest statycznie wyznaczalna a ka

ż

da kratownica budowana przez dostawianie

pól zamkni

ę

tych tworzonych za pomoc

ą

kolejnych dwóch pr

ę

tów jest statycznie

wyznaczalna.

wyznaczalna.

Statyczna wyznaczalno

ść

:

• zewn

ę

trzna – mo

ż

liwo

ść

policzenia reakcji:

3

n

r

= −

• zewn

ę

trzna – mo

ż

liwo

ść

policzenia reakcji:

• wewn

ę

trzna – mo

ż

liwo

ść

policzenia sił w pr

ę

tach:

• całkowita:

gdzie:

r

– liczba reakcji,

p

–

liczba pr

ę

tów,

w

– liczba w

ę

złów.

3

z

n

r

= −

2

3

w

n

p

w

= − ⋅ +

2

n

r

p

w

= + − ⋅

Teoria

Oddziaływania pomi

ę

dzy w

ę

złami i pr

ę

tami

Kratownic

ę

mo

ż

na rozdzieli

ć

w sposób pokazany na rysunku. Zgodnie z trzeci

ą

zasad

ą

dynamiki siły działaj

ą

ce na w

ę

zeł i pr

ę

t dochodz

ą

cy do w

ę

zła maj

ą

takie same warto

ś

ci i

kierunki, ale przeciwne zwroty. Siły, działaj

ą

ce na ko

ń

ce pr

ę

ta, tak

ż

e maj

ą

takie same

warto

ś

ci i kierunki oraz przeciwne zwroty. Wynika to z warunku równowagi pr

ę

ta.

P

N

4

N

4

N

5

N

5

N

6

N

6

N

5

N

5

N

6

N

6

N

7

N

7

N

4

N

4

N

9

N

9

N

11

N

11

N

13

N

13

N

8

N

8

N

10

N

10

N

12

N

12

4

5

6

7

8

9

10

1

1

12

Przy obliczeniach siły normalne, działaj

ą

ce na w

ę

zeł,

zawsze rysujemy zwrócone od w

ę

zła. Uzyskania w

obliczeniach warto

ś

ci dodatniej siły normalnej oznacza,

ż

e pr

ę

t jest rozci

ą

gany, a siły ujemnej,

ż

e pr

ę

t jest

ś

ciskany.

Q

N

1

N

1

N

1

N

1

N

2

N

2

N

2

N

2

N

3

N

3

N

3

N

3

N

7

N

7

N

9

N

9

N

11

N

11

N

13

N

13

N

8

N

8

N

10

N

10

N

12

N

12

1

2

3

1

1

1

3

V

A

V

D

H

D

Teoria

Metody liczenia sił normalnych w pr

ę

tach kratownicy

Reakcje w podporach wyznacza si

ę

z równa

ń

równowagi sił w odniesieniu do układów

płaskich czyli:

suma rzutów wektorów sił zewn

ę

trznych na o

ś

X (kierunek poziomy),

suma rzutów wektorów sił zewn

ę

trznych na o

ś

Y (kierunek pionowy),

Ʃ

X=0

Ʃ

Y=0

suma rzutów wektorów sił zewn

ę

trznych na o

ś

Y (kierunek pionowy),

suma momentów wzgl

ę

dem dowolnego punktu.

Ʃ

M

0

=0

Ʃ

Y=0

Siły normalne w pr

ę

tach mog

ą

by

ć

wyznaczane nast

ę

puj

ą

cymi metodami:

- metoda równowa

ż

enia sił w w

ę

złach – siły normalne w w

ę

złach tworz

ą

układy sił

zbie

ż

nych i musz

ą

spełnia

ć

dwa równania równowagi:

suma rzutów wektorów sił zewn

ę

trznych na o

ś

X (kierunek poziomy),

suma rzutów wektorów sił zewn

ę

trznych na o

ś

Y (kierunek pionowy),

- metoda Rittera (przekrojów) – siły w przekroju kratownicy oraz obci

ąż

enia z jednej

Ʃ

X=0

Ʃ

Y=0

- metoda Rittera (przekrojów) – siły w przekroju kratownicy oraz obci

ąż

enia z jednej

strony tego przekroju musz

ą

spełnia

ć

równania równowagi:

suma rzutów wektorów sił zewn

ę

trznych na o

ś

X (kierunek poziomy),

suma rzutów wektorów sił zewn

ę

trznych na o

ś

Y (kierunek pionowy),

suma momentów wzgl

ę

dem dowolnego punktu.

Ʃ

X=0

Ʃ

M

0

=0

Ʃ

Y=0

Teoria

Twierdzenie Talesa- Je

ż

eli ramiona k

ą

ta przetniemy dwiema

prostymi równoległymi a i b to odcinki wyznaczone na

ramionach kata przez te proste s

ą

proporcjonalne

|

|

|

|

|

|

|

|

||

AB

OA

CD

OC

b

a

=

⇒

Twierdzenie Pitagorasa- Je

ż

eli trójk

ą

t jest prostok

ą

tny to

suma kwadratów długo

ś

ci przyprostok

ą

tnych jest równa

c

α

suma kwadratów długo

ś

ci przyprostok

ą

tnych jest równa

kwadratowi długo

ś

ci przeciwprostok

ą

tnej

2

2

2

c

b

a

=

+

Sinusem k

ą

ta

α

nazywamy stosunek długo

ś

ci

przyprostok

ą

tnej trójk

ą

ta le

żą

cej naprzeciw k

ą

ta

α

do długo

ś

ci

przeciwprostok

ą

tnej

c

b

=

α

sin

Cosinusem k

ą

ta

α

nazywamy stosunek długo

ś

ci

a

b

α

a

b

α

c

Funkcje trygonometryczne w trójk

ą

cie prostok

ą

tnym

Cosinusem k

ą

ta

α

nazywamy stosunek długo

ś

ci

przyprostok

ą

tnej trójk

ą

ta le

żą

cej przy k

ą

cie

α

do długo

ś

ci

przeciwprostok

ą

tnej

c

a

=

α

cos

Rozkładanie siły na składowe

a

α

sin

=

P

Py

α

cos

=

P

Px

P

α

P

cos

α

P

sin

α

P

α

P

x

P

y

P

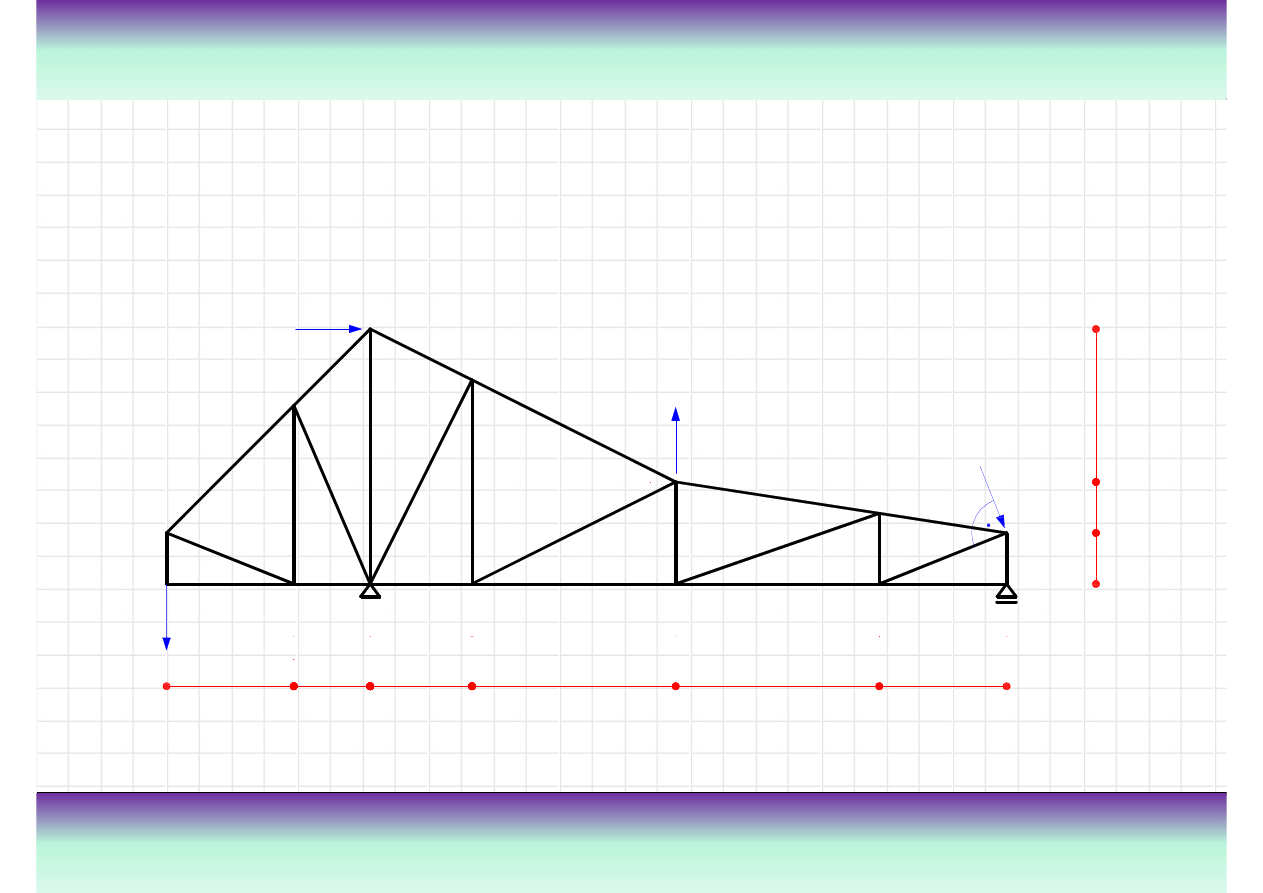
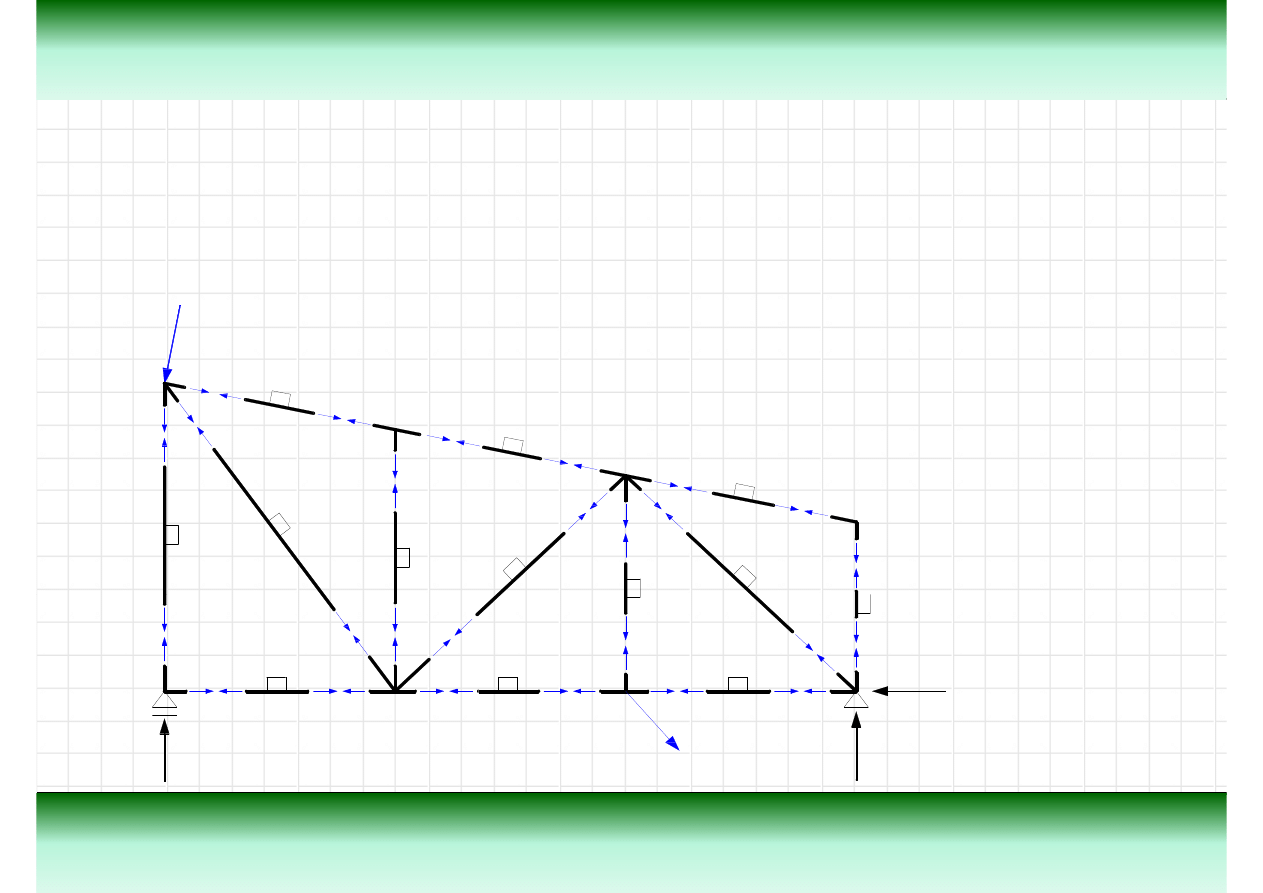
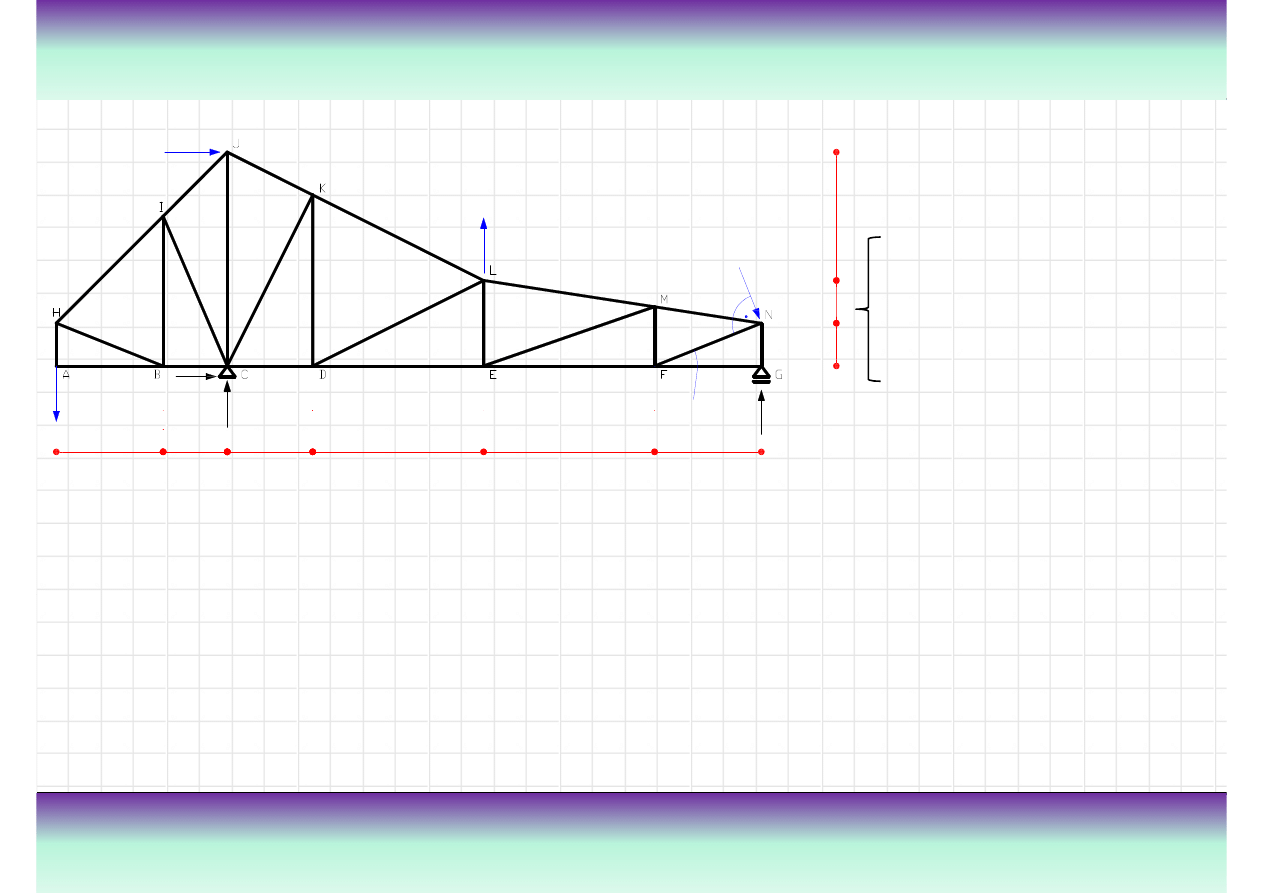
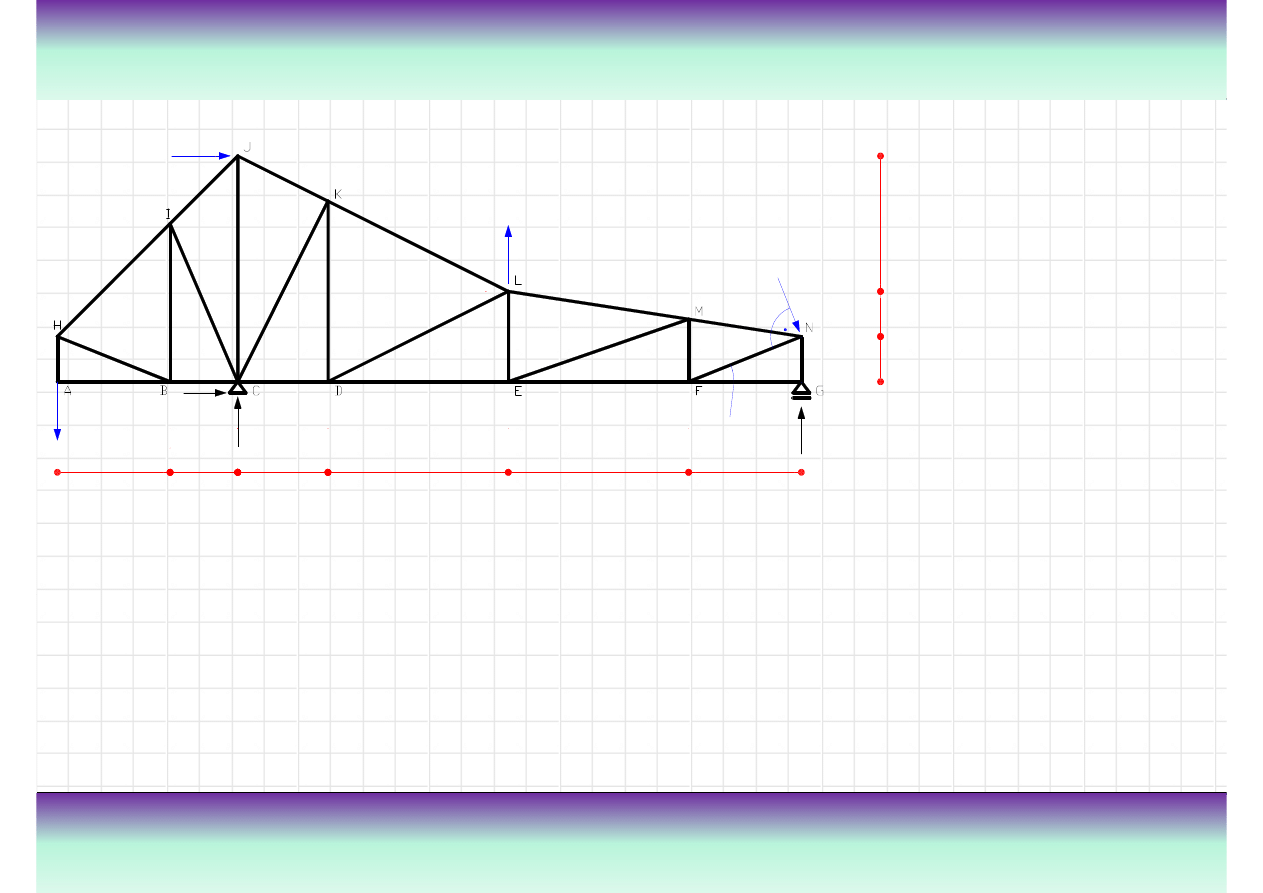
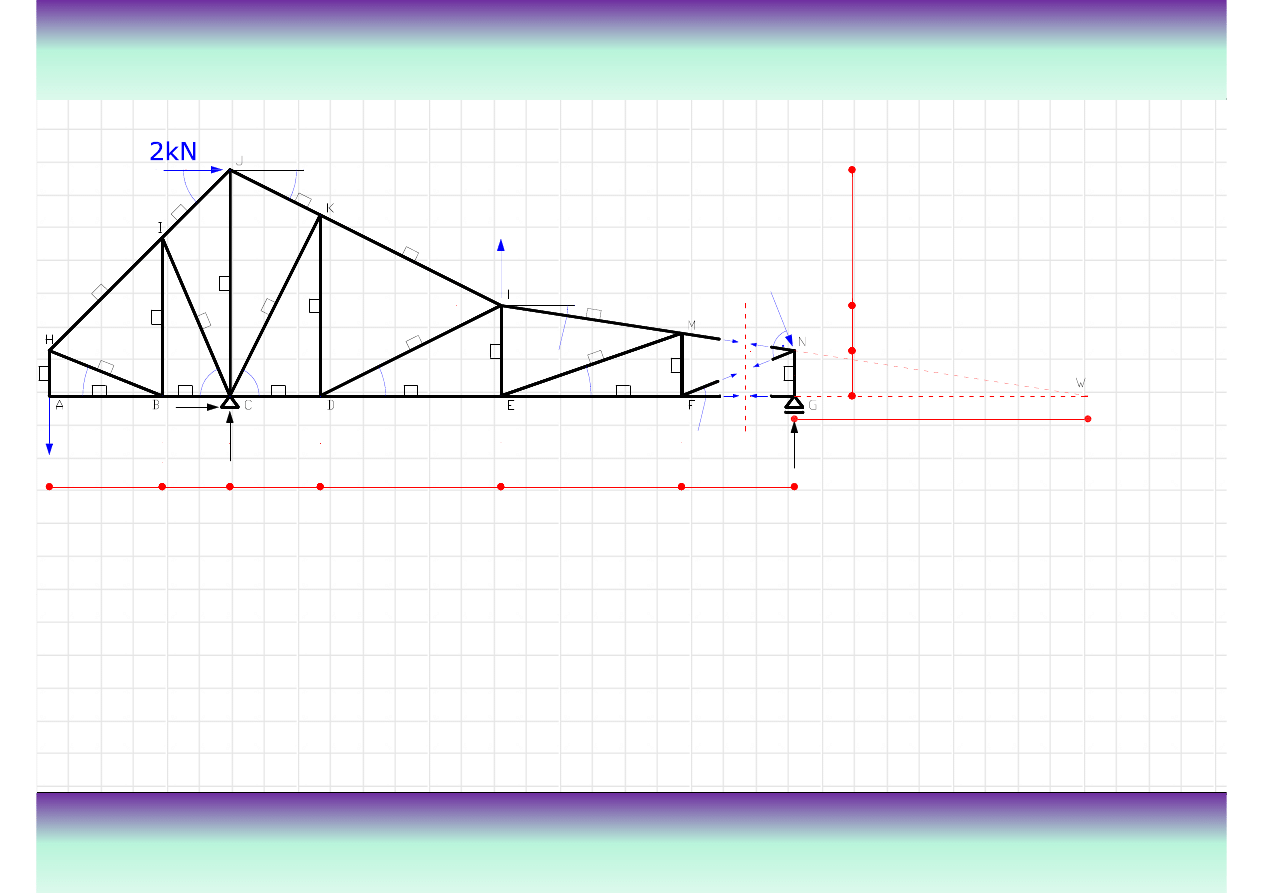
Przykład

Wyznaczy

ć

reakcje w podporach i siły normalne w pr

ę

tach kratownicy pokazanej na

rysunku.

Tre

ść

zadania

2kN

2kN

5kN

3kN

7kN

1

m

1

m

3

m

2.5m

1.5m

2m

4m

4m

2.5m

5kN

1.5m

2m

1.5m

2m

1.5m

2m

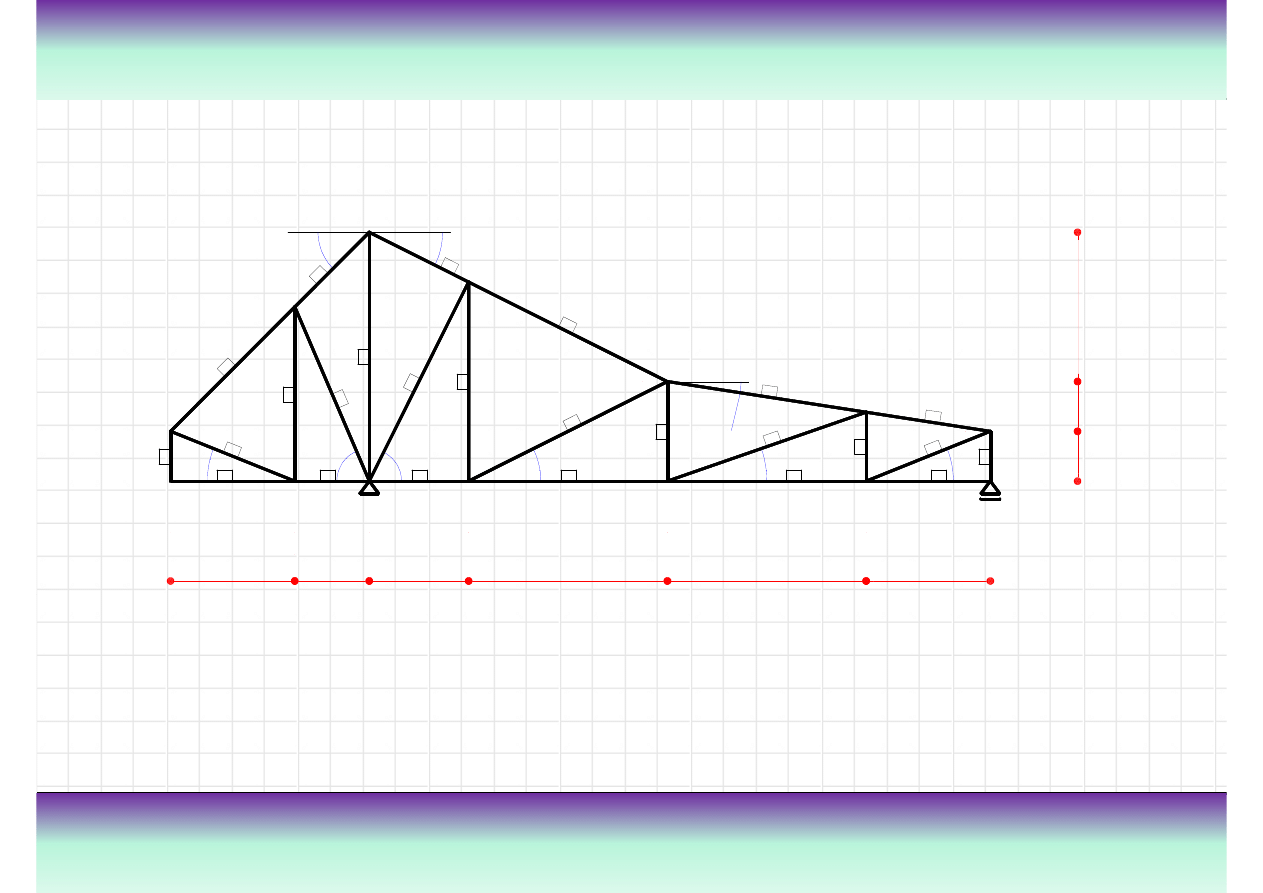
Przykład

Wyznaczanie danych geometrycznych niezb

ę

dnych do dalszych oblicze

ń

3

m

α

2

α

1

8

9

2.5m

1.5m

2m

4m

4m

2.5m

1

m

1

m

3

m

α

8

α

9

α

7

α

6

α

5

α

4

α

3

1

2

3

4

5

6

1

3

1

4

1

5

1

6

1

7

1

8

1

9

20

2

1

2

2

23

24

25

7

10

11

12

Do dalszych oblicze

ń

potrzebne b

ę

d

ą

warto

ś

ci funkcji trygonometrycznych k

ą

tów:

α

1

,

α

2

,

α

3

,

α

4

,

α

5

,

α

6

,

α

7

,

α

8

,

α

9

oraz długo

ś

ci pr

ę

tów nr 14, nr 16 i nr 18.

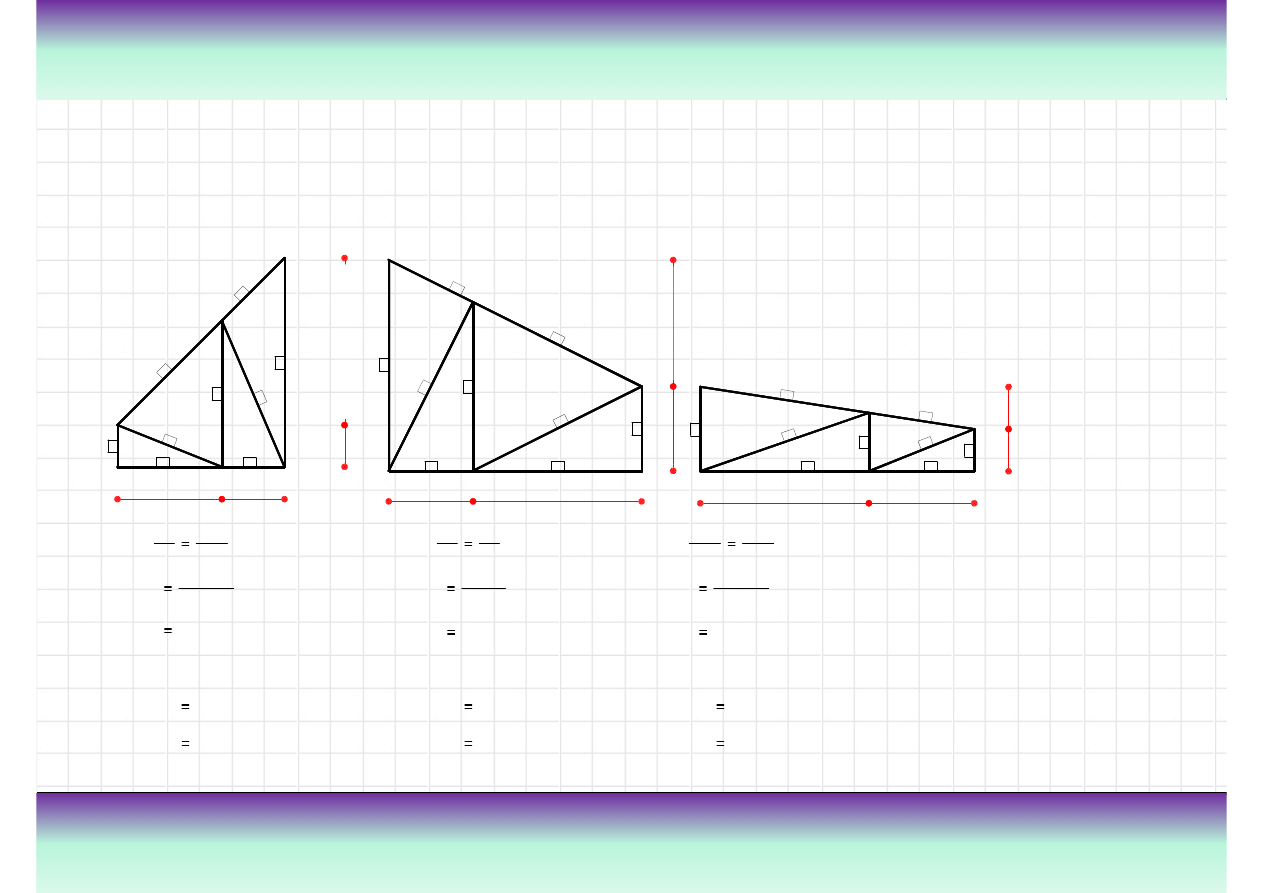
Przykład

Wyznaczanie danych geometrycznych niezb

ę

dnych do dalszych oblicze

ń

Długo

ś

ci pr

ę

tów nale

ż

y wyznaczy

ć

korzystaj

ą

c z

wymiarów kratownicy oraz twierdze

ń

z zakresu

geometrii np. z twierdzenia Talesa

9

8

2m

4m

3

4

1

5

1

6

1

7

2

2

23

10

2

m

3

m

2.5m

1.5m

1

2

1

3

1

4

1

5

20

2

1

7

8

1

m

4

m

5

6

1

7

1

8

1

9

24

25

11

12

4m

2.5m

1

m

1

m

6.5m

1m

2.5m

x

x

2.5m 1

⋅

m

6.5m

4m

4m

2.5m

x

x

2.5m 4

⋅

m

4m

6m

3m

4m

x

x

3m 4

⋅

m

6m

- proporcje na podstawie twierdzenia Talesa

x

6.5m

6.5m

x

0.385m

x

4m

4m

x

2.5m

L14 2.5m 1m

+

L14 3.5m

x

6m

6m

x

2m

L18 0.385m 1m

+

L18 1.385m

L16 2m 2m

+

L16 4m

- rozwi

ą

zanie równa

ń

Ostateczna długo

ść

pr

ę

tów:

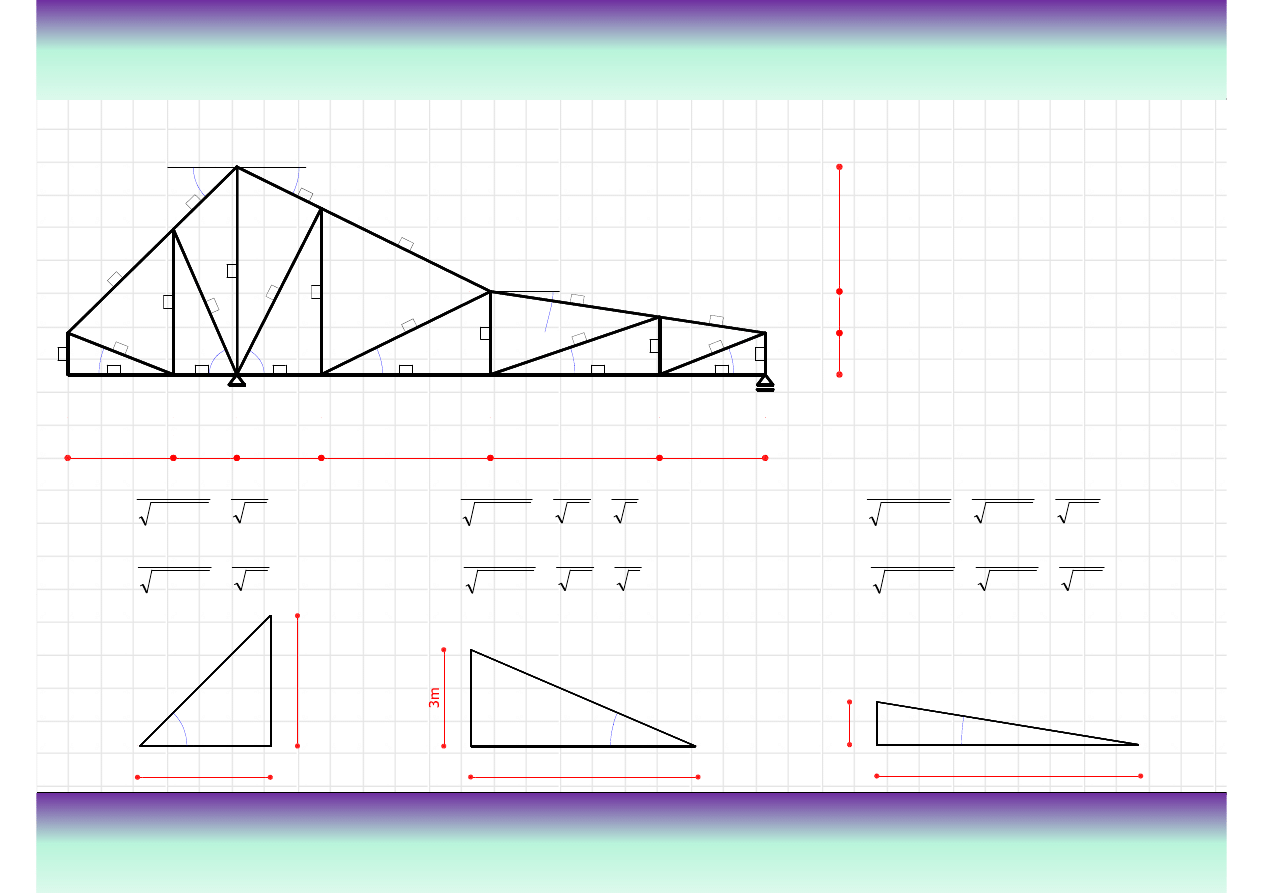
Przykład

Wyznaczanie danych geometrycznych niezb

ę

dnych do dalszych oblicze

ń

3

m

α

2

α

1

1

4

1

5

1

6

2

2

7

8

9

10

11

Warto

ś

ci funkcji trygonometrycznych

k

ą

tów, zaznaczonych na rysunku

nale

ż

y wyznaczy

ć

na podstawie

wymiarów kratownicy, definicji
sinusa i cosinusa k

ą

ta oraz

2.5m

1.5m

2m

4m

4m

2.5m

1

m

1

m

α

8

α

9

α

7

α

6

α

5

α

4

α

3

1

2

3

4

5

6

1

3

1

4

1

6

1

7

1

8

1

9

20

2

1

2

2

23

24

25

11

12

( )

7071

.

0

32

4

4

4

4

sin

2

2

1

=

=

+

=

α

sinusa i cosinusa k

ą

ta oraz

twierdzenia Pitagorasa.

( )

4472

.

0

5

1

45

3

6

3

3

sin

2

2

2

=

=

=

+

=

α

( )

8944

.

0

5

2

45

6

6

3

6

cos

2

2

2

=

=

=

+

=

α

( )

1521

.

0

173

2

25

.

43

1

5

.

6

1

1

sin

2

2

3

=

=

=

+

=

α

( )

9884

.

0

173

13

25

.

43

5

.

6

5

.

6

1

5

.

6

cos

2

2

3

=

=

=

+

=

α

( )

7071

.

0

32

4

4

4

4

cos

2

2

1

=

=

+

=

α

Sinus k

ą

ta jest równy ilorazowi długo

ś

ci przyprostok

ą

tnej, le

żą

cej naprzeciwko k

ą

ta, i długo

ś

ci

przeciwprostok

ą

tnej.

Cosinus k

ą

ta jest równy ilorazowi długo

ś

ci przyprostok

ą

tnej, le

żą

cej przy k

ą

cie, i długo

ś

ci przeciwprostok

ą

tnej.

6

3

+

5

.

6

1

+

4

4

+

4m

4

m

α

1

6m

α

2

6.5m

1

m

α

3

Przykład

Wyznaczanie danych geometrycznych niezb

ę

dnych do dalszych oblicze

ń

3

m

α

2

α

1

1

5

1

6

2

2

7

8

9

10

11

Warto

ś

ci funkcji trygonometrycznych

k

ą

tów, zaznaczonych na rysunku

nale

ż

y wyznaczy

ć

na podstawie

wymiarów kratownicy, definicji
sinusa i cosinusa k

ą

ta oraz

2.5m

1.5m

2m

4m

4m

2.5m

1

m

1

m

α

8

α

9

α

7

α

6

α

5

α

4

α

3

1

2

3

4

5

6

1

3

1

4

1

6

1

7

1

8

1

9

20

2

1

2

2

23

24

25

11

12

( )

3714

.

0

29

2

25

.

7

1

5

.

2

1

1

sin

2

2

4

=

=

=

+

=

α

( )

9191

.

0

58

7

5

.

14

5

.

3

5

.

1

5

.

3

5

.

3

sin

2

2

5

=

=

=

+

=

α

( )

8944

.

0

5

2

20

4

4

2

4

sin

2

2

6

=

=

=

+

=

α

Potrzebne dane:

L

14

=3.5m

L

16

=4.0m

( )

9285

.

0

29

5

25

.

7

5

.

2

5

.

2

1

5

.

2

cos

2

2

4

=

=

=

+

=

α

( )

3939

.

0

58

3

5

.

14

5

.

1

5

.

1

5

.

3

5

.

1

cos

2

2

5

=

=

=

+

=

α

( )

4472

.

0

5

1

20

2

4

2

2

cos

2

2

6

=

=

=

+

=

α

sinusa i cosinusa k

ą

ta oraz

twierdzenia Pitagorasa.

Sinus k

ą

ta jest równy ilorazowi długo

ś

ci przyprostok

ą

tnej, le

żą

cej naprzeciwko k

ą

ta, i długo

ś

ci

przeciwprostok

ą

tnej.

Cosinus k

ą

ta jest równy ilorazowi długo

ś

ci przyprostok

ą

tnej, le

żą

cej przy k

ą

cie, i długo

ś

ci przeciwprostok

ą

tnej.

5

.

2

1

+

5

.

1

5

.

3

+

4

2

+

2.5m

1

m

α

4

1.5m

3

.5

m

α

5

2m

4

m

α

6

Przykład

Wyznaczanie danych geometrycznych niezb

ę

dnych do dalszych oblicze

ń

3

m

α

2

α

1

1

4

1

5

1

6

2

1

2

2

7

8

9

10

11

Warto

ś

ci funkcji trygonometrycznych

k

ą

tów, zaznaczonych na rysunku

nale

ż

y wyznaczy

ć

na podstawie

wymiarów kratownicy, definicji
sinusa i cosinusa k

ą

ta oraz

2.5m

1.5m

2m

4m

4m

2.5m

1

m

1

m

α

8

α

9

α

7

α

6

α

5

α

4

α

3

1

2

3

4

5

6

1

3

1

4

1

6

1

7

1

8

1

9

20

2

1

2

2

23

24

25

11

12

( )

4472

.

0

5

1

20

2

4

2

2

sin

2

2

7

=

=

=

+

=

α

( )

3272

.

0

918225

.

17

385

.

1

385

.

1

4

385

.

1

sin

2

2

8

=

=

+

=

α

( )

3714

.

0

29

2

25

.

7

1

5

.

2

1

1

sin

2

2

9

=

=

=

+

=

α

Potrzebne dane:

L

18

=1.385m

( )

8944

.

0

5

2

20

4

4

2

4

cos

2

2

7

=

=

=

+

=

α

( )

9450

.

0

918225

.

17

4

385

.

1

4

385

.

1

cos

2

2

8

=

=

+

=

α

( )

9285

.

0

29

5

25

.

7

5

.

2

5

.

2

1

5

.

2

cos

2

2

9

=

=

=

+

=

α

sinusa i cosinusa k

ą

ta oraz

twierdzenia Pitagorasa.

Sinus k

ą

ta jest równy ilorazowi długo

ś

ci przyprostok

ą

tnej, le

żą

cej naprzeciwko k

ą

ta, i długo

ś

ci

przeciwprostok

ą

tnej.

Cosinus k

ą

ta jest równy ilorazowi długo

ś

ci przyprostok

ą

tnej, le

żą

cej przy k

ą

cie, i długo

ś

ci przeciwprostok

ą

tnej.

5

20

4

2

+

918225

.

17

385

.

1

4

+

29

25

.

7

5

.

2

1

+

4m

2

m

α

7

4m

1

.3

8

5

m

α

8

2.5m

1

m

α

9

Przykład

Wyznaczanie reakcji

Ʃ

X=0

W celu wyznaczenia reakcji trzeba
zapisa

ć

równania równowagi układu

w nast

ę

puj

ą

cej kolejno

ś

ci:

suma rzutów wektorów sił

zewn

ę

trznych na o

ś

X

(kierunek poziomy);

2kN

3kN

7kN

1

m

3

m

Ʃ

M

C

=0

Ʃ

Y=0

(kierunek poziomy);
suma momentów
wzgl

ę

dem punktu C;

suma rzutów wektorów
sił zewn

ę

trznych na

o

ś

Y (kierunek pionowy).

Ʃ

M

C

=0

V

G

⋅

12.5m+3kN

⋅

6m+5kN

⋅

4m-2kN

⋅

5m-7kN

⋅

sin(

α

9

)

⋅

1m-7kN

⋅

cos(

α

9

)

⋅

12.5m=0

V

G

⋅

12.5m+3kN

⋅

6m+5kN

⋅

4m-2kN

⋅

5m-7kN

⋅

0.3714

⋅

1m-7kN

⋅

0.9285

⋅

12.5m=0

V =4.4675kN

Potrzebne dane:

sin(

α

9

)=0.3714

cos(

α

9

)=0.9285

2.5m

1.5m

2m

4m

4m

2.5m

5kN

1

m

1

m

1.5m

2m

1.5m

2m

1.5m

2m

V

C

H

C

V

G

α

9

Ʃ

X=0

H

C

+2kN+7kN

⋅

sin(

α

9

)=0

H

C

=-2kN-7kN

⋅

0.3714

H

C

=-4.5997kN

Ʃ

Y=0

V

G

=4.4675kN

V

C

+V

G

-7kN

⋅

cos(

α

9

)+3kN-5kN=0

V

C

+4.4675kN-7kN

⋅

0.9285+3kN-5kN=0

V

C

=4.0320kN

Przykład

Wyznaczanie reakcji

Obliczenia reakcji nale

ż

y

sprawdzi

ć

na podstawie

równania równowagi. Nale

ż

y

do tego celu wykorzysta

ć

równanie równowagi, którym
jest suma momentów

2kN

3kN

7kN

3

m

jest suma momentów
wzgl

ę

dem dowolnego punktu,

ale innego ni

ż

przy

obliczeniach reakcji czyli nie
wzgl

ę

dem punktu C. Do

sprawdzenia zostanie
wykorzystane równanie,
opisuj

ą

ce sum

ę

momentów

wzgl

ę

dem punktu A.

Potrzebne dane:

sin(

α

9

)=0.3714

V

C

=4.0320kN

cos(

α

9

)=0.9285

V

G

=4.4675kN

2.5m

1.5m

2m

4m

4m

2.5m

5kN

1

m

1

m

1.5m

2m

1.5m

2m

1.5m

2m

V

C

H

C

V

G

α

9

Ʃ

M

A

=2kN

⋅

4m-V

c

⋅

4m-3kN

⋅

10m+7kN

⋅

sin(

α

9

)

⋅

1m+7kN

⋅

cos(

α

9

)

⋅

16.5m-V

G

⋅

16.5m=

=2kN

⋅

5m-4.0320kN

⋅

4m-3kN

⋅

10m+7kN

⋅

0.3714

⋅

1m+7kN

⋅

0.9285

⋅

16.5m-4.4675

⋅

16.5m=-0.0002kNm

≈

0

Warunek spełniony:

Ʃ

M

A

=0

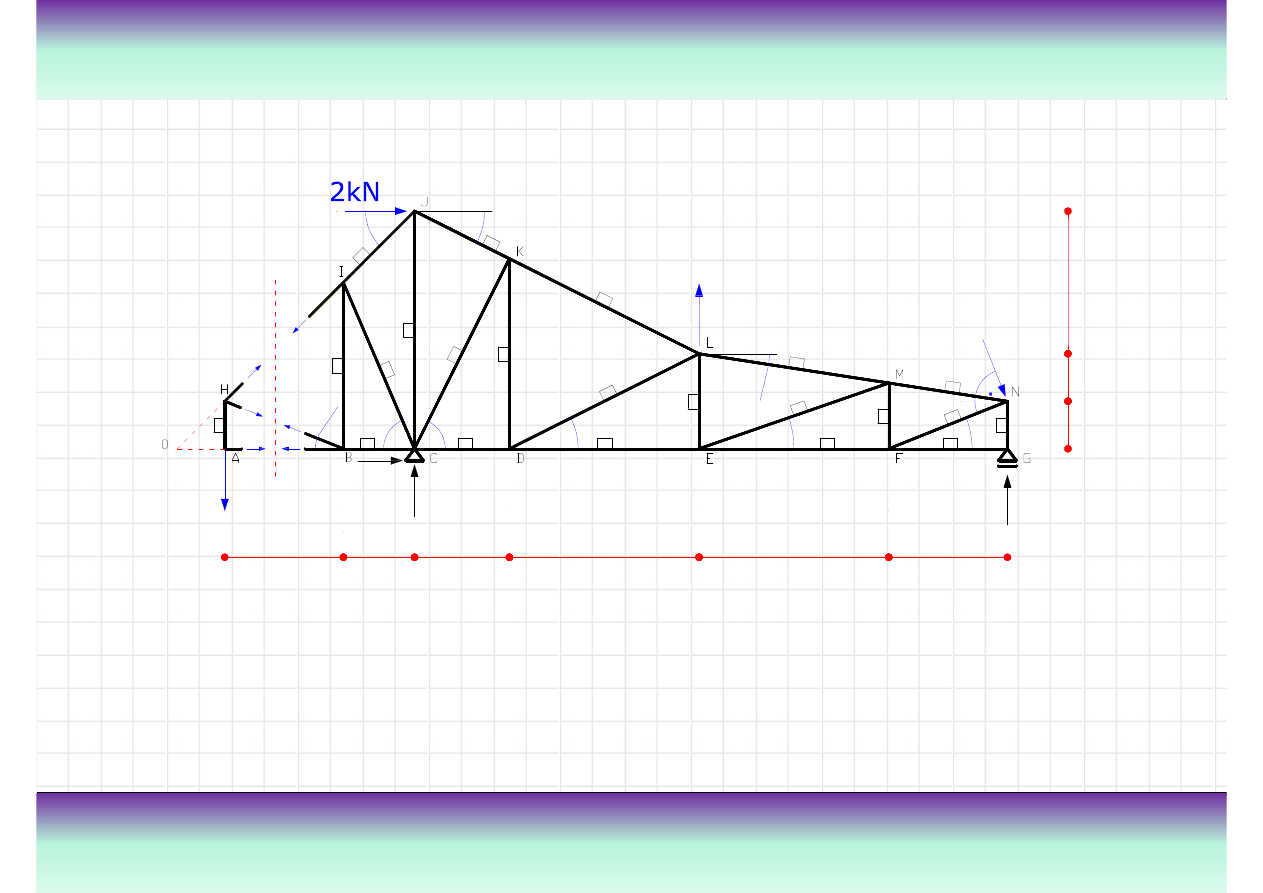
Przykład

Wyznacz warto

ś

ci sił wewn

ę

trznych w poszczególnych pr

ę

tach

8

9

10

3kN

3

m

3

m

α

2

α

1

1

Obliczenia sił wewn

ę

trznych mo

ż

na rozpocz

ąć

od wyznaczenia sił normalnych w pr

ę

tach nr 1, nr 7 i nr 20. W tym celu

2.5m

1.5m

2m

4m

4m

2.5m

1

m

1

m

2

3

4

5

6

1

3

1

4

1

5

1

6

1

7

1

8

1

9

2

1

2

2

23

24

25

10

11

12

2.5m

1.5m

2m

4m

4m

2.5m

5kN

3kN

7kN

1

m

1

m

3

m

2.5m

1.5m

2m

4m

4m

2.5m

1

m

1

m

3

m

α

8

α

9

α

7

α

6

α

5

α

3

N

7

N

7

1

V

C

H

C

α

4

V

G

N

20

N

1

N

1

N

20

Obliczenia sił wewn

ę

trznych mo

ż

na rozpocz

ąć

od wyznaczenia sił normalnych w pr

ę

tach nr 1, nr 7 i nr 20. W tym celu

zostanie wykorzystana metoda Rittera (przekrojów). W metodzie tej nale

ż

y rozdzieli

ć

tak kratownic

ę

, aby w przeci

ę

ciu

znalazły si

ę

trzy pr

ę

ty. W odniesieniu do jednej ze stron mo

ż

na uło

ż

y

ć

trzy równania równowagi, na podstawie których

zostan

ą

wyznaczone siły normalne w pr

ę

tach. Oczywi

ś

cie mo

ż

na napisa

ć

trzy standardowe równania czyli sum

ę

rzutów

wektorów sił na o

ś

X (kierunek poziomy), sum

ę

rzutów wektorów sił na o

ś

Y (kierunek pionowy) i sum

ę

momentów

wzgl

ę

dem dowolnego punktu. Jednak najlepiej, je

ż

eli w równaniu jest tylko jedna niewiadoma, dlatego licz

ą

c sił

ę

normaln

ą

w jednym z pr

ę

tów najlepiej jest skorzysta

ć

z sumy momentów wzgl

ę

dem punktu, który jest punktem

przeci

ę

cia kierunków działania dwóch sił w dwóch pozostałych pr

ę

tach.

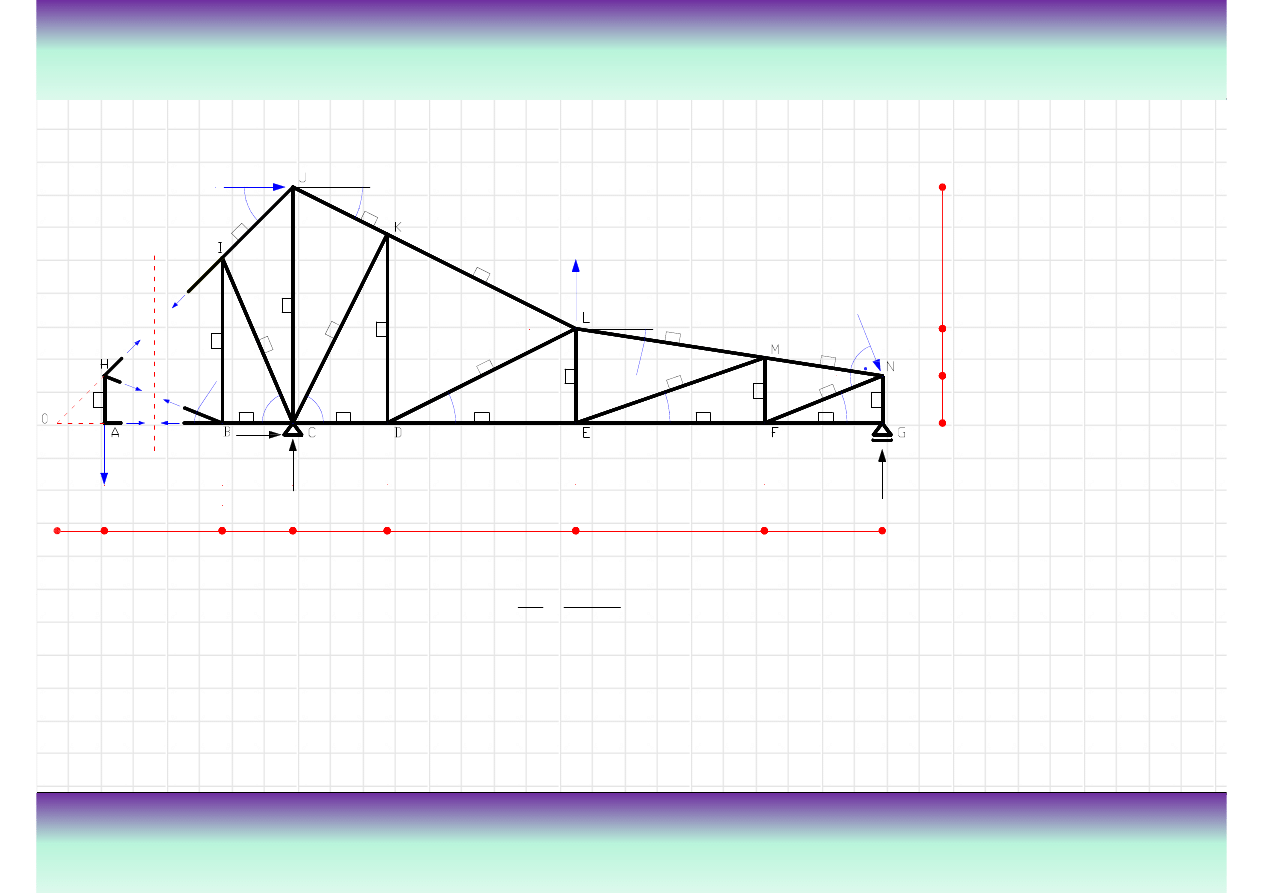
Przykład

Wyznacz warto

ś

ci sił wewn

ę

trznych w poszczególnych pr

ę

tach

Dalsze obliczenia zostan

ą

wykonane w nast

ę

puj

ą

cej

kolejno

ś

ci:

• wyznaczenie siły
normalnej w pr

ę

cie nr 1,

korzystaj

ą

c z sumy

Potrzebne dane:

sin(

α

1

)=0.7071 sin(

α

4

)=0.3714

cos(

α

1

)=0.7071

cos(

α

4

)=0.9285

8

9

10

2kN

3kN

3

m

3

m

α

2

α

1

N

7

1

korzystaj

ą

c z sumy

momentów wzgl

ę

dem

punktu H z lewej strony
przekroju 1-1;
• wyznaczenie siły
normalnej w pr

ę

cie nr 7,

korzystaj

ą

c z sumy

momentów wzgl

ę

dem

punktu B z lewej strony
przekroju 1-1;
• wyznaczenie siły
normalnej w pr

ę

cie nr 20,

korzystaj

ą

c z sumy

momentów wzgl

ę

dem

Ʃ

M

H

L

=0

N

1

⋅

1m=0

Ʃ

M

O

L

=0

m

4

+

=

x

x

m

4

m

1

m

1

m

5

⋅

+

⋅

=

⋅

x

x

m

1

=

x

2.5m

1.5m

2m

4m

4m

2.5m

1

m

1

m

2

3

4

5

6

1

3

1

4

1

5

1

6

1

7

1

8

1

9

2

1

2

2

23

24

25

11

12

2.5m

1.5m

2m

4m

4m

2.5m

5kN

7kN

1

m

1

m

2.5m

1.5m

2m

4m

4m

2.5m

1

m

1

m

α

8

α

9

α

7

α

6

α

5

α

3

N

7

1

V

C

H

C

α

4

V

G

N

20

N

1

N

1

N

20

x

momentów wzgl

ę

dem

punktu O z lewej strony
przekroju 1-1.
Do wyznaczenia
poło

ż

enia punktu O

zostanie wykorzystane
twierdzenie Talesa.

N

1

⋅

1m=0

N

1

=0

Ʃ

M

B

L

=0

N

7

⋅

sin(

α

1

)

⋅

2.5m+N

7

⋅

cos(

α

1

)

⋅

1m-5kN

⋅

2.5m =0

N

7

⋅

0.7071

⋅

2.5m+N

7

⋅

0.7071

⋅

1m-5kN

⋅

2.5m =0

N

7

=5.0508kN

N

20

⋅

sin(

α

4

)

⋅

x

+N

20

⋅

cos(

α

4

)

⋅

x

+5kN

⋅

x

=0

N

20

⋅

0.3714

⋅

1m+N

20

⋅

0.9285

⋅

1m+5kN

⋅

1m =0

N

20

=-3.8464kN

m

5

m

4

m

1

+

=

x

x

m

4

m

1

m

1

m

5

⋅

+

⋅

=

⋅

x

x

m

1

=

x

Przykład

Wyznacz warto

ś

ci sił wewn

ę

trznych w poszczególnych pr

ę

tach

W odniesieniu do przekroju
2-2 zostan

ą

wykonane

nast

ę

puj

ą

ce działania:

• wyznaczenie siły normalnej
w pr

ę

cie nr 2, korzystaj

ą

c z

sumy momentów wzgl

ę

dem

1

5

9

10

2kN

3kN

7kN

3

m

3

m

α

2

α

1

2

N

8

N

8

N

sumy momentów wzgl

ę

dem

punktu I z lewej strony
przekroju 2-2;
• wyznaczenie siły normalnej
w pr

ę

cie nr 8, korzystaj

ą

c z

sumy momentów wzgl

ę

dem

punktu C z lewej strony
przekroju 2-2;
• wyznaczenie siły normalnej
w pr

ę

cie nr 21, korzystaj

ą

c z

sumy momentów wzgl

ę

dem

punktu O z lewej strony
przekroju 2-2.

Ʃ

M

C

L

=0

N

8

⋅

sin(

α

1

)

⋅

1.5m+N

8

⋅

cos(

α

1

)

⋅

3.5m-5kN

⋅

4m =0

Potrzebne dane:

sin(

α

1

)=0.7071 sin(

α

5

)=0.9191

cos(

α

)=0.7071

cos(

α

)=0.3939

N

8

⋅

0.7071

⋅

1.5m+N

8

⋅

0.7071

⋅

3.5m-5kN

⋅

4m =0

2.5m

1.5m

2m

4m

4m

2.5m

1

m

1

m

1

3

4

5

6

1

3

1

4

1

5

1

6

1

7

1

8

1

9

20

2

2

23

24

25

7

11

12

2.5m

1.5m

2m

4m

4m

2.5m

5kN

7kN

1

m

1

m

2.5m

1.5m

2m

4m

4m

2.5m

1

m

1

m

α

8

α

9

α

7

α

6

α

5

α

4

α

3

V

C

H

C

V

G

N

2

2

N

2

N

21

N

21

α

5

x

Ʃ

M

I

L

=0

N

2

⋅

3.5m+5kN

⋅

2.5m=0

N

2

=-3.5714kN

N

8

=5.6569kN

N

21

⋅

sin(

α

5

)

⋅

(

x

+2.5m)+N

21

⋅

cos(

α

5

)

⋅

L

18

+5kN

⋅

x

=0

N

21

=-1.0880kN

cos(

α

1

)=0.7071

cos(

α

5

)=0.3939

x

=1m

L

14

=3.5m

Ʃ

M

O

L

=0

N

8

⋅

0.7071

⋅

1.5m+N

8

⋅

0.7071

⋅

3.5m-5kN

⋅

4m =0

N

21

⋅

0.9191

⋅

3.5m+N

21

⋅

0.3939

⋅

3.5m+5kN

⋅

1m =0

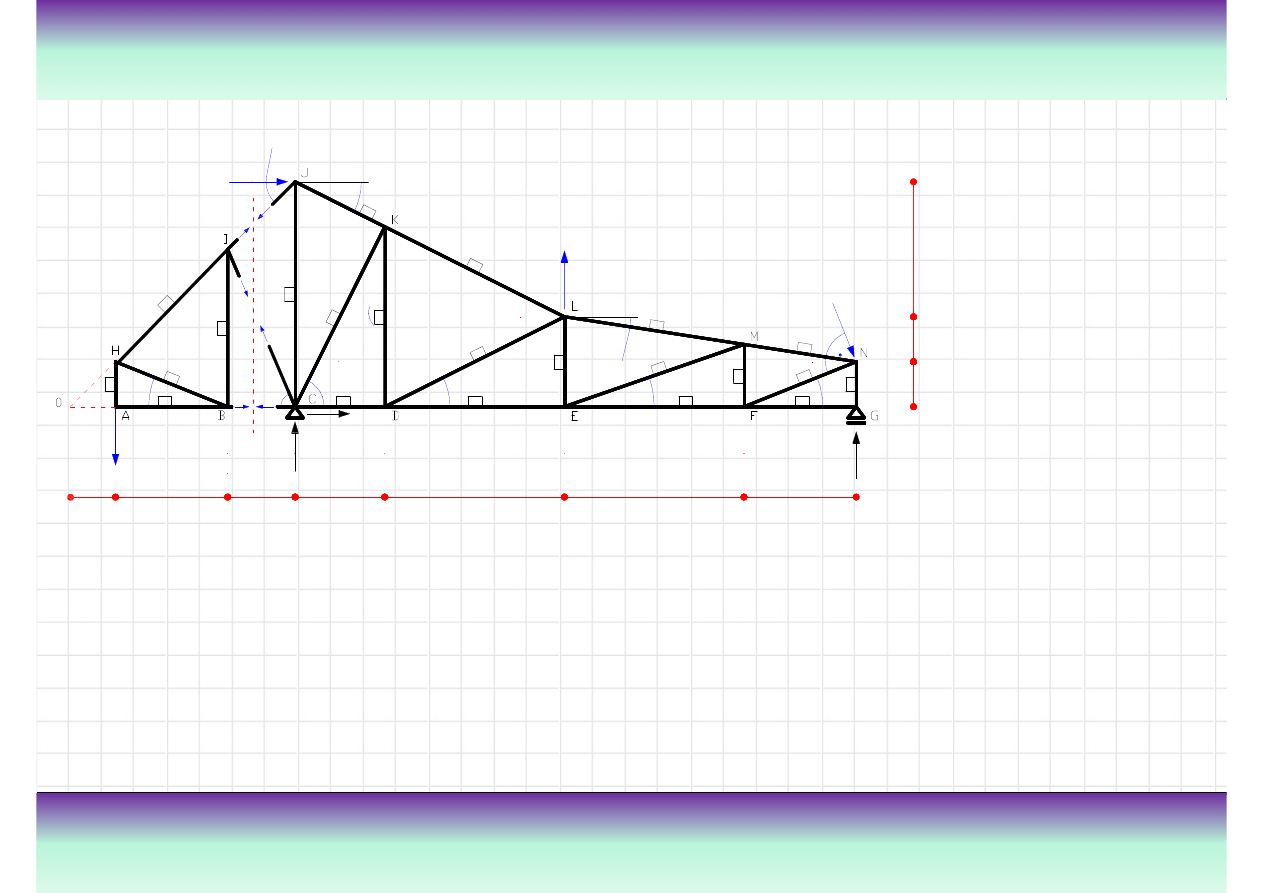
Przykład

Wyznacz warto

ś

ci sił wewn

ę

trznych w poszczególnych pr

ę

tach

W odniesieniu do przekroju
3-3 zostan

ą

wykonane

nast

ę

puj

ą

ce działania:

• wyznaczenie siły normalnej
w pr

ę

cie nr 3, korzystaj

ą

c z

sumy momentów wzgl

ę

dem

8

10

2kN

3kN

3

m

3

m

α

2

α

1

N

3

N

9

N

9

sumy momentów wzgl

ę

dem

punktu K z prawej strony
przekroju 3-3;
• wyznaczenie siły normalnej
w pr

ę

cie nr 9, korzystaj

ą

c z

sumy momentów wzgl

ę

dem

punktu C z prawej strony
przekroju 3-3;
• wyznaczenie siły normalnej
w pr

ę

cie nr 22, korzystaj

ą

c z

sumy momentów wzgl

ę

dem

punktu V z prawej strony
przekroju 3-3.

Potrzebne dane:

sin(

α

9

)=0.3714

L

16

=4.0m

2.5m

1.5m

2m

4m

4m

2.5m

1

m

1

m

1

2

4

5

6

1

3

1

4

1

5

1

6

1

7

1

8

1

9

20

2

1

23

24

25

7

11

12

2.5m

1.5m

2m

4m

4m

2.5m

5kN

3kN

7kN

1

m

1

m

2.5m

1.5m

2m

4m

4m

2.5m

1

m

1

m

α

8

α

9

α

7

α

5

α

4

α

3

V

C

H

C

V

G

N

3

N

3

N

22

N

22

3

α

6

Ʃ

M

K

P

=0

N

3

⋅

L

16

-3kN

⋅

4m-V

G

⋅

10.5m-7kN

⋅

sin(

α

9

)

⋅

3m+7kN

⋅

cos(

α

9

)

⋅

10.5m=0

N

3

=-0.3826kN

9

16

cos(

α

9

)=0.9285

V

G

=4.4675kN

N

3

⋅

4m-3kN

⋅

4m-4.4675kN

⋅

10.5m-7kN

⋅

0.3714

⋅

3m+7kN

⋅

0.9285

⋅

10.5m=0

Dalsze obliczenia na
nast

ę

pnej stronie

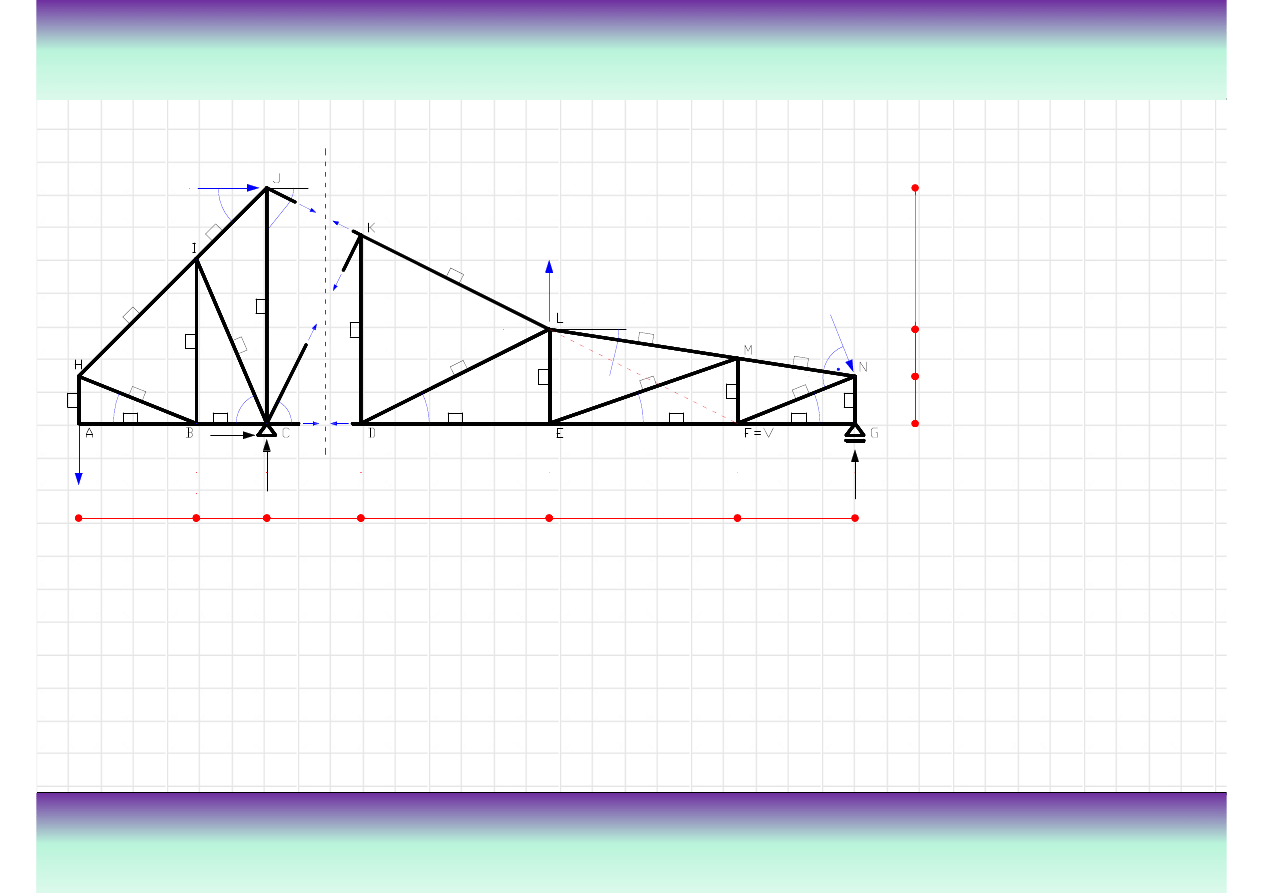
Przykład

Wyznacz warto

ś

ci sił wewn

ę

trznych w poszczególnych pr

ę

tach

W odniesieniu do przekroju
3-3 zostan

ą

wykonane

nast

ę

puj

ą

ce działania:

• wyznaczenie siły normalnej
w pr

ę

cie nr 3, korzystaj

ą

c z

sumy momentów wzgl

ę

dem

8

10

2kN

3kN

3

m

3

m

α

2

α

1

N

22

3

N

9

N

9

sumy momentów wzgl

ę

dem

punktu K z prawej strony
przekroju 3-3;
• wyznaczenie siły normalnej
w pr

ę

cie nr 9, korzystaj

ą

c z

sumy momentów wzgl

ę

dem

punktu C z prawej strony
przekroju 3-3;
• wyznaczenie siły normalnej
w pr

ę

cie nr 22, korzystaj

ą

c z

sumy momentów wzgl

ę

dem

punktu V z prawej strony
przekroju 3-3.

Potrzebne dane:

sin(

α

2

)=0.4472 sin(

α

9

)=0.3714 L

16

=4.0m

2.5m

1.5m

2m

4m

4m

2.5m

1

m

1

m

1

2

4

5

6

1

3

1

4

1

5

1

6

1

7

1

8

1

9

20

2

1

23

24

25

7

11

12

2.5m

1.5m

2m

4m

4m

2.5m

5kN

7kN

1

m

1

m

2.5m

1.5m

2m

4m

4m

2.5m

1

m

1

m

α

8

α

9

α

7

α

5

α

4

α

3

V

C

H

C

V

G

N

3

N

3

N

22

N

22

3

α

6

Ʃ

M

C

P

=0

N

9

⋅

sin(

α

2

)

⋅

2m+N

9

⋅

cos(

α

2

)

⋅

L

16

+3kN

⋅

6m+V

G

⋅

12.5m-7kN

⋅

sin(

α

9

)

⋅

1m-7kN

⋅

cos(

α

9

)

⋅

12.5m =0

N

8

=2.2361kN

cos(

α

2

)=0.8944

cos(

α

9

)=0.9285 V

G

=4.4675kN

N

9

⋅

0.4472

⋅

2m+N

9

⋅

0.8944

⋅

4m+3kN

⋅

6m+4.4675

⋅

12.5m-7kN

⋅

0.3714

⋅

1m-7kN

⋅

0.9285

⋅

12.5m =0

Dalsze obliczenia na
nast

ę

pnej stronie

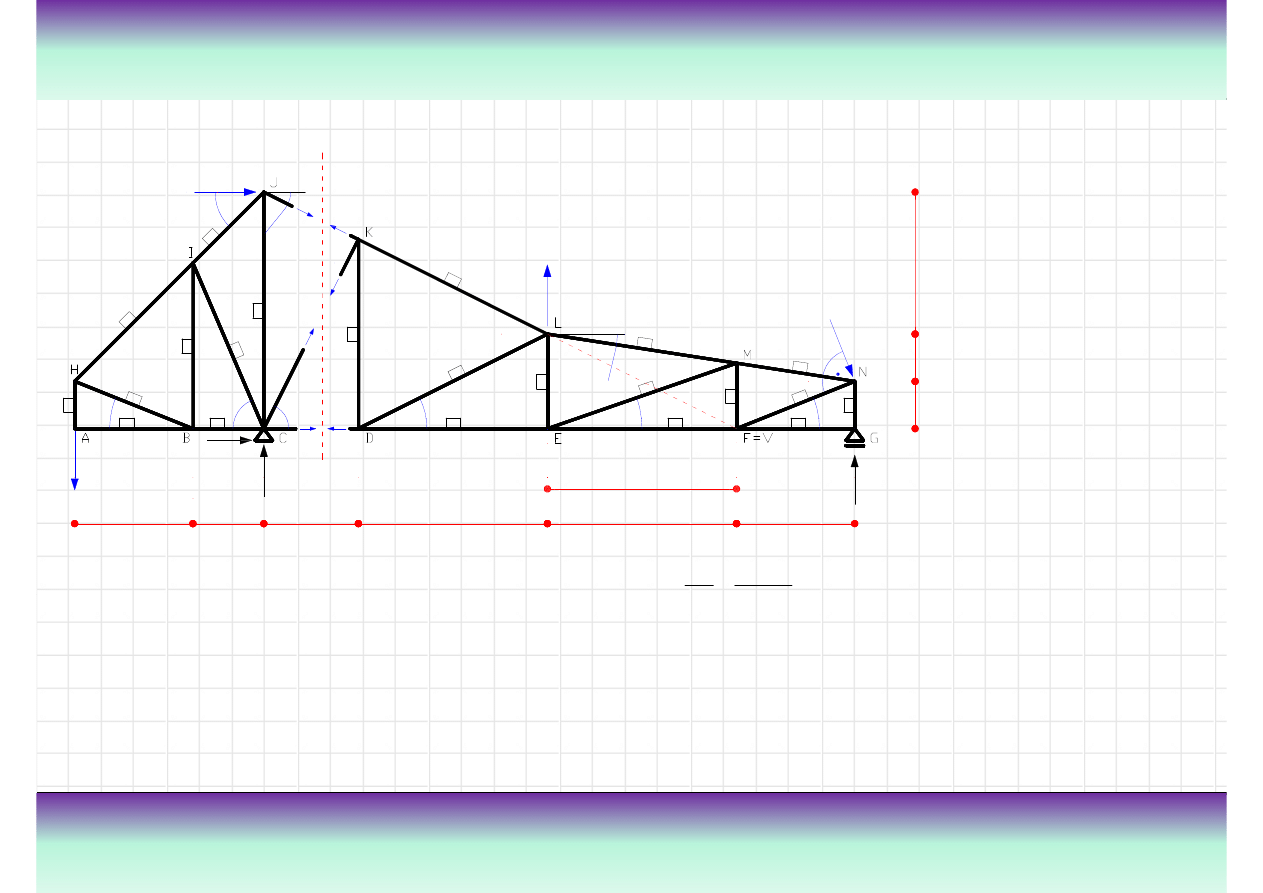
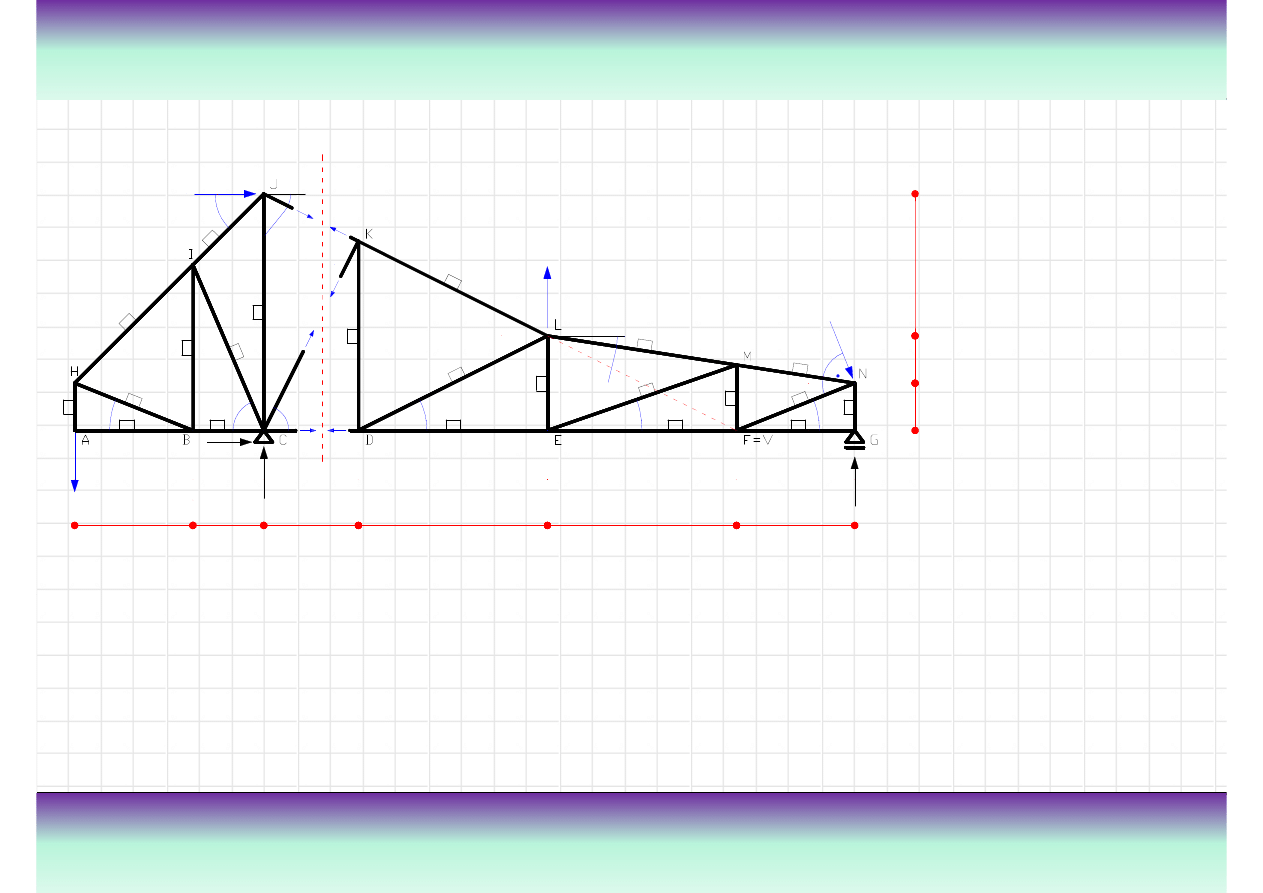
Przykład

Wyznacz warto

ś

ci sił wewn

ę

trznych w poszczególnych pr

ę

tach

W odniesieniu do przekroju
3-3 zostan

ą

wykonane

nast

ę

puj

ą

ce działania:

• wyznaczenie siły normalnej
w pr

ę

cie nr 3, korzystaj

ą

c z

sumy momentów wzgl

ę

dem

8

10

2kN

3kN

3

m

3

m

α

2

α

1

N

3

N

9

N

9

sumy momentów wzgl

ę

dem

punktu K z prawej strony
przekroju 3-3;
• wyznaczenie siły normalnej
w pr

ę

cie nr 9, korzystaj

ą

c z

sumy momentów wzgl

ę

dem

punktu C z prawej strony
przekroju 3-3;
• wyznaczenie siły normalnej
w pr

ę

cie nr 22, korzystaj

ą

c z

sumy momentów wzgl

ę

dem

punktu V z prawej strony
przekroju 3-3. Do
wyznaczenia poło

ż

enia

Potrzebne dane:

sin(

α

6

)=0.8944 sin(

α

9

)=0.3714 L

16

=4.0m

m

5

m

6

m

2

+

=

y

y

Wyznaczenie punktu V:

2.5m

1.5m

2m

4m

4m

2.5m

1

m

1

m

1

2

4

5

6

1

3

1

4

1

5

1

6

1

7

1

8

1

9

20

2

1

23

24

25

7

11

12

2.5m

1.5m

2m

4m

4m

2.5m

5kN

3kN

7kN

1

m

1

m

2.5m

1.5m

2m

4m

4m

2.5m

1

m

1

m

α

8

α

9

α

7

α

5

α

4

α

3

V

C

H

C

V

G

N

3

N

3

N

22

N

22

3

α

6

y

wyznaczenia poło

ż

enia

punktu V zostanie
wykorzystane twierdzenie
Talesa. Z oblicze

ń

wynika,

ż

e punkt V pokrywa si

ę

z

punktem F.

N

22

⋅

sin(

α

6

)

⋅

(

y

+4m)+N

22

⋅

cos(

α

6

)

⋅

L

16

-3kN

⋅

y

+ V

G

⋅

(6.5m-

y

)-7kN

⋅

sin(

α

9

)

⋅

1m-7kN

⋅

cos(

α

9

)

⋅

(6.5m-

y

) =0

N

22

=2.2003kN

sin(

α

6

)=0.8944 sin(

α

9

)=0.3714 L

16

=4.0m

cos(

α

6

)=0.4472 cos(

α

9

)=0.9285

V

G

=4.4675kN

Ʃ

M

V

P

=0

N

22

⋅

0.8944

⋅

8m+N

22

⋅

0.4472

⋅

4m-3kN

⋅

4m+ 4.4675

⋅

2.5m-7kN

⋅

0.3714

⋅

1m-7kN

⋅

0.9285

⋅

2.5m =0

m

5

m

2

m

6

m

2

m

2

m

5

⋅

+

⋅

=

⋅

y

y

m

4

=

y

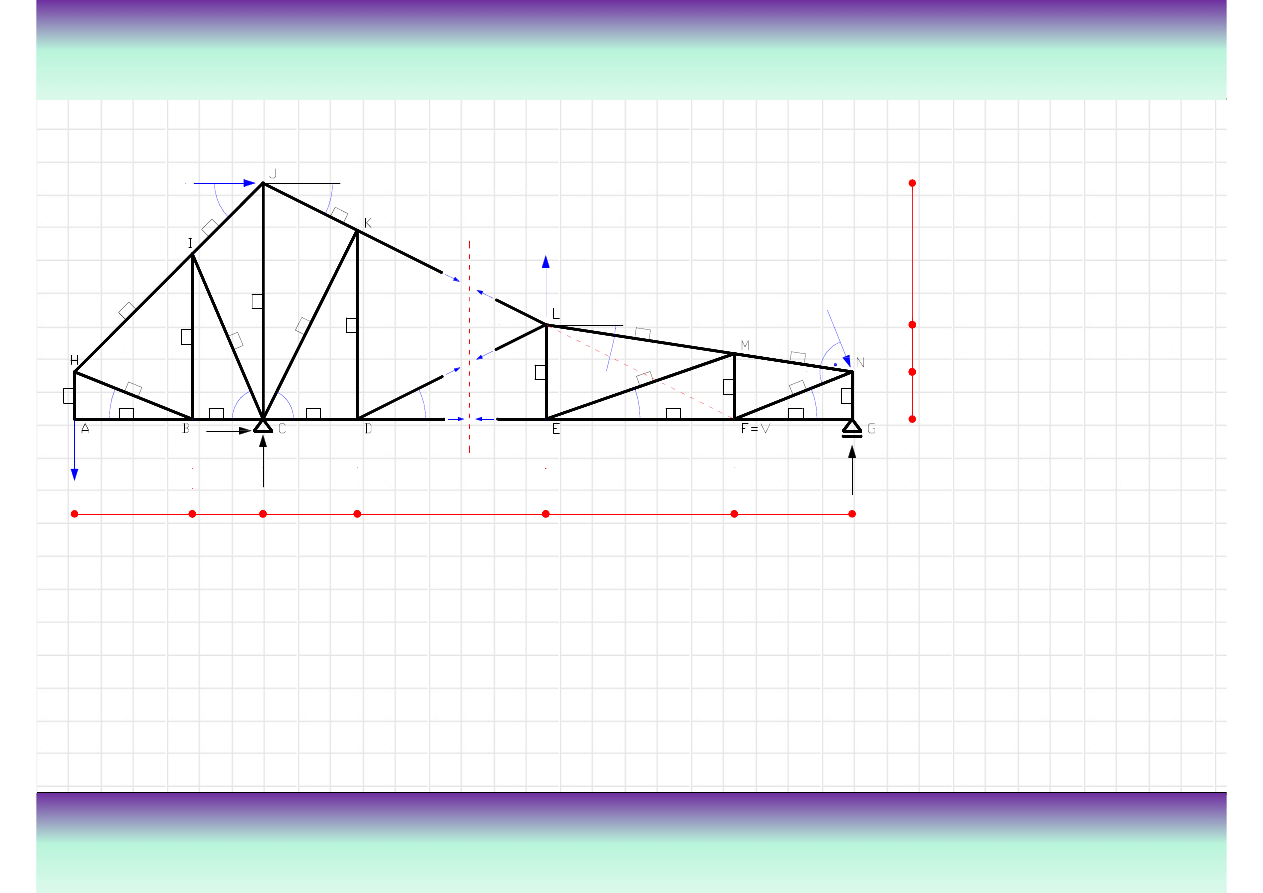
Przykład

Wyznacz warto

ś

ci sił wewn

ę

trznych w poszczególnych pr

ę

tach

W odniesieniu do przekroju
4-4 zostan

ą

wykonane

nast

ę

puj

ą

ce działania:

• wyznaczenie siły normalnej
w pr

ę

cie nr 4, korzystaj

ą

c z

sumy momentów wzgl

ę

dem

1

5

8

9

2kN

3kN

α

2

α

1

4

N

10

3

m

3

m

sumy momentów wzgl

ę

dem

punktu L z prawej strony
przekroju 4-4;
• wyznaczenie siły normalnej
w pr

ę

cie nr 10, korzystaj

ą

c z

sumy momentów wzgl

ę

dem

punktu D z prawej strony
przekroju 4-4;
• wyznaczenie siły normalnej
w pr

ę

cie nr 23, korzystaj

ą

c z

sumy momentów wzgl

ę

dem

punktu V z prawej strony
przekroju 4-4.

Potrzebne dane:

sin(

α

9

)=0.3714

2.5m

1.5m

2m

4m

4m

2.5m

1

m

1

2

3

6

1

3

1

4

1

5

1

6

1

7

1

8

1

9

20

2

1

2

2

25

7

12

2.5m

1.5m

2m

4m

4m

2.5m

5kN

7kN

1

m

2.5m

1.5m

2m

4m

4m

2.5m

1

m

α

9

α

7

α

6

α

5

α

4

V

C

H

C

V

G

N

4

N

4

4

N

10

N

23

N

23

1

m

1

m

1

m

5

24

11

α

8

α

3

N

4

⋅

2m- V

G

⋅

6.5m-7kN

⋅

sin(

α

9

)

⋅

1m+7kN

⋅

cos(

α

9

)

⋅

6.5m =0

N

4

=-5.3041kN

cos(

α

9

)=0.9285

V

G

=4.4675kN

Ʃ

M

L

P

=0

Dalsze obliczenia na
nast

ę

pnej stronie

N

4

⋅

2m- 4.4675kN

⋅

6.5m-7kN

⋅

0.3714

⋅

1m+7kN

⋅

0.9285

⋅

6.5m =0

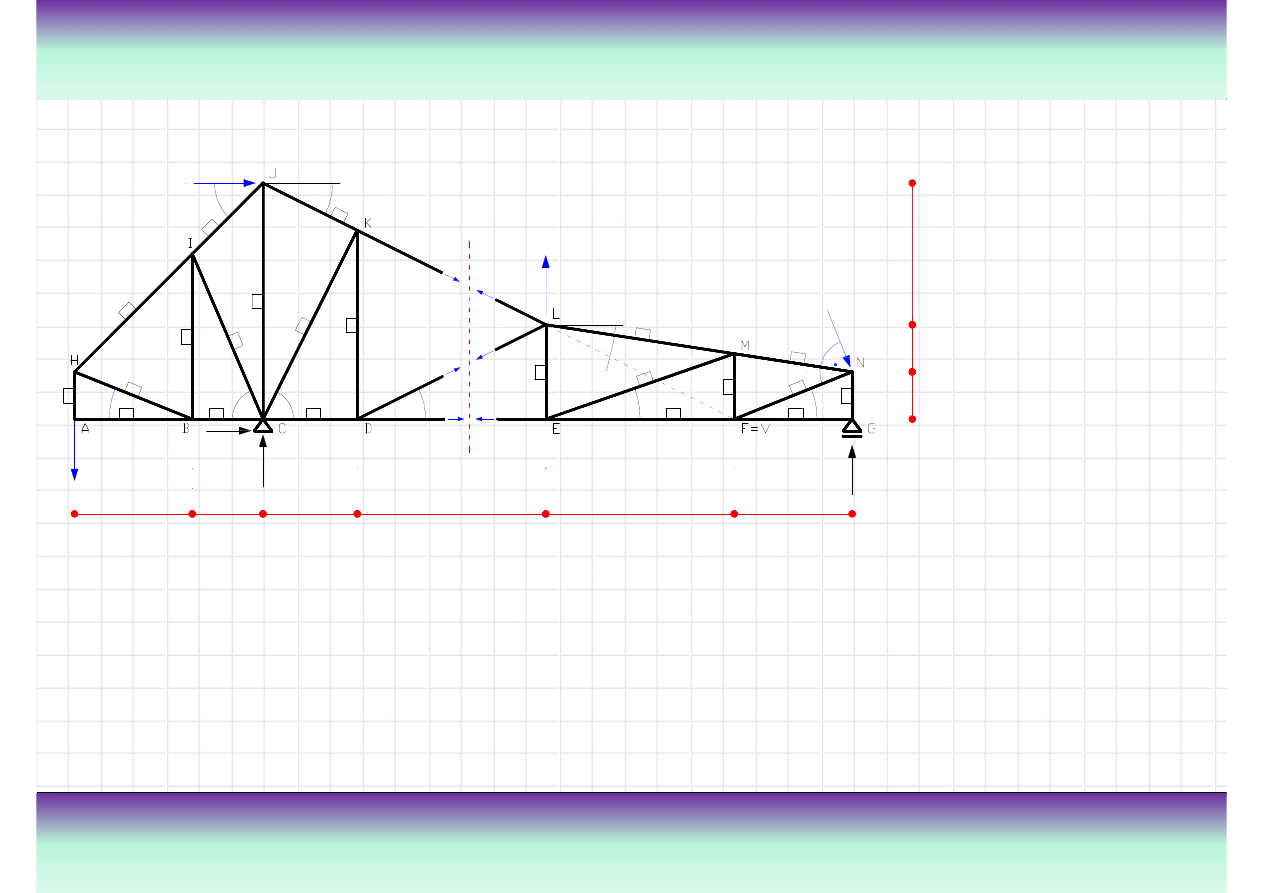
Przykład

Wyznacz warto

ś

ci sił wewn

ę

trznych w poszczególnych pr

ę

tach

W odniesieniu do przekroju
4-4 zostan

ą

wykonane

nast

ę

puj

ą

ce działania:

• wyznaczenie siły normalnej
w pr

ę

cie nr 4, korzystaj

ą

c z

sumy momentów wzgl

ę

dem

1

5

8

9

2kN

3kN

α

2

α

1

4

N

10

3

m

3

m

sumy momentów wzgl

ę

dem

punktu L z prawej strony
przekroju 4-4;
• wyznaczenie siły normalnej
w pr

ę

cie nr 10, korzystaj

ą

c z

sumy momentów wzgl

ę

dem

punktu D z prawej strony
przekroju 4-4;
• wyznaczenie siły normalnej
w pr

ę

cie nr 23, korzystaj

ą

c z

sumy momentów wzgl

ę

dem

punktu V z prawej strony
przekroju 4-4.

Potrzebne dane:

sin(

α

2

)=0.4472 sin(

α

9

)=0.3714

V

G

=4.4675kN

cos(

α

)=0.8944

cos(

α

)=0.9285

2.5m

1.5m

2m

4m

4m

2.5m

1

m

1

2

3

6

1

3

1

4

1

5

1

6

1

7

1

8

1

9

20

2

1

2

2

25

7

12

2.5m

1.5m

2m

4m

4m

2.5m

5kN

7kN

1

m

2.5m

1.5m

2m

4m

4m

2.5m

1

m

α

9

α

7

α

6

α

5

α

4

V

C

H

C

V

G

N

4

N

4

4

N

10

N

23

N

23

1

m

1

m

1

m

5

24

11

α

8

α

3

N

10

⋅

sin(

α

2

)

⋅

4m+N

10

⋅

cos(

α

2

)

⋅

2m+3kN

⋅

4m+V

G

⋅

10.5m-7kN

⋅

sin(

α

9

)

⋅

1m-7kN

⋅

cos(

α

9

)

⋅

10.5m =0

N

10

=3.3363kN

Ʃ

M

D

P

=0

cos(

α

2

)=0.8944

cos(

α

9

)=0.9285

N

10

⋅

0.4472

⋅

4m+N

10

⋅

0.8944

⋅

2m+3kN

⋅

4m+4.4675kN

⋅

10.5m-7kN

⋅

0.3714

⋅

1m-7kN

⋅

0.9285

⋅

10.5m =0

Dalsze obliczenia na
nast

ę

pnej stronie

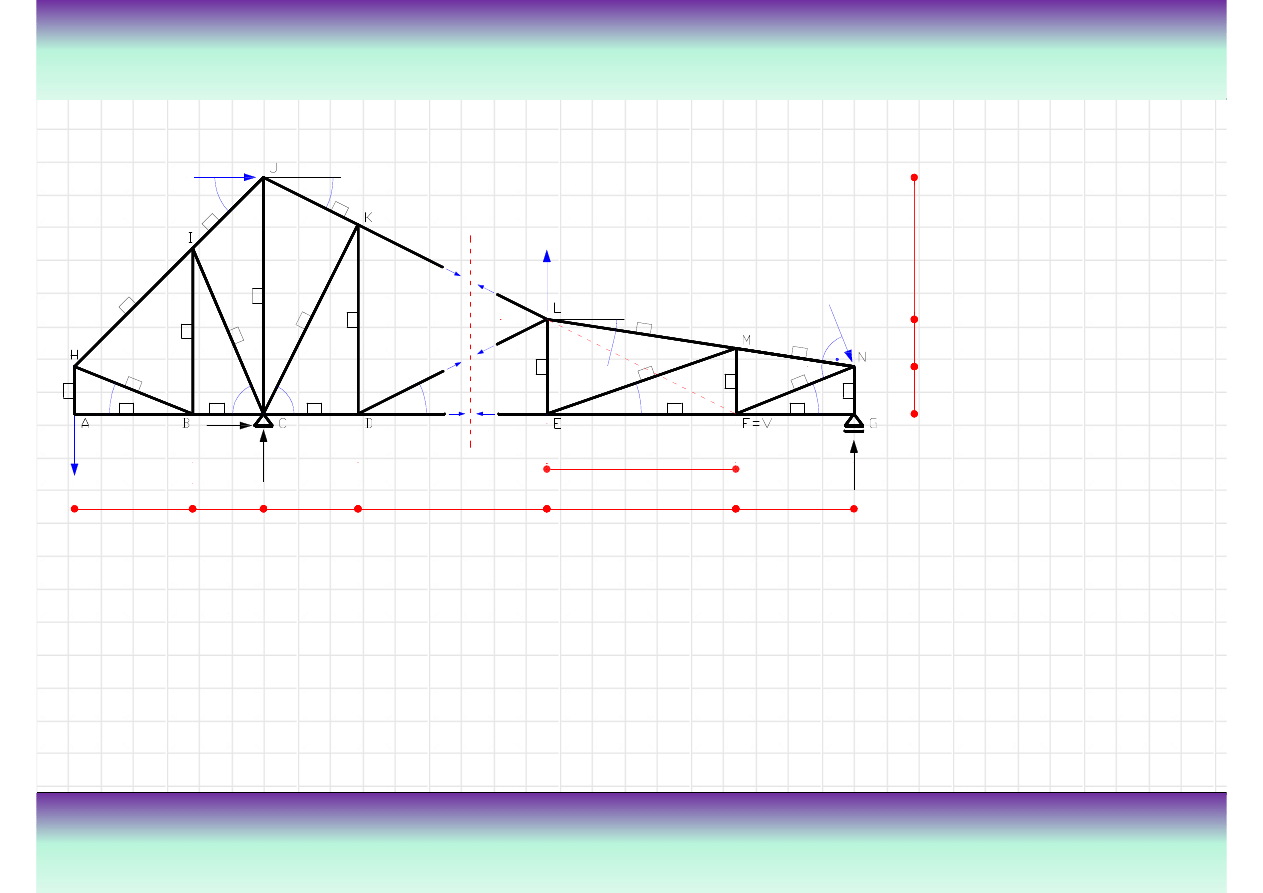
Przykład

Wyznacz warto

ś

ci sił wewn

ę

trznych w poszczególnych pr

ę

tach

W odniesieniu do przekroju
4-4 zostan

ą

wykonane

nast

ę

puj

ą

ce działania:

• wyznaczenie siły normalnej
w pr

ę

cie nr 4, korzystaj

ą

c z

sumy momentów wzgl

ę

dem

1

5

8

9

2kN

3kN

7kN

α

2

α

1

4

N

10

3

m

3

m

sumy momentów wzgl

ę

dem

punktu L z prawej strony
przekroju 4-4;
• wyznaczenie siły normalnej
w pr

ę

cie nr 10, korzystaj

ą

c z

sumy momentów wzgl

ę

dem

punktu D z prawej strony
przekroju 4-4;
• wyznaczenie siły normalnej
w pr

ę

cie nr 23, korzystaj

ą

c z

sumy momentów wzgl

ę

dem

punktu V z prawej strony
przekroju 4-4. Punkt V
pokrywa si

ę

z punktem F.

Potrzebne dane:

sin(

α

7

)=0.4472 sin(

α

9

)=0.3714

y

=4m

cos(

α

)=0.8944

cos(

α

)=0.9285 V =4.4675kN

2.5m

1.5m

2m

4m

4m

2.5m

1

m

1

2

3

6

1

3

1

4

1

5

1

6

1

7

1

8

1

9

20

2

1

2

2

25

7

12

2.5m

1.5m

2m

4m

4m

2.5m

5kN

7kN

1

m

2.5m

1.5m

2m

4m

4m

2.5m

1

m

α

9

α

7

α

6

α

5

α

4

V

C

H

C

V

G

N

4

N

4

4

N

10

N

23

N

23

1

m

1

m

1

m

5

24

11

α

8

α

3

y

pokrywa si

ę

z punktem F.

N

23

⋅

sin(

α

7

)

⋅

y

+N

23

⋅

cos(

α

7

)

⋅

2m-3kN

⋅

y

+V

G

⋅

(6.5m-

y

)-7kN

⋅

sin(

α

9

)

⋅

1m-7kN

⋅

cos(

α

9

)

⋅

(6.5m-

y

)=0

N

23

=5.5008kN

Ʃ

M

V

P

=0

cos(

α

7

)=0.8944

cos(

α

9

)=0.9285 V

G

=4.4675kN

N

23

⋅

0.4472

⋅

4m+N

23

⋅

0.8944

⋅

2m-3kN

⋅

4m+4.4675kN

⋅

2.5m-7kN

⋅

0.3714

⋅

1m-7kN

⋅

0.9285

⋅

2.5m=0

Dalsze obliczenia na
nast

ę

pnej stronie

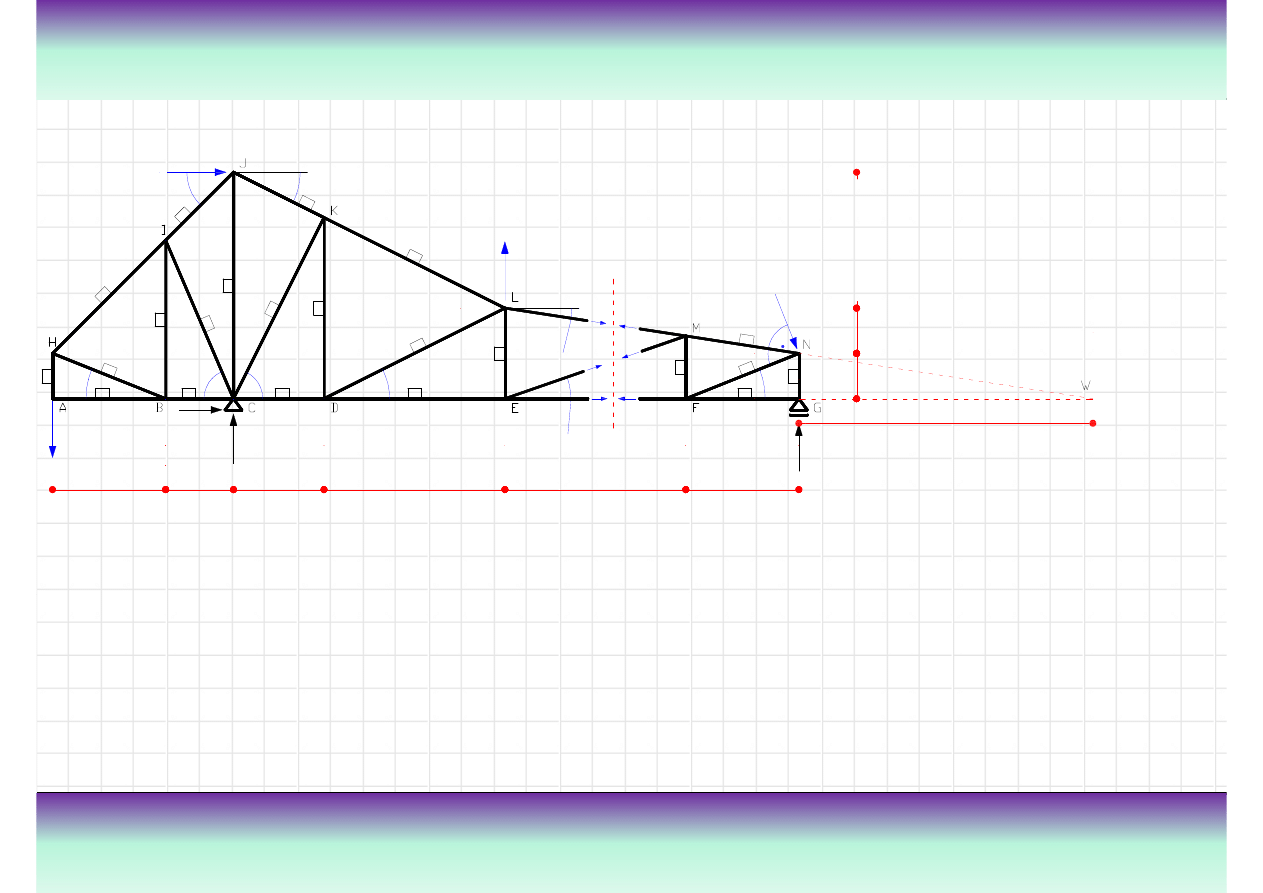
Przykład

Wyznacz warto

ś

ci sił wewn

ę

trznych w poszczególnych pr

ę

tach

W odniesieniu do przekroju
5-5 zostan

ą

wykonane

nast

ę

puj

ą

ce działania:

• wyznaczenie siły normalnej
w pr

ę

cie nr 5, korzystaj

ą

c z

sumy momentów wzgl

ę

dem

1

5

7

8

9

2kN

3kN

7kN

α

2

α

1

10

5

3

m

3

m

sumy momentów wzgl

ę

dem

punktu M z prawej strony
przekroju 5-5;

• wyznaczenie siły normalnej
w pr

ę

cie nr 11, korzystaj

ą

c z

sumy momentów wzgl

ę

dem

punktu E z prawej strony
przekroju 5-5;
• wyznaczenie siły normalnej
w pr

ę

cie nr 24, korzystaj

ą

c z

sumy momentów wzgl

ę

dem

Potrzebne dane:

sin(

α

9

)=0.3714 L

18

=1.385m

cos(

α

)=0.9285 V =4.4675kN

2.5m

1.5m

2m

4m

4m

2.5m

1

m

1

2

3

6

1

3

1

4

1

6

1

7

1

8

1

9

20

2

1

2

2

25

7

12

2.5m

1.5m

2m

4m

4m

2.5m

5kN

7kN

1

m

2.5m

1.5m

2m

4m

4m

2.5m

1

m

α

8

α

9

α

6

α

5

α

4

α

3

V

C

H

C

V

G

N

5

N

24

N

24

N

11

N

5

N

11

4

23

α

7

5

1

m

1

m

1

m

1

m

1

m

1

m

z

sumy momentów wzgl

ę

dem

punktu W z prawej strony
przekroju 5-5.

N

5

⋅

L

18

-V

G

⋅

2.5m-7kN

⋅

sin(

α

9

)

⋅

(L

18

-1m)+7kN

⋅

cos(

α

9

)

⋅

2.5m=0

N

5

=-2.9452kN

Ʃ

M

M

P

=0

cos(

α

9

)=0.9285 V

G

=4.4675kN

N

5

⋅

1.385m-4.4675kN

⋅

2.5m-7kN

⋅

0.3714

⋅

0.385m+7kN

⋅

0.9285

⋅

2.5m=0

Dalsze obliczenia na
nast

ę

pnej stronie

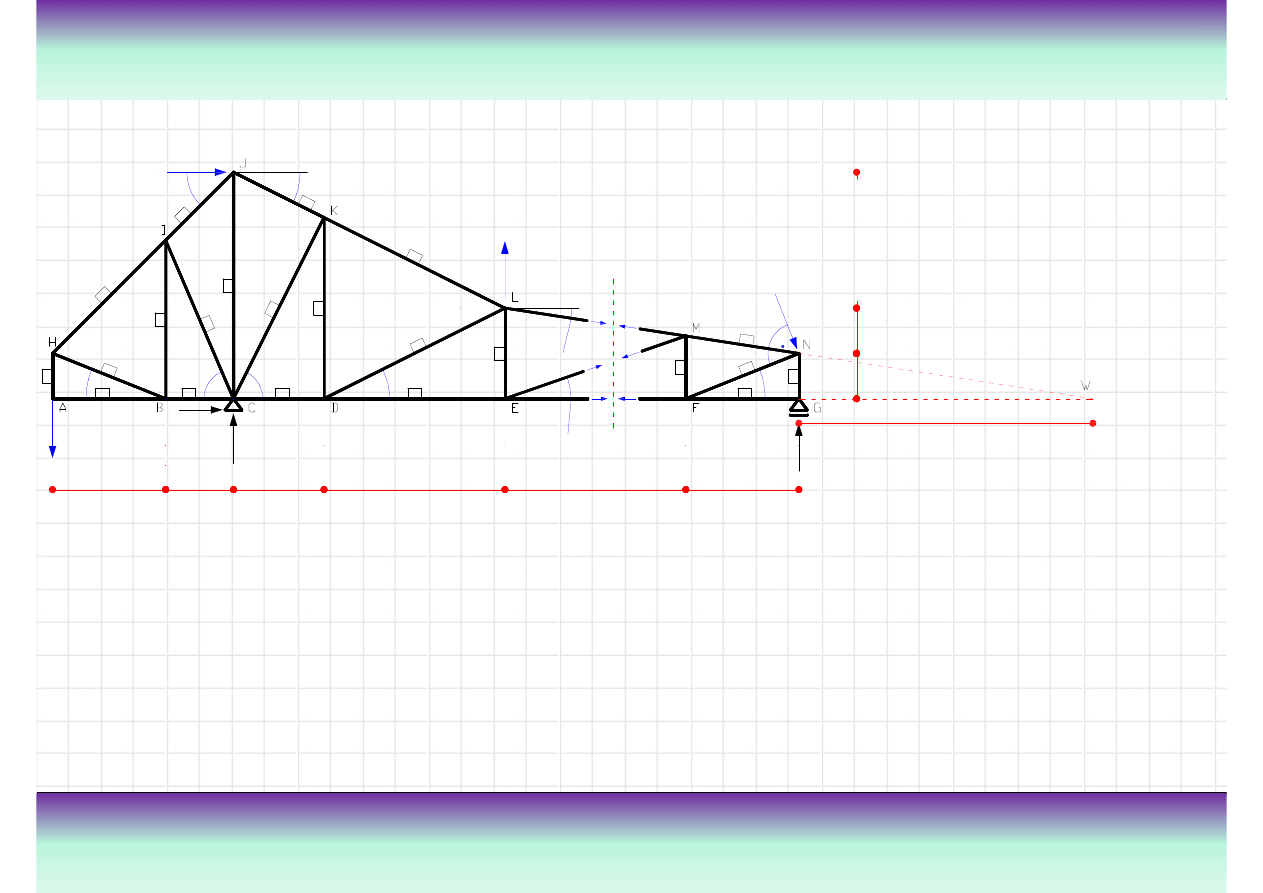
Przykład

Wyznacz warto

ś

ci sił wewn

ę

trznych w poszczególnych pr

ę

tach

W odniesieniu do przekroju
5-5 zostan

ą

wykonane

nast

ę

puj

ą

ce działania:

• wyznaczenie siły normalnej
w pr

ę

cie nr 5, korzystaj

ą

c z

sumy momentów wzgl

ę

dem

1

5

7

8

9

2kN

3kN

7kN

α

2

α

1

10

5

3

m

3

m

sumy momentów wzgl

ę

dem

punktu M z prawej strony
przekroju 5-5;

• wyznaczenie siły normalnej
w pr

ę

cie nr 11, korzystaj

ą

c z

sumy momentów wzgl

ę

dem

punktu E z prawej strony
przekroju 5-5;
• wyznaczenie siły normalnej
w pr

ę

cie nr 24, korzystaj

ą

c z

sumy momentów wzgl

ę

dem

Potrzebne dane:

sin(

α

3

)=0.1521 sin(

α

9

)=0.3714 L

18

=1.385m

cos(

α

)=0.9884

cos(

α

)=0.9285 V =4.4675kN

2.5m

1.5m

2m

4m

4m

2.5m

1

m

1

2

3

6

1

3

1

4

1

6

1

7

1

8

1

9

20

2

1

2

2

25

7

12

2.5m

1.5m

2m

4m

4m

2.5m

5kN

7kN

1

m

2.5m

1.5m

2m

4m

4m

2.5m

1

m

α

8

α

9

α

6

α

5

α

4

α

3

V

C

H

C

V

G

N

5

N

24

N

24

N

11

N

5

N

11

4

23

α

7

5

1

m

1

m

1

m

1

m

1

m

1

m

z

sumy momentów wzgl

ę

dem

punktu W z prawej strony
przekroju 5-5.

N

11

⋅

sin(

α

3

)

⋅

4m+N

11

⋅

cos(

α

3

)

⋅

L

18

+V

G

⋅

6.5m-7kN

⋅

sin(

α

9

)

⋅

1m-7kN

⋅

cos(

α

9

)

⋅

6.5m=0

N

11

=7.9968kN

Ʃ

M

E

P

=0

cos(

α

3

)=0.9884

cos(

α

9

)=0.9285 V

G

=4.4675kN

N

11

⋅

0.1521

⋅

4m+N

11

⋅

0.9884

⋅

1.385m+4.4675

⋅

6.5m-7kN

⋅

0.3714

⋅

1m-7kN

⋅

0.9286

⋅

6.5m=0

Dalsze obliczenia na
nast

ę

pnej stronie

Przykład

Wyznacz warto

ś

ci sił wewn

ę

trznych w poszczególnych pr

ę

tach

W odniesieniu do przekroju
5-5 zostan

ą

wykonane

nast

ę

puj

ą

ce działania:

• wyznaczenie siły normalnej
w pr

ę

cie nr 5, korzystaj

ą

c z

sumy momentów wzgl

ę

dem

1

5

7

8

9

2kN

3kN

7kN

α

2

α

1

10

5

3

m

3

m

sumy momentów wzgl

ę

dem

punktu M z prawej strony
przekroju 5-5;

• wyznaczenie siły normalnej
w pr

ę

cie nr 11, korzystaj

ą

c z

sumy momentów wzgl

ę

dem

punktu E z prawej strony
przekroju 5-5;
• wyznaczenie siły normalnej
w pr

ę

cie nr 24, korzystaj

ą

c z

sumy momentów wzgl

ę

dem

Potrzebne dane:

sin(

α

8

)=0.3272 sin(

α

9

)=0.3714 L

18

=1.385m

cos(

α

)=0.9450

cos(

α

)=0.9285 V =4.4675kN

m

2

m

5

.

6

m

1

+

=

z

z

m

5

.

6

m

1

m

1

m

2

⋅

+

⋅

=

⋅

z

z

Wyznaczenie punktu W:

2.5m

1.5m

2m

4m

4m

2.5m

1

m

1

2

3

6

1

3

1

4

1

6

1

7

1

8

1

9

20

2

1

2

2

25

7

12

2.5m

1.5m

2m

4m

4m

2.5m

5kN

7kN

1

m

2.5m

1.5m

2m

4m

4m

2.5m

1

m

α

8

α

9

α

6

α

5

α

4

α

3

V

C

H

C

V

G

N

5

N

24

N

24

N

11

N

5

N

11

4

23

α

7

5

1

m

1

m

1

m

1

m

1

m

1

m

z

sumy momentów wzgl

ę

dem

punktu W z prawej strony
przekroju 5-5. Do
wyznaczenia poło

ż

enia

punktu W zostanie
wykorzystane twierdzenie
Talesa.

N

24

⋅

sin(

α

8

)

⋅

(

z

+2.5m)+N

24

⋅

cos(

α

8

)

⋅

L

18

-V

G

⋅

z

-7kN

⋅

sin(

α

9

)

⋅

1m+7kN

⋅

cos(

α

9

)

⋅

z

=0

N

24

=-2.4939kN

Ʃ

M

W

P

=0

cos(

α

8

)=0.9450

cos(

α

9

)=0.9285 V

G

=4.4675kN

m

5

.

6

m

1

m

1

m

2

⋅

+

⋅

=

⋅

z

z

m

5

.

6

=

z

N

24

⋅

0.3272

⋅

9m+N

24

⋅

0.9450

⋅

1.385m-4.4675kN

⋅

6.5m-7kN

⋅

0.3714

⋅

1m+7kN

⋅

0.9285

⋅

6.5m=0

Przykład

Wyznacz warto

ś

ci sił wewn

ę

trznych w poszczególnych pr

ę

tach

W odniesieniu do przekroju
6-6 zostan

ą

wykonane

nast

ę

puj

ą

ce działania:

• wyznaczenie siły normalnej
w pr

ę

cie nr 6, korzystaj

ą

c z

sumy momentów wzgl

ę

dem

1

5

7

8

9

10

3kN

7kN

3

m

3

m

α

2

α

1

3

m

3

m

5

sumy momentów wzgl

ę

dem

punktu N z prawej strony
przekroju 6-6;

• wyznaczenie siły normalnej
w pr

ę

cie nr 12, korzystaj

ą

c z

sumy momentów wzgl

ę

dem

punktu F z prawej strony
przekroju 6-6;
• wyznaczenie siły normalnej
w pr

ę

cie nr 25, korzystaj

ą

c z

sumy momentów wzgl

ę

dem

Potrzebne dane:

sin(

α

3

)=0.1521 sin(

α

9

)=0.3714

cos(

α

)=0.9884

cos(

α

)=0.9285 V =4.4675kN

Ʃ

M

N

L

=0

N

6

⋅

1m=0

N =0kN

2.5m

1.5m

2m

4m

4m

2.5m

1

2

3

4

5

1

3

1

4

1

6

1

7

1

8

1

9

20

2

1

2

2

23

24

7

11

2.5m

1.5m

2m

4m

4m

2.5m

5kN

7kN

2.5m

1.5m

2m

4m

4m

2.5m

α

8

α

9

α

7

α

6

α

5

α

4

α

3

V

C

H

C

V

G

N

6

N

6

N

25

N

25

N

12

N

12

5

5

1

m

1

m

1

m

1

m

1

m

1

m

1

m

1

m

1

m

z

sumy momentów wzgl

ę

dem

punktu W z prawej strony
przekroju 6-6.

N

12

⋅

sin(

α

3

)

⋅

2.5m+N

12

⋅

cos(

α

3

)

⋅

1m+V

G

⋅

2.5m-7kN

⋅

sin(

α

9

)

⋅

1m-7kN

⋅

cos(

α

9

)

⋅

2.5m=0

N

12

=5.6112kN

Ʃ

M

F

P

=0

cos(

α

3

)=0.9884

cos(

α

9

)=0.9285 V

G

=4.4675kN

N

6

=0kN

N

12

⋅

0.1521

⋅

2.5m+N

12

⋅

0.9884

⋅

1m+4.4675kN

⋅

2.5m-7kN

⋅

0.3714

⋅

1m-7kN

⋅

0.9285

⋅

2.5m=0

Dalsze obliczenia na
nast

ę

pnej stronie

Przykład

Wyznacz warto

ś

ci sił wewn

ę

trznych w poszczególnych pr

ę

tach

W odniesieniu do przekroju
6-6 zostan

ą

wykonane

nast

ę

puj

ą

ce działania:

• wyznaczenie siły normalnej
w pr

ę

cie nr 6, korzystaj

ą

c z

sumy momentów wzgl

ę

dem

1

5

7

8

9

10

3kN

7kN

3

m

3

m

α

2

α

1

3

m

3

m

5

sumy momentów wzgl

ę

dem

punktu N z prawej strony
przekroju 6-6;

• wyznaczenie siły normalnej
w pr

ę

cie nr 12, korzystaj

ą

c z

sumy momentów wzgl

ę

dem

punktu F z prawej strony
przekroju 6-6;
• wyznaczenie siły normalnej
w pr

ę

cie nr 25, korzystaj

ą

c z

sumy momentów wzgl

ę

dem

Potrzebne dane:

sin(

α

9

)=0.3714

z

=6.5m

cos(

α

)=0.9285 V =4.4675kN

2.5m

1.5m

2m

4m

4m

2.5m

1

2

3

4

5

1

3

1

4

1

6

1

7

1

8

1

9

20

2

1

2

2

23

24

7

11

2.5m

1.5m

2m

4m

4m

2.5m

5kN

7kN

2.5m

1.5m

2m

4m

4m

2.5m

α

8

α

9

α

7

α

6

α

5

α

4

α

3

V

C

H

C

V

G

N

6

N

6

N

25

N

25

N

12

N

12

5

5

1

m

1

m

1

m

1

m

1

m

1

m

1

m

1

m

1

m

z

sumy momentów wzgl

ę

dem

punktu W z prawej strony
przekroju 6-6.

N

25

⋅

sin(

α

9

)

⋅

z

+N

25

⋅

cos(

α

9

)

⋅

1m-V

G

⋅

z

-7kN

⋅

sin(

α

9

)

⋅

1m+7kN

⋅

cos(

α

9

)

⋅

z

=0

N

25

=-3.1736kN

Ʃ

M

W

P

=0

cos(

α

9

)=0.9285 V

G

=4.4675kN

N

25

⋅

0.3714

⋅

6.5m+N

25

⋅

0.9285

⋅

1m-4.4675

⋅

6.5m-7kN

⋅

0.3714

⋅

1m+7kN

⋅

0.9285

⋅

6.5m=0

Przykład

Wyznacz warto

ś

ci sił wewn

ę

trznych w poszczególnych pr

ę

tach

Pozostałe siły normalne zostan

ą

wyznaczone metod

ą

równowa

ż

enia

w

ę

złów. Równania, w których

wszystkie wielko

ś

ci b

ę

d

ą

znane,

1

5

2

2

7

8

9

10

2kN

3kN

7kN

3

m

3

m

α

2

α

1

wszystkie wielko

ś

ci b

ę

d

ą

znane,

posłu

żą

do sprawdzenia oblicze

ń

.

Do wyznaczenia siły normalnej w
pr

ę

cie nr 19 zostanie wykorzystana

suma rzutów wektorów sił na o

ś

Y

(kierunek pionowy) w w

ęź

le G a

drugie równanie zostanie
wykorzystane do sprawdzenia
prawidłowo

ś

ci dot

ą

d

przeprowadzanych oblicze

ń

.

Potrzebne dane:

V

G

=4.4675kN N

6

=0

2.5m

1.5m

2m

4m

4m

2.5m

1

m

1

m

1

2

3

4

5

1

3

1

4

1

6

1

7

1

8

20

2

1

2

2

23

24

25

7

11

12

2.5m

1.5m

2m

4m

4m

2.5m

5kN

7kN

1

m

1

m

2.5m

1.5m

2m

4m

4m

2.5m

1

m

1

m

α

8

α

9

α

7

α

6

α

5

α

4

α

3

V

C

H

C

V

G

N

6

N

19

N

19

N

6

N

19

+V

G

=0

N

19

=-4.4675kN

Ʃ

Y=0

N

19

+4.4675kN=0

Ʃ

X=0

Obliczenia siły normalnej w pr

ę

cie nr 19:

Sprawdzenie oblicze

ń

:

N

6

=0

Warunek spełniony:

Ʃ

X=0

Przykład

Wyznacz warto

ś

ci sił wewn

ę

trznych w poszczególnych pr

ę

tach

Do wyznaczenia siły normalnej w
pr

ę

cie nr 18 zostanie

1

5

7

8

9

10

2kN

3kN

7kN

3

m

3

m

α

2

α

1

pr

ę

cie nr 18 zostanie

wykorzystana suma rzutów
wektorów sił na o

ś

Y (kierunek

pionowy) w w

ęź

le F a drugie

równanie zostanie wykorzystane
do sprawdzenia prawidłowo

ś

ci

dot

ą

d przeprowadzanych

oblicze

ń

.

Potrzebne dane:

N

5

=-2.9452kN N

6

=0 N

25

=-3.1736kN

sin(

α

9

)=0.3714 cos(

α

9

)=0.9285

2.5m

1.5m

2m

4m

4m

2.5m

1

m

1

m

1

2

3

4

1

3

1

4

1

6

1

7

1

9

20

2

1

2

2

23

24

7

11

12

2.5m

1.5m

2m

4m

4m

2.5m

5kN

7kN

1

m

1

m

2.5m

1.5m

2m

4m

4m

2.5m

1

m

1

m

α

8

α

7

α

6

α

5

α

4

α

3

V

C

H

C

V

G

N

6

N

6

α

9

N

6

N

25

N

25

N

18

N

18

N

5

N

5

N

18

+N

25

⋅

sin(

α

9

) =0

N

19

=1.1787kN

Ʃ

Y=0

Ʃ

X=0

Obliczenia siły normalnej w pr

ę

cie nr 18:

Sprawdzenie oblicze

ń

:

Warunek spełniony:

Ʃ

X=0

N

18

-3.1736kN

⋅

0.3714 =0

N

6

+N

25

⋅

cos(

α

9

)-N

5

=

=0-3.1736kN

⋅

0.9285+2.9452kN=-0.0015kN

≈

0

Przykład

Wyznacz warto

ś

ci sił wewn

ę

trznych w poszczególnych pr

ę

tach

Do wyznaczenia siły normalnej w
pr

ę

cie nr 17 zostanie

1

5

7

8

9

10

2kN

3kN

7kN

3

m

3

m

α

2

α

1

pr

ę

cie nr 17 zostanie

wykorzystana suma rzutów
wektorów sił na o

ś

Y (kierunek

pionowy) w w

ęź

le E a drugie

równanie zostanie wykorzystane
do sprawdzenia prawidłowo

ś

ci

dot

ą

d przeprowadzanych

oblicze

ń

.

Potrzebne dane:

N

4

=-5.3041kN N

5

=-2.9452kN N

24

=-2.4939kN

sin(

α

8

)=0.3272 cos(

α

8

)=0.9450

2.5m

1.5m

2m

4m

4m

2.5m

1

m

1

m

1

2

3

6

1

3

1

4

1

6

1

8

1

9

20

2

1

2

2

23

25

7

11

12

2.5m

1.5m

2m

4m

4m

2.5m

5kN

7kN

1

m

1

m

2.5m

1.5m

2m

4m

4m

2.5m

1

m

1

m

α

8

α

9

α

7

α

6

α

5

α

4

α

3

V

C

H

C

V

G

N

5

N

5

N

24

N

24

N

17

N

17

N

4

N

4

N

17

+N

24

⋅

sin(

α

8

) =0

N

17

=0.8160kN

Ʃ

Y=0

Ʃ

X=0

Obliczenia siły normalnej w pr

ę

cie nr 17:

Sprawdzenie oblicze

ń

:

Warunek spełniony:

Ʃ

X=0

N

17

-2.4939kN

⋅

0.3272 =0

N

5

+N

24

⋅

cos(

α

8

)-N

4

=

=-2.9452kN-2.4939kN

⋅

0.9450+5.3041kN=0.0021kN

≈

0

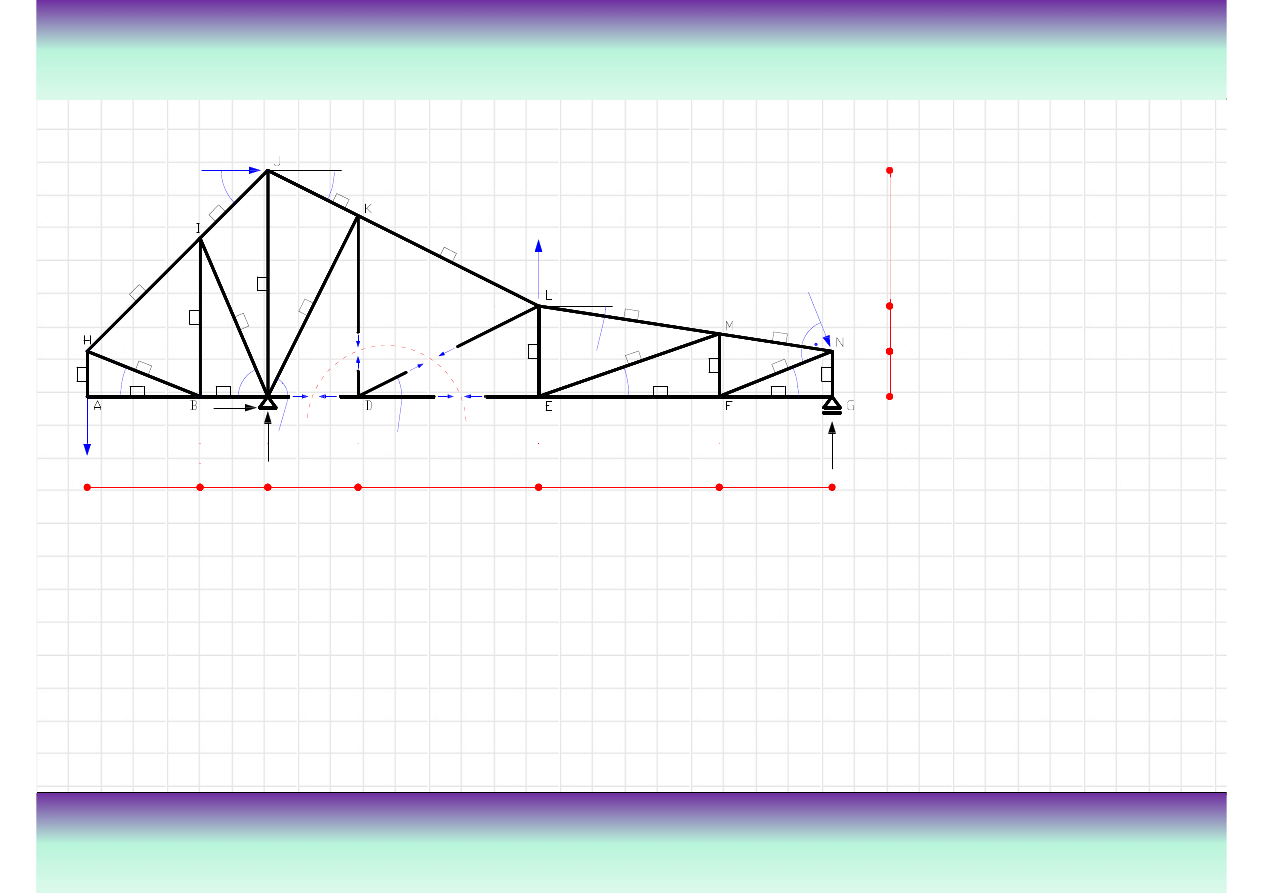
Przykład

Wyznacz warto

ś

ci sił wewn

ę

trznych w poszczególnych pr

ę

tach

Do wyznaczenia siły normalnej w

1

5

7

8

9

10

2kN

3kN

7kN

3

m

3

m

α

2

α

1

Do wyznaczenia siły normalnej w
pr

ę

cie nr 16 zostanie

wykorzystana suma rzutów
wektorów sił na o

ś

Y (kierunek

pionowy) w w

ęź

le D a drugie

równanie zostanie wykorzystane
do sprawdzenia prawidłowo

ś

ci

dot

ą

d przeprowadzanych

oblicze

ń

.

Potrzebne dane:

N

3

=-0.3826kN N

4

=-5.3041kN N

23

=5.5008kN

sin(

α

7

)=0.4472 cos(

α

7

)=0.8944

2.5m

1.5m

2m

4m

4m

2.5m

1

m

1

m

1

2

5

6

1

3

1

4

1

7

1

8

1

9

20

2

1

2

2

24

25

7

11

12

2.5m

1.5m

2m

4m

4m

2.5m

5kN

7kN

1

m

1

m

2.5m

1.5m

2m

4m

4m

2.5m

1

m

1

m

α

8

α

9

α

6

α

5

α

4

α

3

V

C

H

C

V

G

α

7

N

4

N

4

N

23

N

23

N

16

N

16

N

3

N

3

N

16

+N

23

⋅

sin(

α

7

) =0

N

16

=-2.4600kN

Ʃ

Y=0

Ʃ

X=0

Obliczenia siły normalnej w pr

ę

cie nr 16:

Sprawdzenie oblicze

ń

:

Warunek spełniony:

Ʃ

X=0

N

16

+5.5008kN

⋅

0.4472 =0

N

4

+N

23

⋅

cos(

α

7

)-N

3

=

=-5.3041kN+5.5008kN

⋅

0.8944+0.3826kN=-0.0016kN

≈

0

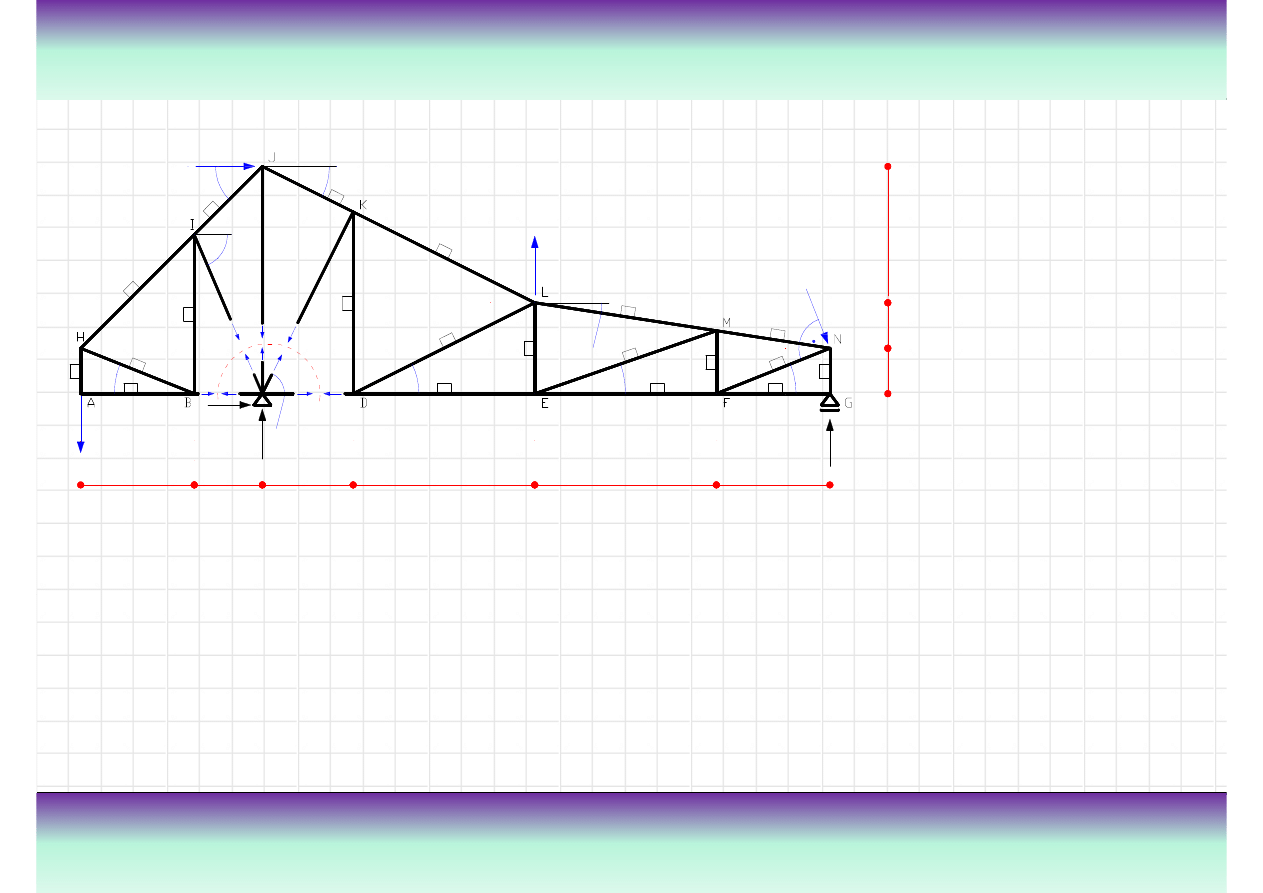
Przykład

Wyznacz warto

ś

ci sił wewn

ę

trznych w poszczególnych pr

ę

tach

Do wyznaczenia siły normalnej w

7

8

9

10

2kN

3kN

7kN

3

m

3

m

α

2

α

1

α

5

Do wyznaczenia siły normalnej w
pr

ę

cie nr 15 zostanie

wykorzystana suma rzutów
wektorów sił na o

ś

Y (kierunek

pionowy) w w

ęź

le C a drugie

równanie zostanie wykorzystane
do sprawdzenia prawidłowo

ś

ci

dot

ą

d przeprowadzanych

oblicze

ń

.

Potrzebne dane:

H

C

=-4.5997kN V

C

=4.0320kN N

2

=-3.5714kN N

3

=-0.3826kN N

21

=-1.0880kN N

22

=2.2003kN

sin(

α

5

)=0.9191 cos(

α

5

)=0.3939 sin(

α

6

)=0.8944 cos(

α

6

)=0.4472

2.5m

1.5m

2m

4m

4m

2.5m

1

m

1

m

1

4

5

6

1

4

1

6

1

7

1

8

1

9

20

23

24

25

11

12

2.5m

1.5m

2m

4m

4m

2.5m

5kN

7kN

1

m

1

m

2.5m

1.5m

2m

4m

4m

2.5m

1

m

1

m

α

8

α

9

α

7

α

6

α

4

α

3

V

C

H

C

V

G

N

3

N

3

N

22

N

22

N

15

N

2

N

2

N

21

N

21

1

3

N

15

+N

22

⋅

sin(

α

6

) +N

21

⋅

sin(

α

5

)+V

c

=0

N

15

=-5.0kN

Ʃ

Y=0

Ʃ

X=0

Obliczenia siły normalnej w pr

ę

cie nr 15:

Sprawdzenie oblicze

ń

:

Warunek spełniony:

Ʃ

X=0

N

3

+N

22

⋅

cos(

α

6

) –N

21

⋅

cos(

α

5

)-N

2

+H

C

=

=-0.3826kN+2.2003kN

⋅

0.4472+0.1.0880kN

⋅

0.3939+

N

15

+2.2003kN

⋅

0.8944 -1.0880kN

⋅

0.9191+4.0320 =0

+3.5714kN-4.5997kN=0.0016kN

≈

0

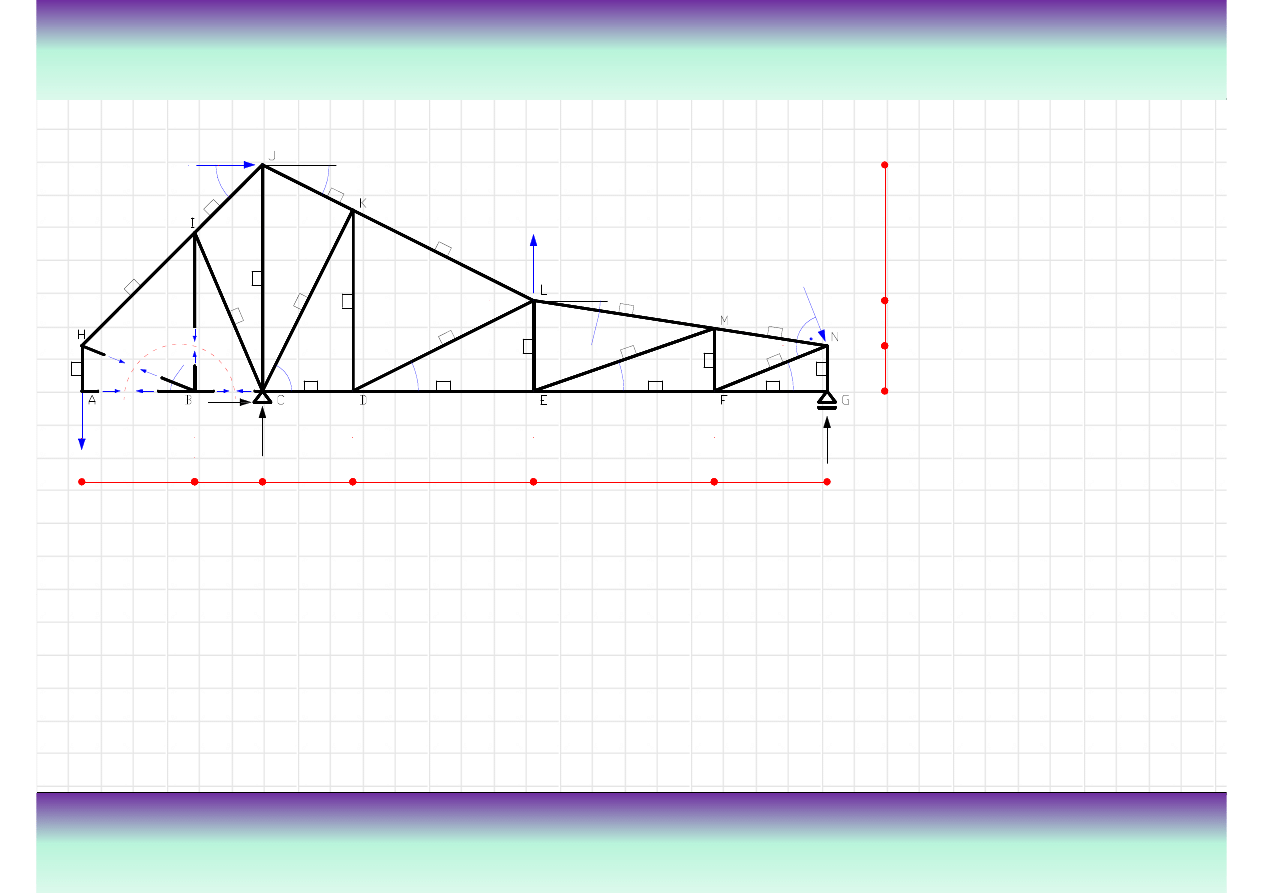
Przykład

Wyznacz warto

ś

ci sił wewn

ę

trznych w poszczególnych pr

ę

tach

Do wyznaczenia siły normalnej w

1

5

1

6

2

2

7

8

9

10

2kN

3kN

7kN

3

m

3

m

α

2

α

1

Do wyznaczenia siły normalnej w
pr

ę

cie nr 14 zostanie

wykorzystana suma rzutów
wektorów sił na o

ś

Y (kierunek

pionowy) w w

ęź

le B a drugie

równanie zostanie wykorzystane
do sprawdzenia prawidłowo

ś

ci

dot

ą

d przeprowadzanych

oblicze

ń

.

Potrzebne dane:

N

1

=0 N

2

=-3.5714kN N

20

=-3.8464kN

sin(

α

4

)=0.3714 cos(

α

4

)=0.9285

2.5m

1.5m

2m

4m

4m

2.5m

1

m

1

m

3

4

5

6

1

3

1

6

1

7

1

8

1

9

2

1

2

2

23

24

25

11

12

2.5m

1.5m

2m

4m

4m

2.5m

5kN

7kN

1

m

1

m

2.5m

1.5m

2m

4m

4m

2.5m

1

m

1

m

α

8

α

9

α

7

α

6

α

4

α

3

V

C

H

C

V

G

N

14

N

14

N

2

N

2

N

20

N

1

N

1

N

20

N

14

+N

20

⋅

sin(

α

4

) =0

N

14

=1.4286kN

Ʃ

Y=0

Ʃ

X=0

Obliczenia siły normalnej w pr

ę

cie nr 14:

Sprawdzenie oblicze

ń

:

Warunek spełniony:

Ʃ

X=0

N

2

-N

20

⋅

cos(

α

4

) –N

1

=

=-3.5714kN+3.8464kN

⋅

0.9285+0=-0.000018kN

≈

0

N

14

-3.8464kN

⋅

0.3714 =0

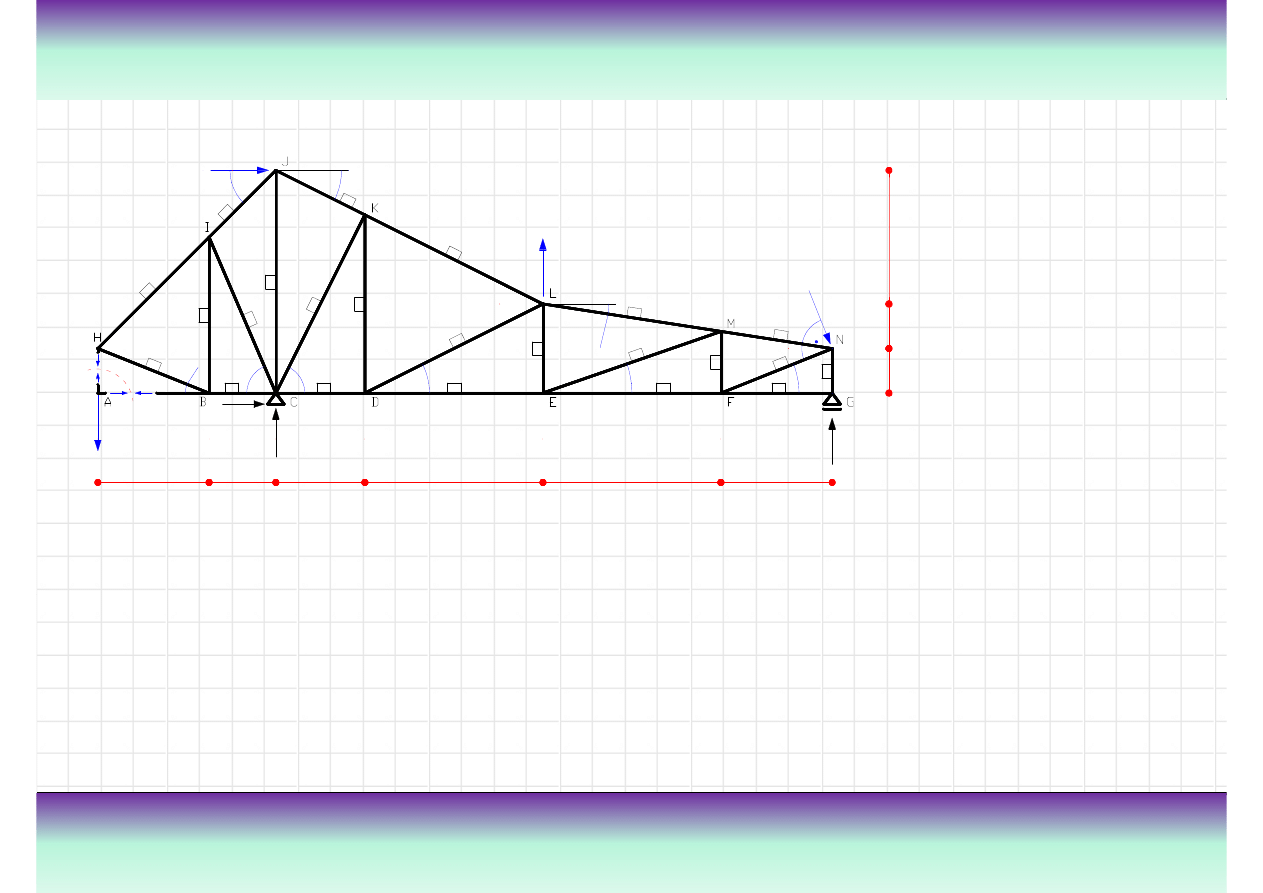
Przykład

Wyznacz warto

ś

ci sił wewn

ę

trznych w poszczególnych pr

ę

tach

Do wyznaczenia siły normalnej w

1

5

2

2

7

8

9

10

2kN

3kN

7kN

3

m

3

m

α

2

α

1

Do wyznaczenia siły normalnej w
pr

ę

cie nr 13 zostanie

wykorzystana suma rzutów
wektorów sił na o

ś

Y (kierunek

pionowy) w w

ęź

le A a drugie

równanie zostanie wykorzystane
do sprawdzenia prawidłowo

ś

ci

dot

ą

d przeprowadzanych

oblicze

ń

.

Potrzebne dane:

N

1

=0

2.5m

1.5m

2m

4m

4m

2.5m

1

m

1

m

2

3

4

5

6

1

4

1

6

1

7

1

8

1

9

20

2

1

2

2

23

24

25

7

11

12

2.5m

1.5m

2m

4m

4m

2.5m

5kN

7kN

1

m

1

m

2.5m

1.5m

2m

4m

4m

2.5m

1

m

1

m

α

8

α

9

α

7

α

6

α

5

α

3

V

C

H

C

V

G

N

1

N

1

α

4

N

13

N

13

N

13

-5kN =0

Ʃ

Y=0

Ʃ

X=0

Obliczenia siły normalnej w pr

ę

cie nr 13:

Sprawdzenie oblicze

ń

:

Warunek spełniony:

Ʃ

X=0

N

1

=0

N

13

=5kN

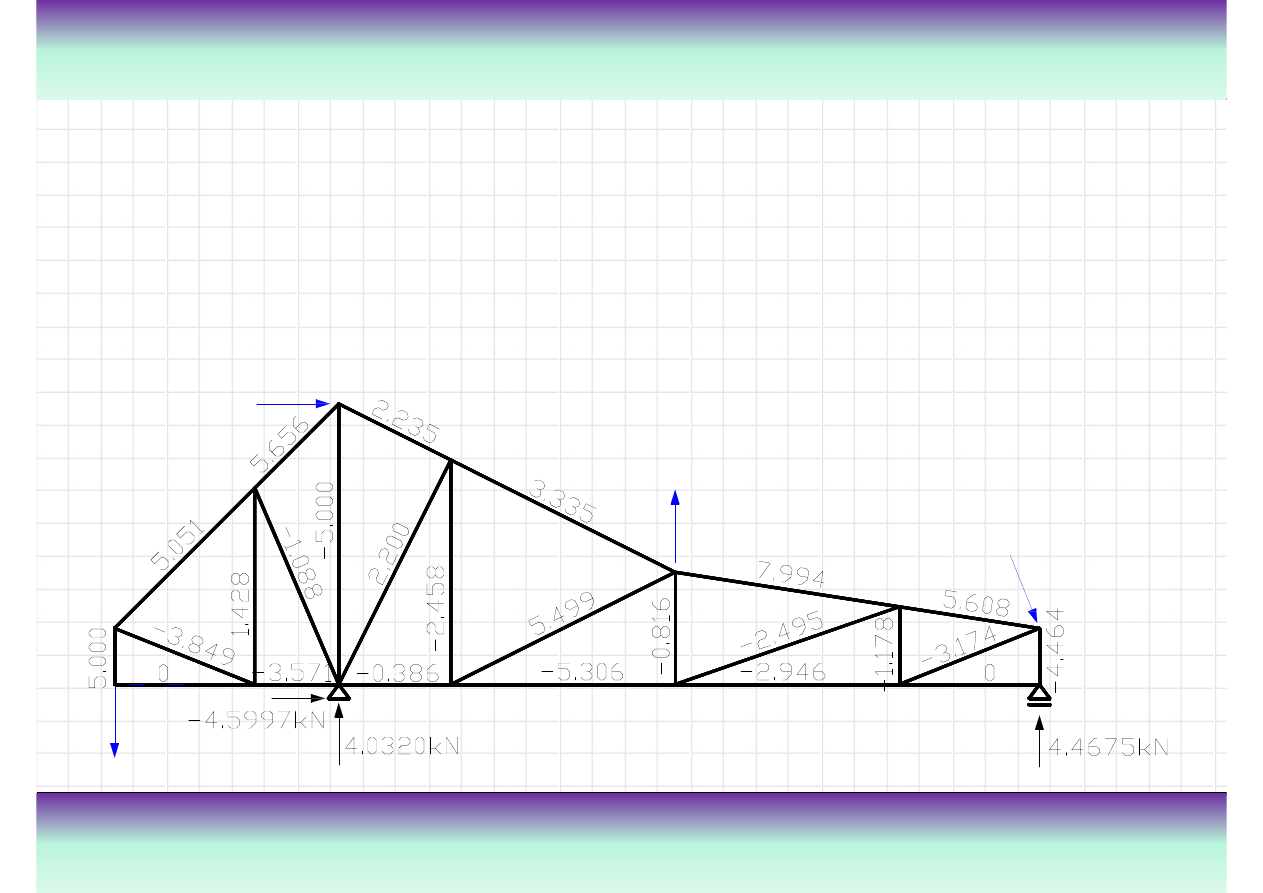
Przykład

Zestawienie sił normalnych w poszczególnych pr

ę

tach kratownicy

Wynikami analizy statycznej kratownicy s

ą

reakcje oraz siły normalne w poszczególnych pr

ę

tach. Siły

normalne zostały przedstawione w formie zestawienia. Liczba przy pr

ę

cie oznacza warto

ść

siły normalnej w

tym pr

ę

cie. Je

ż

eli liczba jest dodatnia, to pr

ę

t jest rozci

ą

gany, a je

ż

eli ujemna, to pr

ę

t jest poddany działaniu

siły

ś

ciskaj

ą

cej.

siły

ś

ciskaj

ą

cej.

Reakcje wynosz

ą

:

H

C

=-4.5997kN

V

G

=4.4675kN

V

C

=4.0320kN

2kN

3kN

7kN

5kN

Podsumowanie

Zastosowanie kratownic płaskich

Jako kratownice mo

ż

na traktowa

ć

konstrukcje, w których elementy s

ą

poł

ą

czone w taki

sposób,

ż

e osie pr

ę

tów, dochodz

ą

cych do jednego w

ę

zła przecinaj

ą

si

ę

w jednym

punkcie. O poł

ą

czeniu przegubowym mo

ż

na te

ż

mówi

ć

w sytuacji gdy poł

ą

czenie

elementu z w

ę

złem (np.. Z blach

ą

w

ę

złow

ą

) ma znacznie mniejsz

ą

sztywno

ść

na

elementu z w

ę

złem (np.. Z blach

ą

w

ę

złow

ą

) ma znacznie mniejsz

ą

sztywno

ść

na

zginanie ni

ż

pr

ę

t. Warunkiem prawidłowego wykorzystania kratownicy jest oczywi

ś

cie

przykładanie obci

ąż

e

ń

w w

ę

złach.

Podsumowanie

Zastosowanie kratownic płaskich

Konstrukcje, które mo

ż

na zamodelowa

ć

kratownic

ą

, s

ą

cz

ę

sto stosowane w praktyce

in

ż

ynierskiej a zwłaszcza jako konstrukcje no

ś

ne przekry

ć

, konstrukcje no

ś

ne mostów i

kładek dla pieszych, konstrukcje wsporcze kominów, itd.

Kładka dla
pieszych nad ul.
Filaretów w Lublinie

Hala supermarketu
Leclerc w Lublinie

Konstrukcja no

ś

na

mostu kolejowego
k. Białej Podlaskiej

Podsumowanie

Zastosowanie kratownic płaskich

W prezentacji przedstawiono analiz

ę

statyczn

ą

układów płaskich, ale od czasu kiedy

in

ż

ynierowie u

ż

ywaj

ą

programów komputerowych do wyznaczania sił wewn

ę

trznych

coraz cz

ęś

ciej stosuje si

ę

przestrzenne konstrukcje kratowe.

Wi

ę

cej informacji na temat analizy statycznej kratownic statycznie wyznaczalnych mo

ż

na znale

źć

w podr

ę

cznikach:

Z. Cywiński: Mechanika budowli w zadaniach. Układy statycznie wyznaczalne, PWN 2008.
Z. Dyląg, E. Krzemińska-Niemiec, F. Filip: Mechanika budowli, PWN 1989.

Konstrukcja no

ś

na

dachu ko

ś

cioła przy ul. Skierki w Lublinie

Ż

urawie na budowie

przy ul. Zana w Lublinie

Aleksander Robak, Ewa Błazik-Borowa

Wy

ż

sza Szkoła Zarz

ą

dzania i Administracji

Katedra Mechaniki Budowli, Politechnika Lubelska

Mamy nadziej

ę

,

ż

e wykład

dostarczył niezb

ę

dnych informacji

o analizie statycznej kratownic

Projekt współfinansowany przez Unię Europejską

Projekt współfinansowany przez Unię Europejską

w ramach Europejskiego Funduszu Społecznego

w ramach Europejskiego Funduszu Społecznego