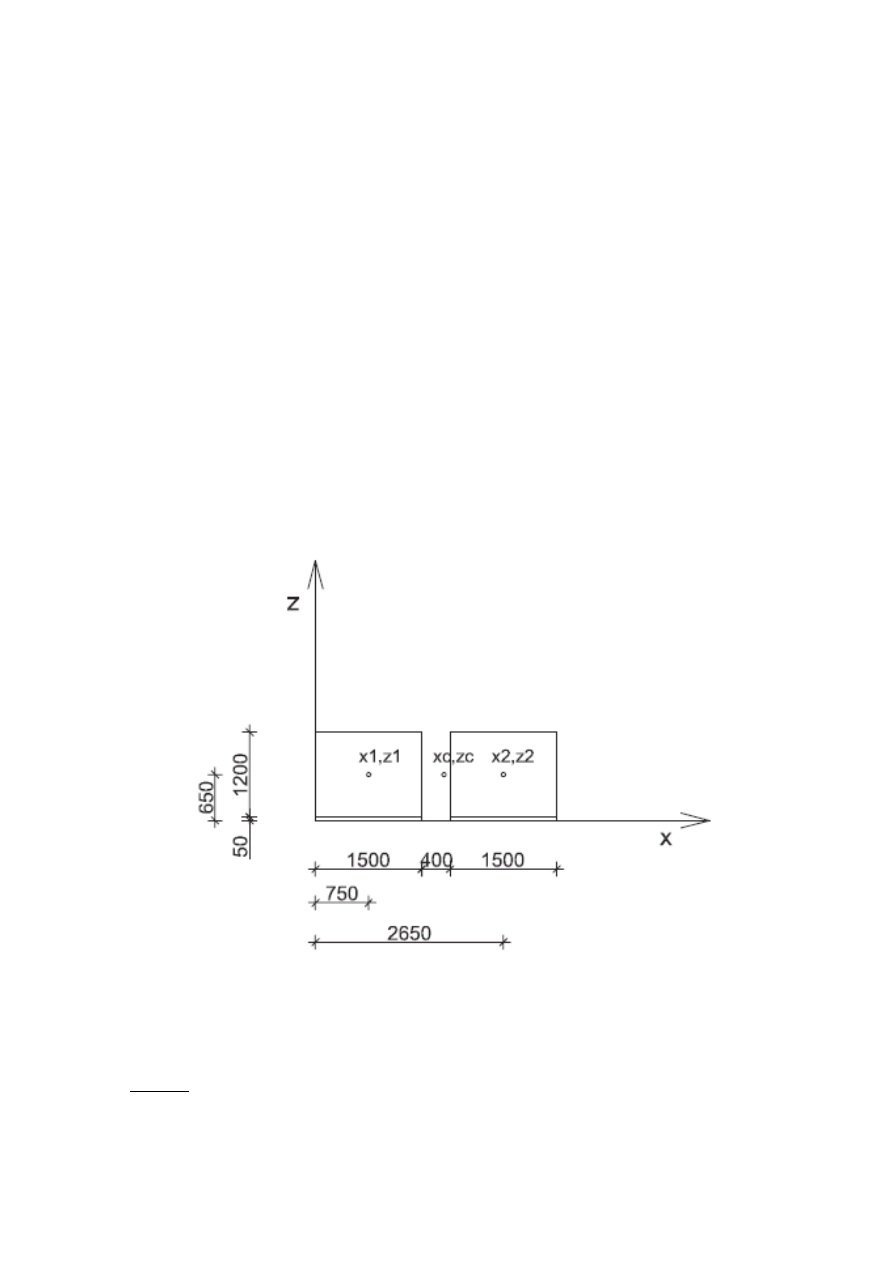
1.Ukształtowanie obiektu – wyznaczenie podstawowych gabarytów konstrukcji.

1.1.Dane:

•

Silnik:

d

1

= 1200mm

l

1

= 1500mm

m

1

= 6,5Mg

•

Wentylator:

d

2

= 1200mm

l

2

= 1500mm

m

2

= 5,00Mg

•

Cokół żelbetowy pod silnikiem:

nie występuje

•

Podbeton pod silnikiem i wentylatorem: 50mm

•

Odległość między silnikiem, a wentylatorem: x = 400mm

1.2. Wyznaczenie środka ciężkości układu:

C

i

i

C

C

C

C

M

m

x

X

)

Z

,

X

(

S

∑

⋅

=

1

C

i

i

C

M

m

z

Z

∑

⋅

=

M

c

= m

1

+ m

2

M

c

= 6,5 + 5,0 = 11,5Mg

Współrzędne środków ciężkości m

1

; m

2

;

Silnik:

m

1

(x

1

, z

1

) = (750, 650)

Wentylator:

m

2

(x

2

, z

2

) = (2650, 650)

S

c

 X

c

, Z

c



X

c

=

750

∗6,52650∗5,0

11,5

=1576,09 mm

Z

c

=

650∗6,5650∗5,0
11,5

=650mm

Przyjęto środek ciężkości układu:

S

c

 X

c

, Z

c



X

c

=

750

∗6,52650∗5,0

11,5

=1576,09 mm

Z

c

=

650∗6,5650∗5,0
11,5

=650mm

2.Obliczenie ciężarów i położenie głównego środka ciężkości całego układu.
2.1. Obliczenie ciężarów:

•

Silnik: m

1

= 6,5Mg

•

Wentylator: m

2

= 5,0Mg

M

c

= m

1

+ m

2

M

c

= 6,5+5,0 = 11,5Mg

2.2. Przyjęcie wymiarów fundamentu:

m

4

= (4 ÷ 5) (m

1

+ m

2

)

(m

1

+ m

2

) = 6,5+5,0 = 11,5Mg

m

4

= (46 ÷ 57,5) Mg

Przyjęto:
d

4

= 2500mm

l

4

= 6000mm

h

4

= 1500mm

m

4

= d

4

·l

4

·h

4

·γ = 2,5·6,0·1,5·2,5 = 56,25Mg

(przyjęto ciężar betonu 2,5T/m

3

)

2.3. Wyznaczenie głównego środka ciężkości:

2

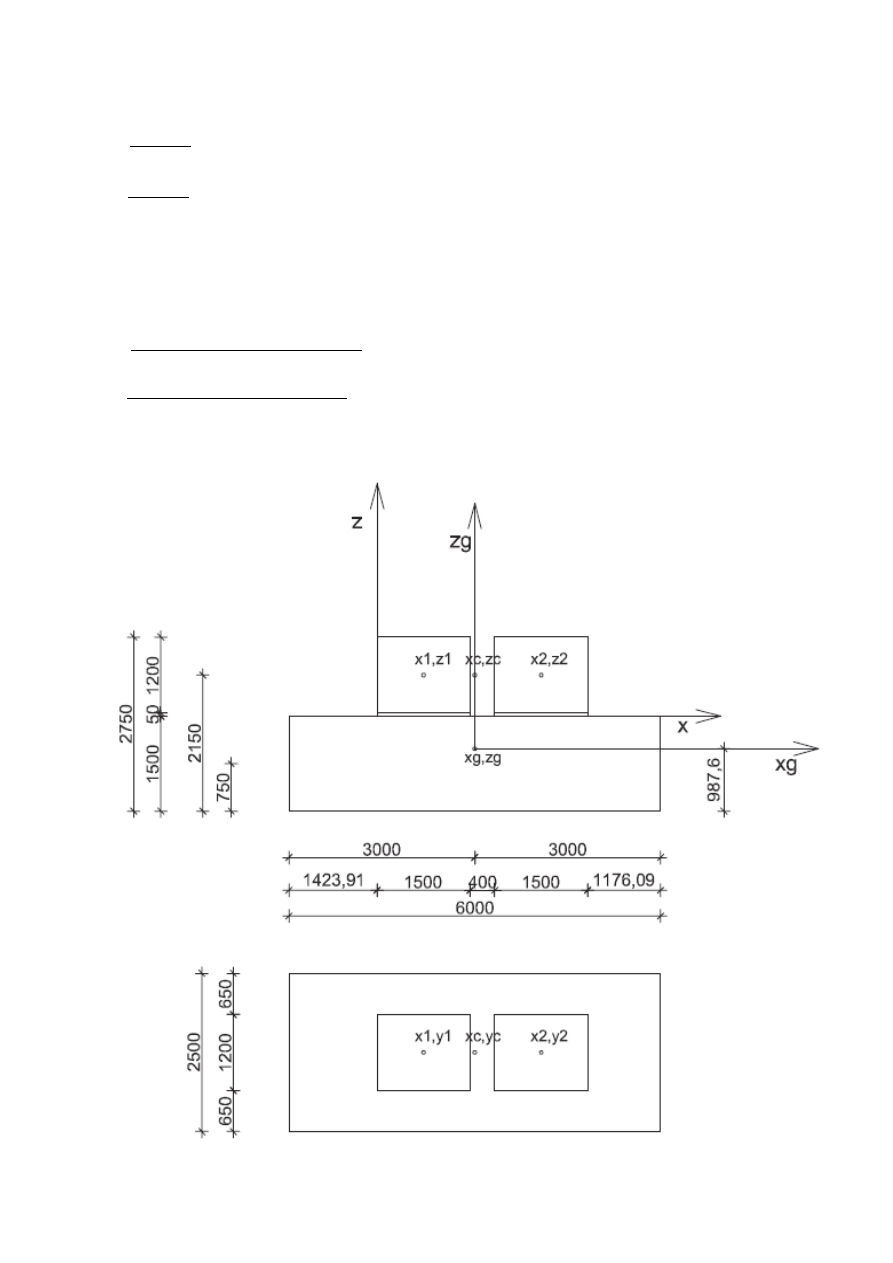
C

i

i

G

G

G

G

M

m

x

X

)

Z

,

X

(

S

∑

⋅

=

C

i

i

G

M

m

z

Z

∑

⋅

=

M

c

= m

1

+ m

2

M

c

= 6,5 + 5,0= 11,5Mg

m

4

= 56,25 Mg

S

c

 X

c

, Z

c



X

c

=

3000

∗11,53000∗56,25

67,75

=3000mm

Z

c

=

2150∗11,5750∗56,25

67,75

=987,6mm

3

3.Wyznaczenie momentów bezwładności mas układu względem płaszczyzn i osi
głównych.

3.1. Momenty bezwładności mas względem płaszczyzn głównych:

3.1.1.Prostopadłościan o wymiarach w kierunku poszczególnych osi: l, b, h:

12

h

m

Y

X

2

1

1

⋅

=

Θ

12

l

m

Z

Y

2

1

1

⋅

=

Θ

12

b

m

Z

X

2

1

1

⋅

=

Θ

•

Fundament:

d

4

= 2500mm

l

4

= 6000mm

h

4

= 1500mm

m

4

= 56,25Mg

 X

1

Y

1

=

56,25

∗1,5

2

12

=10,5469Mg m

2

Y

1

Z

1

=

56,25

∗6,0

2

12

=168,75Mg m

2

 X

1

Z

1

=

56,25

∗2,5

2

12

=29,2969 Mg m

2

3.1.2.Walec o średnicy d i długości l usytuowany wzdłuż osi x

0

:

16

d

m

Y

X

2

1

1

⋅

=

Θ

12

l

m

Z

Y

2

1

1

⋅

=

Θ

16

d

m

Z

X

2

1

1

⋅

=

Θ

•

Silnik:

d

1

= 1200mm

l

1

= 1500mm

m

1

= 6,5Mg

 X

1

Y

1

=

6,5

∗1,2

2

16

=0,585 Mg m

2

Y

1

Z

1

=

6,5

∗1,5

2

12

=1,21875 Mg m

2

 X

1

Z

1

=

6,5

∗1,2

2

16

=0,585 Mg m

2

•

Wentylator:

d

2

= 1200mm

l

2

= 1500mm

m

2

= 5,00Mg

 X

1

Y

1

=

5,0

∗1,2

2

16

=0,45 Mg m

2

Y

1

Z

1

=

5,0

∗1,5

2

12

=0,9375Mg m

2

 X

1

Z

1

=

5,0

∗1,2

2

16

=0,45 Mg m

2

4

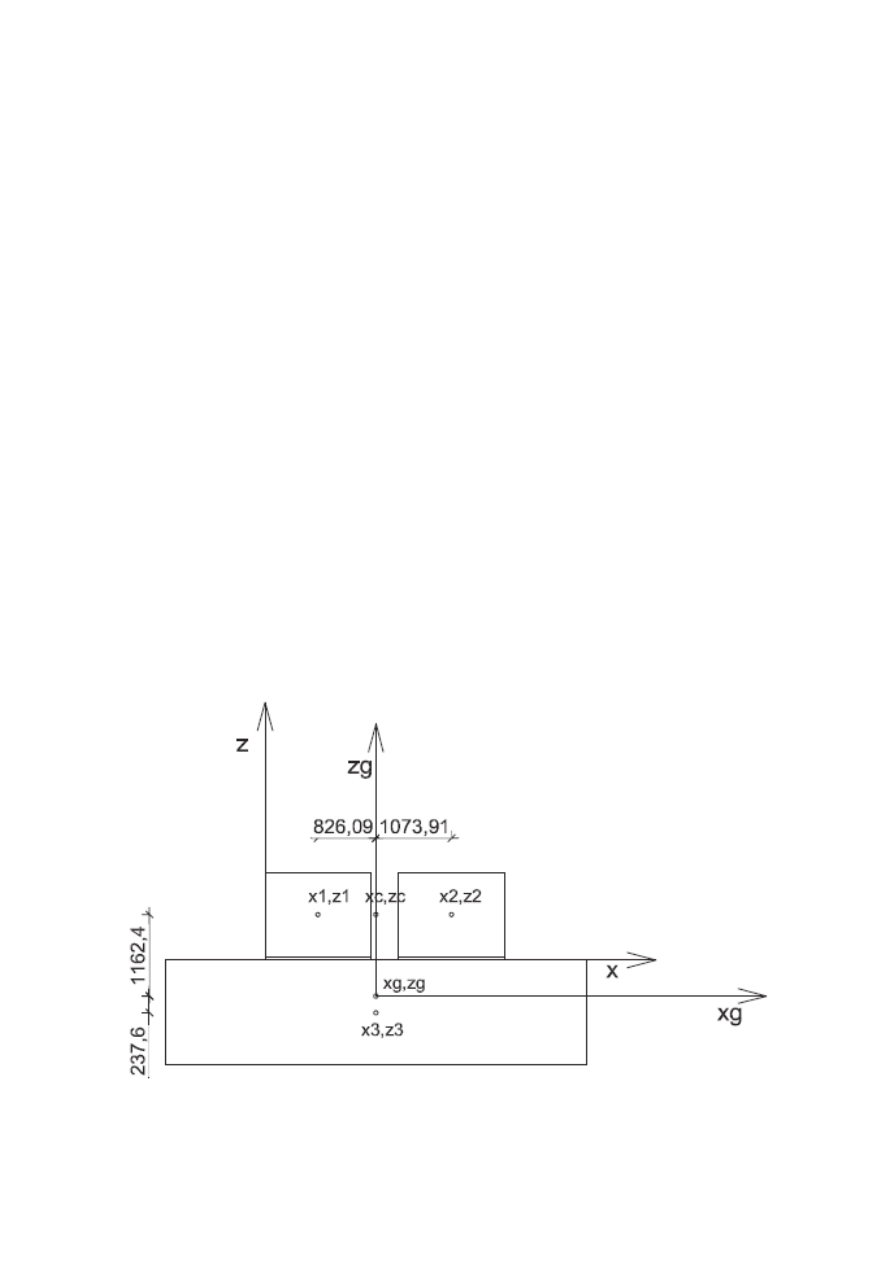
3.2.Momenty bezwładności mas względem płaszczyzn w układzie współrzędnych
przesuniętych o wektor [X, Y, Z]:

2

1

1

0

0

Z

m

Y

X

Y

X

⋅

+

Θ

=

Θ

2

1

1

0

0

X

m

Z

Y

Z

Y

⋅

+

Θ

=

Θ

2

1

1

0

0

Y

m

Z

X

Z

X

⋅

+

Θ

=

Θ

•

Silnik:

 X

0

Y

0

= X

1

Y

1

mZ

2

=0,5856,5∗1,1624

2

=9,3676Mg m

2

Y

0

Z

0

=Y

1

Z

1

mZ

2

=1,218756,5∗0,82609

2

=5,6545Mg m

2

 X

0

Z

0

= X

1

Z

1

mZ

2

=0,5856,5∗0

2

=0,585Mg m

2

•

Wentylator:

 X

0

Y

0

= X

1

Y

1

mZ

2

=0,455,0∗1,1624

2

=7,2059Mg m

2

Y

0

Z

0

=Y

1

Z

1

mZ

2

=0,93755,0∗1,07391

2

=6,7039Mg m

2

 X

0

Z

0

= X

1

Z

1

mZ

2

=0,455,0∗0

2

=0,45 Mg m

2

•

Fundament:

 X

0

Y

0

= X

1

Y

1

mZ

2

=10,548956,25∗0,2376

2

=13,7244 Mg m

2

Y

0

Z

0

=Y

1

Z

1

mZ

2

=168,7556,25∗0

2

=168,75Mg m

2

 X

0

Z

0

= X

1

Z

1

mZ

2

=29,296956,25∗0

2

=29,2969Mg m

2

5

3.3.Momenty bezwładności mas względem osi głównych:

∑ Θ

+

∑ Θ

=

Θ

0

0

0

0

0

Z

X

Y

X

X

∑ Θ

+

∑ Θ

=

Θ

0

0

0

0

0

Z

Y

Y

X

Y

0

0

0

0

0

Z

X

Z

Y

Z

∑ Θ

+

∑ Θ

=

Θ

 X

0

=9,36767,205913,72440,5850,4529,2969=60,6298Mg m

2

Y

0

=9,36767,205913,72445,65456,7039168,75=211,4063Mg m

2

Z

0

=5,65456,7039168,750,5850,4529,2969=211,4403Mg m

2

4.Dobór liczby sprężyn w wibroizolacji, rozmieszczenie i określenie sztywności
wibroizolacji.

4.1. Dane sprężyny wibroizolacji:

•

średnica pręta: d = 20mm

•

średnica podziałowa: D = 136mm

•

wysokość: H

0

= 265mm

•

liczba zwojów: i

0

= 6,5

4.2. Dopuszczalne obliczeniowe obciążenie jednej sprężyny:

w

k

8

d

R

P

2

t

dop

⋅

⋅

⋅

π

⋅

=

R

t

– wytrzymałość obliczeniowa stali sprężynowej na skręcanie, R

t

= 730,0MPa

d – średnica pręta sprężyny [mm]
w – wskaźnik sprężyny, w = D/d

w

=

D
d

=

136
20

=6,8

k – współczynnik poprawkowy uwzględniający nierównomierny stan naprężeń w przekroju
sprężyny

k

=1

5

4

1
w



7
8

1
w

2



1
w

3

=1

5

4

1
6,8



7
8

1
6,8

2



1
6,8

3

=1,2059

P

dop

=

0,73

∗3,14∗20

2



8∗1,2059∗6,8

=13,98

4.3. Wymagana ilość sprężyn w układzie z uwzględnieniem 15% rezerwy obciążenia:

dop

min

P

85

,

0

Q

n

⋅

=

Q – ciężar całkowity układu
Q = M·g
M = m

1

+ m

2

+ m

4

= 6,5 + 5,0 + 56,25 = 67,75Mg

2

s

m

81

,

9

g

=

Q = 67,75·9,81 = 664,6275kN

n

min

=

664,6275

0,85∗13,98

=55,93

6

Przyjęto ilość sprężyn: n = 56szt.

4.4. Sztywność wibroizolacji:

•

sztywność pionowa:

3

Z

w

i

8

d

G

n

K

⋅

⋅

⋅

⋅

=

n – przyjęta całkowita ilość sprężyn w wibroizolacji układu,
G – moduł sprężystości poprzecznej stali sprężynowej, G = 78500MPa
d – średnica pręta sprężyny,
i – liczba pracujących zwojów sprężyny, i = i

0

– 1,5 = 6,5 – 1,5 = 5

w – wskaźnik sprężyny, w = D/d

w

=

D
d

=

136
20

=6,8

K

z

=

56

∗78500∗20

8∗5∗6,8

3



=6990,38

kN
m

•

sztywność pozioma:

K

x

= K

y

zależy od stosunków:

st

st

H

f

oraz

D

H

st

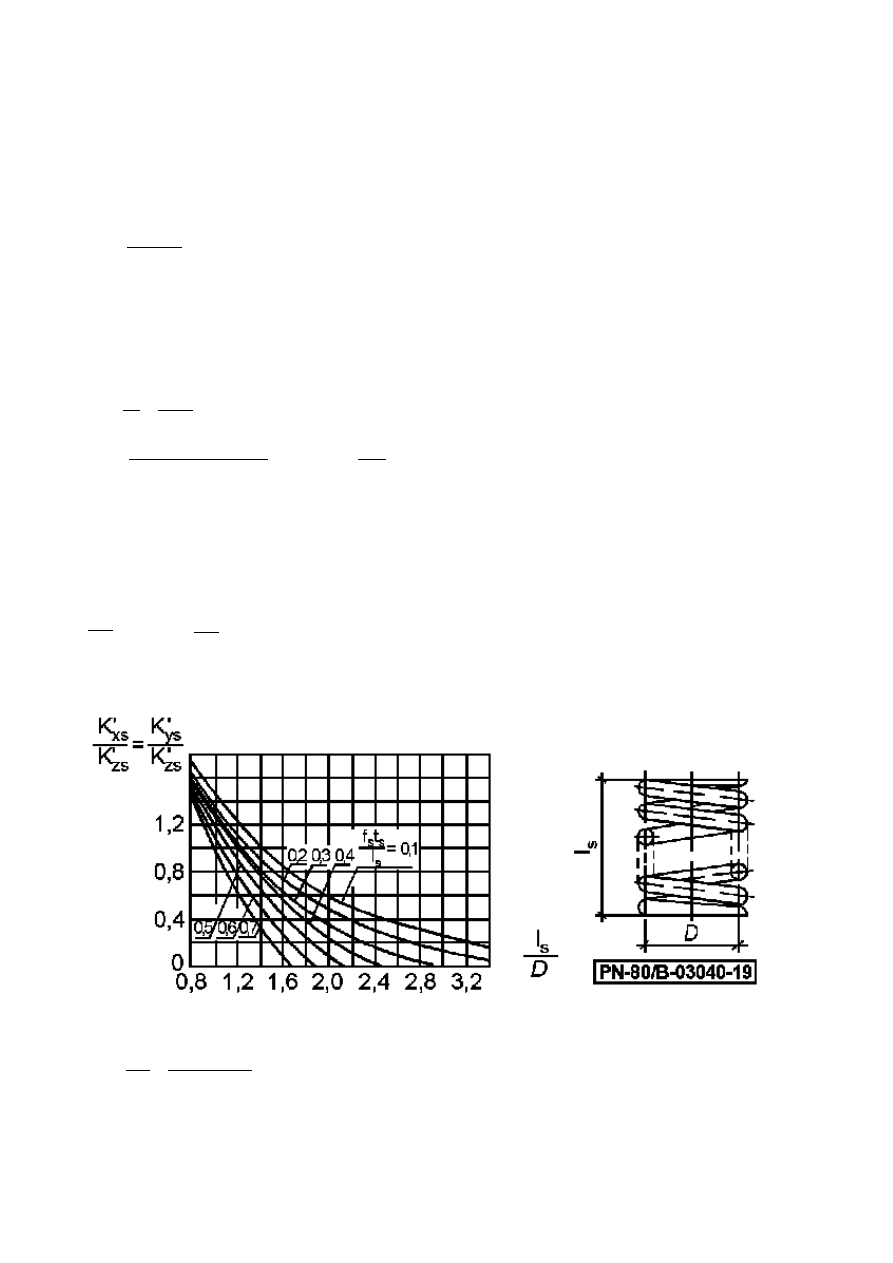
określa się na podstawie rysunku 19 normy PN-80/B-03040

f

st

– ugięcie statyczne sprężyny,

f

st

=

Q

K

z

=

664,6275
6990,38

=0,095m=95mm

H

st

– wysokość sprężyny obciążonej,

H

st

= H

0

– f

st

= 265 – 95 = 170mm

7

D – średnica podziałowa sprężyny

f

st

H

st

=

95,0
170

=0,56

oraz
H

st

D

=

170
136

=1,25

Przyjęto:

K

x

K

z

=

K

y

K

z

=0,75

K

x

=0,75K

z

=0,75∗6990,38=5242,785

kN
m

•

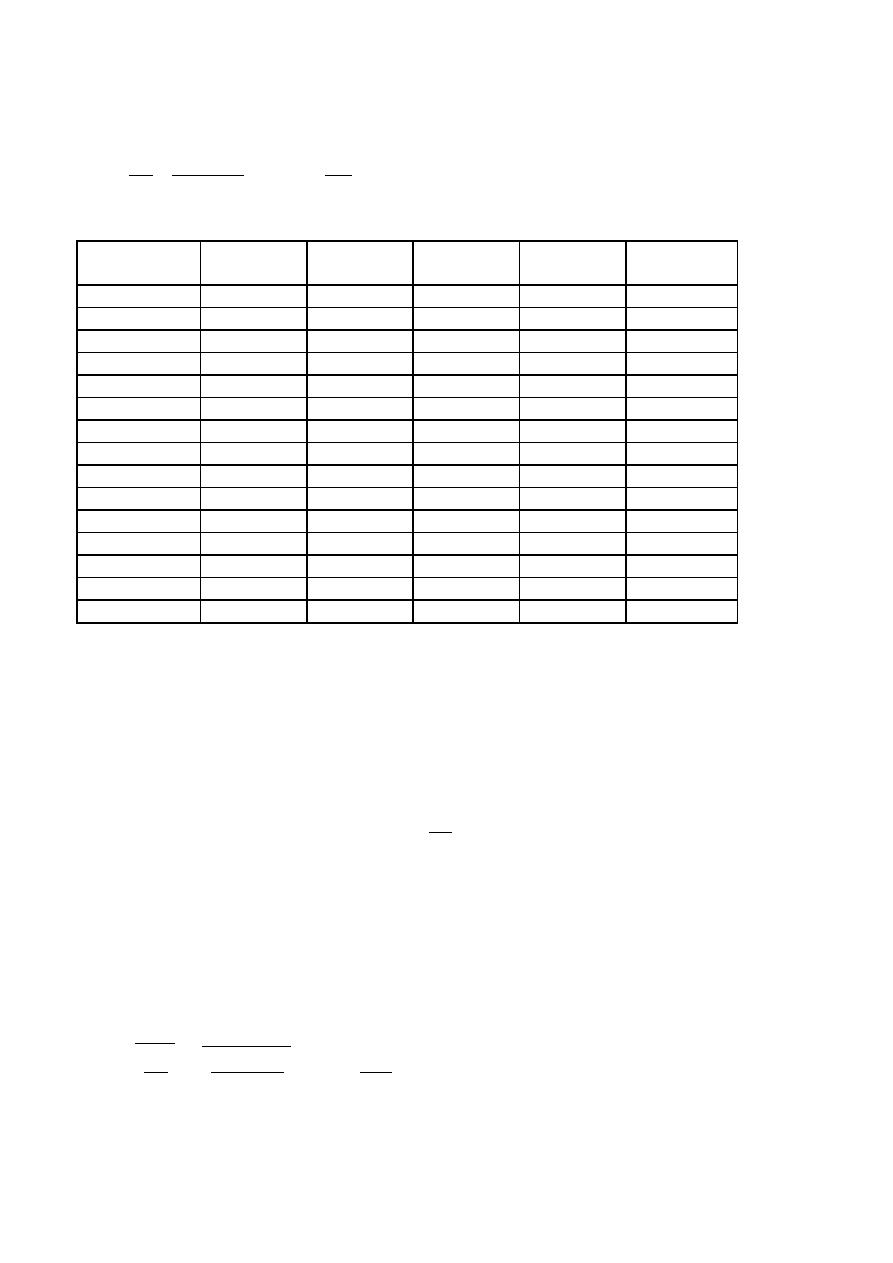
rozmieszczenie wibroizolacji:

•

sztywności wahadłowe:

K

ϕ

xz

= K

z

’

⋅

Σ

x

i

2

K

ϕ

yz

= K

z

’

⋅

Σ

y

i

2

K

z

’– sztywność pionowa jednego wibroizolatora [kN/m],

x

i

– współrzędna x wibroizolatora od osi ciężkości układu [m],

8

y

i

– współrzędna y wibroizolatora od osi ciężkości układu [m]

n – liczba wibroizolatorów

K

z

=

K

z

n

=

6990,38
14

=499,31

kN
m

Nr

wibroizolatora

x

ki

[m]

x

2

ki

[m

2

]

y

ki

[m]

y

2

ki

[m

2

]

x

ki

⋅

y

ki

[m

2

]

1

-2,5

6,25

-0,85

0,7225

2,13

2

-1,25

1,5625

-0,85

0,7225

1,0625

3

0

0

-0,85

0,7225

0

4

1,25

1,5625

-0,85

0,7225

-2,13

5

2,5

6,25

-0,85

0,7225

-1,0625

6

-2,5

6,25

0

0,7225

0

7

-1,25

1,5625

0

0,7225

0

8

1,25

1,5625

0

0,7225

0

9

2,5

6,25

0

0,7225

0

1”

-2,5

6,25

0,85

0,7225

-2,13

2”

-1,25

1,5625

0,85

0,7225

-1,0625

3”

0

0

0,85

0,7225

0

4”

1,25

1,5625

0,85

0,7225

1,0625

5”

2,5

6,25

0,85

0,7225

2,13

Σ

0

46,88

0

10,12

0

K

ϕ

xz

= 499,31

⋅

46,88 = 23407,65kNm

K

ϕ

yz

= 499,31

⋅

10,12 = 5053,02kNm

•

sztywność skrętna

K

ψ

= K

x

’

⋅

(

Σ

x

i

2

+

Σ

y

i

2

)

K

x’

– sztywność pozioma jednego wibroizolatora

K

x’

= 0,75 · K

z

’ = 0,75

⋅

499,31 = 374,4825

m

kN

K

ψ

= 374,4825

⋅

(46,88 + 10,12) = 21345,5025kNm

5.Określenie częstotliwości drgań własnych układu
5.1. Prędkości kątowe drgań własnych-scentrowanego bloku fundamentowego opartego na
sprężystym podłożu gruntowym wyznacza się w [rad/s] wg wzorów:

•

Prędkość kątowa drgań własnych pionowych:



z

=





K

z

M

=





6990,38
67,75

=10,16

rad
s

9

•

Prędkość kątowa drgań własnych skrętnych:





=





K





Z0

=





21345,2025
211,4403

=10,047

rad
s

•

Prędkości kątowe drgań własnych w płaszczyźnie podłużnej:

(

)









µ

⋅

µ

+

λ

−

λ

±

λ

+

λ

=

λ

b

a

2

2

xz

2

x

2

xz

2

x

2

2

,

1

4

2

1



x

2

=

K

x

M

=

5242,785
67,75

=77,38



xz

2

=

K



xz

s

z

2K

∗K

x





Y0

=

23407,651,0926

2

∗5242,785

211,4063

=140,356

- prędkości kątowe drgań podukładów
s – odległość między środkiem ciężkości i środkiem sztywności układu

10



a

=

sK

x

M

=

1,0926

∗5242,785

67,75

=84,55

kN
Mg



b

=

sK

x



Y0

=

1,0926

∗5242,785

211,4063

=27,096

kN
Mg



1

2

=

1
2

[

x

2



xz

2







x

2

−

xz

2



2

4

a



b

]



1

2

=

1
2

[77,38140,356



77,38−140,356

2

4∗84,55∗27,096]=174,243

rad
s



2

2

=

1
2

[

x

2



xz

2







x

2

−

xz

2



2

4

a



b

]



2

2

=

1
2

[77,38140,356−



77,38−140,356

2

4∗84,55∗27,096]=43,4925

rad

s

11

•

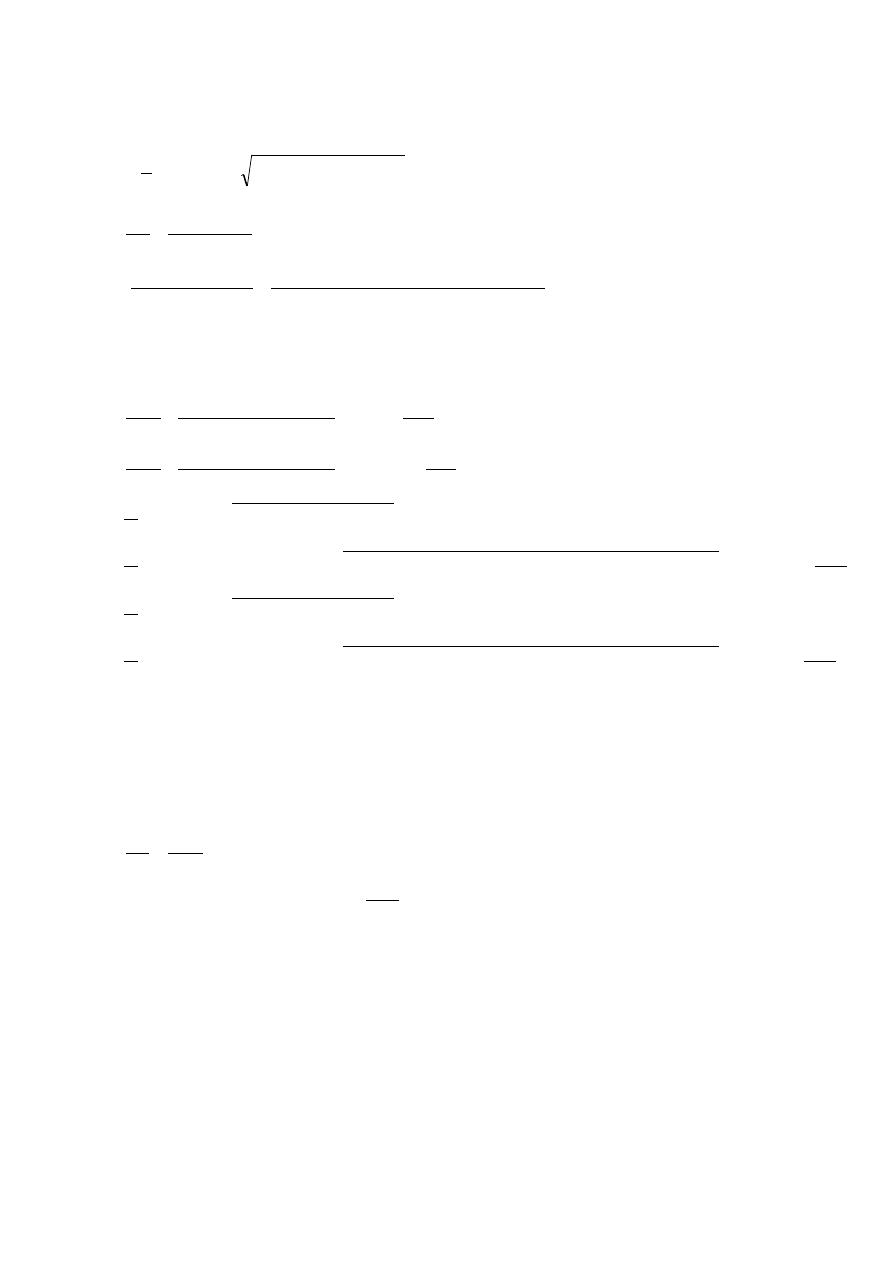
Prędkości kątowe drgań własnych w płaszczyźnie poprzecznej:

(

)









µ

⋅

µ

+

λ

−

λ

±

λ

+

λ

=

λ

b

a

2

2

yz

2

y

2

yz

2

y

2

4

,

3

4

2

1



x

2

=

K

x

M

=

5242,785
67,75

=77,3842



xz

2

=

K



xz

s

z

2K

∗K

x





X0

=

23407,651,0926

2

∗5242,785

60,6298

=489,3032

- prędkości kątowe drgań podukładów
s – odległość między środkiem ciężkości i środkiem sztywności układu



a

=

sK

y

M

=

1,0926

∗5242,785

67,75

=84,55

kN

Mg



b

=

sK

y



X0

=

1,0926

∗5242,785

60,6298

=94,4794

kN
Mg



3

2

=

1
2

[

x

2



xz

2







x

2

−

xz

2



2

4

a



b

]



3

2

=

1
2

[77,3842489,3032



77,3842−489,3032

2

4∗84,55∗94,4794]=507,859

rad
s



2

2

=

1
2

[

x

2



xz

2







x

2

−

xz

2



2

4

a



b

]



2

2

=

1
2

[77,3842489,3032−



77,3842−489,3032

2

4∗84,55∗94,4794]=58,827

rad

s

6.Wyznaczenie amplitud drgań.
n

m

- prędkość obrotowa maszyny, n

m

= 500 obr/min

f

m

– częstotliwość drgań własnych

f

m

=

n

m

60

=

500
60

=8,33Hz

=2 f

m

=2∗3,14∗8,33=52,32

rad
s

Wyznaczanie sił wzbudzających:

P

d

=0,1G

w

- dla maszyn o prędkości obrotowej do 500 obr/min
Silnik:

G

ws

=0,5G

s

G

s

=6,5Mg=63,765kN

G

ws

=0,5∗6,5Mg=31,8825 kN

Pds

=0,10∗0,5∗6,5=3,18825 kN

12

Wentylator:

G

ws

=0,5G

s

G

s

=5,0Mg=49,05 kN

G

ws

=0,5∗5,0Mg=24,525kN

Pds

=0,10∗0,5∗5,0=2,4525kN

Wyznaczenie amplitud drgań:
Schemat I

x

s

= 0,826 m

x

w

= 1,079 m

P

z max

= P

ds

+ P

dw

= 3,188 + 2,453 = 5,641 kN

M

y0

= P

ds

· x

s

- P

dw

· x

w

= 3,188 · 0,826 – 2,453 · 1,079 = -0,013 kNm

Schemat II

x

s

= 0,826 m

x

w

= 1,079 m

P

z

= P

ds

- P

dw

= 3,188 – 2,453 = -0,735 kN

M

y0 max

= P

ds

· x

s

+ P

dw

· x

w

= 3,188 · 0,826 +2,453 · 1,079 = 5,28 kNm

•

Schemat III

x

s

= 0,826 m

x

w

= 1,079 m

z

s

= 1,162 m

P

y

= P

ds

- P

dw

= 3,188 – 2,453 = -0,735 kN

M

x0

= (P

ds

- P

dw

) · z

s

= (3,188 – 2,453) · 1,162 = 0,854 kNm

M

z0

= P

ds

· x

s

+ P

dw

· x

w

= 3,188 · 0,826 +2,453 · 1,079 = 5,28 kNm

•

Schemat IV:

x

s

= 0,826 m

x

w

= 1,079 m

z

s

= 1,162 m

P

y

= P

ds

+ P

dw

= 3,188 + 2,453 = 5,641 kN

M

x0

= (P

ds

+ P

dw

) · z

s

= (3,188 + 2,453) · 1,162 = 6,555 kNm

M

z0

= P

ds

· x

s

- P

dw

· x

w

= 3,188 · 0,826 – 2,453 · 1,079 = -0,013 kNm

13

Wyznaczenie cząstkowych drgań wymuszonych wibroizolowanego układu, bez uwzględnienia
tłumienia, gdy środki ciężkości układu i sztywności wibroizolatorów nie znajdują się w jednym
punkcie:
Założono, że wszystkie obciążenia działają z funkcją sinus:

Amplitudy cząstkowe obrotowe względem osi:

•

Składowe sinusowe:

rad

,

s

K

'

P

B

'

M

'

x

x

y

y

0

y

x

0

x

0

ϕ

∆

⋅

⋅

+

⋅

=

ϕ

rad

,

s

K

'

P

B

'

M

'

y

y

x

x

0

x

y

0

y

0

ϕ

∆

⋅

⋅

+

⋅

=

ϕ

rad

,

)

1

(

K

'

M

'

2

z

z

0

z

0

ϕ

Ψ

η

−

⋅

=

ϕ

K

ϕ

xz

= 499,31

⋅

46,88 = 23407,65kNm

K

ϕ

yz

= 499,31

⋅

10,12 = 5053,02kNm

14

K

ψ

= 374,4825

⋅

(46,88 + 10,12) = 21345,5025kNm



x 

=m

0X



 x1

2

−

2



x2

2

−

2





x 

=67,75∗60,6298507,859

2

−52,32

2

58,827

2

−52,32

2

=7,580998 10

11

B

x 

=K

x 

K

y

S

x

2

−

0X



2

B

x 

=23407,655242,785∗1,0926

2

−60,6298∗52,32

2

=−1,36310

5

B

x

=K

x

−m

2

=5242,785−67,75∗52,32

2

=−1,8024210

5



y 

=m 

0y



y1

2

−

2



 y2

2

−

2





y 

=67,75∗211,4063174,243

2

−52,32

2

43,4925

2

−52,32

2

=−2,29476810

11

B

y 

=K

 x

K

x

S

y

2

−

0Y



2

B

y 

=23407,655242,785∗1,0926

2

−211,4063∗52,32

2

=−5,49033510

5

B

y

=K

y

−m 

2

=5242,785−67,75∗52,32

2

=−1,802149 10

5

λ

i

rad/s

n

i

drg/mi

n

f

i

Hz

Λ

z

=10,16

97,07

1,6178

Λ

ψ

=10,047

95,99

1,5998

60

n

f

i

i

=

π

λ⋅

=

i

i

30

n

•

Schemat I:



0y

=

M

0y

B

x





 y 

=

−0,013∗−180242
−2,294768∗10

11



=−1,021081∗10

−8

rad



z

=




z

=

52,32
10,16

=5,149

a

0z

=

P

0z



K

z

1−

z

2



=

5,641

6990,381−5,149

2



=−0,3163∗10

−4

m

•

Schemat II:



0y

=

M

0y

B

x





 y 

=

5,28∗−180242
−2,294768∗10

11



=−4,147163∗10

−6

rad



z

=




z

=

52,32
10,16

=5,149

a

0z

=

P

0z



K

z

1−

z

2



=−

0,735

6990,381−5,149

2



=0,4121∗10

−5

m

15

•

Schemat III:



0x

=

M

0x

B

y

P

0Y

K

y

s

x





 x

=

0,854∗−180214−0,735∗5242,785∗1,0926
7,580998∗10

11





0x

=−2,085649∗10

−7

rad

a

0y

=

 p

0y

B

y

M

0X

K

y

s

x





x 

=−

0,735

∗−1802140,854∗5242,785∗1,0926

7,580998∗10

11



a

0y

=1,811759∗10

−7

rad



z

=




z

=

52,32
10,16

=5,149



0z

=

M

0z



K

z

1−

z

2



=

5,28
6990,381−5,149

2



=−2,960637∗10

−5

m

•

Schemat IV:



0x

=

M

0x

B

y

P

0Y

K

y

s

x





 x

=

6,555∗−1802145,641∗5242,785∗1,0926
7,580998∗10

11





0x

=−1,515618∗10

−6

rad

a

0y

=

 p

0y

B

y

M

0X

K

y

s

x





x 

=

5,641

∗−1802146,555∗5242,785∗1,0926

7,580998∗10

11



a

0y

=−1,291437∗10

−6

rad



z

=




z

=

52,32
10,16

=5,149



0z

=

M

0z



K

z

1−

z

2



=−

0,013

6990,381−5,149

2



=7,289448∗10

−8

m

Wyznaczenie amplitud przesunięć dowolnego punktu i układu o współrzędnych x

0i

, y

0i

, z

0i

przy działaniu składowej sinusowej:

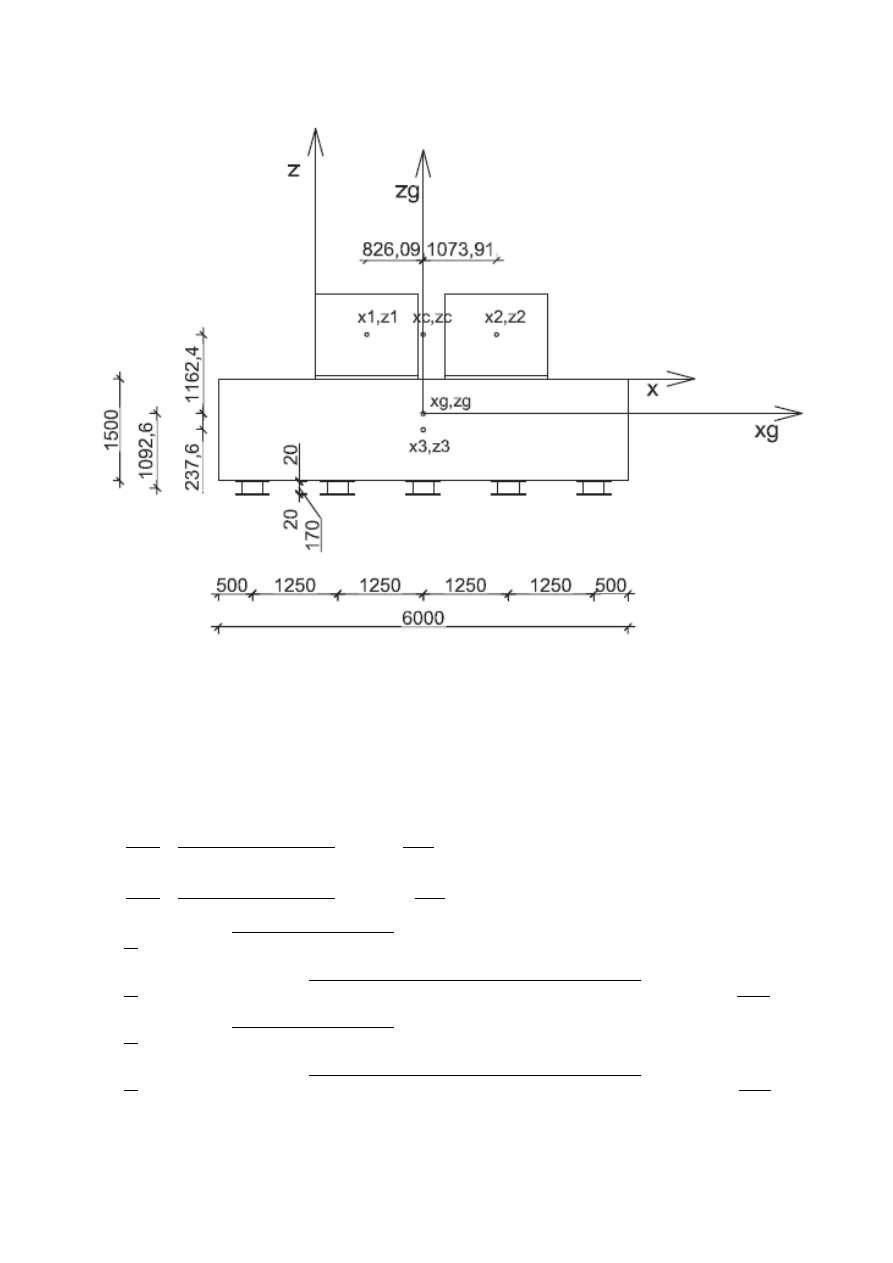
Współrzędne punktów skrajnych układu wibroizolowanego:
x

0i

= ±3000mm

y

0i

= ±1250mm

z

0i

= +512,4mm

z

0i

= -987,6mm

a

xi

=a

0x



oy

Z

oy

−

0z

y

0i

a

xi

=−2,085649∗10

−7

−4,147163∗10

−6

∗0,5124

−−2,96063710∗10

−5

∗−1,25=−0,3934∗10

−4

a

xi

=39,34 m

16

a

yi

=a

0y



oz

X

oi

−

0x

Z

0i

a

yi

=−1,291437∗10

−6

−2,960637∗10

−5

∗3,00

−−2,085649∗10

−7

∗−0,9876=−0,9032∗10

−4

a

yi

=90,32 m

a

zi

=a

0z



ox

Y

oi

−

0y

X

0i

a

zi

=−0,3163∗10

−4

−2,085649∗10

−7

∗1,25

−−4,147163∗10

−6

∗−3,00=−0,4433∗10

−4

a

zi

=44,33m

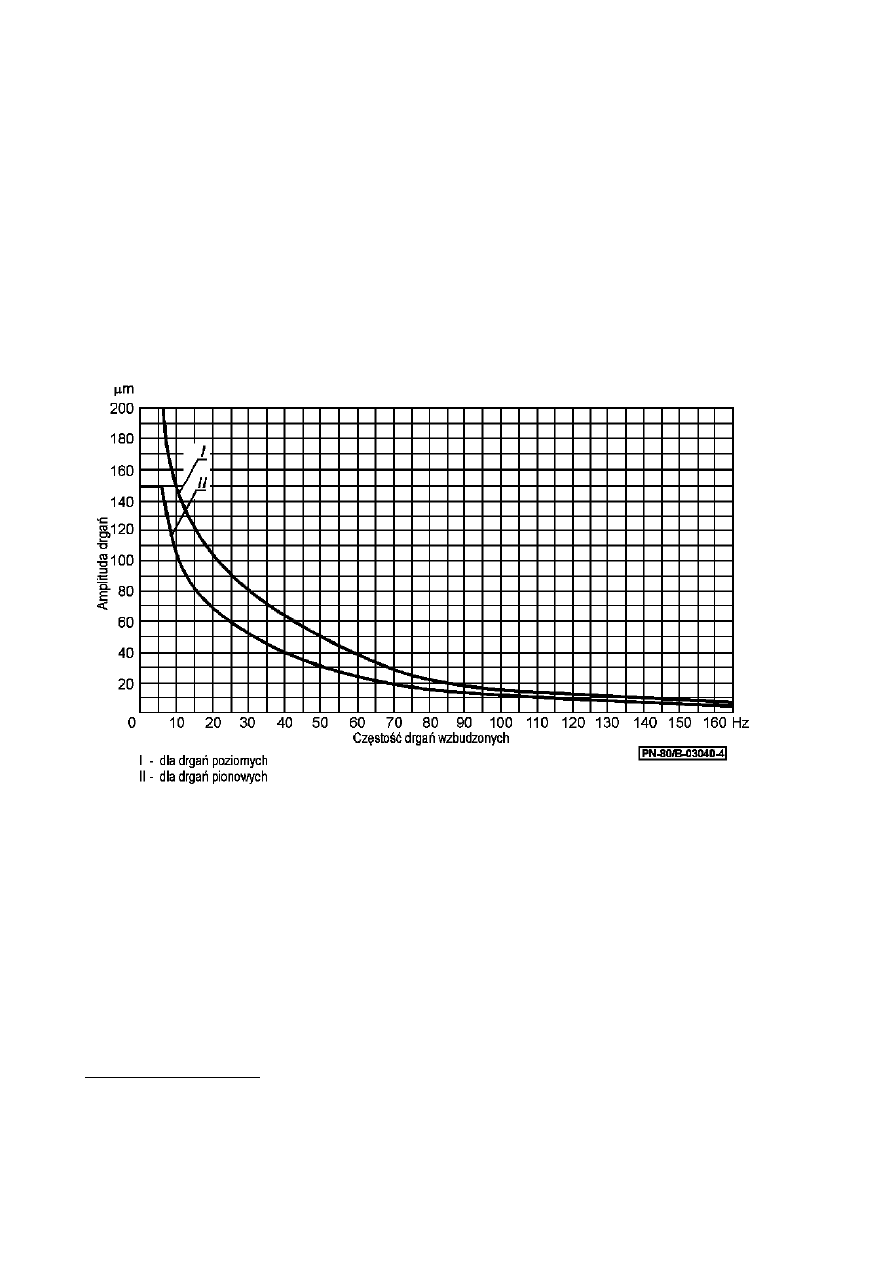
Wartości porównano z wartościami dopuszczalnymi (rys. 4 PN-80/B-03040):

Odczytano dla częstości wzbudzającej 8,33Hz (500obr/min):

•

Dla drgań poziomych:

a

xi

=39,34a

dop

=155 m

a

yi

=90,32a

dop

=155 m

•

Dla drgań pionowych:

a

zi

=44,33a

dop

=108m

Warunki spełnione.

17