Zastosowanie laserów

Kurs inżynierski, IV semestr
Zaliczenie: dwa kolokwia

O zaliczeniu decyduje suma punktów z

obu kolokwiów

Prof.dr hab.inż. Romuald Jóźwicki

Instytut Mikromechaniki i Fotoniki

Pokój 513

Tematyka

Rys historyczny

Właściwości wiązki laserowej

Zasada działania lasera

Przekształcanie wiązki laserowej

Wybrane typy laserów

Tematyka

cd

Zastosowania według właściwości wiązki lasera

Wysoki stopień koherencji (interferometria, holografia,

redefinicja metra i inne)

Mały kąt rozbieżności wiązki (wyznaczanie kierunku,

pomiarowe metody triangulacyjne i inne)

Impulsowa praca lasera (monitorowanie środowiska, pomiar

odległości i inne)

Koncentracja mocy i energii (laserowa obróbka materiałów,

fotolitografia, laserowa mikrosynteza termojądrowa i inne

)

Zastosowanie w medycynie: diagnostyka i terapia zmian

nowotworowych, laserowa chirurgia i wiele innych)

Istota genialności lasera jako źródła

promieniowania

Bezpieczeństwo i higiena pracy z laserem

Polska norma PN-EN 60825-1 z 2005 roku

Tematyka

cd

Uwaga:

Trudności w prezentowaniu zastosowań wymaga elementarnej

wiedzy z różnych dziedzin. Szczególnie kłopotliwe w przypadku

studiów technicznych jest omawianie zastosowania laserów w

medycynie

Literatura

R. Jóźwicki:

Technika laserowa i jej zastosowania

Maszynopis przekazany Oficynie Wydawniczej PW.

Planowany rok wydania

2009

;

R.Jóźwicki:

Podstawy inżynierii fotonicznej

.

Oficyna Wydawnicza PW, 2006, rozdział 11

R. Jóźwicki: Optyka laserów. WNT,

Warszawa 1981;

Wykład:

Technika laserowa

. Kurs magisterski, semestr VIII.

Materiały w Internecie.

Adres: zto.mchtr.pw.edu.pl

;

Inne pozycje podawane podczas wykładu

H. Klejman Lasery - PWN, Warszawa 1979

Nie wszystko będzie jasne

,

chociaż mówimy o zastosowaniu

światła

Filozofia zdobywania wiedzy

Chętnie odpowiadam

na pytania !!!

1. Nie rozumiem, ale piszę o

tym, bo kolokwium

2. Wykonuję projekty, bo tak

mnie nauczono

3.

Końcowy etap po kilku

latach pracy

:

takie to proste

.

Dlaczego tego wcześniej nie

rozumiałem (-am) ?

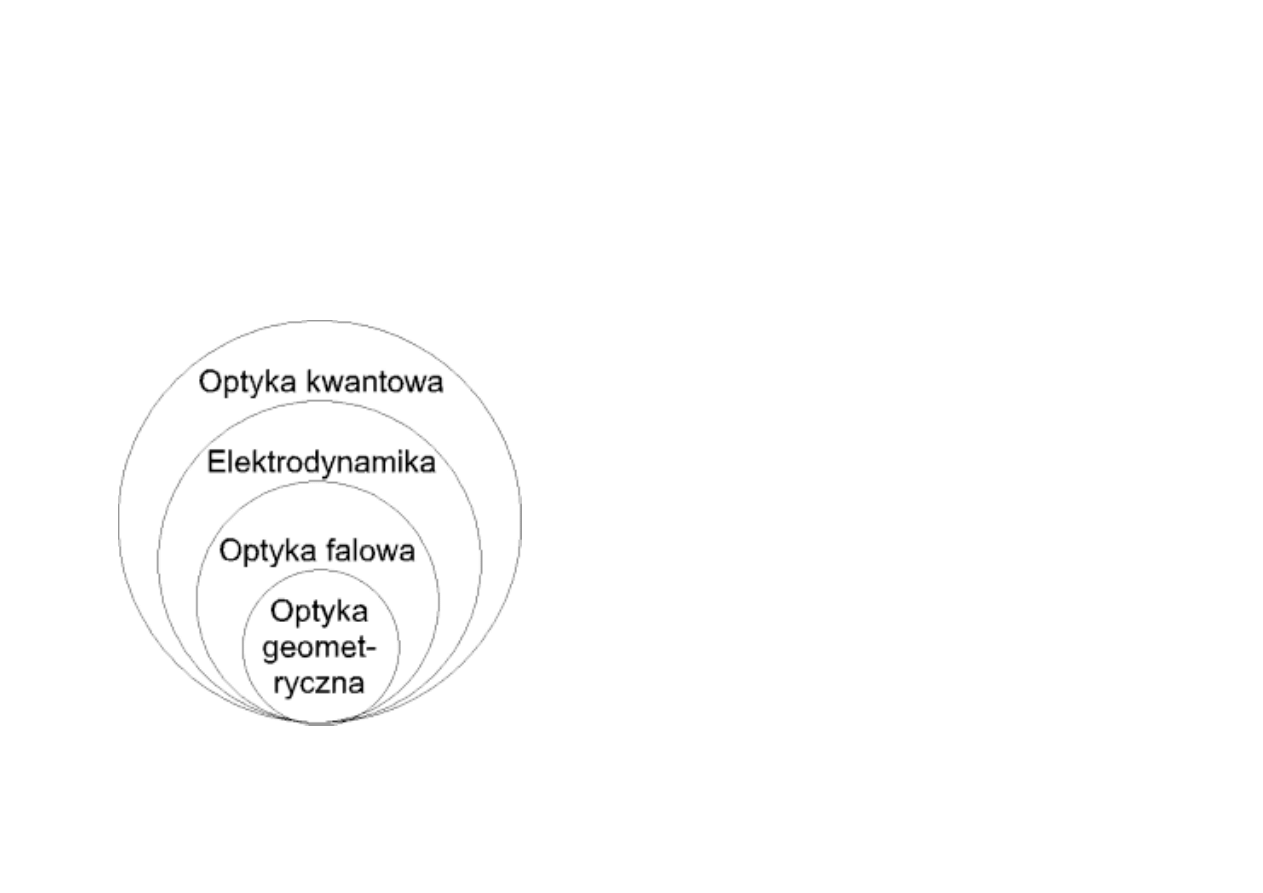
Historyczny rozwój

optyka

→ fotonika

Optyka geometryczna

- promień świetlny

Optyka falowa

- fala nieznanej natury

Elektrodynamika

–

fala ELM

Optyka kwantowa

- kwant

(Max) Planck (1858-1947) wykazał w 1900 roku, że

empiryczna zależność dla

spektralnej emitancji

ciała

doskonale czarnego

1

2

5

1

cz

,

1

T

c

exp

c

M

−

−

⎥

⎦

⎤

⎢

⎣

⎡

−

⎟

⎠

⎞

⎜

⎝

⎛

=

λ

λ

λ

prawo Plancka

może być udowodniona dla skwantowanej struktury energii

c

1

= 37 418.44 Wcm

2

μm

4

i c

2

= 14 387.69

μmK

– stałe promieniowania

T [K] – temperatura

,

λ

[

μm]

–

długość fali

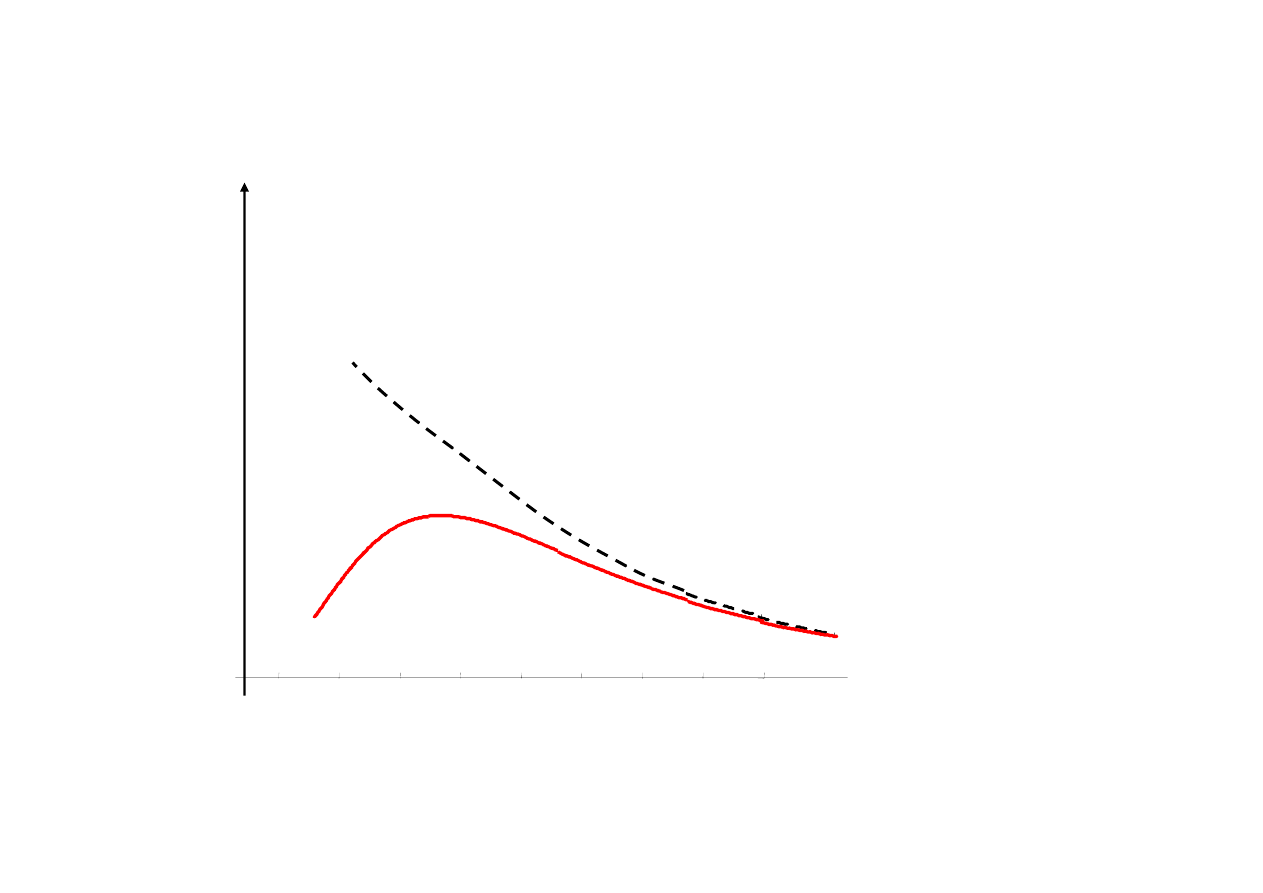
λ

M

λ

Jednostki wzgl

ędne

spektralna emitancja

prawo Jeans’a według klasycznej termodynamiki

promieniowania oscylatorów

rzeczywiste

wyniki

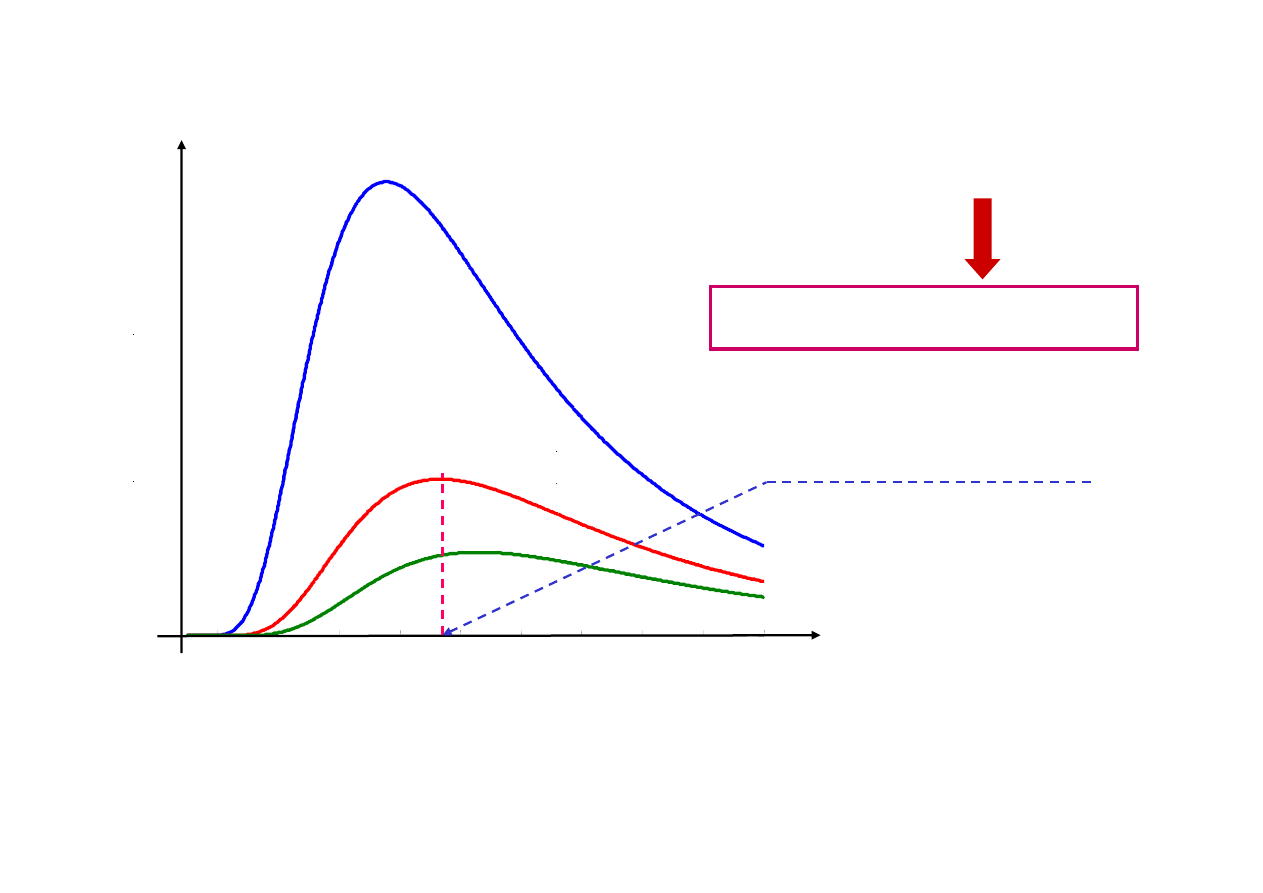
Prawo

(Willy)

Wien’a (1864-1928)

2

6

10

14

18

λ

[

μm

]

M

λ

Jednostki wzgl

ędne

t = 100

0

C

t = 36

0

C

t = 0

0

C

Maksimum spektralnej emitancji dla

λ

max

]

K

m

[

885

.

2897

T

max

⋅

μ

=

λ

Im wyższa temperatura, tym wyższe wartości

M

λ,cz

dla każdego

λ

i tym krótsza długość fali

λ

max

Dla t = 36

0

C T

≈ 309 K

λ

max

≈ 9.6 μm

(Albert)

Einstein

(1879-1955) kwant promieniowania

nazwał

fotonem

Atom (molekuła) jest dipolem absorbującym i

emitującym fotony

Rewolucja w poglądach na budowę atomu

Energia fotonu

ν

= h

E

f

h = 6.62607·10

-34

[Js] -

stała Plancka

ν -

częstotliwość

[Hz = s

-1

]

c = 299 792.4562 ± 0.0011

≈ 300 000 km/s

prędkość światła w próżni

0

c

cT

c

T

1

λ

=

=

=

ν

T [s] - okres

Pasmo optyczne

λ

0

∈ 1nm - 1 mm

ν

∈ 3·10

17

- 3·10

11

Hz

Wysokie wartości częstotliwości !!!

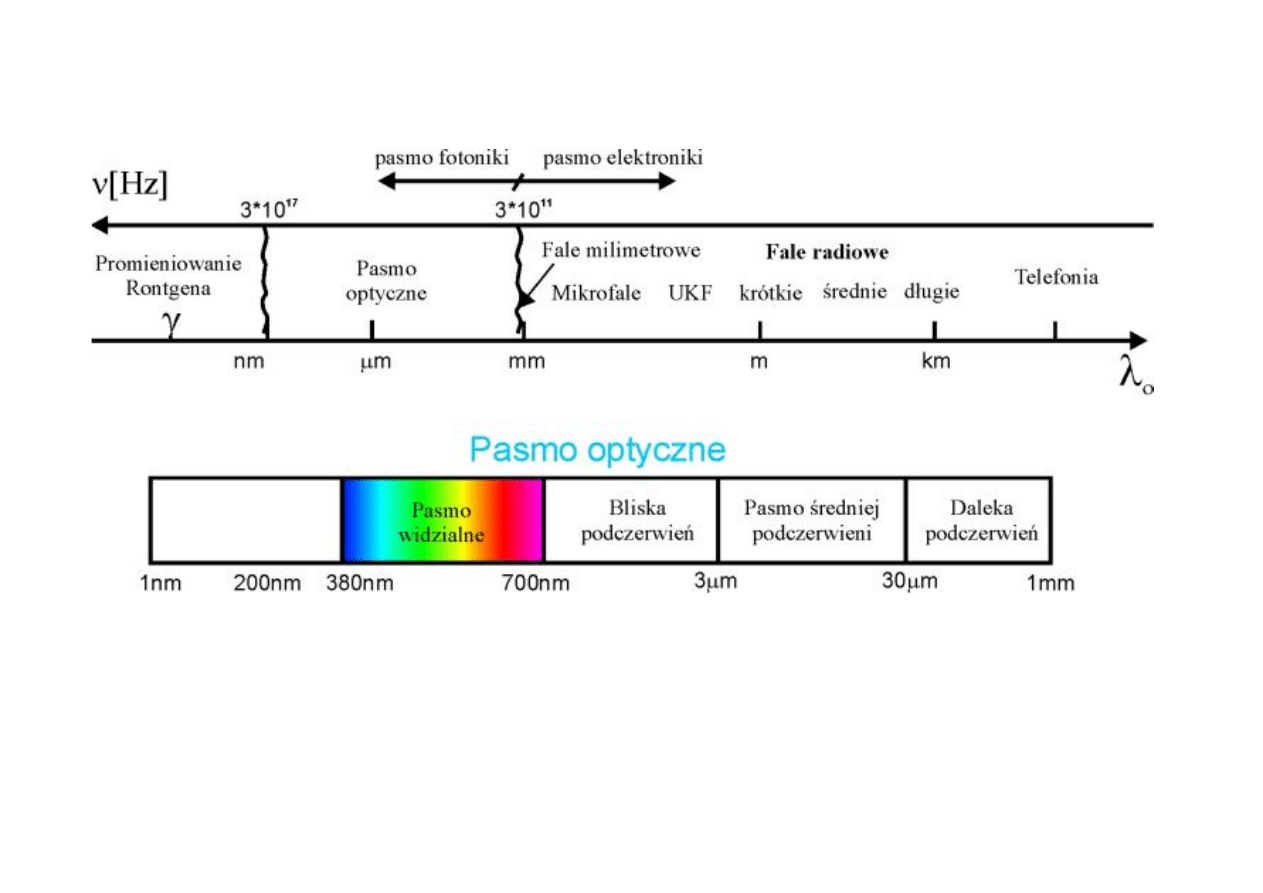
Nadfiolet

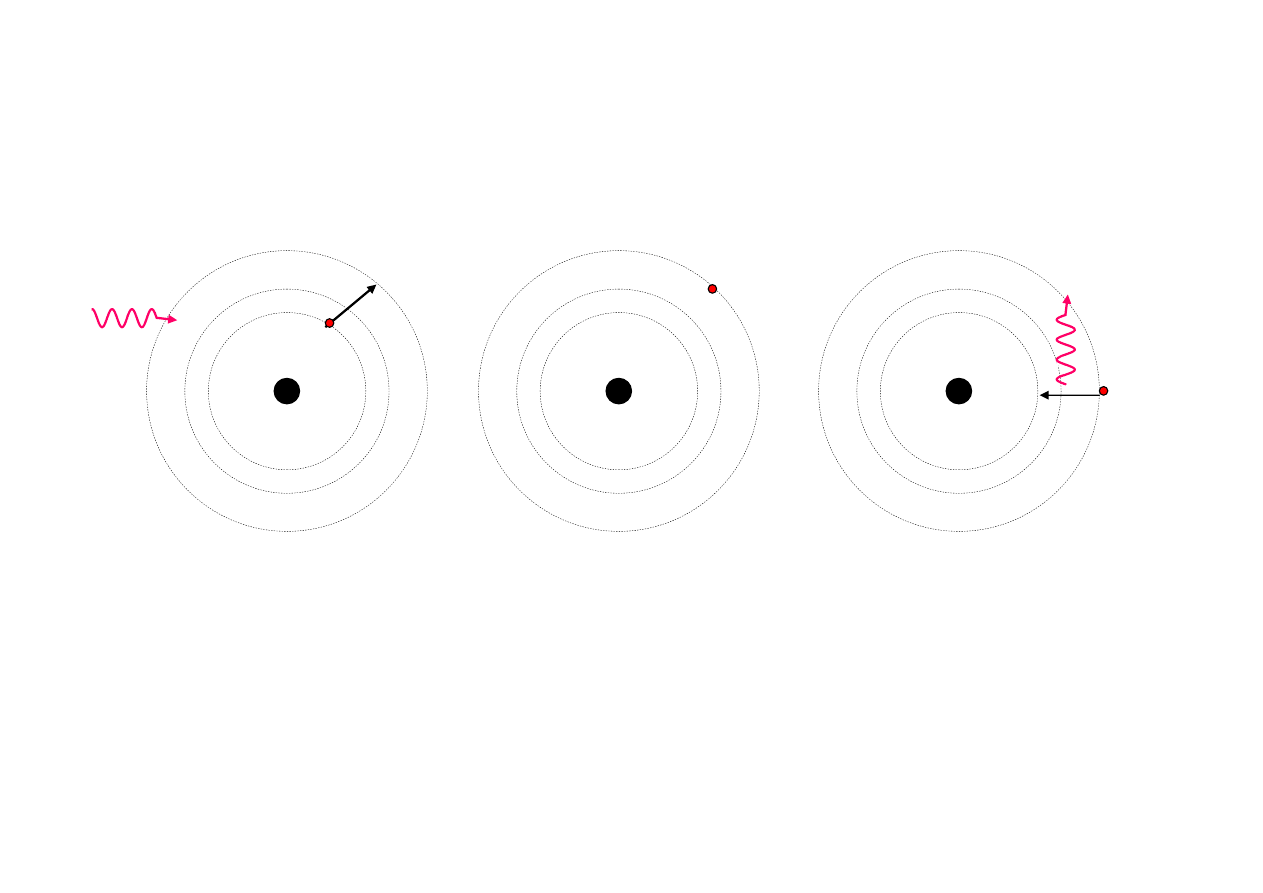
Emisja spontaniczna

absorpcja

kwantu energii

J

e

Atom wodoru Bohra

J

e

J

e

h

ν

h

ν

Przejścia kwantowe w atomie wodoru

Rzeczywiste orbity są eliptyczne

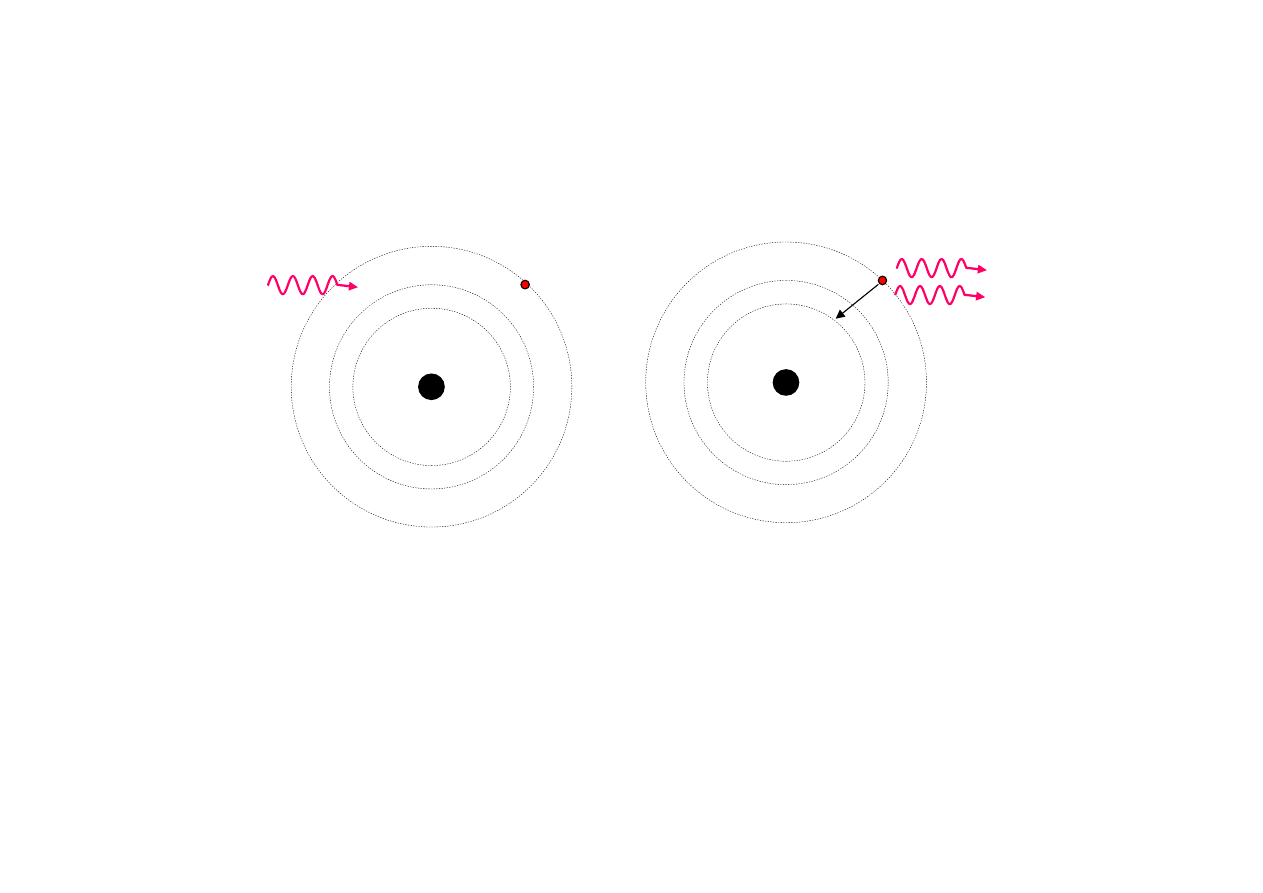
J

e

h

ν

Przejścia kwantowe w atomie wodoru

cd

J

e

Emisja wymuszona

2 h

ν

Obydwa fotony powstałe w drodze emisji wymuszonej są

identyczne

ten sam kierunek propagacji, ta sama częstotliwość,

ta sama faza i stan polaryzacji

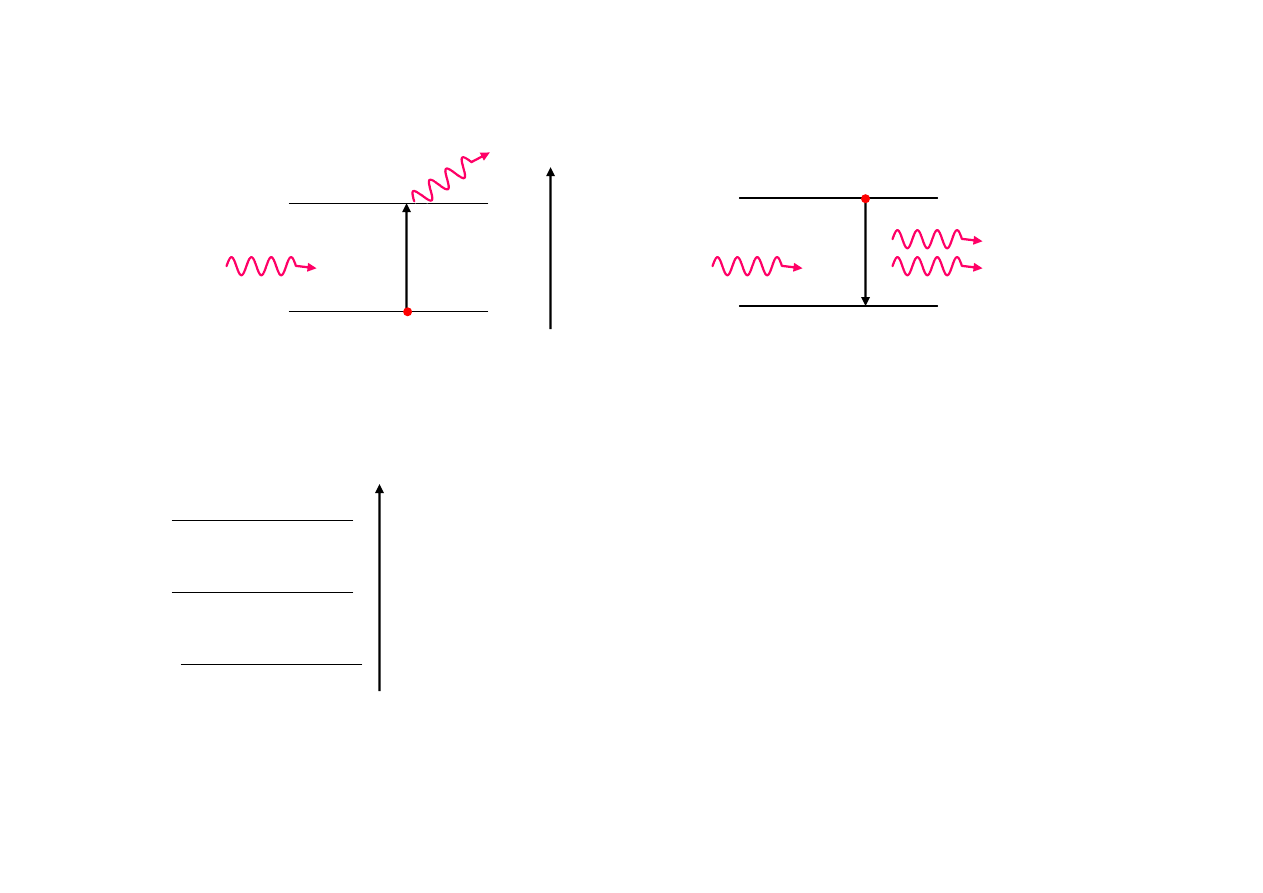
Transmisja i absorpcja fotonów przez ośrodek

• • • •

•

• • • • • • • •

E

Obsadzenie poziomów energetycznych zbioru

atomów

w stanie termodynamicznie ustalonym

Im wyższy poziom energetyczny tym

mniejsze prawdopodobieństwo obsadzenia

Poglądowy rysunek

2

1

h

ν

01

Emisja wymuszona

identyczne

fotony

1

2

h

ν

01

Absorpcja i emisja

spontaniczna

E

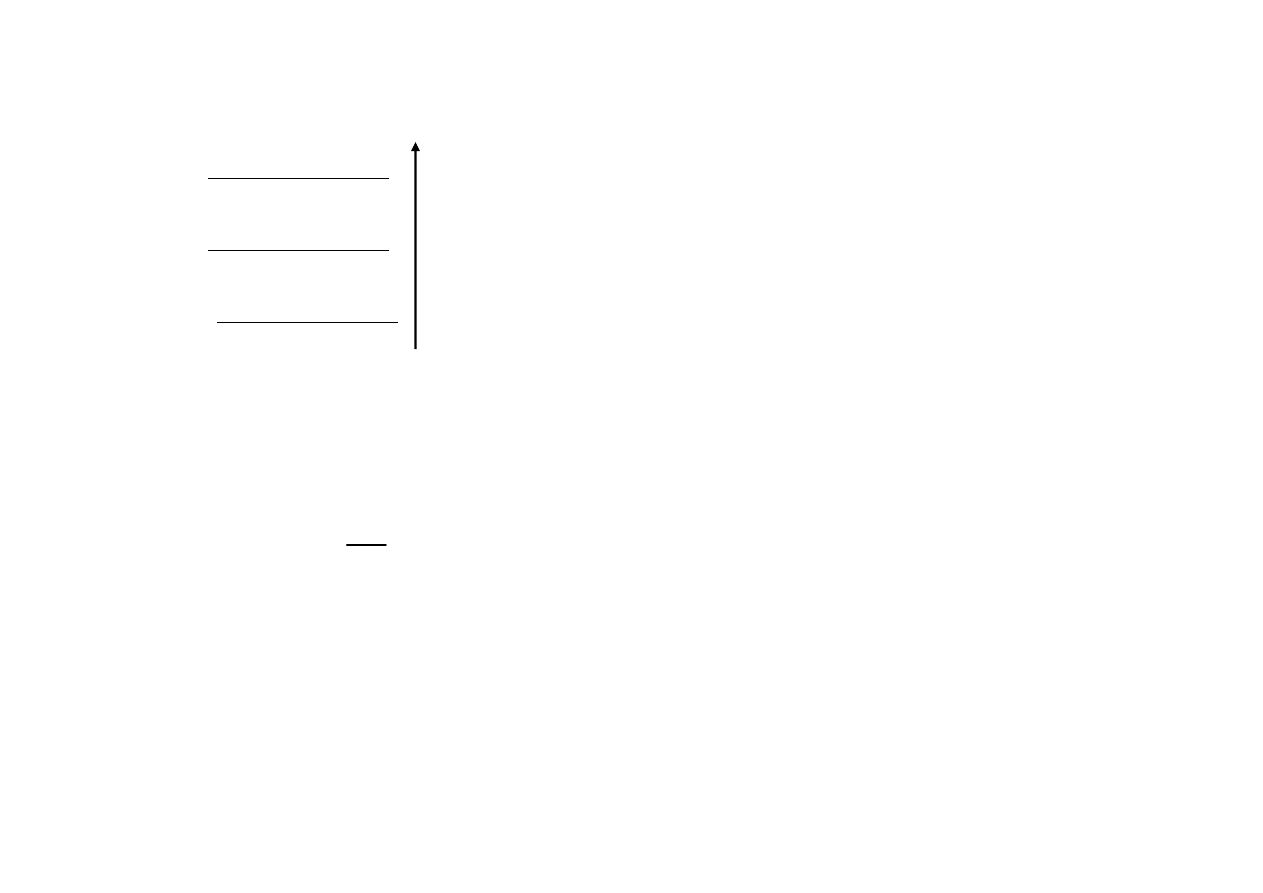
Obsadzenie poziomów

Rozkład

(Ludwig’a)

Boltzmann’a

⎟

⎠

⎞

⎜

⎝

⎛−

∝

kT

E

exp

N

N

i

0

i

∑

=

i

i

0

N

N

E

i

– energia i-tego poziomu

k

– stała Botzmann’a

T

– temperatura [

K

]

• • • •

•

• • • • • • • •

E

N

1

N

3

N

2

N

i

– obsadzenie poziomu

i

Obsadzenie =

liczba atomów

wzbudzonych do poziomu

i

im wyższy poziom energetyczny

tym mniej atomów na tym poziomie

W stanie energetycznie ustalonym

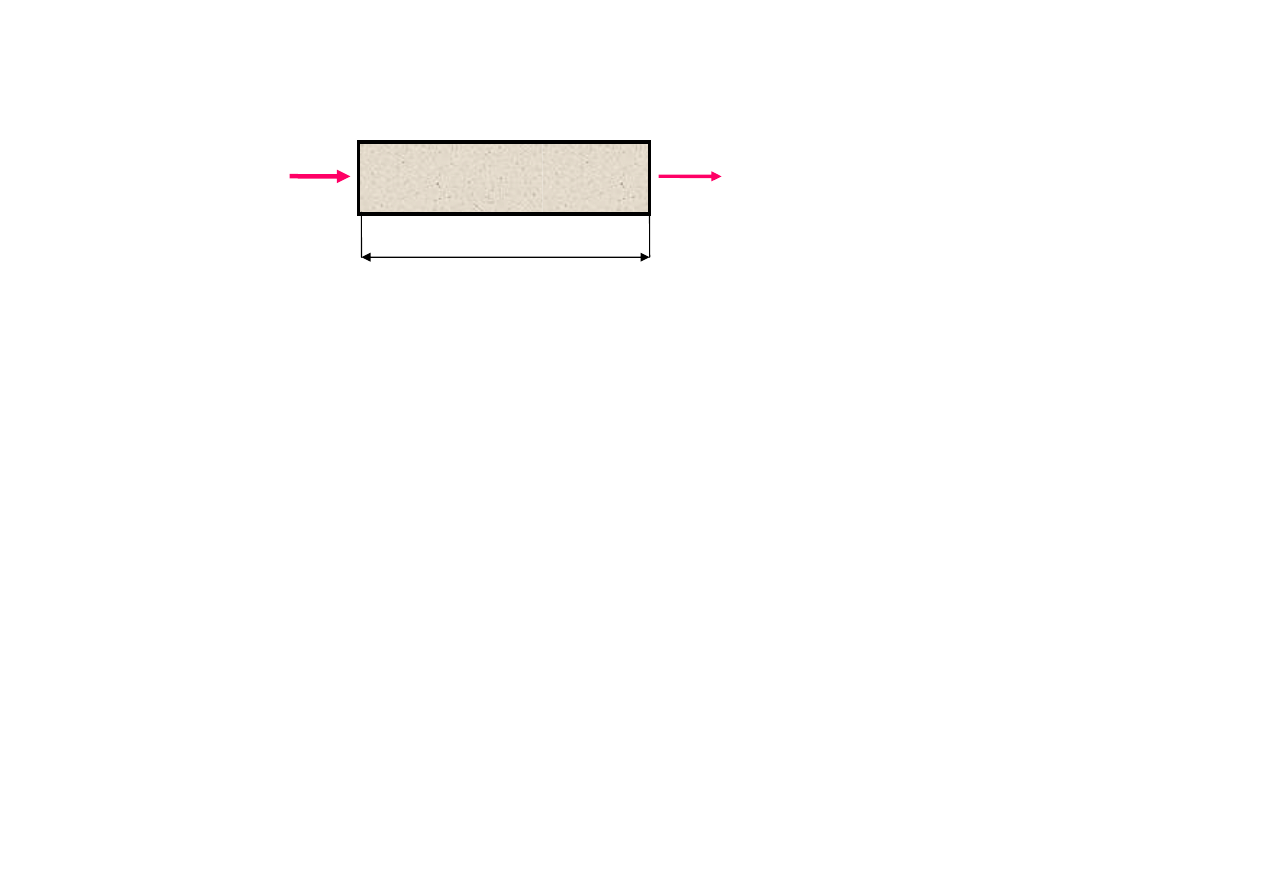
Transmisja fotonów przez ośrodek

0

V

V

>

konieczna inwersja obsadzeń,

kiedy

bardziej prawdopodobna emisja wymuszona niż absorpcja

→

Wzmocnienie

(Alfred)

Kastler (1902-1984) odkrył

zjawisko

pompowania

1966 – nagroda Nobla

(T.H.)

Maiman

1960

pierwszy laser rubinowy

( )

d

exp

V

V

0

α

=

W stanie równowagi termicznej

akty absorpcji

bardziej prawdopodobne

0

V

V

<

0

<

α

→

V

V

0

=

Σhν

d

α

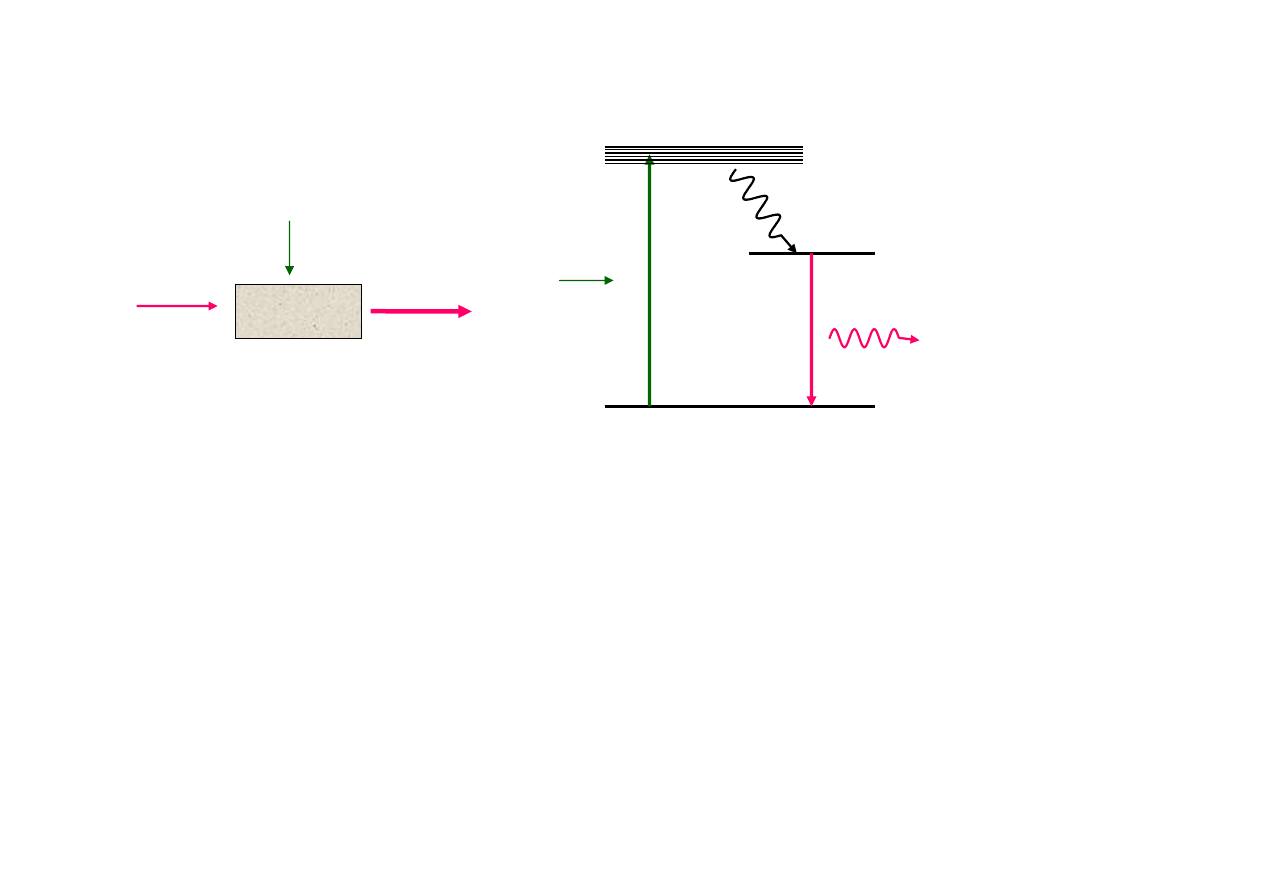
Lasery

pompowanie lasera rubinowego

pompa

h

ν

13

h

ν

12

h

ν

12

rubin

Pompowanie przez

naświetlanie fotonami

ν

13

Wzmocnienie między

poziomami

2

→ 1

Energia

bezpromienistego przejścia

zamienia się na ciepło

niekorzystne zjawisko

Układ poziomów energetycznych

lasera rubinowego -

korund

domieszkowany jonami Cr

3+

pompa

h

ν

13

przejście
bezpromieniste

3

2

1

h

ν

12

poziom
podstawowy

poziom
metastabilny

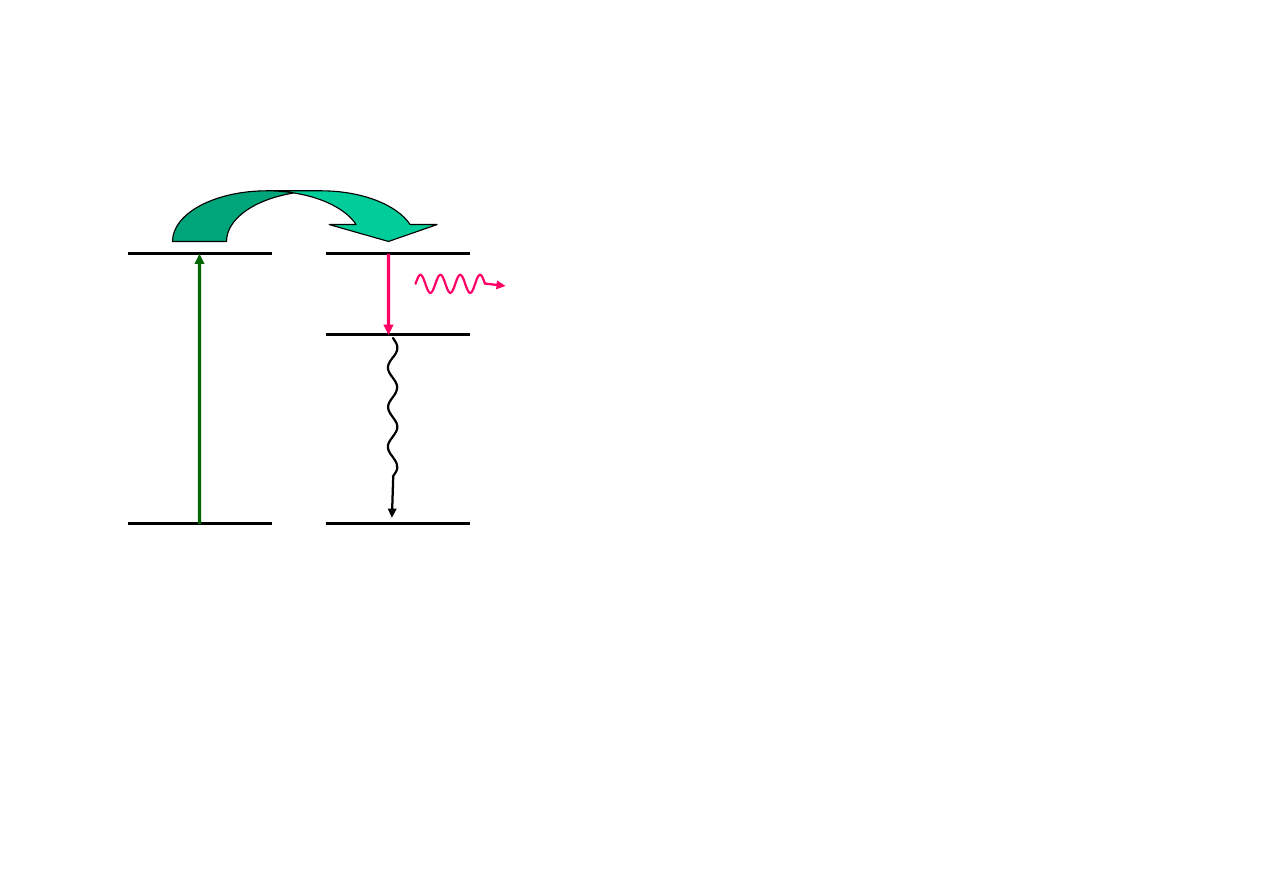
Lasery

pompowanie lasera gazowego na przykładzie lasera

He-Ne

2

He

3

Ne

1

Ne

2

Ne

zderzenie

z elektronami

λ = 0.63 μm

1

He

Hel

Neon

zderzenia ze
ściankami
kapilary

zderzenia atomów

Przepływ prądu w mieszaninie dwóch

gazów

He-Ne

Znacznie więcej atomów

He

niż

Ne

Elektrony zderzają się przede

wszystkim się z

He.

Pompowanie na

He

Hel przekazuje energię do neonu podczas zderzenia

Przejścia laserowe w neonie

Dobór optymalnego prądu. Zbyt duży prąd zaludnia poziom

2

Ne

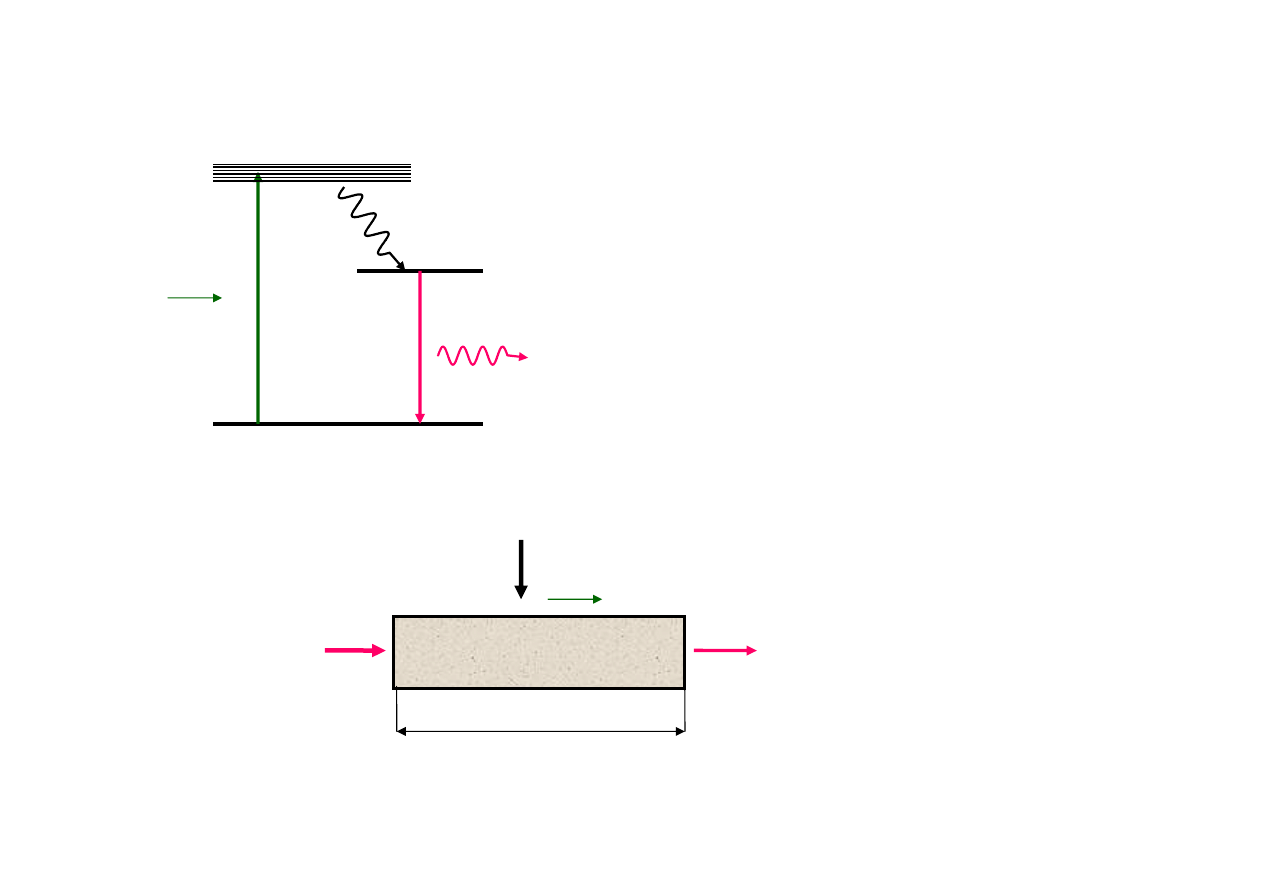
Wzmocnienie promieniowania

pompa

h

ν

13

3

2

1

h

ν

12

poziom
podstawowy

poziom
metastabilny

V

V

0

=

Σhν

12

d

α

pompa

Σ

h

ν

13

( )

d

exp

V

V

0

α

=

0

V

V

>

0

>

α

→

Na przykładzie

lasera rubinowego

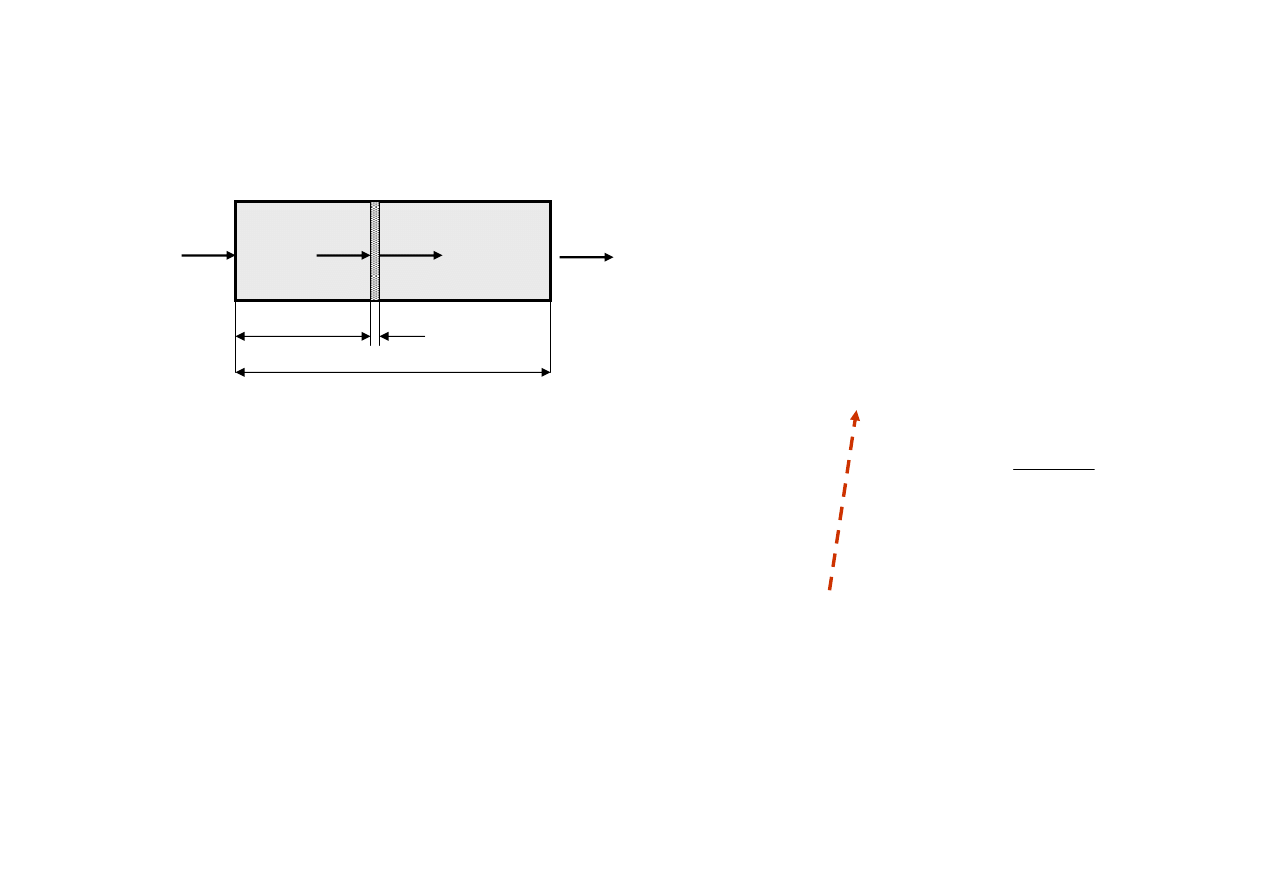
Nasycenie wzmocnienia w

ośrodku wzmacniającym

V

V+dV

x

dx

d

V

0

V

w

Vdx

dV

α

=

Gdy współczynnik wzmocnienia

α

niezależny od sygnału

V

Rozwiązanie równania

różniczkowego dla

warunków brzegowych

( )

d

exp

V

V

0

w

α

=

współczynnik wzmocnienia

α

maleje wraz ze wzrostem sygnału

Przyrost sygnału odbywa się kosztem inwersji obsadzeń

Nasycenie wzmocnienia,

więc

dx

1

V

V

dV

+

α

=

Dla obszaru małego sygnału

(V << 1)

równanie bez nasycenia

Wraz ze wzrostem sygnału maleje przyrost

i w granicy

(V >> 1)

dx

dV

α

=

przyrost liniowy

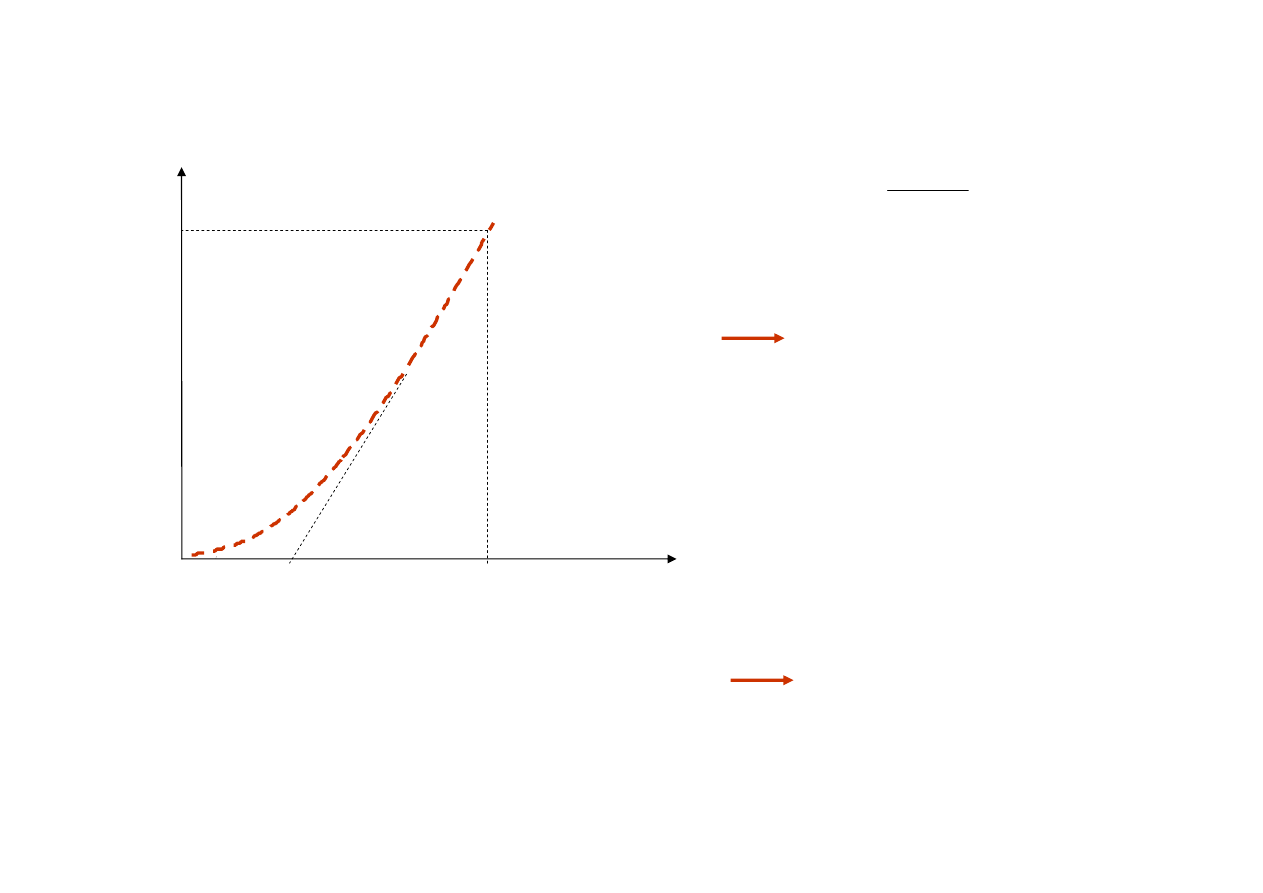
Numeryczne rozwiązanie równania różniczkowego

dx

1

V

V

dV

+

α

=

x

V

0

x

0

V

w

d

dx

dV

α

=

przyrost liniowy dla dużego sygnału

(

)

0

w

x

d

V

−

α

=

Vdx

dV

α

=

( )

d

exp

V

V

0

w

α

=

W obszarze małych

wartości sygnału

brak nasycenia

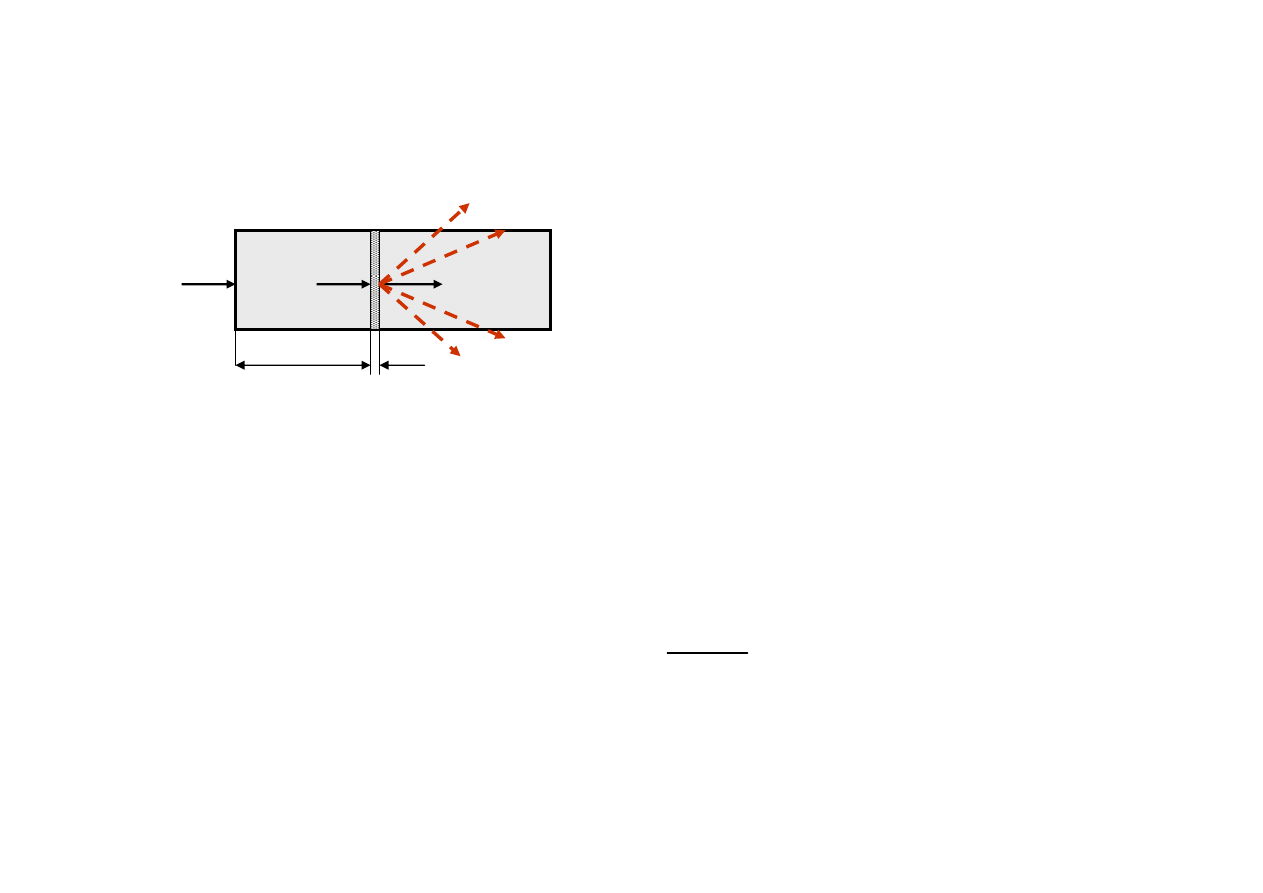
Nasycenie wzmocnienia w ośrodku niejednorodnym

V

V+dV

x

dx

V

0

dV

s

Straty

dV

s

sygnału na skutek

rozproszenia na

niejednorodnościach ośrodka

proporcjonalne do sygnału

Vdx

dV

s

β

−

=

Wartość współczynnika proporcjonalności

β > 0

rośnie wraz ze wzrostem niejednorodności ośrodka

dx

1

V

V

dV

dV

dV

s

⎟

⎠

⎞

⎜

⎝

⎛

β

−

+

α

=

+

=

αβ

Przyrost sygnału uwzględniający wzmocnienie i straty

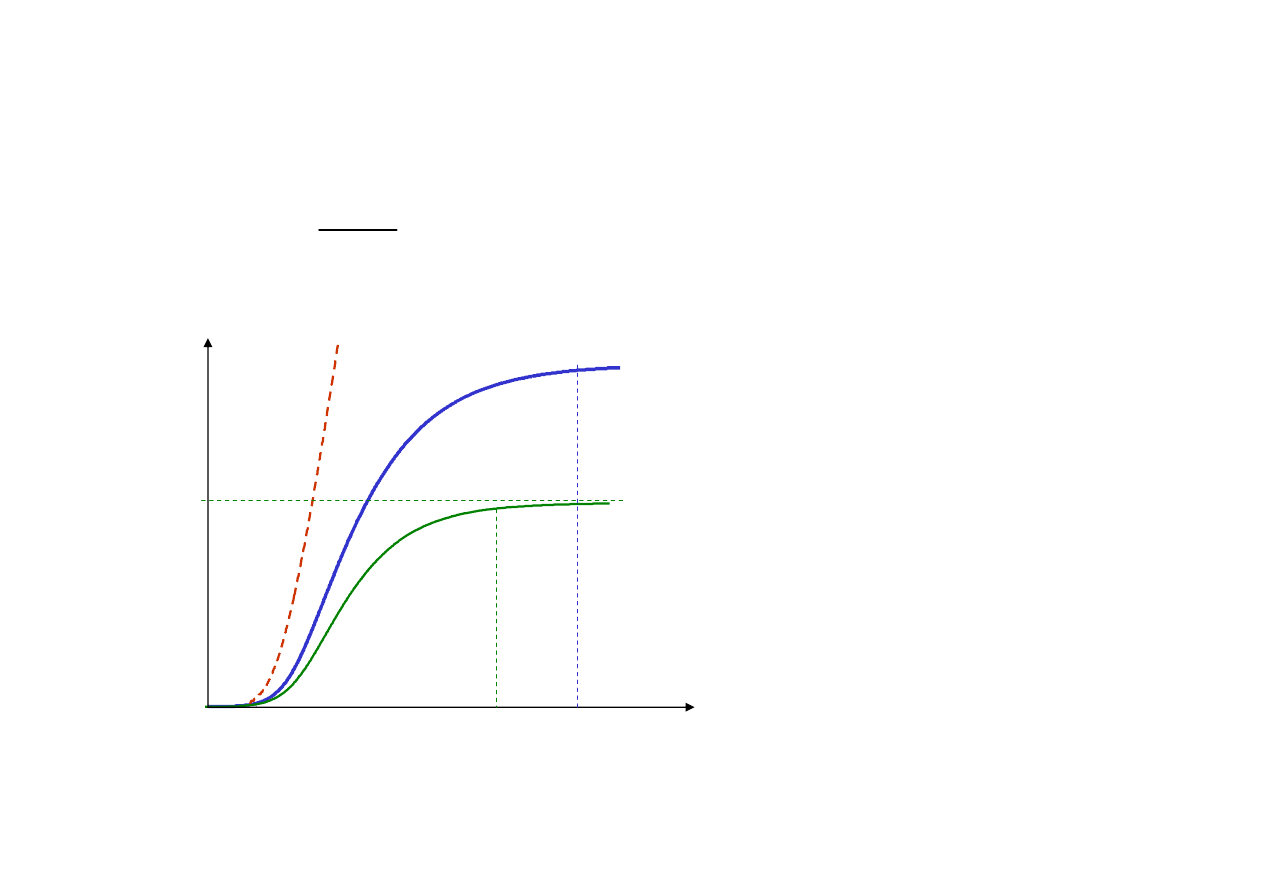
x

V

0

β = 0

β/α = 0.2

β/α = 0.3

x

gr

x

gr

V

n

dx

1

V

V

dV

⎟

⎠

⎞

⎜

⎝

⎛

β

−

+

α

=

Nasycenie wzmocnienia w ośrodku niejednorodnym

Dla każdej wartości współczynnika

strat

β

istnieje graniczna

odległość

x

gr

, po której wartość

sygnału już

nie rośnie

Im większe straty, tym

mniejsza wartość

V

n

i krótsza

odległość

x

g

r

Ośrodki gazowe są wysoce

jednorodne. Można z nich

budować długie ośrodki

wzmacniające

Długość ośrodka na ciele

stałym ograniczona stratami

na niejednorodnościach

ośrodka

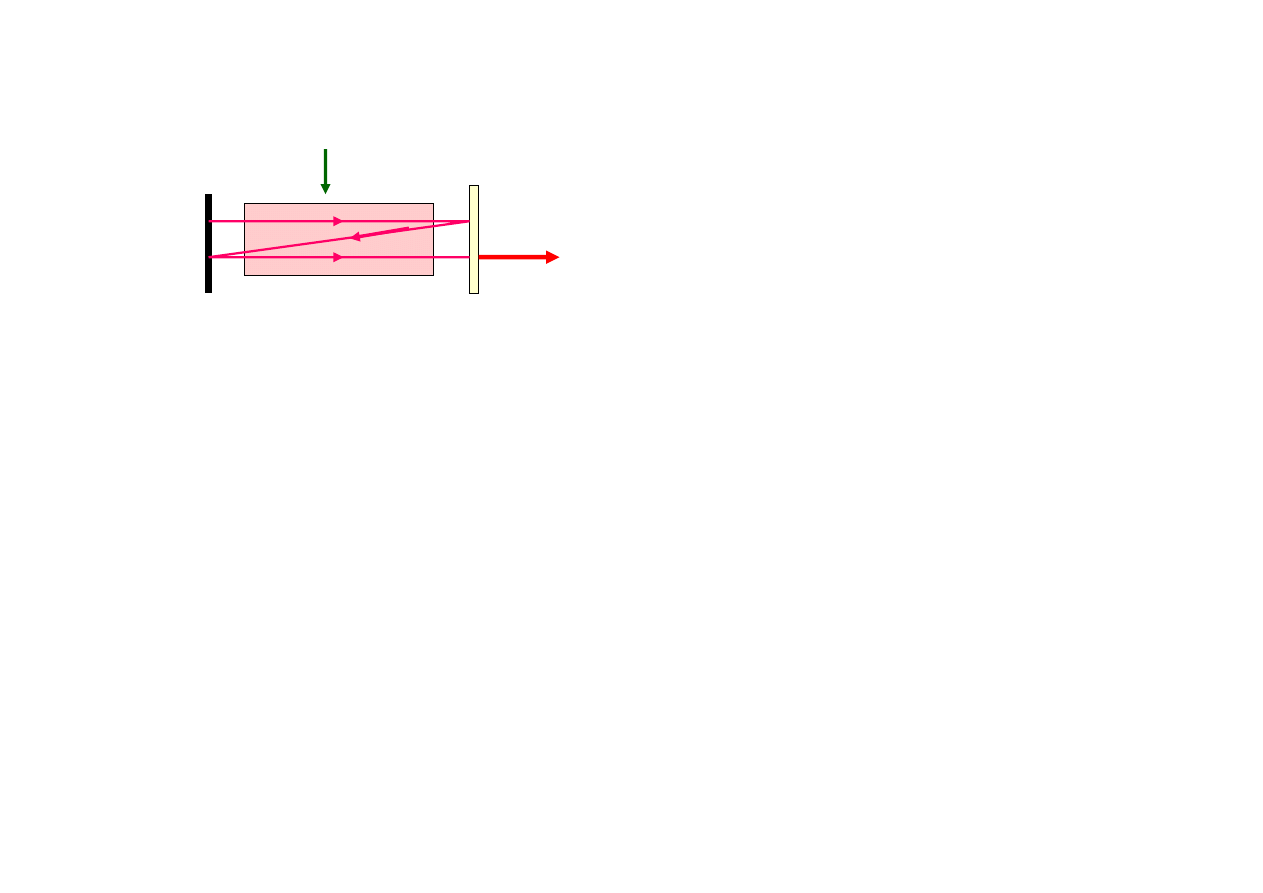
Zasada pracy lasera

Zwierciadła 1 i 2 tworzą

rezonator Fabry-Perot

Strumień fotonów propagując się oscylacyjnie między zwierciadłami

wzmacnia się w napompowanym ośrodku do stanu nasycenia

Przez częściowo przepuszczalne zwierciadło 2 wyprowadzana jest

wiązka użyteczna

λ

las

Zwierciadła rezonatora są sferyczne, aby uniknąć krytycznego warunku

na równoległość zwierciadeł płaskich

Laser jest samowzbudnym generatorem promieniowania

pompa

1

2

λ

las

Praca impulsowa

,

częstotliwość repetycji

do 10 Hz

Duża energia pompowania z powodu trójpoziomowego

układu kwantowego ze środkowym poziomem metastabilnym

Laser historycznie najpierwszy

T.H. Maiman 1960

rubinowy

w korundzie

jony Cr

3+

długość fali

694.3 nm

λ

las

Akronim

L A S E R

jest

mylący

O

pticzeskij

K

wantowyj

G

enierator

OKG

oddaje sens fizyczny lasera

L

ight

A

mplification

by

S

timulated

E

mission of

R

adiation

M

icrowave

A

mplification

by

S

timulated

E

mission of

R

adiation

→

Maser był tylko wzmacniaczem

wywodzi się z masera

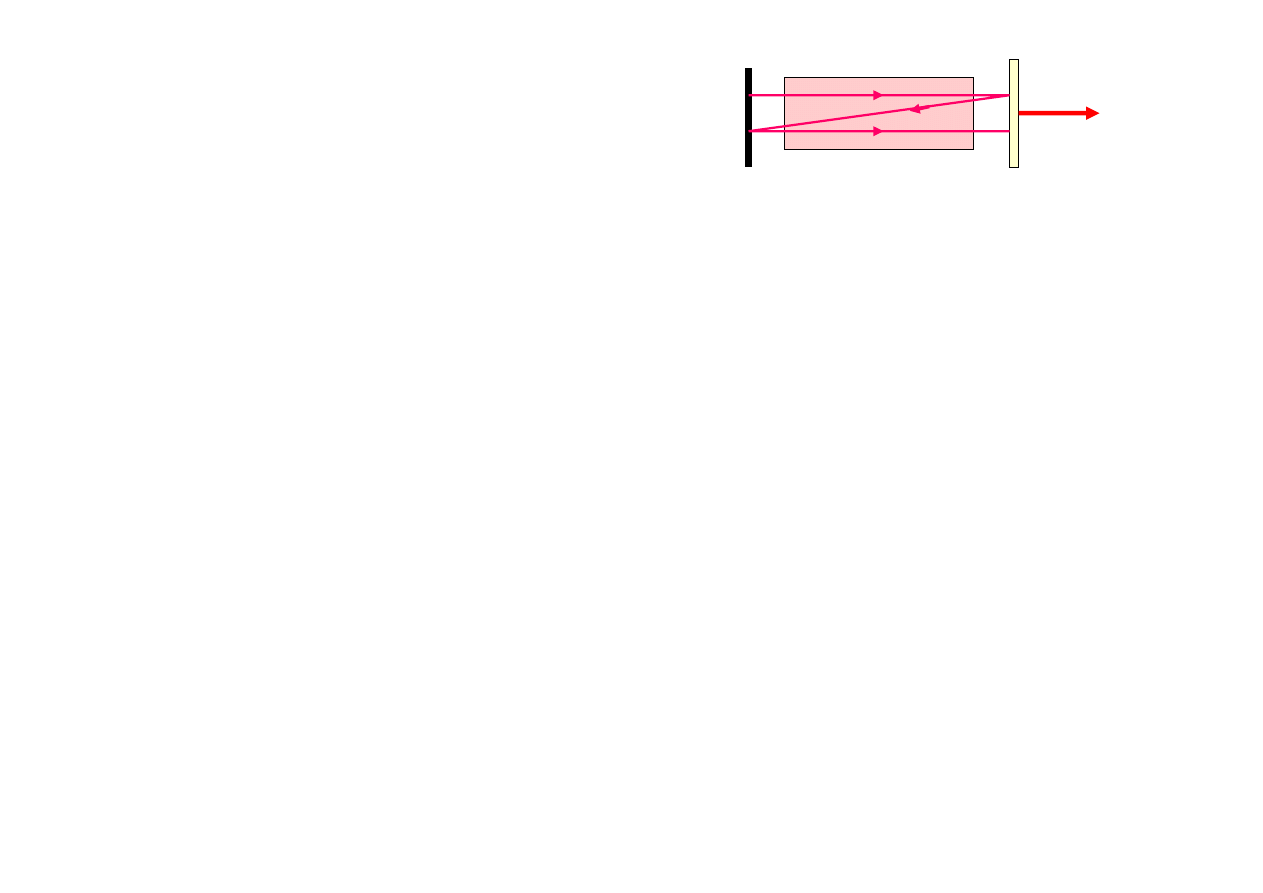
Modowość wiązki laserowej

Rozkłady pola nie spełniające warunku zgodności faz

są tłumione

Konfiguracje pola

spełniające warunek zgodności faz dla

określonej długości fali nazywamy

modami

TEM

– poprzeczne (

T

ransverse

) pole

E

lektryczne i

M

agnetyczne

Oscylacyjna propagacja promieniowania w rezonatorze tworzy zbiór

interferujących wiązek. Ich wzmacnianie jest możliwe tylko przy

pełnej zgodności faz między nimi

λ

las

mody poprzeczne

– rozkłady przestrzenne TEM

mody podłużne

– widmo wiązki dla danego modu poprzecznego

Dla wygody rozróżnia się :

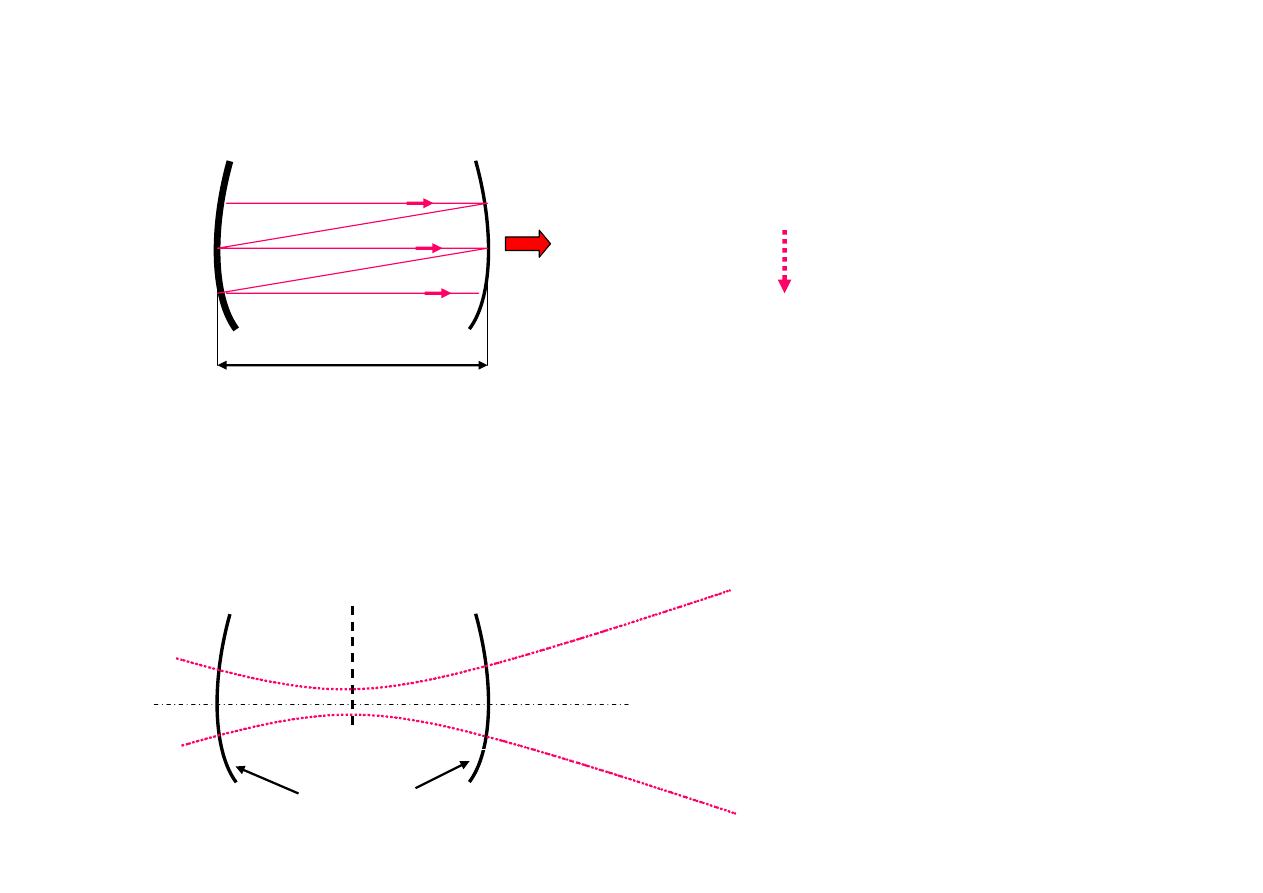
Kształt wiązki laserowej

mody poprzeczne

Różne wartości amplitud na czole fali

– wyniki interferencji

d

1

2

3

Warunek zgodności faz interferujących

wiązek

1, 2, 3

w rezonatorze

czoła fali pokrywają się z

powierzchnią zwierciadeł

TEM

00

wiązka

gaussowska

przewężenie

czoła fali

Poszczególne mody są numerowane

TEM

mn

m, n = 1, 2, 3, .

.

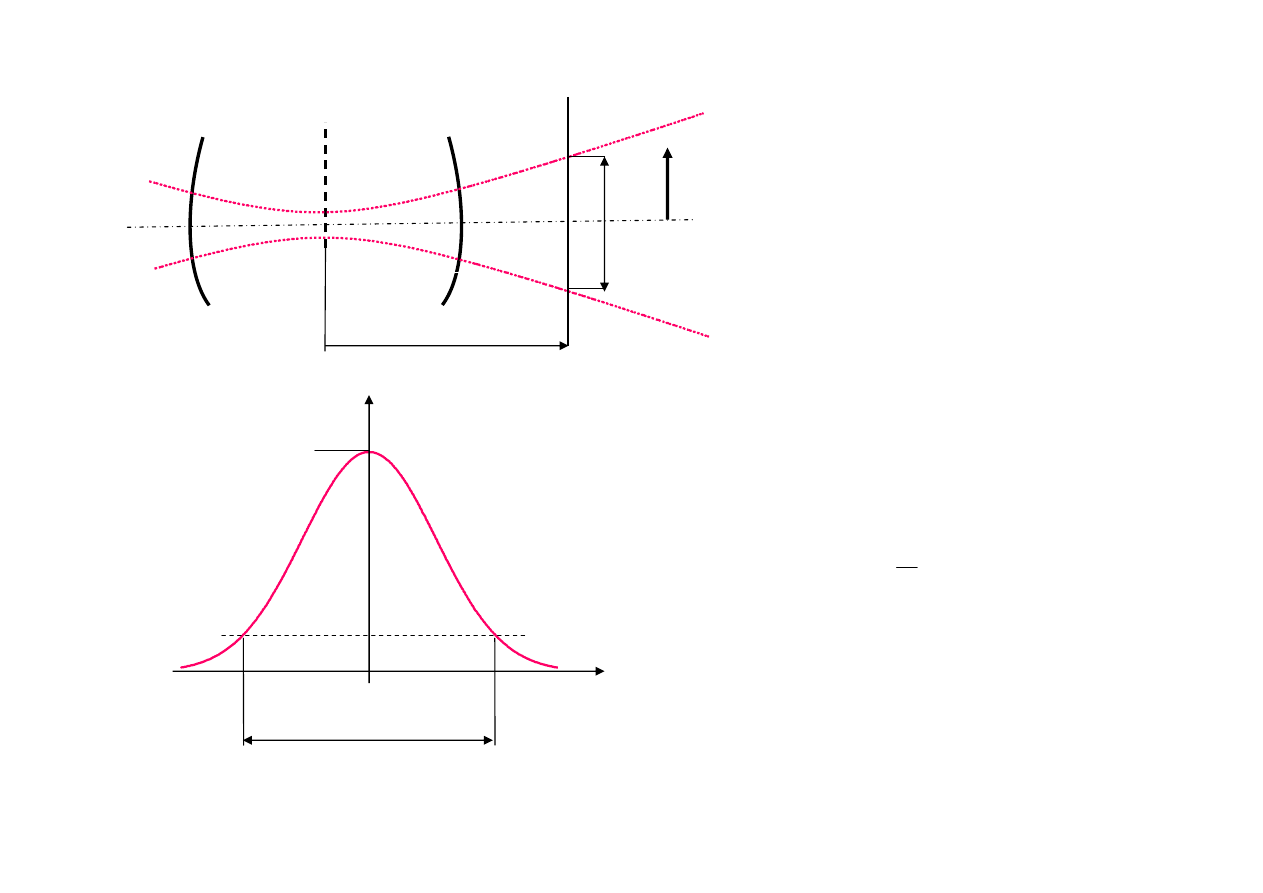
Wiązka gaussowska

2w

- średnica wiązki w

przekroju

π

przewężenie

z

π

2w r

r

0

2w

I

z

I

I

z

/e

2

W każdym przekroju

π

(dla każdego

z

)

gaussowski rozkład intensywności

I

z

– intensywność na osi

( )

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

−

=

2

z

w

r

2

exp

I

z

,

r

I

o obrotowej osi symetrii

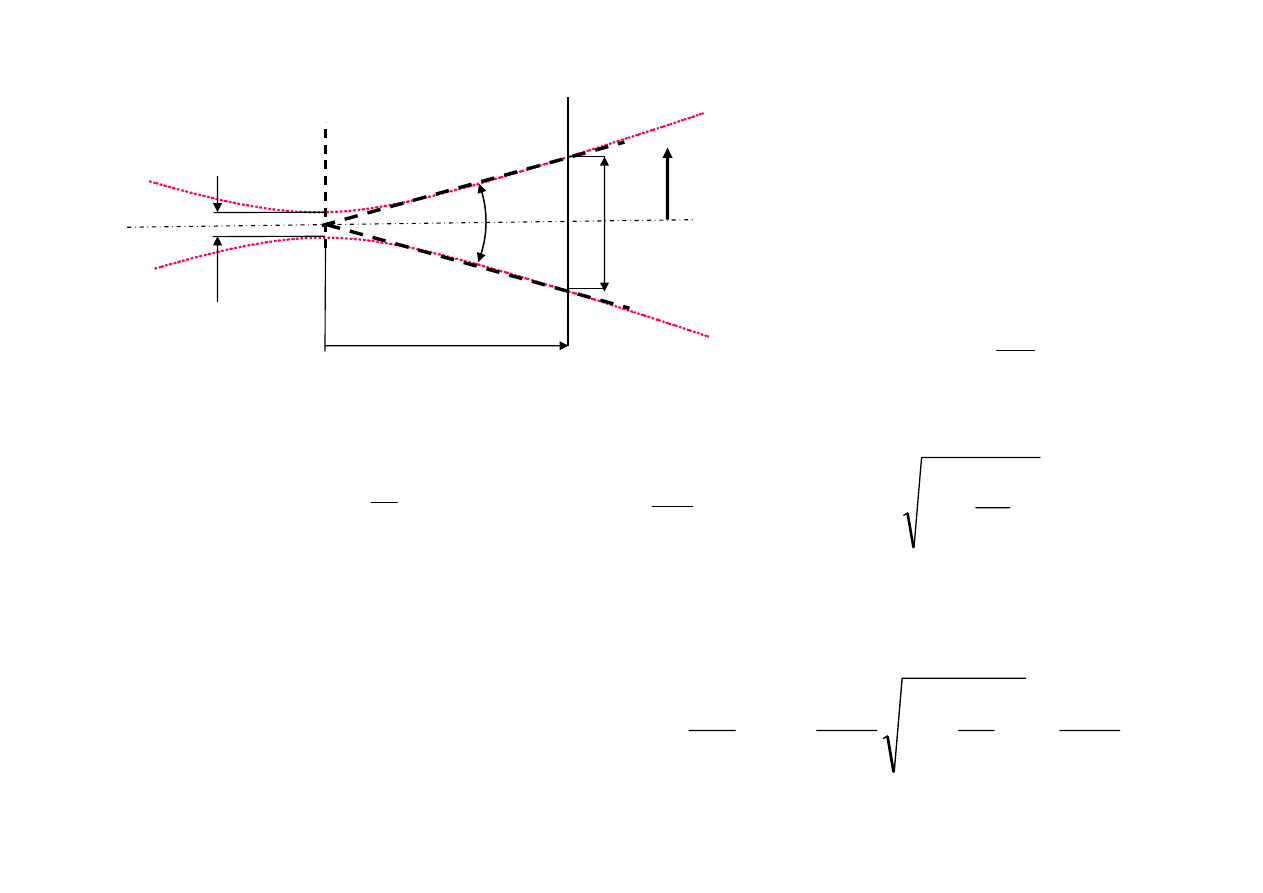
Wiązka gaussowska

przewężenie

z

π

2w r

2

θ

2w

0

2
0

2
0

w

2

kw

D

λ

π

=

=

Parametr konfokalny wiązki

2w

0

– średnica

przewężenia wiązki

podawana przez

producentów lasera

Kąt rozbieżności wiązki

(pojęcie użyteczne dla dużych

odległości

z >> D

)

D

w

4

D

z

2

1

z

w

2

lim

z

w

2

lim

2

0

2

0

z

z

=

⎟

⎠

⎞

⎜

⎝

⎛

+

=

=

ϑ

∞

→

∞

→

2w

– średnica wiązki w danym przekroju (

definiuje kształt wiązki

)

( )

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

−

=

2

z

w

r

2

exp

I

z

,

r

I

( )

2

0

z

w

w

0

,

0

I

I

⎟

⎠

⎞

⎜

⎝

⎛

=

2

0

D

z

2

1

w

2

w

2

⎟

⎠

⎞

⎜

⎝

⎛

+

=

Wyznaczenie rozkładu intensywności

I(r,z)

i kształtu wiązki

I

z

– rozkład intensywności na osi wiązki I(0,0) – w środku przewężenia

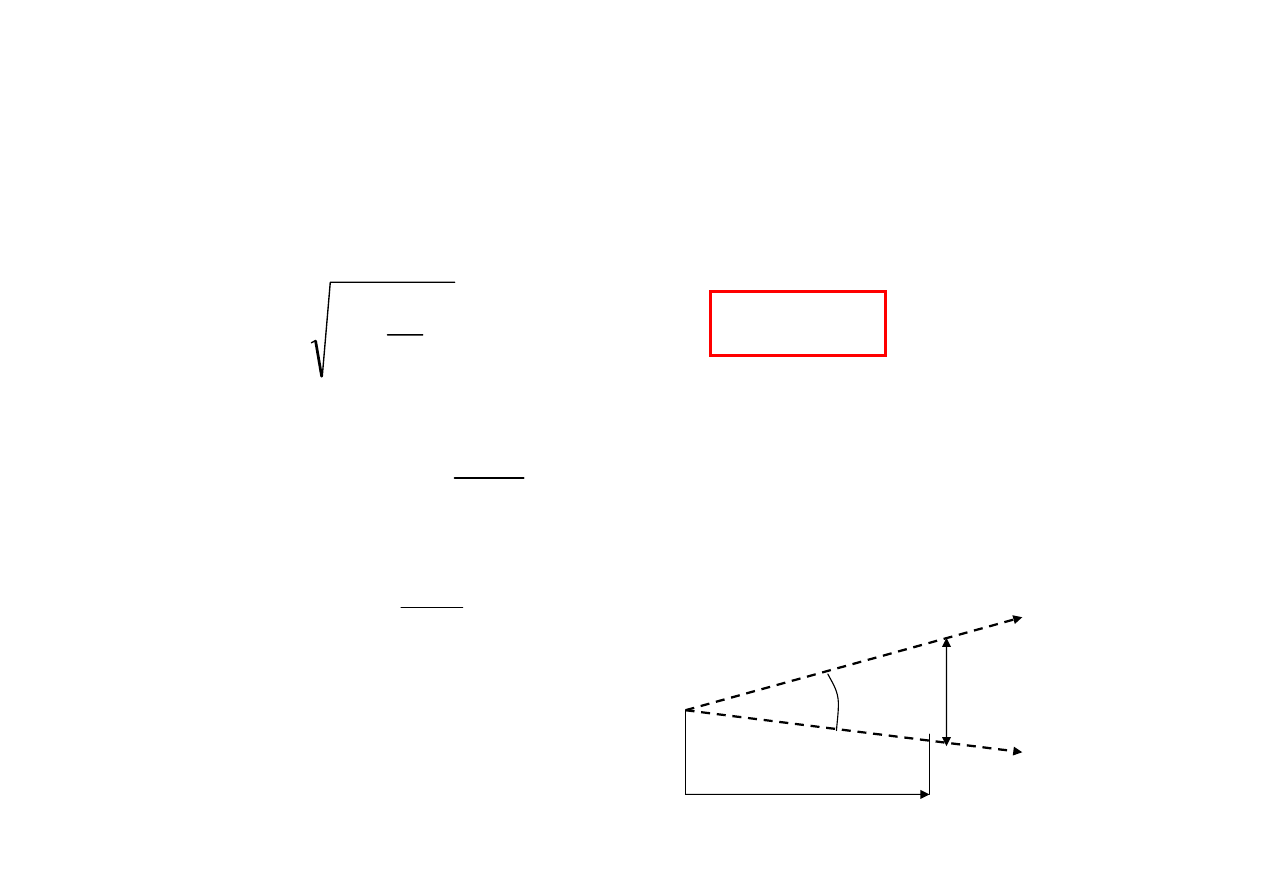
Kształt wiązki laserowej

mody poprzeczne cd

Przybliżenia dla średnic wiązki w różnych odległościach

z

dla

z << D

0

w

2

w

2

≈

2

0

D

z

2

1

w

2

w

2

⎟

⎠

⎞

⎜

⎝

⎛

+

=

dla

z >> D

relacja geometryczna

z

D

w

4

w

2

0

≈

D

w

4

2

0

=

ϑ

gdyż

2w

2

θ

z

z

w

ϑ

2

2

≈

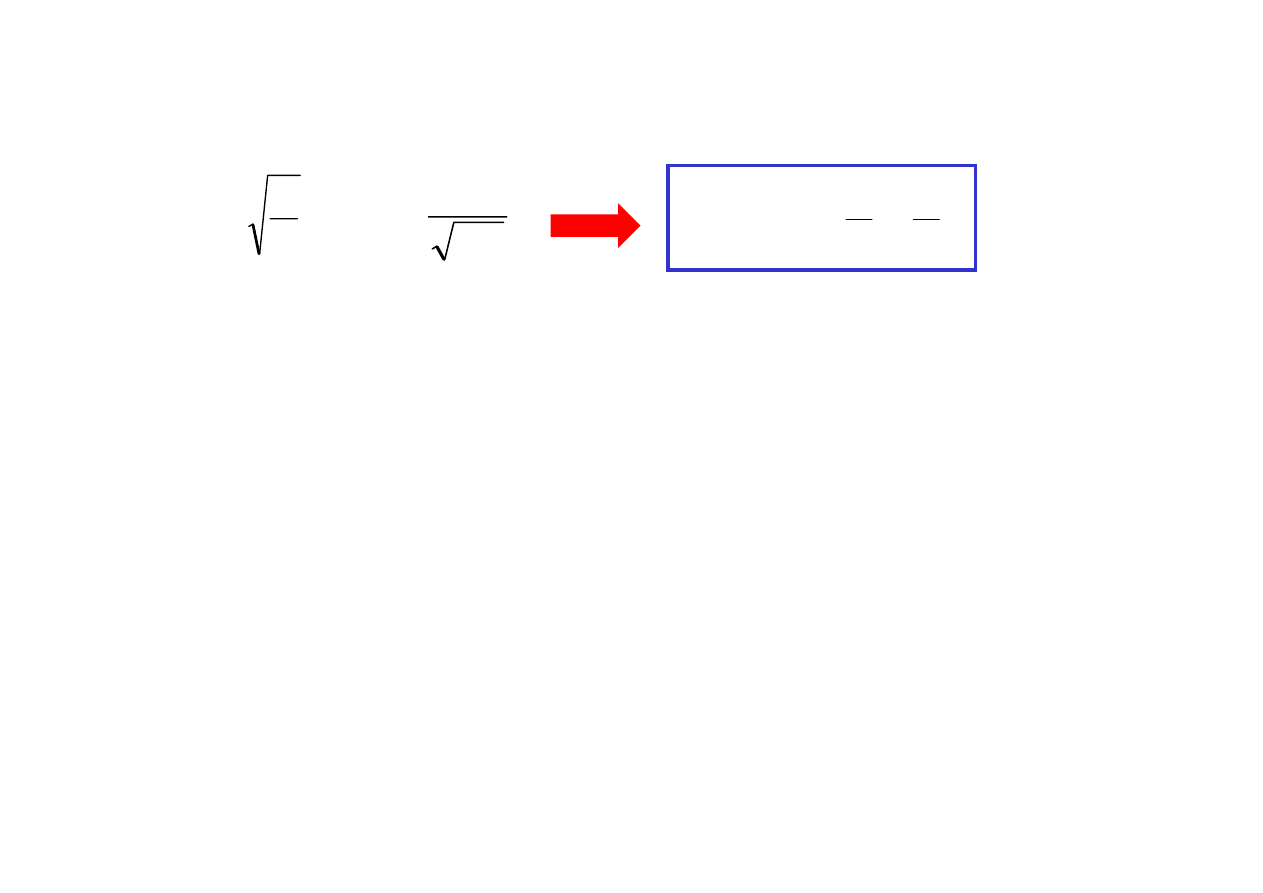
Niezmiennik wiązki gaussowskiej

Dla lasera

He-Ne

i

λ = 0.6328 μm

i typowej średnicy przewężenia

2w

0

= 1 mm

kąt rozbieżności

2

θ

= 0.000806 = 2.77’

Zmniejszenie średnicy przewężenia

2w

0

powoduje jednoczesne

powiększenie kąta rozbieżności

2

θ

Jednoczesne zmniejszanie

2w

0

i

2

θ

jest możliwe tylko przez wybór

lasera generującego promieniowanie

o krótszej długości fali

λ

k

D

2

w

2

0

=

kD

4

2

=

ϑ

λ

π

=

=

ϑ

⋅

4

k

8

2

w

2

0

K !!

Mody poprzeczne wyższych rzędów

Laser może generować jednocześnie różne mody

TEM

mn

Rozkłady intensywności kilku

pierwszych modów

TEM

mn

Wadą jest niejednorodność wiązki

Przy zakupie lasera gazowego zaznaczać pracę jednomodową

Warunek nie do spełnienia

w laserach na ciele stałym

a

szczególnie

w laserach półprzewodnikowych

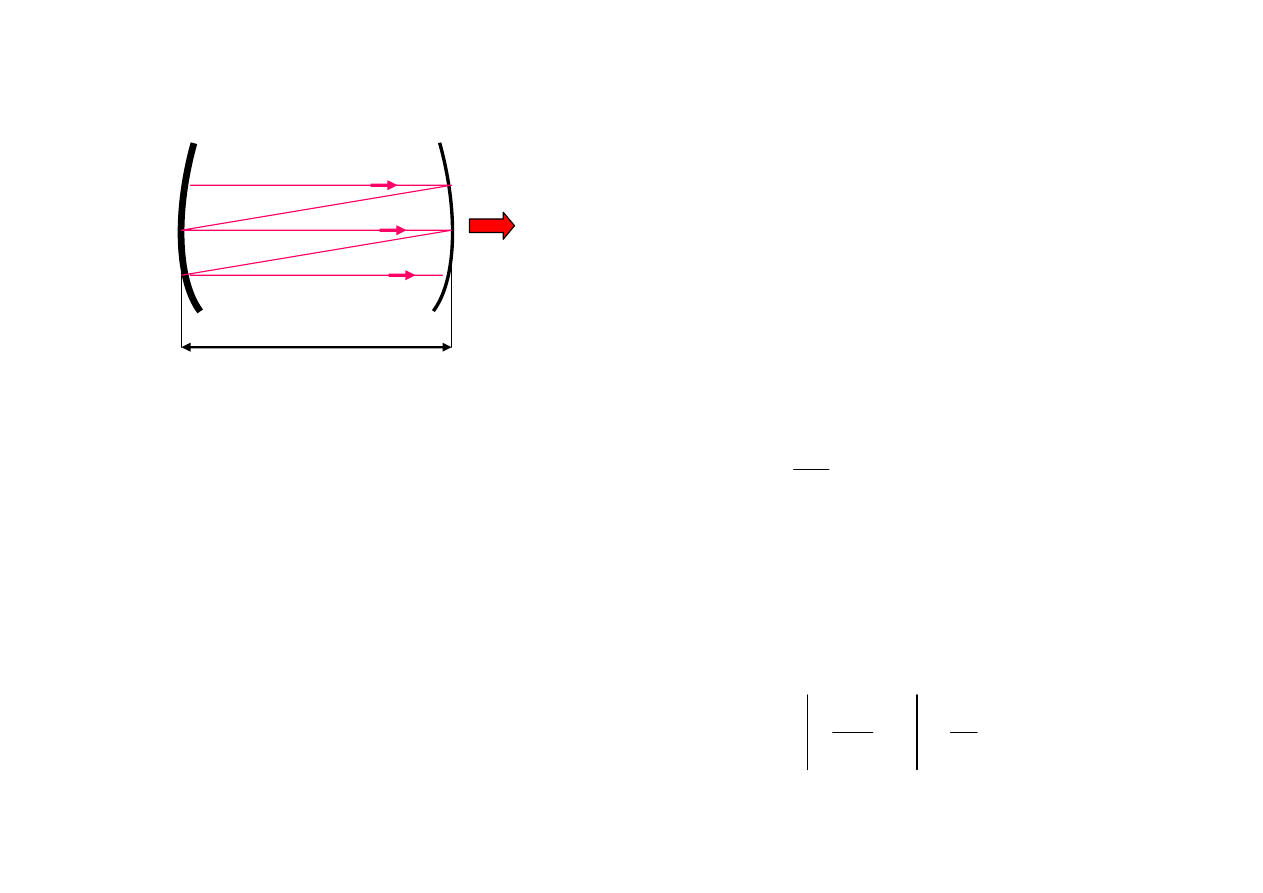
Widmo wiązki laserowej

mody podłużne

,

.

,

2

,

1

K

K

d

2

K

=

=

λ

Każde

λ

K

może być generowane

dla spełnionego warunku generacji

Dla lasera He-Ne

λ ≈ 0.6328.. μm

i długości rezonatora 0.5 m

K

jest rzędu

1.6

⋅10

6

i dokładnie

nie może być znane

Odległość w widmie między sąsiednimi

modami

δK = 1

K

K

K

d

2

2

λ

=

δ

−

=

δλ

W rezonatorze interferencja

promieni

1, 2, 3, ...

Warunek zgodności faz dla

K-tego

modu

K

K

d

2

λ

=

K

–

liczba całkowita

d

1

2

3

sód

wodór

rtęć

hel

neon

Linie widmowe lamp spektralnych

Długość fali

λ

600

550

500

450

400

nm

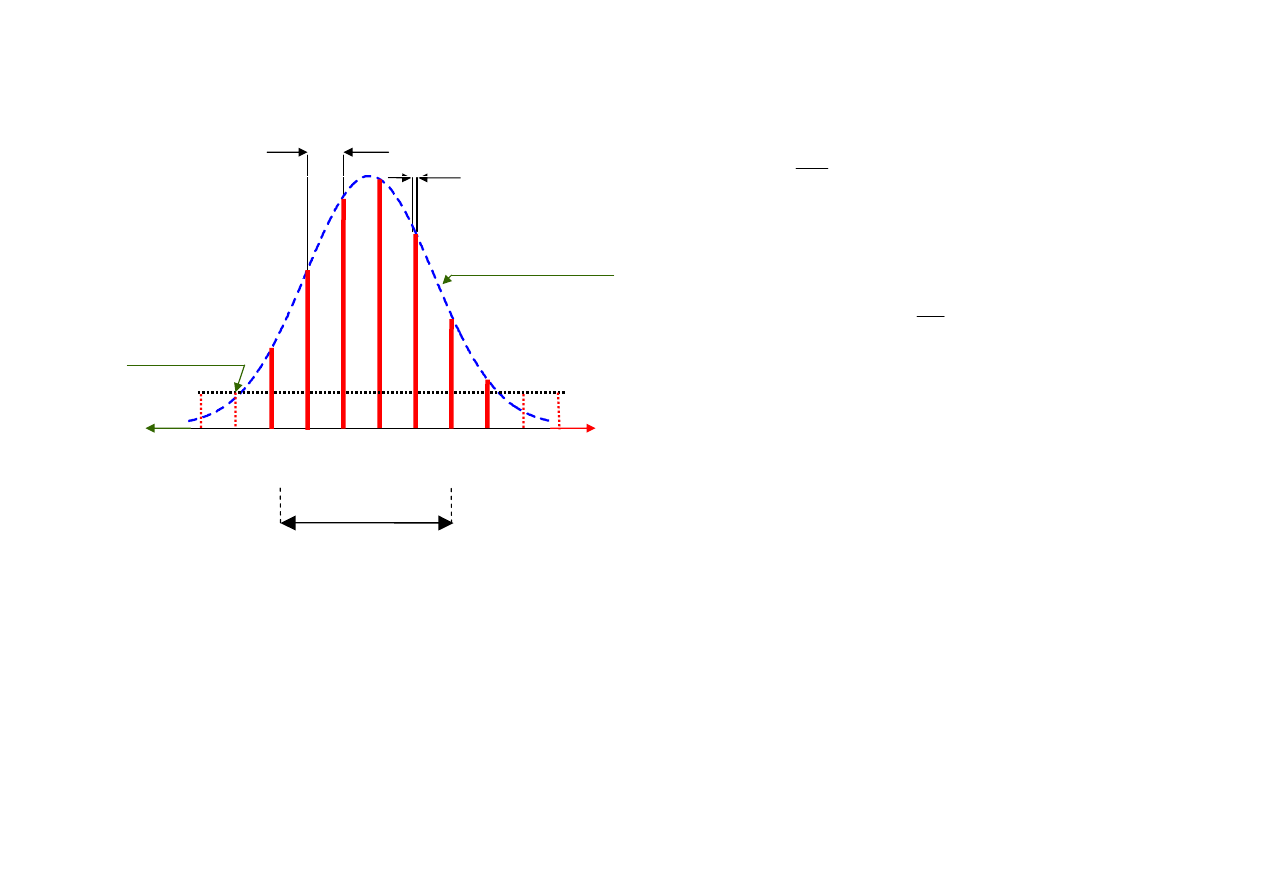
Widmo wiązki lasera

He-Ne

Δλ -

szerokość modu

δλ

odległość
międzymodowa

Δλ

L

≈ 2⋅10

-3

nm

Szerokość połówkowa
linii

Ne

λ = 633 nm

λ

ν

K

K-1

K-2

K+1

K-3

K+2

poziom

generacji

K+3

Linia
widmowa

Ne

potencjalne

mody

eger

int

K

K

d

2

K

−

=

λ

Dla długości rezonatora

d = 0.5 m

i

λ = 632.8 nm

nm

10

4

.

0

K

3

−

⋅

=

λ

=

δλ

Generacja kilku modów podłużnych

Na rysunku 7 modów od

K-3

do

K+3

Wartość K nieznana

Dla lasera z jednym modem szerokość widma

Δλ

bardzo mała,

ale

Δλ ≠0

Laser

potocznie

zwany

jednoczęstotliwościowym

Laser

nie jest

źródłem światła monochromatycznego

K!!

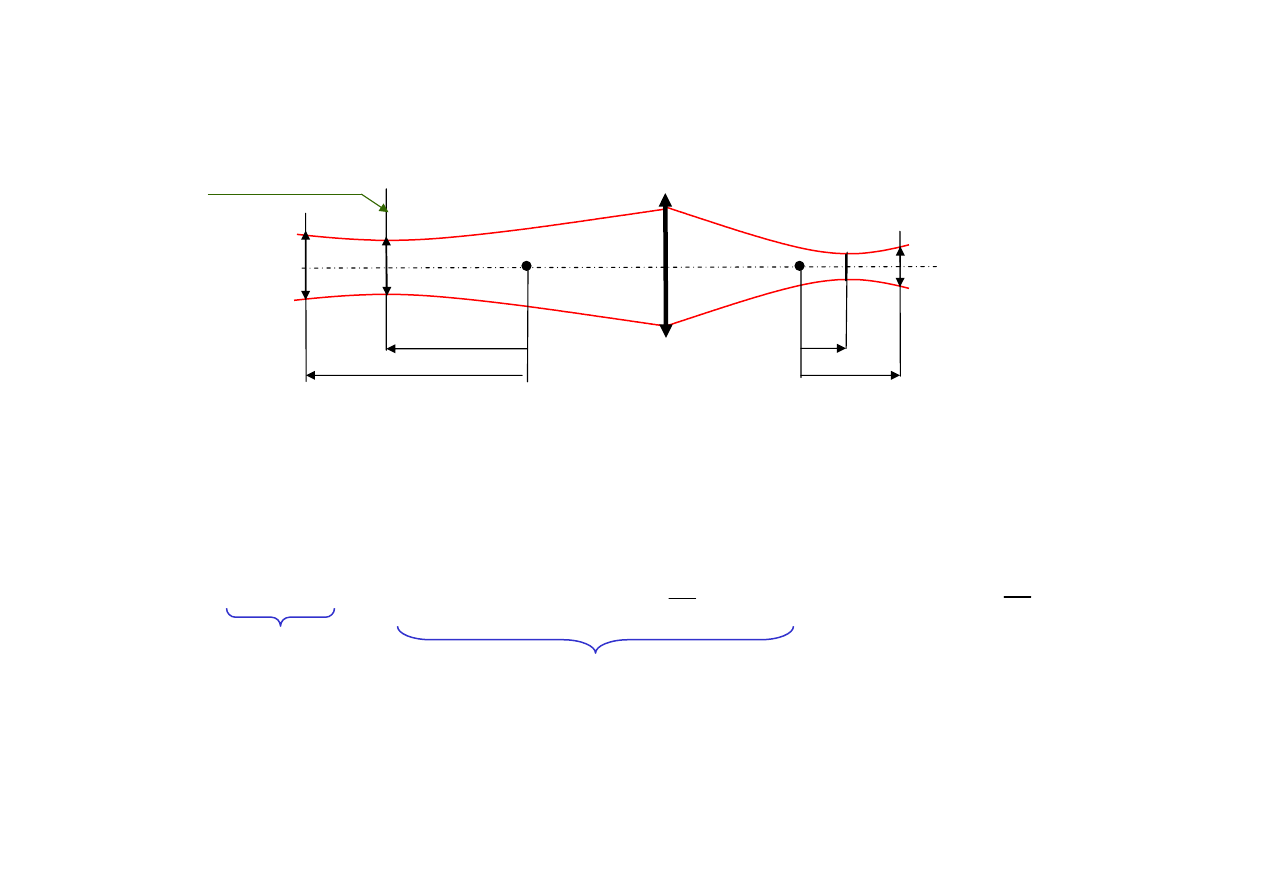
Przekształcanie wiązki przez układy optyczne

Znamy

D

(parametr konfokalny) i

x

p

położenie przewężenia

wiązki przedmiotowej.

Znaleźć

D’

i

x’

p

wiązki obrazowej

-x

p

-x

F

F’

x’

p

x’

2w

2w

0

2w’

n = 1

n = 1

2w’

0

płaszczyzna

przewężenia

π

π’

Obrazem płaszczyzny

π

jest płaszczyzna

π’

, a więc

2

'

f

'

xx

−

=

( )

( )

( )

2

2

2

2

2

w

2

'

f

'

x

w

2

'

w

2

⎟

⎠

⎞

⎜

⎝

⎛

=

β

=

wyznaczenie

położenia

π’

gdyż

'

f

'

x

−

=

β

wyznaczenie kształtu wiązki

obrazowej

Aby wyznaczyć położenia płaszczyzny przewężenia w przestrzeni

obrazowej należy znaleźć takie

x’

, dla którego

2w’ = min

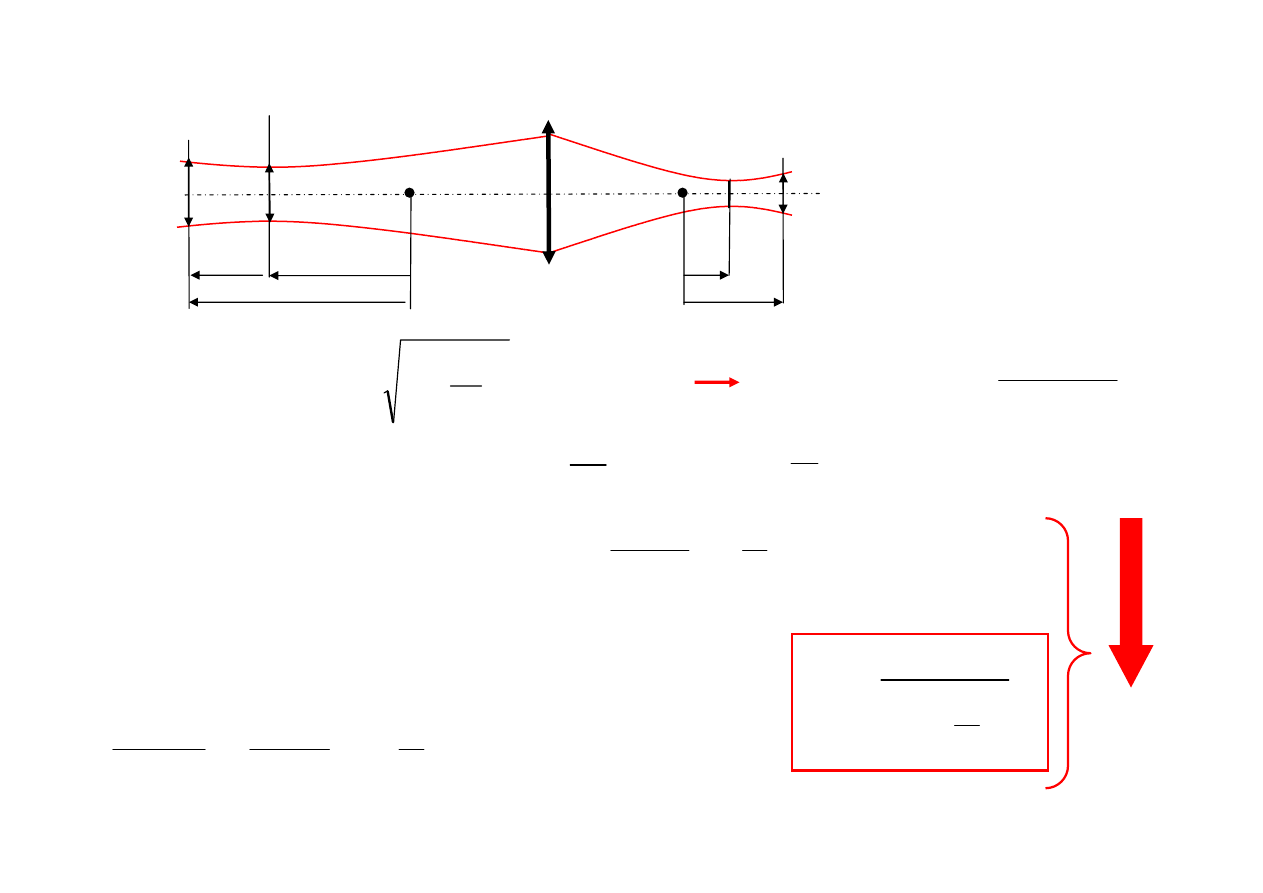
Przekształcanie wiązki przez układy optyczne

cd

-x

p

-x

F

F’

x’

p

x’

2w

2w

0

2w’

n = 1

n = 1

2w’

0

π

π’

-z

( ) (

)

(

)

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

−

+

=

2

2

p

2

0

2

D

x

x

4

1

w

2

w

2

2

0

D

z

2

1

w

2

w

2

⎟

⎠

⎞

⎜

⎝

⎛

+

=

x

x

z

p

−

=

Ponieważ

( )

(

)

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

+

+

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

=

2

p

2

2

2

2

0

2

'

x

x

'

f

'

x

2

D

'

Df

5

.

0

w

2

'

w

2

Po uwzględnieniu relacji

'

x

'

f

x

2

−

=

( )

( )

2

2

2

w

2

'

f

'

x

'

w

2

⎟

⎠

⎞

⎜

⎝

⎛

=

i po przekształceniach

( )

(

)

0

x

'

x

x

'

f

2

'

x

2

D

2

'

Df

5

.

0

w

2

'

x

'

w

2

p

p

p

2

p

2

2

0

2

=

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

+

+

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

=

∂

∂

Z warunku

p

2

2
p

2

p

x

2

D

x

'

f

'

x

⎟

⎠

⎞

⎜

⎝

⎛

+

−

=

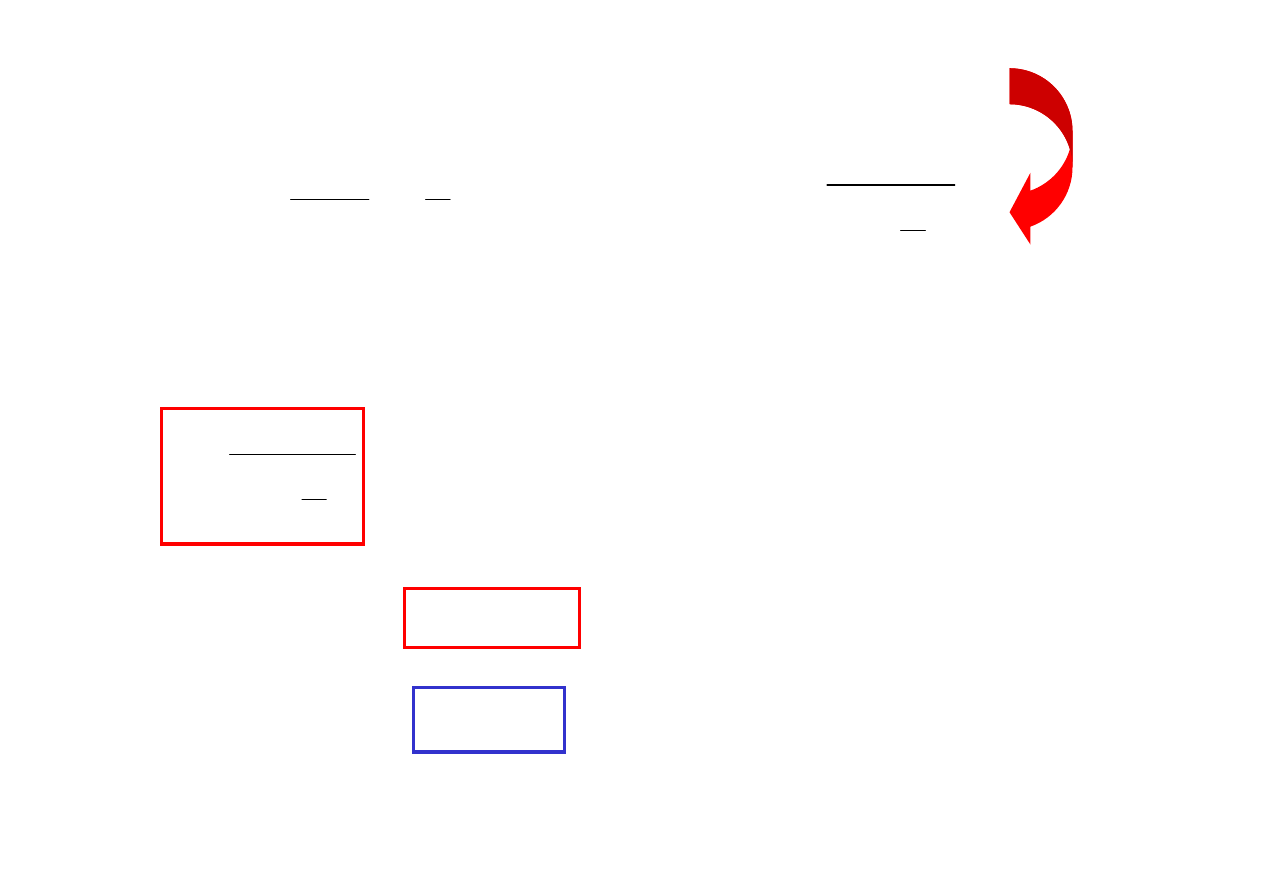
Przekształcanie wiązki przez układy optyczne

cd

2

2
p

2

g

2

D

x

'

f

⎟

⎠

⎞

⎜

⎝

⎛

+

=

α

parametry wiązki

przekształconej

p

g

p

x

'

x

α

−

=

położenie przewężenia

parametr konfokalny

D

'

D

g

α

=

( )

(

)

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

+

+

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

=

2

p

2

2

2

2

0

2

'

x

x

'

f

'

x

2

D

'

Df

5

.

0

w

2

'

w

2

p

2

2
p

2

p

x

2

D

x

'

f

'

x

⎟

⎠

⎞

⎜

⎝

⎛

+

−

=

Podstawiając

x’ = x’

p

znajdziemy

2w’ = 2w’

0

Ponieważ

D’ = kw’

0

2

, ostatecznie oznaczając

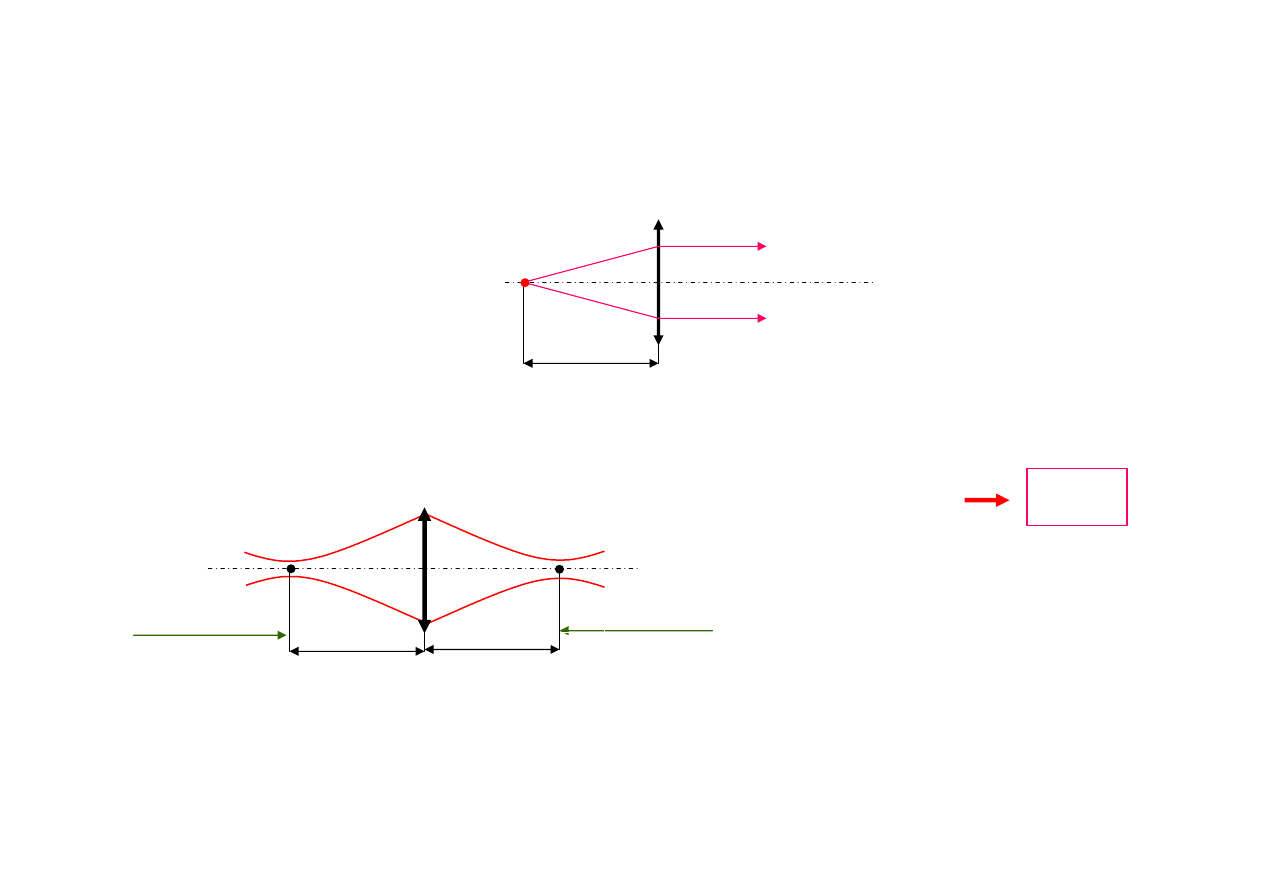
Przekształcanie wiązki przez układy optyczne

cd

Przewężenie wiązki obrazowej

nie jest obrazem

przewężenia wiązki przedmiotowej

Wiązkę gaussowską nie można traktować jako fali sferycznej ani płaskiej

Dla fali sferycznej

F

f’

Ob

Obraz ogniska

przedmiotowego

F

→

∞

przewężenie

x

p

= 0

Dla wiązki gaussowskiej, gdy płaszczyzna przewężenia pokrywa się z

ogniskiem przedmiotowym

F

obiektywu

Ob

Ob

F

F’

przewężenie

f’

f’

0

'

x

p

=

p

g

p

x

'

x

α

−

=

Ponieważ

Paradoks

ogniskowania

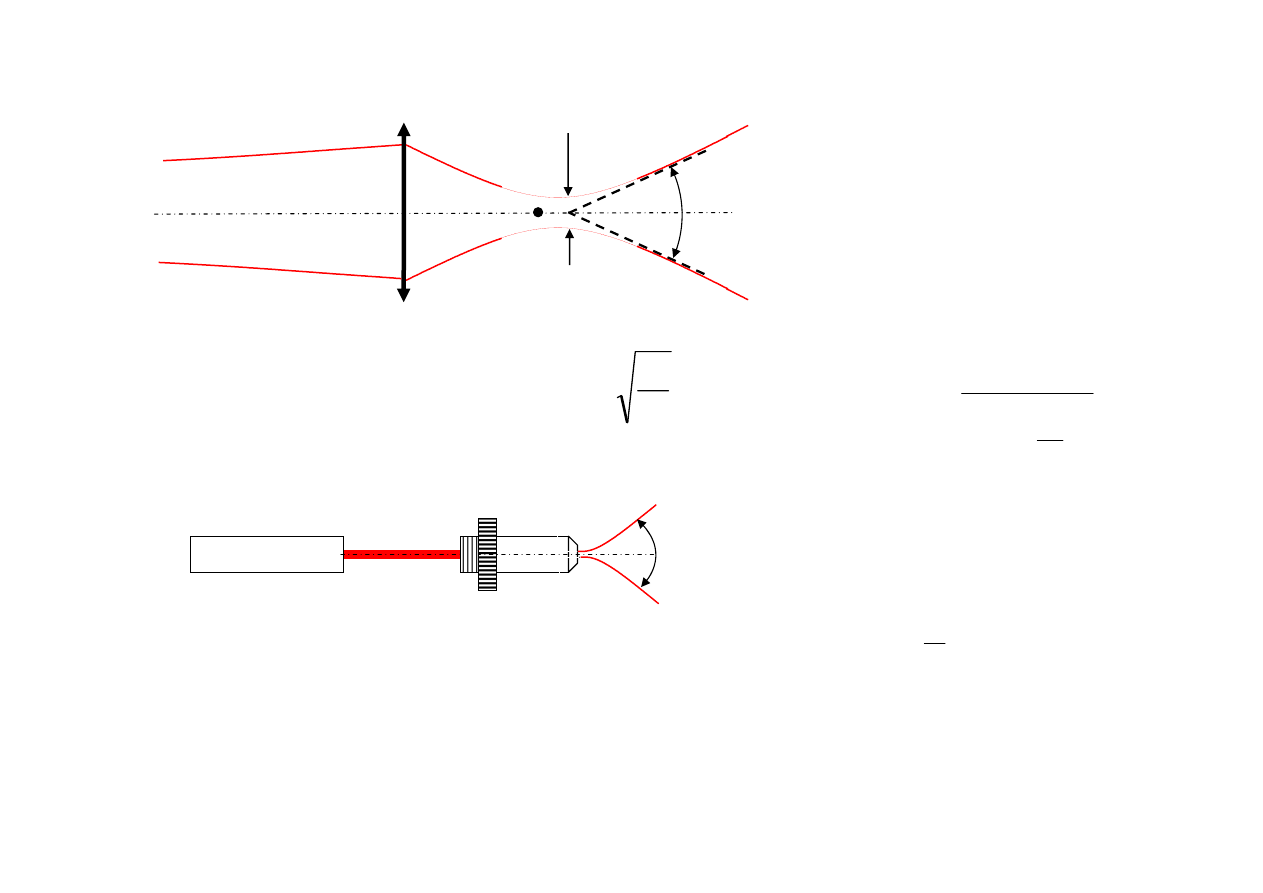
Ogniskowanie wiązki

F’

2w’

0

2

θ’

Średnica przewężenia

wiązki obrazowej

k

'

D

2

'

w

2

0

=

2

2
p

2

2

D

x

'

f

D

'

D

⎟

⎠

⎞

⎜

⎝

⎛

+

=

małe

D’

→

Dla dużych kątów niezmiennik

λ

π

=

ϑ

⋅

2

'

sin

'

w

2

0

Małe

2w’

0

→

duży kąt rozbieżności

2

θ’

Realnie

2w’

0min

≈

λ →

2

θ’

max

≈ 40

0

Najprościej krótka ogniskowa

f’

obiektywu mikroskopowego

Laser

2

θ’

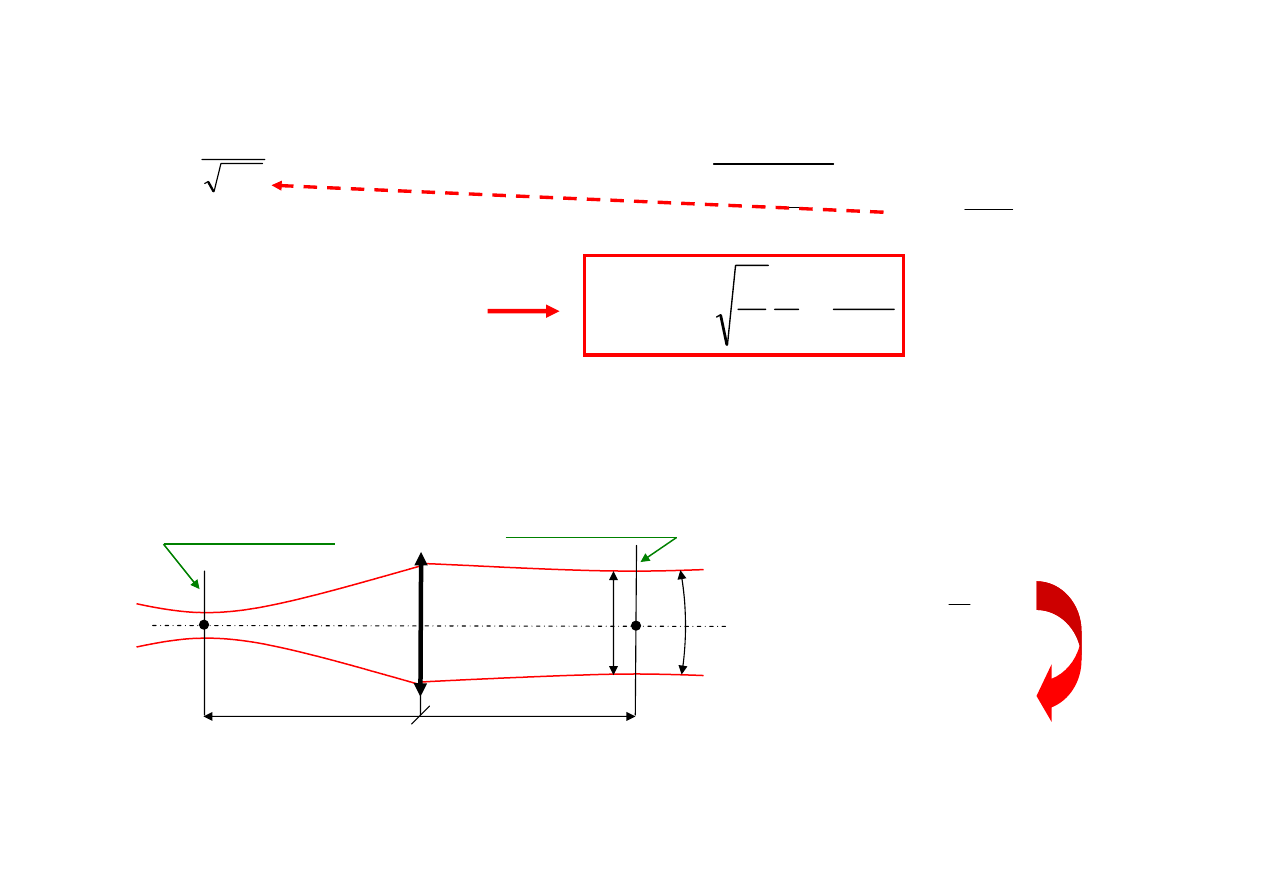
Minimalizacja kąta rozbieżności

2

2
p

2

2

D

x

'

f

D

'

D

⎟

⎠

⎞

⎜

⎝

⎛

+

=

'

kD

4

'

2

=

ϑ

→

D’

max

ponieważ

Aby uzyskać

2

θ’

min

należy pokryć przewężenia wiązki lasera z ogniskiem

F

układu (

x

p

= 0

) i zastosować układ o odpowiednio długiej ogniskowej

f’

D

'f

4

'

D

2

=

należy przyjąć

0

x

p

=

2
0

kw

D

=

'

f

w

2

'

f

1

k

D

2

'

2

0

min

=

=

ϑ

ponieważ

F’

F

f’

f’

przewężenie

przewężenie

2w

0

2w’

0

2

θ’

Z niezmiennika

λ

π

=

ϑ

4

'

2

'

w

2

0

małe

2

θ’

duże

2w’

0

Problem księżycowy

Więc wymagana

ogniskowa obiektywu

m

185

'

2

w

2

'

f

0

≈

ϑ

=

układ technicznie nie

do zrealizowania

Zadanie

: Zaproponować taki układ optyczny, aby na księżycu

średnica oświetlonej powierzchni wynosiła

1 km

Odległość do księżyca

z = 370 tys. km

Typowy laser

He-Ne

λ = 0.6328 μm

Średnica przewężenia

2w

0

= 0.5 mm

, z niezmiennika

mamy

dla wiązki lasera

2

θ = 1.6⋅10

-3

λ

π

=

ϑ

4

'

2

'

w

2

0

Wiązka samego lasera daje plamkę o średnicy

km

592

370

6

.

1

z

2

w

2

=

⋅

=

ϑ

=

"

557

.

0

10

7

.

2

000

.

370

1

z

'

w

2

'

2

6

=

⋅

=

=

=

ϑ

−

Niezbędny kąt rozbieżności

'f

w

2

'

2

0

min

=

ϑ

Dla obiektywu o ogniskowej f’ będzie

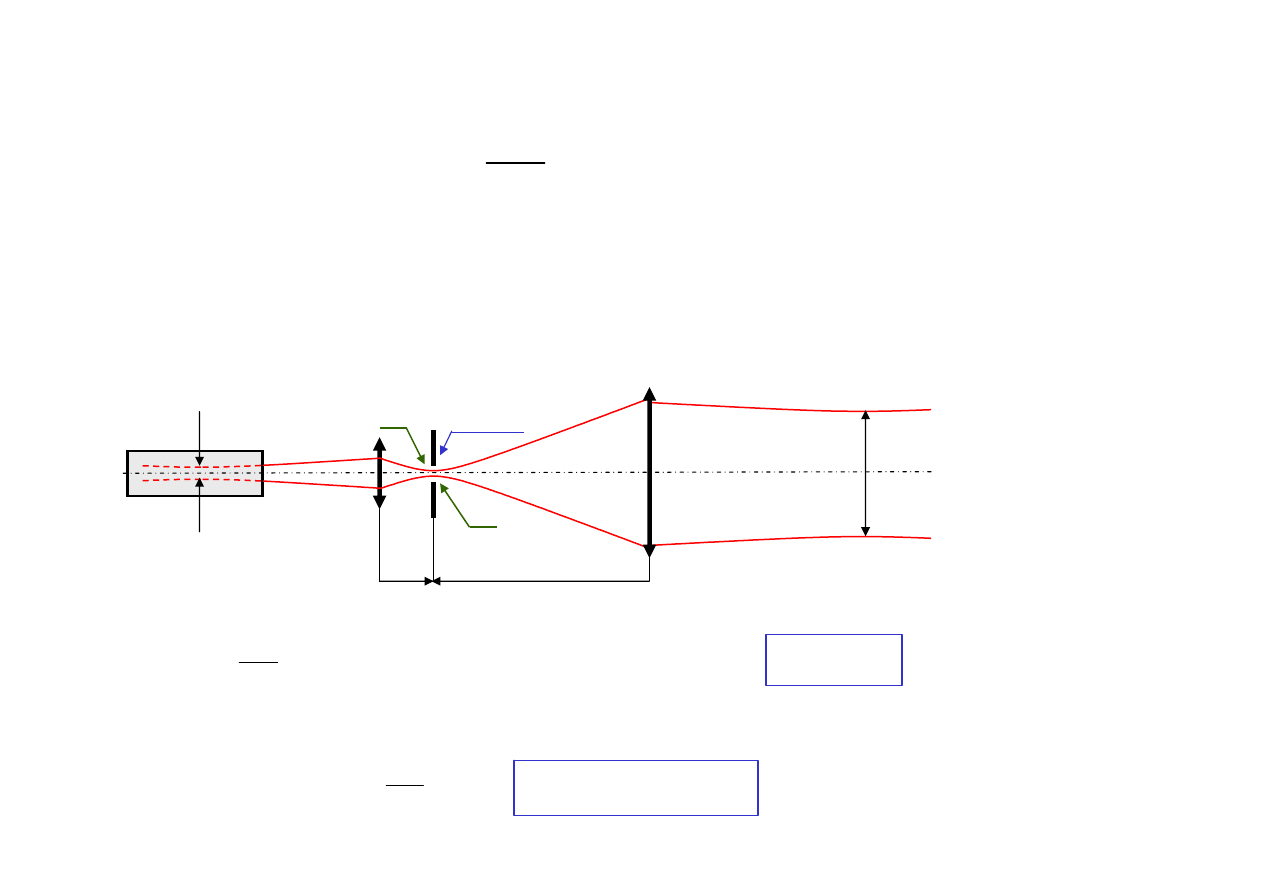
Problem księżycowy

cd

Dlatego stosuje się

układy bezogniskowe

złożone z dwóch elementów,

przy czym

pierwszy

ma za zadanie

zogniskować wiązkę

do małej

średnicy przewężenia

'f

w

2

'

2

0

min

=

ϑ

Zgodnie z relacją

przekształcać wiązkę o mniejszej średnicy przewężenia 2w

0

w celu skrócenia ogniskowej należy

1

2

1

2

2

'

f

'

f

'

2

ϑ

ϑ =

Jeżeli f’

1

= 8 mm wystarczy

m

4

'

f

2

=

ale wtedy

0

2

1

02

w

2

'

f

'

f

'

w

2

=

rozszerzacz wiązki

mm

298

'

w

2

02

=

Laser

•

F’

1

F

2

f’

2

f’

1

pinhol

2

θ’

2

2

θ

1

2w’

02

2w

01