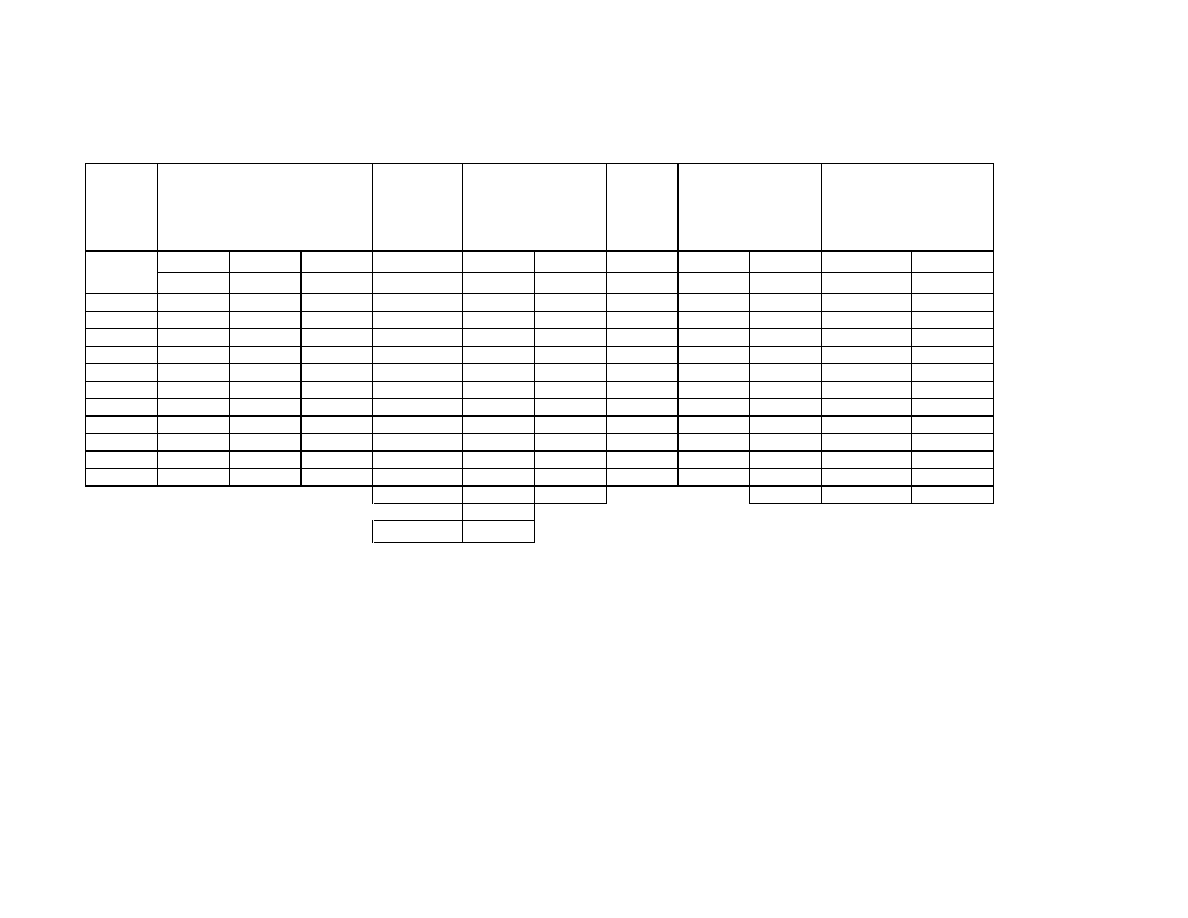
Ozn. Klasy

szerokość

klasy

Częstość
występow
ania danej
klasy

d

imax

d

imin

d

iśr

∆

d

i

q

i

a

i

f(d

i

)

Φ

(d

imax

)

F(d

imin

)

(a

i

/ d

iśr

)

(a

i

* d

iśr

)

mm

mm

mm

mm

g

%

d

h

, mm

d

a

, mm

11

3,2

1,6

2,4

1,6

0

0

0,00

1,000

0

0

0

10

1,6

0,8

1,2

0,8

0,76

0,0076

0,01

1,000

0,0076

0,006333333

0,00912

9

0,8

0,63

0,715

0,17

2,38

0,0238

0,14

0,992

0,0314

0,033286713

0,017017

8

0,63

0,4

0,515

0,23

11,09

0,1109

0,48

0,969

0,1423

0,215339806 0,0571135

7

0,4

0,32

0,36

0,08

9,02

0,0902

1,13

0,858

0,233

0,250555556

0,032472

6

0,32

0,2

0,26

0,12

25,45

0,2545

2,12

0,768

0,487

0,978846154

0,06617

5

0,2

0,16

0,18

0,04

12,18

0,1218

3,05

0,513

0,609

0,676666667

0,021924

4

0,16

0,1

0,13

0,06

19,29

0,1929

3,22

0,391

0,802

1,483846154

0,025077

3

0,1

0,071

0,0855

0,029

6,1

0,061

2,10

0,198

0,863

0,713450292 0,0052155

2

0,071

0,056

0,0635

0,015

3,29

0,0329

2,19

0,137

0,896

0,518110236 0,00208915

1

0,056

0

0,028

0,056

10,44

0,1044

1,86

0,104

1,000

3,728571429 0,0029232

∑

100

1,000

∑

8,605

0,2391

0

Razem

100,00

d

h

=

0,1162

mm

d

a

=

0,2391

mm

i

d

h

= 1/∑(a

i

/d

iśr)

d

a

= ∑ a

i

*d

iśr

Charakterystyka rozkładu wielkości ziaren w oparciu o wyniki analizy sitowej

Wielkość ziaren i - tej klasy

Zawartość klasy

ziarnowej

Wartość funkcji składu

ziarnowego

Ś

rednie średnice ziaren d

ś

r

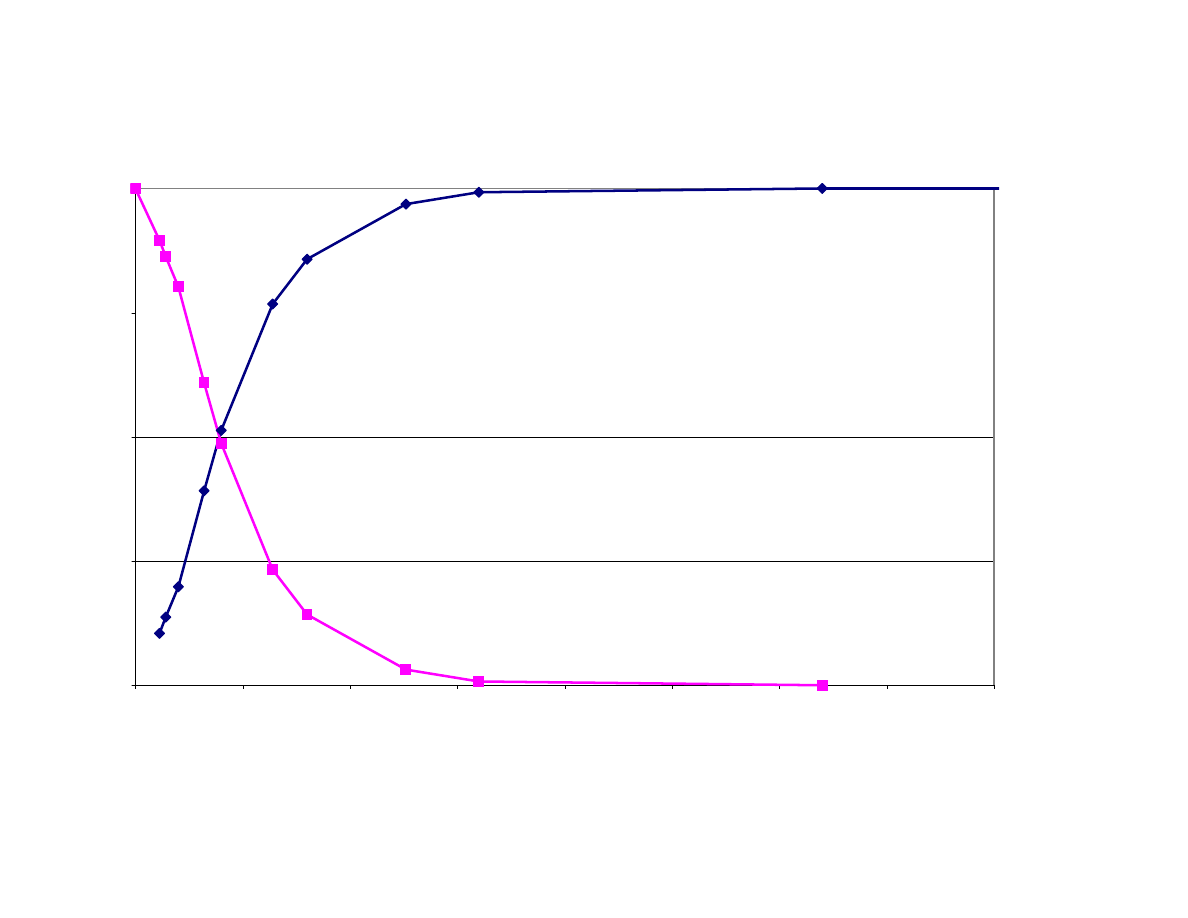
Rys.1. Przebieg funkcji składu ziarnowego

0,00

0,25

0,50

0,75

1,00

0

0,25

0,5

0,75

1

1,25

1,5

1,75

2

d.i., mm

Φ(

Φ(

Φ(

Φ(

d

.i.max

)

F(d

.i.min

)

Φ,

Φ,

Φ,

Φ,

F