29

Politechnika Warszawska
Wydział Fizyki
Laboratorium Fizyki I Płd.
Piotr Jaśkiewicz
Jerzy Antonowicz

OPTYCZNA ANALIZA WIDMOWA

1. P

ODSTAWY FIZYCZNE

Ciało ogrzane do wysokiej temperatury, poddane wyładowaniu elektrycznemu lub

naświetleniu promieniowaniem o odpowiedniej długości fali – samorzutnie emituje promieniowanie
elektromagnetyczne. Jeżeli promieniowanie to zawiera się w zakresie ok. 380 - 780 nm, wtedy
obserwujemy je w postaci światła widzialnego, którego zależność natężenia od długości fali możemy
analizować przy pomocy spektroskopu optycznego. Obserwowaną zależność natężenia
promieniowania od długości fali nazywamy widmem. Widmo promieniowania wysyłanego przez
świecące ciało nazywamy widmem emisyjnym.

Ciało stałe lub ciecz, podgrzane do wysokiej temperatury wysyłają z niezerowym

prawdopodobieństwem fale o różnych długościach, czyli emitują widmo ciągłe.

Jeżeli świecący gaz składa się z oddzielnych, nieoddziałujących ze sobą atomów, to jego

widmo nazywamy atomowym. Widma atomowe są widmami liniowymi (składającymi się
z oddzielnych linii). Jeżeli ciało jest gazem składającym się z wieloatomowych, oddziałujących
ze sobą cząsteczek, to jego widmo jest widmem pasmowym.

Przepuszczając przez badane ciało promieniowanie o widmie ciągłym otrzymujemy widmo

absorpcyjne

∗

, w którym obserwujemy ciemne obszary odpowiadające długościom fal

promieniowania pochłoniętego przez to ciało.

a

b

c

d

λ

1

obszar widzialny

podczerwień

nadfiolet

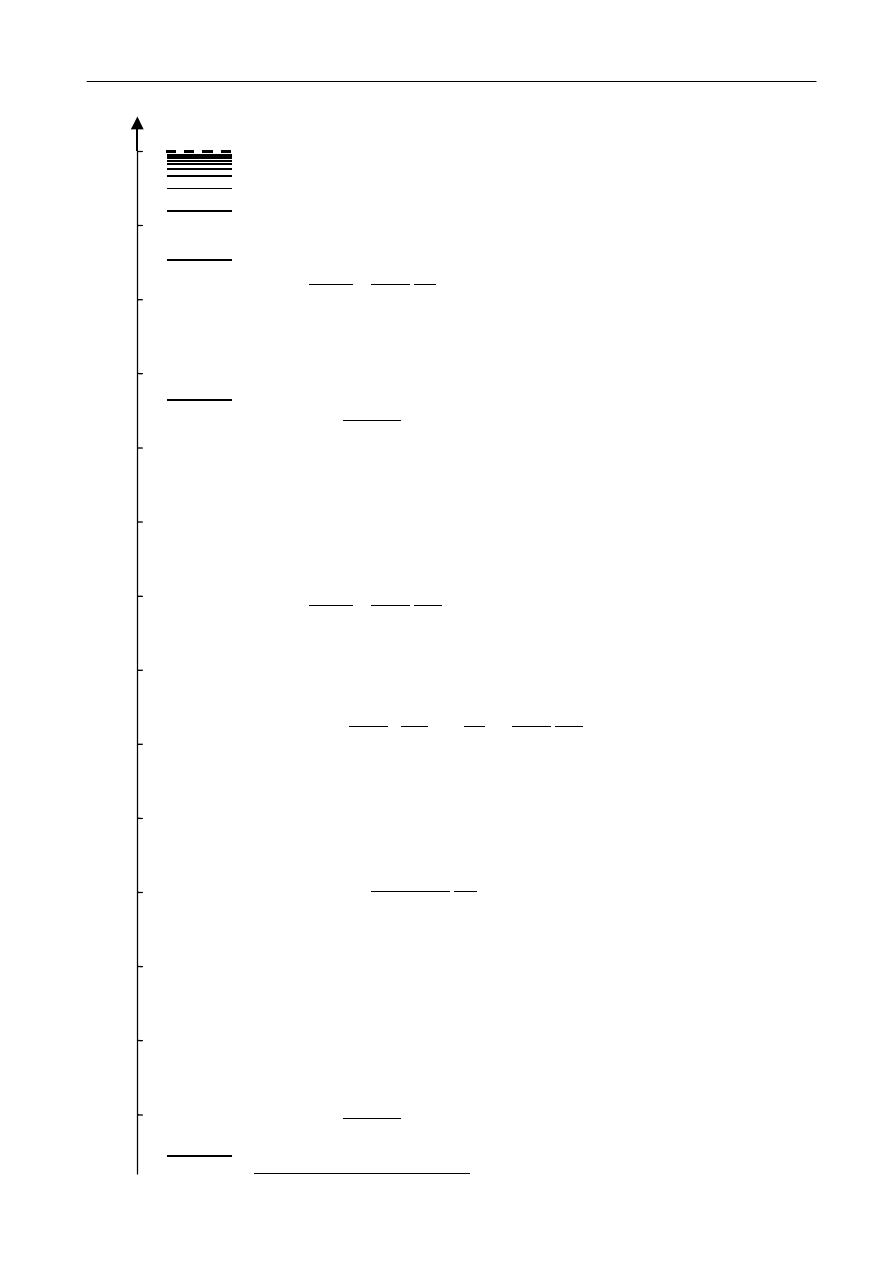
Rys. 1. Rodzaje widm optycznych.

a - widmo pasmowe; b - widmo absorbcyjne; c - widmo ciągłe; d - widmo liniowe.

2. W

IDMO ATOMU WODOROPODOBNEGO

**

Badania widm liniowych atomów różnych pierwiastków, prowadzone przez Rydberga, Ritza

i Kaysera, doprowadziły do sformułowania empirycznego wzoru określającego długości wszystkich
linii widma atomowego:

n

m

T

T

−

=

λ

1

,

(1)

gdzie

λ oznacza długość fali danej linii emitowanego promieniowania a wyrażenia T

m

i T

n

nazywane termami, przyjmują wartości odpowiednio:

∗

Absorpcja - pochłanianie

**

Atom wodoropodobny – układ dwóch ciał, jednego elektronu i jądra atomowego, związanych
oddziaływaniem kulombowskim

Optyczna analiza widmowa

2

2

m

R

T

m

=

i

2

n

R

T

n

=

,

(2)

m = 1, 2 ,3,... , natomiast dla danego m liczba n przyjmuje wartości całkowite zaczynające się od
m+1, a R jest tzw. stałą Rydberga, równą ok. 10967758 m

-1

.

Każdej linii widmowej można przypisać układ dwóch termów, których różnica pozwala

obliczyć odwrotność długości fali emitowanego światła, według zależności:

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

=

2

2

1

1

1

n

m

R

λ

.

(3)

Zespół linii widmowych odpowiadający stałej wartości m nazywamy serią widmową.
Warto zapamiętać nazwiska pierwszych odkrywców poszczególnych serii. I tak serię dla

m = 1 przy (n = 2, 3, 4, ...) nazywamy serią Lymana, m = 2 przy (n = 3, 4, 5, ...) - serią Balmera,
m = 3 przy (n = 4, 5, 6, ...) - serią Paschena - Fowlera, m = 4 przy (n = 5, 6, 7, ...) - serią Bracketta,
m = 5 przy (n = 6, 7, 8, ...) - serią Pfunda, m = 6 przy (n = 7, 8, 9, ...) - serią Humphreusa.

3. M

ODEL

B

OHRA ATOMU WODORU

W roku 1913 duński fizyk Niels Bohr opracował teoretyczny model atomu wodoru. Opierając

się na modelu Rutherforda, Bohr opisał atom w sposób analogiczny do opisu układu planetarnego.
Model swój, częściowo klasyczny, częściowo kwantowy, uzupełnił o dwa postulaty.

Według Bohra atom składa się z ciężkiego jądra zawierającego ładunek dodatni i krążących

wokół jądra lekkich elektronów, obdarzonych ładunkiem ujemnym. Wokół jądra atomu wodoru
krąży jeden elektron, którego ruch można opisać przy pomocy praw mechaniki klasycznej. Elektron
może się poruszać tylko po określonych, kołowych, stacjonarnych orbitach, na których zachowuje
stały, skwantowany

*

moment pędu, będący wielokrotnością stałej Plancka dzielonej przez 2

π

(pierwszy postulat Bohra). Zmiana orbity elektronu jest możliwa tylko w połączeniu z absorpcją
(przeskok z niższej orbity na wyższą) lub emisją (przeskok z wyższej orbity na niższą) kwantu
energii (fotonu) równej różnicy energii elektronu na obu orbitach (drugi postulat Bohra).

Promienie orbit elektronów oraz wartości ich energii na poszczególnych orbitach można

wyliczyć w sposób następujący:

Pierwszy postulat Bohra oznacza, że moment pędu elektronu na n - tej orbicie spełnia

warunek:

h

n

r

m

n

e

=

v

.

(4)

gdzie m

e

jest masą spoczynkową elektronu, n = 1, 2, 3, ... oznacza numer orbity elektronu

(tzw. główną liczbę kwantową),

π

2

h

=

h

, przy czym

h jest stałą Plancka

**

, r

n

jest promieniem n - tej

orbity, v - prędkością elektronu.

Energia elektronu składa się z energii kinetycznej i energii potencjalnej elektronu w polu

elektrostatycznym jądra:

n

e

n

r

e

m

E

2

0

2

4

1

2

v

πε

−

=

.

(5)

gdzie e oznacza ładunek elektronu, a

ε

0

przenikalność dielektryczną próżni.

*

Skwantowany - nieciągły, przyjmujący dyskretne wartości.

**

Wielkość

π

2

h

=

h

nazywamy „h kreślonym”.

Optyczna analiza widmowa

3

R

ys. 2 Rozk

ład warto

ści energii elektronu w atomie wodoru.

E

1

E

2

E

3

E

4

E

5

-13

-12

-11

-10

-9

-8

-7

-6

-5

-4

-3

-2

-1

0

-13,6

energia elektronu [eV]

Przyrównanie siły dośrodkowej i siły kulombowskiego przyciągania

elektronu do jądra przy założeniach, że ciężkie jądro jest nieruchome
a oddziaływanie grawitacyjne elektronu z jądrem jest - przy małej masie
elektronu - zaniedbywalne, prowadzi do równania ruchu elektronu po
kołowej orbicie:

2

2

0

2

4

1

v

n

n

e

r

e

r

m

πε

=

,

(6)

Usuwając z równań (4) i (6) prędkość v elektronu otrzymujemy

dopuszczalne wartości promieni orbit:

2

2

2

0

4

n

e

m

r

e

n

h

πε

=

(n = 1, 2, 3, ...)

(7)

Promień pierwszej orbity elektronowej w atomie wodoru nosi nazwę

promienia Bohra i jest równy r

0

= 0,529177

⋅10

-10

m

*

.

Ponieważ z równania (6) wynika, że:

n

e

r

e

m

2

4

1

2

v

2

0

2

πε

=

,

(8)

zatem równanie (5) można przekształcić do postaci:

n

n

n

n

r

e

r

e

r

e

E

2

4

1

2

4

1

2

0

2

2

0

πε

πε

=

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

−

=

. (9)

Podstawiając do powyższego równania wartość promienia n - tej orbity (7),
otrzymujemy dozwolone wartości energii elektronu w atomie
wodoropodobnym

:

2

2

2

0

2

4

1

32

n

e

m

E

e

n

h

ε

π

−

=

,

(10)

przedstawione w zachowanej skali na rysunku 2 (1 eV = 1,602

⋅10

-19

J).

Jeżeli analogiczne rozważania przeprowadzimy dla ruchu

pojedynczego elektronu wokół jądra dowolnego pierwiastka (atomu
wodoropodobnego) o liczbie atomowej Z, równej liczbie protonów w jądrze
i ładunku Ze, wyrażenia (7) i (10) przekształcą się do postaci:

2

2

2

0

4

n

Ze

m

r

e

n

h

πε

=

, (n = 1, 2, 3, ...)

(11)

*

przyjęto oznaczać promień Bohra przez r

0

lub a

0

zamiast r

1

Optyczna analiza widmowa

4

( )

2

2

2

0

2

4

2

2

2

2

0

2

2

2

1

32

1

32

n

e

Z

m

n

Ze

e

m

E

e

e

n

h

h

ε

π

ε

π

−

=

−

=

(n = 1, 2, 3, ...).

(11)

Atom wodoru z elektronem znajdującym się na poziomie n = 1 znajduje się w stanie

podstawowym

. Z kolei z kwantowej teorii światła wiemy, że falę elektromagnetyczną

o częstotliwości

ν

możemy przedstawić w postaci strumienia cząstek (fotonów), gdzie każdy z nich

niesie energię

ΔE = h

ν

. Gdy atom pochłonie kwant energii o wartości ściśle odpowiadającej różnicy

energii poziomu podstawowego i któregokolwiek poziomu o wyższym n = m , znajdzie się w stanie
wzbudzonym

. Atom przebywa w stanie wzbudzonym dość krótko (rzędu 10

-8

– 10

-9

s), a następnie

powraca do stanu podstawowego, emitując z powrotem kwant energii. W przypadku, gdy
wzbudzony atom emituje jeden kwant energii w postaci fotonu, możemy obliczyć jego energię jako:

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

−

=

−

=

Δ

2

2

2

2

0

2

4

1

1

32

m

n

e

m

E

E

E

e

m

n

h

ε

π

.

(12)

Ponieważ

ΔE = h

ν

=

λ

c

h , zatem można zależność (12) przedstawić w postaci:

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

−

=

2

2

3

2

0

3

4

2

2

2

2

0

2

4

1

1

64

1

1

32

1

n

m

c

e

m

m

n

hc

e

m

e

e

h

h

ε

π

ε

π

λ

. (13)

Porównując zależność (3) z (14) otrzymaliśmy w ten sposób analityczną postać stałej

Rydberga, której wartość po podstawieniu przybliżonych wartości liczbowych:

m

e

= 9,110

⋅10

-31

kg;

e = 1,602

⋅10

-19

C;

ε

0

= 8,854

⋅10

-12

F/m;

h = 1,055⋅10

-34

Js;

c = 2,998

⋅10

8

m/s;

wynosi 10974191,404 m

-1

, co daje bardzo dobrą zgodność ze wartością wyznaczoną doświadczalnie.

Analiza rysunku 2 prowadzi do pytania, jak zachowa się elektron po absorpcji kwantu

o energii większej od 13,6 eV? Przede wszystkim należy zauważyć, że dla energii większej od
13,6 eV nie obowiązują już zasady kwantowania energii elektronu w polu elektrycznym jądra.
Elektron może zaabsorbować kwant o dowolnej energii większej od Ej = 13,6 eV i wydostać się
z atomu, stając się elektronem swobodnym. Dla wodoru Ej jest energią jonizacji, a widmo energii
elektronu będzie widmem ciągłym. Długością fali odpowiadającej krótkofalowej granicy widma
liniowego atomu wodoru będzie:

j

f

E

hc

=

λ

= 91,166 nm (nadfiolet) .

(14)

4. M

ETODY SPEKTROSKOPOWE

Spektroskop jest urządzeniem do badania widma, czyli zależności dowolnej wielkości

fizycznej od długości fali promieniowania padającego na próbkę, emitowanego przez próbkę lub
w inny sposób skojarzonego z badanym układem. Spektroskop optyczny służy do badania rozkładu
widmowego światła w zakresie widzialnym, czyli zależności jego natężenia od długości fali
emitowanej lub przepuszczanej przez próbkę. Elementy optyczne spektroskopu muszą z niewielkimi
stratami przepuszczać badane promieniowanie. Ponieważ wszystkie materiały optyczne posiadają
własną charakterystykę widmową, czyli wykazują różne własności fizyczne dla różnych długości fal,
spektroskopy projektowane są do badania rozkładu widmowego światła w określonym zakresie
długości fali.

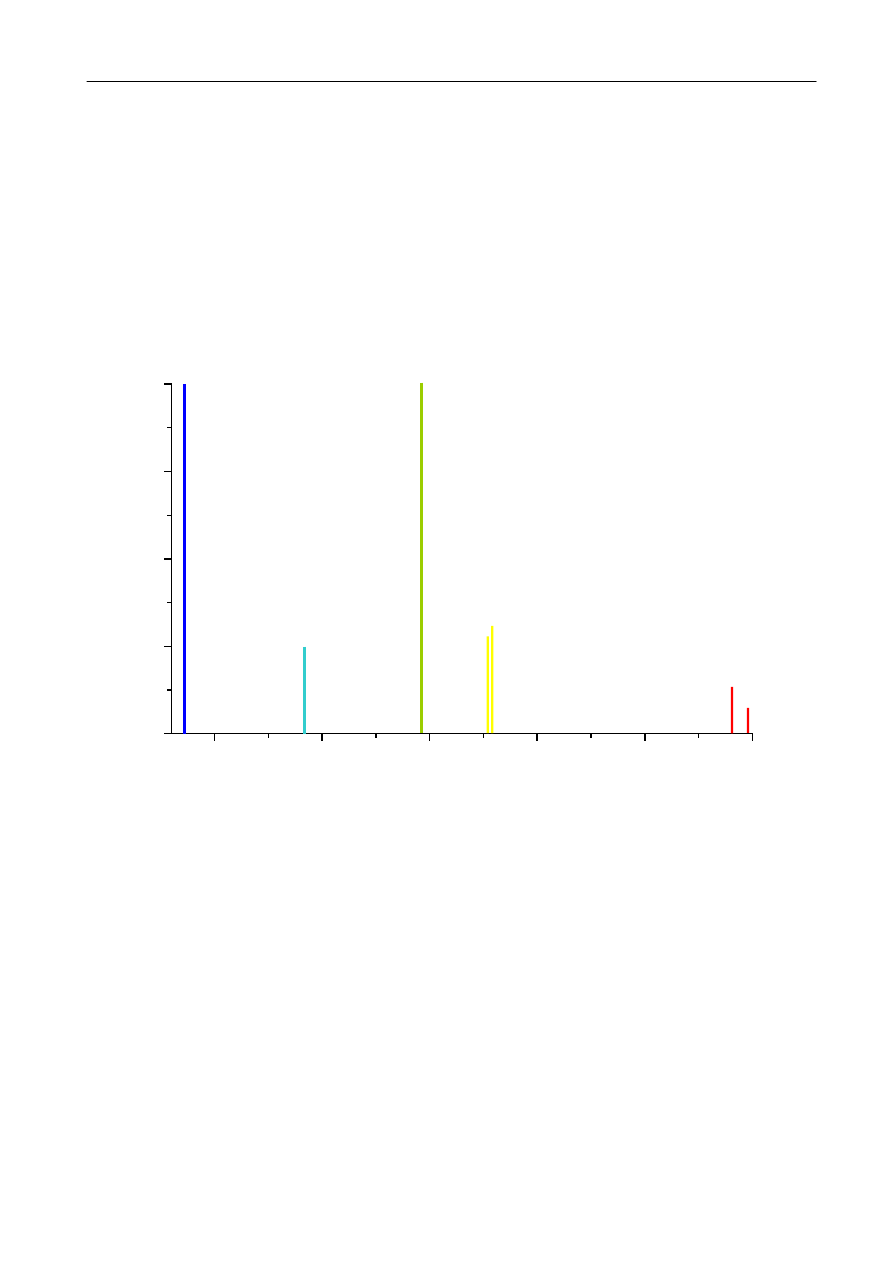
Optyczna analiza widmowa

5

W celu przeprowadzenia analizy widmowej spektroskop optyczny winien być wyposażony

w element rozdzielający analizowane promieniowanie na widmo (według długości fali lub jej
częstości). Najpopularniejszymi spektroskopami optycznymi są spektroskopy pryzmatyczne
(wykorzystujące zjawisko rozszczepienia światła przez pryzmat) i siatkowe (wykorzystujące
zjawisko ugięcia światła na siatce dyfrakcyjnej). Podstawowymi parametrami takiego urządzenia są:
zakres długości fali badanego promieniowania, czułość (minimalna, zauważalna zmiana natężenia
promieniowania o danej długości fali) i rozdzielczość, definiowana jako

λ/Δλ, (stosunek długości

fali do różnicy dwóch długości fal, które jeszcze można przy pomocy danego spektroskopu
rozróżnić).

5. W

YKONANIE ĆWICZENIA

450

500

550

600

650

700

0

1000

2000

3000

4000

698,1

690,8

579,1

577,0

546,1

491,6

435,8

λ

[nm ]

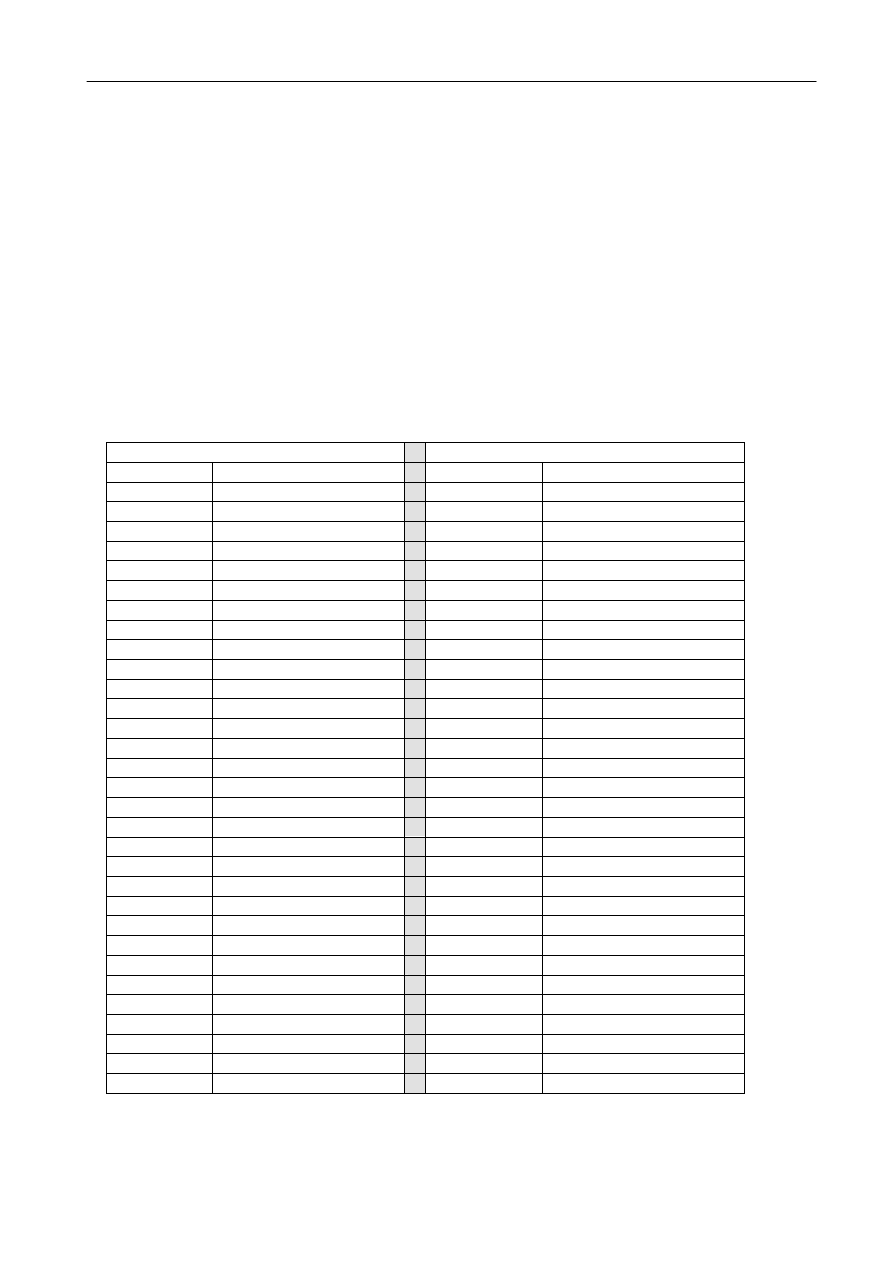
Rys. 3. Widmo rtęci.

N

at

ęż

enie linii [jednostki umowne]

Badane gazy znajdują się w rurkach Geisslera – Plückera, umieszczonych przed szczeliną

spektroskopu.
1. Za pomocą pokrętła należy ustawić rurkę z badanym gazem naprzeciwko szczeliny

spektroskopu, włączyć włącznik główny, zasilacz wysokiego napięcia oraz zasilacz oświetlenia
skali.

2. W pierwszym etapie badań należy wyskalować spektroskop przy pomocy rurki z parami rtęci,

przyporządkowując na podstawie rys. 3 długości fali (

λ) liczbom na skali spektroskopu (s).

3. Korzystając z programu komputerowego wykonać wykres otrzymanej zależności

λ(s).

Do punktów pomiarowych dopasować krzywą drugiego stopnia przyjmując liczbę punktów
ekstrapolacji równą 5000. Oszacować zdolność rozdzielczą spektroskopu, przyjmując jako

Δλ

różnicę długości fal odpowiadającą połowie najmniejszej podziałki na skali spektrometru.
Pozostawić wykres na ekranie komputera.

4. W kolejnym etapie wykonać pomiary długości fal odpowiadających liniom widm emisyjnych

gazów wskazanych przez asystenta, notując względne natężenia (intensywności, według własnej
oceny) prążków oraz wykorzystując wykonaną krzywą skalowania. Wyniki umieścić w tabelach
oznaczonych nazwą badanego gazu.

Optyczna analiza widmowa

6

5. Na podstawie uprzednio wykonanej krzywej skalowania odpowiedzieć na pytanie, czy dublet

sodowy jest możliwy do zaobserwowania przy pomocy używanego w ćwiczeniu spektroskopu.

6. Przed szczeliną spektroskopu umieścić lampę sodową i spróbować zaobserwować dublet

sodowy, a następnie ewentualnie zmierzyć długości fal odpowiadające obu prążkom.

7. Określić maksymalny błąd pomiaru jako różnicę odczytywanych długości fal dla przesunięcia

skali spektroskopu o wartość połowy odległości między działkami.

6.

OPRACOWANIE WYNIKÓW

1. Narysować widma badanych gazów w formie analogicznej do rys. 3.
2. Na podstawie zaobserwowanych linii widma wodoru oraz przy założeniu, że obserwowane linie

emisyjne należą do serii Balmera, obliczyć stałą Rydberga i porównać z wartością teoretyczną.

3. Obliczyć wartości energii odpowiadające prążkom dubletu sodowego. Porównać otrzymane

wartości z danymi tablicowymi.

4. Określić błędy obliczonych wartości.
5. Zidentyfikować gazy o energiach przejść promienistych wymienionych w tabeli poniżej:

gaz I

gaz II

Energia [eV]

Intensywność względna

Energia [eV]

Intensywność względna

2,46978 200

2,47829 40

2,43865 250

2,46225 100

2,41999 400

2,41096 100

2,38162 500

2,32691 250

2,3366 200

2,32241 200

2,32576 500

2,32146 80

2,26844 200

2,29684 600

2,23009 500

2,22986 50

2,22685 2000

2,19285 100

2,22282 80

2,16886 50

2,19561 100

2,15789 120

2,18312 400

2,15186 800

2,17987 200

2,13702 120

2,12661 100

2,13125 400

2,11283 3000

2,11948 5000

2,07006 200

2,11214 1000

2,06949 60

2,10888 1000

2,04821 60

2,10153 600

1,93207 300

2,10012 600

1,93181 100

2,08656 1000

1,92126 200

2,07934 1000

1,88799 150

2,07615 1000

1,85159 60

2,07584 1200

1,7965 100

2,07154 800

1,93207 300

2,05709 1000

1,93181 100

2,04207 1000

1,92126 200

2,03476 800

1,88799 150

2,02404 600

1,85159 60

2,01923 1000

1,7965 100

2,0125 1200

-- --

2,00646 2500

6. We wnioskach spróbować odpowiedzieć na pytanie, co oprócz linii widmowych widać było

w okularze spektroskopu?

Optyczna analiza widmowa

7

7. P

YTANIA KONTROLNE

1. Wymienić postulaty Bohra i wyjaśnić ich sprzeczność z wnioskami wypływającymi z równań

Maxwella.

2. Zdefiniować atom wodoropodobny.
3. Z czego wynikają wartości energii elektronu na poszczególnych orbitach w atomie wodoru ?
4. Co to jest widmo? Wymienić rodzaje widm emisyjnych.

8. L

ITERATURA

1. I.W. Sawieliew, Wykłady z fizyki, t. 3, Wydawnictwo Naukowe PWN W-wa (1998)
2. D. Halliday, R. Resnick, J. Walker, Podstawy Fizyki cz. 5, Wydawnictwo Naukowe PWN W-wa

(2003)

3. C.J. Sansonetti, M.L. Salit, J. Reader, Applied Optics 35, 74-77, (1996)
4. H. Haken, H.C.Wolf, Atomy I kwanty. Wprowadzenie do współczesnej spektroskopii atomowej.

Wydawnictwo Naukowe PWN (1996)

9.

DODATEK

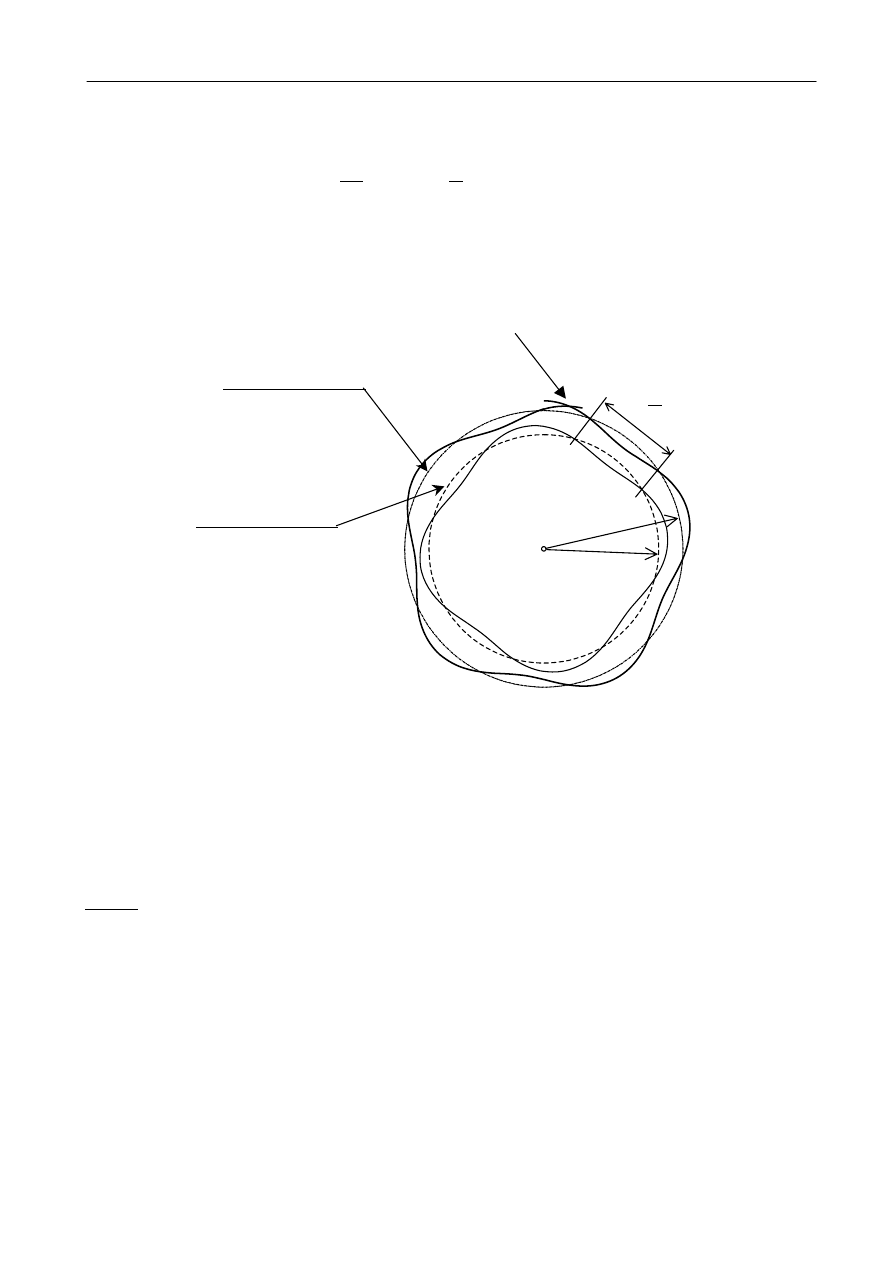
Rys. 4.
Promienie kolejnych orbit elektronu
według modelu Bohra. W skali
rysunku jądro jest niewidoczne z
powodu małych rozmiarów.

n = 4

n = 3

n = 2
n = 1

n = 5

Modelu atomu wodoru Bohra nie dało się zastosować do opisu atomów innych pierwiastków,

głównie z powodu zastosowania w nim częściowo kwantowego, a częściowo klasycznego opisu
ruchu elektronu w polu jądra. Pokazane na rys. 4 kołowe orbity elektronu są jedynie pierwszym
przybliżeniem rzeczywistości. Z praw fizyki współczesnej wiemy, że elektronowi można przypisać
falę materii (patrz instrukcja do ćwiczenia 37) o długości proporcjonalnej do odwrotności pędu
elektronu (teoria de Broglie’a powstała później niż model Bohra). Na podstawie wartości energii
elektronu możemy obliczyć jego pęd :

n

e

n

E

m

p

2

=

,

(15)

a stąd długość fali materii stowarzyszonej z elektronem:

n

n

p

h

=

λ

.

(16)

Optyczna analiza widmowa

8

Pierwszy postulat Bohra można na podstawie (16) przekształcić następująco:

⇒

h

n

r

m

n

e

=

v

π

2

nh

r

p

n

n

=

⇒

nh

r

h

n

=

λ

π

2

⇒

λ

π

n

r

n

=

2

.

(17)

Wynika stąd, że na długości obwodu kołowej orbity odkłada się całkowita wielokrotność

długości fali stowarzyszonej z elektronem, czyli fala stojąca.

orbita „zabroniona”

orbita „dozwolona”

f

ala stojąca związana z elektronem, o długości

λ,

na orbicie o promieniu r

2

istnieć nie może

2

λ

r

2

r

1

= r

n

Rys. 5.

Fala stojąca na orbicie kołowej o promieniu r

n

wyznaczonym z zależności (7)

Oznacza to, że usunięta została sprzeczność wynikająca z konieczności

wypromieniowywania energii przez poruszający się (z przyśpieszeniem dośrodkowym) elektron,
co wynika z klasycznych równań Maxwella.

Na rys. 5 przedstawiono falę materii o długości

λ wzdłuż obwodu kołowej orbity elektronu

z modelu Bohra. Z rysunku 5 oraz z (17) wynika, że fala o długości

λ może utworzyć falę stojącą

jedynie na orbitach o promieniach równym wartościom opisanym zależnością (7).

Sformułowanie modelu wyjaśniającego powstawanie widm atomowych było pierwszym

krokiem do współczesnej wiedzy o budowie atomu. Strukturę energetyczną powłok elektronowych
najprościej zobrazować w formie diagramu, pokazanego na rys. 6. Na rysunku wykreślono poziomy
energetyczne atomu wodoru. Oś pionowa wyznacza wartości energii elektronu wraz z wartościami
głównej liczby kwantowej - n

. Oś pozioma podzielona jest na odcinki odpowiadające drugiej

liczbie kwantowej, l. Wyróżnioną czcionką pokazano tzw. notację spektroskopową, systematyzującą
nazwy powłok (K, L, M, N, ...) i podpowłok (1s, 2s2p, 3s3p3d, 4s4p4d4f, ...) elektronowych
w atomie, pochodzącą z czasów Rydberga i stosowaną do dziś.

Optyczna analiza widmowa

9

-13

-12

-11

-10

-9

-8

-7

-6

-5

-4

-3

-2

-1

0

-13,6

seria
Lymana

seria Balmera

seria
Paschena - Fowlera

seria
Bracketta

seria
Pfunda

n = 1

n = 2

n = 3

n = 4

n = 5

n = 6

n =

∞

l = 0

l = 1

l = 2

l = 3

l = 4

l = 5

l = 6

seria
Humphreusa

energia elektronu [eV]

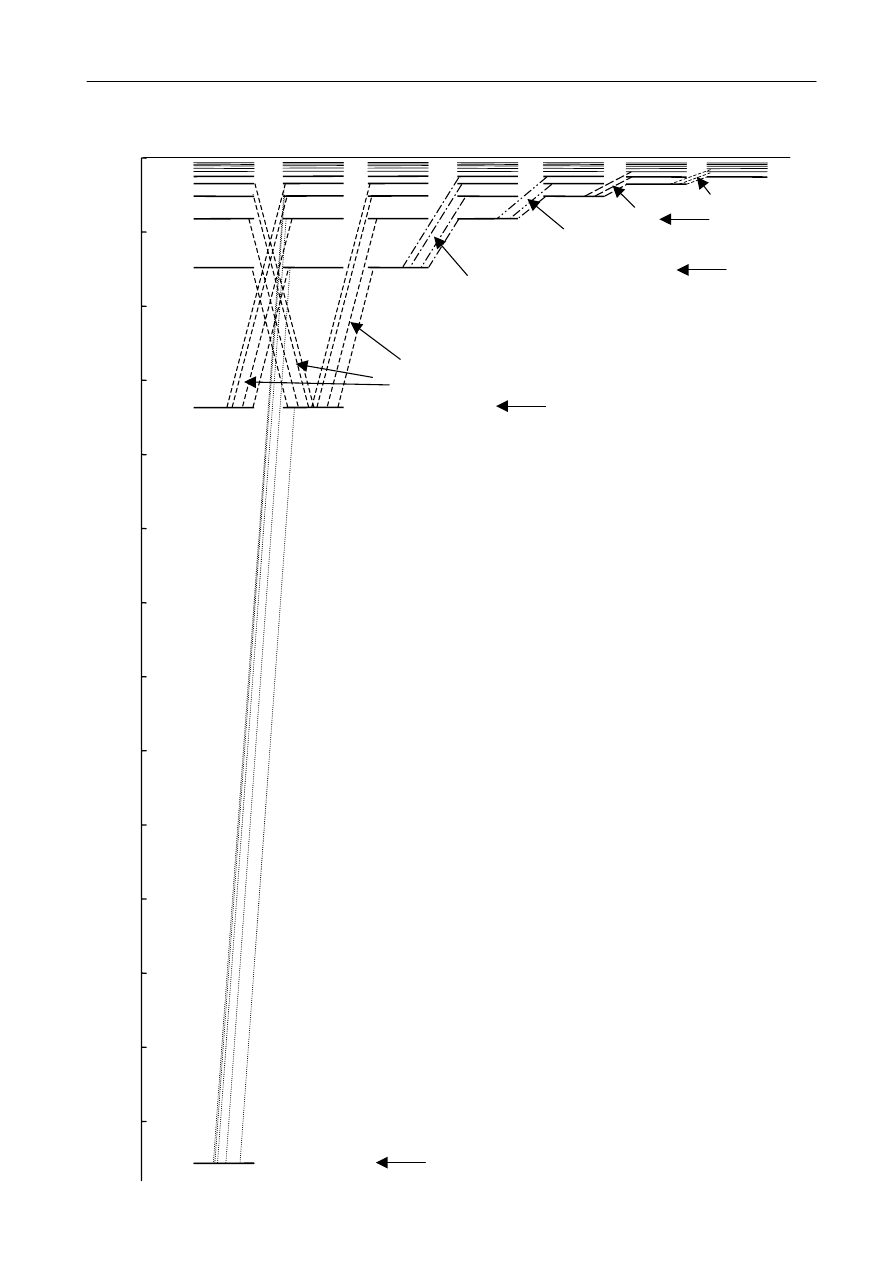
Rys. 6. Struktura poziomów energetycznych

atomu wodoru.

Poziomy energii elektronu w atomie i serie
przejść elektronów między tymi poziomami.
n oznacza numer poziomu energetycznego

(główną liczbę kwantową).

l określa orbitalny moment pędu elektronu

i oznacza poboczną (azymutalną) liczbę
kwantową.

Wyróżnioną czcionką pokazano tzw. notację
spektroskopową, systematyzującą nazwy powłok
(np. K) i podpowłok (np. 2s) elektronowych
w atomie.

1s

2s

2p

3s

3p

3d

4s

4p

4d

4f

N

M

L

K

Optyczna analiza widmowa

10

Dokładne pomiary spektroskopowe widma wodoru ujawniły pewne niejasności w modelu

Bohra. Zaobserwowano mianowicie, że linie widmowe nie są pojedynczymi liniami, ale każda z nich
składa się z kilku linii składowych. Na podstawie tych obserwacji Sommerfeld dokonał rozszerzenia
modelu Bohra. Sommerfeld postulował, że w modelu atomu dopuścić należy, podobnie jak
w problemie Keplera, oprócz orbit kołowych, również orbity eliptyczne. Do rozróżnienia orbit
kołowych i eliptycznych konieczne jest wprowadzenie drugiej liczby kwantowej l (zwanej również
orbitalną)

określającej kształt (spłaszczenie) orbity. Długość większej półosi wyznacza wartość

głównej liczby kwantowej n. Półoś mniejsza jest określana przez drugą liczbę kwantową
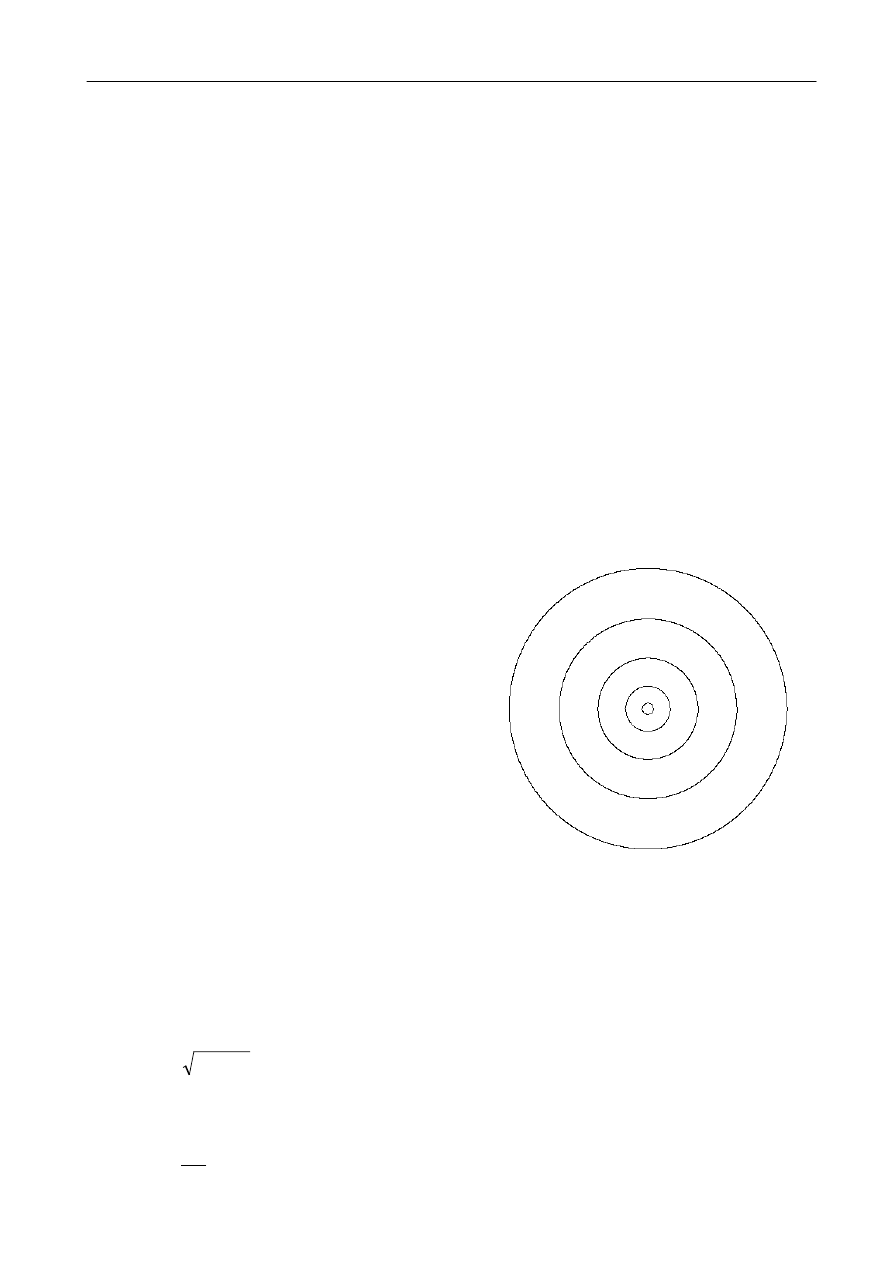
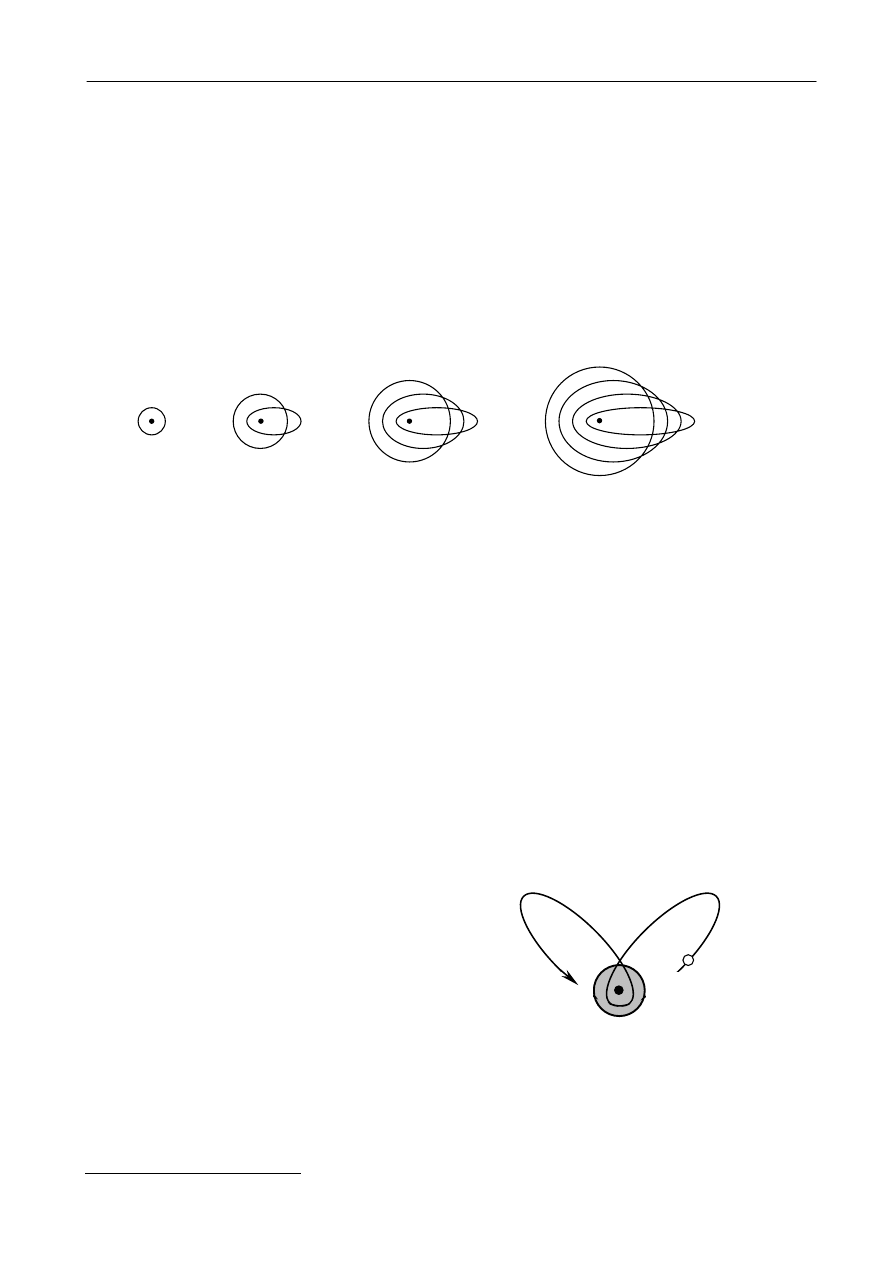
przyjmującą n wartości z zakresu l = 0, ..., n-1. Kształty orbit eliptycznych dla pierwszych czterech
głównych liczb kwantowych n i odpowiadających im liczb orbitalnych l zostały schematycznie
przedstawione na rysunku 7.

Rys. 7.
Kształty orbit elektronu odpowiadające różnym liczbom kwantowym n i l.
Długość większej półosi elipsy określona jest przez liczbę główną n, natomiast długość
mniejszej półosi jest reprezentowana przez kwantową liczbę orbitalną l.

n=1 n=2

n=3

n=4

l=0

l=1

l=0

l=2

l=1

l=0

l=3

l=2

l=1

l=0

Prędkość elektronów na orbicie kołowej jest stała, natomiast na orbitach eliptycznych

prędkość elektronu zależy od odległości od jądra. Pomimo, że prędkość elektronów w atomie
wodoru jest mniejsza niż 1% prędkości światła, relatywistyczna poprawka do energii powoduje
występowanie niewielkich różnic w energiach orbit o różnych małych półosiach. Sommerfeld
pokazał, że to efekt relatywistyczny powoduje rozszczepienie poziomu energetycznego opisywanego
przez liczbę n na n podpoziomów o różnych l, co obserwowane jest jako rozszczepienie
pojedynczych linii widmowych. Efekt relatywistyczny prowadzi do rotacji peryhelium

*

orbity.

W intuicyjnym obrazie, elektron porusza się wokół jądra ruchem rozetowym (rys. 8).

Rys. 8.
Rotacja peryhelium orbity eliptycznej
podczas ruchu elektronu wokół jądra
w atomie wieloelektronowym.
Zacieniowany obszar symbolizuje powłokę
elektronową. Zewnętrzny elektron wędruje
po „orbicie nurkującej”, zagłębiając się
w elektronową powłokę atomu.

-

e

Oprócz głównej liczby kwantowej n, oznaczającej w chemii numer powłoki elektronowej

oraz liczby orbitalnej l odpowiedzialnej za poprawkę relatywistyczną, istnieją jeszcze dwie liczby
kwantowe: magnetyczna - m oraz spinowa - s. Istnienie liczby magnetycznej związane jest

*

Peryhelium – punkt na orbicie znajdujący się najbliżej jądra

Optyczna analiza widmowa

11

z istnieniem skończonej ilości możliwych orientacji przestrzennych orbity elektronu. W obecności
pola magnetycznego każde z takich położeń ma nieco inną energię, co prowadzi do kolejnego
rozszczepienia linii widmowych i znane jest jako efekt Zeemana. Z kolei liczba spinowa jest
świadectwem faktu, że elektron oprócz orbitalnego momentu pędu posiada wewnętrzny moment
pędu charakteryzowany przez kwantową liczbę spinową s = 1/2. Wzajemna relacja pomiędzy
momentem orbitalnym a wewnętrznym momentem pędu elektronu prowadzi do rozszczepienia linii
widmowej na dwie blisko siebie leżące linie. Efekt ten znany jest jako sprzężenie spin-orbita.
W przypadku żółtej linii widmowej sodu rozszczepienie wywołane tym sprzężeniem wynosi
0,0021 eV.

Widma atomów metali alkalicznych

*

są kolejnym, po widmach atomów z jednym

elektronem, stosunkowo prostym przykładem widm. W atomach metalu alkalicznego elektron
walencyjny o ładunku -e porusza się w stosunkowo dużej odległości od jądra w polu
elektrostatycznym układu cząstek o ładunku +Ze, które w znacznym stopniu ekranowane jest przez
Z-1 elektronów. W ten sposób problem wielu ciał można zredukować do problemu jednej cząstki,
a

poziomy energetyczne atomu metalu alkalicznego rozpatrywać w kategoriach atomu

jednoelektronowego. W tym sensie obraz przedstawiony na rysunku 8 pozostaje słuszny nawet
w mechanice kwantowej. Ekranowanie elektronów uwzględnia się wprowadzając tzw. efektywną
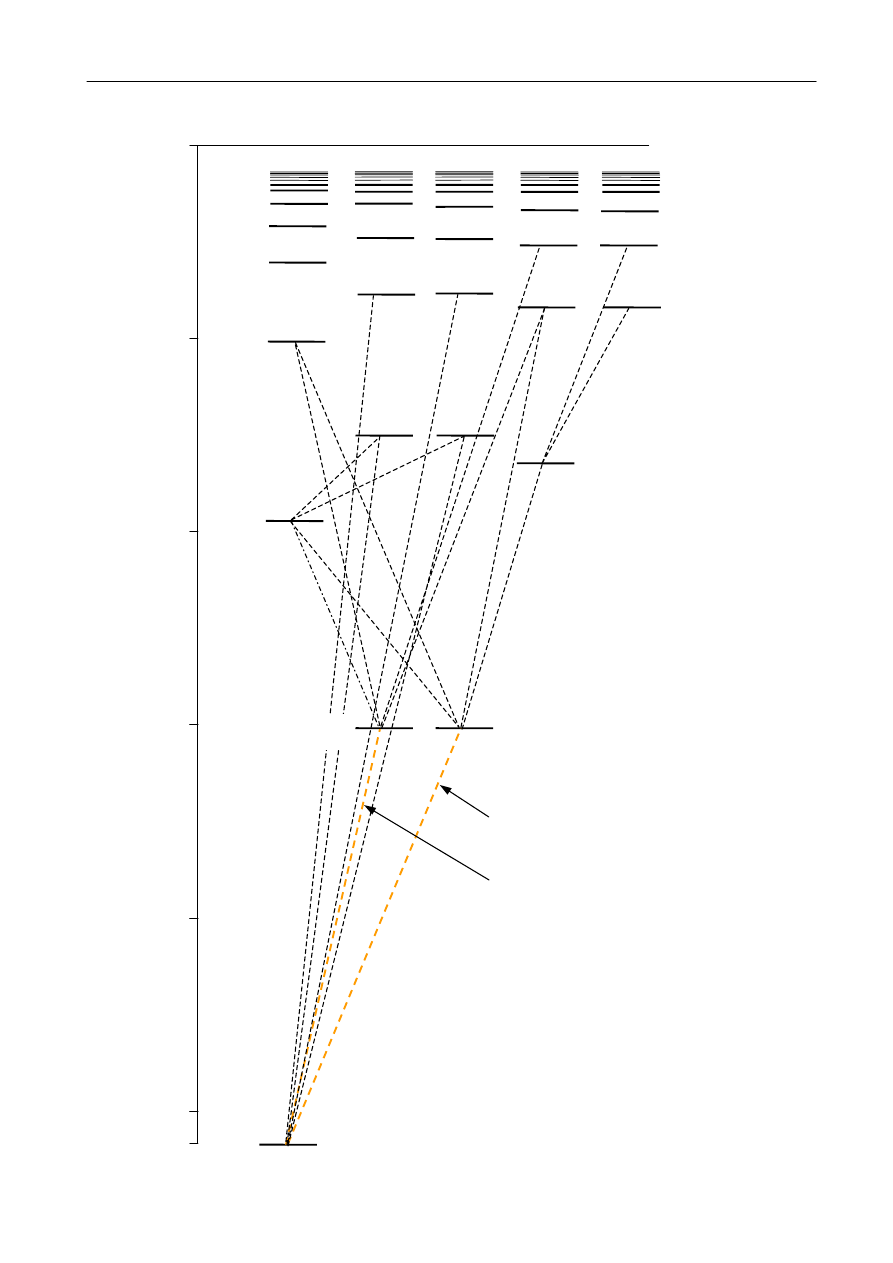
główną liczbę kwantową, nie będącą w ogólności liczbą całkowitą. Diagram poziomów
energetycznych dla sodu obliczony przy użyciu efektywnej liczby kwantowej przedstawiony jest
na rysunku 9.

Należy w tym miejscu nadmienić, że przedstawiony powyżej skrótowo model Bohra-

Sommerfelda należy do tzw. „starej teorii kwantów”, w której próbowano wykorzystać niektóre
pojęcia klasyczne do opisu zjawisk atomowych. W miarę prawidłowo opisuje ona jedynie atom
wodoru, i to bez możliwości wprowadzenia spinu. Już przy obliczeniach dla atomu z dwoma
elektronami, wyniki obliczeń stają się wyraźnie niezgodne z doświadczeniem. Trudności, które
napotykał model Bohra-Sommerfelda zostały usunięte wraz z rozwojem mechaniki kwantowej,
zapoczątkowanym przez Schrödingera, Heisenberga i Diraca. Rozwiązując równanie Schrödingera
dla elektronu poruszającego się w polu dodatniego jądra otrzymamy rozwiązanie, którym nie można
opisać „toru” elektronu. Otrzymujemy za to wartości poziomów energetycznych E

n

oraz funkcje

falowe, które określają prawdopodobieństwo znalezienia elektronu w przestrzeni otaczającej jądro.
Pierwsze trzy liczby kwantowe (n, l, m) wyznaczają znane z teorii wiązań międzyatomowych
orbitale

, których kształt wynika bezpośrednio z analitycznej postaci funkcji falowych, będących

rozwiązaniami równania Schrödingera.

Wszystkie rysunki w niniejszej instrukcji wykonano w skali energii odpowiadającej opisanym
w niej modelom matematycznym.

*

Metale alkaliczne - pierwiastki chemiczne (np.: Li, Na, K) o własnościach metalicznych, których atomy
charakteryzuje obecność pojedynczego, zewnętrznego, słabo związanego elektronu.

Optyczna analiza widmowa

12

2

S

1/2

2

P

3/2

2

P

1/2

2

D

3/2,5/2

2

F

5/2,7/2

-5,12

-5

0

-3

-4

-2

-1

energia elektronu [eV]

n =

∞

n = 3

n = 3

n = 4

n = 5

n = 4

n = 4

n = 4

n = 5

n = 4

Rys. 9.
Diagram poziomów energetycznych dla sodu
obliczony przy użyciu efektywnej liczby
kwantowej. Żółte linie oznaczają przejścia
tworzące dublet sodowy.

589,6 nm

n = 5

589,0 nm

n = 3

n = 3

n = 6

n = 6

n = 5

n = 6

n = 5

n = 7