Transformator o

skończonej indukcyjności

Do tej pory zakładaliśmy, że uzwojenia trans-
formatora, a przynajmniej uzwojenie pierwot-
ne, ma nieskończenie wielką indukcyjność,
co uprościło rozważania, ale nie pozwoliło
uchwycić rzeczywistej zasady pracy transfor-
matora. Okazuje się, że transformator o ogra-
niczonej indukcyjności uzwojeń też może być
transformatorem idealnym, byle tylko uzwo-
jenia te miały zerową rezystancję. Dopiero
rozpatrzenie takiego transformatora bez strat,
ale o ograniczonej indukcyjności uzwojeń,
pozwoli w pełni zrozumieć zasadę działania
transformatora. Początkujący mają problemy
ze zrozumieniem tych zagadnień, jeżeli nie
poukładają sobie w głowie najbardziej podsta-
wowych wiadomości. Częsty błąd polega na
tym, że szukają oni związku napięcia wejścio-
wego z wyjściowym bez należytego zrozumie-
nia roli prądu i strumienia magnetycznego.

My dla uproszczenia rozważmy najpierw

stan jałowy transformatora o skończonej
indukcyjności. Żeby ułatwić analizę, niech
to będzie

transformator sieciowy, czyli taki

dołączony do sieci energetycznej 230V.

Wtedy do źródła napięcia sinusoidalnego o
niezmiennym napięciu 230V podłączone jest
uzwojenie pierwotne, a uzwojenie wtórne
nie jest nigdzie podłączone i tak naprawdę
transformator zachowuje się jak zwyczajna
cewka z dodatkowym, nieczynnym uzwoje-
niem wtórnym. Warto najpierw dokładniej
rozważyć zjawiska zachodzące w tak pracują-
cej zwykłej cewce, a dopiero potem przejść
do transformatora.

Napięcie, prąd, strumień,

napięcie...

Przy omawianiu cewek już wspomnieliśmy
o zjawisku „samopilnowania”. Musimy do
tego wrócić. W obwodzie z rysunku 17
mamy źródło napięcia stałego U

ZAS

, a cewka

jest idealna, więc nie ma rezystancji ograni-
czającej prąd. Dlaczego więc po zamknięciu
obwodu przez cewkę nie zaczyna natych-
miast płynąć ogromny prąd? Co jest

czynni-

kiem hamującym?

Tym czynnikiem hamującym nie jest rezy-
stancja, która w przypadku cewki idealnej
jest równa zeru. Już wcześniej stwierdzili-
śmy, że zmiany prądu płynącego w cewce
powodują powstanie napięcia samoinduk-
cji, którego wartość (SEM) jest wprost
proporcjonalna do szybkości zmian prądu,
co możemy zapisać SEM =

dI/dt (w uprosz-

czeniu SEM =

ΔI/Δt). Wiemy, że czynnikiem

hamującym i wyznaczającym szybkość nara-
stania prądu jest więc napięcie samoindukcji
SEM, które odejmuje się od napięcia zasi-
lającego (kompensuje napięcie zasilające).
Prąd rośnie z dokładnie taką szybkością,
żeby wytworzone napięcie (SEM) było równe
napięciu zasilania Uzas, czyli żeby różnica
między tymi napięciami była... równa zeru.
Jeśliby prąd rósł wolniej, to wytworzona
wartość SEM byłaby mniejsza od U

ZAS

i róż-

nica tych napięć natychmiast spowodowałaby
wzrost szybkości narastania prądu, by dopro-
wadzić do równości SEM=U

ZAS

. Analogicznie

zbyt duża wartość prądu spowodowałaby
wytworzenie zbyt dużego napięcia SEM, co
zahamowałoby szybkość narastania prądu.

W cewce podłączonej do napięcia

stałego

mamy więc do czynienia ze swego rodzaju
autoregulacją, „samopilnowaniem” – szybkość
narastania prądu i wytwarzane napięcie SEM
„pilnują się wzajemnie”. Ale to pilnowanie
wiąże tylko szybkość narastania prądu z napię-
ciem, a nie ogranicza wartości prądu – w
obwodzie prądu stałego prąd narasta liniowo,
teoretycznie aż do nieskończoności, jak poka-
zuje rysunek 17.

Z wcześniejszych rozważań wiemy, że w

przypadku dołączenia cewki do źródła napię-
cia zmiennego, szybkość i kierunek zmian
prądu są wyznaczone przez chwilową wartość
i biegunowość napięcia na cewce. Co dla nas
teraz najważniejsze, istnieje jeden przypadek
szczególny: otóż w przypadku dołączenia
cewki do źródła

napięcia sinusoidalnego,

prąd też jest sinusoidalny, jak ilustruje to
rysunek 18. Już wcześniej podkreślałem, że
podstawowa zasada jest ta sama dla prądu
stałego i zmiennego: podanie napięcia na
cewkę powoduje zmiany płynącego przez
nią prądu, a to skutkuje powstaniem napięcia
samoindukcji.

Teraz dla zrozumienia zasady działania

transformatora, trzeba dokładniej przyjrzeć
się napięciu samoindukcji i rozważyć nastę-
pującą sekwencję przyczynowo-skutkową:
napięcie zasilania

→ prąd w cewce → stru-

mień magnetyczny

→ napięcie samoindukcji.

Otóż dołączenie do cewki

napięcia powoduje

przepływ przez nią

prądu. Ten prąd, przepły-

wając przez cewkę, spowoduje wytworzenie

pola magnetycznego, a konkretnie
strumienia magnetycznego, ściślej

strumienia indukcji magnetycznej.

Zapamiętaj: przepływ prądu przez
cewkę powoduje powstanie stru-
mienia magnetycznego.

Nie musisz rozumieć ze wszyst-

kimi szczegółami, czym jest

pole

magnetyczne, strumień indukcji

magnetycznej, oznaczany Φ, czy

natężenie pola magnetycznego,
oznaczane H i

indukcja magne-

tyczna, oznaczana literą B. Ścisłe
definicje tych pojęć i wielkości są

Rys. 17

Transformator idealny – Wykład 2

Elektronika

Elektronika

(nie tylko) dla informatyków

(nie tylko) dla informatyków

Elementy i układy elektroniczne

Elementy i układy elektroniczne
wokół mikroprocesora

wokół mikroprocesora

32

Elektronika dla informatyków

Elektronika dla Wszystkich

Sierpieñ 2010

Sierpieñ 2010

+ U

ZAS

U

ZAS

I

I

L

U

=

c

o

n

s

t

U=const

pr¹d coraz

wiêkszy

pr¹d coraz

wiêkszy

niezmienne napiêcie

niezmienne napiêcie

t

t

czas

t

czas

I

I

X

L

X

L

dla wartoœci skutecznych

U, I

wystepuje zale¿noœæ:

dla wartoœci skutecznych

U, I

wystepuje zale¿noœæ:

=

I

L

U

ZAS

U

ZAS

U

ZAS

U

ZAS

U

ZAS

U

Z

A

S

Rys. 18

naprawdę skomplikowane, o czym możesz
się przekonać choćby w Wikipedii. Na razie
radykalnie uprośćmy zagadnienie: zapewne
pamiętasz ze szkolnych lekcji lub podręcz-
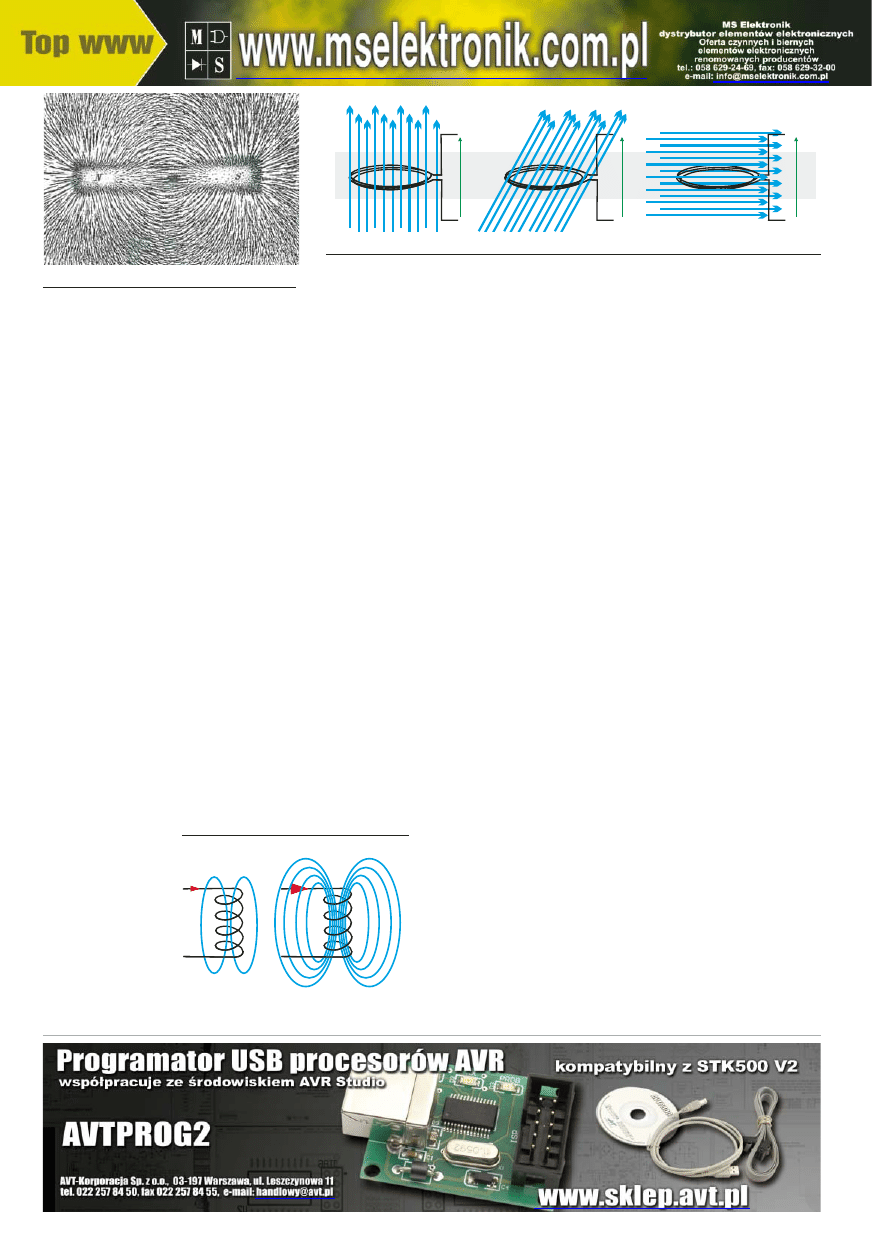
ników fizyki doświadczenie z magnesem i
opiłkami żelaza – opiłki żelaza tworzą wokół
magnesu swego rodzaju linie, pętle – fotogra-
fia 19 (z Wikipedii). Możemy sobie wyobra-
żać, że czym silniejszy magnes, tym więcej
jest tych linii. Przy przepływie prądu przez
cewkę tworzy się elektromagnes i też wystę-
pują takie linie pola magnetycznego. Śmiało
możemy uważać, że strumień magnetyczny
to liczba linii sił pola magnetycznego. W
pierwszym przybliżeniu możemy też przyjąć,
że strumień jest wprost proporcjonalny do
prądu płynącego przez cewkę. Czym większy
prąd, tym większy strumień – rysunek 20.

Żebyśmy nie zgubili obrazu całości, pod-

kreślam, że w zasadzie w cewce i transfor-
matorze „pierwotną przyczyną” jest napięcie
Uzas. Napięcie to powoduje przepływ przez
cewkę prądu. Przepływ prądu przez cewkę
powoduje powstanie strumienia magnetycz-
nego. I tu w grę wchodzi kolejne ważne zjawi-
sko: zjawisko indukcji elektromagnetycznej,
odkryte w roku 1831 przez M. Faradaya. Otóż
zmiany strumienia magnetycznego powodują
indukowanie się napięcia w przewodniku
umieszczonym w tym zmiennym polu mag-
netycznym. Napięcie to bywa też nazywane
siłą elektromotoryczną i oznaczane SEM.
Podkreślam, że napięcie jest wytwarzane nie
pod wpływem

obec-

ności strumienia mag-
netycznego, tylko pod
wpływem zmian stru-
mienia magnetycznego
(lub ruchu przewodnika
w tym polu, ale to inny
przypadek). Jeśli nie ma
zmian strumienia mag-
netycznego, to nie indu-
kuje się napięcie. W
zasadzie zmiany stru-

mienia indukują napięcie w każdym przewod-
niku, ale nas interesuje indukowanie napięcia
w zwoju, a właściwie w wielu zwojach. Nie
wchodząc w szczegóły, możemy powiedzieć,
że zwój w pełni wykorzystuje strumień mag-
netyczny, jeżeli linie pola magnetycznego są
prostopadłe po płaszczyzny zwoju. Gdy linie
pola tworzą z płaszczyzną zwoju kąt inny niż
prosty, „stopień wykorzystania” jest mniej-
szy. W skrajnym przypadku, gdy linie pola
są równoległe do płaszczyzny zwoju, zmiany
tego pola nie indukują żadnego napięcia.
Ilustruje to rysunek 21. Ma to duże znacze-
nie praktyczne, ale nie będziemy wchodzić w
szczegóły. W cewce i w transformatorze linie
pola są prostopadłe do powierzchni zwojów,
według rysunku 21a.

I oto mamy tu pełniejsze wyjaśnienie oma-

wianej wcześniej samoindukcji w cewce: to
zmieniający się strumień magnetyczny powodu-
je powstanie napięcia w każdym zwoju cewki.
Powstające napięcie SEM jest wprost propor-
cjonalne właśnie do szybkości zmian strumienia
magnetycznego, ale strumień zależy od prądu,
dlatego SEM jest wyznaczona przez szybkość
zmian prądu (SEM

≈ dI/dt). Zgodnie z regu-

łą przekory Lenza, tak indukowane napię-
cie (siła elektromotoryczna SEM) będzie się
odejmować od napięcia zasilającego U

ZAS

i

podczas normalnej pracy cewki/transforma-
tora wypadkowa tych obydwu napięć będzie
równa zeru, czy też bardzo bliska zeru, żeby
zapewnić przepływ przez cewkę prądu o
potrzebnej wartości.

To jest proste, ale może znów nasunie Ci

się pytanie: a skąd cewka
wie, jak duże ma być
to indukowane napięcie
SEM i „prąd o potrzebnej
wartości”? Otóż cewka nie
musi niczego wiedzieć:
gdyby sinusoidalny prąd
i powstający sinusoidalny
strumień były za małe, to
powstające sinusoidalne
napięcie samoindukcji
SEM byłoby zbyt małe

i nie skompensowałoby napięcia zasilania.
Wtedy różnica napięć spowodowałaby wzrost
prądu, a tym samym szybkości zmian prądu i
strumienia do takiej wartości, by dokładnie
skompensować napięcie zasilające.

Omawiane zasady dotyczą napięć wej-

ściowych o dowolnym kształcie. Co ważne,
podanie na cewkę napięcia sinusoidalnego
spowoduje przepływ przez nią sinusoidalnego
prądu, przesuniętego o jedną czwartą okresu
(rysunek 18). Podobnie sinusoidalny kształt
ma też przebieg zmian strumienia magnetycz-
nego. W tym szczególnym przypadku sinusoi-
dalnego napięcia zasilającego możemy mówić
o oporności: przy częstotliwości f cewka o
indukcyjności L przedstawia sobą oporność,
reaktancję indukcyjną X

L

, o wartości:

X

L

= 2

ππfL

Oznacza to, że napięcie U

ZAS

powoduje prze-

pływ przez cewkę prądu o wartości wyzna-
czonej przez reaktancję indukcyjną X

L

:

I = U

ZAS

/X

L

Przy przebiegach o innych kształtach, niż
sinusoidalny takich obliczeń nie można wyko-
nywać, bo nie mają one sensu.
A teraz jeszcze inny aspekt zagadnienia: w
idealnej cewce nie występują straty. Oznacza
to, że płynący prąd sinusoidalny w jednej czę-
ści okresu przenosi energię ze źródła zasilania
do cewki (ładuje cewkę), a po chwili, w dru-
giej części okresu, prąd ten przenosi tę energię
w przeciwnym kierunku – z cewki z powro-
tem do źródła zasilania. I tak jest w każdym
cyklu przebiegu zmiennego. W przypadku
idealnym mamy więc jedynie do czynienia z
cyklicznym przekazywaniem energii między
źródłem a cewką raz w jedną, raz w drugą
stronę, bez żadnych strat. Przy przebiegu o
częstotliwości 50Hz, taka cykliczna wymiana
energii następuje 50 razy na sekundę.

I oto mamy wszelkie informacje, potrzeb-

ne do analizy stanu jałowego transformatora,
bo transformator w stanie jałowym to po pro-
stu cewka z dodatkowym, niepodłączonym
uzwojeniem.

Zajmiemy się tym w następnym odcinku.

Piotr Górecki

Rys. 20

Fot. 19

ma³y pr¹d

ma³y pr¹d

ma³y

du¿y

strumieñ

strumieñ

magnetyczny

magnetyczny

du¿y pr¹d

du¿y pr¹d

du¿e

napiêcie

d

u

¿

e

n

a

p

iê

c

ie

brak

napiêcia

b

ra

k

n

a

p

iê

c

ia

U

=

0

a)

b)

c)

ma³e

napiêcie

m

a

³e

n

a

p

iê

c

ie

Rys. 21

R E K L A M A

Elektronika dla informatyków