PADER collection

MATEMATYKA – Semestr II – Rachunek różniczkowy dr Stanisław Kiełtyka

- 1 -

RACHUNEK RÓŻNICZKOWY FUNKCJI

2 i 3 ZMIENNYCH

¾

ZBIORY PŁASKIE

¾

FUNKCJE DWÓCH ZMIENNYCH

¾

GRANICA i CIĄGŁOŚĆ FUNKCJI DWÓCH ZMIENNYCH

¾

WŁASNOŚCI FUNKCJI CIĄGŁYCH

¾

POCHODNA CZĄSTKOWA FUNKCJI DWÓCH

ZMIENNYCH

¾

POCHODNA FUNKCJI ZŁOŻONEJ

¾

PŁASZCZYZNA STYCZNA

¾

RÓŻNICZKA ZUPEŁNA

¾

POCHODNE CAŁKOWE i RÓŻNICZKI WYŻSZYCH

RZĘDÓW

¾

EKSTREMUM FUNKCJI DWÓCH ZMIENNYCH

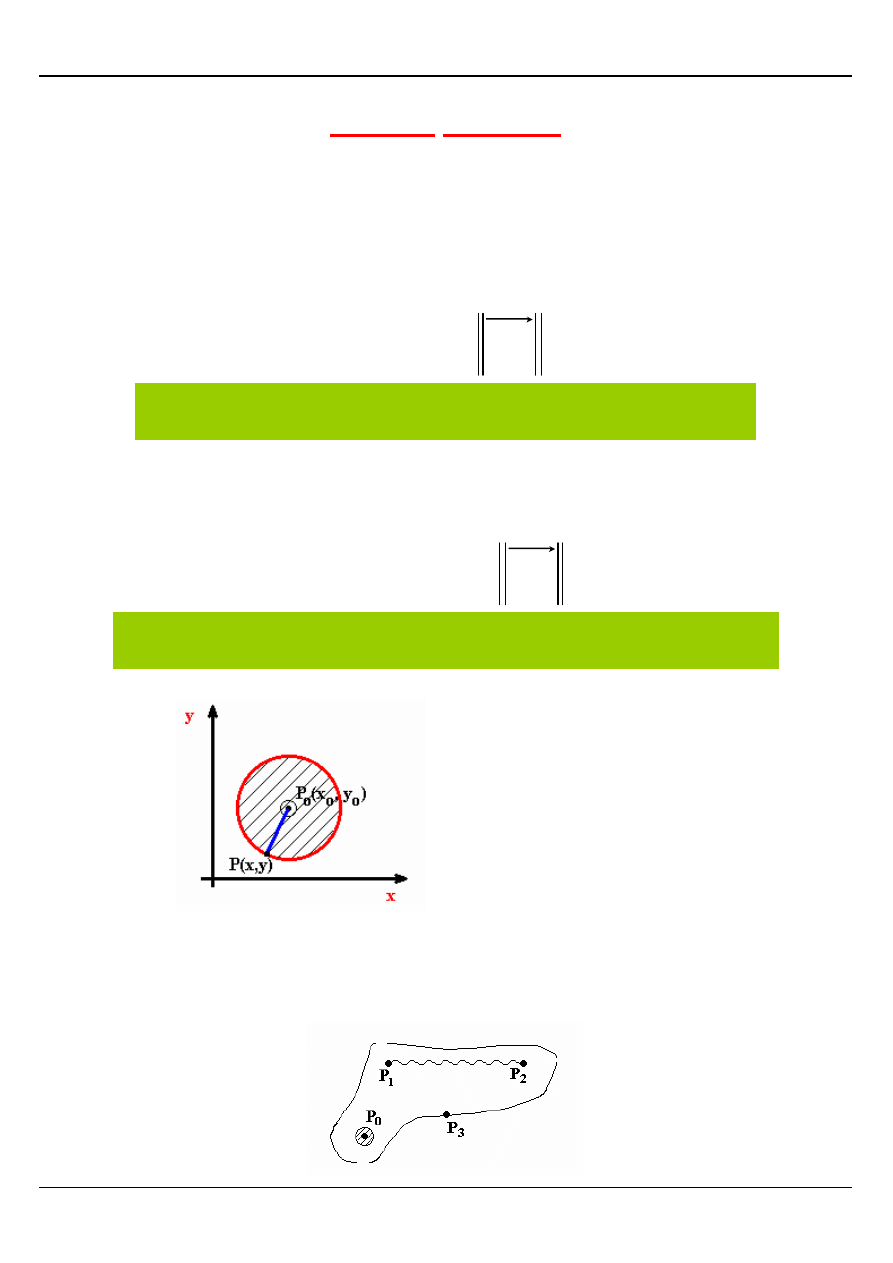
PADER collection

MATEMATYKA – Semestr II – Rachunek różniczkowy dr Stanisław Kiełtyka

- 2 -

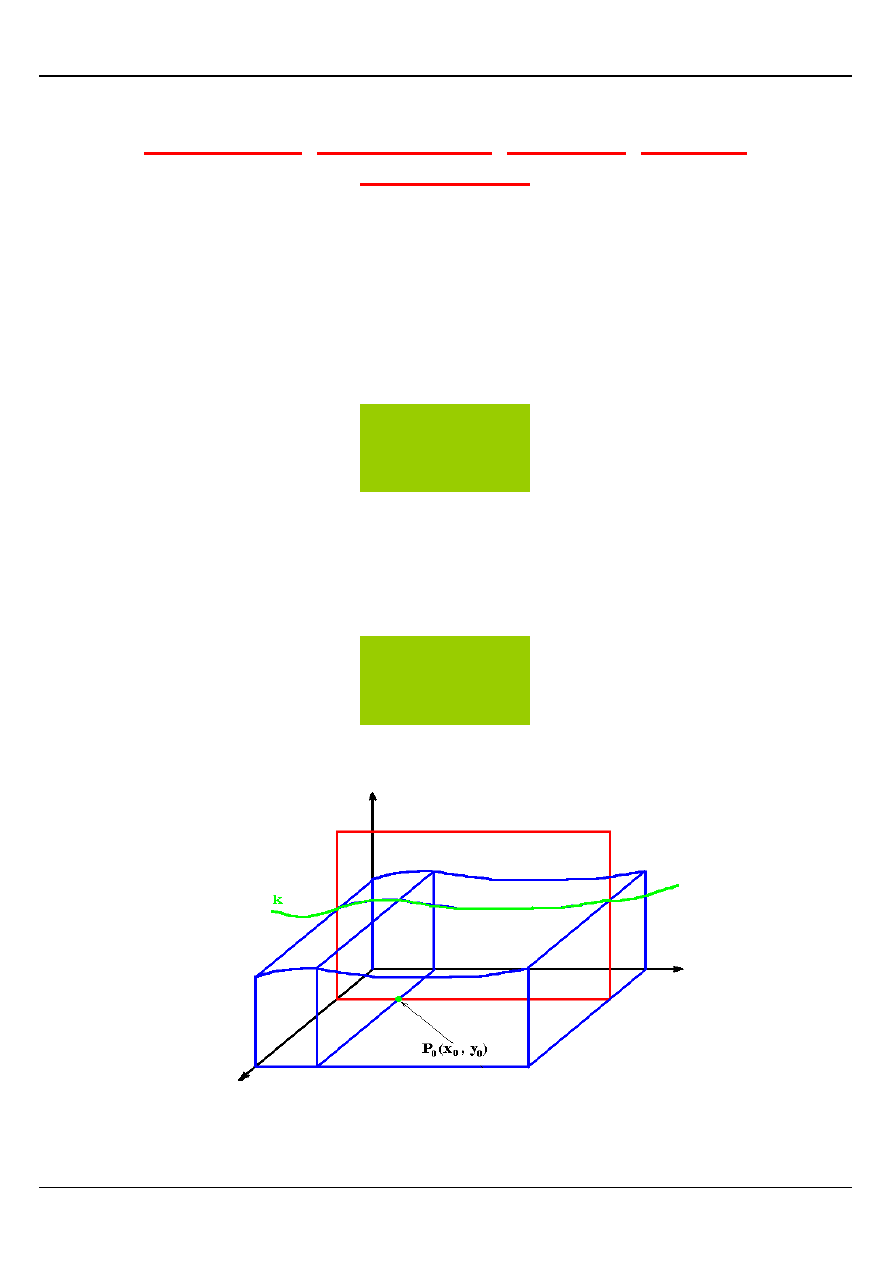
ZBIORY PŁASKIE

Def.

Zbiór płaski to zbiór na płaszczyźnie Oxy.

Def.

Otoczenie punktu P

o

(x

o

, y

o

) o promieniu r to zbiór punktów P(x , y) płaszczyzny

r}

P

P

:

{P

r)

,

O(P

0

0

<

=

}

r

)

y

(y

)

x

(x

:

y)

{(x,

r)

,

O(P

2

2

0

2

0

0

<

−

+

−

=

Def.

Sąsiedztwo punktu P

o

(x

o

, y

o

) o promieniu r to zbiór punktów P(x , y) płaszczyzny

r}

P

P

0

:

{P

r)

,

S(P

0

0

<

<

=

}

r

)

y

(y

)

x

(x

0

:

y)

{(x,

r)

,

S(P

2

2

0

2

0

0

<

−

+

−

<

=

Sąsiedztwo bez środka

Def.

Punkt P

∈ A nazywać będziemy punktem wewnętrznym zbioru A jeżeli należy

do zbioru A pewnego otoczenia puktu P.

PADER collection

MATEMATYKA – Semestr II – Rachunek różniczkowy dr Stanisław Kiełtyka

- 3 -

Dopełnienie Zbioru

Dopełnienie danego zbioru płaskiego to zbiór utworzony ze wszystkich punktów, które do
danego zbioru nie należą.

Punkt Brzegowy

Punkt brzegowy zbioru to punkt, w którego otoczeniu znajdują się punkty zarówno do
zbioru należące jak i nienależące.

Zbiór Spójny

Zbiór płaski nazywamy spójnym jeżeli każde dwa jego punkty można połączyć linią ciągłą
całkowicie zawartą w tym zbiorze.

Mówimy, że odcinek PQ rozcina zbiór jeżeli istnieją takie dwa jego punkty, których nie
można połączyć linią ciągłą w tym zbiorze, która by nie przecinała tego odcinka.

Zbiór Jednospójny

Zbiór spójny nazywamy jednospójnym jeżeli jego dopełnienie do całej płaszczyzny jest
zbiorem spójnym.
W przypadku, gdy zbiór jest ograniczony można podać (inną) równoważną definicję
jednospójności.
Zbiór ograniczony nazywamy jednospójnym, jeżeli każdy odcinek łączący punkty
zewnętrzne tego zbioru i przechodzący przez punkt wewnętrzny zbioru rozcina ten zbiór.

Zbiór Otwarty

Zbiorem otwartym będziemy nazywać zbiór, który zawiera tylko punkty wewnętrzne
(bez brzegu).
Obszar otwarty oznacza zbiór spójny otwarty.

Zbiór Domknięty

Zbiorem domkniętym nazywamy zbiór, który zawiera wszystkie swoje punkty brzegowe.
Obszar domknięty oznacza obszar otwarty z dołączonym brzegiem.

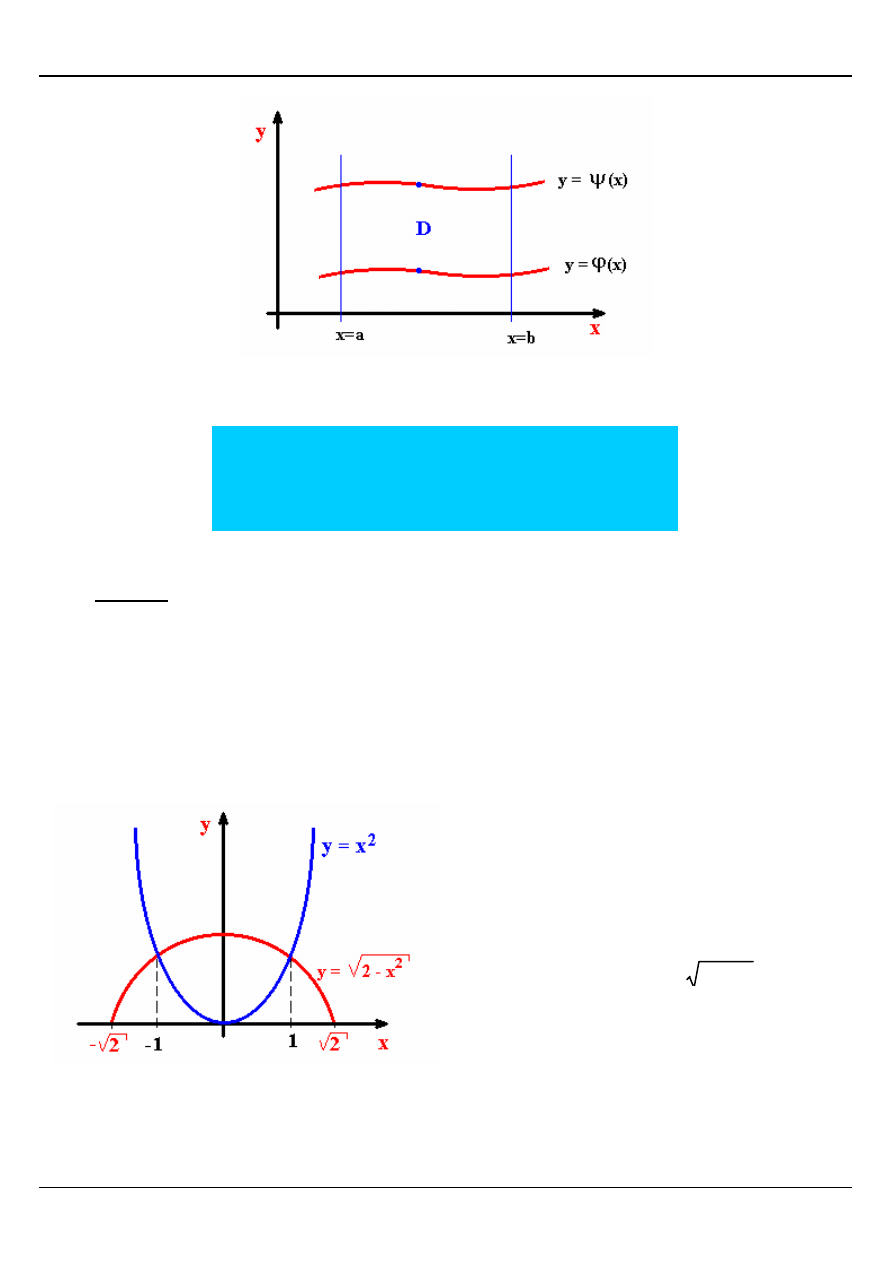
Obszar normalny

Obszar nazywamy normalnym względem danej osi Ox lub Oy jeżeli każda prosta
prostopadła do tej osi i przechodząca przez jego punkt wewnętrzny przecina brzeg obszaru
w dwóch punktach.

PADER collection

MATEMATYKA – Semestr II – Rachunek różniczkowy dr Stanisław Kiełtyka

- 4 -

Zapis analityczny obszaru D normalnego względem osi Ox.













≤

≤

≤

≤

=

ψ(x)

y

(x)

b

x

a

y)

(x,

D

ϕ

Przykład

Narysować i zapisać analitycznie obszar D ograniczony krzywymi

0

x

2

x

2

2

2

≥

=

=

+

y

y

y

















−

≤

≤

≤

≤

=

2

2

x

2

y

x

1

x

1

-

:

y)

(x,

D

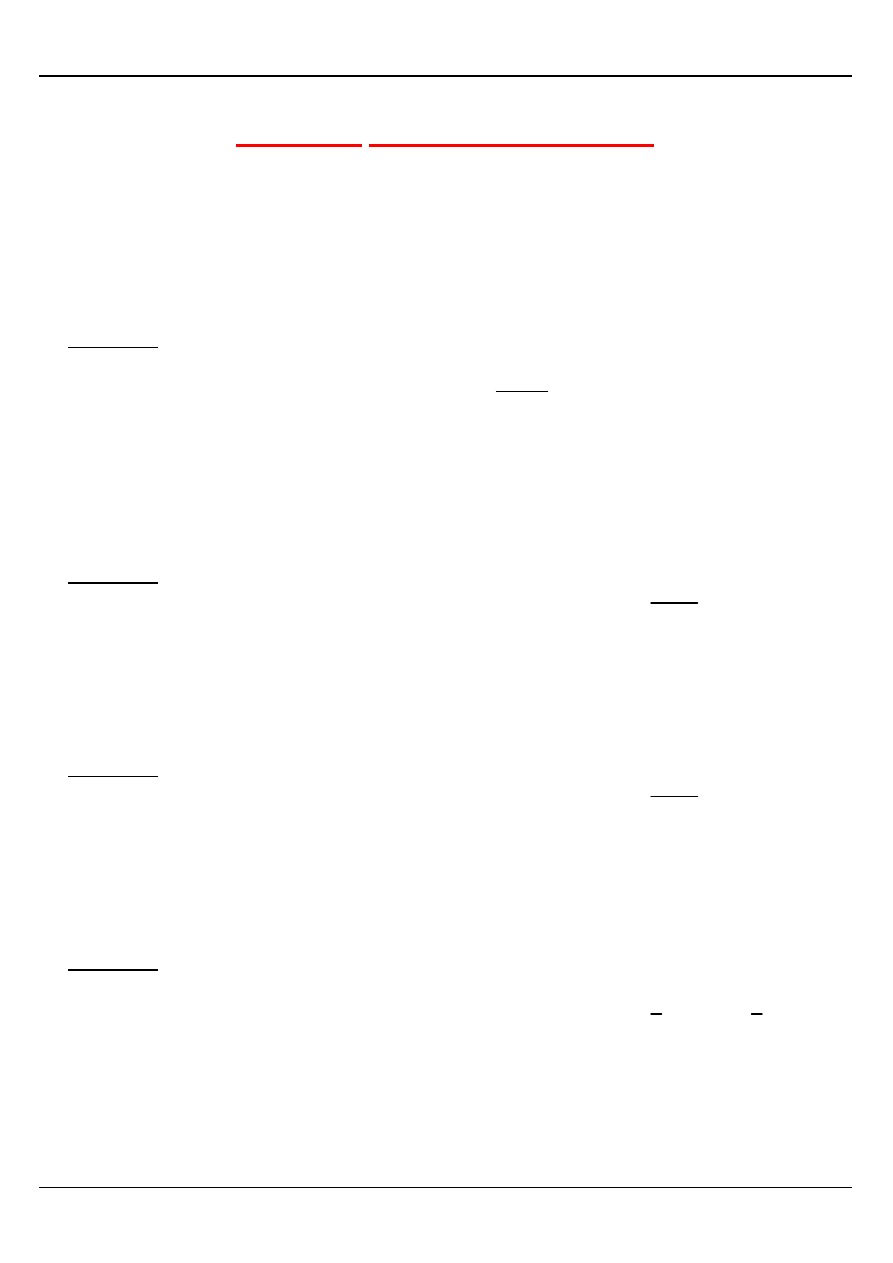
PADER collection

MATEMATYKA – Semestr II – Rachunek różniczkowy dr Stanisław Kiełtyka

- 5 -

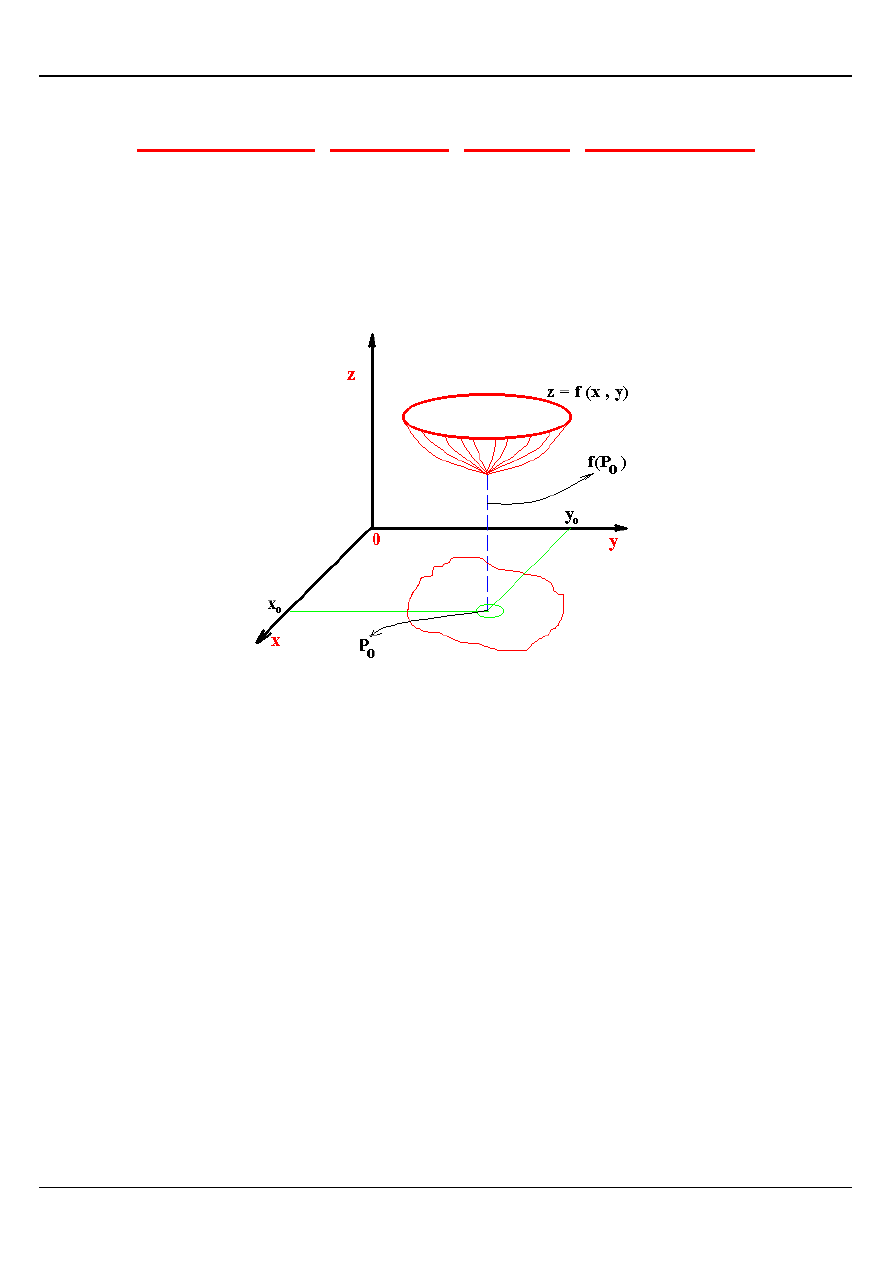
FUNKCJE DWÓCH ZMIENNYCH

Jeżeli każdemu punktowi P(x , y) zbioru płaskiego D przyporządkujemy dokładnie jedną
liczbę rzeczywistą z, to mówimy, że na zbiorze D została określona funkcja dwóch
zmiennych z = f (x , y) [ z = f(D) ].


Przykład 1

Wyznaczyć obszar określoności funkcji

x

sin

1

x

2

y)

f(x,

+

=

Odp.

w tym przypadku

D

f

= R

2

Przykład 2

Wyznaczyć obszar określoności funkcji

2

2

y

x

1

y)

f(x,

+

=

Odp.

D

f

= { (x , y): x ≠ 0

∧

y ≠ 0 }

Przykład 3

Wyznaczyć obszar określoności funkcji

2

2

x

y

x

y)

f(x,

−

=

Odp.

D

f

= { (x , y): y ≠ x

∧

y ≠ -x }

Przykład 4

Wyznaczyć obszar określoności funkcji

4

3

2

arcsin

arcsin

y)

f(x,

+

=

x

Odp.

D

f

= { (x , y): -2 ≤ x ≤ 2

∧

-3 ≤ y ≤ 3 }

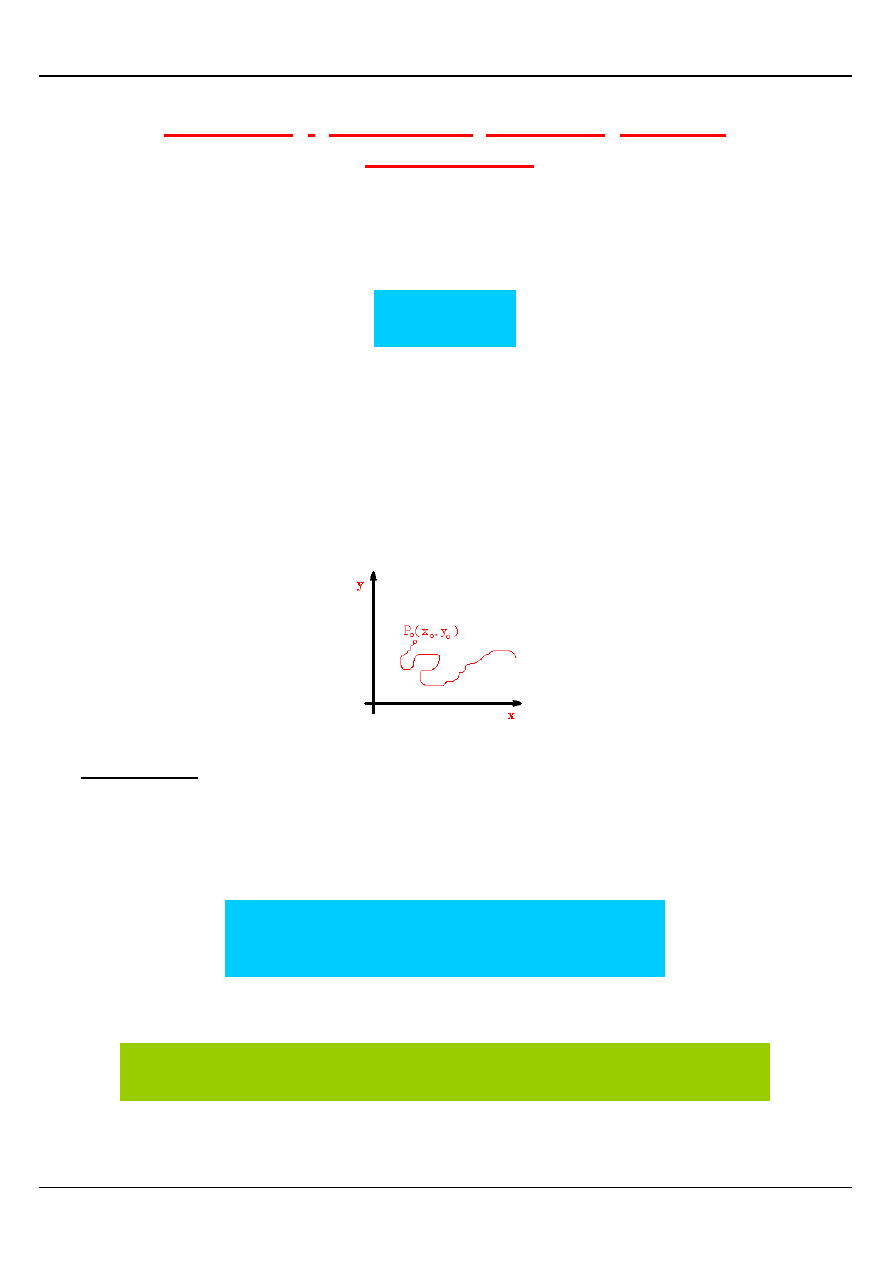
PADER collection

MATEMATYKA – Semestr II – Rachunek różniczkowy dr Stanisław Kiełtyka

- 6 -

GRANICA i CIĄGŁOŚĆ FUNKCJI DWÓCH

ZMIENNYCH

Rozważmy ciąg punktów [P

o

(x

o

, y

o

)] na płaszczyźnie Oxy oraz punkt P

o

(x

o

, y

o

).

Powiemy, że granicą ciągu [P

n

] jest punkt P

o

co zapiszemy:

o

n

n

P

P

lim

=

∞

→

jeżeli w dowolnym otoczeniu punktu P

o

znajdują się prawie wszystkie wyrazy ciągu [P

n

].

Wynika stąd, że:

)

y

y

lim

x

x

lim

(

)

y

,

(x

P

)

y

,

(x

P

lim

o

n

n

o

n

n

o

o

o

n

n

n

n

=

∧

=

↔

=

∞

→

∞

→

∞

→

Def. Heinego

Mówimy, że funkcja f(x , y) posiada w pkt. P

o

(x

o

, y

o

) granicę równą g co zapisujemy













=

=

→

→

g

y)

f(x,

lim

g

f(P)

lim

)

y

,

(x

y)

(x,

P

P

0

0

0

g

)

f(P

P

P

P

P

:

}

{P

g

f(P)

lim

n

0

n

0

n

n

P

P

0

→

⇒

→

∧

≠

⇔

=

→

PADER collection

MATEMATYKA – Semestr II – Rachunek różniczkowy dr Stanisław Kiełtyka

- 7 -

Def.

Funkcję f(P) nazwiemy ciągłą w punkcie P

o

jeżeli:

)

f(P

f(P)

lim

0

P

P

0

=

→

Przykład

Oblicz

granicę

2

2

y

x

xy

(0,0)

y)

(x,

lim

+

→

Rozpatrzmy dwa ciągi punktów

{ }

{

} {

}

)

,

(

''

P

,

)

,

(

'

P

:

P

n

1

n

2

n

n

1

n

1

n

n

Wtedy

5

2

n

1

n

2

n

n

n

2

1

n

1

n

1

n

n

n

)

,

f(

lim

)

''

f(P

lim

)

,

f(

lim

)

'

f(P

lim

=

=

=

=

∞

→

∞

→

∞

→

∞

→

Zatem granica nie istnieje

PADER collection

MATEMATYKA – Semestr II – Rachunek różniczkowy dr Stanisław Kiełtyka

- 8 -

WŁASNOŚCI FUNKCJI CIĄGŁYCH

1 – Jeżeli funkcja f(P) jest ciągła w punkcie P

o

i f(P

o

) > 0 to istnieje takie otocznie P

o

,

że dla każdego punktu P z tego otoczenia będzie f(P) >0.

2 – Funkcja ciągła w obszarze domkniętym i ograniczonym odiąga w nim swoją wartość

największą i najmniejszą.

3 – Funkcja f(P) ciągła w obszarze domkniętym i ograniczonym do którego należą

punkty P

1

i

P

2

, przyjmuje każdą wartość pośrednią zawartą między f(P

1

) i f(P

2

).

PADER collection

MATEMATYKA – Semestr II – Rachunek różniczkowy dr Stanisław Kiełtyka

- 9 -

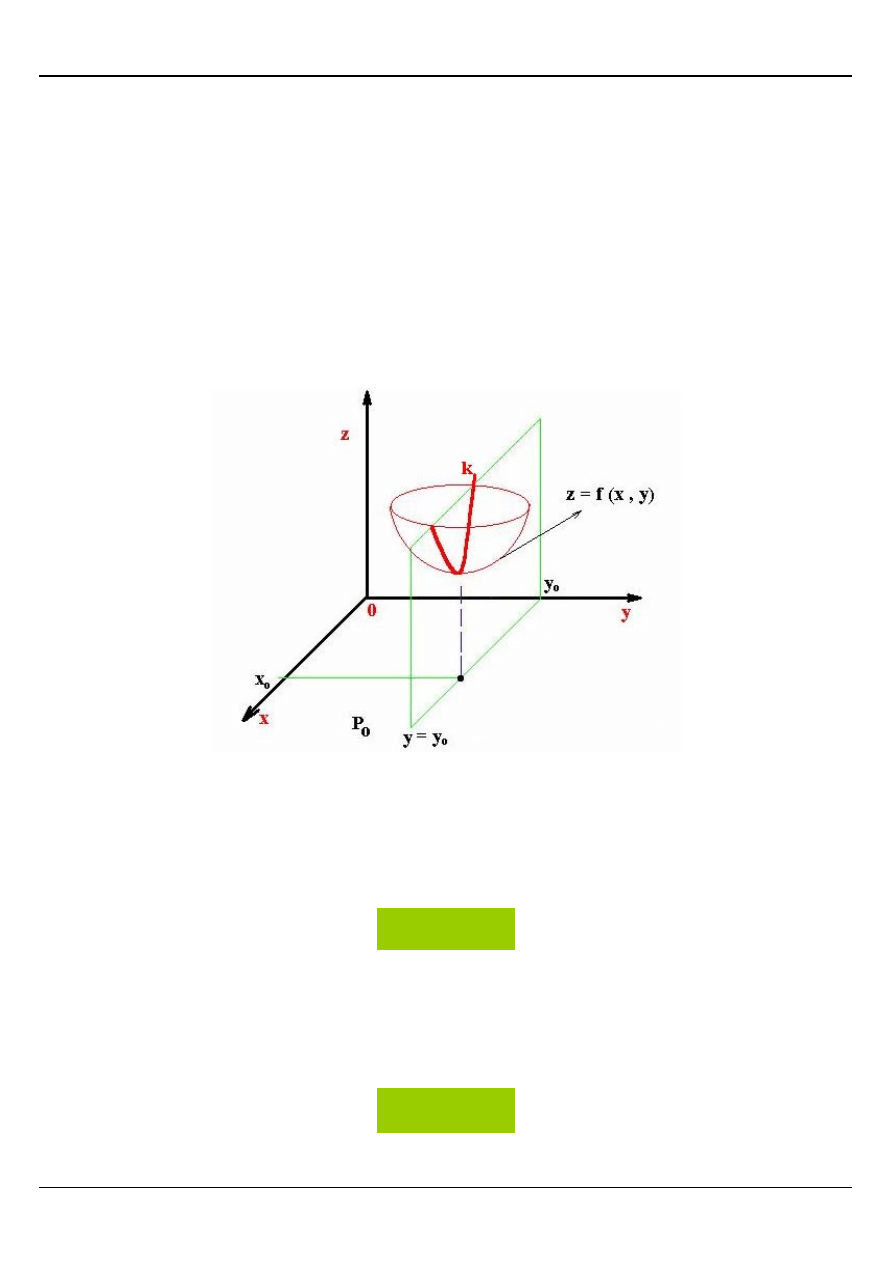
POCHODNA CZĄSTKOWA FUNKCJI DWÓCH

ZMIENNYCH

Rozpatrzmy funkcję z = f(x , y) określoną na obszarze D, przy czym powierzchnia S jest
obrazem geometrycznym tej funkcji.


Jeżeli w funkcji z = f(x , y) podstawimy za x = x

o

to krzywa k powstała przez przecięcie się

powierzchni S i płaszczyzny x = x

o

będzie miała równanie:







=

=

0

0

x

x

y)

,

f(x

z

:

k

Analogicznie jeżeli w funkcji z = f(x , y) podstawimy za y = y

o

to krzywa l powstała przez

przecięcie się powierzchni S i płaszczyzny y = y

o

będzie miała równanie:







=

=

0

0

y

y

)

y

f(x,

z

:

k

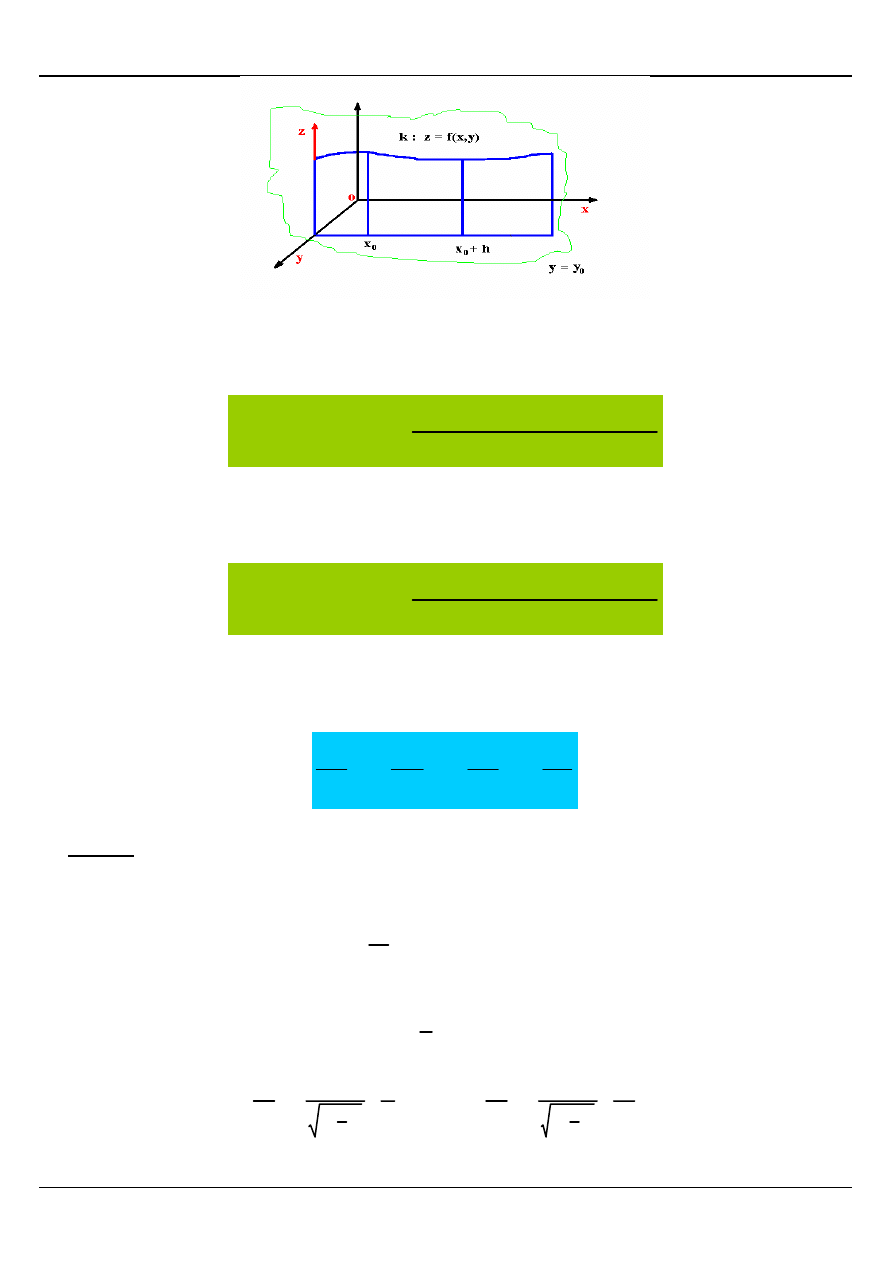
PADER collection

MATEMATYKA – Semestr II – Rachunek różniczkowy dr Stanisław Kiełtyka

- 10 -

Ponieważ funkcja z = f(x , y) jest funkcją jednej zmiennej więc możemy dla niej wyznaczyć
pochodną w pkt. x = x

o

.

Pochodna ta wynosi:

h

)

y

,

f(x

)

y

h,

f(x

lim

)

y

,

(x

'

f

0

0

0

0

0

h

0

0

X

−

+

=

→

i nazywamy ją pochodną cząstkową funkcji dwóch zmiennych z = f(x , y) obliczoną
względem zmiennej x w punkcie (x

o

, y

o

).

Podobnie pochodną

h

)

y

,

f(x

h)

y

,

f(x

lim

)

y

,

(x

'

f

0

0

0

0

0

h

0

0

Y

−

+

=

→

nazywamy pochodną cząstkową funkcji dwóch zmiennych z = f(x , y) obliczoną względem
zmiennej y w punkcie (x

o

, y

o

).

Będziemy też używać oznaczeń:

y

f

,

y

z

,

x

f

,

x

z

∂

∂

∂

∂

∂

∂

∂

∂

Zadanie

Obliczyć pochodne cząstkowe funkcji

3

2

3

3y

y

3x

2x

z

+

+

=

6xy

6x

2

x

z

−

=

∂

∂

Obliczyć pochodne cząstkowe funkcji

y

x

arcsin

z

=

( )

y

1

-

1

1

x

z

2

y

x

⋅

=

∂

∂

( )

2

2

y

x

y

-x

-

1

1

y

z

⋅

=

∂

∂

PADER collection

MATEMATYKA – Semestr II – Rachunek różniczkowy dr Stanisław Kiełtyka

- 11 -

POCHODNA FUNKCJI ZŁOŻONEJ

Niech dana będzie w obszarze D funkcja z = f(x , y) oraz niech funkcje:

v)

φ(u,

y

v)

(u,

x

=

Φ

=

będą określone, ciągłe i różniczkowalne w obszarze ∆.

Zakładamy dodatkowo, że punkt (x , y)

∈D gdy punkt (u , r)∈ ∆.

Wtedy funkcję z = f(x , y) możemy traktować jako funkcję zmiennych (u , v) tj.

[

]

v)

φ(u,

v);

Φ(u,

f

z

=

i możemy wyznaczyć jej pochodne cząstkowe:

v

z

,

u

z

∂

∂

∂

∂

Pochodne te są równe

u

y

y

z

u

x

x

z

u

z

∂

∂

⋅

∂

∂

+

∂

∂

⋅

∂

∂

=

∂

∂

oraz

v

y

y

z

v

x

x

z

v

z

∂

∂

⋅

∂

∂

+

∂

∂

⋅

∂

∂

=

∂

∂

Jeżeli funkcja z = f(x , y) jest funkcją złożoną dwóch funkcji jednej zmiennej, tzn.

)

y(t)

;

x(t)

f(

z

y(t)

y

x(t)

x

=

=

=

PADER collection

MATEMATYKA – Semestr II – Rachunek różniczkowy dr Stanisław Kiełtyka

- 12 -

Wtedy funkcja z = f(x , y) jest ostatecznie funkcją jednej zmiennej t i możemy policzyć jej
pochodną z’

dt

dz

z'

=

która wynosi

t

y

y

z

t

x

x

z

t

z

∂

∂

⋅

∂

∂

+

∂

∂

⋅

∂

∂

=

∂

∂

Przykład

Obliczyć pochodną

u

z

∂

∂

funkcji

x

y

z sin

=

jeżeli

v

u

y

,

x

v

u

+

=

=

(

) (

)

(

)

(

)

u

v

v)

(u

u

v

v

1

u

v

v)

(u

u

v

v)

(u

x

y

x

1

v

1

x

y

x

y

cos

cos

1

sin

cos

-

u

z

2

2

2

⋅

+

⋅

+

⋅

+

⋅

+

⋅

⋅

−

=

⋅

⋅

+

⋅

⋅

=

∂

∂

Obliczyć pochodną całkowitą

t

z

∂

∂

funkcji

)

(

y

x

arctg

z

−

=

jeżeli

2t

t

e

y

e

x

=

=

)

2e

(1

)

e

(e

1

e

2e

1)

(

y)

(x

1

1

e

y)

(x

1

1

t

z

t

2

2t

t

t

2t

2

t

2

−

⋅

−

+

=

⋅

−

⋅

−

+

+

⋅

−

+

=

∂

∂

PADER collection

MATEMATYKA – Semestr II – Rachunek różniczkowy dr Stanisław Kiełtyka

- 13 -

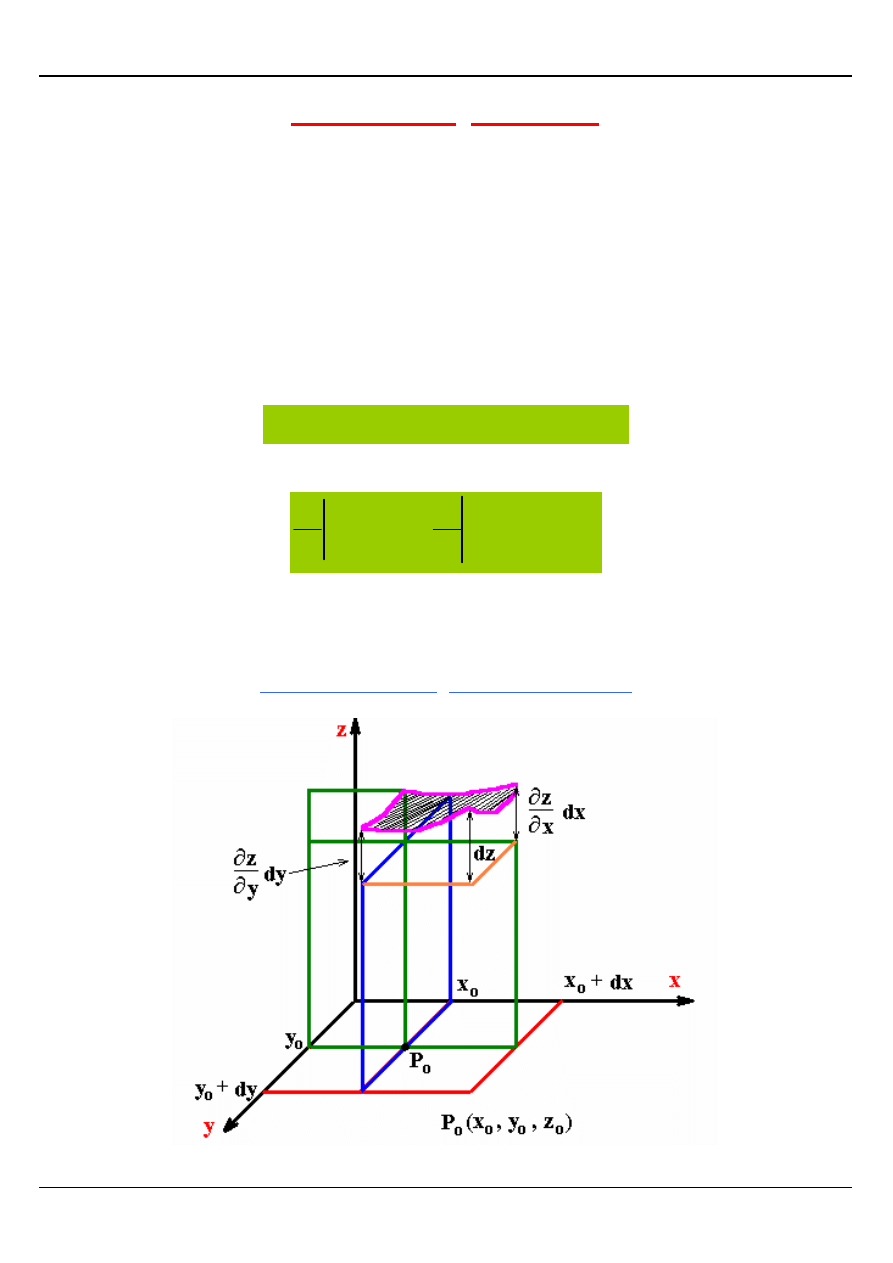
PŁASZCZYZNA STYCZNA

Niech powierzchnia S dana będzie równaniem

y)

f(x,

z

(*)

=

lub

0

z)

y,

F(x,

(**)

=

i niech punkt Q(x

o

, y

o

, z

o

) leży na tej powierzchni:

Przez punkt Q prowadzimy krzywe leżące na powierzchni S, do tych krzywych z kolei
w punkcie Q prowadzimy proste styczne. Takich krzywych krzywych stycznych jest
oczywiście nieskończona ilość.

Jeżeli te wszystkie styczne leżą w jednej płaszczyźnie to tę płaszczyznę nazywamy
płaszczyzną styczną do powierzchni S w punkcie Q.


Równanie płaszczyzny stycznej do powierzchni S w punkcie Q ma postać:

9

w przypadku, gdy S dane jest równaniem (*)

0

)

z

(z

)

y

(y

)

y

,

(x

'

f

)

x

(x

)

y

,

(x

'

f

0

0

0

0

Y

0

0

0

X

=

−

−

−

⋅

+

−

⋅

9

w przypadku, gdy S dane jest równaniem (**)

0

)

z

(z

)

z

,

y

,

(x

'

F

)

y

(y

)

z

,

y

,

(x

'

F

)

x

(x

)

z

,

y

,

(x

'

F

0

0

0

0

Z

0

0

0

0

Y

0

0

0

0

X

=

−

⋅

−

−

⋅

+

−

⋅

Zadanie 1

Wyznaczyć równanie płaszczyzny stycznej do powierzchni S:

z = 2x

2

+ y

2

w punkcie Q (2 , 1 , 9).

4x

x

z =

∂

∂

i

2y

y

z =

∂

∂

PADER collection

MATEMATYKA – Semestr II – Rachunek różniczkowy dr Stanisław Kiełtyka

- 14 -

a stąd

8

x

z

)

1

,

2

(

=

∂

∂

i

2

y

z

)

1

,

2

(

=

∂

∂

Zatem wektor płaszczyzny stycznej do powierzchni S ma postać:

]

1

,

2

,

8

[

−

=

w

a płaszczyzna styczna:

0

9)

1(z

1)

2(y

2)

8(x

:

π

=

−

−

−

+

−

Zadanie 2

Napisać równanie płaszczyzny stycznej do powierzchni S:

z

2

= 16x

2

+ 9y

2

w punkcie Q ( 1 , 1 , 5 ).
Równanie powierzchni S możemy zapisać w postaci

4

4

4

3

4

4

4

2

1

z)

,

y

,

F(x

2

2

2

0

z

9y

16x

:

S

=

−

+

Obliczamy

32x

x

F =

∂

∂

;

18y

y

F =

∂

∂

;

-2z

z

F =

∂

∂

i

32

x

F

)

5

,

1

,

1

(

=

∂

∂

;

8

1

y

F

)

5

,

1

,

1

(

=

∂

∂

;

-10

z

F

(1,1,5)

=

∂

∂

Zatem wektorem szukanej płaszczyzny będzie

10]

,

18

,

32

[

−

=

w

i płaszczyzna styczna ma równanie:

0

5)

10(z

1)

18(y

1)

32(x

:

π

=

−

−

−

+

−

PADER collection

MATEMATYKA – Semestr II – Rachunek różniczkowy dr Stanisław Kiełtyka

- 15 -

RÓŻNICZKA ZUPEŁNA

Jeżeli w równaniu płaszczyzny stycznej

0

)

z

(z

)

y

(y

)

y

,

(x

'

f

)

x

(x

)

y

,

(x

'

f

0

0

0

0

Y

0

0

0

X

=

−

−

−

⋅

+

−

⋅

podstawimy

dx

x

-

x

0

=

;

dy

y

-

y

0

=

;

dz

z

-

z

0

=

to przyjmuje ono postać

dz

dy

)

y

,

(x

'

f

dx

)

y

,

(x

'

f

0

0

Y

0

0

X

=

⋅

+

⋅

lub

dz

dy

y

z

dx

x

z

)

y

,

(x

)

y

,

(x

0

0

0

0

=

⋅

∂

∂

+

⋅

∂

∂

dz nazywamy różniczką zupełną funkcji z = f(x , y) w punkcie (x

o

, y

o

) przy danych

przyrostach dx i dy.

INTERPRETACJA GEOMETRYCZNA

PADER collection

MATEMATYKA – Semestr II – Rachunek różniczkowy dr Stanisław Kiełtyka

- 16 -

Na rysunku widać, że różniczka zupełna dz oznacza przyrost zmiennej zależnej z dla
płaszczyzny stycznej.

Przy dostatecznie małych dx i dy przyrost dz niewiele różni się od przyrostu funkcji

y)

f(x,

dy)

y

dx,

f(x

∆z

−

+

+

=

Można wykazać, że różnica ∆z-dz jest nieskończenie małą wyższego rzędu niż przyrost

dx i dy.

Ta własność różniczki zupełnej ma zastosowanie w rachunkach przybliżonych.

Własność tę możemy zapisać za pomocą wzoru:

dz

∆z

≈

tj.

dy

y

z

dx

x

z

)

y

,

f(x

dy)

y

dx,

x

f(

)

y

,

(x

)

y

,

(x

0

0

0

0

0

0

0

⋅

∂

∂

+

⋅

∂

∂

≈

−

+

+

Przykład

Jak zmieni się przekątna prostokąta o bokach 6m = x i 8m = y jeżeli bok x zwiększymy o
2mm , a bok y zmniejszymy o 5 mm?

Przekątna x prostokąta wynosi

2

2

y

x

z

+

=

a zatem

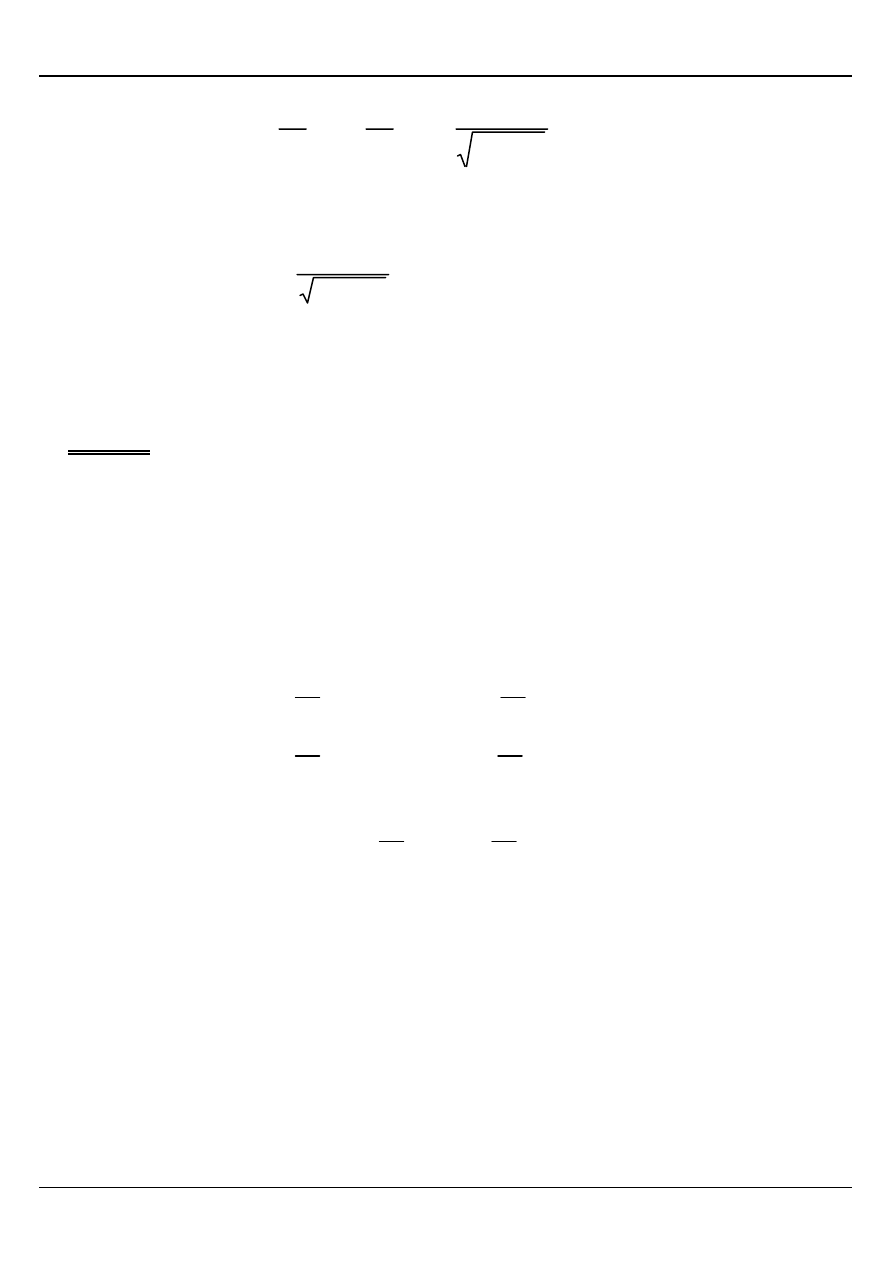
PADER collection

MATEMATYKA – Semestr II – Rachunek różniczkowy dr Stanisław Kiełtyka

- 17 -

ydy)

(xdx

y

x

1

dy

y

z

dx

x

z

∆z

2

2

+

+

=

⋅

∂

∂

+

⋅

∂

∂

≈

W naszym przypadku dx = 0.02 i dy = -0.05, więc

-0,03

0,05)

8

0,02

(6

64

36

1

∆z

≈

⋅

+

⋅

⋅

+

≈

Wynika stąd, że przekątna prostokąta ulegnie skróceniu w przybliżeniu o 3 mm.

Zadanie 1

Korzystając z różniczki zupełnej obliczyć przyblizoną wartość

02

,

2

97

,

0

y

2,02

x

z

(0,97)

=

1

1

)

z(P

(1,2)

P

2

0

0

=

=

2

)

(P

y

z

lnx

y

y

z

2

)

(P

x

z

x

y

x

z

0

y

0

1

y

=

∂

∂

⇒

⋅

=

∂

∂

=

∂

∂

⇒

⋅

=

∂

∂

−

dy

)

(P

y

z

dx

)

(P

x

z

)

dz(P

0

0

0

⋅

∂

∂

+

⋅

∂

∂

=

2)

,

(1

P

0

2,02)

;

(0,97

P

0

0,02

dy

0,03

dx

=

−

=

-0,06

(-0,03)

2

)

dz(P

0

=

⋅

=

1

(0,97)

)

f(P

-

f(P)

∆z

2,02

0

−

=

=

dz

z

≈

∆

PADER collection

MATEMATYKA – Semestr II – Rachunek różniczkowy dr Stanisław Kiełtyka

- 18 -

-0,06

1

(0,97)

2,02

≈

−

0,06

-

1

(0,97)

2,02

≈

Odp.

0,94

(0,97)

2,02

≈

Zadanie 2

Obliczyć przybliżoną wartość wyrażenia

[

]

1

97

,

0

1,02

ln

3

−

+

[

]

1

y

x

ln

z

3

−

+

=

0,97)

;

(1,02

P

1)

;

(1

P

0

0,03

-

dy

0,02

dx

=

=

3

2

3

x

3

1

1

y

x

1

x

z

⋅

⋅

−

⋅

=

∂

∂

3

1

3

1

1

1

1

1

)

(

x

z

0

=

⋅

−

+

=

∂

∂

P

y

1

1

y

x

1

y

z

3

⋅

−

⋅

=

∂

∂

2

1

2

1

1

1

1

1

y

z

=

⋅

−

+

=

∂

∂

0,03)

(

2

1

0,02

3

1

dy

y

z

dx

x

z

)

dz(P

0

−

⋅

+

⋅

=

⋅

∂

∂

+

⋅

∂

∂

=

(

)

(

)

1

1

1

ln

1

97

,

0

02

,

1

ln

)

z(P

-

z(P)

z

3

0

−

+

−

−

+

=

=

∆

(

)

1

97

,

0

02

,

1

ln

z

3

−

+

=

∆

dz

z

≈

∆

różniczka prawie równa przyrostowi

(

)

0,03)

(

0,02

1

0,97

1,02

ln

∆z

2

1

3

1

3

−

+

⋅

≈

−

+

=

PADER collection

MATEMATYKA – Semestr II – Rachunek różniczkowy dr Stanisław Kiełtyka

- 19 -

POCHODNE CAŁKOWE I RÓŻNICZKI WYŻSZYCH

RZĘDÓW

Pochodną cząstkową funkcji dwóch zmiennych są również funkcjami dwóch zmiennych.

z

x

z

∂

∂

y

z

∂

∂













∂

∂

∂

∂

x

z

x













∂

∂

∂

∂

x

z

y









∂

∂

∂

∂

y

z

x









∂

∂

∂

∂

y

z

y

Dla tych pochodnych będziemy używać zapisów

''

XX

2

2

f

x

z

x

z

x

=

∂

∂

=













∂

∂

∂

∂

''

YY

2

2

f

y

z

y

z

y

=

∂

∂

=









∂

∂

∂

∂

''

YX

2

f

x

y

z

x

z

y

=

∂

∂

∂

=













∂

∂

∂

∂

''

XY

2

f

y

x

z

y

z

x

=

∂

∂

∂

=









∂

∂

∂

∂

PADER collection

MATEMATYKA – Semestr II – Rachunek różniczkowy dr Stanisław Kiełtyka

- 20 -

TWIERDZENIE SCHWARZA

3y

2x

x

y

y

3x

z

2

3

2

+

−

+

=

2

y

6xy

x

z

2

3

−

+

=

∂

∂

3

2xy

y

9x

y

z

2

2

+

+

=

∂

∂

3

2

2

6y

x

z =

∂

∂

2y

18xy

x

y

z

2

2

+

=

∂

∂

∂

2x

y

18x

y

z

2

2

2

+

=

∂

∂

y

2

18xy

y

x

z

2

2

+

=

∂

∂

∂

Widać, że pochodne mieszane są sobie równe

x

y

z

y

x

z

2

2

∂

∂

∂

=

∂

∂

∂

Twierdzenie:

Jeżeli funkcja z = f(x , y) ma wewnątrz pewnego obszaru D ciągłą pochodną

x

y

z

,

y

x

z

2

2

∂

∂

∂

∂

∂

∂

to w każdym punkcie tego obszaru te pochodne są sobie równe.

Pochodne cząstkowe pochodnych pierwszego rzędu nazywamy pochodnymi cząstkowymi
drugiego rzędu.

Ogólnie pochodną cząstkową rzędu n nazywamy pochodną cząstkową n-1 rzędu.

Różniczka zupełna dz funkcji dwóch zmiennych z = f(x , y) jest oczywiście funkcją dwóch
zmiennych x i y. Dla tej różniczki możemy obliczyć różniczkę zupełną i otrzymujemy
różniczkę zupełną rzędu d

2

z.

Przykład

Obliczyć d

2

z dla funkcji z = sinxy.

Obliczmy dla tej funkcji dz

cos(xy)dy

x

cos(xy)dx

y

dz

⋅

+

⋅

=

PADER collection

MATEMATYKA – Semestr II – Rachunek różniczkowy dr Stanisław Kiełtyka

- 21 -

Teraz wyznaczamy d

2

z przy założeniu, że dx i dy są stałymi:

(

) (

) (

)

=

⋅

+

⋅

=

⋅

+

⋅

=

cos(xy)dy

x

cos(xy)dx

y

cos(xy)dy

x

cos(xy)dx

y

d

z

d

2

d

d

(

) (

)

=

⋅

+

⋅

+

⋅

⋅

=

sin(xy)dy

x

sin(xy)dx

xy

-

dy

sin(xy)dy

xy

-

sin(xy)dx

y

-

dx

2

2

y

sin(xy)d

x

y

sin(xy)dxd

2xy

-

sin(xy)dx

-y

2

2

2

2

⋅

−

⋅

⋅

=

Różniczka drugiego rzędu d

2

z jest znowu pochodną dwóch zmiennych.

Jeżeli będzie się w dalszym ciągu obliczło różniczki w ten sposób otrzymywanych funkcji,
to będziemy otrzymywali różniczki coraz wyższych rzędów.

Wiemy, że

dy

y

z

dx

x

z

dz

⋅

∂

∂

+

⋅

∂

∂

=

Przy obliczeniach różniczek wyższych rzędów bierzemy pod uwagę fakt, że dx i dy są
stałymi. Tak więc:

y

d

y

z

dxdy

x

y

z

2

x

d

x

z

dy

dy

y

z

dx

y

x

z

dx

dy

x

y

z

dx

x

z

dy

y

z

d

dx

x

z

d

dy

y

z

d

dx

x

z

d

z

d

2

2

2

2

2

2

2

2

2

2

2

2

2

2

∂

∂

+

∂

∂

∂

⋅

+

∂

∂

=

=









∂

∂

+

∂

∂

∂

+









∂

∂

∂

+

∂

∂

=

=









∂

∂

+













∂

∂

=









⋅

∂

∂

+













⋅

∂

∂

=

Analogicznie

( )

( )

( )

( )

3

3

3

2

2

2

2

2

2

3

3

3

3

dy

y

z

dx

dy

x

y

z

3

dx

dy

x

y

z

3

dx

x

z

z

d

∂

∂

+

∂

∂

∂

⋅

+

∂

∂

∂

⋅

+

∂

∂

=

i ogólnie symbolicznie możemy zapisać:

z

''

dy

y

dx

x

z

'

d'













⋅

∂

∂

+

⋅

∂

∂

=

PADER collection

MATEMATYKA – Semestr II – Rachunek różniczkowy dr Stanisław Kiełtyka

- 22 -

EKSTREMUM FUNKCJI DWÓCH ZMIENNYCH

Rozpatrzmy funkcję z = f(x , y), której obraz geometryczny przedstawia rysunek

Widzimy, że dla podanej funkcji istnieje takie otoczenie punktu P

0

O(P

0

, δ), że dla

wszystkich punktów

δ)

,

(P

O

P

0

∈

ma miejsce nierówność

0

)

f(P

f(P)

0

≥

−

W tym przypadku mówimy, że funkcja z = f(x , y) posiada w punkcie

0

P

M INIM UM LOKALNE.

PADER collection

MATEMATYKA – Semestr II – Rachunek różniczkowy dr Stanisław Kiełtyka

- 23 -

WARUNKI KONIECZNE ISTNIENIA EKSTREMUM

FUNKCJI DWÓCH ZMIENNYCH.

Załóżmy, że funkcja z =f(x , y) posiada w pkt. P

o

(x

o

, y

o

) minimum lokalne.

Przecinając powierzchnię z = f(x , y) płaszczyzny y = y

o

otrzymamy na niej krzywą o

równaniu:







=

=

0

y

y

y)

f(x,

y

:

k

W płaszczyźnie y = y

o

funkcja z = f(x , y

o

) jest funkcją jednej zmiennej x, a dla niej

WK na to aby w punkcie x

o

było minimum jest:

0

y)

,

(x

f

0

'

x

=

Podobnie ustalając x = x

o

otrzymujemy warunek

0

)

y

(x,

f

0

'

y

=

PADER collection

MATEMATYKA – Semestr II – Rachunek różniczkowy dr Stanisław Kiełtyka

- 24 -

Dla wyznaczenia punktu (stacjonarnego) P

o

(x

o

, y

o

), w którym funkcja może osiągnąć

ekstremum należy rozwiązać układ równań:

WK!!!









=

=

0

)

y

,

(x

f

0

)

y

,

(x

f

0

0

'

y

0

0

'

x

Przykład 1

Wyznaczyć punkty stacjonarne dla funkcji

3

4y

4x

2y

x

z

2

2

−

+

−

+

=

Aby wyznaczyć punkty stacjonarne należy rozwiązać układ równań.

0

4

4y

0

y)

(x,

f

0

4

-

2x

0

y)

(x,

f

'

y

'

x

=

+

⇒

=

=

⇒

=

stąd P

o

(2 , -1)

Przykład 2

Rozważmy funkcję

2

2

y

-

x

z

=

.

Dla niej WK mają postać.













=

⇒

=

∂

∂

=

⇒

=

∂

∂

0

2y

-

0

y

z

0

2x

0

x

z

i stąd P

o

(0 , 0)

Ale ta funkcja w punkcie P

o

nie ma ekstremum.

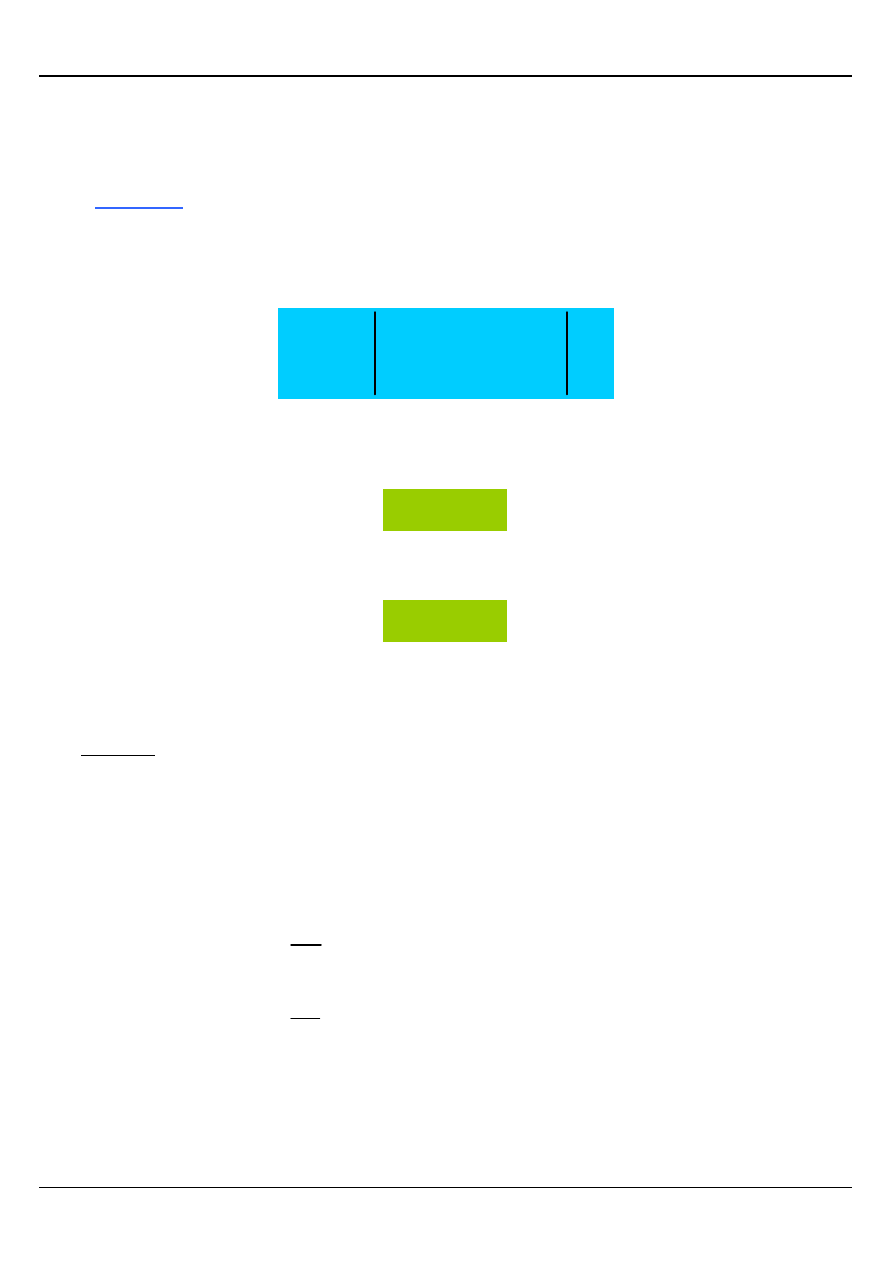
PADER collection

MATEMATYKA – Semestr II – Rachunek różniczkowy dr Stanisław Kiełtyka

- 25 -

WARUNKI WYSTARCZAJĄCE ISTNIENIA EKSTREMUM FUNKCJI

DWÓCH ZMIENNYCH

Tw. WW

Funkcja z = f(x , y) posiada w punkcie stacjonarnym P

o

(x

o

, y

o

) ekstremum, jeżeli

( )

0

)

(P

f

)

(P

f

)

(P

f

)

(P

f

P

W

0

''

YY

0

''

XY

0

''

YX

0

''

XX

0

>

=

przy czym maksimum gdy

0

)

(P

f

0

''

XX

<

i minimum gdy

0

)

(P

f

0

''

XX

>

Przykład

Wyznaczyć ekstremum funkcji

3

4y

4x

2y

x

z

2

2

−

+

−

+

=

Wyznaczmy punkty stacjonarne rozwiązując układ równań:













=

+

⇒

=

∂

∂

=

⇒

=

∂

∂

0

4

4y

0

y

z

0

4

-

2x

0

x

z

stąd P

o

(2 , -1)

tzn., że tylko w tym punkcie funkcja może posiadać ekstrema.

PADER collection

MATEMATYKA – Semestr II – Rachunek różniczkowy dr Stanisław Kiełtyka

- 26 -

Wyznaczamy następnie

2

x

z

2

2

=

∂

∂

,

4

y

z

2

2

=

∂

∂

,

0

y

x

z

2

=

∂

∂

∂

i stąd

( )

0

8

0

4

2

P

W

2

0

>

=

−

⋅

=

Odp. W punkcie P

o

(2 , -1) funkcja posiada ekstremum, przy czym minimum gdyż:

0

2

x

z

2

2

>

=

∂

∂