Wykład 1 i 2 (10h) Rachunek różniczkowy funkcji wielu zmiennych

Przestrzeń euklidesowa *ⁿ jako przestrzeń liniowa i metryczna, uwagi o innych metrykach w *ⁿ.

Kula w przestrzeni metrycznej- otoczenie (kuliste)

Wybrane pojęcia metryczne:

• punkt wewnętrzny zbioru -charakteryzacja otoczeniowa

• zbiór otwarty i zbiór domknięty

• punkt brzegowy zbioru-charakteryzacja otoczeniowa

• brzeg zbioru

• wnętrze zbioru

• punkt skupienia- charakteryzacja otoczeniowa

• punkt izolowany- charakteryzacja otoczeniowa

Norma ||⋅|| (długość wektora) euklidesowa

Granica ciągu w *ⁿ

Oznaczenia

Uwaga. Powyżej zdefiniowana zbieżność jest równoważna zbieżności „po współrzędnych”-uzasadnić.

Przykład.
.

Funkcja rzeczywista n zmiennych rzeczywistych

*ⁿ ⊃ D
x→ f(x)∈ *

Przykład. f(x,y)=arcsin
+ arcsin
jest rzeczywistą funkcją dwóch zmiennych rzeczywistych określoną na prostokącie [-a, a]×[-b, b].

Przykładowe wykresy funkcji 2 zmiennych- przekroje- powierzchnie obrotowe np.:

• paraboloida hiperboliczna (siodło) f(x,y)=x²-y² ,

• paraboloida obrotowa f(x,y)=x²+y² .

• paraboloida eliptyczna f(x,y)=4x²+9y².

Granica funkcji *ⁿ⊃S(x⁰,δ)
x→ f(x)∈ *

Heine
⇔

Cauchy
⇔

Ciągłość funkcji w punkcie.

Funkcja *ⁿ⊃Ot(x⁰,δ)
x→ f(x)∈ * jest ciągła w punkcie x⁰ jeżeli

Ciągłość punktowa i jednostajna funkcji na zbiorze D.

ciągłość jednostajna ⇒ ciągłość punktowa

Pochodne cząstkowe funkcji *ⁿ ⊃ Ot(x,δ)
x→ f(x)∈ * w punkcie :

(skończona granica).

Przykład. Obliczyć pochodne cząstkowe funkcji f(x,y)=
.

(x,y)≠(0,0),
,

(x,y)≠(0,0),
nie istnieje.

Przykład. Funkcja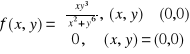
ma obie pochodne cząstkowe w (0,0)
, a nie jest ciągła w (0,0), bo
,
.

Z przykładu widać, że istnienie pochodnych cząstkowych nie może być uznane, za różniczkowalność funkcji, bo różniczkowalność funkcji powinna (jak w przypadku jednowymiarowym) implikować ciągłość.

Pochodna funkcji w punkcie a funkcja pochodna.

Pochodne cząstkowe wyższych rzędów,

Tw. Schwarza. Jeżeli f(x₁,...,x_n) ma w pewnym obszarze D ciągłe pochodne cząstkowe
i
, to są one sobie równe w D.

Pochodne cząstkowe funkcji złożonych.

Twierdzenie Jeżeli

1. f(x₁,...,x_n) ma w pewnym obszarze D⊂ *ⁿ ciągłe pochodne cząstkowe

2. funkcje x_i= x_i (u₁,...,u_m) i=1,...,n mają ciągle pochodne cząstkowe w pewnym obszarze Δ⊂ *^m

3. (x₁(u₁,...,u_m),..., x_n(u₁,...,u_m))∈D , gdy (u₁,...,u_m) ∈Δ

to funkcja złożona F(u₁,...,u_m )=f(x₁(u₁,...,u_m),..., x_n(u₁,...,u_m)) ma ciągłe pochodne cząstkowe w każdym punkcie obszaru Δ i

Przykłady

1. f(x,y)=e^xcosy , x(u,v)=3u+5v, y(u,v)=2u-v, F(u,v)= e^3u+5v cos(2u-v) . Obliczyć pochodne cząstkowe
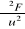
   i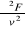
   .

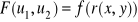
2. 
   gdzie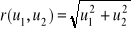
   . Wykazać że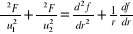
   

Pochodne kierunkowe i pochodne mocne (Frecheta)- różniczkowalność.

Def. Niech f : *ⁿ ⊃ Ot(x,δ)
x→ f(x)∈ * i *ⁿ ∋ k , ||k||=1. Pochodną kierunkową funkcji f w punkcie x w kierunku wektora k nazywamy skończoną granicę
.

Widać, że pochodna cząstkowa jest szczególnym przypadkiem pochodnej kierunkowej w kierunku wersora i-tej osi e_i=(0,...,1,...0)

Def. Funkcja f : *ⁿ ⊃ Ot(x,δ)
x→ f(x)∈ * jest różniczkowalna w sensie Frecheta w punkcie x jeżeli

istnieją stałe A₁,...,A_n takie, że dla dostatecznie małych przyrostów h=(h₁,...,h_n)

f(x+h)-f(x)=A₁h₁+...+A_nh_n+ r(x,h) , przy czym
.

Wyrażenie A₁h₁+...+A_nh_n można zapisać w postaci macierzowej A h , gdzie A=[A₁,...,A_n],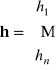
. Pochodną Frecheta funkcji f w punkcie x nazywamy odwzorowanie liniowe L: *ⁿ→* reprezentowane przez macierz A, czyli warunek różniczkowalności można zapisać

f(x+h)-f(x)=L h + r(x,h) , przy czym
.

Uwaga :

• F- różniczkowalność ⇒ ciągłość

• jeżeli f jest różniczkowalna w x , to f ma w x pochodne kierunkowe a więc i cząstkowe przy czym
  

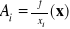
• jeżeli f ma w Ot(x,δ) pochodne cząstkowe ciągłe w x, to f jest różniczkowalna w x

• jeżeli f jest różniczkowalna , to
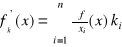
  w zapisie macierzowym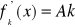
  

Różniczki

Oznaczenia x⁰=(
) Δx=(Δx₁,..., Δx_n)
*

Różniczką funkcji f w punkcie x⁰ dla przyrostu Δx nazywamy wyrażenie

df(x⁰, Δx)=

Różniczki wyższych rzędów

Jeżeli przy ustalonym Δx funkcja d( ⋅ ,Δx) :
* ma różniczkę , to nazywamy ją druga różniczką funkcji f w punkcie x⁰ i oznaczamy d²f (x⁰, Δx).

Przykład. Wyprowadzić wzór na drugą różniczkę funkcji dwóch zmiennych.

Uwagi o zapisie macierzowym drugiej różniczki.

Druga różniczka funkcji wielu zmiennych w danym punkcie jest formą kwadratową przyrostów

Wzór na m-tą różniczkę funkcji n zmiennych

Napisać wzór na drugą różniczkę funkcji trzech zmiennych i trzecią różniczkę funkcji dwóch zmiennych

Wzór Taylora

Jeżeli funkcja f : *ⁿ ⊃ Ot(x⁰,δ)
x→ f(x)∈ * ma ciągłe pochodne cząstkowe do rzędu m w
, to istnieje θ∈(0,1) takie , że dla każdego x ∈Ot(x⁰,δ) prawdziwy jest wzór

gdzie

Uwaga: punkt „pośredni”
leży wewnątrz odcinka o końcach x⁰, x

Przykład. Napisać wzór Taylora dla funkcji f(x,y)=e^xsiny w punkcie (0,0) (wzór Maclaurina) dla m=4.

Odp.

Zastosowanie różniczki w teorii błędów

Dana jest funkcja f wielu zmiennych. Wektorowy argument funkcji nie jest znany lecz dysponujemy jego pomiarem x obarczonym błędem Niech x+Δ x oznacza prawdziwą nieznaną wartość argumentu a błąd bezwzględny pomiaru (wektorowego) nie przekracza b (Δ x ≤ b nierówność wektorowa).

Wówczas
.

Wytłumaczenie przybliżonego charakteru wzoru , kiedy to przybliżenie jest „dobre” i jak postąpić gdy przybliżenia nie jest zadowalające.

Przykład. Oszacować metodą różniczki zupełnej błąd jaki popełniamy obliczając objętość prostopadłościanu o krawędziach 4.1, 3.2, 8.4 zmierzonych odpowiednio z dokładnością 0.1, 0.1, 0.2. Odp. (błąd bezwzględny≤ 8.756, błąd względny 8% (wytłumaczyć jak rozumiemy błąd względny)

Ekstrema lokalne

Def. Funkcja f : *ⁿ ⊃ Ot(x⁰,δ)
x→ f(x)∈ * ma w punkcie x⁰ maksimum lokalne właściwe jeżeli

∀ x∈ S(x⁰,δ) f(x)<f(x⁰) (Uwaga S(x⁰,δ)=Ot(x⁰,δ)-{ x⁰})

Podobnie minimum lokalne właściwe.

Warunek konieczny istnienia ekstremum

Jeżeli funkcja f : *ⁿ ⊃ Ot(x⁰,δ)
x→ f(x)∈ *

• ma w punkcie x⁰ pochodne cząstkowe

• ma w punkcie x⁰ ekstremum

to
, i=1,...,n.

Uwaga: punktami krytycznymi są także punkty w których pochodne cząstkowe nie istnieją.

Warunek wystarczający istnienia ekstremum

Jeżeli f : *ⁿ ⊃ Ot(x⁰,δ)
x→ f(x)∈ *

• jest klasy C²(Ot(x⁰,δ)) (tzn. ma drugie pochodne cząstkowe ciągłe w Ot(x⁰,δ))

• 
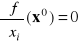
  , i=1,...,n

• d²f(x⁰, Δx) > 0 (<) , ∀Δx≠0

to f ma w punkcie x⁰ maksimum (minimum) lokalne właściwe

Kryterium Sylvestera.

WKW dodatniej określoności drugiej różniczki (d²f(x⁰, Δx) > 0, ∀Δx≠0 ) jest to by wszystkie minory kątowe D_i , i=1,...n macierzy drugiej różniczki były dodatnie.

WKW dodatniej ujemnej drugiej różniczki (d²f(x⁰, Δx) < 0, ∀Δx≠0 ) jest to by wszystkie minory kątowe D_i macierzy drugiej różniczki pomnożone przez (-1)ⁱ (czyli (-1)ⁱ D_i , i=1,...n) czyli były dodatnie.

Wytłumaczyć kiedy kryterium Sylvestera pozwala stwierdzić brak ekstremum a kiedy nie rozstrzyga o istnieniu ekstremum

Przykłady Wyznaczyć ekstrema lokalne funkcji

1. f(x,y)=x⁴+y⁴-2x²+4xy-2y²

( punkty krytyczne (0,0),
,
. WW nie rozstrzyga w (0,0) ( f(x,x)-f(0,0)=2x⁴ >0, f(x,0)-f(0,0)=x²(2-x²)<0 dla dostatecznie małych x≠0 ⇒ brak ekstremum w (0,0) w pozostałych punktach minimum lokalne (-8))

2. f(x,y,z)=x²-2x-y³+3y+5z²

DO TEGO MIEJSCA ZROBIŁEM (Reszta będzie na początku trzeciego wykładu )

Ekstrema globalne

Z twierdzenia Weierstrassa funkcja ciągła (wielu zmiennych) na zbiorze domkniętym i ograniczonym D osiąga swoje kresy.

Algorytm

• szukamy punktów krytycznych we wnętrzu D ( int D )

• szukamy największej i najmniejszej wartości funkcji na brzegu D (to samo zagadnienie ale niższy wymiar)

• obliczamy wartości funkcji w wyznaczonych powyżej punktach i wybieramy ( ze skończonej listy) wartość najmniejszą i największą

Przykład. Znaleźć najmniejszą i największą ) wartość funkcji f(x,y)=x²+y²-xy+x+y w trójkącie domkniętym ograniczonym przez proste x=0, y=0, x+y+3=0.

Odp. Max = f(-3,0)=f(0,-3)=6 Min= f(-1,-1)=-1

Ekstrema warunkowe

Problem. Znaleźć ekstrema funkcji f(x₁,...,x_n)

przy warunkach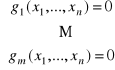

• metoda rozwikłania ograniczeń (wyjaśnić)

• metoda mnożników Lagrange'a

• Tworzymy funkcję Lagrange'a

L(x₁,...,x_n;λ₁,...,λ_m)= f(x₁,...,x_n)+

• WK istnienia ekstremum warunkowego

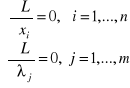
⇒ punkty krytyczne P_i(x₁,...,x_n;λ₁,...,λ_m)

• WW Badamy znak d² L(P_i, Δx₁,...,Δx_n) w punktach krytycznych przy czym przyrosty spełniają układ równań

.

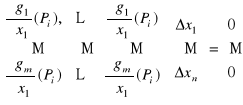
Jeżeli d² L(P_i, Δx₁,...,Δx_n)>0 dla Δx≠0, to f ma w P_i minimum lokalne warunkowe (podobnie maksimum)

Przykład. Wyznaczyć ekstrema warunkowe funkcji f(x,y)=xy przy warunku g(x,y)=x+y-1=0

Pokazać obie metody. W metodzie Lagrange'a zwrócić szczególną uwagę na konieczność krępowania przyrostów w WW.

1

6

---