Rachunek różniczkowy funkcji jednej zmiennej

1 . Obliczyć pochodne z definicji :

Definicja ( pochodnej ) :
.

a)
,
.

b)
,

=
=
=

=
.

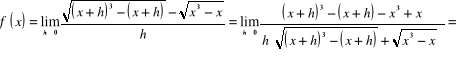
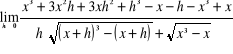
2 . Obliczyć pochodne funkcji :

a)
;

b)
;

c)
;

d)
;

e)
;

f)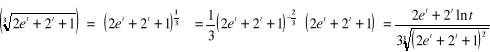
;

g)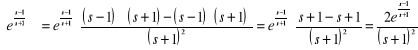
;

h)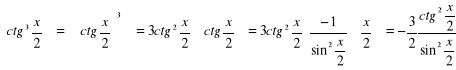
;

i)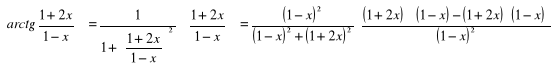
=

=
;

j)
;

k)
=

=
=

=
;

l)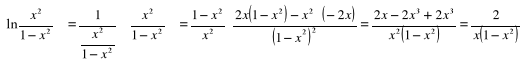
;

m)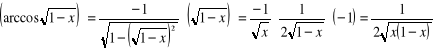
;

3 . Wyznaczyć pochodne funkcji :

{ Korzystamy ze wzoru :
} .

a)
;

b)
;

c)
;

d)
.

4 . Znaleźć równanie stycznej do krzywej :

[ Równanie stycznej do krzywej opisanej równaniem
w punkcie

ma postać :
. ]

, w punkcie
.

Mamy :
,

,
.

Szukane równanie :
, a stąd
.

b)
, w punkcie
.

,
. Zatem


.

5 . Znaleźć przedziały monotoniczności funkcji :

a)
.
.

Badamy , gdzie pochodna funkcji jest dodatnia - tam funkcja jest rosnąca i analogicznie , tam , gdzie pochodna jest ujemna - funkcja maleje .

. Ponieważ funkcja logarytmiczna o podstawie większej od jeden jest rosnąca , to ostatnia nierówność zachodzi dla

. Pochodna badanej funkcji jest dodatnia w przedziale
, więc funkcja jest rosnąca w tym przedziale . Dalej wnioskujemy , że pochodna jest ujemna w przedziale
, więc funkcja jest malejąca w tym przedziale .

b)
.
.

Wyznaczamy przedziały , w których pochodna jest dodatnia ( tam funkcja jest rosnąca ) i w których jest ujemna ( tam funkcja jest malejąca ) :

. Zauważmy , że
. Uwzględniając ten fakt , mamy :




[ parabola o miejscach zerowych
i
i ramionach skierowanych w dół ] . Stąd wynika , że funkcja jest rosnąca w przedziale
.

Dalej wynika już , że funkcja jest malejąca w przedziałach
i
[ bo tam pochodna jest ujemna ] .

c)
,
.

Postępujemy analogicznie jak w wyżej .

.




i


.

Oznacza to , że funkcja
jest rosnąca w przedziałach
i
[ nie wolno tu sumować przedziałów !!! ] ; jest malejąca więc w przedziale

.

d)
. Wyznaczamy dziedzinę :
=
=
.

Postępując jak wyżej , obliczamy pochodną tej funkcji i następnie wyznaczamy przedziały , w których ma ona stały znak . Otrzymujemy :

=
;





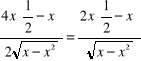
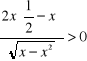
[ uwzględniając dziedzinę funkcji ]


. W tym też przedziale funkcja
jest rosnąca . Stąd dalej wnioskujemy , że funkcja jest malejąca w przedziale
.

e)
. Dziedziną jest zbiór :
.

Dalej postępujemy analogicznie jak wcześniej .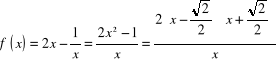
.

.

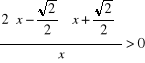
Uwzględniając dziedzinę funkcji otrzymujemy : funkcja jest rosnąca w przedziale
.

Dalej , po uwzględnieniu dziedziny funkcji , funkcja jest malejąca w przedziale
, bo tam jej pochodna jest ujemna .

f)
. Wyznaczamy dziedzinę :

=
.

.

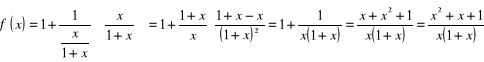
Zauważmy , że licznik ułamka jest zawsze dodatni , bo
<0 i parabola ma ramiona skierowane do góry . Stąd

=
. Stąd wniosek : funkcja jest rosnąca

w przedziałach :
i
; nigdzie nie jest malejąca .

6. Wyznaczyć ekstrema funkcji :

a)
.
.

[ Przeczytać z wykładu warunek konieczny i wystarczający istnienia ekstremum !!! ]

Z warunku koniecznego , wyznaczamy punkty w których funkcja może ( choć nie musi ) mieć ekstremum lokalne . Punktami tymi są miejsca zerowe pierwszej pochodnej . Rozwiążemy więc równanie ;
.

Zatem
.
. Jest to równanie sprzeczne , nie ma rozwiązań a, tym samym , funkcja nie ma ekstremów lokalnych .

b)
.
=
,
.

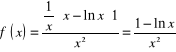
Wyznaczamy punkty w których funkcja może mieć ekstrema . Z warunku koniecznego rozwiązujemy równanie








.

Sprawdzimy teraz , korzystając z warunku dostatecznego , czy funkcja ma ekstremum w wyznaczonym punkcie , tzn. czy pochodna zmienia znak w otoczeniu punktu
.

Funkcja logarytmiczna jest rosnąca , więc dla
,
, a stąd [ przenosząc
na prawą stronę nierówności ] otrzymujemy , że
i , tym samym ,
dla
.

Dalej wnioskujemy , że dla
pochodna jest mniejsza od zera . Ponieważ pochodna zmienia znak w otoczeniu punktu
z „+” na „ - „ , więc funkcja ma w punkcie
maksimum lokalne . Maksimum wynosi
.

c)
.

Funkcja logarytmiczna określona jest dla liczb dodatnich . Wyrażenie
jest dodatnie dla wszystkich liczb rzeczywistych , stąd dziedziną podanej funkcji jest zbiór
:
.

Postępujemy tak jak wyżej .
.

. W wyznaczonym punkcie funkcja może mieć ekstremum lokalne . Sprawdzimy , czy w otoczeniu tego punktu pochodna zmienia znak .

Zauważmy , że dla każdego
wyrażenia
i
są nieujemne co oznacza , że pochodna nie zmienia znaku w otoczeniu punktu
. Stąd i w oparciu o warunek wystarczający istnienia ekstremum , funkcja
nie ma w punkcie
ekstremum lokalnego .

d)
.
.

.

,
.

Pochodna jest funkcją kwadratową , rysując parabolę , która ma ramiona skierowane do góry , to widzimy , że w otoczeniu punktów
i
, pochodna zmienia znak . W otoczeniu punktu
zmienia znak z „ + „ na „ - „ , co , na podstawie warunku wystarczającego , oznacza , że w tym punkcie funkcja ma maksimum lokalne ; w otoczeniu punktu
pochodna zmienia znak z „ - „ na „ + „ zatem funkcja ma w tym punkcie minimum lokalne . Wyznaczamy te ekstrema :

,

.

f)
.
.

.
,
.

Funkcja może mieć ekstrema w wyznaczonych punktach . Łatwo sprawdzić ( samodzielnie ) , że funkcja ma w tych punktach ekstrema , bo pochodna zmienia znak . Stąd w punkcie
ma maksimum lokalne , a w punkcie
ma minimum lokalne .

;
.

2

---