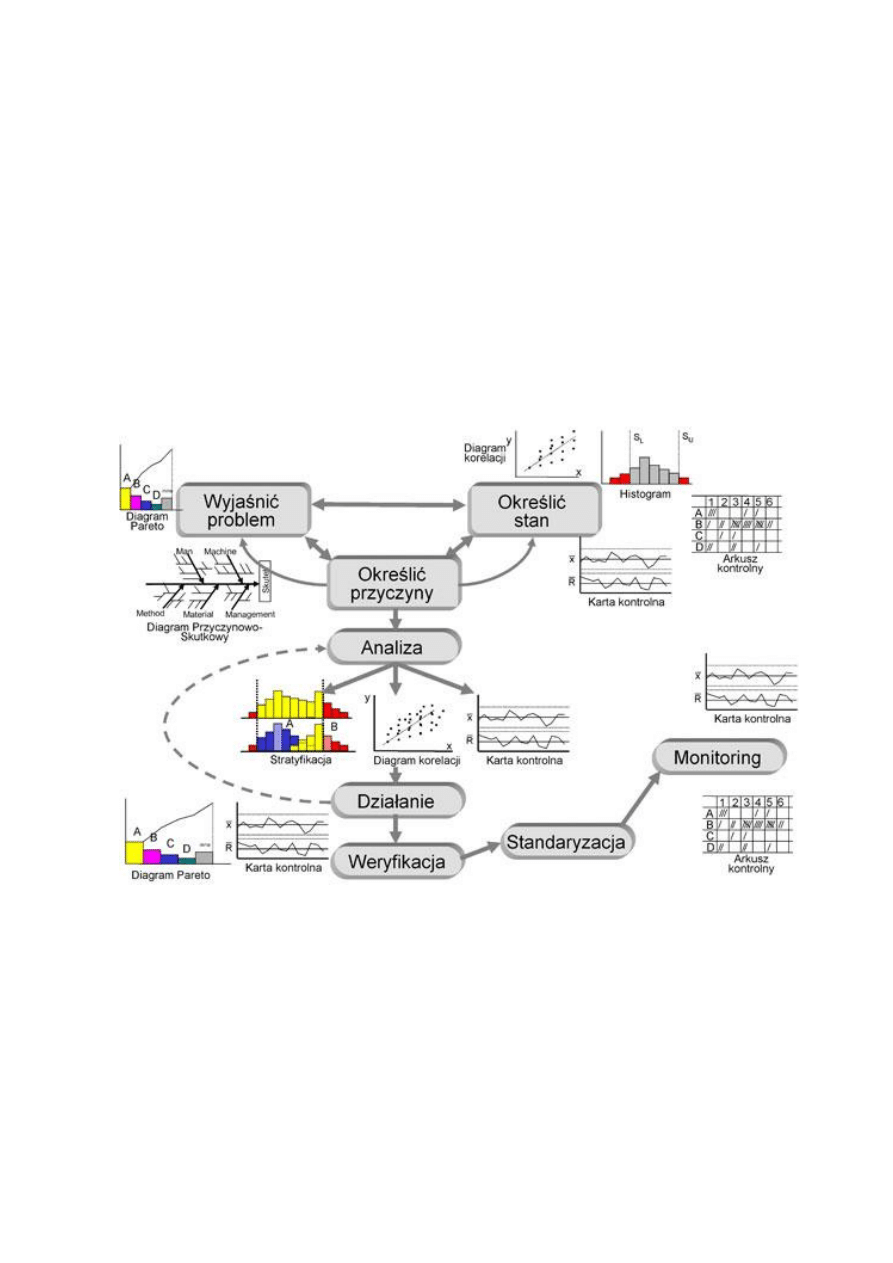
[1]

Narzędzia zarządzania jakością

Doskonalenie systemów jakości przeprowadza się przy pomocy narzędzi i technik
zarządzania jakością. W filozofii TQM kluczowe znaczenie odgrywa ciągłe poszukiwanie
możliwości doskonalenia organizacji we wszystkich aspektach jej działania. Wymaga to
zaangażowania wszystkich pracowników danej organizacji. Skutecznym sposobem
wyzwalania inicjatywy i zaangażowania pracowników jest praca zespołowa i stosowanie
narzędzi zarządzania jakością. Służą one do zbierania i przetwarzania informacji, analiz,
nadzorowania procesu oraz wykrywania błędów, wad i nieprawidłowości w przebiegach
procesów. Pozwalają na wizualizację danych, monitorowanie i diagnozowanie procesów w
całym cyklu życia wyrobu. Dzięki nim można sprawdzić efektywność podjętych działań.

[2]

1. Tradycyjne narzędzia zarządzania jakością

Zestaw opracowany w Japonii w latach 60-tych i składa się z następujących narzędzi:



Diagram Ishikawy



Diagram Pareto-Lorenza



Histogram



Diagram korelacji



Schemat blokowy



Stratyfikacja



Karty kontrolne

Narzędzia te mogą być stosowane samodzielnie. Opierają się one na statystyce
matematycznej i mają szerokie zastosowanie tam, gdzie możliwe jest zebranie dużej ilości
danych umożliwiających ich analizę.

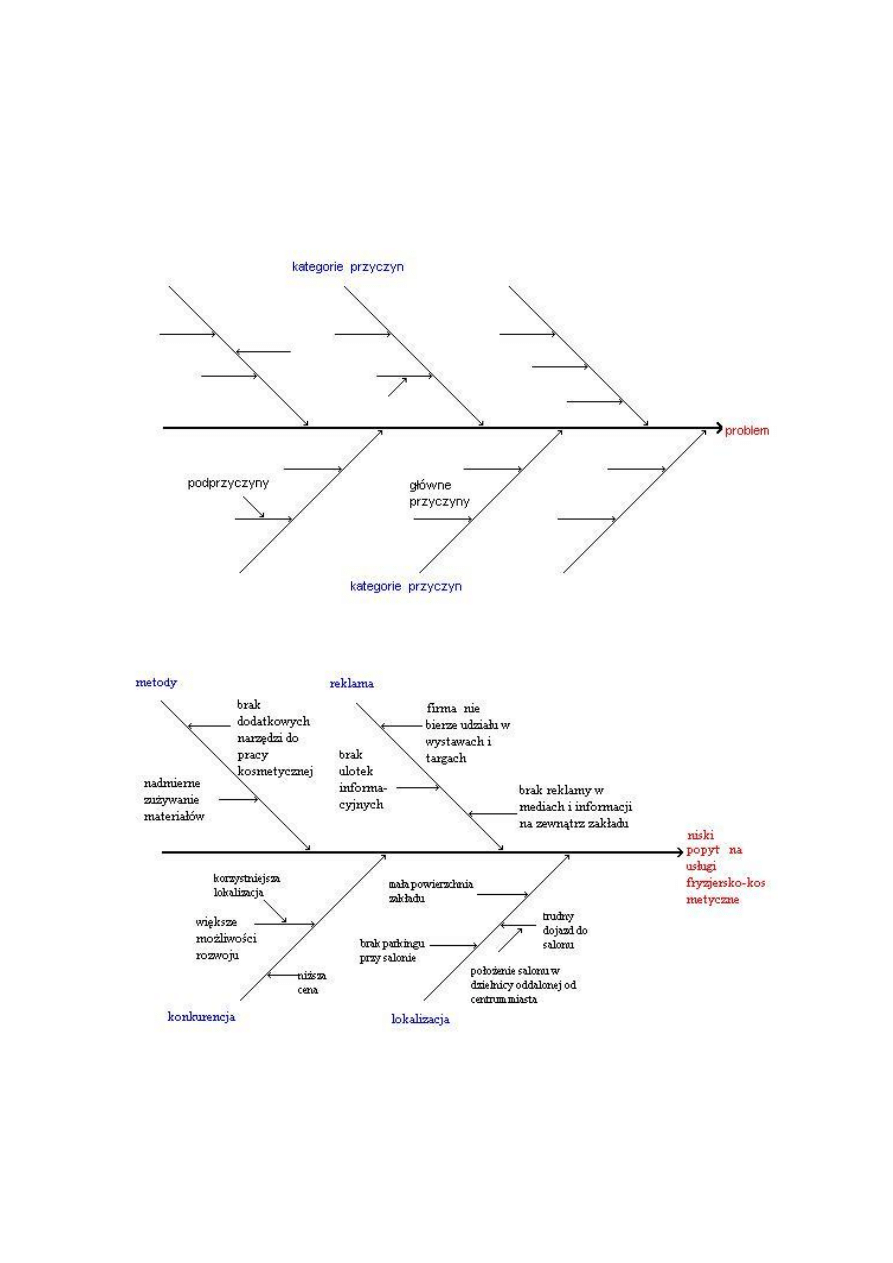
1.1. Diagram Ishikawy

Diagram Ishikawy zwany diagramem przyczynowo – skutkowym jest powszechnie
stosowanym narzędziem w inżynierii jakości. Istotą powstania diagramu jest graficzne
przedstawienie analizy wzajemnych zależności przyczyn, powodujących określony skutek.
Często, ze względna wygląd, diagram jest nazywany jodełkowym lub schematem rybiej ości.
Diagram ten często jest też nazywany schematem jodełkowym lub schematem rybiej ości ze
względu na swoją budowę i kształt. Ogólny obraz schematu j rybiego wykresu symbolizuje:



głowa ryby to skutek, czyli analizowany problem



kręgosłup skupia promieniście rozłożone przyczyny – ości



ości to przyczyny powodujące dany skutek

1.1.1. Fazy budowy diagramu Ishikawy



Faza identyfikacji problemu



Faza rozpoczęcia prac nad diagramem



Faza uszczegółowienia diagramu



Faza analizy diagramu

Punktem wyjścia do budowy diagramu jest zidentyfikowanie problemu, który należy
rozpatrzyć. Następnie należy opisać główne grupy przyczyn wpływających hipotetycznie lub
rzeczywiście na wyłoniony problem. Pomocna może się okazać zasada 5M:



Siła robocza (Manpower)



Metoda (Methods)



Maszyna (Machinery)



Materiał (Material)



Zarządzanie (Managment)

[3]

Można także używać innych kategorii zależnie od dziedziny, w jakiej diagram jest stosowany.
W kolejnym etapie dąży się do uszczegółowienia diagramu Ishikawy. Po tych operacjach
przystępuje się do szczegółowej analizy diagramu, której wynikiem jest rozwiązanie
problemu.

1.1.2. Przykładowe diagramy Ishikawy

[4]

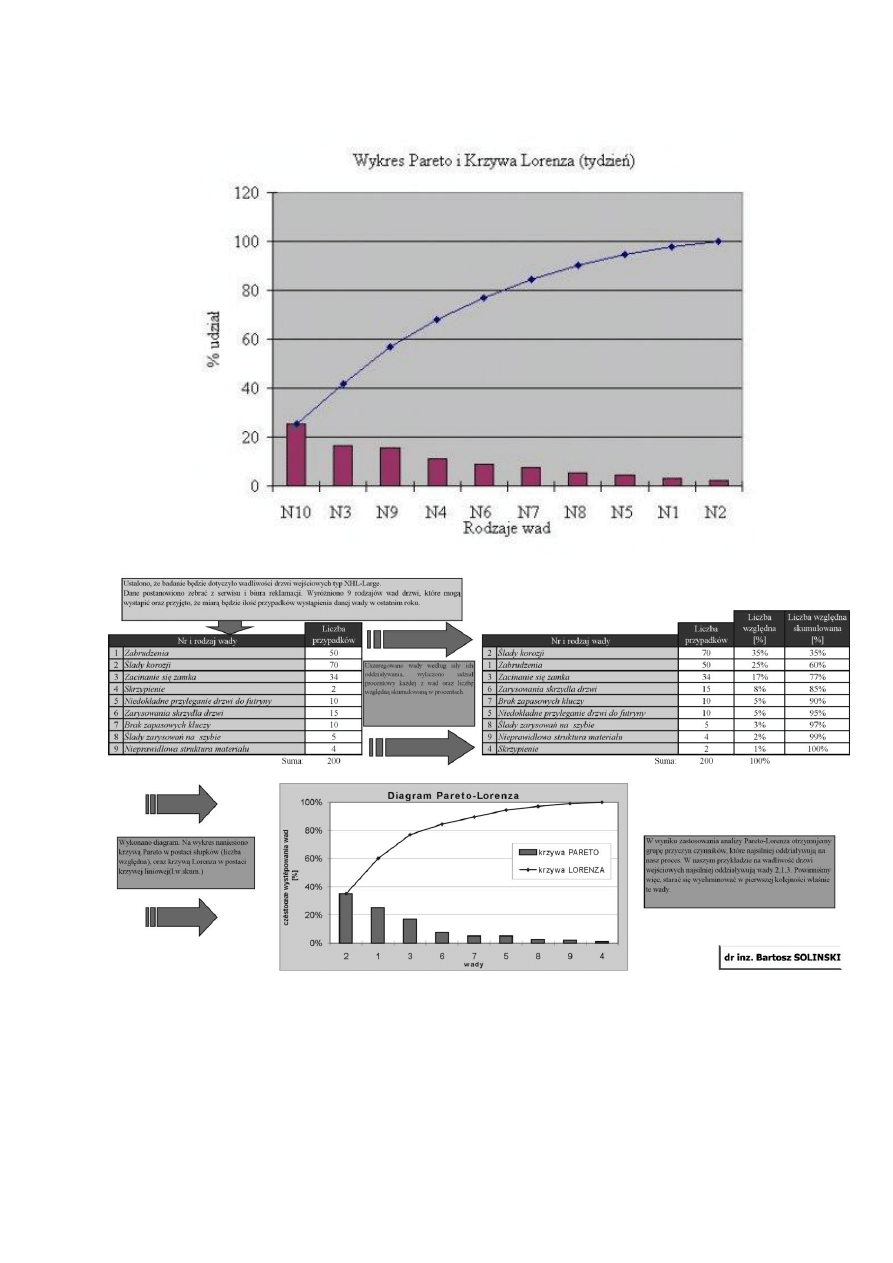
1.2. Diagram Pareto-Lorenza

Diagram Pareto – Lorenza jest narzędziem służącym do nadawania ważności czynnikom
(przyczynom) wywołującym określony problem. Istota tej metody opiera się na pracy
włoskiego ekonomisty Vilfredo Pareto, który sformułował zasadę znaną obecnie jako 80/20,
lub metodą ABC. Mówi ona o tym, że występowanie większości typów zdarzeń można
zaobserwować w małym zaledwie fragmencie możliwych okoliczności. Można stwierdzić na
podstawie tej zasady, że niewielka liczba osób, przyczyn, sytuacji odpowiada za większość
występujących zjawisk. Identyfikowane są te problemy, które mimo stanowienia mniejszości
względem liczebności pozostałych, wywierają dominujący wpływ na rozpatrywane
zagadnienie.

1.2.1. Tworzenie analizy według zasady Pareto – Lorenza

Procedura tworzenia analizy według zasady Pareto – Lorenza:

1) identyfikacja rodzajów rozpatrywanych zagadnień (np. rodzajów wad),
2) określenie przedziału czasowego (dzień, zmiana, rok itp.) w celu późniejszego

porównywania efektów wprowadzonych zmian,

3) ustalenie częstości występowania poszczególnych kategorii (np. przyczyn, wad),
4) uszeregowanie kategorii wg malejącej częstości występowania, obliczenia

częstości procentowych oraz skumulowanych,

5) ustalenie skal na osi pionowej (najczęściej przyjmuje się bezwzględną częstość

występowania oraz procent skumulowany) i poziomej (kategorie),

6) naniesienie na wykres słupków odpowiadających częstości dla poszczególnych

kategorii (wykres Pareto) i krzywej dla procentów skumulowanych (krzywa
Lorenza), w kolejności od największego do najmniejszego nasilenia
oddziaływania.

Dane stosowane do sporządzenia wykresu powinny być zestawione w tabeli, zawierającej
kolumny odpowiadające nazwom (symbolom) poszczególnych kategorii, bezwzględnej
wartości występowania lub nasilenia oddziaływania, procentowemu udziałowi w
rozpatrywanym zagadnieniu oraz procentom skumulowanym.

Metoda ta może służyć nie tylko wskazaniu najważniejszych źródeł problemów, ale również
prezentacji rezultatów działań korygujących w danej dziedzinie. Umieszcza się wówczas
obok siebie dwa wykresy – przed i po podjęciu działań naprawczych, używając oczywiście
tych samych skal i rodzajów danych.

Wykres Pareto-Lorenza:



porządkuje dane pod względem ich ważności



umożliwia wykazanie źródeł powstawania niepotrzebnych kosztów, pozwalając na ich
ograniczenie



pozwala wyciągnąć wnioski i opracować zalecenia odnośnie do podjęcia działań
korygujących i zapobiegawczych



pomaga w natychmiastowym zauważeniu i skorygowaniu niezgodności



jest bardzo przydatny w funkcjonowaniu Systemu Zarządzania Jakością.

[5]

1.2.2. Przykładowe zastosowania diagramu Pareto – Lorenza

[6]

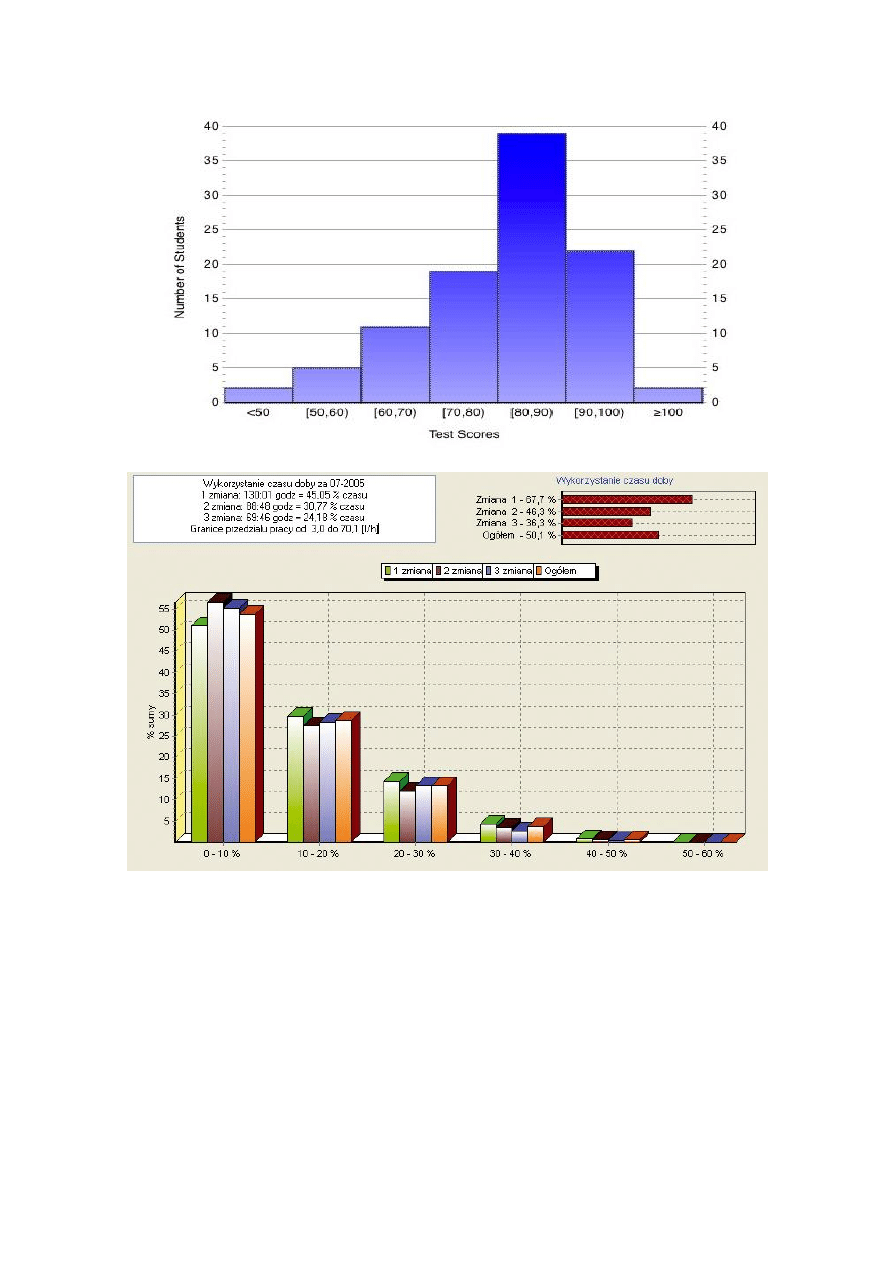
1.3. Histogram

Histogram to jeden z graficznych sposobów przedstawiania rozkładu empirycznego (badania
statystycznego) cechy w postaci wykresu powierzchniowego. Składa się z szeregu
prostokątów umieszczonych na osi współrzędnych. Prostokąty te są z jednej strony
wyznaczone przez przedziały klasowe wartości cechy, natomiast ich wysokość jest określona
przez liczebność (częstość lub gęstość prawdopodobieństwa) elementów przypadających na
określony przedział klasowy. Ilustruje on postać rozkładu i jego usytuowanie w stosunku do
wartości nominalnej i tolerancji. W zarządzaniu jakością jest on pomocny przy wizualizacji
zmienności wyników danego procesu.

1.3.1. Fazy tworzenia histogramu

W pierwszej kolejności należy wyznaczyć przedział zmienności analizowanej wielkości, a
następnie wyznaczyć liczbę przedziałów szeregu rozdzielczego. Liczba przedziałów
uzależniona jest od obszaru zmienności badanej cechy, od liczby zbiorowości oraz od celu
badania (im większy obszar zmienności i liczniejsza zbiorowość, tym więcej musi być
przedziałów).

1.3.2. Budowa histogramu

Histogram podobnie jak pozostałe wykresy statystyczne składa się z kilku części:



Pola



Wykresu



Skali (aby ułatwić czytanie wykresu, stosuje się często, szczególnie w prostokątnym
układzie współrzędnych, dwie jednakowe skale na obu końcach obrazu graficznego, tj.
skalę poziomą oraz dwie skale pionowe po lewej i prawej stronie pola wykresu)



Tytuł (w wykresach popularyzacyjnych tytuł należy umieścić nad obrazem
graficznym, natomiast w publikacjach można go umieścić również pod rysunkiem)



Źródło (jeżeli obok wykresu w tej samej publikacji zamieszczamy tablicę statystyczną
z danymi liczbowymi i opatrzona jest ona opisem źródła informacji, wystarczy pod
wykresem wymienić jako źródło numer kolejny tej tablicy)

[7]

1.3.3. Przykładowe histogramy

1.4. Diagram korelacji

Diagram korelacji występuje także pod innymi nazwami m.in.: wykres rozrzutu, wykres
korelacji, wykres zmiennych. Służy on do graficznego przedstawienia relacji miedzy dwoma
zmiennymi (cechami). Stanowi więc zbiór punktów na płaszczyźnie, odpowiadający zbiorowi
par liczb (x

i

i y

i

), gdzie x

i

oznacza i-tą obserwację zmiennej niezależnej X, y

i

oznacza i-tą

obserwacje zmiennej zależnej Y.

[8]

Na istnienie korelacji zmiennych (cech) wskazuje ich wzajemny związek, który oznacza, że
zmienne wpływają na siebie. Diagram korelacji nie bada natomiast związku przyczynowo-
skutkowego zachodzącego między zmiennymi, a mówi jedynie o tym, czy istnieje pewien
związek korelacyjny między dwiema zmiennymi.

Diagram korelacji używany jest do:



stwierdzenia istnienia zależności pomiędzy zmiennymi



stwierdzenia kierunku związku



pokazania siły związku.

Wyrazem liczbowym korelacji jest współczynnik korelacji:

𝜌 =

cos(𝑋, 𝑌)

𝜎𝑥 ∗ 𝜎𝑦

zawierający się w przedziale

(−1 ÷ 1).

Możliwe wartości współczynnika korelacji:



Gdy ρ = 0, to nie ma korelacji, czyli nie ma liniowego związku między dwiema
zmiennymi losowymi



Gdy ρ = 1, to zachodzi ścisły dodatni związek między dwiema zmiennymi. W tym
przypadku, gdy wartości jednej ze zmiennych rosną, to i wartości drugiej rosną, a gdy
wartości jednej spadają, to i wartości drugiej zmiennej spadają



Gdy ρ = -1, to zachodzi ścisły ujemny związek między dwiema zmiennymi. Gdy jedna
z tych zmiennych przyjmie większe wartości, to druga przyjmuje mniejsze wartości, a
gdy wartości jednaj zmiennej spadają, to wartości drugiej zmiennej rosną



Jeżeli bezwzględna wartość ρ mieści się wewnątrz przedziału [0,1], to mierzy ona siłę
liniowego związku między dwiema zmiennymi

Siła związków korelacyjnych:



poniżej 0,2 - korelacja słaba (praktycznie brak związku)



0,2 – 0,4 - korelacja niska (zależność wyraźna)



0,4 – 0,6 - korelacja umiarkowana (zależność istotna)



0,6 – 0,8 - korelacja wysoka (zależność znaczna)



0,8 – 0,9 - korelacja bardzo wysoka (zależność bardzo duża)



0,9 – 1,0 - zależność praktycznie pełna

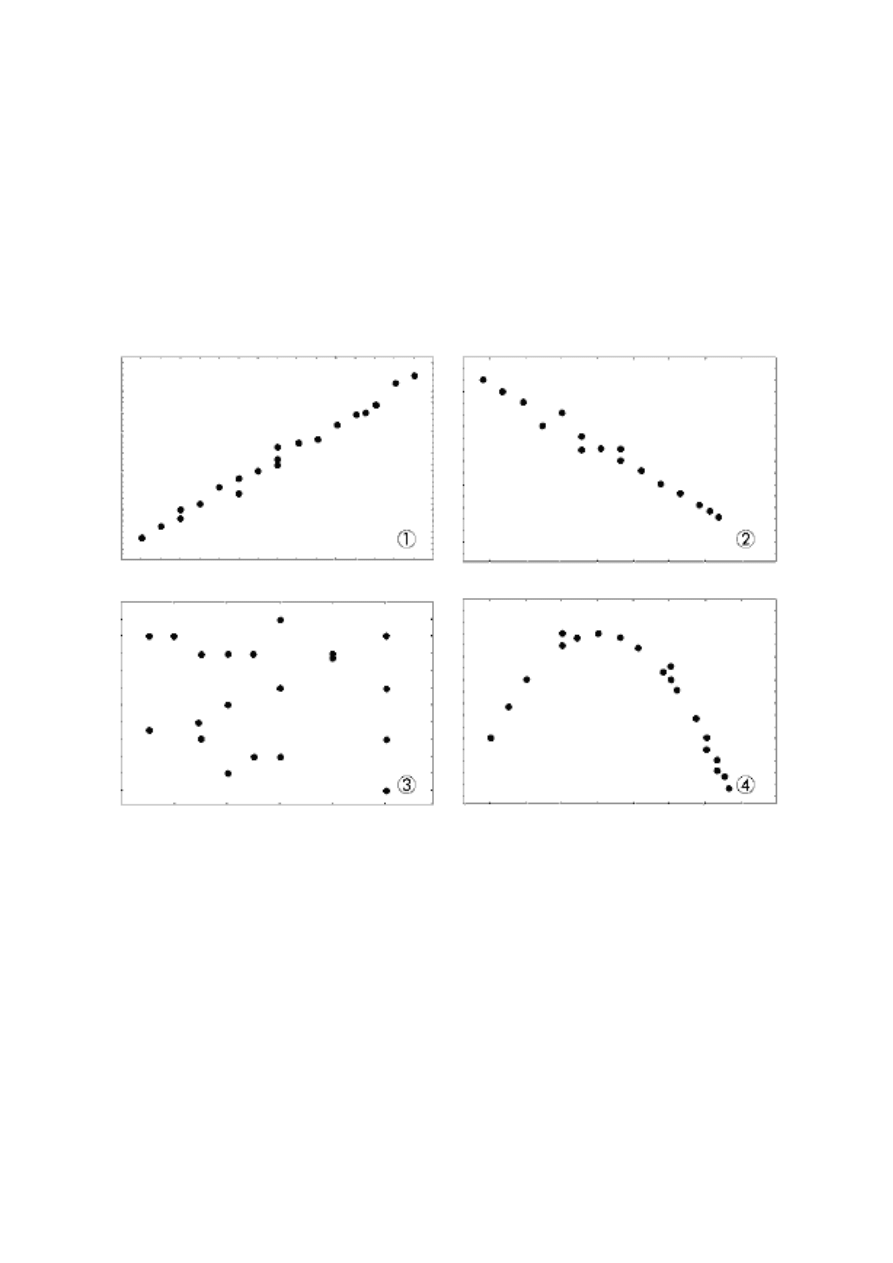
[9]

1.4.1. Tworzenie diagramu korelacji

Diagram korelacyjny w prostokątnym układzie współrzędnych, tworzy się odkładając na
osiach wartości badanych zmiennych. Na osi odciętych zaznaczamy wartości tej zmiennej,
którą przyjmujemy za niezależną (objaśniającą), wyrażającą ilościowo zjawisko traktowane
jako przyczyna, natomiast na osi rzędnych wartości tej zmiennej, którą przyjmujemy za
zależną (objaśnianą), wyrażającą ilościowo zjawisko uznawane za skutek. Punkty
umieszczone w takim układzie współrzędnych tworzą mniej lub bardziej wyraźną „smugę”,
co daje możliwość wstępnej oceny siły i kierunku zależności oraz może być podstawą wyboru
określonej funkcji matematycznej opisującej zależność między badanymi zmiennymi.

1.4.2. Przykładowe diagramy korelacji

1) Korelacja liniowa dodatnia
2) Korelacja liniowa ujemna
3) Brak korelacji
4) Korelacja krzywoliniowa

[10]

1.5. Schemat blokowy

Schemat blokowy w literaturze przedmiotu spotka się także pod nazwami: karta przepływu,
mapa procesu, harmonogram działań.

Schemat blokowy jest graficzną prezentacją wszystkich kroków (przebiegu procesu)
operacyjnych, czynności od momentu ich rozpoczęcia do momentu ich zakończenia.
Narzędzie to daje więc możliwość nie tylko zrozumienia i analizy przebiegu procesu, ale
przede wszystkim przyczynia się do poprawy jego jakości przez wprowadzane korekty czy
modyfikacje. Schemat blokowy ma zastosowanie w odniesieniu do opisu istniejącego procesu
lub zaprojektowania nowego procesu.

Schematy blokowe używane są najczęściej w procesach planowania i kontroli. Możliwość
określenia punktów procesu warunkujących jego dalszy, prawidłowy przebieg (obszarów
krytycznych) jest niewątpliwie zaletą tego narzędzia. Ponadto schemat blokowy może być
wykorzystywany w analizie wykonywanych czynności przez porównanie rzeczywistego
wykonania ze standardem kontroli, czyli z tym, jak dana czynność lub zadanie powinno być
wykonane. Dzięki temu można wykryć błędy popełnione na poszczególnych etapach procesu,
jak również wyeliminować czynności (operacje) zbędne lub powtarzające się.

1.5.1. Sporządzanie schematu blokowego:

1) Nazwanie procesu – najlepiej za pomocą jednego zdania
2) Ustalenie granic procesu – polega na określeniu początku i końca procesu
3) Analiza przebiegu procesu – należy ustalić jak jest wykonywana praca w

poszczególnych fazach procesu

4) Narysowanie schematu
5) Wprowadzenie opisu poszczególnych elementów
6) Połączenie elementów graficznych
7) Wprowadzenie komentarzy

1.5.2. Elementy składowe schematu blokowego



Blok graniczny – oznacza początek lub koniec, zazwyczaj w postaci owalnej



Skrzynka operacyjna – oznacza wykonywanie różnych działań, ma postać prostokąta



Skrzynka wejścia / wyjścia – oznacza wprowadzanie lub wyprowadzanie danych, ma
postać równoległoboku, wchodzi i wychodzi z niej jedno połączenie



Skrzynka warunkowa – oznacza sprawdzenie warunku i dokonanie wyboru, ma kształt

rombu, wychodzą z niej dwa połączenia: TAK i NIE



Strzałka – wskazuje jednoznacznie powiązania i kierunek przepływu informacji

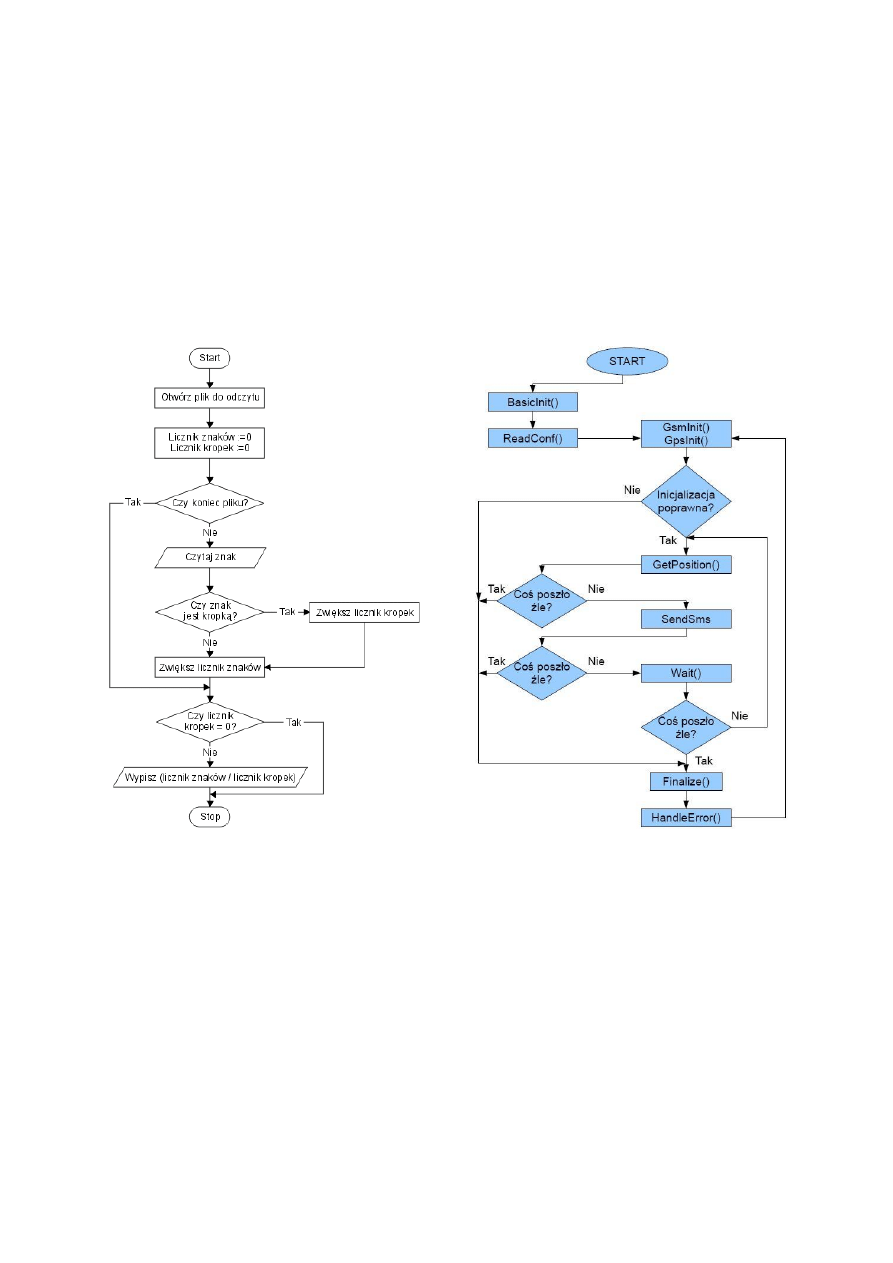
[11]

1.5.3. Budowa schematu blokowego

1) Każda operacja jest umieszczona w skrzynce
2) Schemat ma tylko jedną skrzynkę "początek" i przynajmniej jedną skrzynkę "koniec"
3) Skrzynki są ze sobą połączone
4) Ze skrzynki wychodzi jedno połączenie; wyjątek stanowią skrzynki: "koniec" (z której

nie wychodzą już żądne połączenia) oraz "warunkowa" (z której wychodzą dwa
połączenia opisane TAK i NIE - w zależności od tego, czy warunek jest spełniony czy
nie, można wyjść jedną z dwóch dróg)

1.5.4. Przykładowe schematy blokowe

1.6. Stratyfikacja

Stratyfikacja jest techniką polegającą na zbieraniu danych dotyczących przedmiotu dostawy,
produkcji lub przebiegu procesu na specjalnie przygotowanych formularzach w celu ich
dalszego przetwarzania (np. w celu analizy procesu, poszukiwania przyczyn problemów).
Zastosowanie techniki pozwala na łatwiejszą identyfikację źródła i przyczyn ewentualnych
błędów.

W procesie produkcyjnym zbieranie informacji w formularzach mogą obejmować np.:nr
wydziału, nr partii, symbol materiału, symbol dostawcy, nr pracownika, nr kontrolera,
temperaturę powietrza, czas obróbki itp.

[12]

W sytuacji gdy zaistnieje problem, np. pojawią się uszkodzenia materiałów, można
wykorzystując informacje z formularzy, dokonać „rozwarstwienia” informacji (stratyfikacji) i
wskazać główne źródło problemu.

1.6.1. Przykładowy arkusz zbierania informacji na potrzeby stratyfikacji

ARKUSZ PRZYJĘCIA

MATERIAŁU

Data ………………….
Nr partii ….………………
Symbol materiału ………………….
Symbol dostawcy ………………….
Środek transportu ………………….
Sposób kontroli .…………………
Warunki środowiska:

- temperatura …...…………….
- wilgotność ….………………

1.7. Karty kontrolne

Karty kontrolne są to podstawowe i najwcześniejsze historycznie narzędzia statystycznego
sterowania procesami. Pomysł karty kontrolnej zawdzięczamy Shewhartowi, a pierwsze
praktyczne zastosowanie tego pomysłu nastąpiło w 1924 roku. Karta kontrolna to graficzny,
usystematyzowany i ciągły sposób obserwacji kontrolowanego procesu / analiz.

1.7.1. Rodzaje kart kontrolnych

Wyróżniamy dwa rodzaje kart kontrolnych Shewharta:

1) Karty kontrolne dla cech ocenianych liczbowo (mierzalne)

a) Karta X-średnie - na tej karcie wykreślane są średnie z próbki, aby

monitorować średnie wartości zmiennej obserwowanej (np. rozmiar pierścieni
tłokowych, wytrzymałość materiału itd.)

b) Karta R - na tej karcie wykreślane są wartości rozstępu z próbki, otrzymywane

w rezultacie kolejnych badań zmienności obserwowanej zmiennej

c) Karta S - na tej karcie wykreślane są wartości odchylenia standardowego z

próbki, otrzymywane w rezultacie kolejnych badań zmienności obserwowanej
zmiennej

d) Karta S

2

- na tej karcie wykreślane są wartości wariancji z próbki,

otrzymywane w rezultacie kolejnych badań zmienności obserwowanej
zmiennej

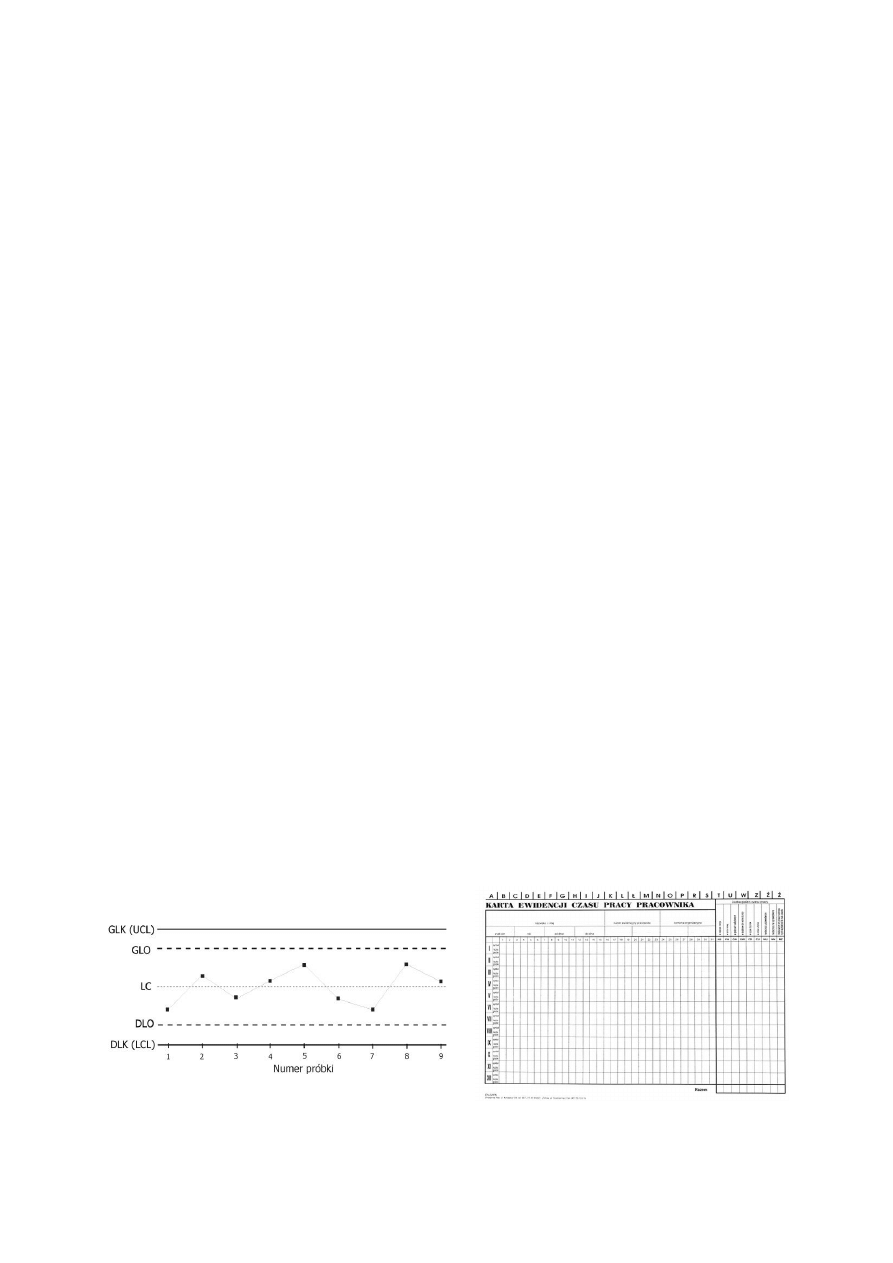
[13]

2) Karty kontrolne dla cech ocenianych alternatywnie (niemierzalne)

a) Karta C - na tej karcie wykreśla się liczbę wad, niezgodności (na partię, na

dzień, na maszynę, na 100 metrów długości rury itd.)

b) Karta U - na tej karcie wykreśla się wskaźnik liczby wad, niezgodności,

obliczany jako stosunek liczby wad do liczby badanych jednostek

c) Karta Np. - na tej karcie wykreśla się liczbę jednostek (elementów) wadliwych

(niezgodnych) w próbkach o stałej liczności (podobnie jak na karcie C)

d) Karta P - na tej karcie wykreśla się frakcję (procent) jednostek (elementów)

wadliwych (niezgodnych) w próbkach produktu (podobnie jak na karcie U)

Wszystkie te karty kontrolne mogą być dostosowane do produkcji krótkoseryjnej, a także do
procesów wieloźródłowych.

Karty kontrolne mają na celu sprawdzenie czy badany proces przebiega zgodnie z
założeniami. Natomiast w dłuższym okresie czasu służą ocenie stabilności procesu.

1.7.2. Tworzenie karty kontrolnej

Karty kontrolne buduje się z zebranych, w określonych odstępach czasu procesu
produkcyjnego, próbek o danej liczebności. Następnie są one zapisywane w arkuszach, co
pozwala na sprawdzenie czy dany proces przebiega prawidłowo. Na osi poziomej, zaznacza
się pobrane próbki, zaś na pionowej – wartości obserwowanej zmiennej. Tworząc karty
kontrolne należy przestrzegać następujących procedur:



wybór cechy, która będzie badana



wybór rodzaju karty



pobranie danych do obliczeń



wyznaczenie linii centralnej



wyznaczenie górnej i dolnej linii kontrolnej.

1.7.3. Przykładowe karty kontrolne

[14]

2. Nowe narzędzia zarządzania jakością

Pod koniec lat 70-tych opracowano w Japonii nowe narzędzia zarządzania jakością, w skład
których wchodzą:



Diagram pokrewieństwa



Diagram relacji



Wykres drzewa



Diagram macierzowy



Diagram strzałkowy



Macierzowa analiza danych

Większość narzędzi wymaga pracy zespołowej. Wszystkie narzędzia służą do zdefiniowania
problemu, znalezienia sposobu jego rozwiązania i zaplanowania działań doskonalących w
procesie zarządzania.

2.1. Diagram pokrewieństwa

Diagram pokrewieństwa nazywany jest inaczej wykresem podobieństw, wykresem
współzależności lub diagramem powinowactwa.

Diagram pokrewieństwa jest narzędziem wykorzystywanym do porządkowania
rozproszonych danych i informacji powstałych przykładowo w wyniku burzy mózgów. Jest to
narzędzie uniwersalne, które doskonale sprawdza się w analizie pomysłów, problemów, opcji
czy rozwiązań, a ich sortowanie ma charakter intuicyjny. W pracy z diagramem
pokrewieństwa wykorzystywana jest metoda pracy zespołowej. Istotą jest zatem
wykorzystywanie intuicji członków zespołu, którymi są specjaliści z badanego zagadnienia.

Diagram ten może być stosowany do generowania i zbierania informacji opisowych takich jak
idee, pomysły, opinie, czy koncepcje, a następnie porządkowania ich w grupy obejmujące
pokrewne pomysły. Porządkowanie powinno polegać na tworzeniu nie więcej niż dziesięciu
kategorii pojęć. Pomysły zebrane w trakcie tworzenia diagramu pokrewieństwa można
opracowywać dalej, wykorzystując pozostałe narzędzia takie jak na przykład diagram
Ishikawy, czy diagram zależności.

2.1.1. Schemat diagramu pokrewieństwa

Na górze tablicy lub kartki, w centralnym miejscu należy wpisać problem, który chcemy
rozwiązać. Przed grupowaniem kartki z zapisanymi pomysłami rozłożone są w sposób
przypadkowy, natomiast po grupowaniu pomysłów w kategorie kartki wykazują
uporządkowanie

[15]

2.1.2. Przykładowy diagram pokrewieństwa

2.2. Diagram relacji

Diagram relacji określany jest również jako diagram zależności, drzewo relacji, lub wykres
współzależności przyczyn. Jest on techniką wyjaśniania związków przyczynowych. Został
zaprojektowany dla ukazania logicznych powiązań i zależności zespołu czynników
wpływających na analizowane zagadnienia. Diagram relacji wykazuje znaczne podobieństwa
do diagramu przyczynowo skutkowego Ishikawy, jednak definiuje on nie tylko powiązania ,,
przyczyna - skutek’’, ale określa i odzwierciedla również powiązania ,, przyczyna-
przyczyna’’. Diagram relacji jest podstawą do planowania działań korygujących.

2.2.1. Tworzenie diagramu relacji dzielimy na trzy fazy:

1) W pierwszej fazie definiujemy problem, który chcemy przeanalizować
2) W drugiej fazie przy pomocy innych metod (np. burzy mózgów) określamy przyczyny

wywołujące zdefiniowany problem. Za pomocą strzałek łączymy przyczyny ze
skutkami, łącząc także zależności międzyprzyczynowe

3) W trzeciej fazie otrzymane informacje analizujemy w grupie badawczej i rysujemy

diagram relacji

Rozróżnia się trzy formy diagramu relacji:



Prosty



Ukierunkowany



Scentralizowany

[16]

2.2.2. Przykładowe diagramy relacji

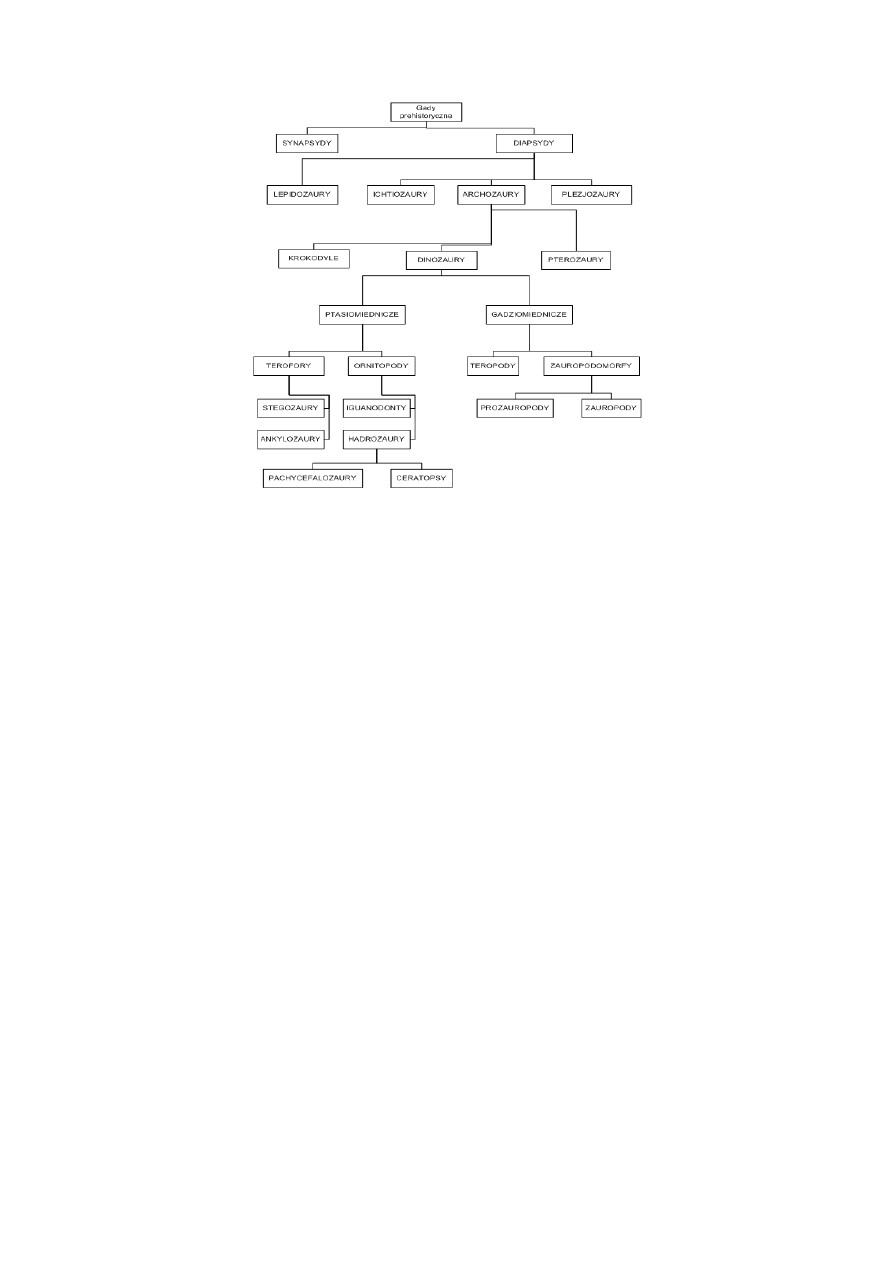
2.3. Wykres drzewa

Wykres drzewa zwany inaczej diagramem systematyki, wykres typu drzewo lub drzewem
decyzyjnym. Stosuje się go w procesach planowania. Jest to graficzne uporządkowanie
czynników powodujących występowanie problemu (przypomina wykres Ishikawy) lub
czynności niezbędnych w ramach danego procesu (nawiązuje do schematu blokowego).
Przyczyny i zadania są porządkowane w sposób logiczny i chronologiczny, zgodnie z zasadą
„od ogółu do szczegółu". Jego weryfikacja polega na skontrolowaniu, czy czynności
szczegółowe umożliwiają realizację celu głównego i odwrotnie. Diagram decyzyjny stanowi
dalsze uporządkowanie informacji zawartych w wykresach pokrewieństwa i współzależności.

Główne zastosowanie to ukazanie związków między rozpatrywanym zagadnieniem, a jego
elementami składowymi. Pomysły powstałe przy tworzeniu, mogą być przekształcone w
wykres drzewa z uwzględnieniem logiki i kolejności powiązań.

2.3.1. Tworzenie wykresu drzewa

1) określić w sposób jasny i prosty badane zagadnienie
2) wyznaczyć główne kategorie zagadnienia (wg burzy mózgów lub kart tytułowych z

wykresu współzależności)

3) zbudować wykres umieszczając zagadnienie po lewej stronie, a odgałęzienia

głównych kategorii po prawej

4) dla każdej głównej kategorii ustalić elementy składowe i podrzędne
5) elementy składowe i podrzędne umieścić z prawej strony kategorii jako boczne

gałęzie

6) zweryfikować wykres ze względu na kompletność i logikę

[17]

2.3.2. Przykładowy wykres drzewa

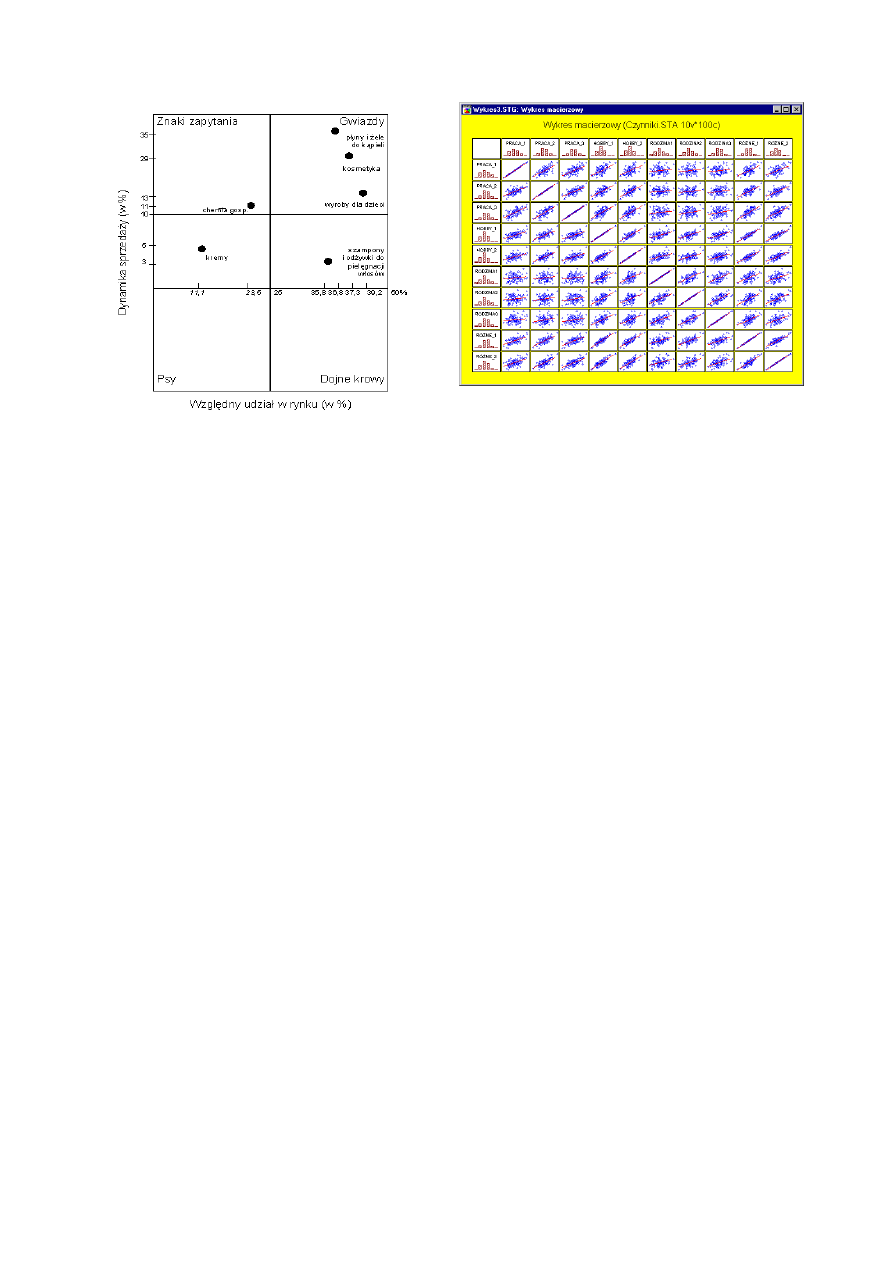
2.4. Diagram macierzowy

Diagram macierzowy- nazywany także diagramem tablicowym. Przedstawi powiązania
elementów (zadań, czynności, procesów, proponowanych rozwiązań) oraz rodzaj i „siłę"
związku. Dobór elementów diagramu może stanowić efekt prac, wykorzystujących inne
narzędzia, np. burze mózgów lub analizę oddziaływań. W zależności od liczby grup
czynników oraz rodzaju powiązań między nimi są stosowane różne typy diagramów. Metoda
ta powstała w celu rozpoznania zależności pomiędzy wymaganiami klienta a parametrami
wyrobu i umożliwiającego ustalenie jego cech Diagram macierzowy może także stanowić
uszczegółowienie wykresu typu drzewo zdarzeń.

2.4.1. Tworzenie diagramu macierzowego

1) Wybór informacji prezentowanej w wierszu (np. etykieta funkcji)
2) Wybór informacji prezentowanej w kolumnie (np. nazwa encji)
3) Wybór informacji prezentowanej w komórce macierzy (np. operacje wykonywane

przez funkcję encji)

[18]

2.4.2. Przykładowe diagramy macierzowe

2.5. Diagram strzałkowy

Diagram strzałkowy inaczej wykres sieciowy. Wykorzystuje się do planowania działań oraz
ustalania ich kolejności (np. realizacji projektów). Oraz do planowania powtarzalnych
procesów. Przy definiowaniu procesu ustalane są chronologie działań oraz czas potrzebny na
ich wykonanie. Działania dotyczące czasu łączone są na schemacie liniami, działania
realizowane równocześnie – są oznaczone strzałkami. Węzły powstającego diagramu
oznaczają stany, a łączące je linie czynności powodujące przejście do kolejnego stanu.
Technika ta stosowana jest do tzw. analizy ścieżek krytycznych.

2.5.1. Tworzenie diagramu strzałkowego

1) Zdefiniowanie planowanego przedsięwzięcia (określenie m.in. początku i końca

przedsięwzięcia)

2) Określenie listy czynności niezbędnych do wykonania przedsięwzięcia
3) Oszacowanie czasu trwania (realizacji) poszczególnych czynności (należy przyjąć

jednakową jednostkę czasu)

4) Określenie kolejności występowania czynności (niektóre czynności mogą być

wykonywane jednocześnie)

5) Narysowanie diagramu (sieci działań) (w zależności od rodzaju rysowanej sieci należy

odpowiednio oznaczyć wierzchołki i strzałki; wpisuje się na wykresie czynności i czas
realizacji każdej z nich, czasami uzupełnia się diagram o dodatkowe informacje, np. o
najwcześniejsze i najpóźniejsze terminy rozpoczęcia czynności, jednostki
odpowiedzialne za ich wykonanie itp.)

6) Przeprowadzenie analizy diagramu

a) określenie zapasów czasowych dla poszczególnych czynności
b) wyznaczenie ścieżki krytycznej (najdłuższej drogi w sieci, która wyznacza

najkrótszy możliwy czas ukończenia przedsięwzięcia, a w której znajdują się
czynności krytyczne, tj. takie, które nie mają zapasu czasu)

c) obliczenie czasu potrzebnego do wykonania całego przedsięwzięcia
d) dokonanie analizy środków, jakich należy użyć, aby zrealizować przedsięwzięcie

w terminie

[19]

2.5.2. Przykładowe schematy strzałkowe

2.6. Macierzowa analiza danych

Macierzowa analiza danych - określana także jako wykres analizy danych lub tablicowa
analiza danych. Celem jej stosowania jest analiza danych zawartych w diagramach
macierzowych. Ukazuje zależności między dwoma zbiorami danych nie powiązanych ze sobą
funkcjonalnie. Narzędzie to stanowi sposób prezentacji danych wyjściowych, których
otrzymanie muszą poprzedzić wielowariantowe analizy danych zawartych w diagramach
macierzowych. Taki sposób prezentacji danych jest wykorzystywany przede wszystkim w
marketingu, np. w trakcie szukania nisz rynkowych.

Macierzowa analiza danych jest techniką numeryczną, wykorzystującą liczby i formuły
matematyczne, jednak prezentacja danych odbywa się w formie graficznej. Technika ta
prezentowana jest w formie wykresu opartego na układzie współrzędnych, gdzie analizowane
są dane na podstawie dwóch zmiennych.

2.6.1. Zastosowanie macierzowej analizy danych

Macierzowa analiza danych stosowana jest głównie do:



Badania runku produktów i usług



Planowania i prac badawczych nad nowym produktem



Analizy niejednorodnych przyczyn problemów, tworzących duży zbiór danych



Kompleksowych ocen jakości

[20]

3. Dodatkowe narzędzia zarządzania jakością



Wizualizacja danych



Analiza pola sił



Metoda ABCD



Analiza oddziaływań



Burza mózgów

3.1. Wizualizacja danych

Wizualizacja danych polega na prezentacji danych numerycznych w postaci graficznej.
Dzięki prezentacji danych w atrakcyjnej wizualnie formie, użytkownik może szybko
zapoznać się z informacją i w prawidłowy sposób ją zinterpretować.

Dane (a tym samym informacje) pełnią istotną rolę w zarządzaniu jakością. Dane numeryczne
posiadają walory informacyjne, jednak są trudne do szybkiej interpretacji. Dane
przedstawione w postaci graficznej (np. wykresu kołowego lub słupkowego) niosą te same
informacje, ale w sposób bardziej efektywny. Należy przy tym podkreślić, że wizualizacja nie
powoduje zmiany oryginalnych danych numerycznych.

Dobra wizualizacja danych posiada trzy następujące cechy:



dokładność prezentacji danych (odpowiedni wybór skali i typu wykresu)



estetyczny wygląd



elastyczność umożliwiająca zmianę stylu wizualizacji

Właściwe techniki wizualizacji zależności danych są jednym z ważniejszych czynników
decydującym o zrozumieniu danych. Techniki wizualizacji mogą być stosowane jako jedna ze
skuteczniejszych form eksploracji danych, która może powiedzieć na ich temat więcej niż
same liczby.

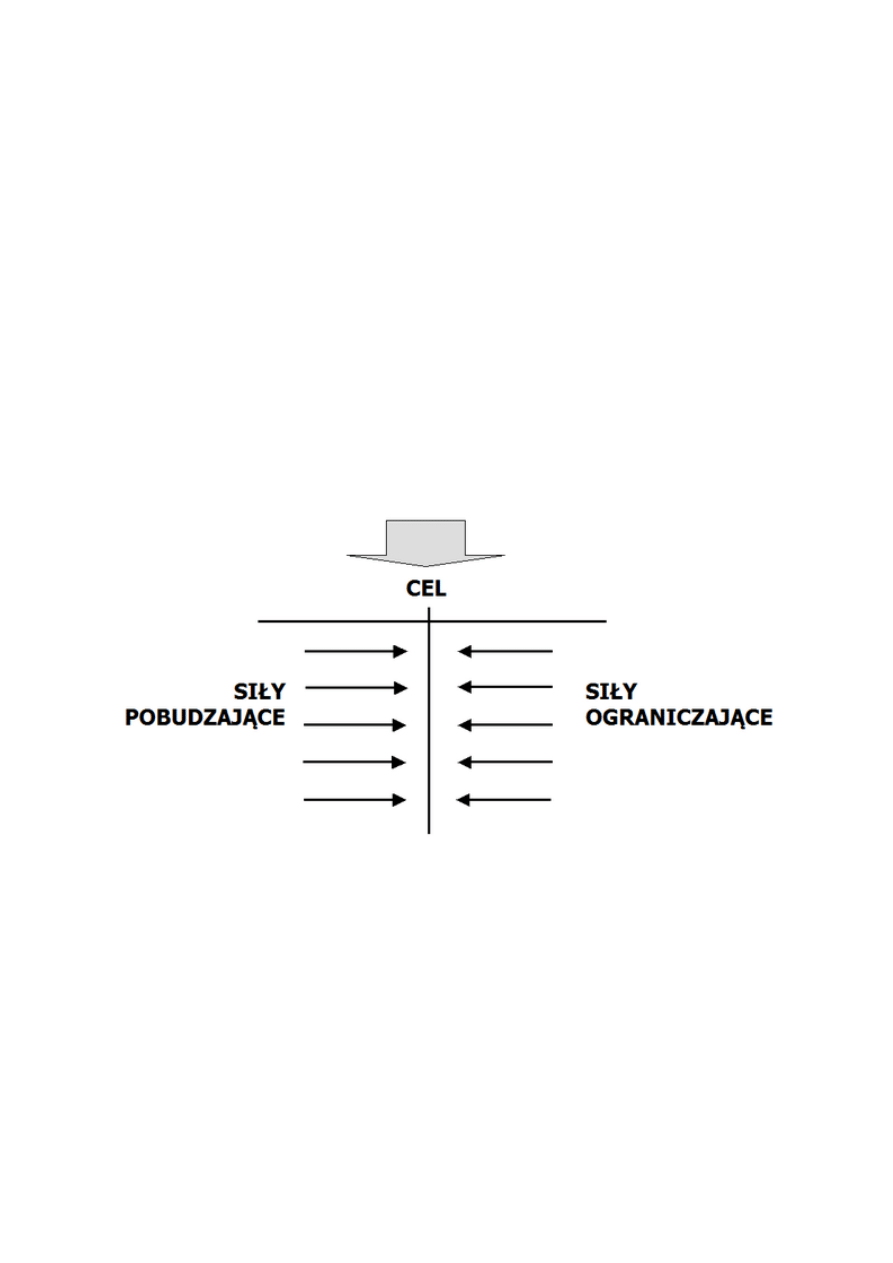
3.2. Analiza pola sił

Analiza pola sił - metoda (narzędzie, technika) doskonalenia jakości ułatwiająca ocenę
zaistniałego problemu. Można ją wykorzystać, gdy zidentyfikowaliśmy już dany problem i
musimy wybrać najlepsze rozwiązanie. Pozwala przeprowadzić pewnego rodzaju symulację
następstw podjęcia określonych działań oraz pomaga rozważyć wiele alternatywnych
rozwiązań w sposób przemyślany i systematyczny.

Zastosowania :

W analizie pola sił konfrontuje się przeciwstawne siły: sprzyjające i ograniczające osiągnięcie
zamierzonego celu. Można bowiem przyjąć, że nawet najbardziej statyczny układ jest efektem
określonego stanu równowagi czynników sprzyjających i przeszkadzających. W celu
wykorzystania analizy pola sił, należy spojrzeć na dany problem jak na układ dwóch grup sił.

[21]

3.2.1. Etapy prowadzenia analizy sił

1) Wpisanie aktualnej sytuacji pośrodku diagramu
2) Wpisanie sytuacji docelowej poniżej
3) Określenie sił pobudzających i umieszczenie ich na diagramie
4) Określenie sił ograniczających i umieszczenie ich na diagramie
5) Przeanalizowanie diagramu pod kątem możliwości zmian określonych czynników dla

osiągnięcia zamierzonego celu:

a) Ustalamy 3 podstawowe czynniki pobudzające
b) Ustalamy 3 podstawowe czynniki hamujące
c) Określamy działania, które mogą wzmocnić czynniki sprzyjające
d) Określamy działania mogące osłabić czynniki hamujące

6) Określenie, czy wybrane rozwiązanie jest możliwe do wykonania

a) Jeśli TAK - przygotowujemy plan działania(dokładne określenie działań: kto?

co? czym? kiedy? gdzie?)

b) Jeśli NIE - szukamy innego rozwiązania

3.2.2. Przykładowy diagram pola sił

3.3. Metoda ABCD

Metodyka ABCD pozwala ocenić i zweryfikować efektywność realizacji procesów
zarządzania względem tzw. najlepszych praktyk - czyli grupy procesów o kluczowym
znaczeniu dla funkcjonowania przedsiębiorstwa.

W ramach każdego procesu, zostały również wyodrębnione jego cechy charakterystyczne.
Następnie informacje te zostały pogrupowane w odpowiednie kategorie zastosowań,
opatrzone przejrzystymi komentarzami i przedstawione w formacie umożliwiającym
stosunkowo proste przeprowadzenie samooceny.

[22]

Posługiwanie się Metodą ABCD polega na określeniu, czy dane cechy procesu zarządzania
oraz sam proces występują w praktyce działania przedsiębiorstwa. A następnie na weryfikacji
funkcjonowania procesów. Odpowiedzi odnośnie efektywności realizacji samych procesów są
punktowane. Efektywność jest mierzona za pomocą czterech klas: A, B, C oraz D - stąd
nazwa metody.

Klasa A jest najwyższą oceną a jej uzyskanie stanowi wyższy stopień trudności niż popularne
standardy jakościowe ISO 9000, ponieważ oceniana jest rzeczywista efektywność operacyjna
przedsiębiorstwa, jego systemowy mechanizm w działaniu.

Warunkiem osiągnięcia certyfikatu klasy A jest udowodnienie mierzalnych efektów w
dziedzinie obsługi klientów oraz szeroko rozumianej jakości produktów i działań w
połączeniu z systematycznym obniżaniem kosztów.

W Metodzie ABCD wyróżnia się pięć kategorii procesów zarządzania. Są to procesy
związane z:

1) Planowaniem strategicznym
2) Zespołami ludzkimi
3) Zarządzaniem przez jakość i ciągłym usprawnianiem działalności
4) Opracowywaniem nowych produktów
5) Planowaniem i sterowaniem produkcją.

3.4. Burza mózgów

Burza mózgów to zespołowy sposób poszukiwania pomysłów dotyczących metod
rozwiązywania problemów. Podczas burzy mózgów dochodzi do utworzenia i wyjaśnienia
listy pomysłów, problemów lub spraw, wykorzystuje się twórcze myślenie całego zespołu, w
formie dyskusji.

3.4.1. Fazy burzy mózgów



faza tworzenia



faza wyjaśnienia

3.4.2. Etapy burzy mózgów

1) Wyznaczenie osoby prowadzącej
2) Jasne określenie celu sesji
3) Każdy wypowiada kolejno pojedynczą myśl
4) Rozwijanie pomysłów wcześniej zgłoszonych
5) Niedyskutowanie i niekrytykowanie wcześniejszych pomysłów
6) Widoczne dla wszystkich zapisywanie
7) Kontynuowanie aż do wyczerpania pomysłów
8) Dokonanie przeglądu wszystkich pomysłów w celu ich wyjaśnienia

[23]

Bibliografia:

1) „Inżynieria jakości – projektowanie projakościowe” Hieronim Suterski, Sławomir

Miedziarek

2) Zasoby sieci Internet:

a)

http://umbrella.org

b)

http://www.zarz.agh.edu.pl

c)

http://jakosc.biz

d)

http://www.tuv.com

e)

http://mfiles.pl

f)

http://www.studenci.pl

g)

http://www.centrum.jakosci.pl

h)

http://www.portfel.pl

i)

http://aragorn.pb.białystok.pl

j)

http://www.goldenline.pl