Autor: Martin Slota

  

Zdroj: http://www.zones.sk 

Používanie  materiálov  zo  ZONES.SK  je  povolené  bez 
obmedzení  iba  na  osobné  ú

č

ely  a  akéko

ľ

vek  verejné 

publikovanie je bez predchádzajúceho súhlasu zakázané.

 

 

1/3

 

MATURITNÉ PRÍKLADY Z MATEMATIKY 

M

ATURITNÝ OKRUH 

16:

 

K

OMBINATORIKA

 

1.  príklad (177/Pr. 2) 

Zadanie: Dokážte identitu 

(

)

1

2

1

1

2

2

1

1

−

⋅

=













⋅

+













−

⋅

−

+

+













⋅

+













⋅

n

n

n

n

n

n

n

n

n

n

K

 

a)  úpravou jednotlivých 

č

lenov 

ľ

avej strany. 

b)  kombinatorickou úvahou. 

Riešenie: 

a)  Dôkaz (priamy): 

Priamo z definície kombina

č

ného 

č

ísla dostávame: 

(

)

(

) (

)

(

)

(

)

(

) (

)

(

)

(

)

(

)

( ) ( )

Č

BTD

2

1

!

1

!

!

1

!

1

!

0

!

!

2

!

1

!

!

1

!

2

!

!

1

!

!

!

0

!

!

1

!

1

!

1

!

2

!

2

!

2

!

1

!

1

!

1

1

1

2

2

1

1

1

1

0

1

1

−

−

=

=

=

⋅

=













−

⋅

=

−

−

−

⋅

=

−

+

−

+

+

−

+

−

=

=

⋅

+

−

⋅

−

+

+

−

⋅

+

−

⋅

=













⋅

=













⋅

+













−

⋅

−

+

+













⋅

+













⋅

∑

∑

∑

n

n

i

n

i

n

i

n

i

n

n

i

i

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

i

n

i

n

n

n

n

n

n

n

n

K

K

K

 

b)  Dôkaz (priamy): 

Predstavme  si,  že  by  sme  vypísali  zoznam  všetkých 

1

2

−

n

  neprázdnych  podmnožín 

množiny 

{

}

n

A

,

,

2

,

1

K

=

.  Ko

ľ

ko 

č

ísel  by  sme  pritom  napísali?  Je  zrejmé,  že  každé  z 

č

ísel 

n

,

,

2

,

1

K

  sme  napísali  rovnako  ve

ľ

akrát,  a to  presne  to

ľ

kokrát,  v ko

ľ

kých  podmnožinách  sa 

vyskytuje.  ich  po

č

et  môžeme  zisti

ť

  nasledujúcou  úvahou:  Každú  podmnožinu  množiny 

A

 

obsahujúcu  prvok 

k

  môžeme  zapísa

ť

  v tvare 

{ }

k

A

k

∪

,  kde 

k

A

  je 

ľ

ubovo

ľ

ná  podmnožina 

(

)

−

−

1

n

prvkovej  množiny 

{ }

k

A

−

.  Týchto  podmnožín  je 

1

2

−

n

,  teda  každé 

č

íslo 

A

k

∈

 

napíšeme 

−

−

1

2

n

krát. Ke

ď

že 

č

ísel je spolu 

n

, je celkový po

č

et napísaných 

č

ísel 

1

2

−

⋅

n

n

. 

Teraz  si  predstavme,  že  by  sme  zoznam  podmnožín  množiny 

A

  robili  systematicky  – 

pod

ľ

a po

č

tu prvkov. Najskôr vypíšeme  všetky 1-prvkové podmnožiny. Tých je 













1

n

 a každá 

obsahuje  jedno 

č

íslo.  Potom  vypíšeme  všetky  dvojprvkové  podmnožiny  –  tých  je 













2

n

 

a každá  obsahuje  dve 

č

ísla,  teda  pritom  zapíšeme 













⋅

2

2

n

 

č

ísel  at

ď

.  Spolu  týmto  postupom 

napíšeme 

(

)













⋅

+













−

⋅

−

+

+













⋅

+













⋅

n

n

n

n

n

n

n

n

1

1

2

2

1

1

K

 

č

ísel.  

Ke

ď

že  obe  správne  úvahy  musia  vies

ť

  k rovnakému  výsledku,  je  správnos

ť

  danej 

identity dokázaná. 

2.  príklad (179/Pr. 3) 

Zadanie:  Ko

ľ

ko  je  všetkých  štvorciferných 

č

ísel  neobsahujúcich  nulu,  v ktorých  dekadickom  zápise 

platí, že sú

č

et prvých dvoch cifier sa rovná sú

č

tu druhých dvoch cifier? 

Riešenie: 

 

     

Autor: Martin Slota

  

Zdroj: http://www.zones.sk 

Používanie  materiálov  zo  ZONES.SK  je  povolené  bez 
obmedzení  iba  na  osobné  ú

č

ely  a  akéko

ľ

vek  verejné 

publikovanie je bez predchádzajúceho súhlasu zakázané.

 

 

2/3

 

MATURITNÉ PRÍKLADY Z MATEMATIKY 

M

ATURITNÝ OKRUH 

16:

 

K

OMBINATORIKA

 

Ozna

č

me 

M

  množinu  všetkých 

č

ísel  požadovaných  vlastností, 

i

M

  nech  je  množina 

štvorciferných prirodzených 

č

ísel, v ktorých sa sú

č

et prvých dvoch aj druhých dvoch cifier rovná 

i

. 

Potom  platí 

18

3

2

M

M

M

M

∪

∪

∪

=

K

,  pri

č

om 

θ

=

∩

j

i

M

M

  pre 

j

i

≠

.  Vy

č

íslime  teda 

i

M

  pre 

18

,

,

3

,

2

K

=

i

 a použijeme pravidlo sú

č

tu. 

Nech 

i

M

k

∈

  pre 

10

≤

i

.  Pre  prvé  dve  cifry 

č

ísla 

k

  máme  možnosti 

[

] [

] [

]

1

,

1

,

,

2

,

2

,

1

,

1

−

−

−

i

i

i

K

, 

spolu 

1

−

i

  možností.  Pre  druhé  dve  cifry 

č

ísla 

k

  máme  tých  istých 

1

−

i

  možností,  pri

č

om  vo

ľ

ba 

druhej dvojice je nezávislá od vo

ľ

by prvých dvoch cifier. Pod

ľ

a pravidla sú

č

inu teda 

( )

2

1

−

=

i

M

i

.  

Nech  teraz 

i

M

k

∈

  pre 

11

≥

i

.  Potom  pre  prvé  dve  cifry 

č

ísla 

k

  máme  možnosti 

[

] [

] [

]

9

,

9

,

,

8

,

8

,

9

,

9

−

−

−

i

i

i

K

, spolu 

i

−

19

 možností, teda pre 

11

≥

i

 platí 

(

)

2

19

i

M

i

−

=

. 

Pod

ľ

a  pravidla  sú

č

tu  potom  dostávame 

489

1

2

8

9

8

2

1

2

2

2

2

2

2

2

=

+

+

+

+

+

+

+

+

=

K

K

M

. 

Č

ísel 

požadovaných vlastností je teda 489. 

3.  príklad (180/5) 

Zadanie: Nech 

12

1

1

,

,

,

A

A

A

K

 sú vrcholy pravidelného 12-uholníka. Ko

ľ

ko existuje  

a)  rovnoramenných 

b)  pravouhlých 

c)  tupouhlých 

trojuholníkov s vrcholmi v týchto dvanástich bodoch? 

Riešenie: 

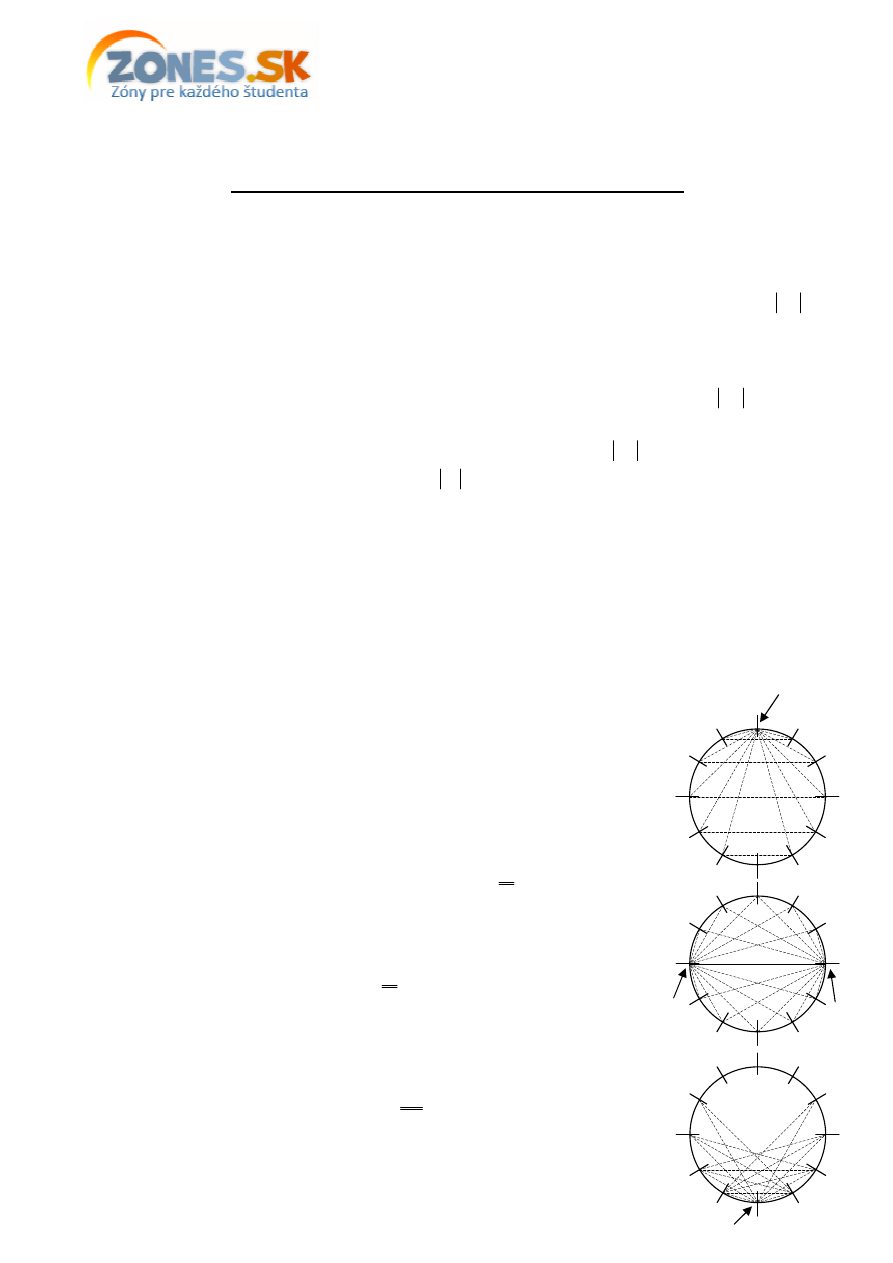
a)  Ku  každému  z dvanástich  vrcholov  vieme  dokresli

ť

  práve  5 

rovnoramenných  trojuholníkov  s vrcholmi  v niektorých  z ostatných 
z dvanástich vrcholov (pozri obr.). Z každého z dvanástich vrcholov však 
zostrojíme aj jeden rovnostranný trojuholník, ktorý tým pádom zarátame 
z každého  jeho  vrcholu  raz  – 

č

iže  dohromady  trikrát.  Preto  ho  musíme 

zárove

ň

  dvakrát  odráta

ť

.  Rovnoramenných  trojuholníkov  je  teda 

P(vrcholov)*P(trojuholníkov 

prislúchajúcich 

jednému 

vrcholu) 

– 

2*P(rovnostranných trojuholníkov) = 

52

2

4

12

5

=

⋅

−

⋅

. 

b)  Pokia

ľ

  si  zoberieme  jeden  z priemerov  kružnice  dvanás

ť

uholníku 

opísanej,  všetky  trojuholníky  vytvorené  s niektorým  z 

ď

alších  vrcholov 

budú  pravouhlé  (Tálesova  kružnica;  pozri  obr.).  Každému  priemeru 
prislúcha  teda  10  trojuholníkov  a  priemerov  je  6, 

č

iže  dohromady  bude 

pravouhlých trojuholníkov 

60

6

10

=

⋅

. 

 
 
 
 

c)  Tupouhlých  trojuholníkov  vieme  ku  každému  z vrcholov  zostroji

ť

  10, 

a preto je ich celkový po

č

et 

120

12

10

=

⋅

. 

 
 
 

 

     

Autor: Martin Slota

  

Zdroj: http://www.zones.sk 

Používanie  materiálov  zo  ZONES.SK  je  povolené  bez 
obmedzení  iba  na  osobné  ú

č

ely  a  akéko

ľ

vek  verejné 

publikovanie je bez predchádzajúceho súhlasu zakázané.

 

 

3/3

 

MATURITNÉ PRÍKLADY Z MATEMATIKY 

M

ATURITNÝ OKRUH 

16:

 

K

OMBINATORIKA

 

 

4.  príklad (181/9) 

Zadanie:  Na  orienta

č

ný  beh  sa  prihlásilo 

n

  pretekárov,  medzi  nimi  aj  Adamec,  Behú

ň

  a Cerový. 

Pretekári  vybiehajú  na  tra

ť

  jednotlivo,  v pevných  intervaloch.  Ur

č

te,  ko

ľ

kými  spôsobmi  možno 

zostavi

ť

  rozvrh  štartov  tak,  aby  žiadni  dvaja  z menovaných  pretekárov  neštartovali  bezprostredne 

po sebe. 

Riešenie: 

P (žiadni dvaja neštartujú po sebe) = P (všetkých štartovacích rozvrhov) – P (niektorí dvaja štartujú 
v 

ľ

ubovo

ľ

nom  poradí  po  sebe)  +  P  (všetci  traja  štartujú  v 

ľ

ubovo

ľ

nom  poradí  po  sebe)  = 

(

)

(

)

(

)

(

)

!

2

6

!

1

6

!

!

2

!

3

!

1

2

3

!

2

!

−

⋅

+

−

⋅

−

=

−

⋅

+

−

⋅













⋅

−

n

n

n

n

n

n

. 

5.  príklad (181/11) 

Zadanie: Ko

ľ

kými spôsobmi možno 

č

íslo 

6

10

 rozloži

ť

 na sú

č

in troch prirodzených 

č

inite

ľ

ov, ak berieme 

do úvahy aj ich poradie? 

Riešenie: 

Ke

ď

že 

⇒

⋅

=

6

6

6

5

2

10

  všetky  h

ľ

adané 

č

ísla  budú  v tvare 

{

}

(

)

6

,

,

2

,

1

,

0

,

5

2

K

∈

⋅

j

i

j

i

.  Pri  vytváraní 

trojíc 

č

inite

ľ

ov,  ktorých  sú

č

inom  je 

6

10

,  v podstate  rozdelíme  šes

ť

  dvojok  a nezávisle  na  tomto 

rozdelení aj šes

ť

 pätiek medzi h

ľ

adané 

č

initele. Po

č

et rôznych trojíc 

č

inite

ľ

ov sa teda bude rovna

ť

 

po

č

tu rôznych rozdelení dvojok znásobenému po

č

tom rôznych rozdelení pätiek medzi 

č

initele.  

Predstavme si teraz, že máme dve prepážky rozde

ľ

ujúce jednotlivé 

č

initele a šes

ť

 dvojok, ktoré 

medzi  alebo  za  tieto  prepážky  dávame.  Tým  pádom  v podstate  máme  osem  „vecí“,  ktoré  sa 
snažíme usporiada

ť

 v 

ľ

ubovo

ľ

nom poradí. Zárove

ň

 je nám však jedno, ktorá dvojka bude kde a tiež 

ktorá prepážka bude kde. Po

č

et rôznych rozdelení dvojok bude teda zodpoveda

ť

 

č

íslu 

28

!

6

!

2

!

8

=

⋅

. 

Správne  matematicky  povedané  sme  vypo

č

ítali  permutácie  s opakovaním  prvkov  dvoch  druhov, 

pri

č

om po

č

et prvkov jedného druhu je 6 a po

č

et prvkov druhého druhu je 2. Zápis: 

( )

2

,

6

P

. 

Výpo

č

et  po

č

tu  rôznych  rozdelení  pätiek  je  úplne  rovnaký  až  na  to,  že  namiesto  dvojok 

rozde

ľ

ujeme medzi 

č

initele pä

ť

ky. 

Celkový po

č

et výberu trojice 

č

inite

ľ

ov je teda 

784

28

28

=

⋅

.