Wojciech Calów

177153

Politechnika Wrocławska
Wydział Elektryczny
Rok studiów : III
Semestr : VI
Rok akad.: 2012/13

 Laboratorium Metod Numerycznych

Data: 

Temat : 

Różniczkowanie

Ocena: 

1. Cel ćwiczenia:

Zapoznanie się z metodami rozwiązywania równań różniczkowych metodą jawna i 
niejawną Eulera oraz metodą trapezów na podstawie następującego równania:

  

dy

(

t)

dt

=

2⋅t−0.2⋅y(t)

Warunki początkowe : 

y (0)=1

2. Program:

% Ró¿niczkowanie =======================

h=0.005;
x=0:h:1;

n=length(x);
y=[zeros(size(x))];

y1=[zeros(size(x))];
y2=[zeros(size(x))];

y(1)=1;
y1(1)=1;

y2(1)=1;
yp=2*(x) - 0.2*y;

yp1=2*(x) - 0.2*y1;
yp2=2*(x) - 0.2*y2; 

% Metoda Eulera Jawna ==================

for

 k=2:n

    y(k)=y(k-1)+h*yp(k-1);

end

% Metoda Eulera niejawna ===============

for

 k=2:n

    y1(k)=y1(k-1)+h*yp1(k);

end

% Metoda Trapezowa =====================

for

 k=2:n

    y2(k)=y2(k-1)+h/2*(yp2(k-1)+yp2(k));

end

      

% PLOT =================================

figure(1); hold 

on

; grid 

on

;

title(

'Ró¿niczkowanie dy/dt=2*(t)-0.2*y;'

);

plot(x,y, 

'r'

,x,y1,

'g'

,x,y2,

'b'

);

legend(

'm.trapez'

,

'm.Eulera jaw.'

,

'm.Eulera niejaw.'

);

axis([0 1 1 2]);

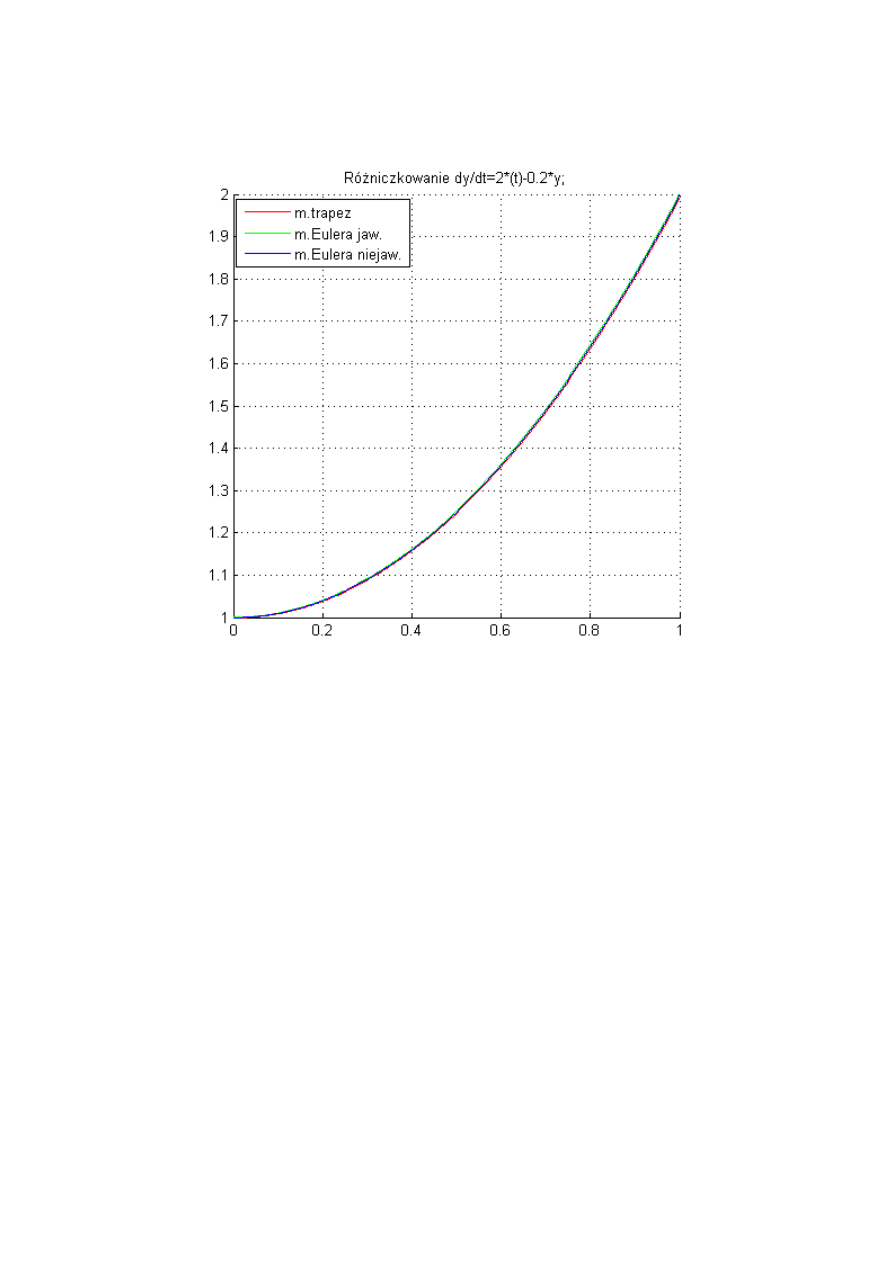
3. Wykresy

Rys. 1.Wykres rozwiązania równania różniczkowego

4. Wnioski

a) Uzyskane wyniki pozwoliły nam stwierdzić, że błąd wynosi ok 0,5% podczas 
porównywania metody trapezowej i jawnej Eulera. 
b) Wartość średnia wszystkich trzech rozwiązań pokrywa się z metodą niejawną 
Eulera.