Politechnika Wrocławska

Wydział Elektryczny

Wojciech Calów

Rok studiów : III
Semestr : VI
Rok akad. : 2012/13

Laboratorium Metod Numerycznych

Data:

Temat :

Całkowanie funkcji.

Ocena:

1. Cel ćwiczenia

Celem ćwiczenia jest zapoznanie się z metodami całkowania zadanej funkcji i porównanie
otrzymanych wyników w mat labie z obliczeniami analitycznymi.

S=

∫

0

0.01

(

sin(100 π t )−e

(−

10 t)

)

dt

2. Program

% CALKOWANIE NUMERYCZNE

clc; clear

all

; close

all

;

T=0.001;
t=0:T:0.01;

y=(sin(100*pi*t)) - (exp(-10*t));

% Metoda prostok¹tow

yp=0;

for

k=1:10

yp=yp+ T*y(k);

end

% Metoda trapezow

yt=0;

for

k=1:10

yt=yt+ T*(y(k)+y(k+1))/2;

end

% Metoda Simpson'a

ys=0;

for

k=1:2:10-1;

ys=ys+(T/3)*( y(k) + 4*y(k+1) + y(k+2));

end

figure(4);
plot(t,y);

grid

on

;

title(

'Interpolowana funkcja'

);

disp(

'Metoda Prostokatow'

); disp(yp);

disp(

'Metoda Trapezow'

); disp(yt);

disp(

'Metoda Simpspna'

); disp(ys);

2. Wyniki całkowania

Metoda Prostokątów
-0.003250167274730

Metoda Trapezow
-0.003202585983748

Metoda Simpspna
-0.003149711868816

Wartość otrzymana na stronie WolframAlpha
-0.00315006

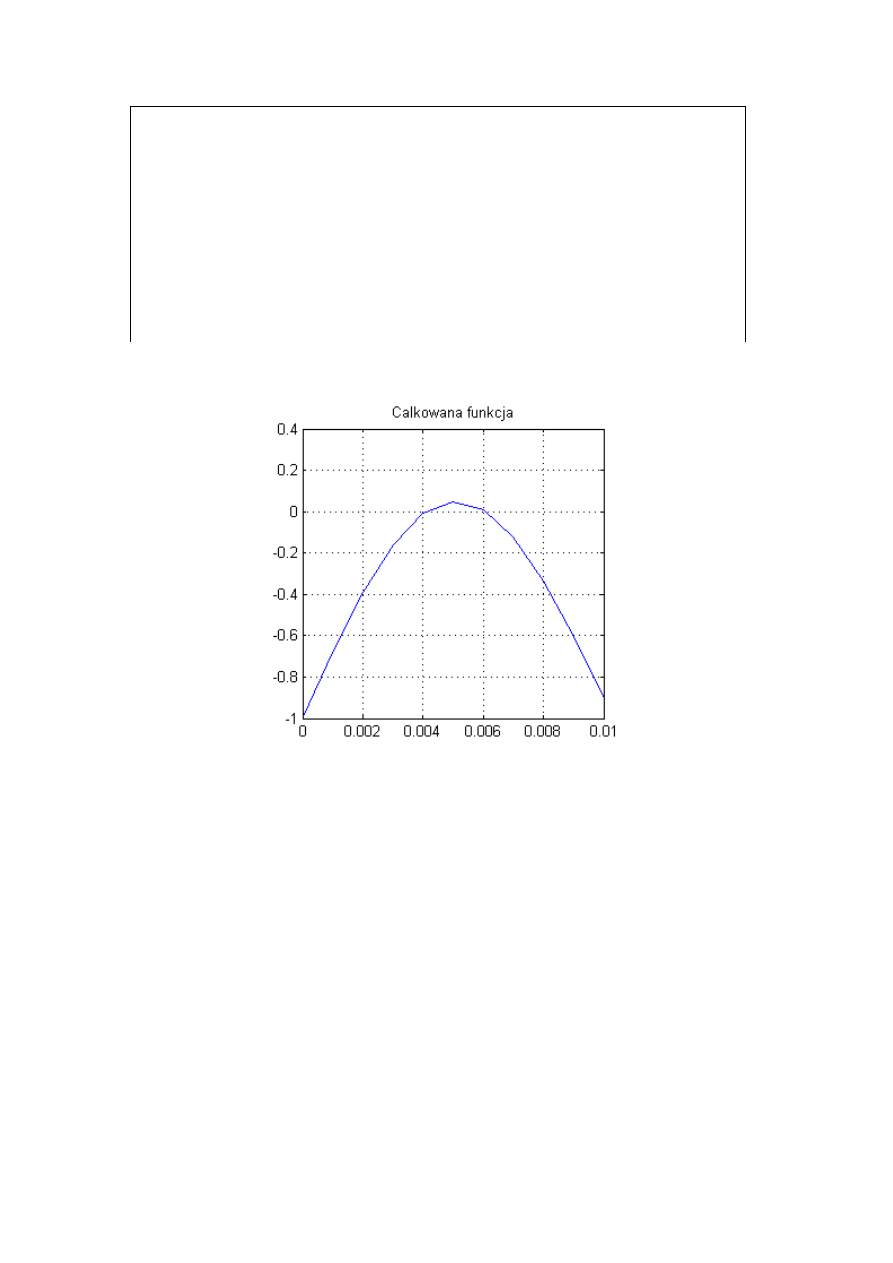
3. Wykres calkowanej funkcji