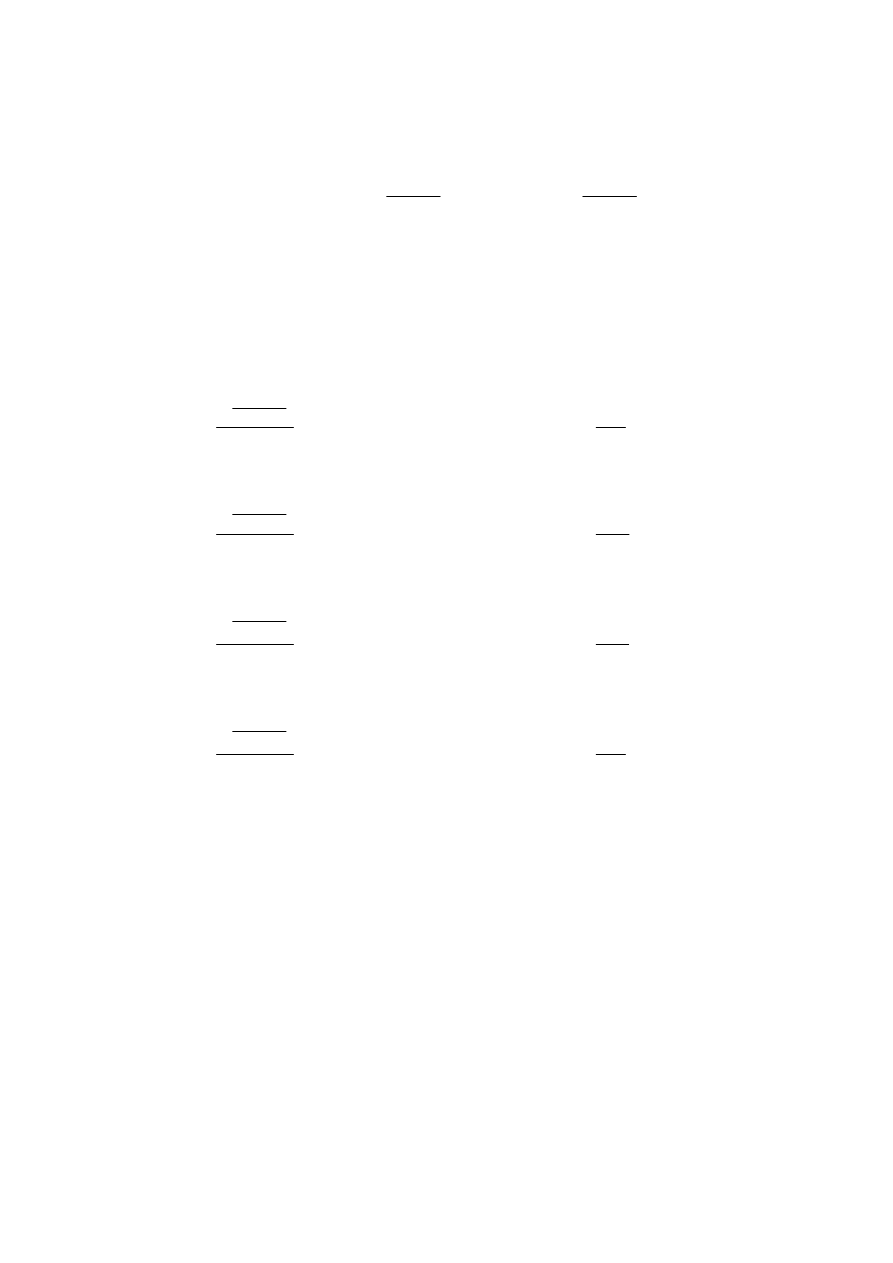
4.4. Pochodne cząstkowe drugiego rzędu

Pochodne cząstkowe z’

x

=

'

x

f

(x, y) =

x

y

x

f

∂

∂

)

,

(

, z’

y

=

'

y

f

(x, y) =

y

y

x

f

∂

∂

)

,

(

funkcji z = f(x, y)

obliczone w punkcie (x, y) są również funkcjami dwóch zmiennych x, y.

Dla każdej z tych funkcji pochodnych możemy wyznaczyć pochodne cząstkowe

względem x (pochodne po x ) oraz względem y (pochodne po y) – jeżeli tylko te pochodne

istnieją . Otrzymamy wówczas cztery nowe funkcje:

[

'

x

f

(x, y)]’

x

=

x

x

y

x

f

∂

∂

∂

∂

)

)

,

(

(

; funkcję tę oznaczamy krótko

'

2

x

f

bądź

2

2

x

f

∂

∂

,

[

'

x

f

(x, y)]’

y

=

y

x

y

x

f

∂

∂

∂

∂

)

)

,

(

(

; funkcję tę oznaczamy krótko

'

xy

f

bądź

y

x

f

∂

∂

∂

2

,

[

'

y

f

(x, y)]’

x

=

x

y

y

x

f

∂

∂

∂

∂

)

)

,

(

(

; funkcję tę oznaczamy krótko

'

yx

f

bądź

x

y

f

∂

∂

∂

2

,

[

'

y

f

(x, y)]’

y

=

y

y

y

x

f

∂

∂

∂

∂

)

)

,

(

(

; funkcję tę oznaczamy krótko

'

2

y

f

bądź

2

2

y

f

∂

∂

.

Otrzymane funkcje nazywamy pochodnymi cząstkowymi drugiego rzędu funkcji z = f(x,y).

Pochodne

'

yx

f

,

'

yx

f

różnią się tylko kolejnością liczenia (po x, po y). Nazywamy je

pochodnymi mieszanymi rzędu drugiego.

Twierdzenie

Jeżeli dla funkcji z = f(x, y) pochodne

'

yx

f

,

'

yx

f

istnieją i są funkcjami ciągłymi w obszarze

D, to w każdym punkcie tego obszaru są sobie równe.

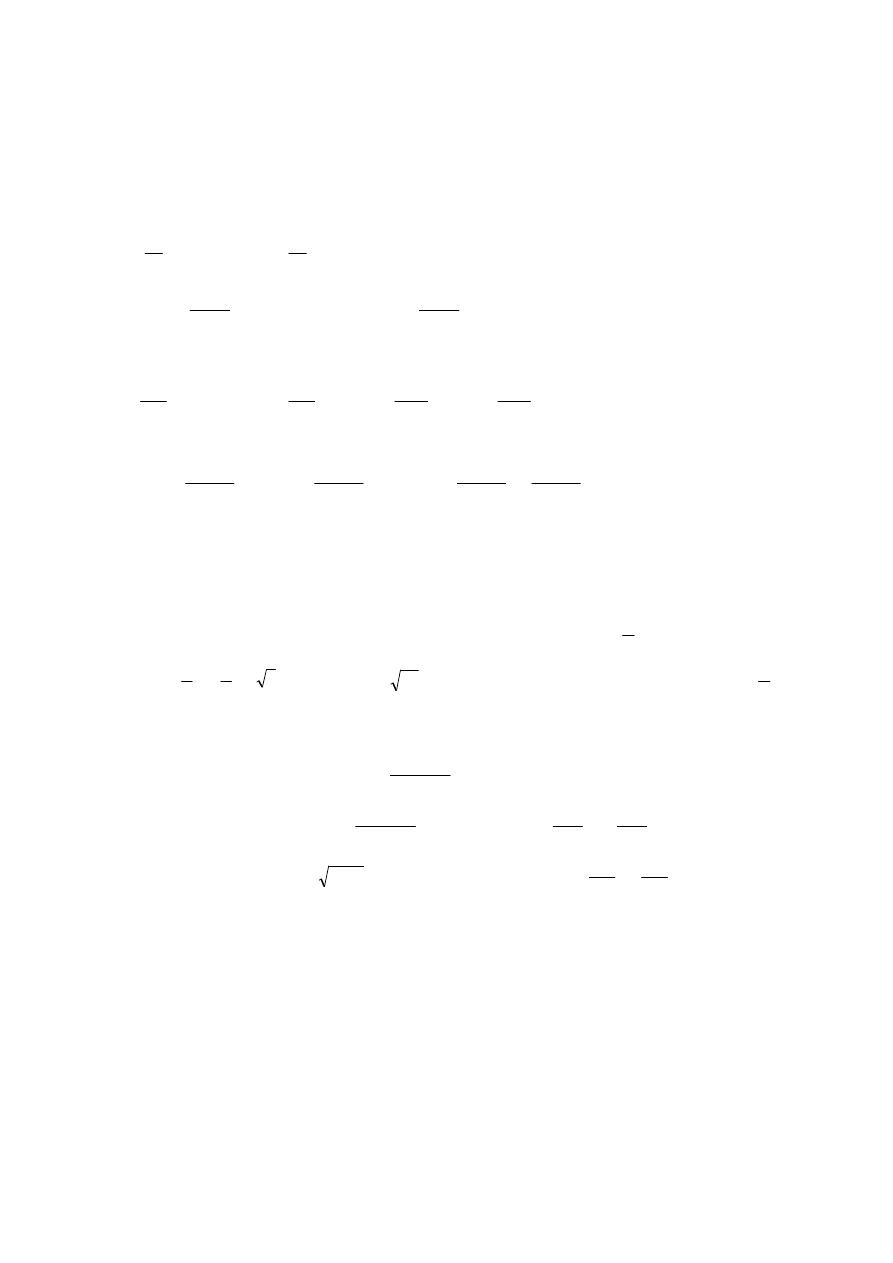
Przykład

Dana jest funkcja z = y

3

+ 2x

2

y – x

4

+ 5 określona w R

2

. Wyznacz pochodne cząstkowe

pierwszego i drugiego tej funkcji w dowolnym punkcie P(x, y) oraz w punkcie A(2, -3).

Mamy:

x

z

∂

∂

= 4xy – 4x

3

,

y

z

∂

∂

= 3y

2

+ 2x

2

; są to funkcje zmiennych x, y określone w R

2

.

x

A

z

∂

∂

)

(

= 4

⋅

2(–3) – 4

⋅

2

3

= –56 ;

y

A

z

∂

∂

)

(

= 35.

2

2

x

z

∂

∂

= 4y – 12x

2

,

2

2

y

z

∂

∂

= 6y ,

y

x

z

∂

∂

∂

2

= 4x ,

x

y

z

∂

∂

∂

2

= 4x.

2

2

)

(

x

A

z

∂

∂

= – 50 ;

2

2

)

(

y

A

z

∂

∂

= – 18 ;

y

x

A

z

∂

∂

∂

)

(

2

=

x

y

A

z

∂

∂

∂

)

(

2

= 8.

Zadania

1. Wyznacz pochodne rzędu drugiego funkcji:

a) z = x – 1, b) z = x

2

ln(y – 3) , c) z = x

y

, d) z = arc tg

y

x

,

e) z =

v

u

–

u

v

+

3

, f) z = x

2

ln(

xy

– 3) , g) z = x cos y – tg x , h) z = arc sin

y

x

.

2. Oblicz pochodne

xx

z

''

,

xy

z

''

,

yy

z

''

funkcji:

a) z = e

x

(cosy + xsiny) , b) z =

2

2

3x

y

y

−

.

3. Uzasadnij, że funkcja f(x, y) =

2

2

3x

y

y

−

spełnia równanie

2

2

x

f

∂

∂

= 9

2

2

y

f

∂

∂

.

4. Uzasadnij, że funkcja z =

y

x

−

+ sin(x – y) spełnia równanie

2

2

x

z

∂

∂

=

2

2

y

z

∂

∂

.