4.2. Pochodne cząstkowe funkcji.

Przyrost zmiennej i przyrost wartości funkcji

Niech będzie dana funkcja n – zmiennych z = f (x

1

, x

2

, .... x

n

). Niech także

P

0

( x

01

, x

02

, … ,x

0n

) będzie ustalonym, konkretnie wybranym punktem dziedziny D tej

funkcji.

Rozważamy inny punkt P

1

tej dziedziny i taki, który tylko jedną współrzędną różni się

od punktu P

0

albo dwiema, a nawet równocześnie wszystkimi współrzędnymi. Mówimy

wówczas, że nastąpiła zmiana odpowiednich zmiennych.

Jeśli zmieniamy tylko jedną zmienną (współrzędną punktu), np. x

0k

o

∆

x

01

, to

∆

x

01

nazywamy przyrostem zmiennej x

k

. Obliczając różnicę wartości funkcji f(P

1

) – f(P

0

)

otrzymamy przyrost funkcji ze względu na zmienną x

k

; nazywamy go przyrostem

częściowym funkcji.

Jeśli rozważymy punkt P dziedziny, w którym zmieniają się wszystkie zmienne

(współrzędne) równocześnie, to różnicę wartości funkcji f(P) – f(P

0

) nazywamy przyrostem

zupełnym funkcji.

Zinterpretujmy te określenia w przypadku funkcji dwóch zmiennych.

Załóżmy, że z = f(x, y) jest daną funkcją o dziedzinie D

f

.

Niech P

0

(x

0

, y

0

) będzie danym punktem.

Zmieniamy tylko x

0

o

∆

x, czyli przechodzimy

od P

0

( x

0

, y

0

) do P

1

(x

0

+

∆

x, y

0

).

Odpowiadająca tej zmianie częściowa

zmiana wartości funkcji wyraża się wzorem:

∆

f

x

= f(x

0

+

∆

x, y

0

)

−

f(x

0

, y

0

).

W przypadku zmiany y

0

o

∆

y mamy przejście ze stanu (x

0

, y

0

) do stanu (x

0

, y

0

+

∆

y).

Odpowiadająca temu częściowa zmiana wartości funkcji wynosi:

∆

f

y

= f(x

0

, y

0

+

∆

y)

−

f(x

0

, y

0

).

W przypadku zmiany obu współrzędnych mamy przejście ze stanu (x

0

, y

0

) do stanu

(x

0

+

∆

x, y

0

+

∆

y) i odpowiadający temu przyrost zupełny funkcji:

∆

f = f(x

0

+

∆

x, y

0

+

∆

y) - f(x

0

, y

()

).

x

0

+

∆

x

x

0

x

y

P

0

P

1

Przykład

Funkcję f określono wzorem f(x,y) = -3x + 5y + 7. Jej dziedziną jest zbiór R

2

.

Rozważamy punkty P

0

(1, -3), P

1

(0,7; -3); P

2

(1; -2,5); P

3

(0,7; -2,5);

Przyrosty zmiennych:

∆

x = 0,7 – 1 = - 0,3 ;

∆

y = -2,5 – (-3) = 0,5.

Wartości funkcji:

f(P

0

) = f(1, -3) = -3 -15 + 7 = - 11; f(P

1

) = f(0,7; -3) = -3

⋅

0,7 - 15 + 7 = - 10,1;

f(P

2

) = f(1, -2,5) = -3 -5(-2,5) + 7 = - 8,5; f(P

3

) = f(0,7; -2,5) = - 7,6.

Przyrosty funkcji:

∆

f

x

= f(P

1

)

−

f(P

0

) = 0,9 ;

∆

f

y

= f(P

2

)

−

f(P

0

) = 2,5 ;

∆

f = f(P

3

)

−

f(P

0

) = 3,4.

Pochodne cząstkowe

Analogicznie jak w przypadku funkcji jednej zmiennej interesuje nas stosunek przyrostu

częściowego wartości funkcji do przyrostu zmiennej, a więc ilorazy

x

f

x

∆

∆

,

y

f

y

∆

∆

określające

średnią prędkość zmiany funkcji w kierunku osi Ox oraz Oy, odpowiadającą zmianie

zmiennych odpowiednio o

∆

x albo

∆

y.

Ogólnie

Rozważamy ilorazy

1

1

x

f

x

∆

∆

,

2

2

x

f

x

∆

∆

, …,

n

x

x

f

n

∆

∆

określające średnią prędkość zmiany funkcji

z = f (x

1

, x

2

, .... x

n

) odpowiadające zmianie kolejnych zmiennych o

∆

x

1

,

∆

x

2

, …,

∆

x

n

w

stosunku do punktu P

0

( x

01

, x

02

, … ,x

0n

)..

Skończone granice ilorazów

1

1

x

f

x

∆

∆

,

2

2

x

f

x

∆

∆

, …,

n

x

x

f

n

∆

∆

, gdy przyrosty zmiennych

∆

x

1

,

∆

x

2

, …,

∆

x

n

zmierzają do 0 nazywamy pochodnymi cząstkowymi funkcji z = f (x

1

, x

2

, .... x

n

) w

punkcie P

0

( x

01

, x

02

, … ,x

0n

)

Symbolicznie (w przypadku zmiennej x

1

):

'

1

x

f

(P

0

) =

1

0

)

(

x

P

f

∂

∂

=

lim

0

1

→

∆

x

1

1

x

f

x

∆

∆

.

Podobnie w przypadku kolejnych zmiennych.

Zinterpretujmy tę definicję w przypadku funkcji dwóch zmiennych.

Definicja

Niech z = f(x, y) jest daną funkcją o dziedzinie D

f

oraz P

0

(x

0

, y

0

) wraz ze swoim

otoczeniem należy do tej dziedziny. Nadajmy zmiennej y wartość stałą y

0

. Wówczas z = f(x,

y

0

) jest funkcją jednej zmiennej x. Oznaczmy ją z = g(x).

O ile funkcja g ma pochodną g’(x) w punkcie x

0

, to nazywamy ją pochodną cząstkową

rzędu pierwszego funkcji dwóch zmiennych z = f(x, y) względem x w punkcie (x

0

, y

0

) i

oznaczamy ją symbolem

'

x

f

(x

0

, y

0

) lub

0

0

,

y

y

x

x

x

f

=

=













∂

∂

lub

x

y

x

f

∂

∂

)

,

(

0

0

.

Jest ona granicą ilorazu różnicowego:

'

x

f

(x

0

, y

0

) =

x

y

x

f

∂

∂

)

,

(

0

0

=

lim

0

→

∆

x

x

f

x

∆

∆

.

Podobnie definiujemy pochodną cząstkową rzędu pierwszego funkcji dwóch

zmiennych z = f(x, y) względem y w punkcie (x

0

, y

0

) i oznaczamy ją symbolem

'

y

f

(x

0

, y

0

) lub

0

0

,

y

y

x

x

y

f

=

=













∂

∂

lub

y

y

x

f

∂

∂

)

,

(

0

0

.

Definicja

Pochodna cząstkowa rzędu pierwszego funkcji dwóch zmiennych z = f(x, y) względem x

w punkcie P(x, y) jest funkcją zmiennych x, y; oznaczamy ją krótko

'

x

f

lub













∂

∂

x

f

lub

x

y

x

f

∂

∂

)

,

(

. Mówimy krótko: pochodna funkcji f po iksie.

Pochodna cząstkowa rzędu pierwszego funkcji dwóch zmiennych z = f(x, y) względem y

w punkcie (x, y) jest funkcją zmiennych x, y; oznaczamy

'

y

f

lub













∂

∂

y

f

lub

y

y

x

f

∂

∂

)

,

(

.

Mówimy krótko: pochodna funkcji f po igreku.

Przykład

Niech f(x, y) = 3x

2

– 4xy

3

+ 5. Wyznacz pochodne cząstkowe rzędu pierwszego tej funkcji

względem x, względem y w punkcie P(-2,3).

Zgodnie z definicją tworzymy funkcje:

f(x, 7) = 3x

2

– 4x

⋅

3

3

+ 5 = 3x

2

–108 x + 5.

f(-2, y) = 3(-2)

2

– 4 (-2)y

3

+ 5 = 8y

3

+ 17.

Wtedy

'

x

f

(-2,3) = (3x

2

–108 x + 5)

’

x = -2

= (6x –108 )

x = -2

= - 120.

'

y

f

(-2,3) = (8y

3

+ 17)

’

y =3

= (24y

2

)

y = 3

= 216.

Ostatecznie

'

x

f

(-2,3) =- 120,

'

y

f

(-2,3) =216.

Przykład

Gdy f(x, y) = 3x

2

– 4xy

3

+ 5. Wtedy

'

x

f

(x,y) = 6x –4y

3

,

'

y

f

(x,y) = –12x y

2

.

Gdy f(x, y) = yx

2

– 4

x

y

−

4

+ x, wtedy

'

x

f

(x,y) = 2xy – 2y

−

4

x

−

0,5

+ 1;

'

y

f

(x,y) = x

2

+16

x

y

−

5

.

Obliczanie pochodnych cząstkowych

'

x

f

,

'

y

f

funkcji f nazywamy różniczkowaniem

funkcji f po x , po y. Funkcję f mającą pochodne

'

x

f

,

'

y

f

nazywamy różniczkowalną.

Interpretacja geometryczna pochodnych cząstkowych

Niech f będzie funkcją określoną w zbiorze D. Wykresem funkcji f jest zbiór punktów

P = (x, y, z) przestrzeni (powierzchnia), których współrzędne spełniają związek z = f(x, y),

gdzie (x, y)

∈

D,

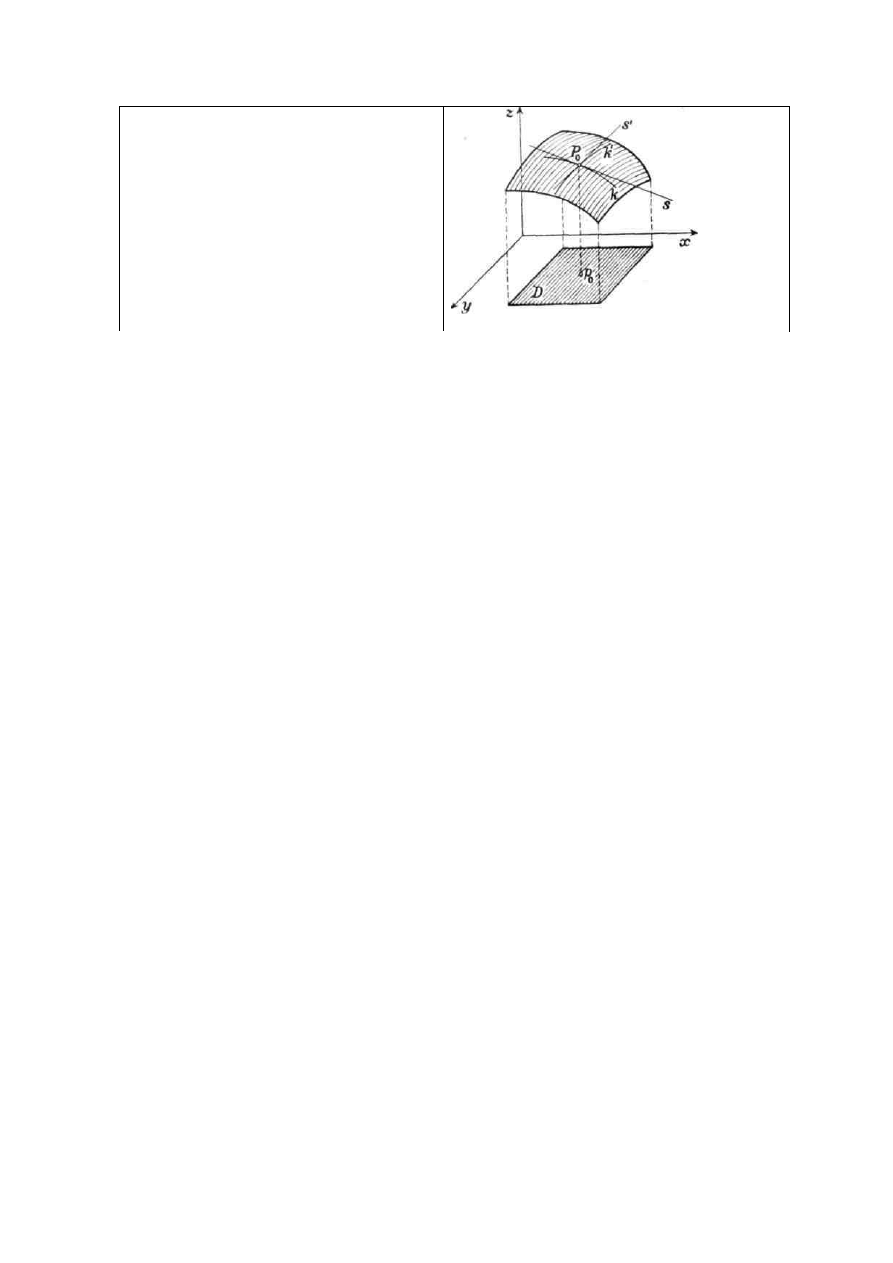
Płaszczyzna o równaniu y = y

0

przecina tę

powierzchnię wzdłuż krzywej k o

równaniu z = f(x, y

0

) i wobec tego

pochodna cząstkowa

'

x

f

(x

0

, y

0

) jest

tangensem kąta nachylenia stycznej s do

krzywej k względem osi x w punkcie P

0

(x

0

, y

0

, z

0

) tej powierzchni.

Analogicznie, płaszczyzna x = x

0

przecina powierzchnię wzdłuż krzywej k' o równaniu

z = f(x

0

,y) i pochodna

'

y

f

(x

0

, y

0

) równa się tangensowi kąta nachylenia stycznej do k'

względem osi y w punkcie P

0

(x

0

, y

0

, z

0

).

Funkcja f może mieć w punkcie P

0

pochodne cząstkowe i nie być ciągła w tym

punkcie.

Zadania

1. Oblicz przyrost funkcji f ze względu na x, na y oraz przyrost zupełny, gdy punkt P(-4, 2)

przesunięto do punktu Q(3, 0), zaś funkcję f definiujemy wzorem:

a) f(x,y) = x – y, b) f(x,y) = x

2

y – 2xy

2

+ 3, c) z = x

2

– y

2

, d) z = |x| - |x – y|.

2. Oblicz przyrost funkcji f ze względu na x, na y oraz przyrost zupełny, gdy nastąpił

przyrost zmiennej x o

∆

x = ½ , przyrost zmiennej y o

∆

y = - ½ , poczynając od punktu

P(-4, 2), zaś funkcję f definiujemy wzorem:

a) f(x,y) = 2x – y, b) f(x,y) = x

2

y

2

– 2xy + 5, c) z = x

2

– (y+1)

2

.

3. Oblicz przyrost funkcji f ze względu na x, na y oraz przyrost zupełny, gdy nastąpił przyrost

zmiennej x o

∆

x = 0,1 , przyrost zmiennej y o

∆

y = - 1 , poczynając od punktu

P(x, y), zaś funkcję f definiujemy wzorem:

a) f(x,y) = 2x – 3y +2, b) f(x,y) = x

2

y

2

– 2x(y + 5), c) z = 3x

2

– (y+1)

2

.

4. Oblicz pochodne cząstkowe rzędu pierwszego funkcji:

a) z = 2x – 3y +2, b) f(x,y) = x

2

y

2

– 2x(y + 5), c) z = 3x

2

– (y+1)

2

,

d) z =

y

x

+

- 2y

3

, e) f(x,y) = ln (y

2

– 3xy

2

- 5), f) z = ln xy.

5. Oblicz pochodne cząstkowe rzędu pierwszego funkcji:

a) z =

x

y

y

x

−

, b) z =

3

2

2

+

−

x

y

x

, c) z = sin (x +xy

3

), d) z =

xy

ye

cos

, e) z =

x

y

x

sin

5

2

+

.