Instrukcje do ćwiczeń laboratoryjnych z Teorii Maszyn i Mechanizmów
Laboratorium Teorii Maszyn i Mechanizmów
Bielsko-
Biała 2011
o
o
o
p
p
p
r
r
r
a
a
a
c
c
c
o
o
o
w
w
w
a
a
a
ł
ł
ł
A
A
A
r
r
r
k
k
k
a
a
a
d
d
d
i
i
i
u
u
u
s
s
s
z
z
z
T
T
T
r
r
r
ą
ą
ą
b
b
b
k
k
k
a
a
a
ĆWICZENIE NR ...
DOŚWIADCZALNE WYZNACZANIE MASOWEGO MOMENTU
BE
ZWŁADNOŚCI KORBOWODU SILNIKA SPALINOWEGO
1. Cel ćwiczenia
Celem ćwiczenia jest określenie masowego momentu bezwładności korbowodu
względem osi równoległej do osi otworów i przechodzącej przez środek masy
metodą doświadczalną.
2. Zależności obowiązujące w metodzie doświadczalnej
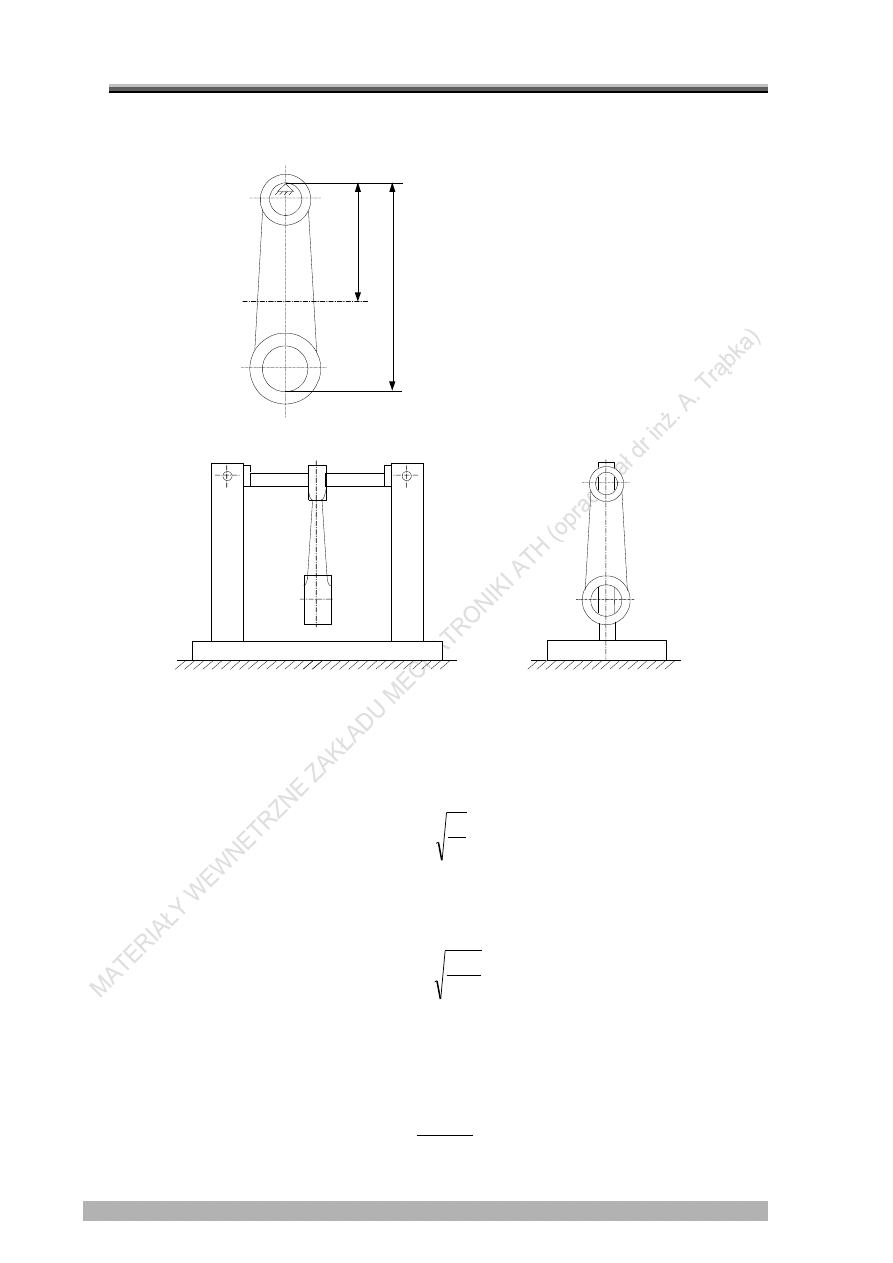
Korbowód zawieszony w punkcie A lub B (rys.1a) w przyrządzie pomiarowym
składającym się z pionowych podpór, w których osadzona jest pryzma (rys. 1b) jest
wahadłem fizycznym o długości zredukowanej l
z
.
Dla zawieszenia w punkc
ie A długość zredukowaną określamy wg zależności (1):
a
m
I
l
A
z
(1)
gdzie:
I
A
-
moment bezwładności względem osi przechodzącej przez punkt
zawieszenia,
m - masa korbowodu,
a -
odległość między osiami przechodzącymi przez środek masy i punkt
zawieszenia.
DOŚWIADCZALNE WYZNACZANIE MASOWEGO MOMENTU BEZWŁADNOŚCI...
Labora
torium Teorii Maszyn i Mechanizmów
2
l
a
S
B
A
a)
b)
Rys. 1.
Schemat korbowodu wraz z przyrządem: a) schemat podparcia korbowodu,
b) schemat przy
rządu
Okres drgań wahadła fizycznego wynosi (2):
g
l
2
T
Z
(2)
Wstawiając zależność (1) do zależności (2) otrzymuje się wzór (3) na okres drgań
wa
hadła podwieszonego w punkcie A:
g
a
m
I
2
T
A
A
(3)
Z kolei przek
ształcając zależność (3) otrzymuje się wzór (4) na masowy moment
bezwładności korbowodu, określony względem osi zawieszenia poprowadzonej
przez punkt A:
2
2
A
A
4
a
g
m
T
I
(4)
Instrukcje do ćwiczeń laboratoryjnych z Teorii Maszyn i Mechanizmów
Laboratorium Teorii Maszyn i Mechanizmów
3
Dokonując analogicznych przekształceń możemy wyznaczyć zależność (5) na
masowy moment bezwładności korbowodu względem osi przechodzącej przez punkt
zawieszenia B:
2
2
A
B
4
a
l
g
m
T
I
)
(
(5)
Stosując twierdzenie Steinera można zapisać zależność (6) na masowy moment
bezwładności korbowodu względem osi przechodzącej przez jego środek masy S:
2
B
S
2
A
S
a
l
m
I
I
a
m
I
I
(6)
Wprowadzając do równań (6) wielkości I
A
oraz I
B
określone przez wyrażenia (4) i (5)
zależność na masowy moment bezwładności korbowodu względem osi
przechodzącej przez jego środek masy S przyjmie postać (7):
2
2
2
A
S
a
m
4
a
g
m
T
I
(7)
2
2
2
B
S
a
l
m
4
a
l
g
m
T
I
)
(
Dokonując porównania prawych stron równań (7) otrzymamy wyrażenie (8) na
odległość między osiami przechodzącymi przez środek masy i punkt zawieszenia A:
l
l
8
T
T
g
l
4
T
g
a
2
2
B
2
A
2
2
B
(8)
Wyznaczenie doświadczalne wartości wielkości T
A
, T
B
, m i l pozwala na obliczenie
odl
egłości „a” między osiami przechodzącymi przez środek masy i punkt
zawieszenia, następnie z pierwszego z wzorów (7) momentu bezwładności I
S
korbowodu względem osi przechodzącej przez jego środek masy.
3. Analiza błędów
Błędy pomiaru wyznaczanych doświadczalnie wielkości T
A
, T
B
,
m oraz l są od siebie
nieza
leżne i wynoszą:
T
A
,
T
B
,
m oraz
l.
Bezwzględny błąd z jakim wyznaczona została wartość masowego momentu
bezwładności korbowodu względem osi przechodzącej przez jego środek masy S
można określić na podstawie zależności (9):
DOŚWIADCZALNE WYZNACZANIE MASOWEGO MOMENTU BEZWŁADNOŚCI...
Labora
torium Teorii Maszyn i Mechanizmów
4
2
S
2
S
2
B
B
S
2
A
A
S
S
l
l
I
m
m
I
T
T
I
T
T
I
I
(9)
Pochodne cząstkowe wchodzące do wzoru (9) określimy na podstawie zależności
(10), (11), (12) i (13):
l
8
T
T
g
T
g
2
a
m
I
4
a
g
m
T
2
T
I
2
2
B
2
A
A
2
S
2
A
A
S
(10)
l
8
T
T
g
a
l
T
m
g
2
g
a
2
4
T
T
I
2
2
B
2
A
B
2
2
A
2
B
S
(11)
2
2
2
A
S
a
4
g
a
T
m
I
(12)
l
8
T
T
g
a
l
8
gT
g
m
g
a
2
4
T
l
I
2
2
B
2
A
2
2
B
2
2
A
S
)
(
(13)
Błąd względny wartości masowego momentu bezwładności korbowodu wynosi (14):
%
100
S
S
I
I
(14)
4. Przebieg ćwiczenia
Zważyć korbowód (zanotować także dokładność wskazań wagi) - pomiary
wykonać trzykrotnie;
Zmierzyć odległość l pomiędzy punktami podwieszenia korbowodu A i B
(z
anotować także dokładność wskazań suwmiarki), pomiary wykonać trzykrotnie;
Podwiesić korbowód w punkcie A (rys.1a) zwracając uwagę na to, aby oś
otwo
rów była równoległa do krawędzi pryzmy (rys.1b);
Wprawić korbowód w ruch wahadłowy o kącie wahań
< 10
0
i zmierzyć
trzykrotnie czas t
A
50 wahnięć (zanotować także dokładność wskazań stopera);
Podwiesić korbowód w punkcie B zwracając uwagę na to, aby oś otworów była
równoległa do krawędzi pryzmy;
Wprawić korbowód w ruch wahadłowy o kącie wahań
< 10
0
i zm
ierzyć
trzykrotnie czas t
B
50 wahnięć;
Na podstawie wartości czasów wahań t
A
i t
B
obliczyć okresy wahań T
A
i T
B
na
podstawie zależności (15) i (16):
Instrukcje do ćwiczeń laboratoryjnych z Teorii Maszyn i Mechanizmów
Laboratorium Teorii Maszyn i Mechanizmów
5
wahniec
liczba
t
A
A
T
(15)
wahniec
liczba
t
B
B
T
(16)
Obliczyć według wzorów (7), (8) moment bezwładności względem osi równoległej
do osi otworów i przechodzącej przez środek masy oraz położenie środka masy
korbowodu;
Wyznaczyć wartości błędów pomiaru okresów wahań
T
A
,
T
B
,
biorąc pod uwagę
fakt, że dokładność pomiaru wykonanego stoperem odnosi się do przyjętej
łącznej liczby wahnięć;
Określić błąd bezwzględny i względny wartości masowego momentu bezwładności
korbowodu
według wzorów (9) - (14).
5. Zawartość sprawozdania
Cel ćwiczenia;
Przebieg ćwiczenia (w punktach);
Schemat stanowiska laboratoryjnego (z opisem);
Dane wejściowe do przeprowadzanego ćwiczenia;
Zestawienie wyników pomiarów;
Pełny przebieg obliczeń z podaniem wzorów oraz podstawień do wzorów;
Zestawienie wyni
ków obliczeń;
Sporządzony w trakcie ćwiczeń protokół;
Wnioski, spostrzeżenia i uwagi.