Autor: dr inż. Piotr Wyciślok

Strona 1 / 3

INSTRUKCJA

LABORATORIUM KOMPUTEROWE

WSPOMAGANIE W TECHNICE.

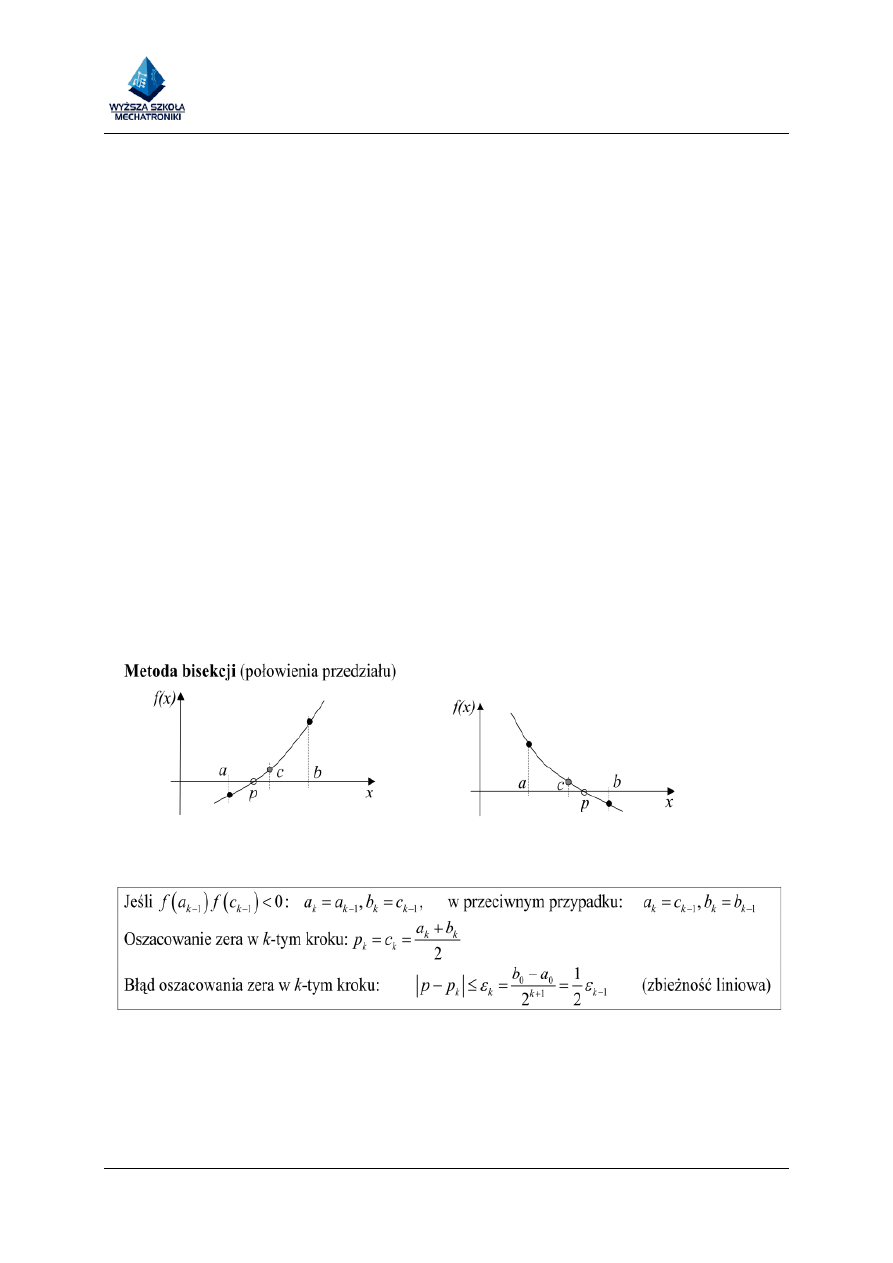
METODA BISEKCJI I METODA

SIECZNYCH ZNAJDOWANIA

PIERWIASTKÓW RÓWNAŃ

NIELINIOWYCH

Ćwiczenie 4

Autor: dr inż. Piotr Wyciślok

Strona 2 / 3

CEL
Celem ćwiczenia jest zapoznanie się z metodami rozwiązywania równań nieliniowych ze
szczególnym uwzględnieniem wpływu błędów (metody i numerycznego) na uzyskany wynik.

WSTĘP TEORETYCZNY
Wyznaczanie pierwiastków równania nieliniowego (miejsc zerowych funkcji nieliniowej) -
trudności i podstawowe idee:
Trudności:
• możliwość braku miejsc zerowych (np. wielomian z zerami zespolonymi kiedy szukamy
rzeczywistych).
• duże nagromadzenie miejsc zerowych w przedziale (np. dla funkcji sin(l/x) w pobliżu zera),
• możliwość braku zmiany znaku (np. dla miejsc zerowych wielomianu o parzystej krotności),
• nieciągłości, osobliwości. Pomysły na rozwiązanie:
• zgrubnie narysować przebieg funkcji dla zorientowania się w problemie,
• znaleźć przedział, w którym funkcja zmienia znak i iteracyjnie go zawężać,
• wystartować z dowolnego punktu i podążać w kierunku malejących co do modułu wartości.
Informacja do wykorzystania:
• wartości funkcji.
• wartości lub przybliżenie pochodnych funkcji,
• poprzednio znalezione zera. Sposób kontroli dokładności:
• różnica między wartością funkcji a zerem
• różnica między bieżącym oszacowaniem zera a rozwiązaniem (ale to jest nieznane)
• różnica między dwoma kolejnymi oszacowaniami

W każdym kroku następuje wybór dwóch nowych punktów ograniczających przedział z
miejscem zerowym spośród dwóch starych punktów ograniczających i punktu środka
przedziału.

Autor: dr inż. Piotr Wyciślok

Strona 3 / 3

ZADANIE DO REALIZACJI:

Napisać procedurę rozwiązania równania nieliniowego:

4

2

3

10

993

3

165

0

-

.

+

x

.

-

x

x

f

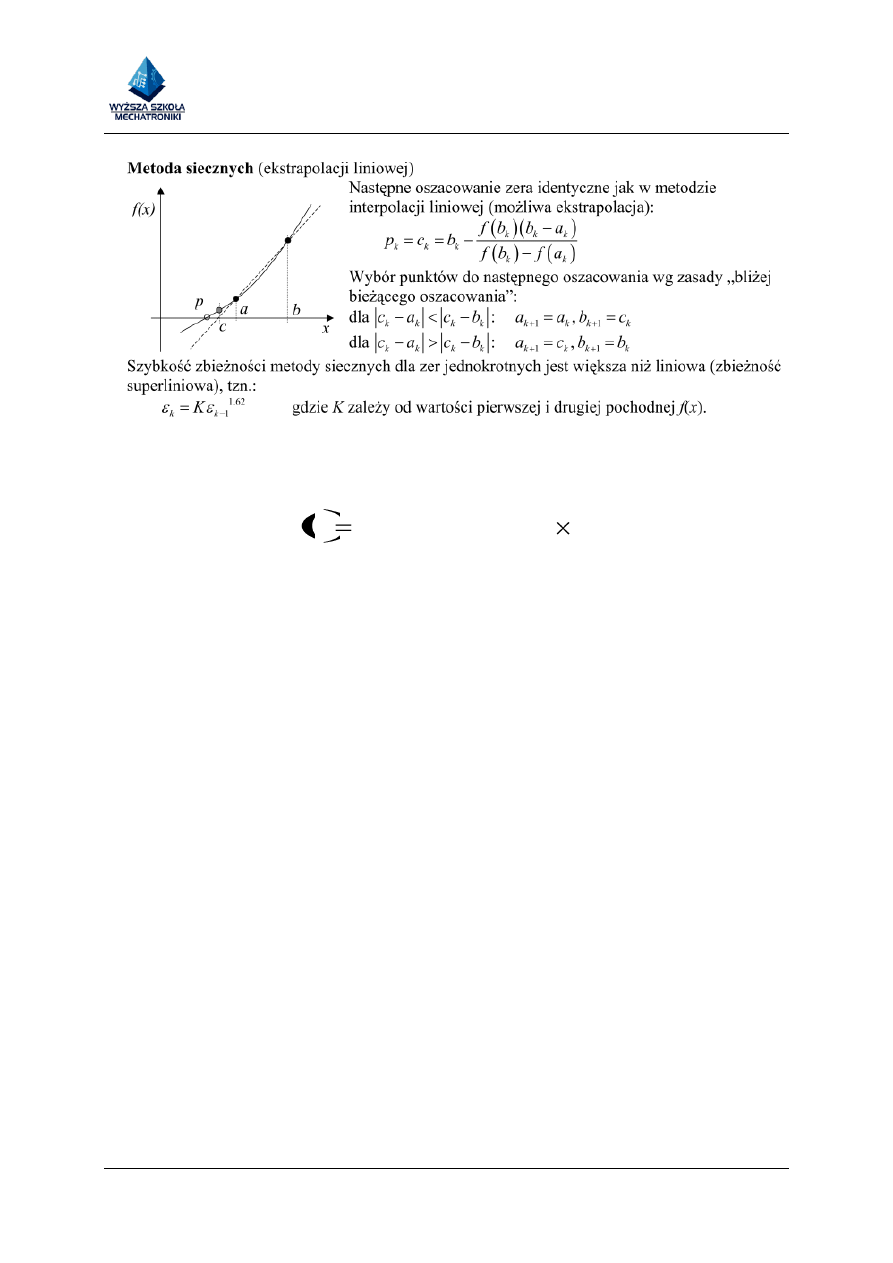
metodą bisekcji i metodą siecznych

Podjąć dyskusję błędu.

PRZEBIEG ĆWICZENIA

1. Podział na grupy.
2. Test wiadomości.
3. Wybór oprogramowania (Excel, MathCAD, MatLab, Scilab Octave…)
4. Adaptacja algorytmów postępowania do platformy programowej.
5. Wykonanie obliczeo na zadaniu testowym z wykorzystaniem obu metod, próba

znalezienie co najmniej dwu pierwiastków równania.

6. Wybranie co najmniej dwu par punktów startowych.
7. Wykonanie obliczeo dla dokładności obliczeo do 1 miejsca po przecinku i dla pełnej

reprezentacji liczbowej w wybranym programie.

8.

Dyskusja błędu z uwzględnieniem błędu numerycznego.