Metody numeryczne

szukanie pierwiastka metodą bisekcji

Dawid Rasała

Pierwiastki równania f(x) = 0 na ogół nie wyrażają się zamkniętymi 

wzorami,  dlatego  rozwiązując  równania  nieliniowe  stosujemy  na 

ogół  metody  przybliżone,  opierające  się  zazwyczaj  na  kolejnych 

przybliżeniach pierwiastka. Są to metody iteracyjne, co oznacza, że 

startując  od  jednego  lub  kilku  przybliżeń  początkowych 

pierwiastka, metody te dają ciąg x

0

, x

1

, x

2

, … kolejnych przybliżeń 

pierwiastka.

Rozwiązywanie równań

Metody numeryczne 
Dawid Rasała

Metoda  równego  podziału  (metoda  połowienia,  metoda 

bisekcji,  metoda  połowienia  przedziału)  -  jedna  z  metod 

rozwiązywania  równań  nieliniowych.  Opiera  się  ona  na 

następującym twierdzeniu:

Metoda bisekcji

Jeżeli  funkcja  ciągła  f(x)  ma  na  końcach  przedziału  domkniętego 

wartości różnych znaków, to wewnątrz tego przedziału, istnieje co 

najmniej jeden pierwiastek równania f(x) = 0.

Metody numeryczne 
Dawid Rasała

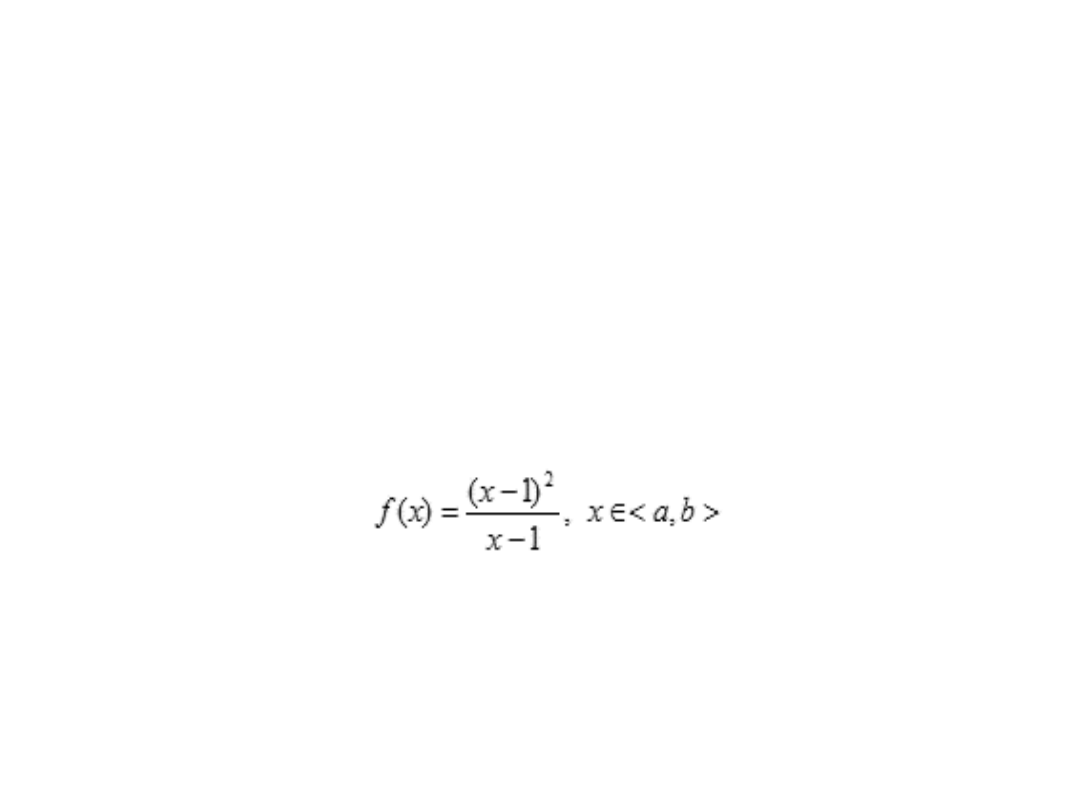
Mamy daną funkcję f(x) oraz przedział <a,b>, w którym będziemy 

poszukiwali  miejsca  zerowego.  Aby  można  było  zastosować 

algorytm połowienia muszą być spełnione poniższe warunki:

1. Funkcja f(x) jest określona w każdym punkcie przedziału <a,b>.  

Określoność funkcji oznacza, iż dla każdej wartości argumentu x z 

przedziału <a,b> potrafimy policzyć wartość funkcji. Dla przykładu 

rozważmy prostą funkcję:

W  punkcie  x = 1  tak  podana  funkcja  ma  nieokreśloną  wartość. 

Musimy  dzielić  przez  0,  a  jak  wiadomo  jest  to  zadanie 

niewykonalne.

Metoda bisekcji

Metody numeryczne 
Dawid Rasała

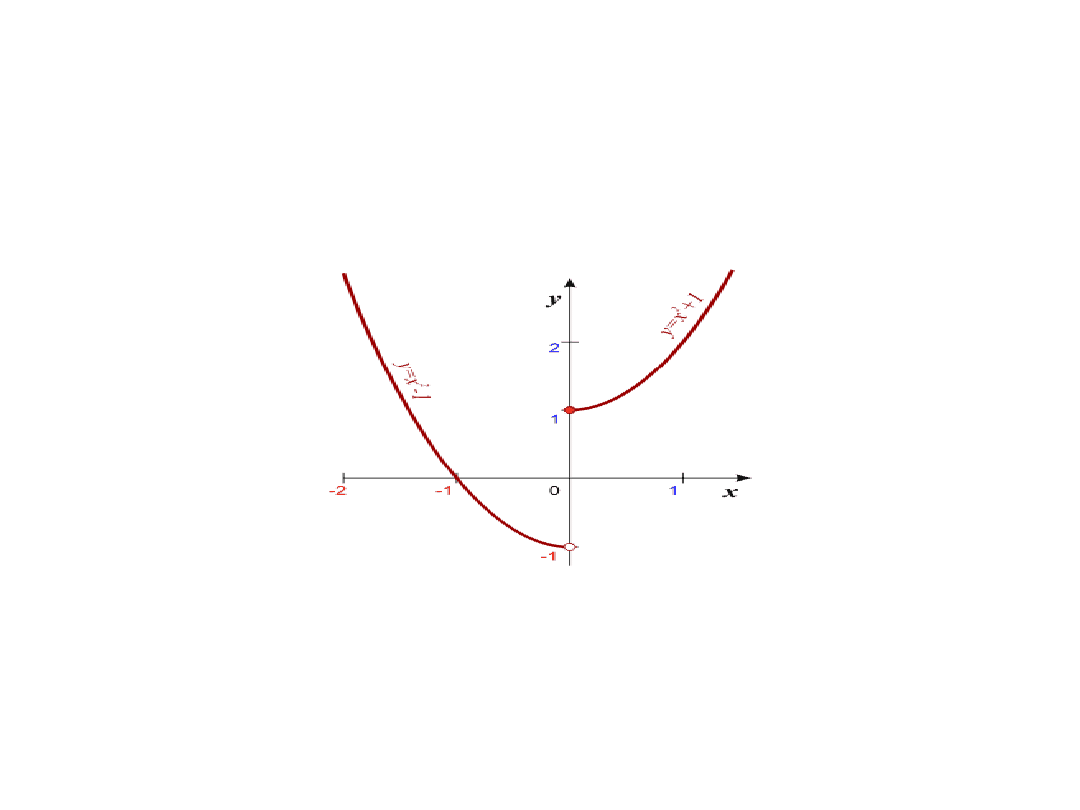
2.  Funkcja  f(x)  jest  ciągła.  Ciągłość  funkcji  oznacza  z  kolei,  iż  jej 

wartości  nie  "wykonują"  nagłych  skoków,    nie  istnieją  przerwy  w 

kolejnych  wartościach  funkcji.  Dla  przykładu  rozważmy  taką  oto 

funkcję:

Nieciągłość  występuje  w  punkcie  x = 0,  czyli  w  miejscu  zmiany 

przepisu funkcji.

Metoda bisekcji

Metody numeryczne 
Dawid Rasała

3.  Funkcja  f(x)  na  krańcach  przedziału  <a,b>  przyjmuje  różne 

znaki.  Ponieważ  funkcja,  zgodnie  z  poprzednim  wymogiem,  jest 

ciągła,  to  przyjmuje  w  przedziale  <a,b>  wszystkie  wartości 

pośrednie pomiędzy f(a) i f(b).  Wartości te mają różne znaki (czyli 

leżą po różnych stronach osi OX), zatem musi być taki punkt x

o

 w 

przedziale  <a,b>,  dla  którego  funkcja  przyjmuje  wartość 

pośrednią. 

Metoda bisekcji

Metody numeryczne 
Dawid Rasała

Gdy  funkcja  f(x)  spełnia  powyższe  trzy  warunki,  to  w  przedziale 

<a,b>  zagwarantowane  jest  istnienie  pierwiastka  i  możemy  go 

wyszukać algorytmem połowienia. Zasada jest następująca:

Kroki algorytmu

1. Wyznaczamy punkt x

o

 jako środek przedziału <a,b>.

2.  Obliczamy  wartość  funkcji  w  punkcie  x

o

.  Sprawdzamy,  czy  f(x

o

) 

znajduje się dostatecznie blisko 0:

Metody numeryczne 
Dawid Rasała

3. Jeśli nierówność jest spełniona, to x

o

 jest poszukiwaną wartością 

pierwiastka. Zwracamy wynik i kończymy algorytm. W przeciwnym 

razie  za  nowy  przedział  poszukiwań  pierwiastka  przyjmujemy  tą 

połówkę  <a,x

o

>  lub  <x

o

,b>,  w  której  funkcja  zmienia  znak  na 

krańcach i przechodzimy ponownie do punktu 1. 

Kroki algorytmu

Metody numeryczne 
Dawid Rasała

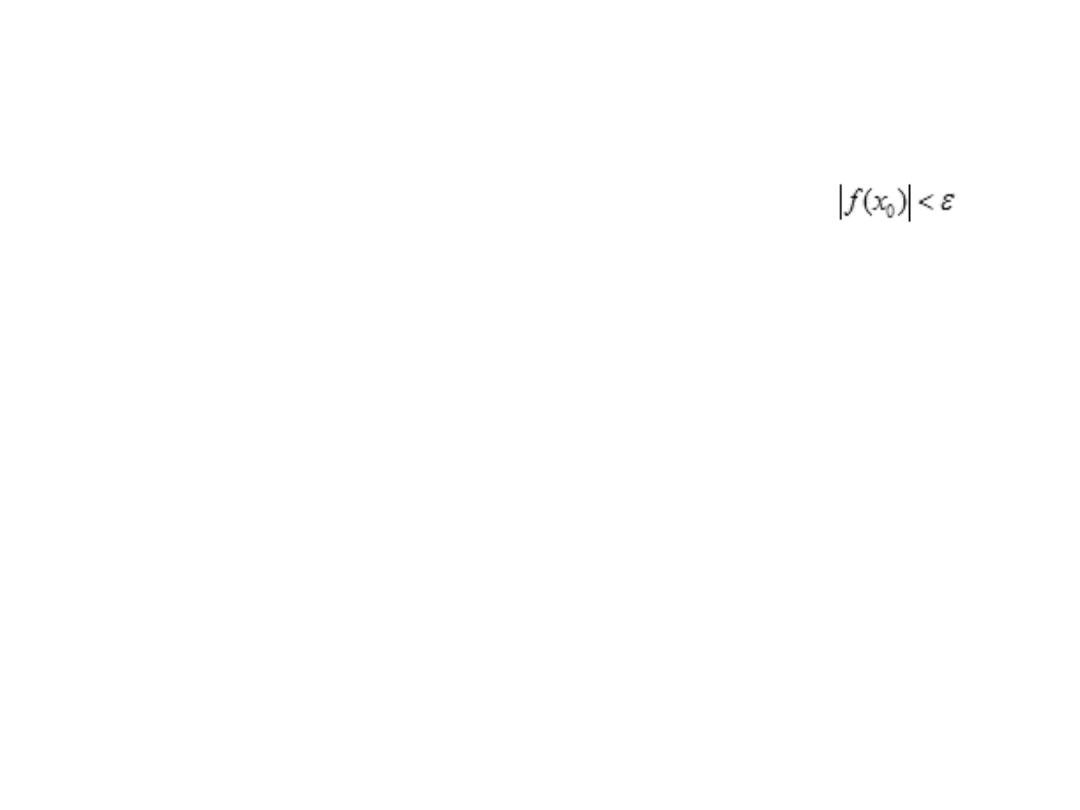
Algorytm powtarzamy od początku dotąd, aż:

1.znajdziemy pierwiastek, czyli spełniona będzie nierówność 

2.przedział <a,b> osiągnie założoną długość (może to być również 

epsilon)

3.wykonamy określoną ilości iteracji.

Warunki zakończenia obliczeń

Metody numeryczne 
Dawid Rasała

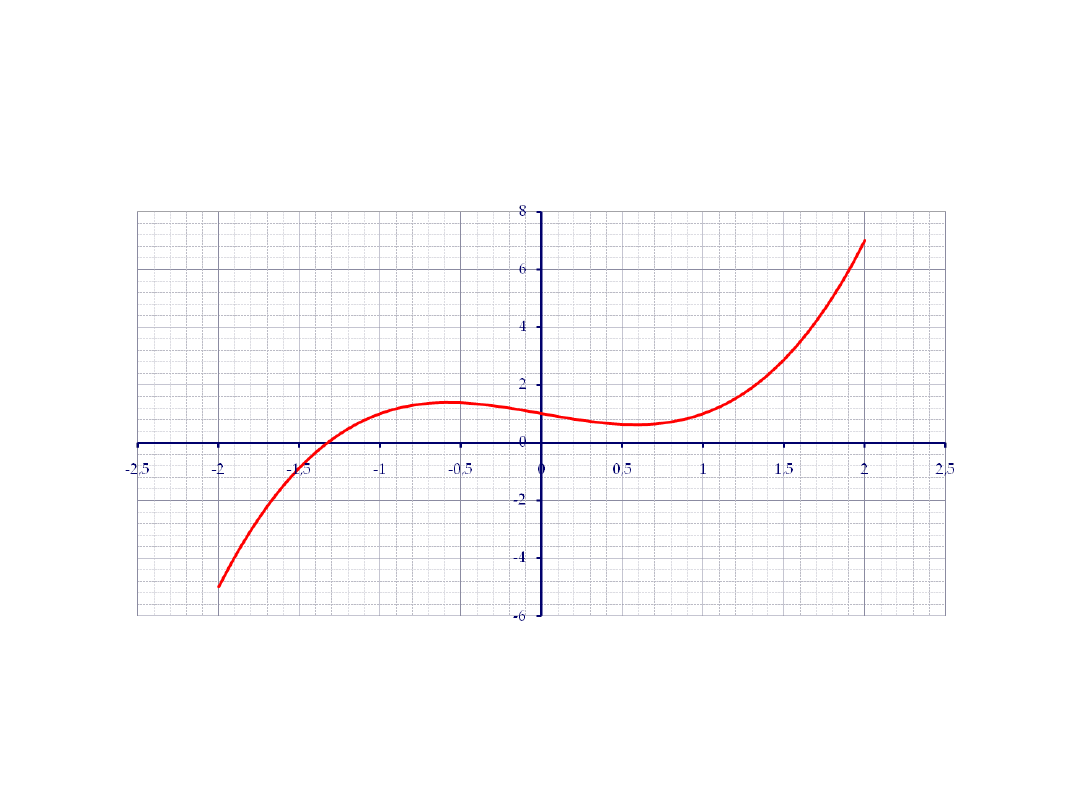
Wyznaczyć pierwiastek równania  x

3

 − x + 1 = 0 w przedziale [ − 

2;0].

Przykład

Metody numeryczne 
Dawid Rasała

1. Wszystkie poniższe równania maja pierwiastek w przedziale (0, 

1.6).  Wyznaczyć  te  pierwiastki  metodą  bisekcji  z  błędem 

mniejszym od 0,02:

a) x * cos(x) = - ln(x);

b) 2 x - e

-x

 = 0.

2. Napisać  w  dowolnym  języku  program,  który  realizuje  meodę 

bisekcji dla zadanej funkcji. 

Zadania

Metody numeryczne 
Dawid Rasała