Algorytmy i Struktury Danych

Wojciech Palacz

2009/2010

(na podst. materiałów dr Anny Paszyńskiej)

1. T.H.Cormen, C.E.Leiserson, R.L.Rivest, C.Stein:

Wprowadzenie do algorytmów. WNT, Warszawa 2004.

2. L.Banachowski, K.Diks, W.Rytter: Algorytmy i struktury

danych. WNT, Warszawa 1996.

3. Richard Neapolitan, Kumaris Naimipour: Podstawy

algorytmów z przykładami w C++.

4. Adam Drozdek: C++. Algorytmy i Struktury Danych.

5. Materiały z wykładów.

Literatura

1.Projektowanie i analiza algorytmów.
2.Rekurencja (silnia, liczby Fibonacciego, algorytm

Euklidesa obliczania największego wspólnego
dzielnika, algorytm obliczania symbolu Newtona).

3.Algorytmy sortowania.
Abstrakcyjne Typy Danych (ADT):
1.ADT LIST - reprezentacja wskaźnikowa listy.
2.ADT LIST - reprezentacja tablicowa listy.
3.ADT LIST - lista podwójnie wiązana.
4.Tablice haszujące.

Zakres materiału

1.ADT STACK – wskaźnikowa i tablicowa

reprezentacja stosu, Odwrotna Notacja Polska.

2.ADT QUEUE - kolejka cykliczna.
3.ADT QUEUE – reprezentacja wskaźnikowa.
4.ADT TREE – wskaźnikowa reprezentacja drzewa

binarnego wraz z operacjami inorder, preorder,
postorder.

5.Drzewa BST (?)
6.Drzewa AVL (?)

Zakres materiału

Kolejne etapy pisania programów:
1.Sformułowanie problemu i specyfikacja.
2.Projekt rozwiązania.
3.Implementacja (zapis w wybranym języku

programowania i uruchomienie na

konkretnym komputerze).
4.Testowanie i dokumentacja.
5.Ocena rozwiązania.

Projektowanie i analiza algorytmów

1.

Sformułowanie problemu i specyfikacja

Poszukiwanie modelu, w którego terminach
można sformułować problem (najczęściej
model matematyczny).

2. Projekt rozwiązania
Jeśli problem jest już sformułowany,
poszukujemy rozwiązania w postaci
algorytmu.

Projektowanie i analiza algorytmów

Algorytm

– skończony, uporządkowany ciąg

jasno zdefiniowanych czynności (instrukcji),
koniecznych do wykonania pewnego zadania.

Algorytm musi, dla dowolnego zestawu
danych wejściowych, zakończyć się po
wykonaniu skończonej liczby instrukcji.

Projektowanie i analiza algorytmów

3. Implementacja

4.Testowanie i dokumentacja

Dokumentacja:
- projektowa
- komentarze w kodzie programu
- użytkowa

Projektowanie i analiza algorytmów

4. Testowanie i dokumentacja

Testowanie – eksperymentalny dowód poprawności.
Zawsze konieczne, choćby do wyeliminowania przypadkowych błędów.
Liczba wykonywanych testów zależy od różnorodności danych.
Jak dobierać testy? Dane celowe i przypadkowe; typowe i graniczne.

Formalny dowód poprawności.
Proste algorytmy najczęściej nie wymagają szczegółowej formalnej analizy
poprawności. Po wykonaniu projektu i napisaniu programu, program jest
testowany i po skończonej liczbie znalezionych i usuniętych błędów uznaje się,
że algorytm (program) jest poprawny.
Taka metoda nie zawsze jest właściwa (zły projekt, niewystarczające testy, …).

Powszechnie stosowaną metodą wykazywania częściowej poprawności
algorytmów jest metoda niezmienników.

Projektowanie i analiza algorytmów

Proces rozwiązywania problemu:

model matematyczny + nieformalny algorytm

abstrakcyjne typy danych + program
w pseudojęzyku

struktury danych + program w języku
programowania (C, Java, …)

Projektowanie i analiza algorytmów

Abstrakcyjny typ danych

– model

matematyczny wraz ze zbiorem operacji
zdefiniowanych na tym modelu.

Np. zbiór liczb całkowitych z operacjami
sumy, iloczynu i różnicy mnogościowej, graf
z operacjami dodawania i usuwania
wierzchołków oraz krawędzi, ...

Projektowanie i analiza algorytmów

Argumentami operacji zdefiniowanych dla
danego Abstrakcyjnego Typu Danych
mogą być nie tylko elementy tego ADT, ale
również elementy innego ADT lub np.
liczby całkowite. Jednak przynajmniej
jeden argument lub rezultat musi być
elementem tego ADT.

Projektowanie i analiza algorytmów

Problem składowania substancji chemicznych:

Zakłady chemiczne wykorzystują przy produkcji n
surowców chemicznych.
Wiadomo, że niektóre substancje nie mogą być
przechowywane razem, gdyż zetknięcie ich ze sobą
spowodowałoby 'zniszczenie magazynu'.

Jaka jest minimalna liczba magazynów potrzebna do
przechowywania wszystkich surowców chemicznych
używanych w tej fabryce?
W jaki sposób przydzielić surowce do magazynów?

Projektowanie algorytmu – przykład

1.Sformułowanie problemu i specyfikacja

Projektowanie i analiza algorytmów

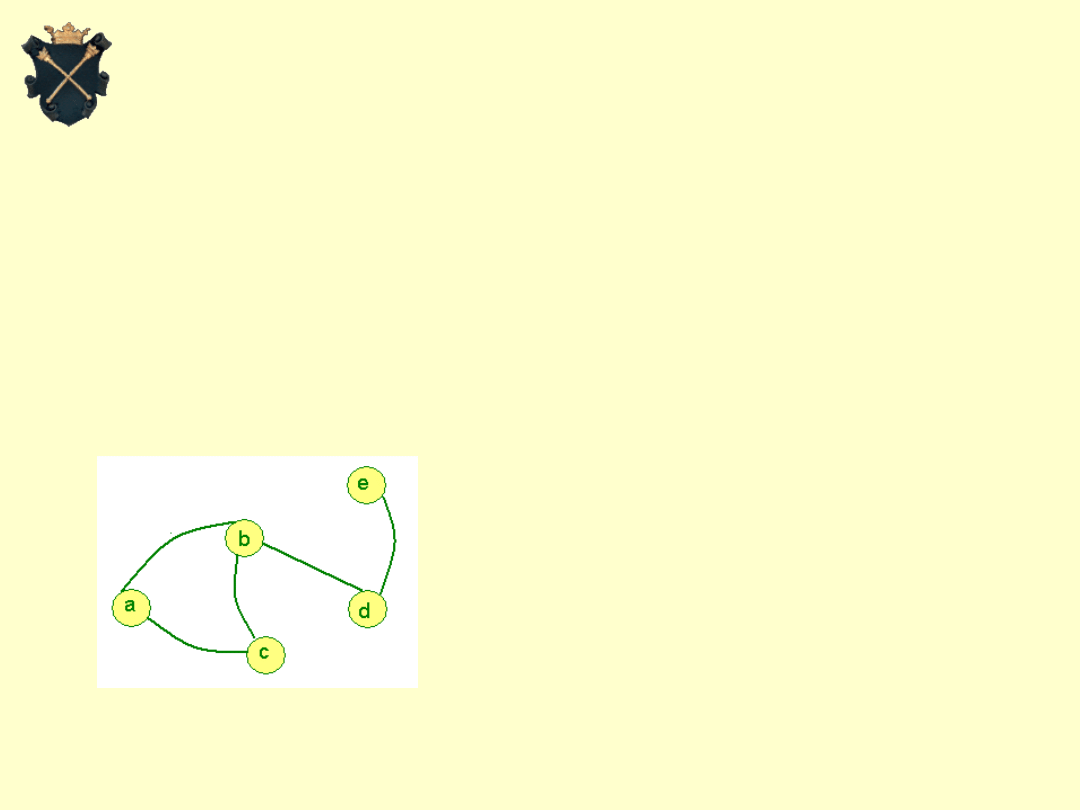
wierzchołki: a, b, c, d, e.

krawędzie: (a,c), (a,b), (b,c),
(b,d), (d,e)

Poszukiwanym modelem może być graf.

Graf jest to zbiór wierzchołków i krawędzi:

Tworzymy graf, którego n wierzchołków
odpowiada poszczególnym surowcom chemicznym.

Projektowanie i analiza algorytmów

Surowce:

A, B, C, D, E, F, G, H.

Dwa wierzchołki łączymy krawędzią, jeżeli
reprezentowane przez nie surowce nie mogą
być przechowywane razem.

Projektowanie i analiza algorytmów

Projektowanie i analiza algorytmów

Surowiec A nie może być przechowywany z
surowcami: B, D, E, F, G

Surowiec B nie może być przechowywany z : A, D, E,
F, H

Surowiec C nie może być przechowywany z : D, G, H

Surowiec D nie może być przechowywany z : A, B, C

Surowiec E nie może być przechowywany z : A, B, F,
G, H

Surowiec F nie może być przechowywany z : A, B, E,
G

Surowiec G nie może być przechowywany z: A, C, E,
F

Surowiec H nie może być przechowywany z: B, C, E

2. Projekt rozwiązania

Kolorowanie grafu polega na takim
przyporządkowaniu kolorów wierzchołkom,
aby
każde dwa wierzchołki połączone krawędzią
miały różne kolory.

Projektowanie i analiza algorytmów

2. Projekt rozwiązania

Problem znalezienia minimalnej liczby
magazynów potrzebnej do przechowywania
wszystkich surowców chemicznych sprowadza
się do pokolorowania grafu surowców
najmniejszą możliwą liczbą kolorów.

Surowce odpowiadające wierzchołkom
pokolorowanym tym samym kolorem mogą być
przechowywane w tym samym magazynie.

Projektowanie i analiza algorytmów

2. Projekt rozwiązania – cd.

Problem pokolorowania grafu jak
najmniejszą liczbą kolorów jest problemem
NP-zupełnym

(nondeterministic polynomial time)

(wszystkie znane rozwiązania
są typu „wypróbuj wszystkie możliwości”).
Wybieramy więc rozwiązanie szybkie, dające
małą (ale niekoniecznie najmniejszą) liczbę
kolorów – algorytm zachłanny (greedy)
kolorowania grafu.

Projektowanie i analiza algorytmów

2. Projekt rozwiązania – cd.
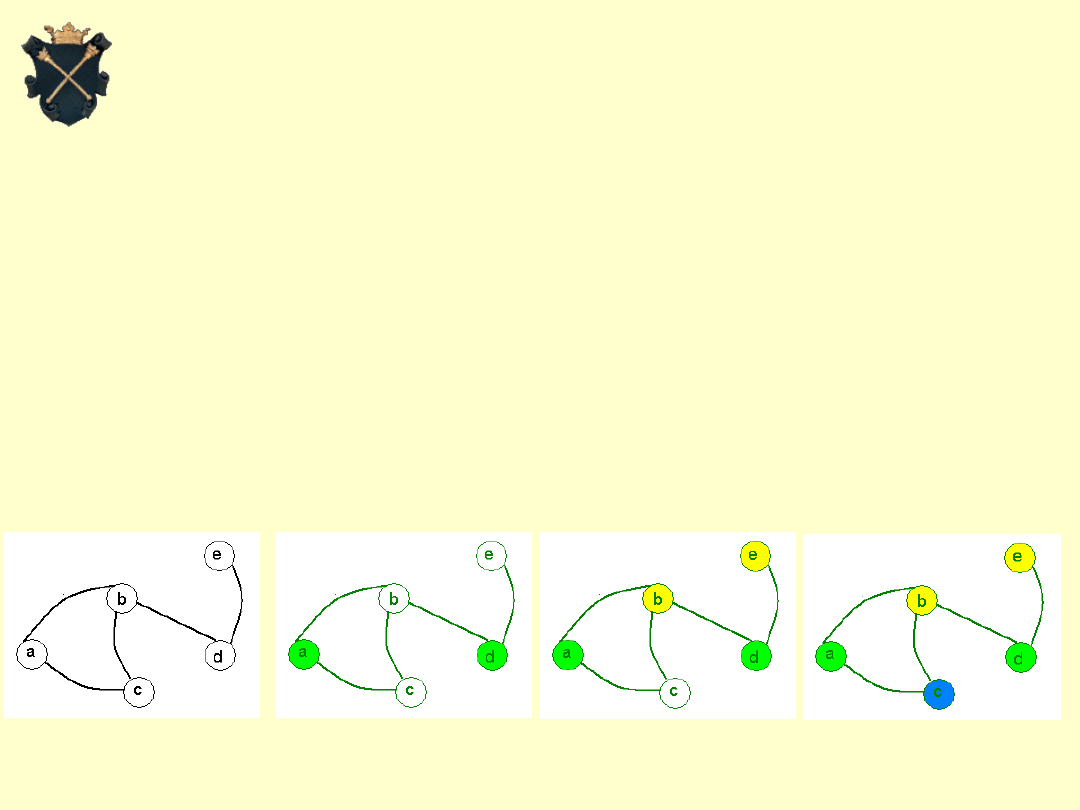
Algorytm zachłanny kolorowania grafu:
Kolorujemy pierwszym kolorem tyle
wierzchołków, ile się da, następnie drugim
kolorem, ile się da z pozostałych wierzchołków
itd…

Projektowanie i analiza algorytmów

2. Projekt rozwiązania – cd.
Aby pokolorować wierzchołki nowym kolorem
należy:
1.Wybrać nie pokolorowany wierzchołek

i pokolorować go nowym kolorem

2.Przeglądnąć listę nie pokolorowanych
wierzchołków. Dla każdego nie

pokolorowanego wierzchołka sprawdzić, czy
ma krawędź łączącą z wierzchołkiem już
pokolorowanym nowym kolorem. Jeśli nie ma,
to pokolorować go nowym kolorem.

Projektowanie i analiza algorytmów

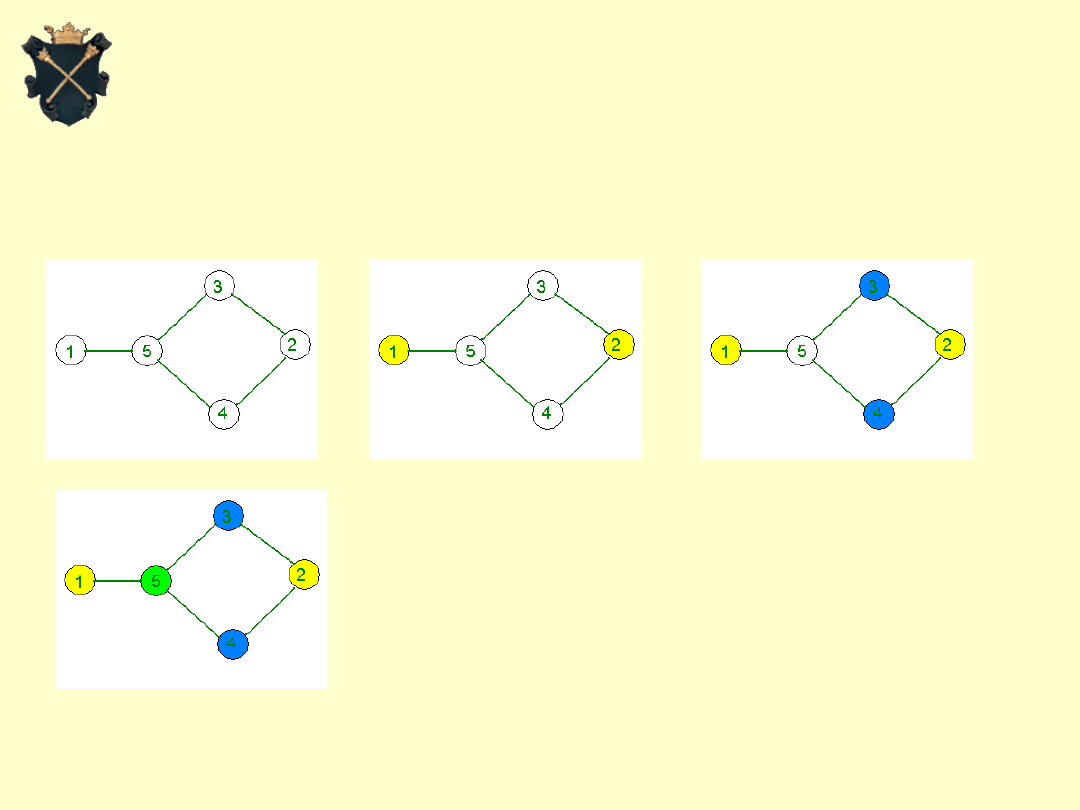
Kolorowanie grafu – algorytm zachłanny

Projektowanie i analiza algorytmów

Takie pokolorowanie nie jest optymalne!

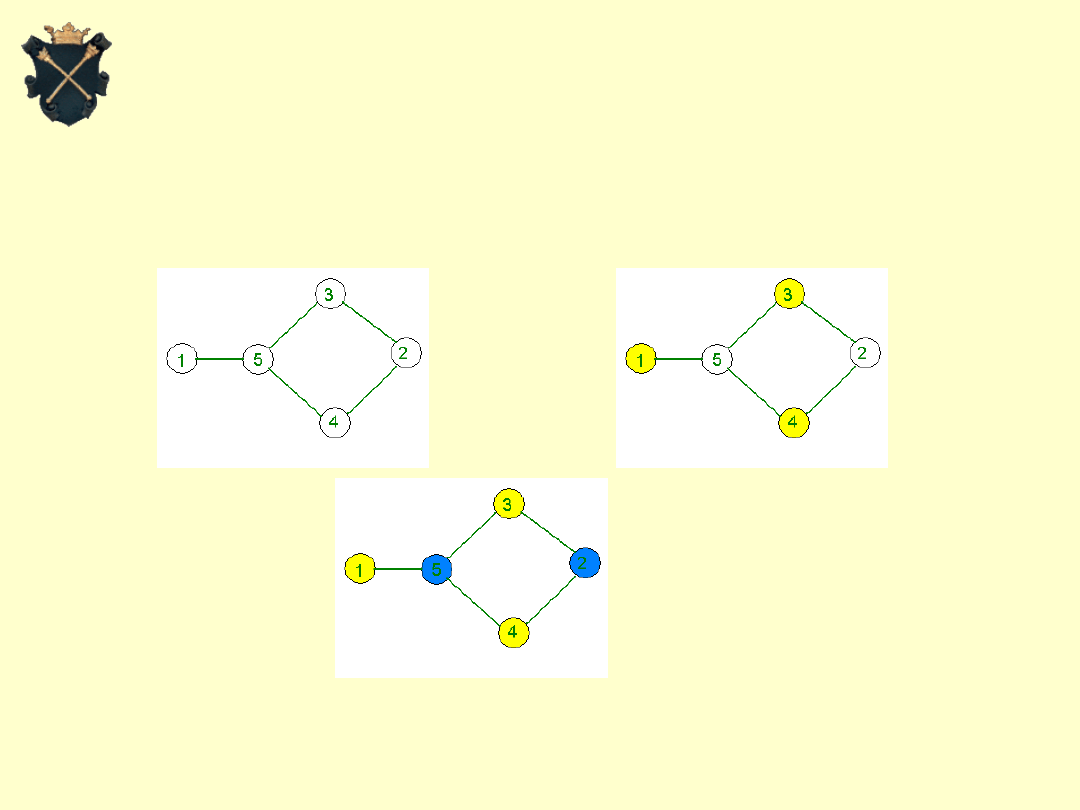
Kolorowanie grafu – algorytm zachłanny

Projektowanie i analiza algorytmów

Kolorowanie optymalne

3. Implementacja

• Gdy mamy już model matematyczny oraz

nieformalny algorytm, przechodzimy do
następnego etapu: abstrakcyjne typy danych
oraz program w pseudojęzyku.

• Niech Newclr będzie zbiorem

wierzchołków, które mogą być pokolorowane
nowym kolorem. Program będzie
wykonywany aż do momentu, gdy wszystkie
wierzchołki grafu będą pokolorowane.

Projektowanie i analiza algorytmów

3. Implementacja - cd.
• Funkcja greedy umieszcza w Newclr te

wierzchołki, które mogą być pokolorowane
nowym kolorem.

• GRAPH (graf), SET(zbiór) – abstrakcyjne typy

danych.

• GRAPH i SET zostaną później zdefiniowane

jako typy w C wraz z odpowiednimi funkcjami
– operacjami związanymi z ADT.

Projektowanie i analiza algorytmów

3. Implementacja - cd.

greedy (GRAPH G; SET Newclr)
{
Newclr:=Ø
For każdy niepokolorowany wierzchołek v w G do

if v nie jest związany w G krawędzią z żadnym

wierzchołkiem z Newclr then
{
Zaznacz, że v jest pokolorowany
Umieśc v w Newclr
}
}

Projektowanie i analiza algorytmów

3. Implementacja - cd.

Metodą kolejnych uściśleń dochodzimy
do abstrakcyjnych typów danych oraz
szczegółowego opisu algorytmu
w pseudojęzyku, a następnie do odpowiednich
struktur danych oraz opisu algorytmu w języku
programowania.

Projektowanie i analiza algorytmów

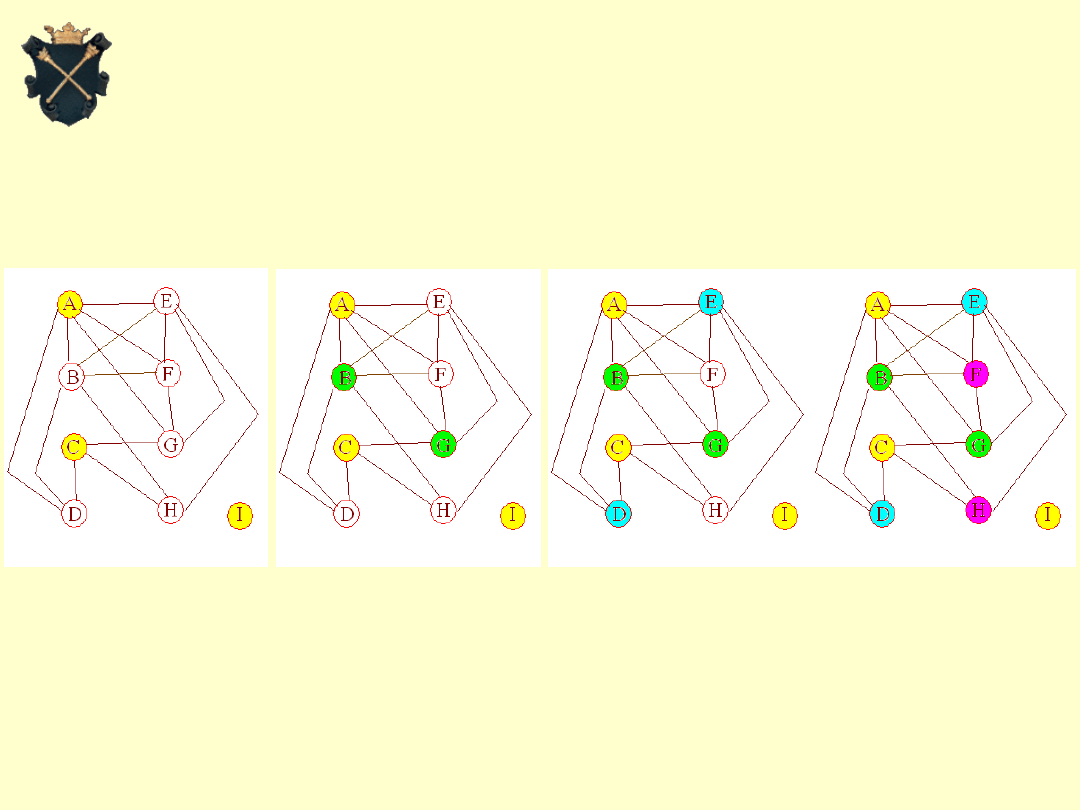
5. Ocena rozwiązania

Projektowanie i analiza algorytmów

Wynik otrzymany w wyniku zastosowania
algorytmu do naszego problemu

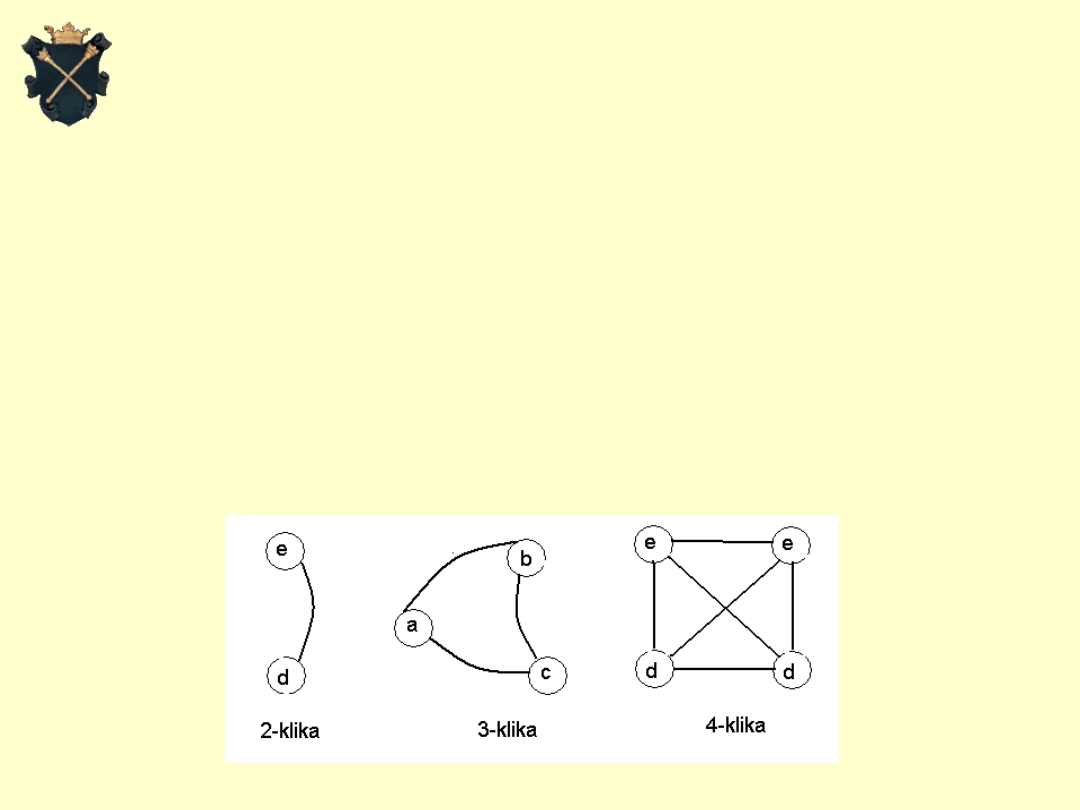
5. Ocena rozwiązania - cd.

Aby ocenić otrzymany rezultat, odwołujemy się do
teorii grafów.
Definicja:
K-Klika jest to zbiór złożony z k wierzchołków grafu,
które są połączony każdy z każdym krawędziami.

Projektowanie i analiza algorytmów

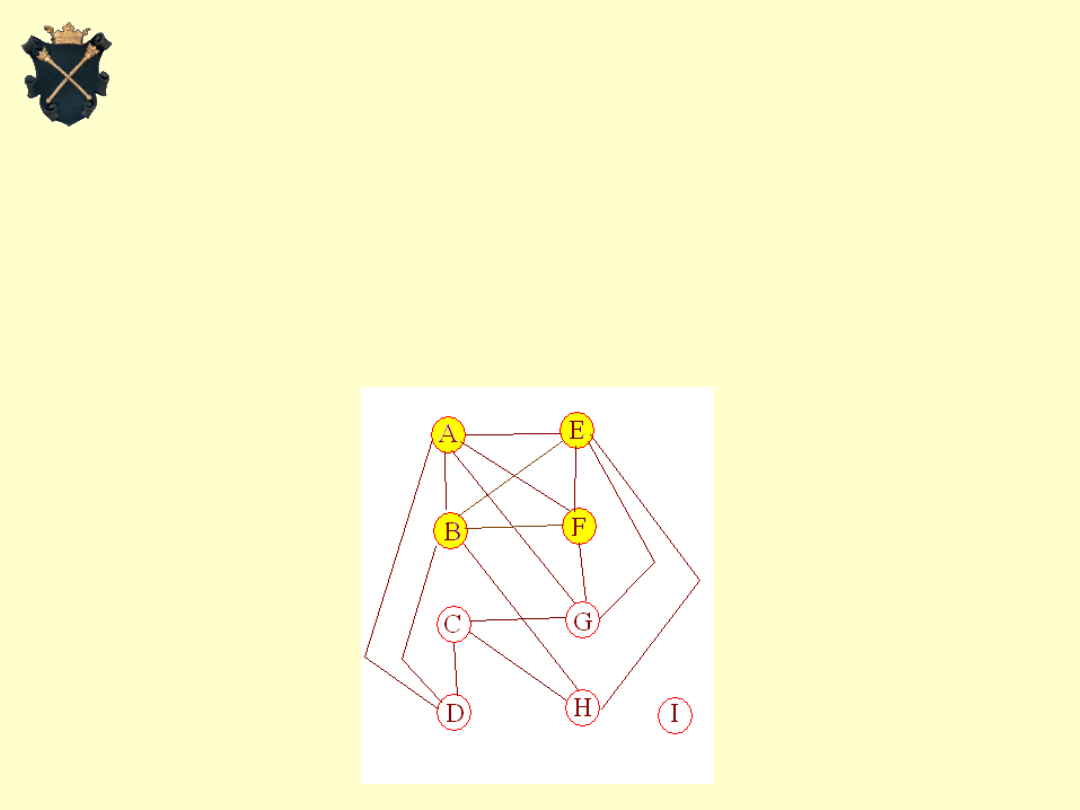
5. Ocena rozwiązania - cd.
Tw. Do pokolorowania grafu, który posiada
k-klikę, potrzeba co najmniej k kolorów.
W naszym grafie mamy 4-klikę: A,B,E,F.

Projektowanie i analiza algorytmów

5. Ocena rozwiązania - cd.

Naszego grafu nie można pokolorować
mniejszą liczbą kolorów. Nasze rozwiązanie jest
optymalne. Do przechowywania surowców
potrzebne są cztery magazyny.

Projektowanie i analiza algorytmów

Przez prostą zamianę (bąbelkowe):

Wartości do posortowania zapisane są w tablicy, której
elementy ponumerowane są od 1 do n.

dla i od n-1 do 1
dla j od i do n-1
porównaj wartości j, j+1
jeśli są w złej kolejności to
zamień miejscami j, j+1

Proste algorytmy sortowania

Przez prostą zamianę (bąbelkowe):

Wartości do posortowania zapisane są w tablicy, której
elementy ponumerowane są od 1 do n.

dla i od n-1 do 1

dla j od i do n-1 <- błąd! od 1 do i

porównaj wartości j, j+1
jeśli są w złej kolejności to
zamień miejscami j, j+1

Proste algorytmy sortowania

Przez proste wybieranie:

Z jeszcze nieuporządkowanego fragmentu wybieramy minimum
i wstawiamy na jego właściwe miejsce.

dla i od 1 do n-1
znajdź minimum z wartości od i do n
zamień wartość i oraz znalezione minimum

Nie powiedzieliśmy jak szukać minimum; patrz pseudokod na
następnym slajdzie.

Proste algorytmy sortowania

Przez proste wybieranie (uszczegółowiony):

dla i od 1 do n-1
k = i
dla j od i+1 do n
jeśli tab[j] < tab[k] to
k = j
# w k mamy zapisane gdzie jest minimum
zamień miejscami tab[i] oraz tab[k]

Proste algorytmy sortowania

Przez proste wybieranie (kompletny):

dla i od 1 do n-1
k = i
dla j od i+1 do n
jeśli tab[j] < tab[k] to
k = j
# w k mamy zapisane gdzie jest minimum
tymcz = tab[i]
tab[i] = tab[k]
tab[k] = tymcz

Proste algorytmy sortowania

Przez proste wstawianie:

Stopniowo powiększamy uporządkowany fragment tablicy
wstawiając w jego środek nowe elementy.

dla i od 2 do n
tymcz = tab[i]
j = i - 1
jak długo j >= 1 oraz tab[j] > tymcz
tab[j+1] = tab[j]
j = j - 1
tab[j] = tymcz

Proste algorytmy sortowania