
1
TRAINING
M1-1
Hydraulic Foundations
Index
Comparison of energy transferring systems
Pressure due to external forces
Pipe friction / flow resistance
Pressure dependence of volume flow

2
TRAINING
Hydraulic Foundations
M1-1
1. General basics
1.1 Definition of hydraulic
Hydraulics is a part of fluid-power, which also includes the pneumatic.
The word „hydraulic“ is derived the greek word „hydor“ and means „water“.
Nowadays the term „hydraulics“ signifies the
transfer and control of forces and movements
by means of a liquid.
As an agent of energy transfer liquid is thus used, because liquids are nearly incompressible and free
of friction.
1.2 Hydro-mechanics
The “Hydro-mechanic” ( mechanic of fluids) is divided into to fields:
•
Hydro-statics
The mechanic of still fluids
Pressure is produced by the gravity force of fluids.
•
Hydro-kinetics
The mechanic of moving fluids (former Hydro-dynamics)
Pressure is produced by machines, which are acting on the fluid.

3
TRAINING
M1-1
Hydraulic Foundations
1.3 Where hydraulic is used
MOBIL HYDRAULIC
Used in mobile machines on wheels, chains ...
Valves are often acted directly by hand.
Working machines
Workman baskets
Hydraulic loaders
Excavators
Agricultural machines
Mining machines
Special trucks
Vehicle technology
Brakes
Steering
Loading facilities
Gears for special machines
Construction site
Stone drilling machines
Inspection- spanning- lifting- and loading facilities
Ships and aeroplanes
Stabilisers
Winches
Driving motors
Flaps
STATIONARY HYDRAULIC
Fixed to it’s location
Mostly controlled electrically
Production machines
Forging machines
Power press
Material testing machines
Feed gearboxes
Workholding fixtures
Transport technology
Belt conveyors
Loading ramps
Power plants
Weir actuation
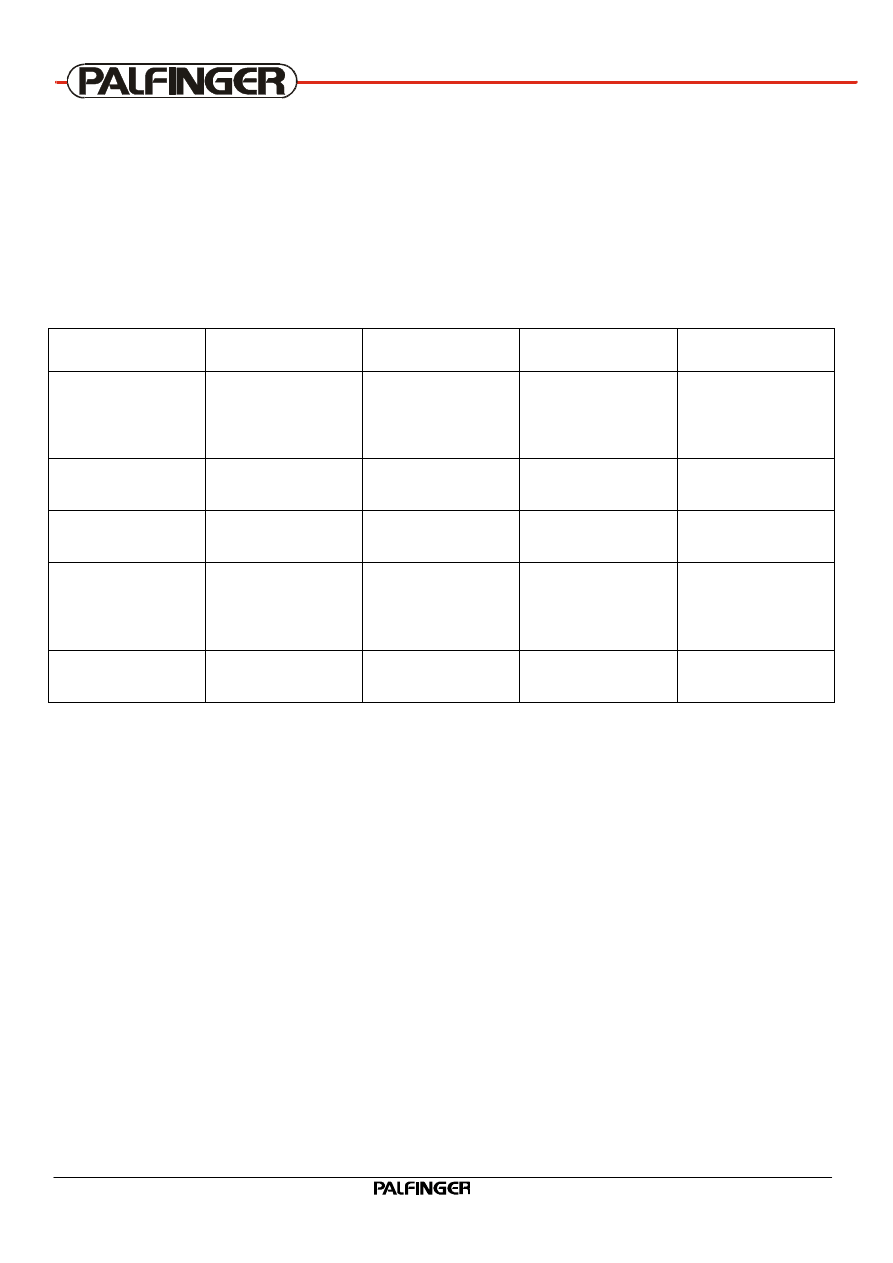
4
TRAINING
Hydraulic Foundations
M1-1
1.4 Comparison of energy transferring systems
Comparison between:
Hydraulics
Pneumatics
Electric
Mechanics
Hydraulics
Pneumatics
Electrics
Mechanics
Energy source
E-Motor
Combustion engine
Hydro accumulator
E-Motor
Combustion engine
Pressure tank
Power supply
Battery
E-Motor
Combustion engine
Weight force
Spring force
Energy transferred by pipes
hoses
pipes
hoses
cable
magnetic field
levers, shafts
mechanical parts
Transfer carrier
Fluids
Air
Electrons
Rigid and elastic
objects
Efficiency
high
high pressure
high forces
small components
relatively small
low pressure
small
(efficiency rate
E-motor to Hydro-
motor approx. 1:10)
high
but mostly
complicated and big
parts
proportional
controllability
Very good because of
pressure and flow
controllability
Good because of
pressure and flow
controllability
Very good because of
electronic controls
good
Advantages of hydraulics
•
Transfer of high forces with small parts
•
Precise and very good controllability
•
Small and compact components
•
No gear boxes necessary
•
Positioning without switches
•
Start-up with maximum load possible
Disadvantages of hydraulic
•
Production of components very expensive (tolerances)
•
Leakage possible, bad for the environment
•
Relatively high maintenance necessary
•
Expensive filtration necessary
•
Danger due to high pressure
•
Temperature dependence

5
TRAINING
M1-1
Hydraulic Foundations
1.5 Quantities, units, formulas
1.5.1
Mass
SI unit:
kilograms
[kg]
Symbol:
m
A mass is the weight of an object, defined by the Ur-kilogram made of Platiniridium.
The mass is not depending on a certain location.
One dm
3
of water has a mass of 1 kg if its temperature is 4
o
Celsius.
1.5.2
Force
Symbol:
F
SI unit:
Newton
[N]
1N = 1kgm/s
2
According to Newton’s law:
F = m * a
Force = mass * acceleration
If the general acceleration is replaced by the acceleration due to gravity (g = 9,81 m/s
2
), the
following is obtained:
F = m * g
Force = masse * gravity acceleration
A mass of 1 kg creates on the earth a force of 9,81 N.
In practice, it is generally adequate to use 10 N or 1daN instead of 9,81 N for a weight of 1 kg.
1.5.3
Work
Symbol:
W
SI unit:
Joule [J]
1J = 1Nm = Ws
If an object is move by a force F a certain distance s, the force has done the work W.
W = F * s
Work = force (in the direction of the distance) * distance
W = V * Äp
Hydraulic Work
V in m
3
Äp in Pa

6
TRAINING
Hydraulic Foundations
M1-1
1.5.4
Energy
Symbol:
E
SI unit:
Joule [J]
1J = 1Nm = Ws
If an object is capable of work, it has “stored work”.
This type of “stored work” is known as energy.
Work and energy hence have the same unit.
Depending on the type of “stored work”, there are two types of energy.
•
Potential Energy
E
p
An object may sink to a particular level due to its high initial position and it hence carries out
work. The amount of work stored is dependent on the weight force of the object m*g and
the height h.
E
p
= m * g * h
•
Kinetic Energy
E
k
If a moving object meets an object at rest, the moving object performs work to the body at
rest (e.g. deformation work).
The work stored is contained in the movement of the object in this case.
E
k
= m * v
2
/ 2
1.5.5
Power
Symbol:
P
SI unit:
Watt
[W]
1W = 1J/s
Power is given by work divided by time.
P = W / t
Power = work / time
1.5.6
Velocity
Symbol:
v
SI unit:
metre/second [m/s]
1m/s = 3,6 km/h
Velocity v is the distance s divided by the time t taken to cover the distance.
v = s / t
Velocity = distance / time

7
TRAINING
M1-1
Hydraulic Foundations
1.5.7
Acceleration
Symbol:
a
SI unit:
metre / second squared [m/s
2
]
g = 9,81 m/s
2
If an object does not move at a constant velocity, it experiences an acceleration a.
The change in velocity may be positive (increase in velocity/acceleration) or negative (decrease in
velocity/acceleration).
The linear acceleration a is given by velocity v divided by time t.
a = v / t
Acceleration = speed / time
g = 9,81 m/s
2
Gravity acceleration
1.5.8
Pressure
Symbol:
p
SI unit:
Pascal
[Pa]
1Pa = 1N/m
2
= 10
-5
bar
In descriptions of processes involving fluids, pressure is one of the most important quantities.
If a force acts perpendicularly to a surface and acts on the whole surface, then the force F divided
by the area of the surface A is the pressure p.
p = F / a
Pressure = force / surface
1 Pa = 1 N /m
2
Pressure in Pascal or Million-Pascal [MPa]
1 bar = 1kp / cm
2
Pressure in bar (not SI, but more common)
1 bar = 100 000 Pa = 0,1 MPa
1.5.9
Volume flow
Symbol:
Q
SI unit:
metre cubed / second
[m
3
/s]
1 m
3
/s = 60000 l/min
The Volume flow Q is Volume V divided by time t.
Q = V / t
Volume flow = volume / time
V = A * s
Q = A * s / t
and
v = s / t
Q = A * v
Volume flow = area * velocity
The most common unit for the volume flow Q is [l/min] in the hydraulic field.

8
TRAINING
Hydraulic Foundations
M1-1
1.5.10 Hydraulic power
Power is calculated by work divided through a certain time.
P = W / t
see 1.5.5
P = F * s / t
W = F * s (replaced)
Valid for hydraulics:
F = p * A
P = p * A * s / t
(replaced)
further :
V = A * s
P = p * V / t
Q = V / t
P = p * Q
hydraulic power
Different formulas to calculate the hydraulic power (different units):
P = p * Q
[W] = [Pa] * [m
3
/s]
P = p * Q /1000
[kW] = [Pa] * [m
3
/s] / 1000
P = p * Q * 100
[kW] = [bar] * [m
3
/s] * 100
P = p * Q / 600
[kW] = [bar] * [l/min] / 600
P = p * Q / 10
[kW] = [bar] * [l/s] / 10
P = p * Q / 450
[PS] = [bar] * [l/min] / 450

9
TRAINING
M1-1
Hydraulic Foundations
2. PHYSICAL BASICS
2.1 Hydrostatic pressure
Hydrostatic pressure is the pressure in a liquid column, which occurs due to the weight of the liquid
mass over a given surface.
Hydrostatic pressure:
p =
ρρ . g . h
p
pressure
[Pa]
ρρ
density
[kg/m
3
]
g
gravity acceleration
[m/s
2
]
h
liquid height
[m]
The hydrostatic pressure only depends on the height of the liquid column and on the density of the
liquid itself. The shape of the column is not important.
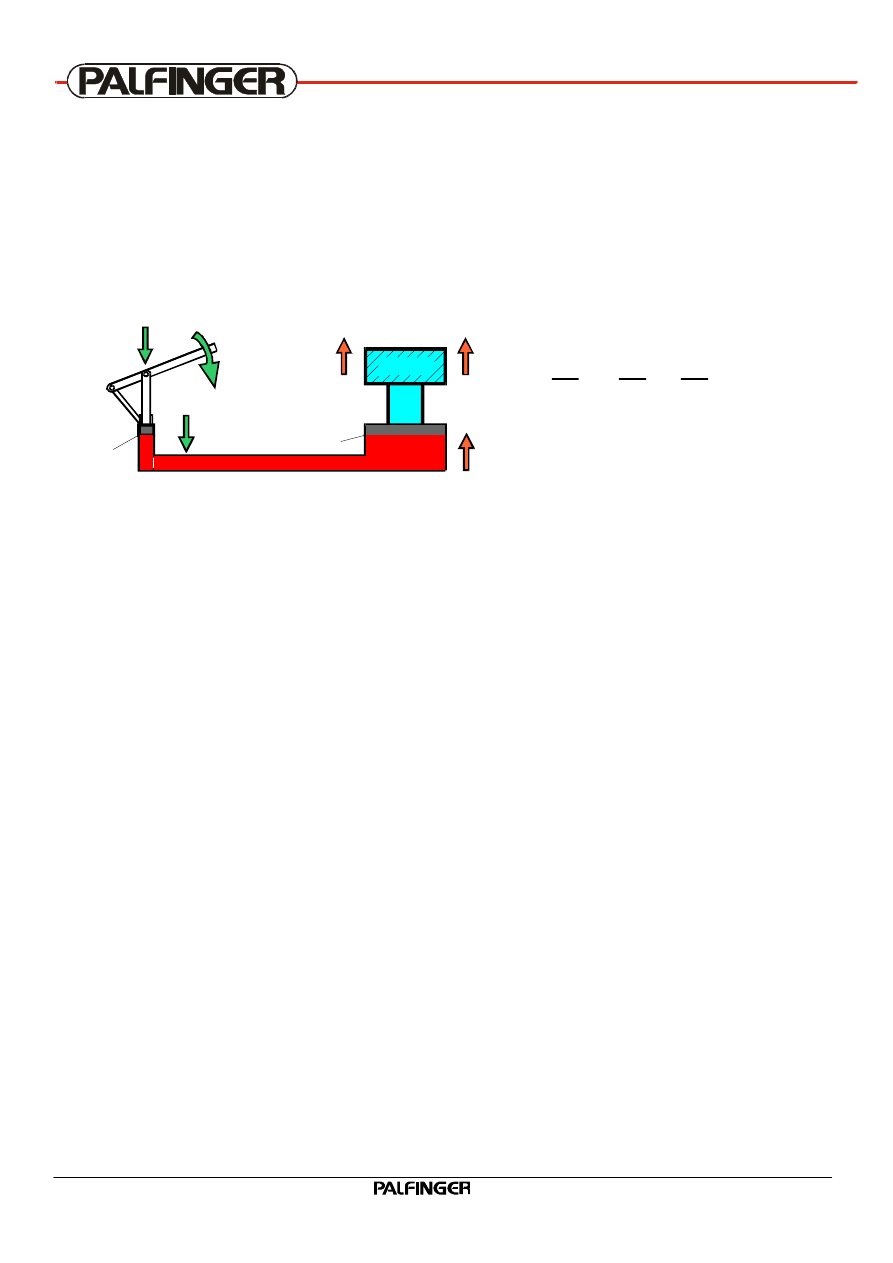
2.2 Pressure due to external forces
If a force “F” acts perpendicularly on a fluid over a given surface “A”, pressure “p” occurs. The
pressure in the liquid acts to all sides with the same value.
This law is called “Pascal’s law”.
Law of Pascal:
(pressure through external forces)
p = F / A
p
pressure
[Pa]
F
force
[N]
A
surface
[m
2
]
1 Pa = 1 N / m
2
1 bar = 1 kg / 1 cm
2
This calculation only includes the pressure due to the external force, the gravity pressure of the liquid
is not included. But compared to the (mostly) very high working pressures, the gravity pressure is not
relevant in hydraulic calculations.
10
TRAINING
Hydraulic Foundations
M1-1
2.3 Force transmission
In a closed system, the created pressure acts with the same value everywhere in the system.
If the system has one small surface, where the pressure is created and a big one, where the load is
placed, the forces can be transmitted.
LO AD
Pum p
Cylinder
A
1
F
1
F
2
A
2
S
1
S
2
A
1
F
1
F
2
A
2
S
1
S
2
=
=
This example shows
p
1
= F
1
/ A
1
pressure in the first cylinder
p
2
= F
2
/ A
2
pressure in the second cylinder
p
1
= p
2
pressure is equal everywhere in the system
F
1
/ A
1
= F
2
/ A
2
law of force transmission
The principle of force transmission is a very common tool in hydraulic systems to create very high
working forces with relatively small pumps.
2.4 Distance transmission
If (with the above mentioned principle) a load F
2
should be lifted over a distance s
2
, the piston K
1
has
to push a certain liquid volume, which moves the piston K
2
over the distance s
2
.
Then therefore necessary liquid volume is calculated as follows:
V
1
= s
1
* A
1
Volume cylinder 1
V
2
= s
2
* A
2
Volume cylinder 2
s
1
* A
1
= s
2
* A
2
Continuity law
The displacements s
1
and s
2
of the pistons vary in inverse proportion to the areas A
1
and A
2
.
11
TRAINING
M1-1
Hydraulic Foundations
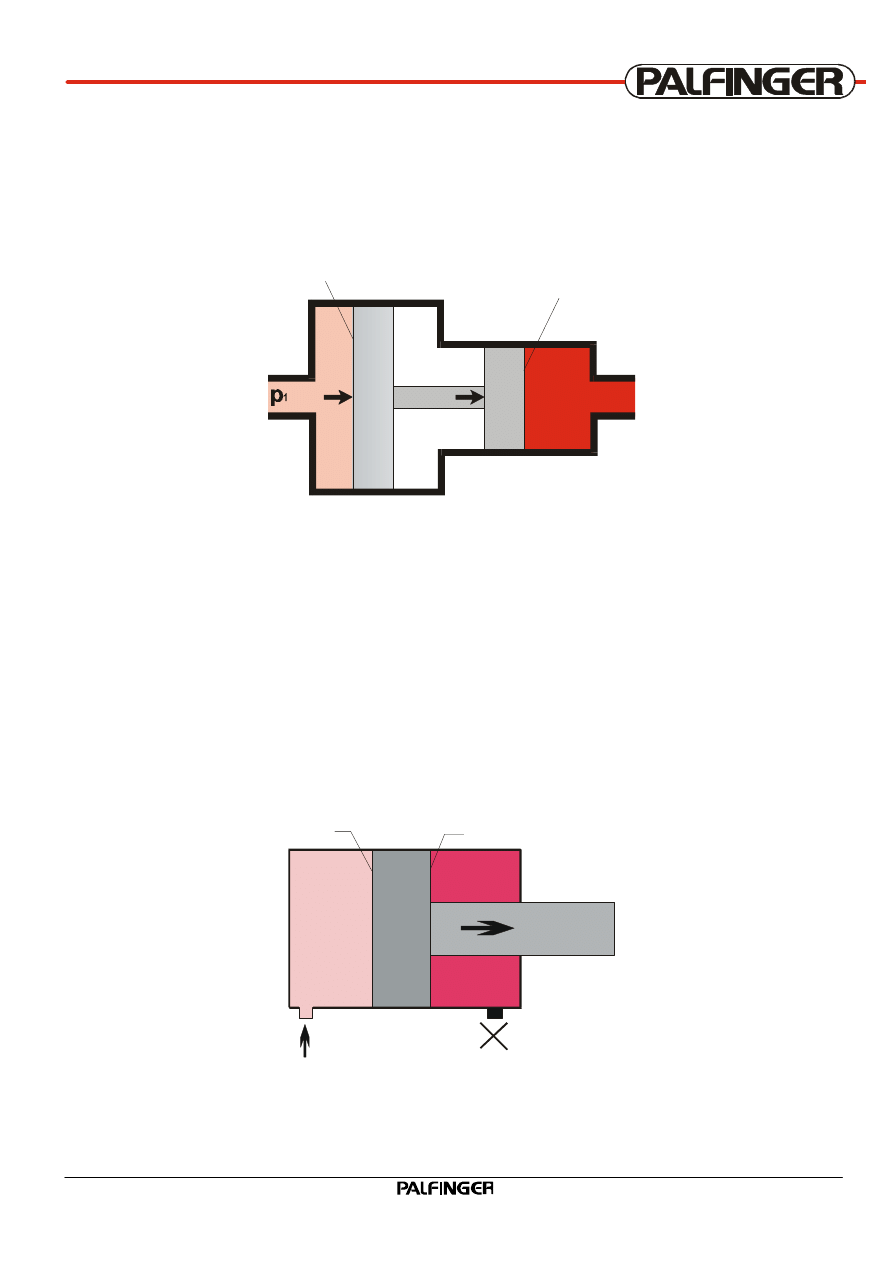
2.5 Pressure transmission
Two pistons of different sizes are fixed together by means of a rod.
If area A
1
is pressurised with pressure p
1
, a force F
1
is produced at piston 1.
Force F
1
is transferred via the rod to area A
2
of piston 2 and hence pressure p
2
is obtained there.
F
1
A
1
F
2
A
2
p
2
F
1
= F
2
and p
1
* A
1
= p
2
* A
2
p
1
/ p
2
= A
2
/ A
1
In pressure transfer the pressures vary in inverse proportion to the areas.
On single rod cylinders, this can create a dangerously high pressure p
2
, if the retracting port is closed.
The operating pressure p1 acts on area A
1
and increases the pressure p
2
by the area transmission
ratio A
1
/A
2
. This can cause damages to the cylinder.
p1
F
p2
A2
A1
12
TRAINING
Hydraulic Foundations
M1-1
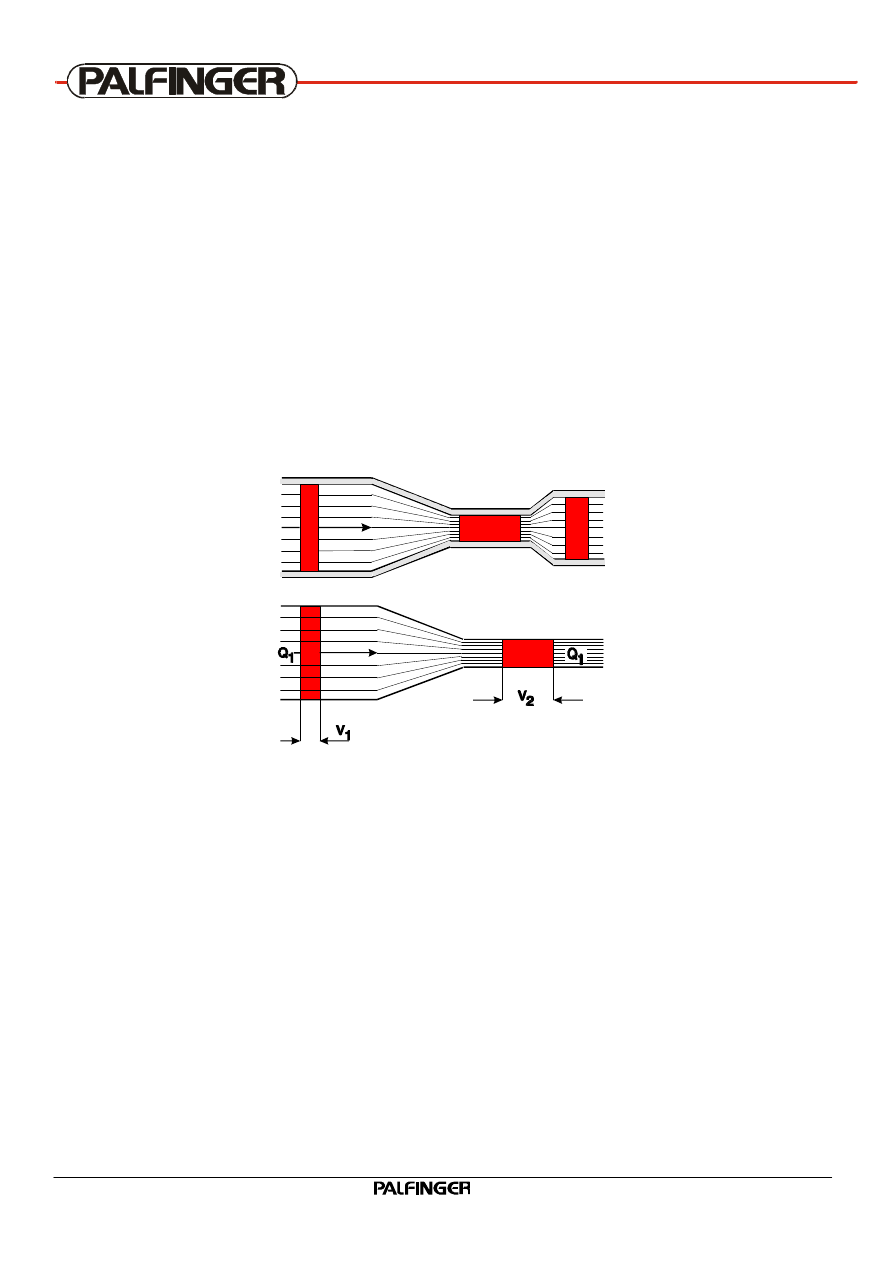
2.6 Continuity law
In all hydraulic systems, a certain (constant or variable) flow is used to operate the system.
Q = V / t
volume flow
(see chapter 1.5.9)
The flow can also be calculated with the following formula:
Q = A * v
Q ... volume flow
[m
3
/s]
A ... area
[m
2
]
v ... moving speed
[m/s]
If liquid flows through a pipe with varying diameters, at any particular time at the same volume flows
at all points. This means, that the velocity of liquid flow must increase at a narrow point.
Q = constant
the flow will not change
A
1
*v
1
= A
2
*v
2
Continuity law (flow law)
Friction and pressure losses
Hydraulic energy cannot be transferred trough pipes without losses. Friction occurs at the pipe
surface and within the liquid, which generates heat.
Mainly the pressure loss is dependent upon:
•
Length and dimension of pipe
•
Roughness of pipe surface
•
Number of pipe bends
•
Velocity of flow
•
Viscosity of the liquid

13
TRAINING
M1-1
Hydraulic Foundations
2.7 Law of conservation of energy
The law of conservation of energy, with respect to a flowing fluid, states that the total energy of a flow
of liquid does not change, as long as the energy is not supplied from the outside or drained to the
outside.
Neglecting the types of energy do not change during flow, the total energy is made up of:
Potential energy
Positional energy, dependent on the height of head of liquid and on static pressure
Kinetic energy
Movement energy, dependent on the velocity of flow and on back pressure
Hence Bernoulli’s equation is produced
p
ges
= p
st
+
ρρ * g * h + ρρ / 2 * v
2
p
st
static pressure
ρ
* g * h
potential energy
ρ
/ 2 * v
2
kinetic energy
Let’s now consider both to the continuity equation and the Bernoulli equation.
If the velocity increases as the cross-section decreases, movement energy increases.
As the total energy remains constant, potential energy and/or pressure must become smaller as the
cross section decreases.
That means, that the pressure in the area with the smaller cross section is less than before and
behind this area.

14
TRAINING
Hydraulic Foundations
M1-1
2.8 Types of flow
There are two different types of flow:
Laminar flow:
Up to a certain velocity, liquid move along pipes in layers (laminar). The
inner-most liquid layers travels at the highest speed. The outer-most liquid
layer does not move.
Turbulent flow:
If the velocity of flow is increased, at the critical velocity the type of flow
changes and becomes whirling (turbulent).
Reynold’s number
The type of flow may be roughly determined using Reynold’s number
R
e
= v * d
h
/ v
R
e
Reynold’s number
v
velocity of flow
[m/s]
d
h
hydraulic diameter
[m]
with circular cross-sections equal to the pipe internal diameter
otherwise calculated as
d
h
= 4 * A / U
v
kinetic viscosity
[m
2
/s]
R
ecrit
= 2300
If the value is less than 2300, the flow is laminar, otherwise turbulent.
The value only applies for round, technically smooth, straight pipes.

15
TRAINING
M1-1
Hydraulic Foundations
2.9 Pipe friction / flow resistance
Hydraulic energy cannot be transferred trough pipes without losses. Friction occurs at the pipe
surface and within the liquid, which generates heat.
Mainly the pressure loss is dependent upon:
•
Length and dimension of pipe
•
Roughness of pipe surface
•
Number of pipe bends
•
Velocity of flow
•
Viscosity of the liquid
Friction in pipes
The friction in pipes can be measured as pressure loss in a system.
Mainly the pressure loss depends on the cross section, further on the velocity of the liquid and on
the roughness of the pipe.
The following formula shows how to calculate the pressure loss (roughly)
d
p = L * l *
ρρ * v
2
/ (2*d)
d
p
Pressure loss (difference) in Pa
L
Pipe friction factor = 75/R
e
(gr. letter Lambda)
ρ
Density in kg/m
3
v
Velocity in m/s
l
Length in m
d
Internal diameter in m
Pressure loss through fittings
Pressure loss also occurs, if the liquid flows through fittings (also pipe bends, reducing parts, T-
connections, L-connections, etc.)
The pressure loss mostly depends on the design of the fitting, further also on the velocity of the
liquid.
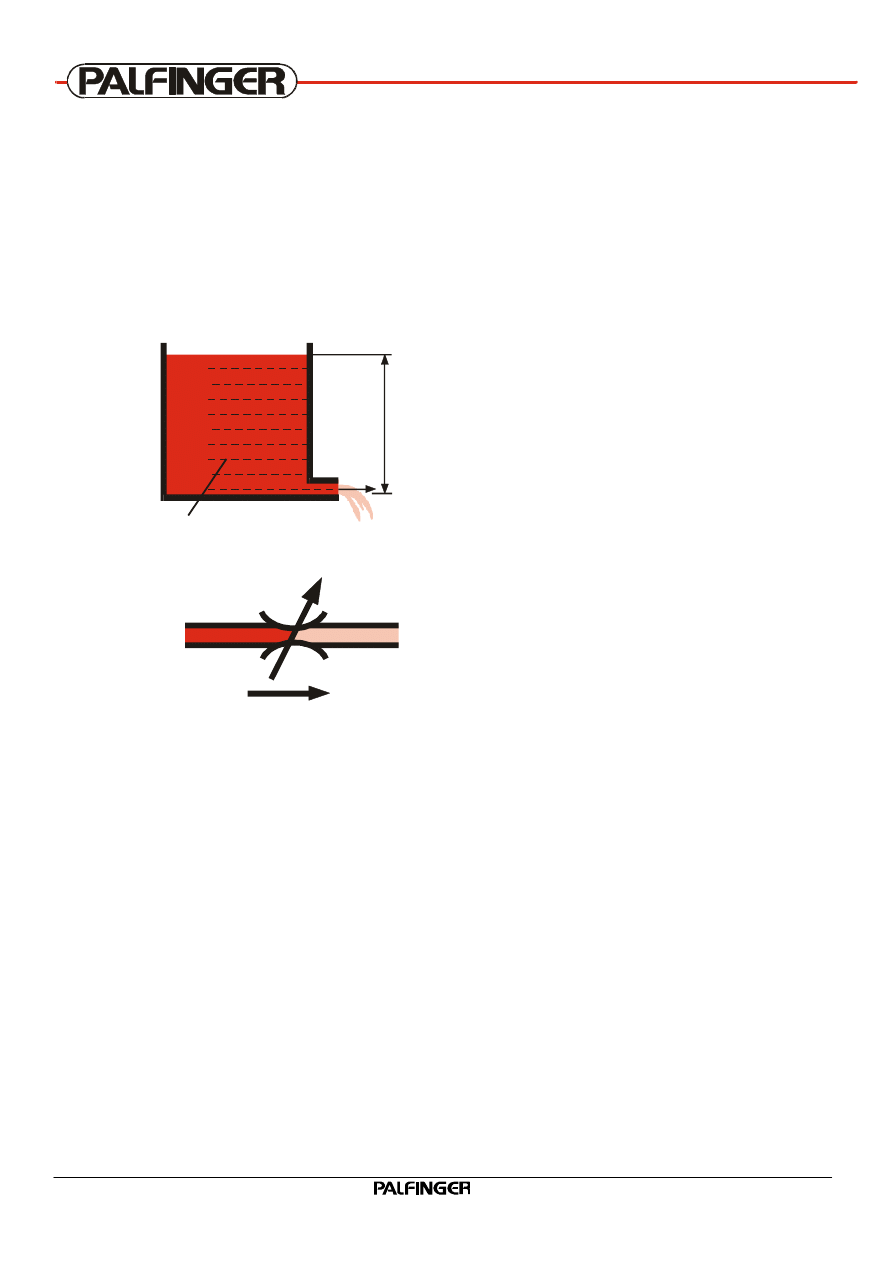
16
TRAINING
Hydraulic Foundations
M1-1
2.10 Pressure dependence of volume flow
The volume flow over narrow areas depends on the cross section and (mainly) on the pressure
difference before and behind the narrow area (passage).
If the pressure before the narrow area increases, also the flow increases (without changes on the
cross section).
Q
h
p
h
Flow out of objects
Q
p
2
p
1
Volume flow on narrow passages
The volume flow can be determined with the law of Hagen and Poiseuille:
Q = a* A
D
* SQRT ( 2 /
ρρ *
d
p)
a
Resistance factor (gr. letter Alpha)
A
D
Cross section (m
2
)
ρ
Density of liquid (kg/m
3
)
d
p
Pressure difference (Pa)
SQRT
stands for square root

17
TRAINING
M1-1
Hydraulic Foundations
2.11 Efficiency rate of hydraulic systems
Due to power losses, the power which can be taken from a hydraulic system is less than the power
which has to be given to the system.
The ratio between the taken power and the given power is called efficiency rate.
The symbol for the efficiency rate is usually the Greek letter Eta, in this documentation replaced by
the capital letter:
E
In practice, the total efficiency rate is a sum of the hydraulic-mechanic efficiency rate and the
volumetric efficiency rate, which occurs due to leakage and friction in the system.
Volumetric efficiency rate E
v
Covers all losses given by hydraulic friction and leakage on pump, on the valves, on cylinders
and motors.
Hydraulic mechanic efficiency rate E
hm
Covers all losses given by mechanic friction on power packs, valves, cylinders (seals) and all
other hydraulic parts in the system.
Total efficiency rate E
ges
E
ges
= E
v *
E
hm
The total efficiency rate depends on the size and complexity of the hydraulic system and is
usually between 70 and 90 %.
The total efficiency rate decreases with the age of a hydraulic system.

18
TRAINING
Hydraulic Foundations
M1-1
2.12 Cavitation
Unter Kavitation (cavitare = aushöhlen) versteht man das Herauslösen von kleinsten Partikeln aus
der Werkstoffoberfläche.
Kavitation kann bei Hydraulikgeräten (Pumpen und Ventilen) and Steuerkanten auftreten.
Der Grund dafür ist schnelle Temperaturerhöhung oder schnelle Druckänderung (Unterdruck).
Dies kann bei Engstellen (Drosseln) durch Erhöhung der Geschwindigkeit und damit verbundenem
Druckabfall auftreten. Durch den Druckabfall (ab ca. 0,3 bar Unterdruck) löst sich Luft aus dem Öl.
Steigt nun nachher der Druck bedingt durch einen Geschwindigkeitsverlust wieder an, stürzt das
Öl in die Gasbläschen und kann folgende Kavitationseffekte auslösen:
Druckspitzen:
An der Stelle der Querschnittserweiterung werden kleine Partikel aus dem Werkstoff
herausgelöst. Dies führt zu Materialermüdung und ist mit erheblichen Geräuschen begleitet.
Selbstentzündung:
Beim Zusammenbrechen der Luftblasen stürzt das Öl in die Gasbläschen, dadurch treten
aufgrund des Komprimierens der Luft sehr hohe Temperaturen (Blitztemperaturen) auf.
Dadurch kann es zur Selbstentzündung des Öls kommen (Dieseleffekt).
Air in the hydraulic system:
Luft ist in einem Hydrauliksystem immer vorhanden, normalerweise sind ca. 9% im Öl gelöst.
This value varies in dependence of pressure and temperature.
Luft kann auch von außen (Saugleitungen, undichte Drosselstellen ..) in das System kommen.
Because of the air in the hydraulic liquid, hydraulic liquids are also compressible (even they
are a liquid).
Approximate value:
1 volume per cent pre 100 bar pressure difference
19
TRAINING
M1-1
Hydraulic Foundations
3. The simple hydraulic circuit
3.1 Principle of a simple system
The piston of a hand pump is loaded with a force. The force divided by the piston area results in the
attainable pressure.
The greater the force on the piston is, the higher the pressure rises.
LAST
Pumpe
Zylinder
A
1
F
1
F
2
A
2
S
1
S
2
However, the pressure rises until, with respect to the cylinder area, it is in a position to overcome the
load (F=p*A). If the load remains constant, the pressure does not increase any further.
This basic principle says:
The pressure in the system is always depending on the resistance given by the load.
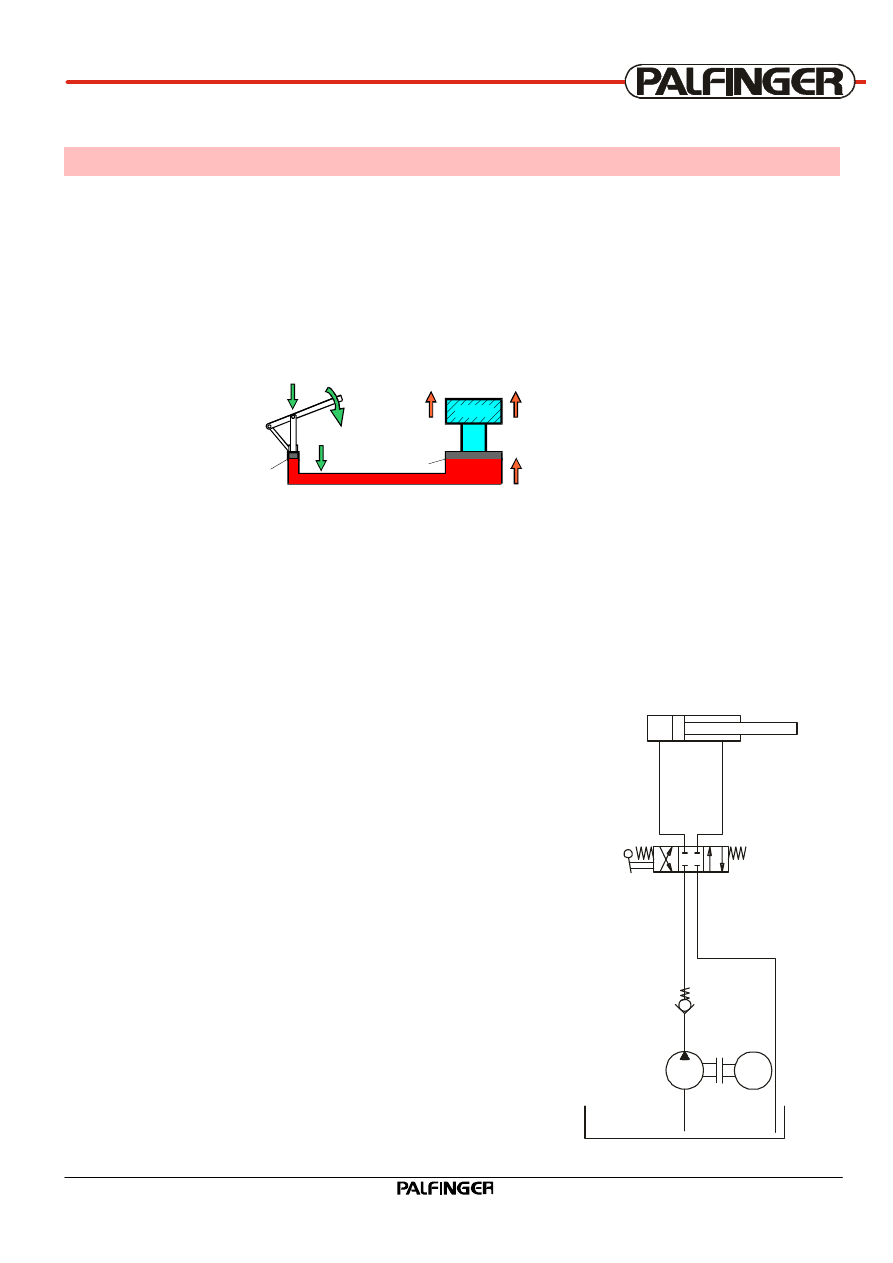
3.2 The first system
A hydraulic pump is driven by a motor (electric or com-
bustion engine). It sucks fluid from a tank and pushes it
into the lines of the hydraulic circuit.
Via a directional valve, a cylinder is connected to the
system.
Cylinder at the en of the line represents a resistance to
flow. Pressure increases until it is in a position to over-
come the resistance.
The direction of movement of the piston is controlled via
the directional valve.
At rest, the hydraulic circuit is prevented from being
drained via the hydraulic pump by check valve.
M
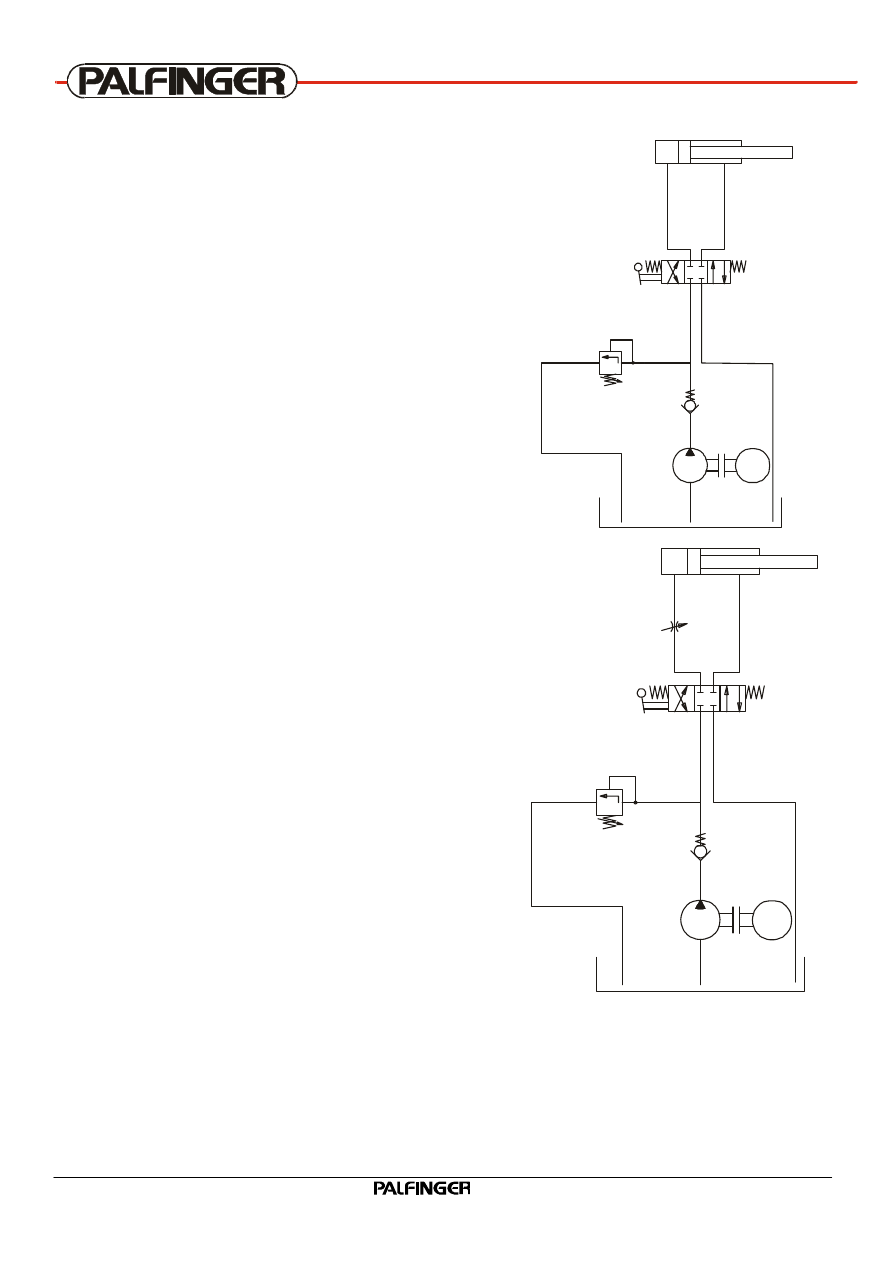
20
TRAINING
Hydraulic Foundations
M1-1
3.3 Pressure limitation
So that the hydraulic pressure is protected from excess
pressures an hence from overloading, the maximum
pressure must be limited.
This is achieved using a pressure relief valve.
The energy transferred to tank is changed to temperature
(P = p * Q).
The pressure can not increase any further.
With the adjusted limit, also the maximum working
pressure is given to the system.
3.4 Control of working speed
In order to change the speed of movement of the piston
in the hydraulic cylinder, the amount of flow to the
cylinder must be controlled.
This may be achieved using a flow control valve.
The cross section area of the pipe may be changed,
using a flow control valve. If the area is decreased, less
liquid per unit time reaches cylinder. The piston in the
cylinder hence moves slower.
The excess liquid, which is now delivered by the pump, is
drained to tank via pressure relief valve.
The following pressure occur in the system:
Ø Main relief pressure acts between pump and flow
control valve
Ø Pressure dependent on load acts between flow
control valve and cylinder
M
M
Document Outline
Wyszukiwarka
Podobne podstrony:
m11 id 274932 Nieznany
Abolicja podatkowa id 50334 Nieznany (2)
4 LIDER MENEDZER id 37733 Nieznany (2)
katechezy MB id 233498 Nieznany
metro sciaga id 296943 Nieznany
perf id 354744 Nieznany
interbase id 92028 Nieznany
Mbaku id 289860 Nieznany
Probiotyki antybiotyki id 66316 Nieznany
miedziowanie cz 2 id 113259 Nieznany
LTC1729 id 273494 Nieznany
D11B7AOver0400 id 130434 Nieznany
analiza ryzyka bio id 61320 Nieznany
pedagogika ogolna id 353595 Nieznany
Misc3 id 302777 Nieznany
cw med 5 id 122239 Nieznany
D20031152Lj id 130579 Nieznany
więcej podobnych podstron