Tradycyjny rachunek nazw

Wstęp

3

1. Zdania kategoryczne

4

1.1. Logika Arystotelesa

4

1.2. Zdania kategoryczne

4

1.3. Prawdziwość zdań kategorycznych

5

1.4. Reprezentacja graficzna

6

2. Wnioskowania bezpośrednie

8

2.1. Kwadrat logiczny

8

2.2. Znaczenie zwrotu „niektóre”

9

2.3. Prawa kwadratu logicznego

9

2.4. Wnioskowania bezpośrednie

9

2.5. Konwersja

10

2.6. Negacja przynazwowa

10

2.7. Obwersja

10

2.8. Kontrapozycja

11

3. Sylogizmy

12

3.1. Wnioskowania pośrednie

12

3.3. Tryby i figury

12

3.4. Tryby poprawne

13

3.5. Kryteria poprawności sylogizmu

13

3.6. Entymematy

14

4. Graficzne sprawdzanie sylogizmów

15

4.1. Diagram Venna dla trzech nazw

15

4.2. Tryb poprawny

15

4.3. Tryb niepoprawny

16

4.4. Przesłanki szczegółowe

17

4.5. Zaznaczanie istnienia w zdaniach ogólnych

19

5. Język KRK

5.1. Ograniczenia logiki arystotelesowskiej

20

5.2. Nazwy i predykaty

20

5.3. Formuły atomowe

21

5.4. Zdania proste a złożone

21

5.5. Kwantyfikatory

22

5.6. Zdania kategoryczne

23

5.7. Relacje

23

Bibliografia

24

Słownik

25

Spis symboli

30

3

Wstęp

W tym module zajmiemy się

rachunkiem nazw

, zwanym często po prostu logiką

tradycyjną albo arystotelesowską. Jest to system o możliwościach zbyt ograniczonych,
aby pozwolić na analizę wielu rozumowań w języku naturalnym. Mimo to, zakres
jego zastosowań pod pewnym względem przewyższa możliwości rachunku zdań
omawianego w poprzednim module. Zademonstrujemy to na prostym przykładzie.
Poniższe rozumowanie jest poprawne:

Wszystkie słonie są ssakami. Każdy ssak jest kręgowcem. Zatem każdy słoń jest
kręgowcem.

Jednak próba wykazania jego poprawności przy użyciu KRZ jest skazana na
niepowodzenie, gdyż nie występują tu w ogóle spójniki. Na gruncie KRZ schemat
powyższego rozumowania wygląda więc następująco:

p, q / r

Wystarczy użyć wartościowania V(p) = V(q) = 1 i V(r) = 0, aby taki schemat poddać
falsyfikacji. Aby wykazać, że interesujące nas rozumowanie jest poprawne, musimy
umieć poddać analizie strukturę wewnętrzną jego zdań składowych, a to umożliwia
rachunek nazw.

Poświęcimy prezentacji rachunku nazw cztery tematy. W ostatnim przedstawimy
język

klasycznego rachunku kwantyfikatorów

(w skrócie KRK), który jest współczesną

formą logiki klasycznej i zawiera w sobie zarówno rachunek zdań, jak i rachunek
nazw. Jednak KRK to dużo bardziej skomplikowany system i dlatego więcej uwagi
poświęcimy prostszemu systemowi, czyli rachunkowi nazw.

4

1. Zdania kategoryczne

1.1. Logika Arystotelesa

Historycznie pierwszy system logiczny, zbudowany przez Arystotelesa blisko
2,5 tysiąca lat temu, nie był logiką zdań, ale logiką nazw. Arystoteles wprawdzie
intuicyjnie stosował niektóre zasady klasycznego rachunku zdań, ale nie rozwinął go
w systematyczny sposób. Zbudował natomiast ograniczoną wersję rachunku nazw,
czyli takiej logiki, w której występują zmienne nazwowe.

Ograniczenia logiki Arystotelesa są dość istotne. Po pierwsze, w jego systemie
występują tylko zmienne reprezentujące n a z w y o g ó l n e , czyli posiadające więcej
niż jeden desygnat. Po drugie, analizowane są tylko wybrane rodzaje zdań, tzw.
z d a n i a k a t e g o r y c z n e . Po trzecie, w jego systemie mamy ujęcie tylko bardzo
specyficznej klasy rozumowań, tzw. wnioskowań bezpośrednich oraz pośrednich,
określanych tradycyjnie jako s y l o g i z m y. Ze względu na ważność tych ostatnich,
logikę Arystotelesa określa się często jako sylogistykę.

Współczesna logika matematyczna, czyli tzw. klasyczny rachunek kwantyfikatorów
(KRK) — z powodu jej zasięgu — jest znacznie przydatniejszym narzędziem analizy
rozumowań. Zarówno rachunek zdań, jak i sylogistyka, są po prostu jej częściami.
Jednak KRK jest systemem złożonym i jego dokładna prezentacja przekracza
ramy tego kursu. W ostatnim temacie ograniczymy się tylko do bardzo krótkiego
wprowadzenia do języka KRK, natomiast resztę modułu przeznaczymy na prezentację
systemu Arystotelesa.

Mimo swoich ograniczeń, sylogistyka jest bardzo pożytecznym narzędziem. Przede
wszystkim jest to system znacznie prostszy od KRK i dlatego można go sobie
przyswoić nawet w ramach krótkiego kursu logiki. Poza tym w ramach sylogistyki
formalizuje się bardzo popularne rodzaje rozumowań, które często nam w życiu
towarzyszą. Dlatego, chociaż nie powinno się przeceniać znaczenia i zasięgu tego
systemu, to warto opanować jego zasady.

1.2. Zdania kategoryczne

Są to zdania proste podmiotowo-orzecznikowe, w których występują dwie
nazwy ogólne. Arystoteles dzielił je na 3 grupy, w zależności od siły orzekania.
Jeżeli stwierdzamy, że pewna relacja między podmiotem i orzeczeniem zachodzi
z konieczności, to jest to

zdanie apodyktyczne

. Jeżeli zachodzenie tej relacji stwierdzamy

jako coś możliwego, to jest to

zdanie problematyczne

. W przypadku braku takiej

kwalifikacji modalnej mamy do czynienia ze

zdaniem asertorycznym

.

W dalszym ciągu ograniczymy się do wykładu logiki zdań asertorycznych. Wyróżniamy
cztery rodzaje takich zdań. Poniżej podamy ich przykłady oraz tradycyjny sposób
formalizacji, w którym litery S i P to zmienne nazwowe, reprezentujące odpowiednio
podmiot (subiectum) i orzecznik (praedicatum) zdania kategorycznego.

5

Zdanie:

1.

Każdy pies jest zwierzęciem

to przykład

zdania ogólno-twierdzącego

, którego schemat zapiszemy następująco:

2.

SaP, gdzie S — pies, P — zwierzę, a — Każdy... jest...

Schemat

zdania ogólno-przeczącego

, np.:

3.

Żaden pies nie jest rybą

zapiszemy tak:

4.

SeP, gdzie S — pies, P — ryba, e — Żaden... nie jest...

Zdanie:

5.

Niektóre psy są inteligentne,

które reprezentuje tzw.

zdania szczegółowo-twierdzące

, zapiszemy:

6.

SiP, gdzie S — pies, P — inteligentny, i — Niektóre... są...

Natomiast

zdanie szczegółowo-przeczące

, np:

7.

Niektóre psy nie szczekają

zapiszemy tak:

8.

SoP, gdzie S — pies, P — stworzenie szczekające, o — Niektóre... nie są...

Ostatni przykład pokazuje, że wiele zdań w języku polskim wymaga drobnego
przeformułowania, aby uznać je za zdania kategoryczne w sensie ścisłym. Litery „a”,
„e”, „i”, „o” oznaczają specyficzne stałe logiczne rachunku nazw, których znaczenie
określa zarówno rodzaj kwantyfikacji występującej w zdaniu kategorycznym, jak
i rodzaj orzekania. Z tego względu zdania kategoryczne dzieli się według

ilości

i

jakości

. Według jakości wyróżniamy zdania twierdzące i przeczące, według ilości

— zdania ogólne i szczegółowe.

1.3. Prawdziwość zdań kategorycznych

Zastanówmy się nad warunkami prawdziwości zdań kategorycznych. Korzystając
z tego, że ekstensją dowolnej nazwy ogólnej jest niepusty zbiór, wprowadzimy
teoriomnogościową interpretację tych warunków. Symbole S i P oznaczać będą dalej
nie tylko nazwy występujące jako podmiot i orzecznik, ale również ich ekstensje.
a) SaP jest prawdziwe wtw, S ⊆ P, co jest równoważne stwierdzeniu, że S − P = ∅,
b) SeP jest prawdziwe wtw, S ∩ P = ∅,
c) SiP jest prawdziwe wtw, S ∩ P ≠ ∅,
d) SoP jest prawdziwe wtw, S − P ≠ ∅.

Jak widać, prawdziwość każdego zdania kategorycznego da się sprowadzić do tego,
czy pewien zbiór jest pusty, czy nie.

6

1.4. Reprezentacja graficzna

Powszechnie stosowanym i wygodnym sposobem sprawdzania poprawności
rozumowań zbudowanych ze zdań kategorycznych są różnego rodzaju diagramy. Do
analizy rozumowań sylogistycznych moglibyśmy np. zastosować diagramy Eulera,
jednak efektywniejszą metodą okazują się

diagramy Venna

.

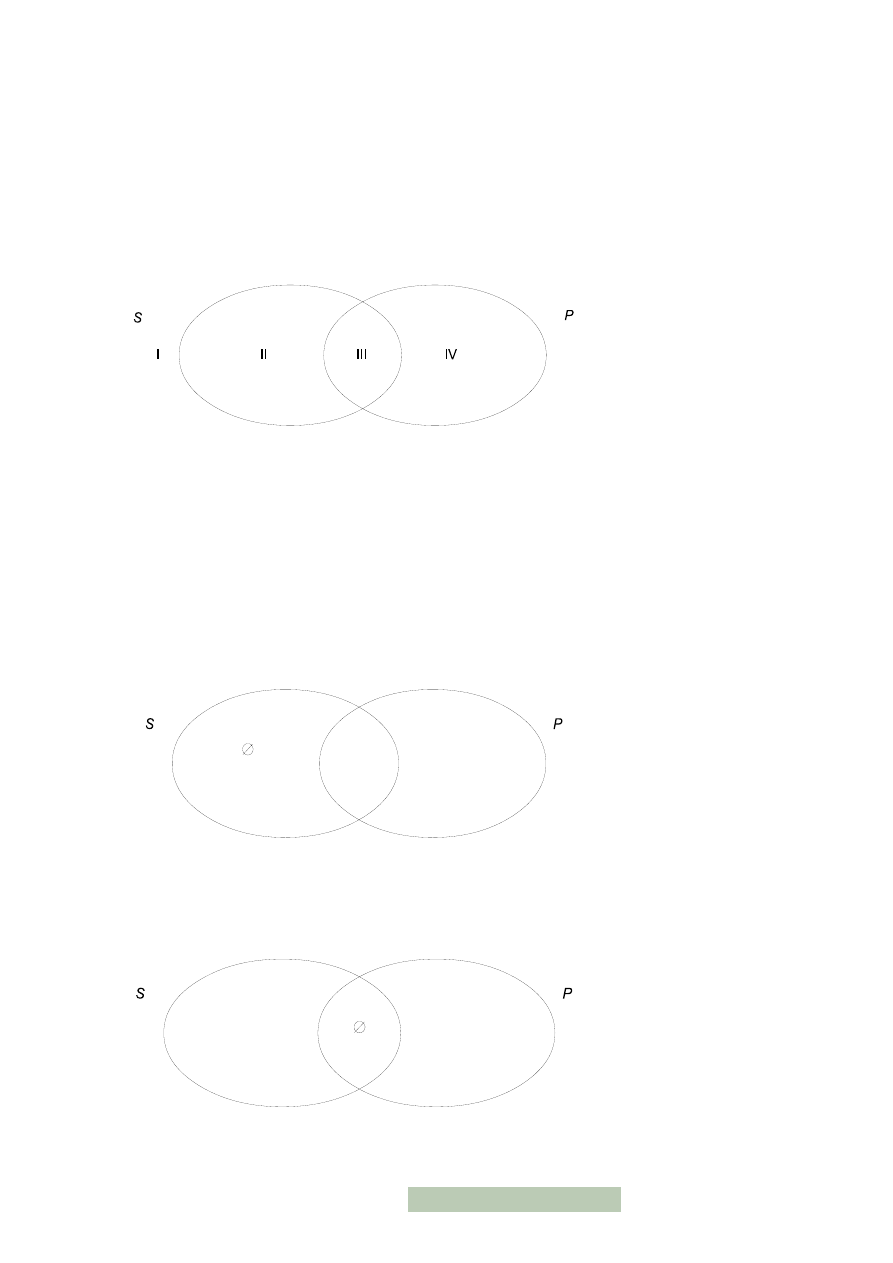
Diagram Venna dla dwóch zbiorów składa się z dwóch krzyżujących się okręgów:

Obszar I oznacza tu zbiór −S ∩ −P, II — S − P, III — S ∩ P, a IV — P − S. Problem
graficznej reprezentacji prawdziwości zdań kategorycznych sprowadza się zatem do
zaznaczenia na diagramie Venna pustości lub niepustości pewnego zbioru. Przyjmijmy,
że w przypadku niepustości, na danym obszarze postawimy symbol X, a w przypadku
pustości — ∅. Obszar, o którym nie mamy informacji, nie będzie zawierał żadnych
symboli. Zgodnie z tą konwencją prawdziwość zdań kategorycznych będą wyrażać
następujące diagramy:

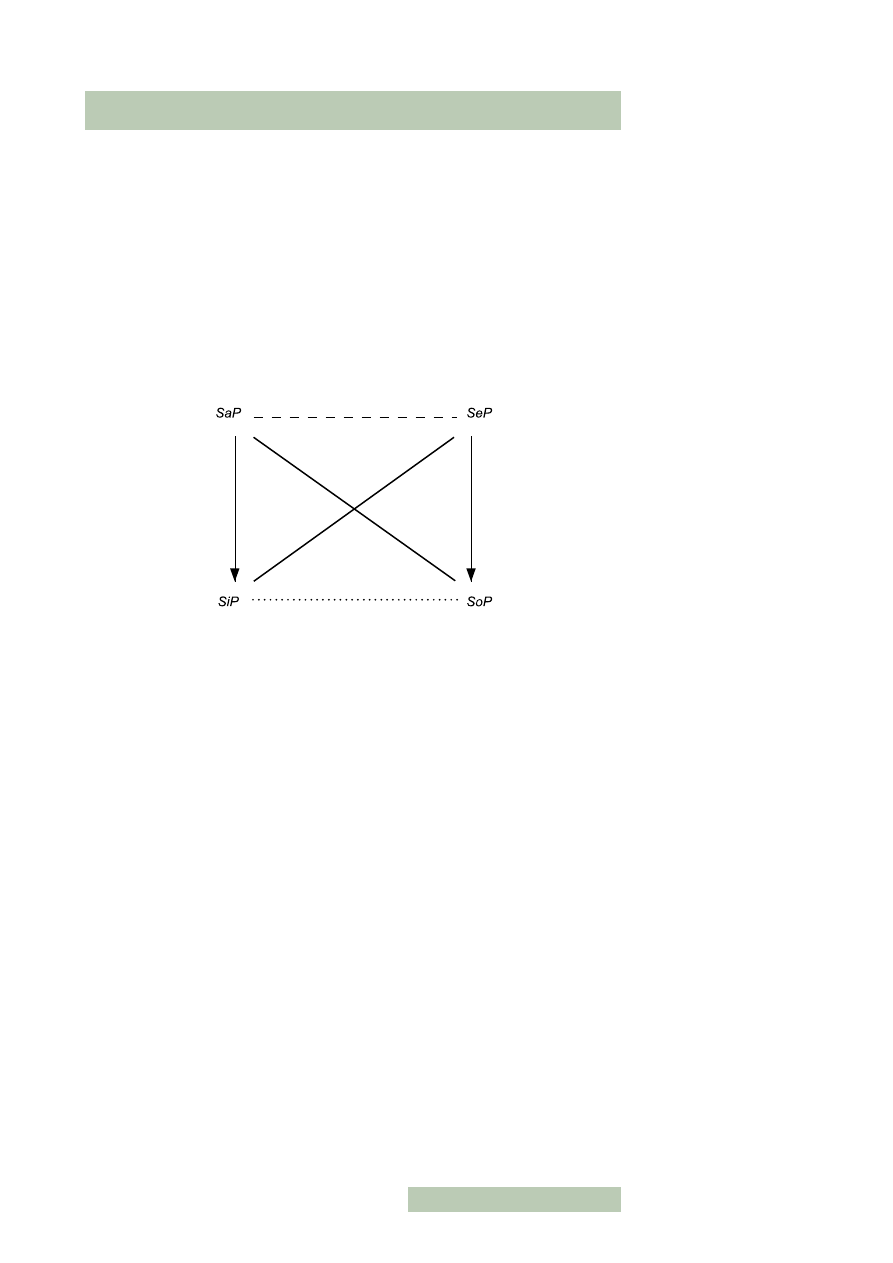
a)

SaP

b)

SeP

Rysunek 1

Rysunek 2

Rysunek 3

7

c)

SiP

d)

SoP

Rysunek 4

Rysunek 5

8

2. Wnioskowania bezpośrednie

2.1. Kwadrat logiczny

Zastanówmy się, jakie relacje logiczne zachodzą między różnymi zdaniami
kategorycznymi o tym samym podmiocie i orzeczniku. W średniowieczu dla lepszego
przedstawienia tych związków używano diagramu zwanego kwadratem logicznym.

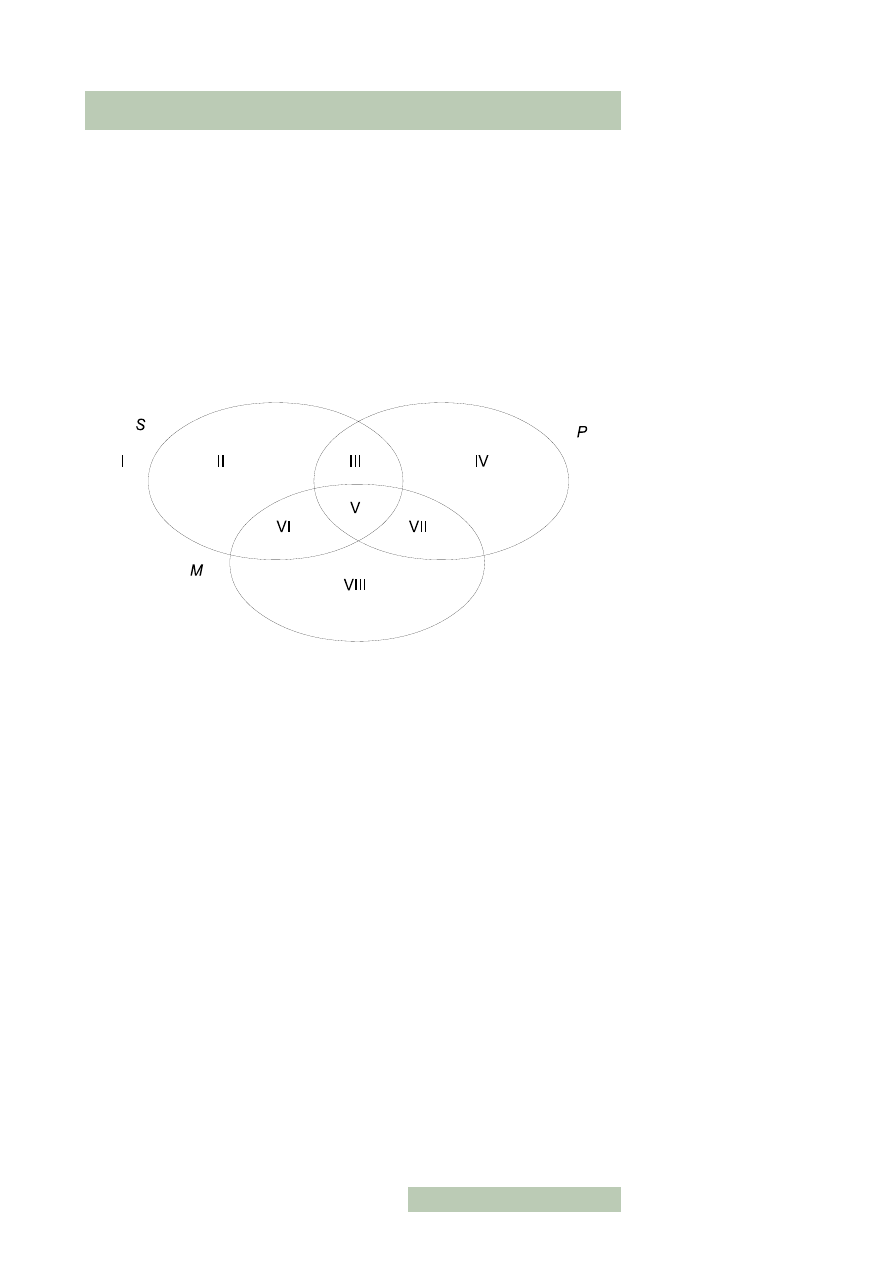
Najłatwiej zauważyć, jaka relacja zachodzi w pionie pomiędzy zdaniami ogóln-
ymi i szczegółowymi tej samej jakości. Jest to relacja wynikania, określana też w
logice tradycyjnej jako r e l a c j a p o d p o r z ą d k o w a n i a . Strzałki zaznaczają
kierunek tej relacji, tzn. ze zdania ogólnego wynika zdanie szczegółowe (jest mu
podporządkowane), ale nie odwrotnie.

Między zdaniami ogólnymi o różnej jakości (szczyt kwadratu) zachodzi relacja
wykluczania (sprzeczności), zwana w logice tradycyjnej r e l a c j ą p r z e c i w i e ń s t w a
i oznaczona linią przerywaną. Oznacza to, że choć zdania takie mogą być zarazem
fałszywe, to prawdziwe oba być nie mogą. Przykładowo, podstawienie S — ssak,
P — kręgowiec daje nam prawdziwość jednego ze zdań, a fałszywość drugiego.
Podstawienie S — Polak, P — pijak daje nam fałszywość obu zdań.

Dół kwadratu (linia kropkowana) to relacja dopełniania, zwana tradycyjnie r e l a c j ą
p o d p r z e c i w i e ń s t w a . Zatem dwa zdania szczegółowe o różnej jakości nie mogą
być zarazem fałszywe, choć oba mogą być prawdziwe. Przykładowo podstawienie
S — krowa, P — łaciata daje prawdziwość obu zdań. Podstawienie S — ssak,
P — kręgowiec daje nam prawdziwość jednego ze zdań a fałszywość drugiego.

Gruba linia łącząca zdania po przekątnej oznacza relację mocnej sprzeczności.
W dowolnej parze zdań o różnej jakości i ilości zawsze jedno będzie prawdziwe
a drugie fałszywe, choć możemy nie wiedzieć, które z nich jaką wartość logiczną
posiada.

Rysunek 6

9

2.2. Znaczenie zwrotu „niektóre”

Warto podkreślić, że zwrot „niektóre” używany jest tutaj w znaczeniu „co najmniej
jeden”, co oznacza, że zdanie szczegółowe jest prawdziwe również wtedy, gdy
wszystkie desygnaty podmiotu mają własność wyrażaną przez orzecznik (w zdaniach
twierdzących) lub jej nie mają (w zdaniach przeczących). Jest to istotne wyjaśnienie,
gdyż potocznie często zwrotu tego używamy w znaczeniu „pewne, ale nie
wszystkie”. W tym drugim znaczeniu nie moglibyśmy uznać np. zdania „Niektóre
ssaki są kręgowcami” za prawdziwe (jak to zrobiliśmy powyżej). Co więcej, przy
takim rozumieniu zwrotu „niektóre” nie zachodzi większość relacji logicznych
zaznaczonych na kwadracie logicznym.

2.3. Prawa kwadratu logicznego

Tradycyjny rachunek nazw jest systemem logicznym nadbudowanym nad rachunkiem
zdań. Oznacza to, że oprócz czterech nowych stałych logicznych, które budują zdania
proste (czyli kategoryczne) możemy używać również spójników KRZ do budowy
zdań złożonych. Skorzystamy z tego obecnie. Zachodzenie powyższych relacji
pozwala nam stwierdzić, że poniższe formuły są prawami logicznymi (tautologiami)
tradycyjnego rachunku nazw:

1. SaP → SiP
2. SeP → SoP
3. ¬SiP → ¬SaP
4. ¬SoP → ¬SeP
5. ¬(SaP ∧ SeP)
6. SaP → ¬SeP
7. SeP → ¬SaP
8. SiP ∨ SoP
9. ¬SiP → SoP

10. ¬SoP → SiP
11. SaP ↔ ¬SoP
12. SeP ↔ ¬SiP
13. SiP ↔ ¬SeP
14. SoP ↔ ¬SaP

Prawa 1–4 są pochodną wynikania; w szczególności 3 i 4 otrzymujemy z 1 i 2 przez
kontrapozycję. Prawa 5–7 są konsekwencją wykluczania zdań ogólnych, a 8–10
— dopełniania zdań szczegółowych. Ostatnie cztery wzory charakteryzują sprzeczność
mocną.

2.4. Wnioskowania bezpośrednie

Taką nazwą określa się w logice tradycyjnej proste schematy rozumowań z jednej
przesłanki, w których zarówno przesłanka, jak i wniosek są zdaniami kategorycznymi,
względnie ich negacjami.

10

Pamiętając o zależności między tautologicznymi implikacjami a schematami
poprawnych rozumowań, można z podanych wyżej tautologii uzyskać szereg takich
schematów. W szczególności prawa 11–14 dają podstawę do 8 schematów, np. z 11.
mamy dwa schematy o postaci: SaP / ¬SoP i ¬SoP / SaP. Tylko prawa 5. i 8. nie
uzasadniają żadnego schematu wnioskowań bezpośrednich.

Nie są to jedyne formy wnioskowania bezpośredniego uznawane w logice tradycyjnej.
Poniżej omówimy najważniejsze rodzaje pozostałych.

2.5. Konwersja

Jest to wnioskowanie, w którym dokonujemy przestawienia podmiotu i orzecznika.
Oddają to następujące schematy:

SaP / PiS

SiP / PiS

SeP / PeS

W przypadku SaP dodatkowo zmienia się ilość wniosku. Jest to tak zwana konwersja
z ograniczeniem. W pozostałych wypadkach mamy konwersję prostą.

Gdyby dla zdania SaP dopuścić konwersję prostą, to można by ze zdania „Każdy
pies jest drapieżnikiem” wywnioskować zdanie „Każdy drapieżnik jest psem”, co
uzasadnia konieczność dodatkowej zmiany we wniosku. Zdanie postaci SoP w ogóle
nie poddaje się konwersji, np. ze zdania „Niektórzy ludzie nie są politykami” wbrew
pozorom nie wynika zdanie „Niektórzy politycy nie są ludźmi”.

2.6. Negacja przynazwowa

W rozważanych rozumowaniach dopuszcza się również negację przynazwową, która
w języku naturalnym wyrażana jest często za pomocą prefiksów „nie-”, „a-”, „non-”,
„bez-”, dołączonych do zaprzeczanej nazwy. Tworzymy w ten sposób antonim
dla danej nazwy. Przykładowo: „niepospolity”, „anormalny”, „nonsensowny”,
„bezkręgowiec”. Oczywiście, nie zawsze fakt, że dana nazwa tak się zaczyna oznacza,
że mamy do czynienia z nazwą zaprzeczoną. Na przykład „alkoholik” to nie forma
zaprzeczona nazwy „lkoholik” a „absurd” to nie zaprzeczenie „bsurdu”.

Jeżeli w języku naturalnym nie występuje dla danej nazwy odpowiedni antonim,
zawsze możemy go wprowadzić sztucznie przez dodanie zwrotu „nie-”, przykładowo:
„pies”–„nie-pies”. Symbolicznie będziemy negację przynazwową zaznaczać, stawiając
apostrof za nazwą zaprzeczaną.

2.7. Obwersja

Jest to forma rozumowania, w której dokonuje się zmiana jakości przesłanki
z jednoczesnym zanegowaniem orzecznika. W przeciwieństwie do konwersji jest

11

to operacja uniwersalna, tzn. rezultat obwersji zawsze wynika z przesłanki, co daje
cztery schematy:

SaP / SeP’

SiP / SoP’

SeP / SaP’

SoP / SiP’

Przykładowo ze zdania „Niektórzy politycy nie są uczciwi” wynika przez obwersję
„Niektórzy politycy są nieuczciwi”.

2.8. Kontrapozycja

W rozumowaniu takim jednocześnie przestawiamy podmiot z orzecznikiem
i dokonujemy ich zanegowania, podobnie jak w KRZ, gdzie dokonuje się przestawienia
członów implikacji wraz z ich zanegowaniem. Poprawne są następujące formy:

SaP / P’aS’

SeP / P’oS’

SoP / P’oS’

W tym wypadku zdanie typu SeP wymaga kontrapozycji ograniczonej, tzn.
z jednoczesną zmianą ilości przesłanki, gdyż w przeciwnym wypadku można np.
ze zdania „Żaden owad nie jest kręgowcem” wywnioskować „Żaden bezkręgowiec
nie jest nie-owadem”, co jest oczywiście fałszem, gdyż do bezkręgowców należą nie
tylko owady. Zdania typu SiP nie poddają się kontrapozycji.

12

3. Sylogizmy

3.1. Wnioskowania pośrednie

Oprócz wnioskowań bezpośrednich, które są po prostu formą przekształcenia zdania
kategorycznego, w logice tradycyjnej rozważa się również wnioskowania z większej
ilości przesłanek, zwane wnioskowaniami pośrednimi. Szczególną rolę odgrywają
pewne formy rozumowań o dwóch przesłankach zwane sylogizmami.

Teoria sylogizmu obrosła w ciągu wieków skomplikowaną terminologią, którą
omówimy przy okazji podania jego definicji. Istnieje też wiele pomysłowych
metod sprawdzania poprawności sylogizmów, w szczególności metody graficzne.
W tym temacie omówimy dwie metody o charakterze pamięciowym, w następnym
pokażemy jak wykorzystać diagramy Venna, wprowadzone w pierwszym temacie.

3.2. Sylogizm

Jest to forma wnioskowania pośredniego, która składa się z trzech zdań
kategorycznych (dwie przesłanki), w których występują tylko trzy różne nazwy,
zwane t e r m i n a m i sylogizmu. Każdy termin występuje w sylogizmie tylko dwa
razy, a oba wystąpienia są w różnych zdaniach sylogizmu. Podmiot wniosku to
t e r m i n m n i e j s z y, jego orzecznik to t e r m i n w i ę k s z y, natomiast nazwa, która
występuje w obu przesłankach, to t e r m i n ś r e d n i (pośredniczący). Litery S i P
nadal będą oznaczać podmiot i orzecznik wniosku, natomiast M (od łac. medius)
oznaczać będzie termin średni.

Przesłanka zawierająca termin mniejszy to p r z e s ł a n k a m n i e j s z a , natomiast
przesłanka zawierająca termin większy to p r z e s ł a n k a w i ę k s z a . Przesłankę
większą zwykło się podawać jako pierwszą przesłankę sylogizmu. Pozwala to
dokonać pewnego uporządkowania możliwych form, gdyż z logicznego punktu
widzenia kolejność przesłanek nie ma żadnego znaczenia. Oto przykład rozumowania
sylogistycznego:

1.

Każdy pies jest drapieżnikiem. Każdy ratlerek jest psem. Zatem każdy ratlerek jest

drapieżnikiem.

Schemat tego rozumowania wygląda następująco:

2.

MaP, SaM / SaP

(M — pies, S — ratlerek, P — drapieżnik).

3.3. Tryby i figury

Schematy rozumowań sylogistycznych nazywa się

trybami sylogizmu

. Ze względu na

usytuowanie terminu średniego, wszystkie tryby można podzielić na cztery

figury

o schematach:

13

Fig. I

Fig. II

Fig. III

Fig. IV

M…P

P…M

M…P

P…M

S…M

S…M

M…S

M…S

S…P

S…P

S…P

S…P

Podstawiając w miejsce „...” symbol dowolnej stałej (tzn. a, e, i lub o), uzyskujemy
konkretny tryb danej figury. Można bez trudu wyliczyć, że wszystkich trybów jest
256 (4 x 4 x 4 x 4), jednak poprawnych jest znacznie mniej, bo tylko 24, po 6
w każdej figurze.

Ze względu na niewielką ilość, można po prostu wypisać wszystkie poprawne
tryby i nauczyć się ich na pamięć. Aby to ułatwić, w średniowieczu wprowadzono
dźwięczne nazwy dla poprawnych trybów, w których użyte samogłoski podawały,
jakie stałe występują w trzech kolejnych zdaniach trybu.

3.4. Tryby poprawne

W pierwszej figurze mamy tryby:
MaP, SaM / SaP MaP, SaM / SiP MeP, SaM / SeP
MeP, SaM / SoP MaP, SiM / SiP MeP, SiM / SoP
O nazwach: Barbara, Barbari, Celarent, Celaront, Darii, Ferio.

W drugiej:
PeM, SaM / SeP PeM, SaM / SoP PaM, SeM / SeP
PaM, SeM / SoP PeM, SiM / SoP PaM, SoM / SoP
O nazwach: Cesare, Cesaro, Camestres, Camestros, Festino, Baroco.

W trzeciej:
MaP, MaS / SiP MiP, MaS / SiP MaP, MiS / SiP
MeP, MaS / SoP MoP, MaS / SoP MeP, MiS / SoP
O nazwach: Darapti, Disamis, Datisi, Felapton, Bocardo, Ferison.

W czwartej:
PaM, MaS / SiP PaM, MeS / SeP PaM, MeS / SoP
PiM, MaS / SiP PeM, MaS / SoP PeM, MiS / SoP
O nazwach: Bramantip, Camenes, Camenos, Dimaris, Fesapo, Fresison.

3.5. Kryteria poprawności sylogizmu

Pamięciowe opanowanie schematów lub ich nazw nie jest jednak najlepszym sposobem
opanowania sylogistyki, zwłaszcza jeżeli na względzie mamy szybkie rozpoznawanie
rozumowań niepoprawnych. Analiza trybów poprawnych ujawnia bowiem szereg
prawidłowości, które proces sprawdzania sylogizmów czynią zadaniem wręcz
mechanicznym.

14

Oto one:
1. Obie przesłanki nie mogą być przeczące.
2. Obie przesłanki nie mogą być szczegółowe.
3. Jeżeli jedna z przesłanek jest przecząca, to wniosek też musi taki być.
4. Jeżeli jedna z przesłanek jest szczegółowa, to wniosek też musi taki być.
5. Termin środkowy musi być rozłożony przynajmniej w jednej przesłance.
6. Jeżeli termin jest rozłożony we wniosku, to musi być rozłożony w przesłance.

Aby zrozumieć dwa ostatnie warunki, musimy wyjaśnić, co to znaczy, że termin jest
rozłożony. Termin jest rozłożony wtedy, gdy używając go, mamy na myśli wszystkie
jego desygnaty. Warunek ten spełniają podmioty zdań ogólnych i orzeczniki zdań
przeczących. Stąd w SeP oba terminy są rozłożone, a w SiP żaden, natomiast w SaP
— S, a w SoP — P.

Każdy tryb poprawny spełnia wszystkie podane wyżej warunki, natomiast każdy
niepoprawny łamie co najmniej jeden z nich. Rozważmy następujący sylogizm:

3.

Żadna ryba nie jest gadem. Żaden ssak nie jest rybą. Zatem żaden ssak nie jest

gadem.

Rozumowanie jest niepoprawne, gdyż łamie 1. kryterium. Istotnie, w oparciu o jego
tryb (MeP, SeM / SeP) można zbudować rozumowanie falsyfikujące (kontrprzykład),
np.:

4.

Żadna ryba nie jest gadem. Żaden wąż nie jest rybą. Zatem żaden wąż nie jest

gadem.

Inny przykład:

5.

Każdy ssak jest kręgowcem. Każdy kot jest kręgowcem. Zatem każdy kot jest

ssakiem.

Tutaj złamane jest 5. kryterium, gdyż termin średni (kręgowiec) nie jest rozłożony
w żadnej przesłance. Aby otrzymać kontrprzykład, wystarczy np. za termin większy
(ssak) wstawić nazwę „ptak”.

3.6. Entymematy

Na zakończenie rozważmy jeszcze jeden przykład:

6.

Każdy tygrys jest ssakiem. Więc każdy tygrys jest kręgowcem.

Rozumowanie to intuicyjnie wydaje się poprawne, jednak nie jest ono ani
sylogizmem (tylko jedna przesłanka), ani wnioskowaniem bezpośrednim (trzy różne
nazwy). Po namyśle możemy jednak powyższe rozumowanie uznać za poprawny
entymemat, w którym pominięto, jako oczywistą, przesłankę większą „Każdy ssak
jest kręgowcem”. Po jej dołączeniu rozumowanie powyższe okazuje się kolejnym
reprezentantem trybu Barbara.

Analizując rozumowania sylogistyczne, musimy pamiętać, że często mogą one
występować w postaci entymematycznej, jednoprzesłankowej, przy założeniu
oczywistości twierdzenia ogólnego, będącego treścią pominiętej przesłanki.

15

4. Graficzne sprawdzanie sylogizmów

4.1. Diagram Venna dla trzech nazw

Zastosujemy teraz metodę diagramów Venna do sprawdzania poprawności
sylogizmów. W przypadku takich rozumowań pojawia się pewna trudność
dodatkowa, gdyż mamy wyrazić na diagramie ekstensje trzech terminów. Dlatego
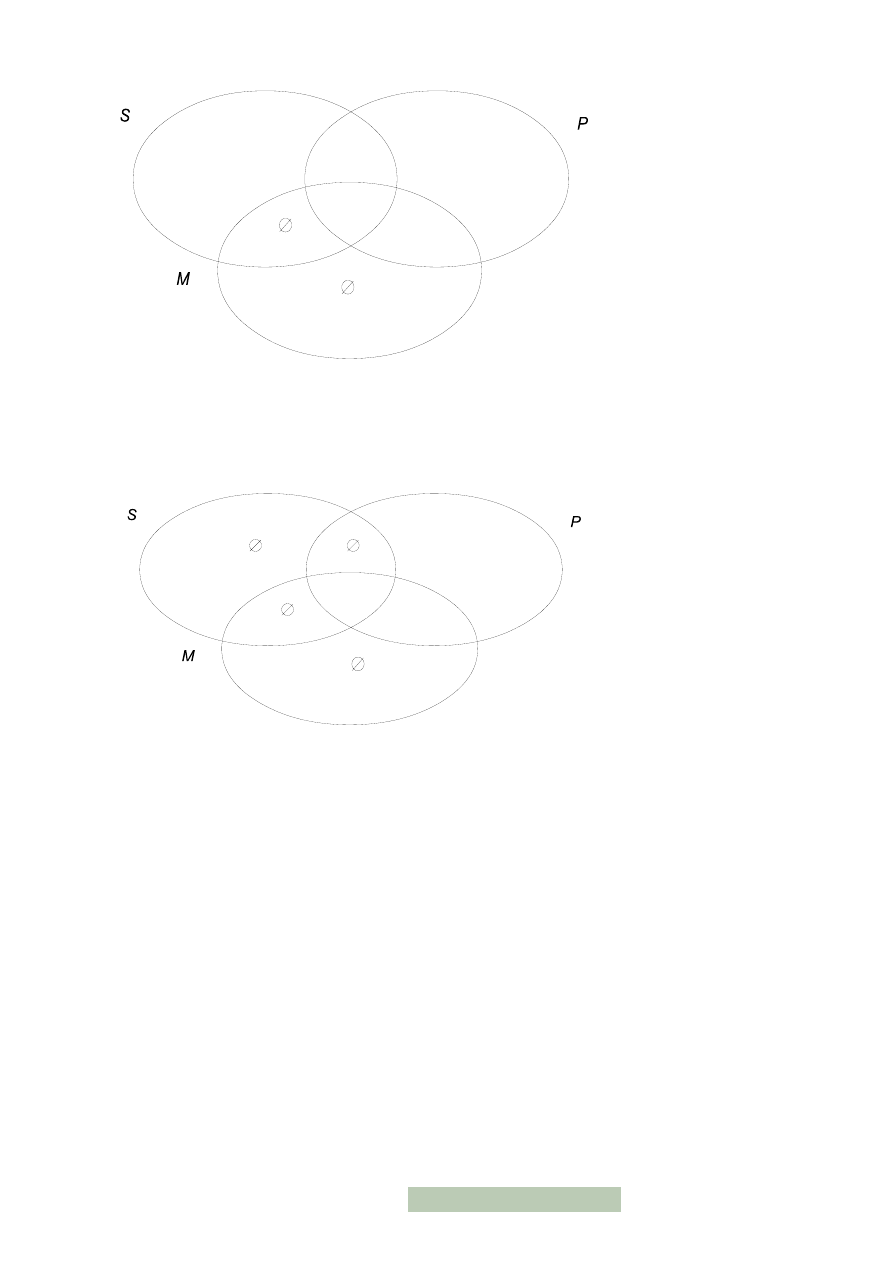
będziemy używać trzech krzyżujących się okręgów:

Kolejne obszary reprezentują tu: I — −S ∩ −P ∩ −M; II — (S − P) − M; III
— (S ∩ P) − M; IV — (P − S) − M; V — S ∩ P ∩ M; VI — (S ∩ M)−P; VII — (P

∩ M) − S; VIII — (M − S) − P.

Generalna zasada będzie taka: na diagramie zaznaczamy warunki prawdziwości obu
przesłanek i sprawdzamy, czy z diagramu można odczytać prawdziwość wniosku.
Jeżeli tak, to rozumowanie jest poprawne, w przeciwnym wypadku jest niepoprawne
i możemy postarać się o znalezienie przykładu falsyfikującego.

4.2. Tryb poprawny

Przeanalizujmy następujące rozumowanie:

1.

Każdy ssak jest kręgowcem. Każdy tygrys jest ssakiem. Zatem każdy tygrys jest

kręgowcem.

Jest to poprawny tryb Barbara (M — ssak, S — tygrys, P — kręgowiec). Po naniesieniu
na diagram warunków prawdziwości przesłanki większej, mamy następującą
sytuację:

Rysunek 7

16

Po uwzględnieniu dodatkowo prawdziwości drugiej przesłanki otrzymujemy
następujący diagram:

Jak widać, zarówno obszar II, jak i VI zostały zaznaczone jako puste, a to oznacza,
że nie ma takich desygnatów S (tygrysów), które nie należą również do ekstensji
P (kręgowców). Jeżeli jakieś desygnaty S w ogóle istnieją, to muszą się znajdować
na obszarze V, symbolizującym część wspólną wszystkich trzech zbiorów. Oznacza
to, że wniosek jest prawdziwy, przy założeniu prawdziwości przesłanek, a zatem
rozumowanie jest poprawne.

4.3. Tryb niepoprawny

W dalszym ciągu będziemy dla uproszczenia prawdziwość obu przesłanek zaznaczali
od razu na jednym diagramie. Zbadajmy rozumowanie:

2.

Żaden tygrys nie jest żabą. Żadna żaba nie jest wilkiem. Zatem żaden wilk nie jest

tygrysem.

Rysunek 8

Rysunek 9

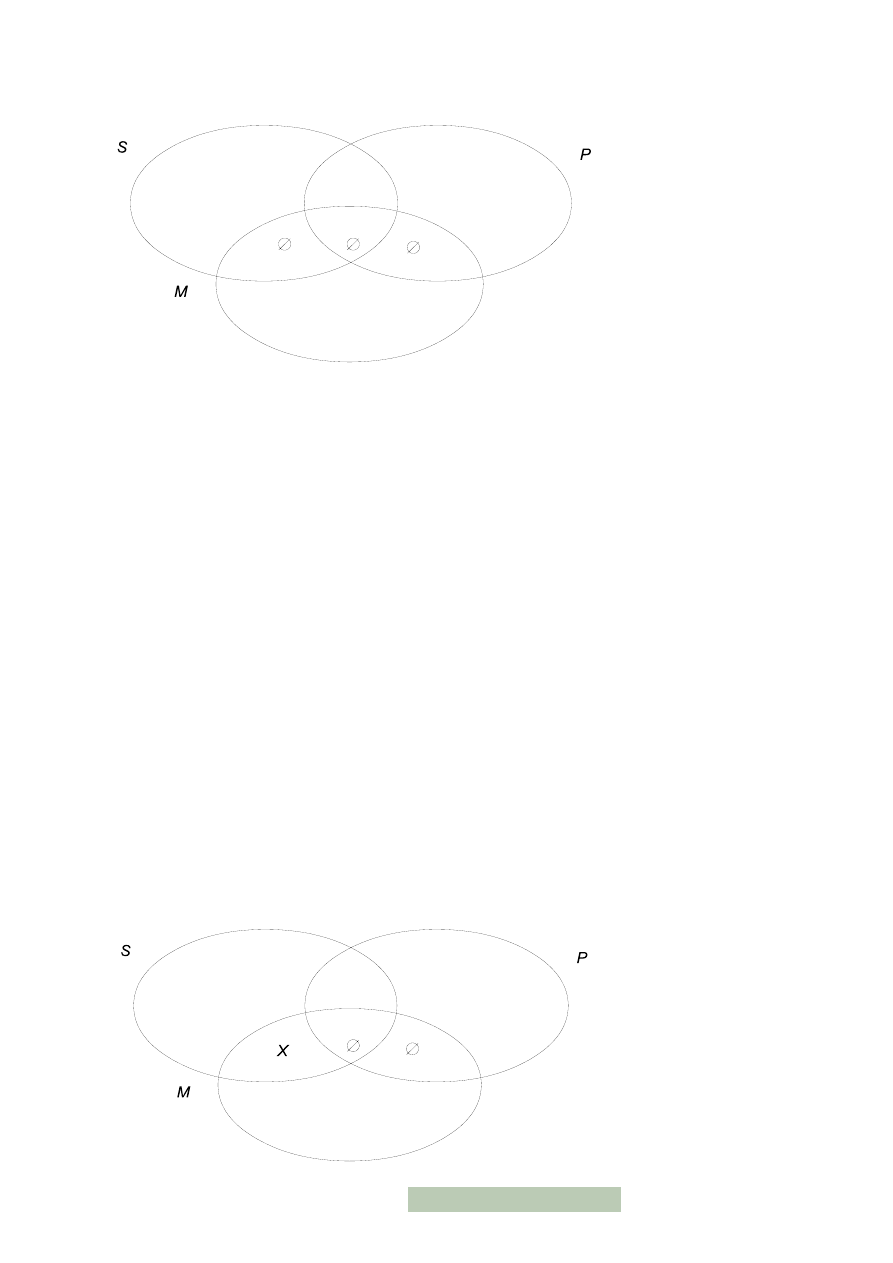
17

Ma ono następujący schemat: PeM, MeS / SeP, którego diagram ma postać:

Tutaj prawdziwość pierwszej przesłanki dała pustość obszaru V i VII, a drugiej VI
i ponownie V. Jednak aby wniosek był prawdziwy, musimy mieć gwarancję pustości
iloczynu S i P, który jest symbolizowany łącznie przez obszar V i III. Wprawdzie V
jest pusty, ale III nie jest wcale zaznaczony, więc jest możliwe, że reprezentuje zbiór
niepusty.

Rozumowanie powyższe nie jest zatem poprawne, gdyż struktura przesłanek nie
gwarantuje (przy ich prawdziwości) prawdziwości wniosku o zadanej strukturze.
Niepoprawność rozumowania pokazuje diagram, ale możemy też łatwo znaleźć
interpretację falsyfikującą. Rozważmy poniższe rozumowanie:

3.

Żaden tygrys nie jest żabą. Żadna żaba nie jest ssakiem. Zatem żaden ssak nie jest
tygrysem.

Reprezentuje ono taki sam tryb, ale wniosek jest ewidentnie fałszywy, chociaż
przesłanki prawdziwe. Warto też sprawdzić, które kryterium poprawności sylogizmu
zostało

złamane.

Kolejne przykłady podajemy od razu ze schematem i diagramem.

4.4. Przesłanki szczegółowe

4.

Żaden ssak nie jest rybą. Niektóre ryby są drapieżnikami. Zatem niektóre

drapieżniki nie są ssakami (PeM, MiS / SoP).

Rysunek 10

Rysunek 11

18

Rozumowanie jest poprawne, gdyż X stoi w obszarze VI, wskazując na niepustość
zbioru S poza obszarem zbioru P. Warto zauważyć, że zaznaczając prawdziwość
przesłanki drugiej, mamy do dyspozycji dwa obszary — V i VI. Jednak V jest już
zaznaczony jako zbiór pusty, zatem X możemy postawić tylko w obszarze VI. Dla
prawdziwości wniosku potrzeba, żeby X stało bądź w obszarze VI, bądź w obszarze
V — nie jest istotne, w którym. Przeanalizujmy kolejny przykład.

5.

Każdy ssak to kręgowiec. Niektóre kręgowce to drapieżniki. Więc niektóre

drapieżniki są ssakami (PaM, MiS / SiP).

Powyższy przykład może wydać się poprawny. Wniosek jest prawdziwy, przesłanki
również, ale to nie powinno już nikogo zwieść. Skoncentrujmy się na formie, a nie
na treści. Żeby wniosek był prawdziwy, X powinien stać w obszarze III lub V.
Pierwszy z nich jest wprawdzie pusty, ale V zawiera X. Zwróćmy jednak uwagę, że
X stoi także w obszarze VI. Zaznaczając prawdziwość drugiej przesłanki, mieliśmy
bowiem do dyspozycji oba te obszary. Inaczej niż w przykładzie 4., gdzie z dwóch
teoretycznie możliwych, jeden został wstępnie wykluczony przez prawdziwość
przesłanki większej.

To, że mieliśmy do dyspozycji dwa obszary, zaznaczyliśmy, łącząc oba X-y kreską.
Taką sytuację (dwa obszary, na których może znaleźć się X) interpretujemy jako
świadectwo niepoprawności trybu. Przesłanka będąca zdaniem szczegółowym
w takim przypadku może być prawdziwa na trzy różne sposoby:
a) kiedy zarówno obszar V, jak i VI są niepuste,
b) kiedy V jest niepuste, a VI puste,
c) kiedy V jest puste, a VI niepuste.

Łatwo zauważyć, że prawdziwość wniosku gwarantuje tylko przypadek a) i b). Jeżeli
zajdzie c), to wniosek jest fałszywy, mimo prawdziwości przesłanki.

A zatem w sytuacji, kiedy zaznaczając prawdziwość zdania szczegółowego, jesteśmy
zmuszeni postawić X na dwóch polach, sygnalizujemy to, łącząc je kreską. X
połączony kreską z innym X-em interpretujemy jako znak mówiący, że jest możliwe,
iż dany zbiór jest niepusty, ale nie jest tak w każdej sytuacji. A to oznacza, że jeżeli
wniosek też jest zdaniem szczegółowym i X stoi w miejscu, w którym gwarantuje
prawdziwość tego zdania, to bierzemy go pod uwagę tylko wtedy, gdy nie występuje
z kreską. W przeciwnym wypadku traktujemy rozumowanie jako niepoprawne. Kogo
nie przekonały powyższe wywody, niech zwróci uwagę na następujące rozumowanie
falsyfikujące analizowany tryb:

6.

Każdy ssak to kręgowiec. Niektóre kręgowce to ryby. Więc niektóre ryby to

ssaki.

Rysunek 12

19

4.5. Zaznaczanie istnienia w zdaniach ogólnych

Diagramy Venna pozwalają sprawdzić poprawność każdego trybu. Zaznaczmy
jednak, że w przypadku poprawnych trybów, w których obie przesłanki są ogólne
a wniosek szczegółowy (jest 9 takich trybów), należy dodatkowo zaznaczyć za
pomocą X niepustość jednego z terminów. Nie będziemy jednak szerzej objaśniać
tego problemu, zilustrujemy go tylko przykładem.

7.

Każdy tygrys jest drapieżnikiem. Każdy tygrys jest ssakiem. Zatem niektóre ssaki

są drapieżnikami (MaP, MaS / SiP).

Na diagramie nie ma krzyżyka ani w obszarze V, ani w III, a żeby wniosek był
prawdziwy, to jeden z nich powinien być niepusty. Jednak powyższe rozumowanie
jest poprawne (tryb Darapti). Otóż musimy pamiętać, że wszystkie terminy sylogizmu
są niepuste, a zatem — skoro trzy obszary M są zaznaczone jako puste — to mamy
prawo dostawić X w V, gdyż jest to na powyższym diagramie jedyny potencjalnie
niepusty obszar, który jest częścią zbioru M. Takie uzupełnienie diagramu gwarantuje
nam zarazem prawdziwość wniosku.

Rysunek 13

20

5. Język KRK

5.1. Ograniczenia logiki arystotelesowskiej

We wstępie do tego modułu wskazaliśmy na ograniczenia KRZ w analizie rozumowań
z języka potocznego. Rachunek nazw pozwala poszerzyć zakres analizy, ale tylko
w ograniczony sposób. Rozważmy następujące rozumowanie:

1.

Adam jest niższy od Bogdana. Bogdan jest niższy od Cezarego. Zatem Adam jest
niższy od Cezarego.

Rozumowanie to jest intuicyjnie poprawne, chociaż entymematyczne. Jednak nawet
po uzupełnieniu go przesłanką charakteryzującą relację „niższości” o postaci: „Jeżeli
ktoś jest niższy od drugiej osoby, a ta jest niższa od trzeciej, to i on jest niższy od tej
trzeciej”, nie jesteśmy w stanie wykazać jego poprawności. Nie jest to możliwe na
gruncie KRZ, gdyż brak tu spójników i poprawność rozumowania zależy od struktury
wewnętrznej zdań. Jednak w rachunku nazw też nie możemy tego zrobić, gdyż
rozumowanie to nie składa się ze zdań kategorycznych. Dopiero klasyczny rachunek
kwantyfikatorów (KRK) jest logiką wystarczającą do analizy takich rozumowań.

5.2. Nazwy i predykaty

W języku KRK też wyróżnia się nazwy i — podobnie jak w rachunku nazw
— kategorię tę rozumie się wąsko. Jednak podczas gdy w logice tradycyjnej za nazwy
uznawaliśmy jedynie nazwy ogólne, to w KRK za nazwy uznajemy tylko nazwy
jednostkowe, a nawet węziej — tylko nazwy indywidualne.

Nazwy te dzielimy na dwie grupy. S t a ł e n a z w o w e to nazwy o ustalonym
desygnacie, czyli imiona własne. Będziemy je oznaczać literami: a, b, c, d. Oprócz
stałych potrzebne są z m i e n n e n a z w o w e , które nie mają w danym kontekście
ustalonego znaczenia. Będziemy je oznaczać literami: x, y, z.

W języku KRK rozważamy funktory zdaniotwórcze od argumentów nazwowych
zwane predykatami. Dzielimy je na predykaty 1-argumentowe (kategorii z/n),
2-argumentowe (z/n, n), 3-argumentowe (z/n, n, n). Teoretycznie można też
wprowadzić predykaty o większej liczbie argumentów, ale zazwyczaj nie ma takiej
potrzeby. Przykładami predykatów są wyrażenia: „...biegnie”, „...jest wysoki”,
„...kocha...”, „...jest niższy od...”, „...leży między...a...”, gdzie za pomocą „...”
zaznaczyliśmy położenie i liczbę argumentów nazwowych dla danego predykatu.

Funkcją predykatów 1-argumentowych jest wyrażanie własności (cech)
obiektu, którego nazwa jest ich argumentem. Natomiast predykaty dwu-, trój-
i więcejargumentowe wyrażają relacje zachodzące między parami, trójkami,
... obiektów.

Zauważmy, że w języku KRK nazwy ogólne (np. „wysoki”) są traktowane jako
składnik predykatu, podobnie jak funktor „jest”, który w rachunku nazw był częścią
stałych logicznych (a, e, i, o).

21

5.3. Formuły atomowe

Predykaty oznaczać będziemy za pomocą liter od A do Z, w miarę możliwości
wybierając pierwszą literę odpowiedniego wyrażenia z języka polskiego. Argumenty
predykatu będziemy zawsze podawać na prawo od jego symbolu, w ustalonej
kolejności.

Zdania typu: „Adam biegnie” czy „Adam jest mężczyzną” zapiszemy jako proste
formuły atomowe: „Ba”, „Ma”. W przypadku obu zdań nie ma innej możliwości,
gdyż oba przypisują pewnemu obiektowi pewną własność. W szczególności w drugim
z nich mamy do czynienia z tzw. predykatywnym użyciem funktora „jest”, które
oznacza, że obiekt jest elementem pewnego zbioru. Weźmy pod uwagę zdanie:

2.

Adam czyta Kocią kołyskę.

Można je również potraktować jako formułę tego typu („Ca”), ale bardziej wskazane
jest potraktowanie go jako

formuły relacyjnej

o schemacie: „Cab”, gdzie „b” denotuje

tę konkretną powieść, a „C” dwuargumentowy predykat „...czyta...”.

W przypadku zdań relacyjnych najważniejszym problemem jest przestrzeganie
kolejności argumentów predykatu wobec możliwości pojawienia się różnych
form gramatycznych. Np. zdanie „Adam kocha Beatę” i „Beata jest kochana przez
Adama” należy wyrazić taką samą atomową formułą relacyjną Kab, gdzie K denotuje
„...kocha...”. Błędem jest zarówno użycie do każdego z tych zdań innego symbolu
predykatu, jak i przepisanie w drugim przypadku nazw argumentów w takiej
kolejności, jaką dyktuje zdanie.

5.4. Zdania proste a złożone

Osobny problem to wyrażanie w języku KRK c h a r a k t e r y s t y k z ł o ż o n y c h .

Rozważmy zdanie:

3.

Adam jest wysokim blondynem.

Należy je ująć jako koniunkcję dwóch zdań atomowych, czyli „Wa ∧ Ba”. Jak
widać, w języku KRK używamy spójników KRZ w standardowy sposób, po prostu
zamiast zmiennych zdaniowych występują formuły atomowe KRK. Podana przez nas
formalizacja 3. jest poprawna, gdyż zachowuje logiczne własności tego zdania, np.
z formuły tej wynika zarówno formuła „Wa”, jak i „Ba”. Analogicznie ze zdania 3.
wynika zarówno zdanie „Adam jest wysoki”, jak i „Adam jest blondynem”.

Z drugiej strony zdania:

4.

Adam jest niskim koszykarzem

nie możemy potraktować tak samo. Ktoś, kto jest niskim koszykarzem, ma np. 1,80 m
wzrostu, a to nie daje podstaw do uznania za prawdziwe zdania „Adam jest niski”.
Zdania 3. i 4. mają taką samą formę gramatyczną, ale inną

formę logiczną

. W 3.

o obiekcie orzeka się dwie niezależne charakterystyki, natomiast w 4. orzeka się
o nim jedną złożoną charakterystykę, w której „niski” stosuje się nie do Adama, ale
do dowolnego koszykarza. W związku z tym 4. należy zapisać jako formułę atomową,
np. „Na”. Konsekwencją tego jest niestety utrata pewnych logicznych własności
zdania 4., np. wynika z niego zdanie „Adam jest koszykarzem”, ale z formuły „Na”
nie wynika formuła „Ka” (gdzie „K” denotuje „...jest koszykarzem...”). Ważniejsze

22

jest jednak tutaj raczej to, że — na szczęście — formalizacja zdania „Adam jest niski”
(np. „Ma”) również nie będzie wynikała z „Na”.

5.5. Kwantyfikatory

Spójniki KRZ to nie jedyne stałe logiczne języka KRK. Gdyby tak było, to pod
pewnymi względami język ten byłby uboższy od języka rachunku nazw. Dopiero
dodanie kwantyfikatorów czyni z niego potężne narzędzie formalizacji. Wyróżniamy
dwa kwantyfikatory:
— o g ó l n y (który czytamy: „dla każdego...”) o symbolu ∀,
— s z c z e g ó ł o w y („dla pewnego...”, „istnieją takie, że...”) o symbolu ∃.

Oba kwantyfikatory będą występowały zawsze w połączeniu ze zmiennymi
nazwowymi, które mają wiązać (czyli do których się odnoszą) w danej formule
w następujący sposób: „∀x” (czytamy: „dla każdego x”), „∀xyz” (czytamy:
„dla każdego x, y, z”). Podobnie jak predykaty, stawiamy je z lewej strony zdań,
które poddawane są kwantyfikacji. Jeżeli zdanie kwantyfikowane jest złożone, to
dodatkowo bierzemy je w nawias, podobnie jak w przypadku negacji.

Wyrażenia z języka polskiego, dla których formalizacji można użyć kwantyfikatora
ogólnego to:

„każdy”, „wszystko”, „zawsze”, „wszędzie”,

natomiast formalizowane przez kwantyfikator szczegółowy to:

„pewne”, „niektóre”, „coś”, „istnieje”, „kiedyś”, „gdzieś”.

Łącząc kwantyfikator ogólny z negacją, można też formalizować zwroty typu:

„nie każdy”, „żaden”, „nigdy”, „nigdzie”.

Podejmując decyzję o użyciu kwantyfikatora, trzeba dobrze rozważyć, czy dane
wyrażenie wymaga formalizacji przez ogólny, czy szczegółowy kwantyfikator.
Przykładowo zdanie „Cokolwiek jest psem, jest zwierzęciem” jest zdaniem typu SaP
i wymaga użycia kwantyfikatora ogólnego (patrz niżej). Natomiast zdanie „Adam
czyta cokolwiek” wymaga raczej użycia kwantyfikatora szczegółowego, co zaraz
zademonstrujemy.

Zdania typu: „Coś jest ciężkie”, „Wszystko ma masę” wymagają użycia
kwantyfikatorów — odpowiednio: „∃xCx”, „∀xMx”. Zdania: „Wszystko jest
większe od czegoś” i „Coś jest większe od wszystkiego” zapiszemy odpowiednio:
„∀x∃yWxy”, „∃x∀yWxy”. Zdanie „Adam kogoś kocha” zapiszemy „∃xKax”
— w analogiczny sposób zapiszemy formę wspomnianego wyżej zdania „Adam czyta
cokolwiek”.

Są to proste przykłady kwantyfikacji zdań atomowych. Natomiast zdanie „Adam
czyta j a k ą ś książkę” jest już przykładem kwantyfikacji zdania złożonego, którą
zapiszemy: „∃x(Kx ∧ Cax)” (gdzie K denotuje „...jest książką”, a C — „...czyta...”).
Tutaj jesteśmy już zmuszeni do użycia dodatkowego predykatu kwalifikującego
zmienną kwantyfikowaną i zastosowania jakiegoś spójnika łączącego, zatem zdanie,
którego forma gramatyczna jest bardzo nieskomplikowana, okazuje się zdaniem
złożonym.

23

5.6. Zdania kategoryczne

W języku KRK bez problemu możemy formalizować zdania kategoryczne według
schematu:
SaP

oddamy przez ∀x(Sx → Px)

SeP

oddamy przez ∀x(Sx → ¬Px)

SiP

oddamy przez ∃x(Sx ∧ Px)

SoP

oddamy przez ∃x(Sx ∧ ¬Px)

Jak widać, zdania proste rachunku nazw są tutaj traktowane jako formuły złożone.
Co więcej, jeżeli chcemy dokładnie oddać znaczenie obu zdań ogólnych, należy je
jeszcze bardziej skomplikować. SaP należy zapisać jako ∀x(Sx → Px) ∧ ∃xSx, a SeP
jako ∀x(Sx → ¬Px) ∧ ∃xSx. W ten sposób dodatkowo informujemy o niepustości
nazwy S.

5.7. Relacje

Język KRK, który pozwala nam analizować strukturę wewnętrzną dowolnych zdań
a nie tylko zdań kategorycznych, pozwala sformalizować również rozumowanie
1., które zawiera zdania relacyjne. Jego zapis, po dodaniu dodatkowej przesłanki,
wygląda następująco:

5.

Nab, Nbc, ∀xyz[(Nxy ∧ Nyz) → Nxz] / Nac

Dodana przesłanka mówi o tym, że relacja wyrażana predykatem „...jest niższy od...”
jest

przechodnia

. Na gruncie KRK łatwo możemy potwierdzić nasze intuicje dotyczące

poprawności analizowanego rozumowania. Jeżeli w przesłance charakteryzującej
relację „N” odłączymy kwantyfikator, a za zmienne podstawimy stałe nazwowe
według schematu: x – a, y – b, z – c, to otrzymamy schemat:

6.

Nab, Nbc, (Nab ∧ Nbc) → Nac / Nac

Operacja odłączania kwantyfikatora i zamieniania zmiennych na stałe to przykład
poprawnej reguły wnioskowania KRK, której intuicyjny sens jest następujący: jeżeli coś
jest orzekane o wszystkich obiektach (danej kategorii), to można to orzec o każdym
konkretnie wybranym obiekcie. Otrzymany schemat można sprawdzić za pomocą
metody skróconej, co wykaże, że jeżeli przesłanki są prawdziwe, to wniosek też.

Korzystając z języka KRK, można wyrazić wiele innych interesujących własności
relacji dwuargumentowych, takich jak zwrotność czy symetria.

24

Bibliografia

1. Ajdukiewicz K., 1959: Zarys logiki, PZWS,Warszawa.
2. Arystoteles, 1990: Dzieła wszystkie, t. 1, PWN,Warszawa.
3. Borkowski L., 1976: Elementy logiki formalnej, PWN, Warszawa.
4. Bremer J., W., 2004: Wprowadzenie do logiki, Wydawnictwo WAM, Kraków.
5. Chodkowski T., Nieznański E., Świętorzecka K., Wójtowicz A., 2000: Elementy

logiki prawniczej, PWP Iuris, Warszawa.

6. Gumański L., 1990: Wprowadzenie w logikę współczesną, PWN, Warszawa.
7. Mill J., S., 1962: System logiki dedukcyjnej i indukcyjnej, t. I–II, PWN,

Warszawa.

8. Przybyłowski J., 2001: Logika z ogólną metodologią nauk, Wydawnictwo

Uniwersytetu Gdańskiego, Gdańsk.

9. Skarbek W., 2004: Logika dla humanistów, NWP, Piotrków Trybunalski.
10. Szymanek K., 2001: Sztuka argumentacji. Słownik terminologiczny, PWN,

Warszawa.

11. Tokarz M., 1984: Wprowadzenie do logiki, Uniwersytet Śląski, Katowice.
12. Trzęsicki K., 1996: Logika, nauka i sztuka, Temida, Białystok.
13. Wójcicki R., 2003: Wykłady z logiki z elementami teorii wiedzy, Scholar,

Warszawa.

14. Ziembiński Z., 1993: Logika praktyczna, PWN, Warszawa.

Bibliografia stron WWW

15. John Carroll University. Witryna internetowa.,
www.jcu.edu/philosophy/gensler, stan z 20.12.2005.

25

Słownik

Argumenty

— typowe sposoby uzasadniania poglądów stosowane w dyskusji. Ich

ocena dotyczy raczej skuteczności, nie zaś logicznej poprawności. Niektóre można
jednak zdecydowanie uznać za nieuczciwe sposoby przekonywania, toteż określa
się je często jako fortele (sztuczki) erystyczne i traktuje jako rodzaj błędnych
rozumowań. Do najbardziej znanych należą argumentum ad autoritatem (odwołanie
się do autorytetu, odwoływanie się do litości dyskutanta lub audytorium),
argumentum ad verecundiam (odwoływanie się do nieśmiałości dyskutanta),
argumentum ad vanitatem (odwoływanie się do próżności naszego rozmówcy),
argumentum ad hominem (odwołanie się do poglądów oponenta, aby wykorzystać
je dla własnych celów), argumentum ad personam (argumenty, w których poglądy
oponenta podważa się w sposób pośredni, wskazując, że jest to osoba nieuczciwa,
niemoralna, niekompetentna itp.), argumentum ad baculum (odwołanie się „do kija”,
do gróźb), argumentum ad misericordiam (odwoływanie się do litości dyskutanta
lub audytorium), argumentum ad populum (używanie rozmaitych chwytów
demagogicznych „pod publiczkę”, aby zyskać jej poparcie).

Błędy definicji

— błędy popełniane podczas definiowania. Wyróżnić można m.in. błąd

ignotum per ignotum (niezrozumiałe przez niezrozumiałe) oraz błąd idem per idem,
zwany też błędnym kołem (circulus vitiosus) w definicji. Tutaj dodatkowo występują
dwa typy — błędne koło bezpośrednie (ten sam termin w definiendum i definiensie
tej samej definicji) oraz błędne koło pośrednie, gdzie mamy do czynienia z ciągiem
definicji takim, że każda następna wyjaśnia pewien termin występujący w definiensie
poprzedniej, a w definiensie ostatniej pojawia się ponownie termin z definiendum
pierwszej definicji. Inne rodzaje błędów dotyczą niezgodności zakresów definiensa
i definiendum. Definicja jest za szeroka, gdy zakres definiendum jest podrzędny
względem zakresu definiensa, natomiast za wąska, gdy zakres definiendum jest
nadrzędny względem zakresu definiensa.Może też zachodzić krzyżowanie się zakresów
lub tzw. błąd kategorialny, gdy zakresy obu członów definicji są rozłączne.

Błędy logiczne

— różne rodzaje wykroczeń przeciwko regułom użycia języka,

powodujące zakłócenia w komunikacji, wynikające m.in. z wieloznaczności,
nieostrości, niedookreśloności, używania wyrażeń okazjonalnych, niezrozumiałych.
Typowym przykładem takiego błędu jest amfibologia, czyli wadliwa składnia
umożliwiająca różną interpretację tekstu.

Błędy rozumowań

— tradycyjnie dzieli się je na materialne (fałszywość przynajmniej

jednej przesłanki) i formalne (niepoprawny schemat rozumowania). Dodatkowo
wyróżnia się wiele szczególnych przypadków. Do najważniejszych należą ekwiwokacja
(użycie pewnego terminu w różnych znaczeniach w obrębie jednego rozumowania)
oraz logomachia (użycie pewnego terminu w różnych znaczeniach w dyskusji).

Błąd formalny

— brak wynikania w rozumowaniu, które przedstawia się jako

poprawne (niezawodne).

Błąd materialny

— fałszywość co najmniej jednej przesłanki w rozumowaniu.

Definicja

— językowy sposób wyjaśnienia znaczenia jakiegoś wyrażenia (definicja

nominalna) lub podanie charakterystyki przedmiotu (definicja realna). Definicja
składa się z trzech części: definiendum (część zawierająca termin definiowany),
łącznika definicyjnego (zwanego często spójką definicyjną) i definiensa (część
wyjaśniająca znaczenie). Ze względu na spełniane zadania wyróżnia się trzy

26

rodzaje definicji: definicje sprawozdawcze — inaczej słownikowe — które służą
do wyjaśniania, w jakim znaczeniu dane wyrażenie jest obecnie w pewnym języku
używane; definicje regulujące — które służą precyzacji znaczenia danego wyrażenia,
np. w przypadku nazw nieostrych podają propozycję uściślenia ich zakresu; definicje
projektujące — powstające wówczas, gdy pojawia się potrzeba nazwania nowego
zjawiska w danym języku.

Funkcje komunikacyjne

— ogół celów realizowanych przez użycie języka. Do funkcji

komunikacyjnych należą: funkcja ekspresywna (wyrażanie stanów wewnętrznych
użytkownika języka), funkcja perswazyjna (oddziaływanie na słuchacza), funkcja
fatyczna (utrzymywanie kontaktu między użytkownikami), funkcja opisowa
(przekazywanie informacji).

Indukcja

— ogólna nazwa klasy schematów rozumowania, z których większość jest

zawodna, ale często wykorzystywana w praktyce. Można tu wyróżnić: indukcję
eliminacyjną, indukcję enumeracyjną oraz indukcję matematyczną. Najpopularniejsza
(często zwana po prostu indukcją) jest indukcja enumeracyjna, czyli przez wyliczenie.
Na podstawie skończonej liczby przesłanek, które są zdaniami szczegółowymi,
dochodzi się do wniosku ogólnego. W indukcji eliminacyjnej stosuje się tzw. kanony,
czyli pewne dodatkowe schematy rozumowania. Należą do nich m.in. kanony:
jedynej zgodności i jedynej różnicy.

Języki sztuczne

— języki konstruowane do specjalnych celów, np. w logice do analizy

znaczenia wybranych wyrażeń. Charakteryzują się prostą i konsekwentną gramatyką,
a w semantyce brakiem wieloznaczności.

Kategoria syntaktyczna

— zbiór wyrażeń, które mogą być wzajemnie wymienialne bez

utraty składniowej spójności kontekstu, w którym ta wymiana się odbywa. Kategorie
syntaktyczne dzielimy na samodzielne (zdania i nazwy) oraz niesamodzielne
(funktory).

Klasyczny rachunek kwantyfikatorów (KRK)

— podstawowy rachunek logiczny, zwany

często po prostu logiką klasyczną (również rachunek predykatów, rachunek 1-go
rzędu, rachunek funkcyjny).

Klasyczny rachunek zdań (KRZ)

— elementarna część logiki klasycznej, w której jedyne

wyróżnione stałe logiczne to pewne spójniki ekstensjonalne.

Klasyfikacja odpowiedzi

— wśród wielu rodzajów możliwych odpowiedzi na różne

rodzaje pytań można wyróżnić odpowiedź właściwą — uzupełnienia pewnego
schematu, który sugeruje pytanie; odpowiedź częściową — zdanie, z którego nie
wynika żadna odpowiedź właściwa, ale które wyklucza niektóre spośród nich;
odpowiedź wyczerpującą — zdanie prawdziwe, z którego wynikają wszystkie
odpowiedzi właściwe i prawdziwe.

Kwadrat logiczny

— graficzny sposób prezentacji relacji logicznych zachodzących

między zdaniami kategorycznymi o tym samym podmiocie i orzeczniku.

Kwantyfikatory

— wyrażenia określające, czy chodzi o wszystkie elementy danego

zbioru (kwantyfikator ogólny), czy o ich część (kwantyfikator szczegółowy).
Kwantyfikator zawsze występuje wraz z symbolem zmiennej nazwowej, która jest
przez niego związana.

Operacja formalizacji tekstu

— przekład z języka naturalnego na język KRK lub inny

język sztuczny w celu wyeliminowania wieloznaczności. Poprawna formalizacja musi
zachować co najmniej warunki prawdziwości zdań tłumaczonych.

Podział logiczny

— jest to podstawowy zabieg porządkujący określoną dziedzinę

badań. Podział — aby był logiczny — musi spełniać warunek adekwatności (suma
zbiorów będących członami podziału musi dawać w rezultacie zbiór dzielony),

27

warunek rozłączności (zbiory będące członami podziału muszą być parami rozłączne),
warunek niepustości (każdy człon podziału musi coś zawierać). Skrzyżowanie różnych
podziałów to klasyfikacja, zaś uporządkowanie członów podziału to systematyzacja.

Pytania

— wypowiedzi, których zasadniczym celem jest zdobycie informacji. Składają

się zazwyczaj z partykuły pytajnej i tzw. datum questionis (danej pytania). Wyróżnić
można pytania otwarte i pytania zamknięte (pytania zamknięte dopełnienia, pytania
zamknięte rozstrzygnięcia).

Rachunek nazw (tradycyjny)

— system logiki stworzony przez Arystotelesa,

w którym analizuje się pewne formy rozumowań zachodzących pomiędzy zdaniami
kategorycznymi.

Reguły niezawodne

— schematy rozumowań, w których wniosek wynika z przesłanek,

np. modus ponendo ponens, sylogizm hipotetyczny, dylemat konstrukcyjny prosty.

Relacje logiczne

— zachodzą między zdaniami w sensie logicznym. Do najważniejszych

należy pięć niżej wymienionych:
— Z

2

w y n i k a z Z

1

wtw, „Jeżeli Z

1

, to Z

2

” jest zdaniem analitycznie prawdziwym.

— Z

1

i Z

2

są r ó w n o w a ż n e wtw, „Z

1

wtw, Z

2

” jest zdaniem analitycznie

prawdziwym.

— Z

1

i Z

2

w y k l u c z a j ą s i ę wtw, „Z

1

i Z

2

” jest zdaniem kontradyktorycznym.

— Z

1

i Z

2

d o p e ł n i a j ą s i ę wtw, „Z

1

lub Z

2

” jest zdaniem analitycznie

prawdziwym.

— Z

1

i Z

2

są s p r z e c z n e wtw, „Z

1

wtw, Z

2

” jest zdaniem kontradyktorycznym.

Relacje między zakresami nazw

— w przypadku nazw ogólnych można wyróżnić pięć

rodzajów relacji zachodzących między ich zakresami. Ekstensje dwóch nazw mogą:
— być r ó w n o w a ż n e (tożsame), gdy jest to ten sam zbiór, np. „kobieta”

i „niewiasta”,

— być w relacji p o d r z ę d n o ś c i (ostrego zawierania się), gdy każdy desygnat jednej

nazwy jest desygnatem drugiej, ale nie odwrotnie (ta druga nazwa jest wtedy
w relacji n a d r z ę d n o ś c i względem pierwszej), np. „ssak”, „kręgowiec”,

— w y k l u c z a ć s i ę (być rozłączne), gdy nie mają wspólnych desygnatów, np.

„piernik” i „wiatrak”,

— k r z y ż o w a ć s i ę , gdy mają jakieś desygnaty wspólne i każda z nich ma

desygnaty, które nie należą do zakresu drugiej, np. „ssak”, „drapieżnik”.

Rozumowanie

— jako czynność: proces psychiczny zmierzający do uznania pewnych

zdań (wniosków) na podstawie innych zdań (przesłanek); jako rezultat: tekst
językowy, w którym pewne zdania występują w funkcji przesłanek, a inne w funkcji
wniosków.

Rozumowanie entymematyczne

— rozumowanie, w którym pominięto przesłanki lub

uznano za oczywiste, lub zdania w oczywisty sposób z nich wynikające a prowadzące
do wniosku końcowego.

Rozumowanie poprawne (dedukcyjne, niezawodne)

— takie rozumowanie, w którym

pomiędzy przesłankami a wnioskiem zachodzi relacja wynikania.

Rozumowanie uprawdopodobniające

— rozumowanie, w którym nie zachodzi

wynikanie między przesłankami a wnioskiem, ale w którym prawdziwość przesłanek
zwiększa prawdopodobieństwo zachodzenia wniosku, np. różne formy indukcji czy
rozumowania przez analogię.

Semiotyka logiczna

— dział logiki zajmujący się badaniem systemów znakowych.

Dzieli się na syntaktykę, badającą reguły składni, semantykę, badającą relacje między
znakami i ich znaczeniem oraz pragmatykę, badającą relacje między znakami a ich
użytkownikami.

28

Semantyka KRZ

— (czyli teoria znaczenia języka) jest ekstensjonalna — oznacza to,

że nie uwzględnia się w niej formalnie sądów logicznych, a tylko wartości logiczne
zdań. Podstawowe jest tutaj pojęcie wartościowania zmiennych. Wartościowaniem
nazywamy dowolne odwzorowanie V ze zbioru zmiennych zdaniowych w zbiór
{1,0}. Definicje znaczenia spójników pokazują, w jaki sposób dane wartościowanie
należy poszerzyć na dowolną formułę złożoną.

Sprzeczność w KRZ

— zbiór formuł X jest sprzeczny wtw, nie istnieje wartościowanie,

przy którym wszystkie formuły z tego zbioru są prawdziwe.

Stałe logiczne

— są to wyróżnione wyrażenia, których znaczenie jest precyzyjnie

ustalone na gruncie semantyki danej logiki. W KRZ są to spójniki, czyli funktory
zdaniotwórcze: funktor negacji oraz dwuargumentowe funktory koniunkcji,
alternatywy, implikacji, równoważności.

Tautologia KRZ

— formuła, która jest prawdziwa przy każdym wartościowaniu

(prawda logiczna). Formuła, która przy każdym wartościowaniu jest fałszywa, to
kontrtautologia albo fałsz logiczny. Formuły, których wartość logiczna nie jest stała,
lecz zmienia się — w zależności od wartościowania — to formuły kontyngentne.
Przykłady tautologii KRZ:
— prawo wyłączonego środka p∨¬p,
— prawo (nie)sprzeczności ¬(p∧¬p),
— prawo tożsamości p → p (lub, w mocniejszej postaci p ↔ p),
— sylogizm hipotetyczny [(p → q) ∧ (q → r)] → (p → r),
— modus ponendo ponens [(p → q) ∧ p] → q.

Wynikanie w KRZ: ze zbioru X wynika p wtw, dla dowolnego wartościowania V,
przy którym V(X) = 1, to V(p) = 1.

Wnioskowania bezpośrednie

— reguły niezawodne, w których wniosek wyprowadza

się z jednej przesłanki (np. obwersja, konwersja, kontrapozycja).

Wnioskowania pośrednie (sylogizmy)

— reguły niezawodne, w których wniosek

wyprowadza się z dwóch przesłanek. W sylogizmie występują trzy różne terminy,
każdy po dwa razy w całym rozumowaniu ale tylko raz w danym zdaniu. Termin
występujący w obu przesłankach to termin średni, orzecznik wniosku to termin
większy a podmiot wniosku to termin mniejszy.

Wynikanie

— wniosek wynika z przesłanek wtw, jeżeli jest n i e m o ż l i w e , żeby

wszystkie przesłanki były prawdziwe, a wniosek fałszywy.

Zasada brzytwy Ockhama

— zasada nawołująca do tego, by nie mnożyć bytów bez

potrzeby.

Zasada dwuwartościowości

— każde zdanie (w sensie logicznym) posiada jedną

z dwóch wartości logicznych: jest prawdziwe lub fałszywe.

Zasada niesprzeczności

— żadne zdanie stwierdzające jakiś stan rzeczy nie może być

zarazem prawdziwe i fałszywe. Innymi słowy, nie jest możliwe, aby jakiś stan rzeczy
zachodził i nie zachodził zarazem.

Zasada racji dostatecznej

— zasada mówiąca, że dla każdego twierdzenia należy podać

wystarczające uzasadnienie, czyli dostateczną rację dla jego uznania.

Zasada życzliwej interpretacji

— taki sposób interpretowania tekstu w procesie

formalizacji, który stara się zachować logiczne relacje i własności (np. wynikanie
i niesprzeczność).

Zbiór uporządkowany

— zbiór, na którego elementy nałożono pewną relację

porządkującą. Dwa ważne rodzaje takich relacji to relacja częściowego porządku
i relacja liniowego porządku.

29

Zdania kategoryczne (asertoryczne)

— zdania podmiotowo-orzecznikowe, których

analizą zajmował się już Arystoteles, tworząc pierwszy system logiki. Wyróżniamy:
zdania ogólno-twierdzące (Każde S jest P — SaP), zdania ogólno-przeczące (Żadne
S nie jest P — SeP), zdania szczegółowo-twierdzące (Niektóre S są P — SiP), zdania
szczegółowo-przeczące (Niektóre S nie są P — SoP).

Znaczenie wyrażeń

— informacja przekazywana przez wyrażenie. Wyróżnia się dwa

rodzaje znaczenia:

ekstensję

(zakres, odniesienie, denotację),

intensję

(sens, treść).

W przypadku nazw ekstensją jest zbiór desygnatów nazwy (obiektów, do których
odnosi), a intensją zbiór cech desygnatów. W przypadku zdań ekstensją jest ich
wartość logiczna, a intensją sąd logiczny (komunikowany w zdaniu stan rzeczy).

30

Spis symboli

n — nazwa

z — zdanie

z/z — funktor zdaniotwórczy od jednego argumentu zdaniowego

z/z,z — funktor zdaniotwórczy od dwóch argumentów zdaniowych

z/n — funktor zdaniotwórczy od jednego argumentu nazwowego

z/n,n — funktor zdaniotwórczy od dwóch argumentów nazwowych

n/n — funktor nazwotwórczy od jednego argumentu nazwowego

n/n, n — funktor nazwotwórczy od dwóch argumentów zdaniowych

(z/n)/(z/n) — funktor funktorotwórczy (tworzy funktor o kategorii z/n) od jednego
argumentu funktorowego kategorii z/n

Z

1

, Z

2

— zdania oznajmujące

p, q, r, s, t — zmienne zdaniowe (dowolne zdania oznajmujące)

X — zbiór zdań

X / p — schemat rozumowania o przesłankach X i wniosku p ( X, zatem p)

¬p — negacja p (nieprawda, że p)

(p ∧ q) — koniunkcja p i q (p i q)

(p ∨ q) — alternatywa p i q (p lub q)

(p → q) — implikacja o poprzedniku p i następniku q (jeżeli p, to q)

(p ↔ q) — równoważność p i q (p wtedy i tylko wtedy, gdy q)

1 — symbol prawdy

0 — symbol fałszu

S — podmiot (subiectum) zdania kategorycznego

P — orzecznik (predicatum) zdania kategorycznego

T — termin średni

S’ — nazwa zaprzeczona (nie-S)

SaP — zdanie ogólno-twierdzące (Każde S jest P)

SeP — zdanie ogólno-przeczące (Żadne S nie jest P)

SiP — zdanie szczegółowo-twierdzące (Niektóre S są P)

SoP — zdanie szczegółowo-przeczące (Niektóre S nie są P)
∅ — zbiór pusty

S∪P — suma zbiorów S i P

S∩P — iloczyn (przekrój) zbiorów S i P

31

S−P — różnica zbiorów S i P

−S — dopełnienie zbioru S

S ⊆ P — relacja zawierania (S jest podzbiorem P)

a, b, c — stałe nazwowe

x, y, z — zmienne nazwowe

A – Z — predykaty
∀x — kwantyfikacja ogólna (duża, uniwersalna) zmiennej x (dla każdego x)
∃x — kwantyfikacja szczegółowa (mała, egzystencjalna) x (dla pewnego x)