Przemysław Mudryk, grupa 092 MAI
Akademia Marynarki Wojennej
Wydział Mechaniczno–Elektryczny
Instytut Elektrotechniki i Automatyki Okrętowej

Temat pracy dyplomowej inżynierskiej:

„Projekt stanowiska do badania regulatora PID”

WPROWADZENIE (definicja, rodzaje, cel pracy)
1. ANALIZA WŁASNOŚCI REGULATORÓW PID

1. Zasada regulacji PID
2. Charakterystyki czasowe i częstotliwościowe regulatora idealnego i rzeczywistego PID
3. Struktury realizacji praktycznych regulatorów PID
4. Metody doboru nastaw regulatora PID

1.

Metoda Zieglera-Nicholsa wyznaczania wzmocnienia krytycznego

2.

Metoda Zieglera-Nicholsa bazująca na odpowiedzi skokowej

2. OPIS SPRĘŻARKI GAZU FP SPOMAX DR JAKO OBIEKTU REGULACJI

1. Zasada działania sprężarki
2. Budowa sprężarki
3. Charakterystyki eksploatacyjne sprężarki

3. UKŁADU REGULACJI CIŚNIENIA SPRĘŻARKI Z REGULATOREM PID

1. Schemat blokowy układu regulacji
2. Wymagania dla układu regulacji
3. Charakterystyki układu rzeczywistego

4. STANOWISKO DO BADANIA REGULATORA PID SPRĘŻARKI GAZU

1. Opis stanowiska
2. Zadawanie nastaw rzeczywistych i wyznaczanie odpowiedzi skokowych regulatora PI
3. Zadawanie nastaw rzeczywistych i wyznaczanie odpowiedzi skokowych regulatora PD
4. Zadawanie nastaw rzeczywistych i wyznaczanie odpowiedzi skokowych regulatora PID p
5. Porównanie charakterystyk rzeczywistych i odpowiedzi skokowych badanych regulatorów

ZAKOŃCZENIE (wnioski końcowe)

Literatura:
1. Gierusz W.: Laboratorium podstaw automatyki. Wyd. Akademii Morskiej w Gdyni, Gdynia,

2010.

Brzózka J.: Regulatory i układy automatyki. Wyd. MIKOM, Warszawa, 2003.

Wprowadzenie

1

Zarys historyczny

za początki automatyki przemysłowej uważa się rok 1784 , kiedy

James Watt opatentował odśrodkowy regulator do stabilizacji

prędkości obrotowej silników parowych W roku 1820 zastosowano regulator cienienia gazu w

sieci gazowej służącej do oświetlania ulic dużych miast. Rok 1830 wynalezienie bimetalicznego

regulatora temperatury.

Okres poprzedzający wybuch I wojny światowej był sprzysięgający do rozwoju automatycznej

regulacji

- 1907 firma C.J. Opracowała Tagliabue pneumatyczny, regulator temperatury

na obiekcie pasteryzacji mleka.

w roku 1912 przyznano nagrodę Nobla G. Dalenowi

za skonstruowanie w 1907 r. układu automatycznej regulacji wielkości płomienia

i częstotliwości jego pulsacji w palnikach acetylenowych stosowanych w bojach

świetlnych i latarniach morskich.

W tym czasie nastąpił dynamiczny rozwój serwomechanizmów hydraulicznych przeznaczonych do

sterowania działami okrętowymi oraz regulatorów kursu statku i torped.

Okres dwudziestolecia międzywojennego przyniósł pierwszy regulator PID dzięki pracy N.

Minorskiego który zaimplementował go do na statek New Mexico Marynarki Wojennej USA.

Regulator odpowiedzialny był za sterowanie kursem statku.

W latach dwudziestych XX w. dostępne były dwustawne regulatory elektryczne a w laboratorium

regulatory PI wykorzystujące silniki dające efekt całkowania. W tym okresie były powszechnie

wykorzystywane regulatory pneumatyczne, zapewniające szybkie działanie dwustawne i tylko

wąski zakres działania proporcjonalnego (od 5 do 7% zakresu pełnej skali). Pneumatyczny

regulator PI został wyprodukowany przez firmę Foxboro we wrześniu 1931 r.

Był to regulator Model 10 Stabilog. Prace Ralph'a Clarridge nad działaniem różniczkującym w

regulator pneumatycznych zaowocowały pojawienie się handlowych wersji regulatorów PID

produkowanych przez firmy Taylor i Foxboro

Pod koniec lat dwudziestych XX wieku Vannevar Bush z MIT (Massachusetts

Institute of Technology) realizował prace badawcze nad technicznym sposobem do

rozwiązywania równań różniczkowych , co zaowocowało wprowadzeniem na rynek coraz

doskonalszych regulatorów.

W czsie II wojny światowej trwały intensywne prace nad regulatorami pneumatycznymi oraz

2

elektro- elektronicznymi. Większość z nich dotarła na rynek po zakończeniu działań wojennych ze

względu na tajemnice wojskową. W 1945 r. A.J. Young opisał już sześć elektronicznych

regulatorów PID różnych firm (Evershed &

Vignolles n Wielka Brytania; Hartman & Braun oraz Schoppe & Faeser n Niemcy;

Leeds & Northrup Manning, Maxwell & Moore, The Swartwout Company n USA).

W roku 1957 G.P.L. Wiliams z firmy George Kent Company zakomunikował

o realizacji dodatkowych funkcji w elektronicznych regulatorach PID, takich jak:

dodawanie, mnożenie, podnoszenie do kwadratu.

W roku 1959 firma Foxboro wyprodukowała w pełni tranzystorowy, przemysłowy

regulator PID.

Lata 60 to czas kiedy zaczęto wprowadzać do sterowania procesami produkcyjnymi komputery.

1970 r. to rozwój sterowania cyfrowego zwiększa się liczba komputerów z ok. 5000 w 1970 r. do

50 000 w roku 1975.

Okres lat osiemdziesiatych to prace badawcze nad układami opartymi na sztucznych sieciach

neuronowych w latach 90 tych uczenia sieci neuronowych zastosowano algorytmy genetyczne i

strategie ewolucyjne.

Badania nad sieciami neuronowymi pozwoliły zastosować ich efekty do wielowymiarowych

regulatorów rozmytych, ich strojenia i adaptacji nastaw.

Koniec XX wieku to przede wszystkim zastosowanie regulatorów cyfrowych, które powoli

wypierały regulatory analogowe. Dużą role odegrała także informatyka w automatyce, dzięki tej

dyscyplinie można było pracować w sieci wymieniać informację z dużą prędkością. Rozwój

języków programowania, systemów operacyjnych dał nieograniczone możliwości rozwoju

regulatorów i sterowników.

3

1. ANALIZA WŁASNOŚCI REGULATORÓW PID

1.1 Zasada regulacji PID

Regulator to urządzenie, które w momencie odchylenia sygnału regulowanego od sygnału

zadanego powoduje, za pośrednictwem oddziaływania na obiekt regulacji, powrót przebiegu

sygnału regulowanego do przebiegu zgodnego z sygnałem zadanym. Sygnałem wejściowym

regulatora jest błąd regulacji, a sygnałem wyjściowym - sterowanie oddziaływające na obiekt

regulacji. Zależność sterowania od sygnału błędu regulacji jest algorytmem liniowym

Ze względu na własności dynamiczne rozróżnia się cztery rodzaje regulatorów liniowych:
• proporcjonalne (typu P),
• proporcjonalno-całkujące (typu PI),
• proporcjonalno-różniczkujące (typu PD),
proporcjonalno-całkująco-różniczkujące (typu PID)

Regulator typu P jest członem proporcjonalnym,pozbawionym inercji, którego zastosowanie
zmniejsza uchyb ustalony wraz ze wzrostem wzmocnienia kp (uchyb ustalony jest odwrotnie
proporcjonalny do współczynnika wzmocnienia),

zależność sygnału sterującego od błędu regulacji można opisać

u t=k

p

e t

Postać operatorowa

U  s=k

p

E  s

zatem

U s 

E s 

=

k

p

transmitancja regulatora

G

r



s=k

p

odpowiedz skokowa regulatora wykres

4

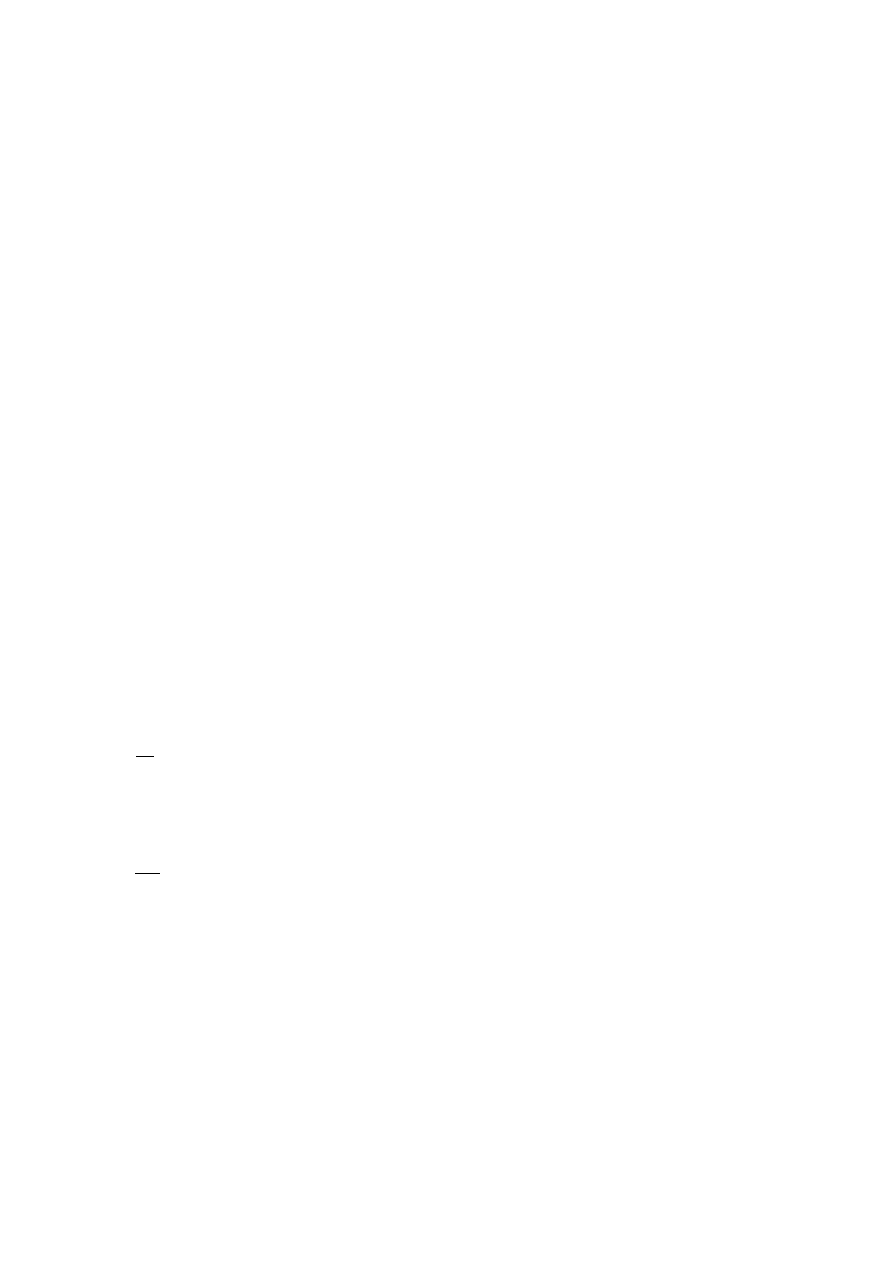
Regulator typu I z członem całkującym, właściwości pozwalają sprowadzić uchyb regulacji do

zera, jednak w stosunku do regulatora typu P wpływa to na wydłużenie czasu regulacji - sygnał

wyjściowy przyjmie wartości równe sygnałowi sterującemu u(t) z regulatora typu P po upływie

czasu stałej czasowej całkowania T

i

(s)

Właściwości całkujące sprawią iż sygnał sterujący u (t) czyli sygnał wyjściowy regulatora,

będzie zmieniał się tak długo, aż uchyb przyjmie wartość równą zeru.

Idealny regulator całkujący będzie charakteryzował się tym, iż sygnał wyjściowy u(t) jest

jest proporcjonalny do całki sygnału wejściowego e(t) zgodnie ze wzorem

u t=

1

T

i

∫

0

t

e dt 

T

i

czas całkowania

Transmitancja regulatora ma postać

G

I



s 

1

sT

i

Odpowiedz skokowa wykres

5

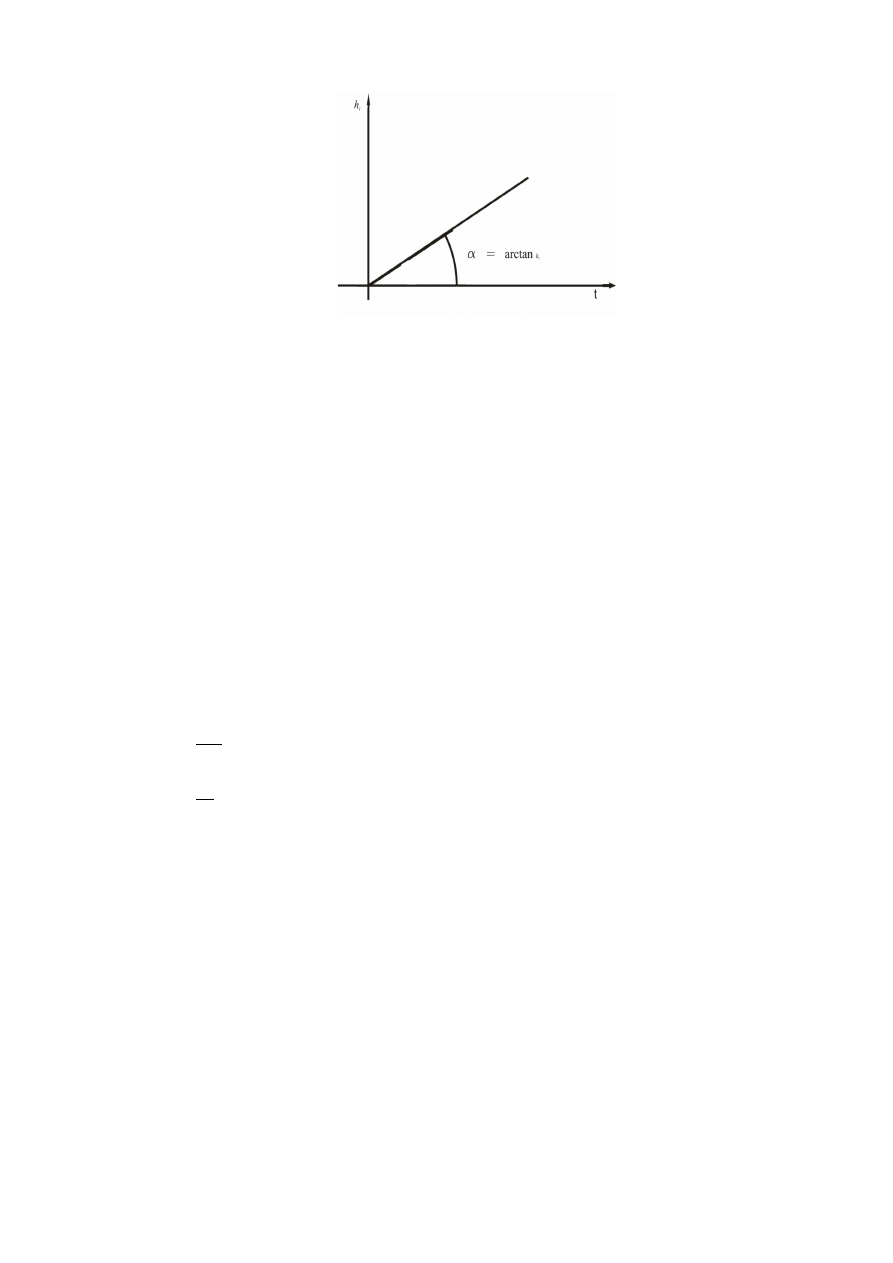
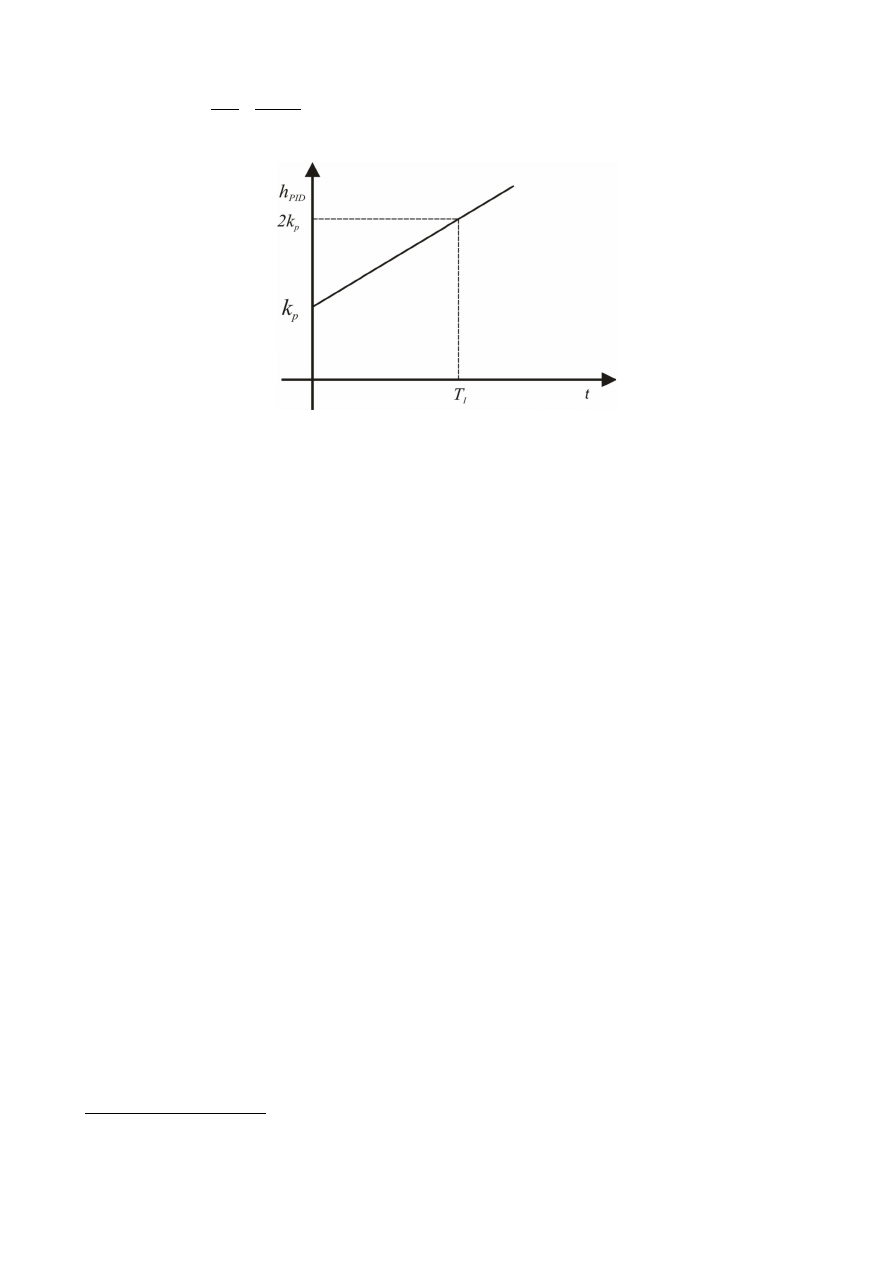
Regulator typu PI to połączenie właściwości dwóch poprzednich. Ma za zadanie sprowadzenie

uchybu do zera i skrócenie czasu regulacji, jednak ze względu na właściwości całkujące będzie on

i tak dłuższy od czasu regulacji w układzie z regulatorem typu P.

Stała czasowa elementu całkującego regulatora PI nazywa się stałą zdwojenia, ponieważ

przy skokowej zmianie uchybu po upływie czasu T

1

sygnał sterujący osiągnie dwukrotnie większą

wartość niż w regulatorze typu P.

Charakterystyka Logarytmiczna modułu wskazuje , że warunkiem zerowego uchybu ustalonego

jest, aby moduł transmitancji regulatora przy częstotliwości bliskiej zeru dążył do nieskończoności.

Transmitancja i odpowiedź skokowa na wymuszenie przedstawia się następująco

G

r



s=k

p



1

1

sT

i



u t=k

p

e 1

t

T

i



gdzie

k

p

współczynnik wzmocnienia

2k

P

Stała zdwojenia

T

i

stała zdwojenia –stała całkowania

6

1. Rysunek: Odpowiedź skokowa reg.I

Opowiedz skokowa

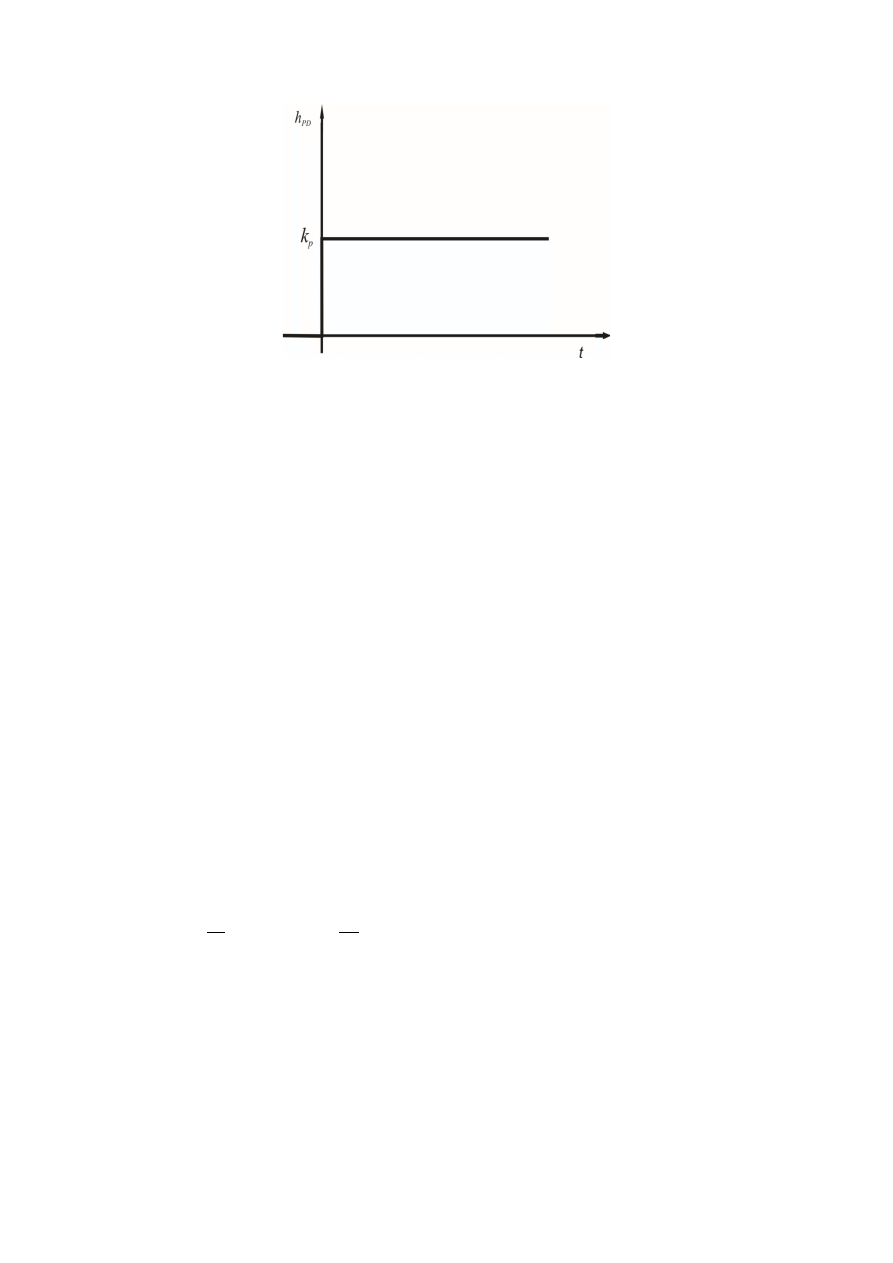
W idealnym regulatorze PD sygnał wyjściowy u(t) jest proporcjonalny do sygnału wejściowego

e(t) oraz jego różniczki

de t

dt

Regulator typu PD ze względu na brak członu całkującego nie zapewnia sprowadzenia uchybu do

zera. Ponadto dziabnie D nie zapewnia likwidacji uchybu ma tylko go korygować. T

d

czas

wyprzedzenia to czas. jaki musi upłynąć, aby po wystąpieniu uchybu narastającego liniowo sygnał

e(t) zrównał się z sygnałem wyjściowym z regulatora u(t)

równanie regulatora PD ma postać

u t=k

p

[

e t T

d

de

dt

]

k

p –

wzmocnienie regulatora

T

d

czas wyprzedzenia ( czas różniczkowania )

odpowiedz na skok jednostkowy

h t=k

p

[

1tT

d

d 1t 

dt

]

h t=k

p

[

1tT

d

 

t]

Transmitancja ma postać

G

PD

=

k

p

[

1T

d

s ]

7

2. Rysunek: Odpowiedź skokowa reg.
PI

Odpowiedz skokowa

Regulator typu PID stanowi najbardziej uniwersalny typ regulatora, który przy odpowiednio dużym

dozwolonym zakresie zmian parametrów umożliwia sterowanie różnymi typami obiektów.

Pozwala on połączyć zalety regulatorów PI oraz PD, umożliwiając uzyskanie krótkiego czasu

narastania i regulacji, małego prze regulowania i zerowego uchybu ustalonego.

Regulator typu PID (rzeczywisty) Podobnie jak w przypadku regulatora PD człon różniczkujący

został zastąpiony członem różniczkującym z inercją, co skutkuje ograniczeniem wartości modułu

dla częstotliwości dążącej do nieskończoności, przy zachowaniu właściwości regulatora typu PID z

idealnym różniczkowaniem.

Regulator PID z idealnym różniczkowaniem ma trzy parametry: kp, T. oraz Tj, dzięki czemu, z

uwagi na możliwość spełnienia wielu wymagań, jest najczęściej stosowanym regulatorem.

Równanie idealnego PID

u t=k

p



e t

1

T

i

∫

0

1

e  d T

d

de

dt



Gdzie
k

p

współczynnik wzmocnienia

T

i

czas całkowania (stała zdwojenia )

T

d

czas różniczkowania ( czas wyprzedzania )

Transmitancja regulatora PID ma postać

8

3. Rysunek: Odpowiedz regul. typu PD

G

PID



s =k

p



1

1

sT

c



sT

d

1sT



Odpowiedz skokowa

1.2 Charakterystyki czasowe i częstotliwościowe regulatora idealnego i rzeczywistego

PID

Transmitancja operatorowa jest bardzo wygodna dla analizy pracy liniowych układów i

dlatego jest powszechnie stosowana. Umożliwia ona również przedstawienie zasadniczych cech

układów w postaci graficznej, pozwalającej na pierwszy rzut oka ocenić właściwości dynamiczne.

Biorąc pod uwagę dziedzinę, w jakiej przedstawia się te właściwości, można wyróżnić:

•

charakterystyki czasowe

•

charakterystyki częstotliwościowe.

Elementy liniowe automatyki zazwyczaj rozważane są w dziedzinie czasu, czyli interesowała na

odpowiedz układu na skok jednostkowy jeżeli na element linowy podamy sygnał harmoniczny

Charakterystyki czasowe dają możliwość (w odniesieniu do układów jednowymiarowych)

bezpośredniej oceny układu, ponieważ charakterystyka czasowa jest przebiegiem w czasie

odpowiedzi układu dynamicznego y(t) na określone wymuszenie x(t).

Najczęściej stosowanymi wymuszeniami są:

1

−

odpowiedź na skok jednostkowy 1(t) mamy wtedy do czynienia z charakterystyką czasową

h(t)

−

odpowiedź na impuls Diraca δ( t) mamy wtedy do czynienia z charakterystyką impulsową

g(t)

1 Charakterystyki Czasowe i Częstotliwościowe Układów Automatyki WAT Warszawa 2004r

9

4. Rysunek: Odpowiedź skokowa reg. PID

w obydwóch przypadkach muszą być spełnione warunki początkowe

0 dla t< 0

x(t) = 1(t) = 1 dla t ≥ 0

0 dla t≠ 0

x(t) = g(t) =

∞ dla t= 0

Charakterystyki częstotliwościowe

Jeżeli na wejście układu linowego podamy sygnał harmoniczny z zaleznością x(t) = A

1

(ω) sin(ωt)

to otrzymamy na wyjściu także sygnał harmoniczny y(t) = A

2

(ω) sin(ωt)

Wyróżnia się następujące rodzaje charakterystyk częstotliwościowych układu:

•

charakterystykę amplitudowo-fazową

•

charakterystykę amplitudową

•

charakterystykę fazową

•

charakterystyki logarytmiczne (amplitudową i fazową).

2

Charakterystyka amplitudowo-fazowa idealnego regulatora PID jest prostą pionową przechodzącą

w odległości k

p

od osi urojonej

2 Charakterystyki Czasowe i Częstotliwościowe Układów Automatyki WAT Warszawa 2004r

10

5. Rysunek: Charakterystyka Amplitudowa reg
idelnego PID

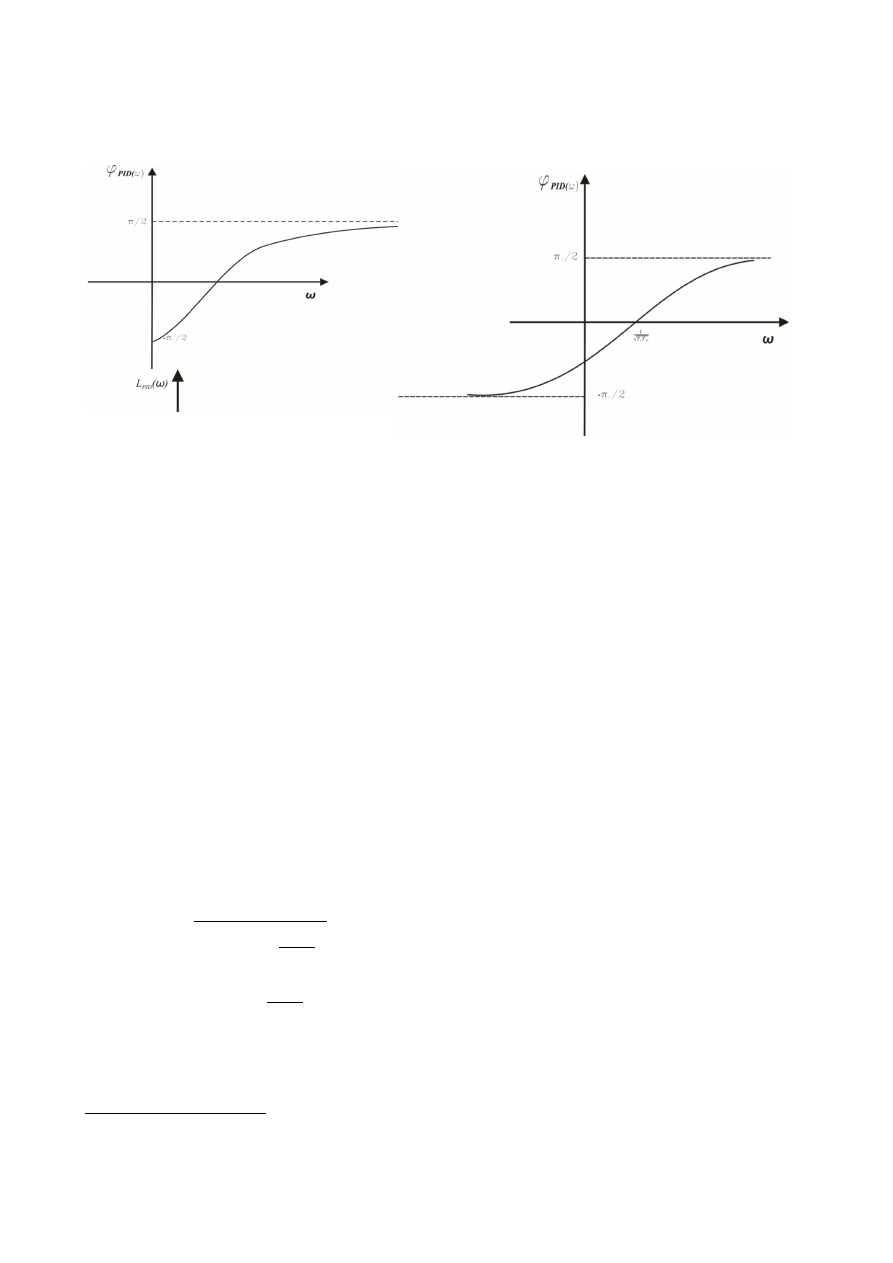
Charakterystyki amplitudowa i fazowa opisane są zależnościami:

3

A

PID

=

k

p



1T

D

−

1



T

1

2





PID

=

arctg T

D

−

1



T

1



Logarytmiczna charakterystyka ma postać

3 Wybrane Zagadnienia Sterowania Obiektami Morskimi B. Żak A. Żak Gdynia 2010

11

7. Rysunek: Charakterystyka Logarytmiczna fazowa
reg idelnego PID

8. Rysunek: Charakterystyka logarytmiczna
amplitudowa reg idelnego PID

L

PID



20log k

p



20log



1T

D

−

1



T

1

2



1.3

Struktury realizacji praktycznych regulatorów PID

W dzisiejszych czasach najczęściej regulatory PID implementuje się w rożnych urządzeniach oto

najpopularniejsze z nich :

−

przetwornicach częstotliwości popularnie zwanych Falownikami

−

sterownikach PLC

−

mikro-kontrolerach

Falowniki służą głowinie do płynnej regulacji obrotów silnika indukcyjnego, a także

odpowiedzialne są za jego powalmy rozruch ( funkcja soft start) oraz łagodne hamowanie.

Regulacją obrotów następuje przez zmianę częstotliwości na wyjściu z przetwornicy. Zmiany

można dokonywać w zakresie od 0 do 60 Hz. Większość Inwerterów ma zaimplementowany

regulator PID , który umożliwia pracę urządzenia w zamkniętej pętli sprzężenia zwrotnego z

czujnikiem np. ciśnienia temperatury itp. Aby tego dokonać należy w menu wybrać odpowiednie

nastawy:

−

wybór pracy włączenie PID

−

wybór sygnału zadającego

Mamy tu wiele możliwości w zależności od typu przetwornicy może to być klawiatura, sygnał

napięciowy w zakresie od 0 do 10 V lub prądowy (4...20mA), sygnał impulsowy, transmisja po

porcie RS 485 z komputera za pomocą aplikacji udostępnionej przez producenta urządzania.

−

wybór sygnału sprzężenia zwrotnego

Sygnał sprzężenia zwrotnego może pochodzić od czujników i być wyrażony w postaci napięciowej

prądowej lub dyskretnej w zależności od zastosowanego czujnika.

Poszczególnych nastaw odnośnie samego regulatora PID dokonujemy w memu w zależności

od wybranego sygnału zadającego

I tak można za pomocą wbudowane klawiatury lub klawiatury zewnętrznej i potencjometrów.

Najczęściej jednak wykonuje się przy użyciu komputerów i aplikacji.

W sterownikach PLC Funkcja PID przeprowadza obliczenia oparte na wzorze PID na

podstawie aktualnej wartości zmiennej procesowej (PV) wyznaczonej z zewnętrznego sygnału

12

analogowego oraz nastaw (SP) procesu. Wynikiem obliczeń jest wyjściowy sygnał sterujący dla

sterowanego procesu, który może zostać podany bezpośrednio do modułu analogowego lub innego

interfejsu wyjściowego lub też pozostawiony do realizacji kolejnego procesu. Prawidłowe

wykorzystanie sterowania PID w procesie umożliwia otrzymanie szybkiego i dokładnego wyniku

PV podążającego za zmianą SP oraz uodparnia proces na zakłócenia.

4

Wzór PID w formie cyfrowej:

[

D4005

Pb

⋅

E

n

]

∑

0

n

[

4005

Pb

⋅

T

i

⋅

T

s

⋅

En]−[



D4005

Pb

⋅

T

d

⋅

PV

n

−

PV

n−1



T

s

]

BIAS

Mn wyjście sterujące w czasie „n”

D4005 : Stała wzmocnienia wartością domyślną jest 1000. Można ją ustawić w zakresie 1~5000.

Pb : Pasmo proporcjonalne ( zakres : 2~5000, jednostka 0.1%. Kc (wzmocnienie) =1000/ Pb )

Ti Całkująca stała czasowa ( zakres : 0~9999 odpowiada 0.00~99.99 powtórzeniom/minutę

Td Różniczkująca stała czasowa ( zakres : 0~9999 odpowiada 0.00~99.99 minutom )

PV Wartość procesowa w czasie ”n”

Pvn-1 Wartość procesowa w czasie ”n-1”

En Błąd w czasie ”n” =nastawa ( SP) – wartość procesowa w czasie ”n” (PVn)

Ts Przedział czasowy obliczeń PID ( zakres: 1~3000, jednostka : 0.01 s )

Bias : Offset wyjścia sterującego ( zakres: 0~16380 )

4 Podręcznik użytkownika sterownika PLC firmy Fatek rozdział 7 s. 9

13

Wraz z upowszechnieniem mikrokontrolerów mamy możliwość w prosty sposób zaimplementować

algorytm PID w takim właśnie urządzeniu . Producent mikrokontrolerów Atmel udostępnia

gotowy kod napisany w języku „C” diagram działania programu przedstawiono poniżej

W strukturze pid są przechowywane ostatnie dane procesowe np. mierzona temperatura (wartości

całki i różniczki) współczynniki (K

p

K

i

K

p)

) Całkowanie odbywa się metodą kwadratów , po

obliczeniu wartości wyjściowej układ sprawdza czy nie zostały przekroczone wartości

14

10. Rysunek: Schemat Blokowy Microkontrolera ATMEGA 8 kB

9. Rysunek: opis instrukcji i przykład programu dla regulacjiw pętli PID (FUN30) FBs-PLC

maksymalne. Jeżeli wartości zostaną przekroczone to układ stara się przez sprawdzanie

kolejnych danych procesowych doprowadzić do jak najmniejszego uchybu .

Jednak w przypadku większości urządzeń które regulowane są przez PID nie mamy modelu

matematycznego dlatego potrzebne są metody doboru nastaw które opiszę w następnym punkcie.

1.4 Metody doboru nastaw regulatora PID

1.4.1 Metoda Zieglera-Nicholsa wyznaczania wzmocnienia krytycznego

Dobór nastaw regulatorów uwzględnia dynamikę obiektu jak i wymagania stawiane zamkniętemu

układowi regulacji .

Projektowanie układów regulacji obejmuje m.in. wybór typu regulatora oraz dobór jego nastaw.

Dobór nastaw regulatora jest bezproblemowy kiedy znamy charakterystyki dynamiczne obiektu.

Taka sytuacja w praktyce zdarza się niezmiernie rzadko. Za zwyczaj mamy do czynienia z regulacją

obiektu nam nie znanego. Wtedy pozostaje korzystanie z metod przybliżonego doboru nastaw

regulatorów o których będzie mowa w tym referacie.

Przy wyznaczaniu nastaw regulatora PID stosuje się wiele rożnych metod ich doboru.

Jednak do właściwego określenia nastaw konieczna się staje znajomość dynamiki obiektu.

Własności dynamiczne obiektu wyznaczane mogą być w oparciu o charakterystyki

częstotliwościowe , lub o charakterystyki czasowe. Korzystniejsza jest synteza w oparciu o

charakterystyki częstotliwościowe. Wymaga ona jednak dużego doświadczenia.

W roku 1942 Ziegler i Nichols jako pierwsi podali zasady przybliżonego doboru nastaw

regulatorów oparte na znajomości tylko dwóch parametrów charakterystycznych układu, które w

łatwy sposób możemy wyznaczyć eksperymentalnie. poniżej przedstawiony został algorytm

postępowania przy doborze nastaw metodą z wyznaczaniem wzmocnienia krytycznego:

1.Nastawiamy regulator na działanie proporcjonalne (człon P)
2.

Zwiększamy wzmocnienie aż do momentu osiągnięcia granicy stabilności

3.

Mierzymy okres oscylacji T

osc

4.

Mierzymy współczynnik wzmocnienia przy którym wystąpiły oscylacje

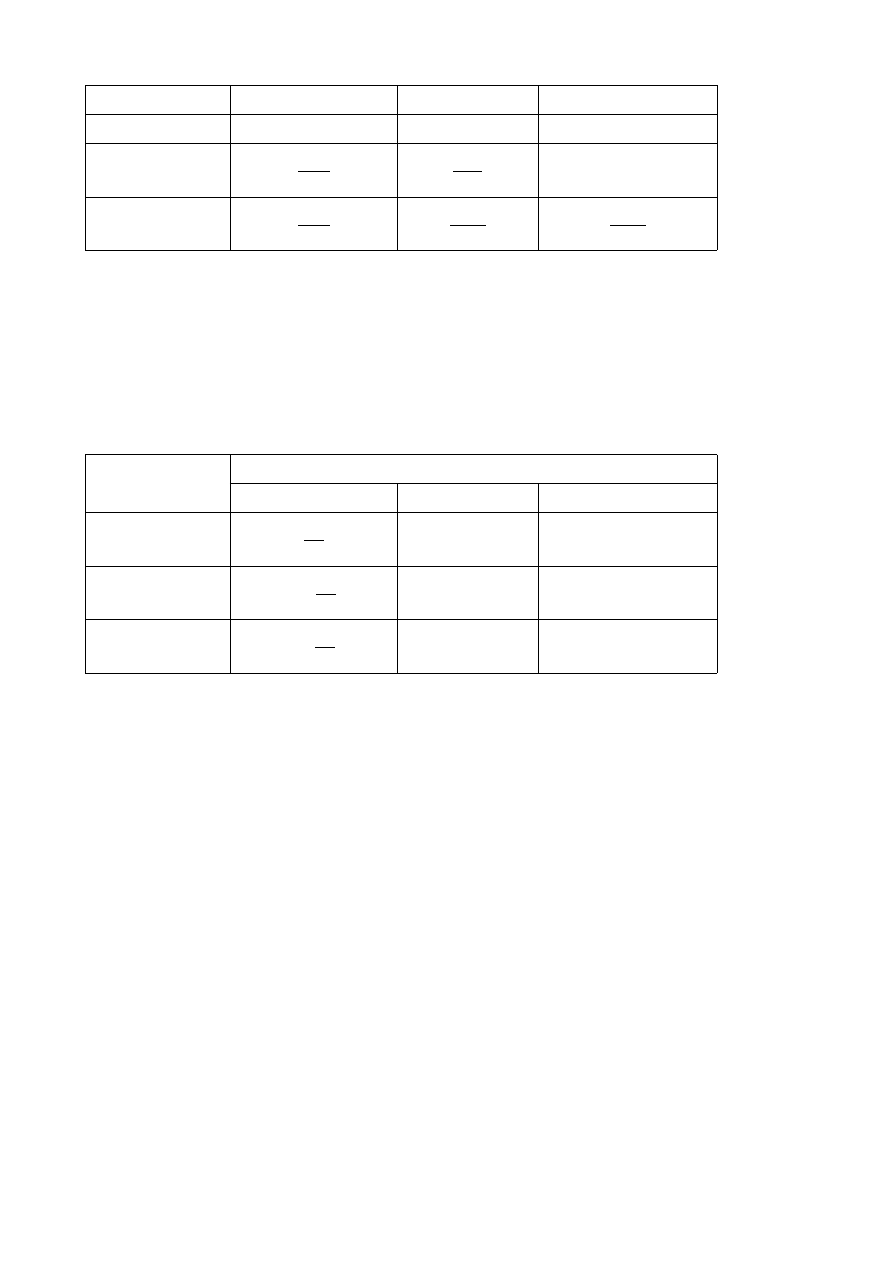
5. Przyjmujemy nastawy w zależności od rodzaju regulatora zgodnie z tabelą

5

Typ regulatora

Optymalne wartości parametrów

5 Wybrane Zagadnienia Sterowania Obiektami Morskimi B. Żak A. Żak Gdynia 2010

15

K

p

T

i

T

d

P

0,5K

KR

-

-

PI

K

KR

2,2

T

osc

1,2

-

PID

K

KR

1,7

T

OSC

2

T

OSC

8

1. Tabela:

Nastawy określone w powyższy sposób powinny zapewnić przeregulowanie nie przekraczające
30%.

Typ regulatora

Optymalne wartości parametrów

K

p

T

i

T

d

P

T

0

R

-

-

PI

0,9

T

0

R

3T

0

-

PID

1,2

T

0

R

2T

0

0,5 T

0

2. Tabela:
W powyższej tabeli umieszczono również nastawy parametrów wynikające z drugiej metody

zaproponowanej przez Zieglera i Nicholsa, a mianowicie z metody bazującej na odpowiedzi

skokowej.

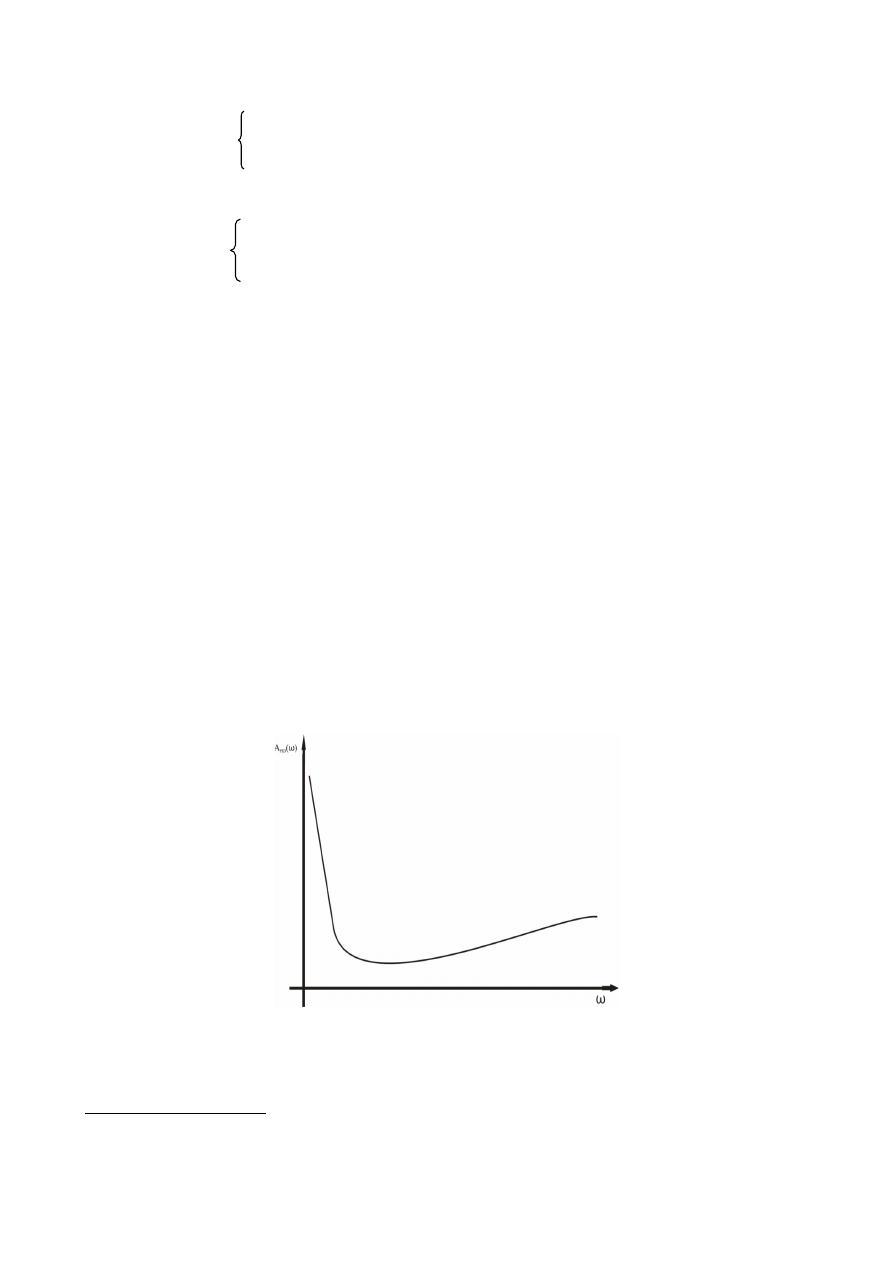
Ziegler i Nichols zauważyli, że odpowiedź skokowa większości układów sterowania ma kształt

podobny do tego z poniższego rysunku. Krzywa ta może być otrzymana z danych

eksperymentalnych lub symulacji dynamicznej obiektu.

Krzywa o kształcie S jest charakterystyczna dla układów wyższych rzędów.

Transmitancja aproksymuje układy wyższych rzędów prostym układem I rzędu z

dodatkowym opóźnieniem To wyrażonym w sekundach. Jeśli styczna narysowana jest w punkcie

przegięcia krzywej odpowiedzi, wówczas nachylenie linii jest wyznaczane ze wzoru R=K/T, a

przecięcie stycznej z osią czasu określa czas opóźnienia To. Parametry T0 i T można również

16

znaleźć graficznie tak jak pokazano to na powyższym rysunku.

Metoda Zieglera-Nicholsa bazująca na odpowiedzi skokowej daje dobre rezultaty

gdy spełniony jest następujący warunek :

Klasyczne metody doboru nastaw Zieglera-Nicholsa zyskały na popularności wraz z pojawieniem

się na rynku sterowników z funkcjami samostrojenia.

\

2.1 Zasada działania sprężarki

17

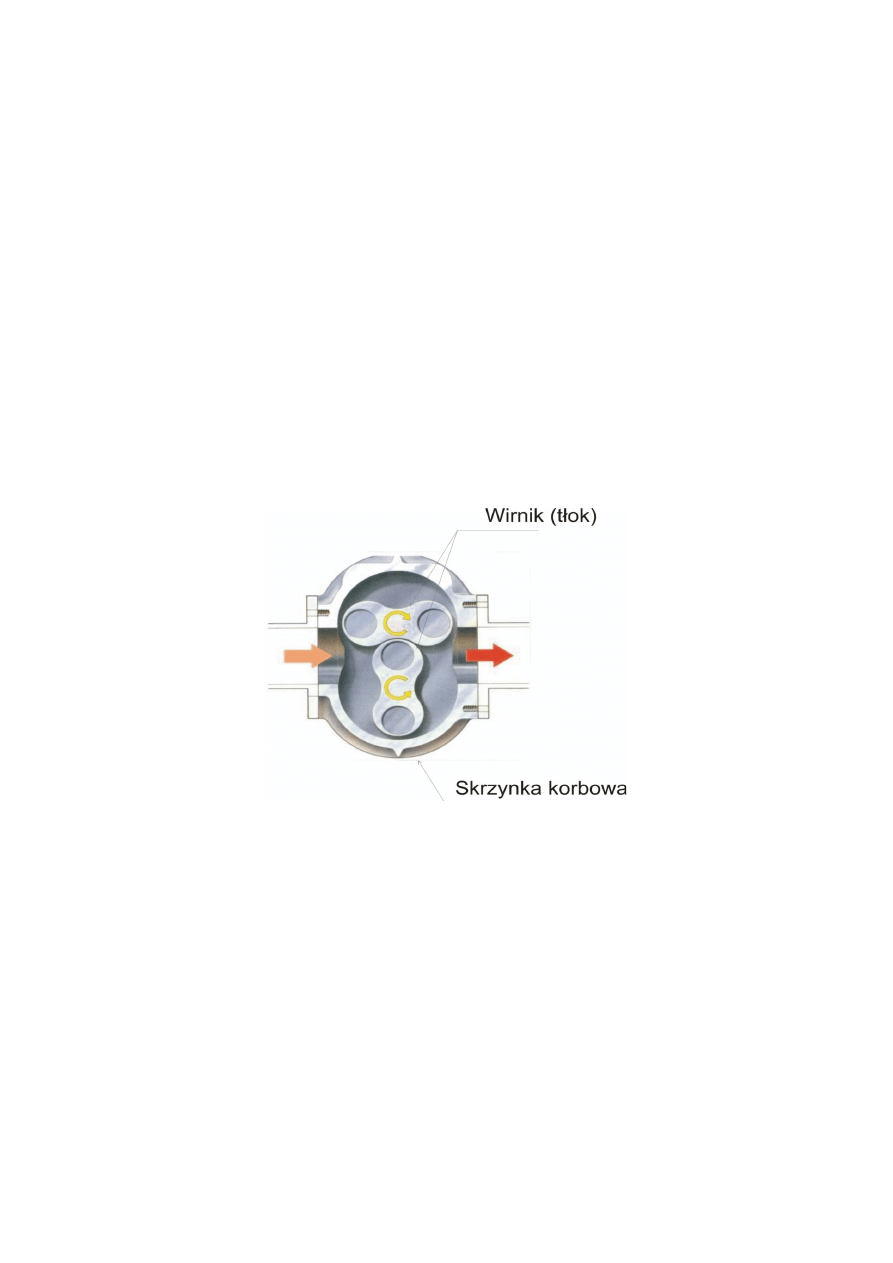
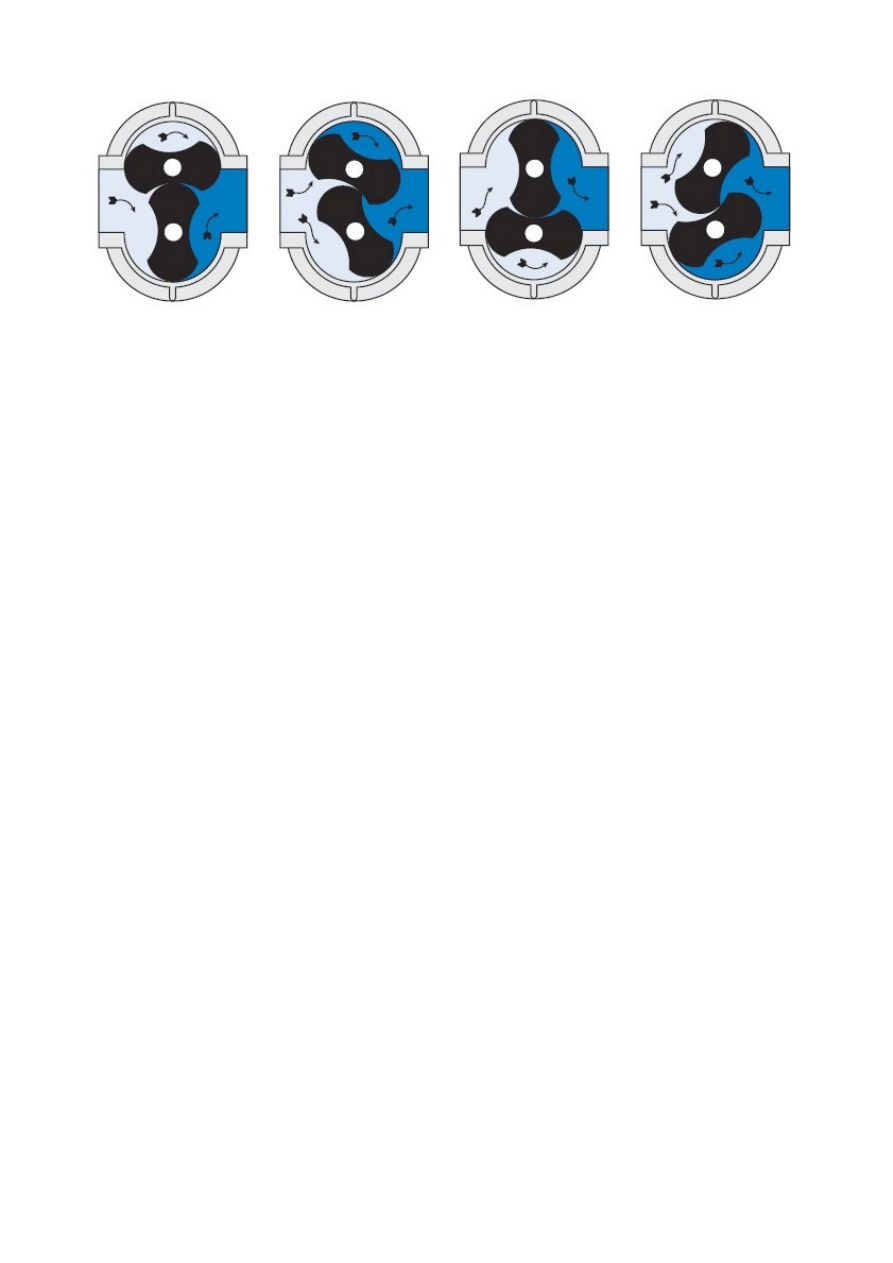
Dmuchawy typu Rootsa, zastosowane są dwa wirniki tłoki dwu zębne lub trzy zębne ,

które obracając się wewnątrz obudowy, zasysają medium do komory kompresji, by następnie

wypchnąć ją do otworu wylotowego. Tłoki obracają się w przeciwną stronę za pomocą kół

zębatych Ciśnienie powietrza podczas procesu jest stałe aż do momentu odsłonięcia otworu

wylotowego przez tłoki rotacyjne. Część powietrza przepływa z powrotem do komory sprężania,

zwiększając ciśnienie i zmniejszając objętość w zamkniętej przestrzeni. Wirniki tłokowe obracają

się dalej aż do momentu wypchnięcia powietrza z przestrzeni obudowy. W czasie jednego obrotu

wirników (tłoków) dochodzi do czterokrotnego lub sześciokrotnego (w zależności od wersji

wykonania wirnika) przetłaczania gazu. Podstawową zaletą układu jest to iż tłoki ( wirniki) pracują

między sobą i obudową z minimalnymi odległościami przez co nie występuje efekt tarcia . Brak

styku współpracujących elementów wyklucza potrzebę smarowania . Dzięki takim parametrom

uzyskujemy przetłaczany czynnik pozbawiany drobin ojeju , także obsługa takiego urządzenia jest

mniej kłopotliwa ponieważ nie trzeba wymieniać oleju .

Poniżej kolejne fazy przetłaczania medium wlotu do wylotu

18

11. Rysunek: Budowa sprężarki Rootsa

2.2 Budowa sprężarki

Dmuchawy w wykonaniu standardowym przeznaczone są do sprężania i odsysania

powietrza oraz gazów obojętnych. Sprężony pozostaje wolne od oleju oraz innych zanieczyszczeń.

W Ofercie firmy Spomax jest aż 30 wielkości dmuchaw o wydajności od 20 do 20000 m3/h i

sprężu do 1100 mbar. Proponowane dmuchawy mogą pracować także jako pompy próżniowe o

podciśnieniu roboczym do 500 mbar, a w wykonaniu specjalnym o podciśnieniu do 800 mbar (200

mbar ciśnienia absolutnego).

Dmuchawy produkowane są w wielu odmianach konstrukcyjnych i z różnym wyposażeniem.

Dostarczane są do odbiorców w postaci agregatów. Podstawowym elementem każdego agregatu jest

stopień sprężania.

Wykonanie materiałowe:

- korpus, płyty boczne, pokrywy: ŻL 250 wg PN 92/H-83101.

- koła zębate w klasie wykonania 6-D/II: stal 20 HG wg PN 90/M-88522.

- tłoki: dmuchaw w wielkościach DR 80T do DR 240T - stal 40HwgPN 93/M-84019.

- tłoki dmuchaw w wielkościach DR 250T do DR 2000T część robocza tłoka wykonana jest z
żeliwa ŻL 250 wg PN 92/H-83101 a wał tłoka ze stali 40H wg PN 93/M-84019.

- łożyska SKF lub FAG z luzem C3.

19

12. Rysunek: fazy pracy sprężarki

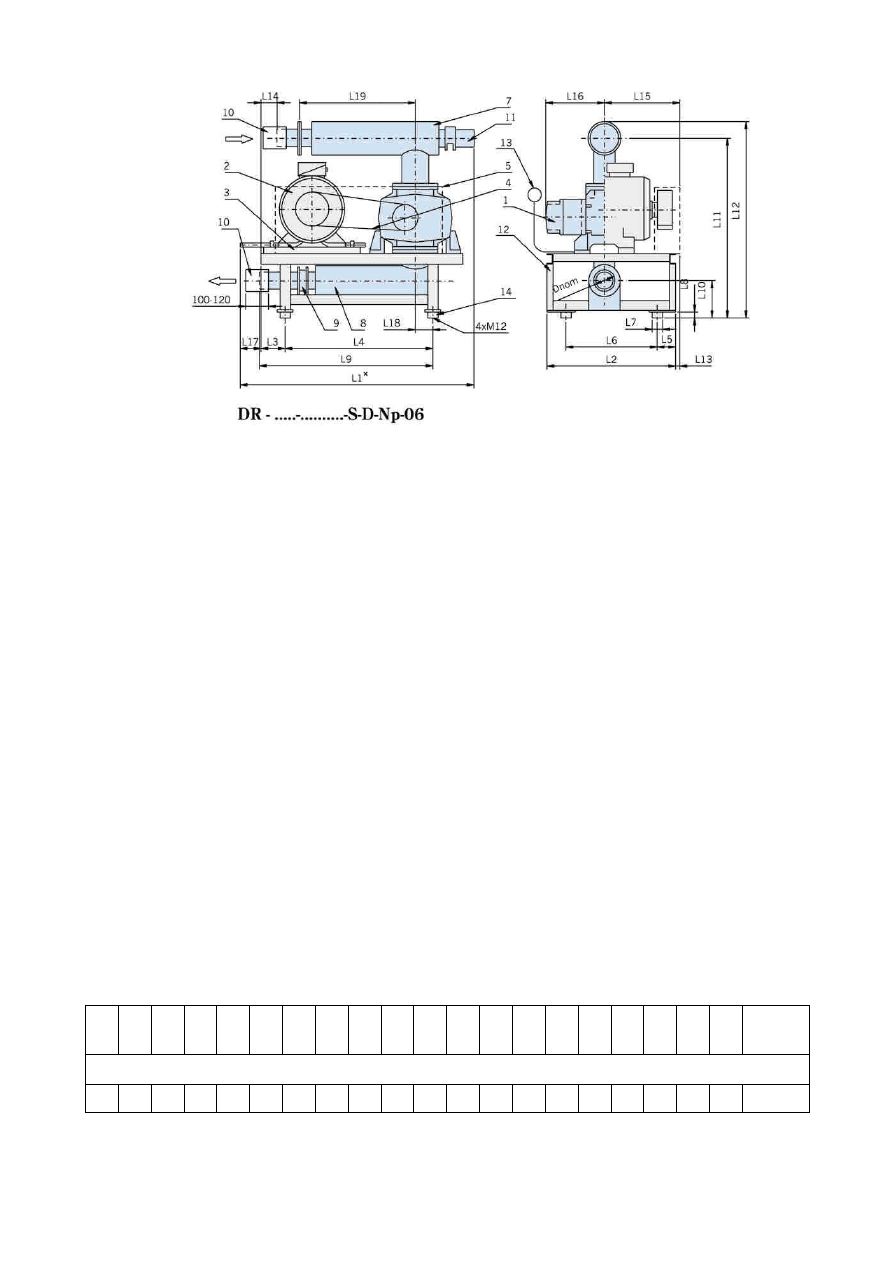
2.

Dmuchawa rotacyjna

3.

Silnik

4.

Sanie naciągowe

5.

Przekładnia pasowa

6.

Osłona przekładni

7.

Filtr

powietrza

8.

Tłumik hałasu wlotowy

9.

Tłumik hałasu wylotowy

10.

Zawór zwrotny

11.

Króciec ze złączem elast.

12.

Zawór przeciążeniowy

13. Rama

wsporcza

14.

Zespół kontroli ciśnienia

15.

Wibroizolator

2.3 Charakterystyki eksploatacyjne sprężarki

L

1

L

2

L

3

L

4

L

5

L

6

L

7

L

8

L

9

L

10

L

11

L

12

L

13

L

14

L

15

L

16

L

17

L

18

L

19

mm

1520

1470

680

142

816

60

80

45

981

215

1009

1115

5

418

327

56

115

519

20

3. Tabela: Wymiary

21