Komputerowe

Wspomaganie

Projektowania

Akademia Morska w Gdyni

Wydział Elektryczny

mgr inż. Andrzej Rak [e-mail]

2

Programy wspomagania obliczeń inżynierskich

Komercyjne

• MATLAB
• MathCAD
• Mathematica
• Statistica
• Maple
• ...

Wolne

• Octave
• Scilab
• Maxima
• Euler
• Scigraphica
• ...

3

Co to jest MATLAB?

MAT

rix

LAB

oratory

Język programowania wysokiego poziomu (IV

generacji)

Producent: The MathWorks Inc. USA

http://www.mathworks.com

news:comp.soft-sys.matlab

4

Literatura

1. Dokumentacja w Internecie:

http://www.mathworks.com/access/helpdesk/help/helpdesk.shtml

2. Pratap R., Matlab 7 dla naukowców i inżynierów, PWN (Mikom), Warszawa,

2007.

3. Dobroczyński L., Matlab. Środowisko obliczeń naukowo technicznych, Mikom,

Warszawa, 2005.

4. Mrozek B. Mrozek Z., Matlab. Leksykon kieszonkowy, Helion, Warszawa

2005.

5. Mrozek B. Mrozek Z., Matlab i Simulink Poradnik Użytkownika, Helion,

Warszawa 2004.

5,5. Mrozek B. Mrozek Z., Matlab 6 (5 Simulink 2) Poradnik Użytkownika, PLJ, Warszawa 2001

(1998)

6. Zalewski A. Cegieła R., Matlab - obliczenia numeryczne i ich zastosowania,

Nakom, Poznań 1996.

5

Cechy MATLAB-a

• Otwarte środowisko
• Ogromna ilość rozszerzeń (toolbox-y)
• Integracja obliczeń numerycznych i funkcji

graficznych

• Wieloplatwormowość (PC, UNIX, Macintosh)
• Interfejs API (C, Fortran, Ada, ActiveX)

6

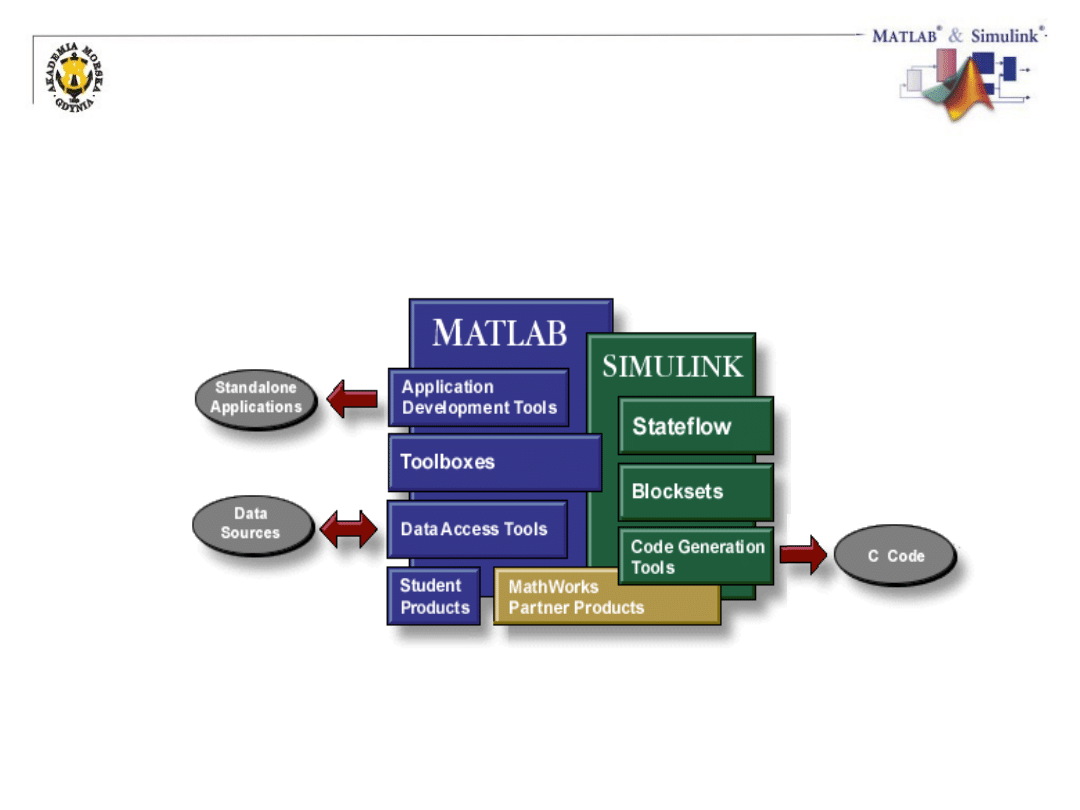
Struktura środowiska MATLAB

7

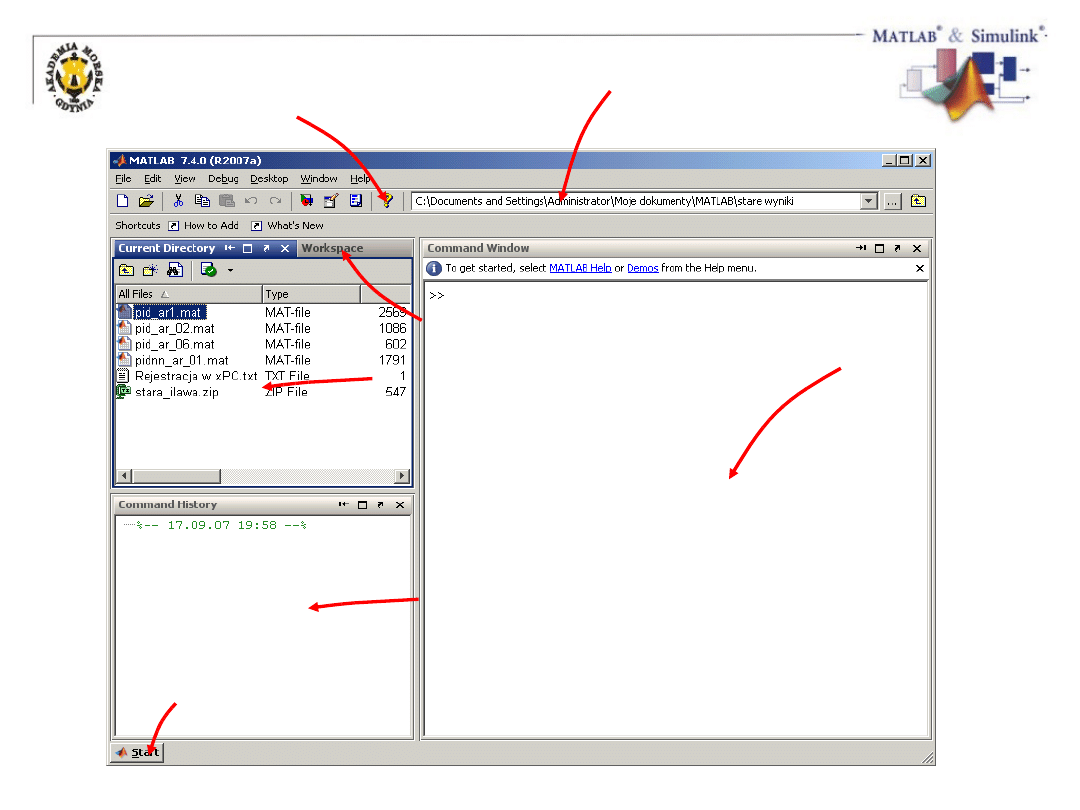
Główne okno MATLAB-a

Okno poleceń

Podgląd przestrzeni roboczej

Historia poleceń

Dostęp do programów narzędzi i plików pomocy

Operacje w bieżącym katalogu

Ustalanie bieżącego katalogu

Pomoc

8

Podstawowe polecenia - Pomoc

• Pomoc na temat

>> help

• Okno pomocy

>> helpwin

• Poszukiwanie ciągu znaków

>> lookfor

»

lookfor serial

FREESERIAL Release MATLAB's hold on serial port.
INSTRCB Wrapper for serial object M-file callback.
INSTRFIND Find serial port objects with specified property values.
DATENUM Serial date number.

. . . .

» help instrfind
INSTRFIND Find serial port objects with specified property values.

OUT = INSTRFIND returns all serial port objects that exist in

memory.

The serial port objects are returned as an array to OUT

.....

9

Tryby pracy z MATLAB-em

• Tryb interakcyjny

zmienna = polecenie;
polecenie, polecenie, zmienna = polecenie;

• Tryb wsadowy

m-file (skrypt)

Uwaga! MATLAB rozróżnia

WIELKIE

i

małe

litery

10

Znaki specjalne

=

przypisanie

[ ]

tworzenie tablic, listy argumentów wyjściowych

{ }

tworzenie i indeksowanie tablic blokowych

( )

argumenty wejściowe funkcji, kolejność obliczeń

...

kontynuacja linii

:

generowanie wektorów, indeksowanie macierzy

.

kropka dziesiętna, element operatorów
arytmetycznych, wskazywanie pól struktury

11

Znaki specjalne cd.

;

koniec wiersza macierzy, wstrzymanie „echo”

,

separator indeksów, argumentów funkcji, poleceń

%

komentarz

‘

wprowadzanie łańcuchów, operator transpozycji lub
sprzężenia macierzy

!

wyjście do systemu operacyjnego

..

katalog macierzysty („jeden wyżej”)

12

Podstawowe polecenia - Pliki i zmienne

>> cd / pwd, ls / dir

- zmiana, listowanie bieżącego katalogu

>> what

- listowanie plików bieżącego katalogu (z podziałem na grupy)

>> which

- lokalizowanie funkcji lub zmiennej za pomocą nazw

>> clear

- usuwanie zmiennej / funkcji z pamięci

>> who (whos)

- listowanie nazw zmiennych w przestrzeni roboczej

(rozmiar macierzy, zajętość pamięci, typ)

>> size

- zwraca rozmiar macierzy

13

Operatory arytmetyczne

>> 2/3

ans =

0.6667

>> 2\3

ans =

1.5000

Operatory Arytmetyczne

^ potęgowanie

* mnożenie

/ dzielenie prawostronne

\ dzielenie lewostronne

+ dodawanie

- odejmowanie

’ sprzężenie macierzy

.’ transpozycja macierzy

14

» kasa = [-2 10 NaN 30 -11 Inf 31];
» all_pos = all(kasa>=0)
all_kasa =
0
» each_pos = kasa>=0
each_pos =
0 1 0 1 0 1 1
» pos_fin = (kasa>=0)&(isfinite(kasa))
pos_fin =
0 1 0 1 0 0 1

1 = PRAWDA
0 = FAŁSZ

Operatory Logiczne
= = równe

> większe niż

< mniejsze niż

~ nie

& i

| lub

isempty()

isfinite(), etc. . . .

any()

all()

Operatory logiczne

15

Zmienne i stałe specjalne

ans

Domyślna nazwa nie zadeklarowanej zmiennej

pi

Pi

≡

π

= 3.141592…

eps

Precyzja zmiennoprzecinkowa: 2.206x10

-16

= 2

-52

(

realmax, realmin

)

inf

Nieskończoność

∞

1

−

i,j

Jednostka urojona

nan

0/0 lub

∞ / ∞

flops

Licznik operacji zmiennoprzecinkowych

16

Wprowadźmy liczbę rzeczywistą
Reprezentacja stałoprzecinkowa

format short

= 0.3333

(5 cyfr)

format long

= 0.33333333333333

(15 cyfr)

Reprezentacja zmiennoprzecinkowa (e)

format short e

= 3.3333e-001

(5 cyfr)

format long e

= 3.333333333333333e-001

(15 cyfr)

Postać ułamkowa (przybliżenie)

format rat

= 1/3

Reprezentacja szesnastkowa

format hex

= 3fd5555555555555

(15 cyfr)

Wybrane formaty

wyświetlania

liczb



3333

.

0

3

1

=

=

x

17

Macierz - podstawowy typ danych w MATLAB-ie

MATLAB == MATrix LABoratory

»load durer

»image(X);

»colormap(map)

»load detail

»image(X);

»colormap(map)

18

Macierz - indeksowanie

4

10

1

6

2

8

1.2

9

4

25

7.2

5

7

1

11

0

0.5

4

5

56

23

83

13

0

10

1

2

Wiersze (m)

3

4

5

Kolumny

(n)

1 2 3 4 5

1

6

11

16

21

2

7

12

17

22

3

8

13

18

23

4

9

14

19

24

5

10

15

20

25

A =

A (2,4)

A (17)

Tablica prostokątna:
Skalar: macierz 1-na-1
Wektor: macierz m-na-1

macierz 1-na-n

Macierz: macierz m-na-n

19

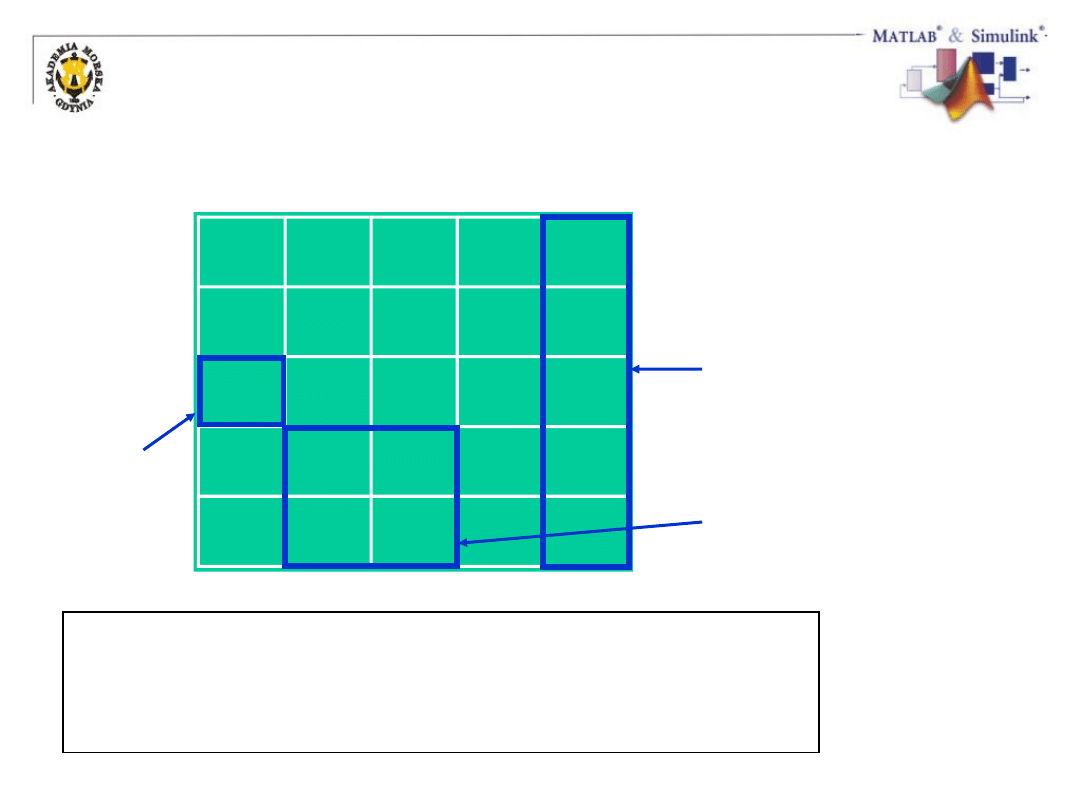
Wybór elementów macierzy

4

10

1

6

2

8

1.2

9

4

25

7.2

5

7

1

11

0

0.5

4

5

56

23

83

13

0

10

1

2

3

4

5

1 2 3 4 5

1

6

11

16

21

2

7

12

17

22

3

8

13

18

23

4

9

14

19

24

5

10

15

20

25

A =

A(3,1)

A(3)

A(1:5,5)
A(:,5)

A(21:25)

A(4:5,2:3)

A([9 14;10 15])

• Używaj nawiasów () do określania indeksów
• Dwukropek (:) określa zakres: “Wszystko”
• Nawiasy [ ] pozwalają zdefiniować macierz indeksów
• ‘end’ określa największą wartość indeksu

A(1:end,end)
A(:,end)

A(21:end)

’

20

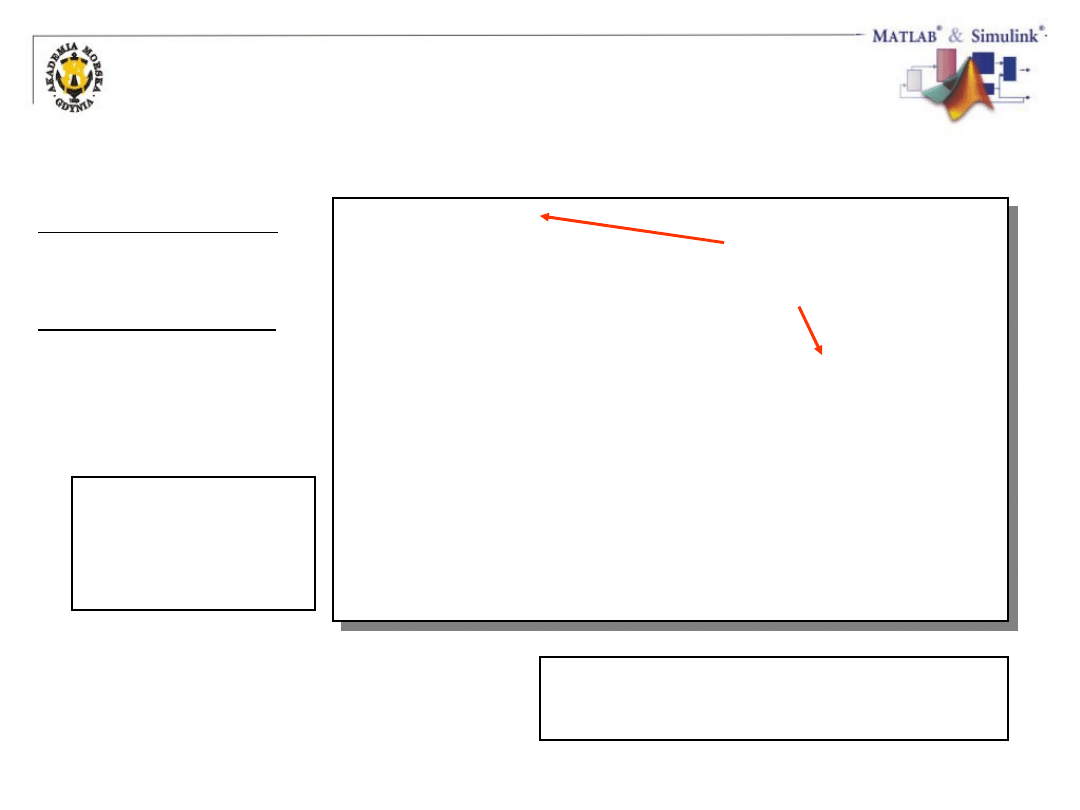
Definiowanie macierzy

Elementem macierzy może być
dowolne wyrażenie MATLAB-a

» a=[1 2;3 4]
a =
1 2
3 4
» b=[-2.8, sqrt(-7), (3+5+6)*3/4]
b =
-2.8000 0 + 2.6458i 10.5000
» b(2,5) = 23
b =
-2.8000 0 + 2.6458i 10.5000 0 0
0 0 0 0 23.0000

Separator wierszy:
średnik (;)

Separator kolumn:
spacja / przecinek (,)

Macierze muszą
być prostokątne

(za brakujące
elementy wstaw 0)

Pamiętaj o
nawiasach [ ]

21

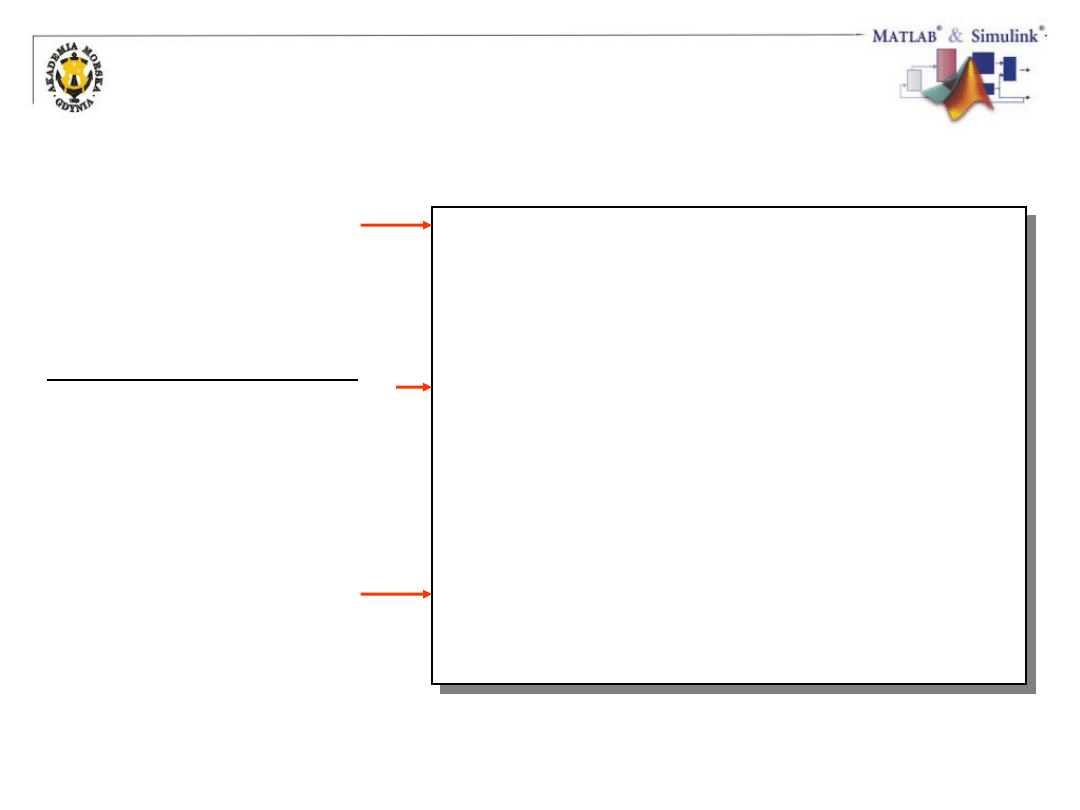
Definiowanie macierzy cd.

» w=[1 2;3 4] + 5
w =
6 7
8 9
» x = 1:5
x =
1 2 3 4 5
» y = 2:-0.5:0
y =
2.0000 1.5000 1.0000 0.5000 0
» z = rand(2,4)
z =
0.9501 0.6068 0.8913 0.4565
0.2311 0.4860 0.7621 0.0185

Operacje
algebraiczne

Generowanie ciągów:
operator dwukropek (:)

Specjalizowane
funkcje

22

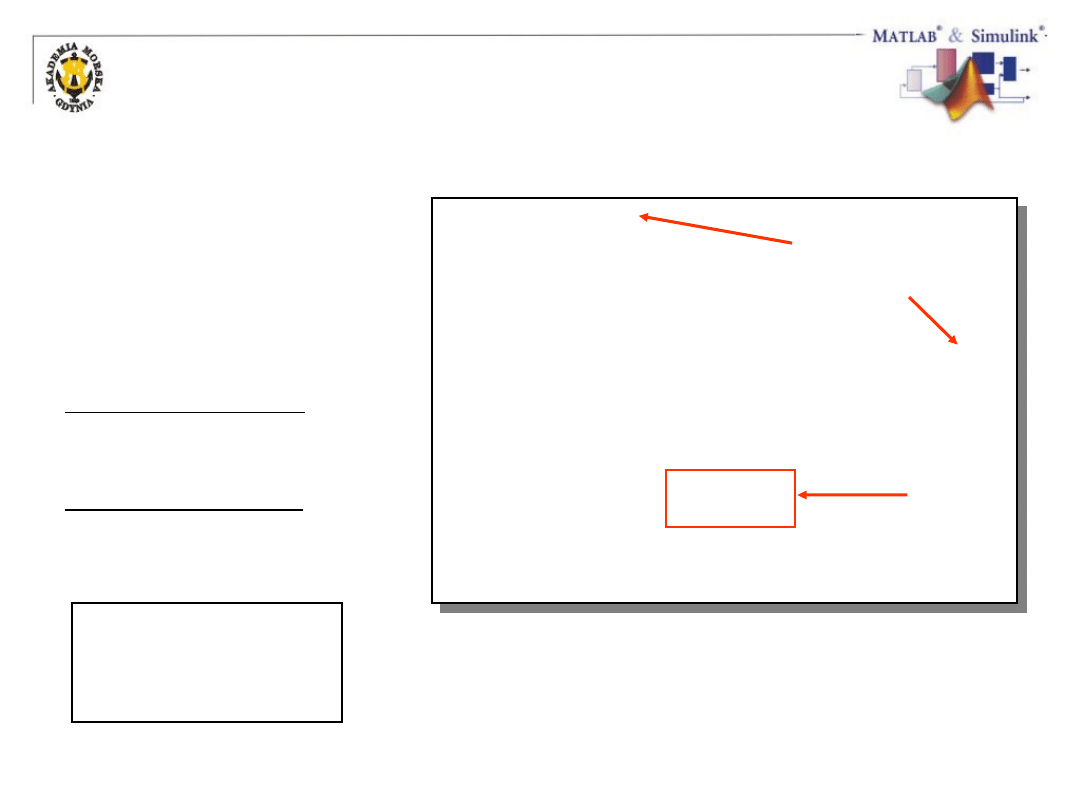
Łączenie macierzy

» a=[1 2;3 4]
a =
1 2
3 4
» cat_a=[a, 2*a; 3*a, 4*a; 5*a, 6*a]
cat_a =
1 2 2 4
3 4 6 8
3 6 4 8
9 12 12 16
5 10 6 12
15 20 18 24

Stosuj [ ] do łączenia
zdefiniowanych
macierzy jako
“elementów” nowych

Pamiętaj o
nawiasach [ ]

Macierz
wynikowa musi
być prostokątna

4*a

Separator wierszy:
średnik (;)

Separator kolumn:
spacja / przecinek (,)

23

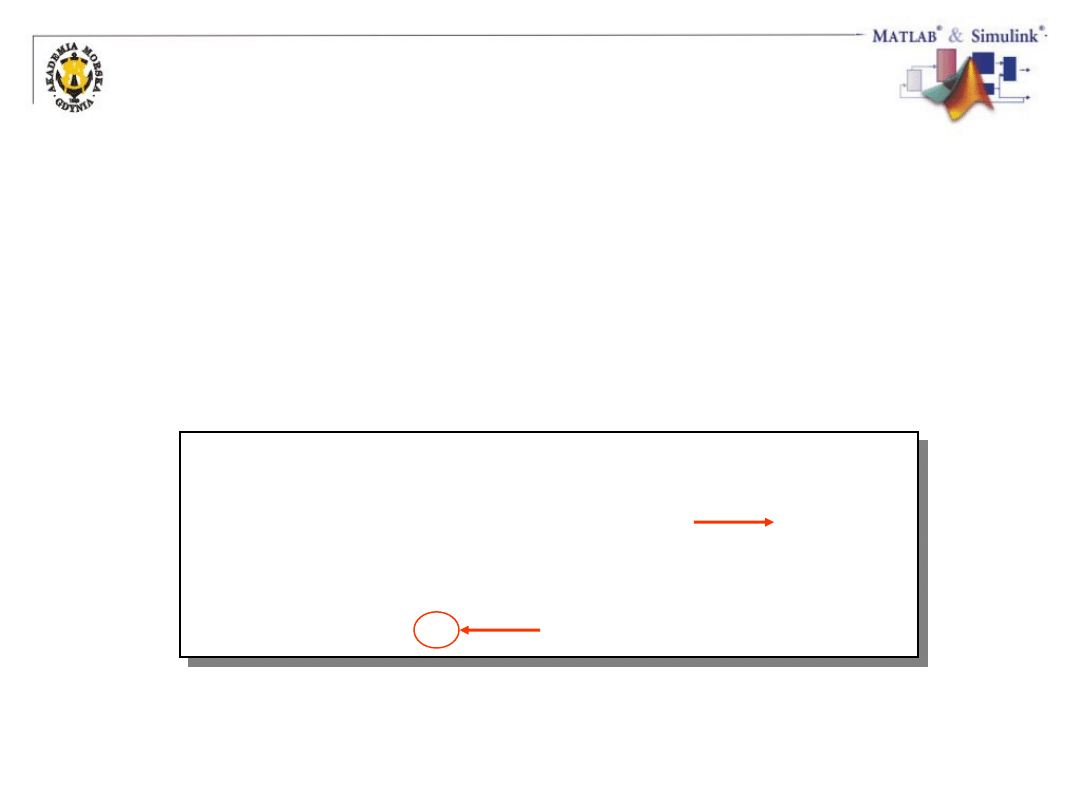
Mnożenie macierzy

• “Wewnętrzne” wymiary muszą być równe
• Wymiar macierzy wynikowej = “zewnętrzne” wymiary macierzy

mnożonych

• Elementy macierzy wynikowej = suma iloczynów wierszy

pierwszej macierzy z kolumnami drugiej

» a = [1 2 3 4; 5 6 7 8];
» b = ones(4,3);
» c = a*b
c =
10 10 10
26 26 26

[2x4]
[4x3]

[2x4]*[4x3] [2x3]

a(2gi wiersz) * b(3cia kolumna)

24

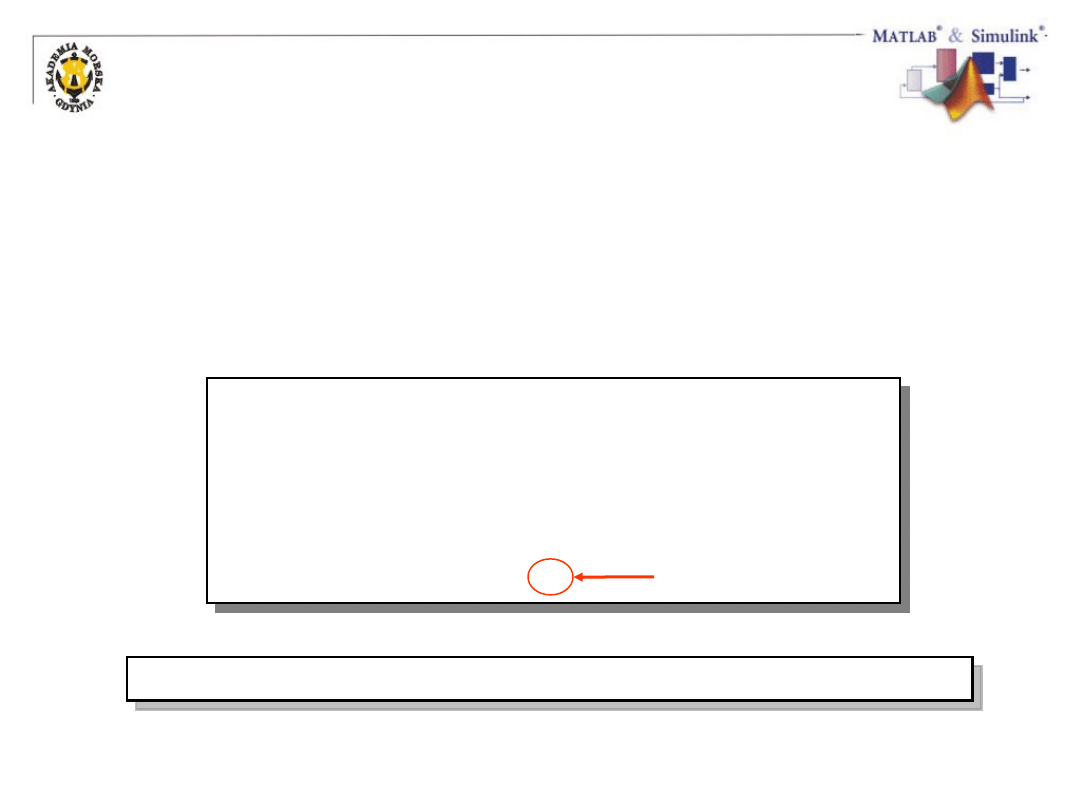
Mnożenie tablicowe

• Macierze muszą mieć identyczne wymiary
• Wymiar macierzy wynikowej = Wymiary macierzy mnożonych
• Elementy macierzy wynikowej = iloczyny odpowiednich

elementów macierzy mnożonych

» a = [1 2 3 4; 5 6 7 8];
» b = [1:4; 1:4];
» c = a.*b
c =
1 4 9 16
5 12 21 32

c(2,4) = a(2,4)*b(2,4)

Uwaga! Analogiczne reguły odnoszą się do pozostałych działań

25

Co to jest wektoryzacja?

•

Inne języki programowania - pętle

•

MATLAB - operacje macierzowe:

»

tic; Gestosc = Masa./(Dlug.*Szer.*Wys); toc

elapsed_time =
0

» tic;

for I = 1:1000

Gestosc(I) = Masa(I)/(Dlug(I)*Szer(I)*Wys(I));
end; toc
elapsed_time =
0.0500

TIC i TOC -

pomiar czasu

Kod wektoryzowany

jest znacznie szybszy

26

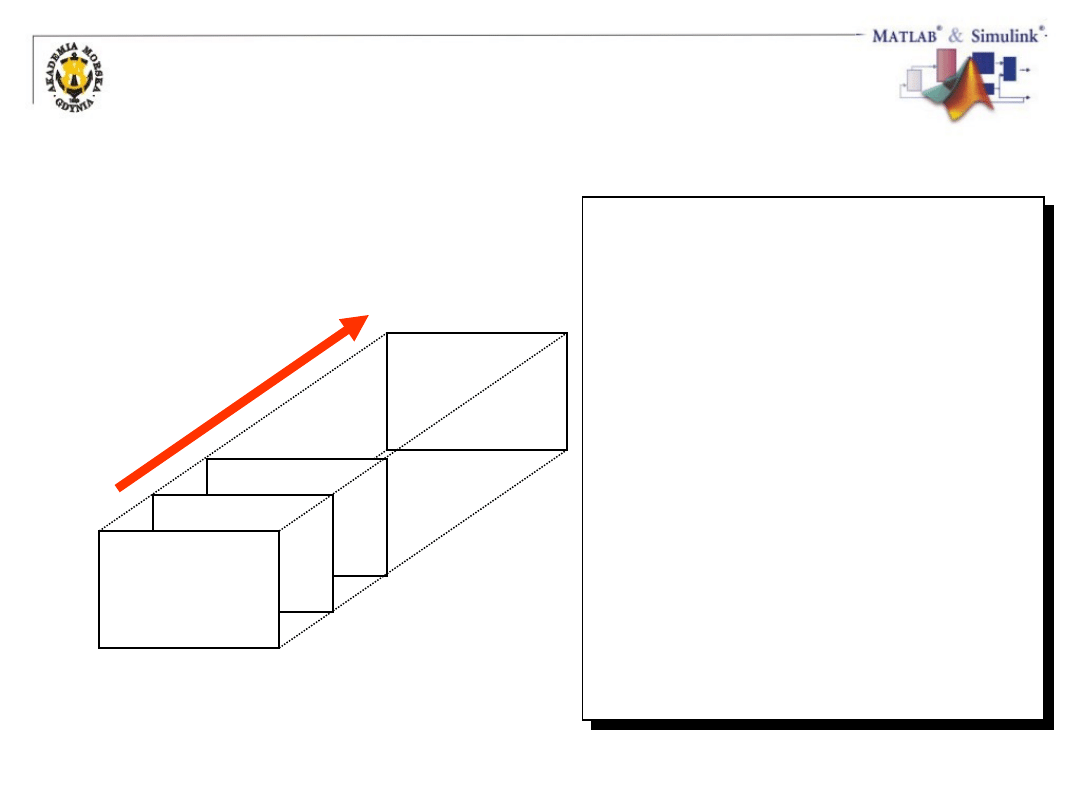
Macierze wielowymiarowe

1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1

» A = pascal(4);
» A(:,:,2) = magic(4)
A(:,:,1) =
1 1 1 1
1 2 3 4
1 3 6 10
1 4 10 20
A(:,:,2) =
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
» A(:,:,9) =

diag(ones(1,4));

Warstwa N

0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0

16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1

1 1 1 1
1 2 3 4
1 3 6 10
1 4 10 20

27

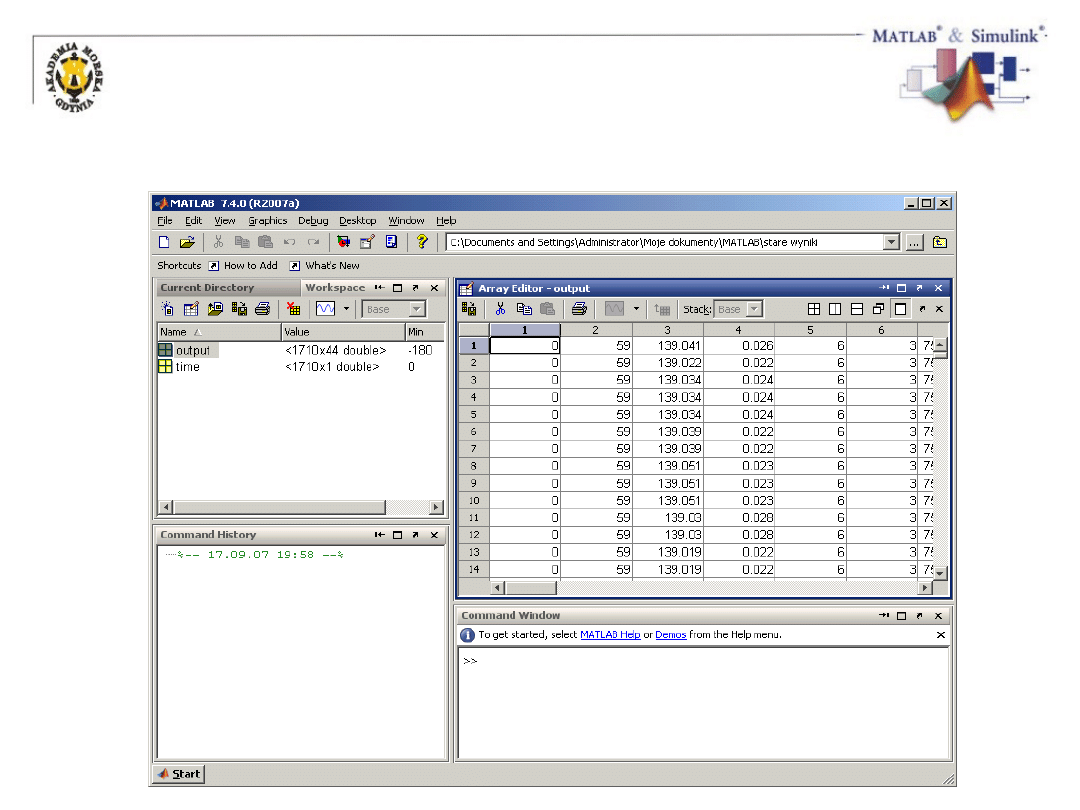
Edytor macierzy

28

>> -5/(4.8+5.32)^2
ans =
-0.0488
>> (3+4i)*(3-4i)
ans =
25
>> cos(pi/2)
ans =
6.1230e-017
>> exp(acos(0.3))
ans =
3.5470

» a = 2;
» b = 5;
» a^b
ans =
32
» x = 5/2*pi;
» y = sin(x)
y =
1
» z = asin(y)
z =
1.5708

Wynik zapisany
do zmiennej “ans”
(bez nazwy)

argumenty funkcji
w nawiasach ()

Wstrzymanie
wypisania
odpowiedzi

MATLAB jako kalkulator

Deklarowanie zmiennych

Liczby zapisywane są w notacji
zmiennoprzecinkowej podwójnej precyzji

Praca interakcyjna

29

» [sred, odch] = ourstat([6 3 8 6 1 8 7 2 3 9 7 1])

sred =

5.0833

odch =

2.7826

Praca wsadowa

Wykonanie m-pliku funkcyjnego

Zmienne
wyjściowe
(wynikowe)

Nazwa m-pliku

Dane
wejściowe
(wektor)

30

• Pliki skryptowe

• Działają tak jakby wpisywano szereg poleceń MATLAB-a w

oknie poleceń

• Zmienne przechowywane są w

globalnej

przestrzeni roboczej

• Pliki funkcyjne

• Pozwalają na tworzenie własnych poleceń MATLAB-a
• Wszystkie zmienne wewnątrz funkcji są

lokalne

• Informacja do funkcji może być przekazywana tylko w formie

parametrów

Pliki skryptowe i funkcyjne

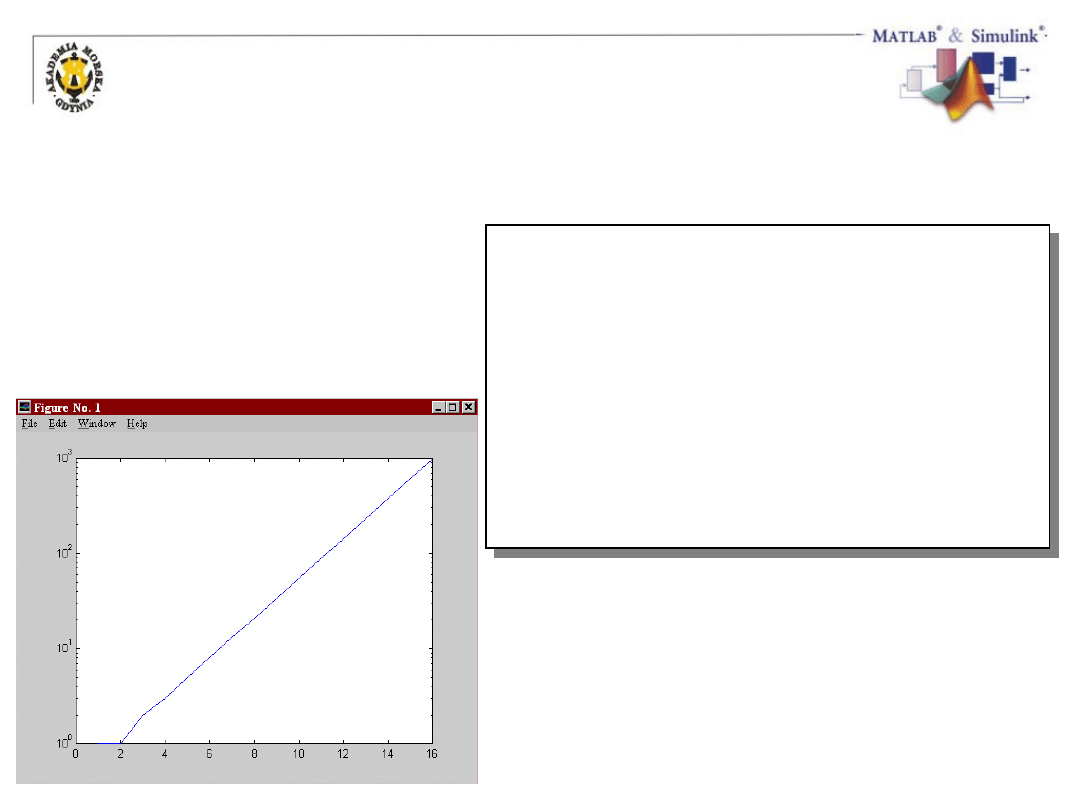
31

% m–plik obliczjący
% ciąg Fibonacciego

f = [1 1]; i = 1;
while f(i) + f(i+1) < 1000

f(i+2) = f(i) + f(i+1);
i = i + 1;

end
semilogy(f)

• Standardowy plik

tekstowy ASCII

• Wykonuje ciąg poleceń

MATLAB-a w przestrzeni
roboczej.

M-plik skryptowy

32

M-plik funkcyjny (funkcja)

function

y = mean (x)

% MEAN Average or mean value.
% For vectors, MEAN(x) returns the mean value.
% For matrices, MEAN(x) is a row vector
% containing the mean value of each column.

[m,n] = size(x);

if

m == 1

m = n;

end

y = sum(x)/m;

Argumenty wyjściowe

Argumenty wejściowe

Nazwa funkcji

Pomoc

Kod funkcji

33

Wybrane polecenia związane z programowaniem

funkcji

function

definiowanie funkcji

global

definiowanie zmiennych globalnych

persistent

definiowanie zmiennych lokalnych z pamięcią wartości

nargchk

sprawdzanie zakresu wartości parametrów

nargin

liczba argumentów wejściowych

nargout

liczba argumentów wyjściowych

return

powrót do miejsca wywołania funkcji

error

komunikat o błędzie i przerwanie wykonywania funkcji

eval

wykonanie łańcucha jako polecenia MATLAB-a

feval

wykonanie funkcji zapisanej jako łańcuch

input

tekst jako zachęta do wprowadzania danych

keyboard

wywołanie klawiatury

menu

generacja graficznego lub tekstowego menu

pause

oczekiwanie na reakcję użytkownika

34

Struktury programowania

• pętla

for

for

indx = 1:10

y(indx)= 3*indx

end

• pętla

while

indx=1;

while

indx <= 10

y(indx)=3*indx
indx=indx+1;

end

35

• instrukcja warunkowa

if

for

indx = 1:41

if

indx <= 10

y(indx)= 2*indx;

elseif

indx <=20

y(indx)= 3*indx;

else

y(indx)= indx-1;

end

end

• “wektoryzuj” gdzie się da!

y = [2:2:20 33:3:60 20:40]

Struktury programowania cd.

36

Struktury programowania cd.

• Instrukcja wyboru

switch

switch

inputval

case

1,

y = 2*indx;

case

2,

y = 4*indx;

otherwise

, disp(

‘unknown option‘

);

end

• nie “przelatuje” (w przeciwieństwie do C nie potrzeba instrukcji

break)

case

TrueValue, y=1;

case

NextValue, y=2;

%Warunek nie sprawdzany

37

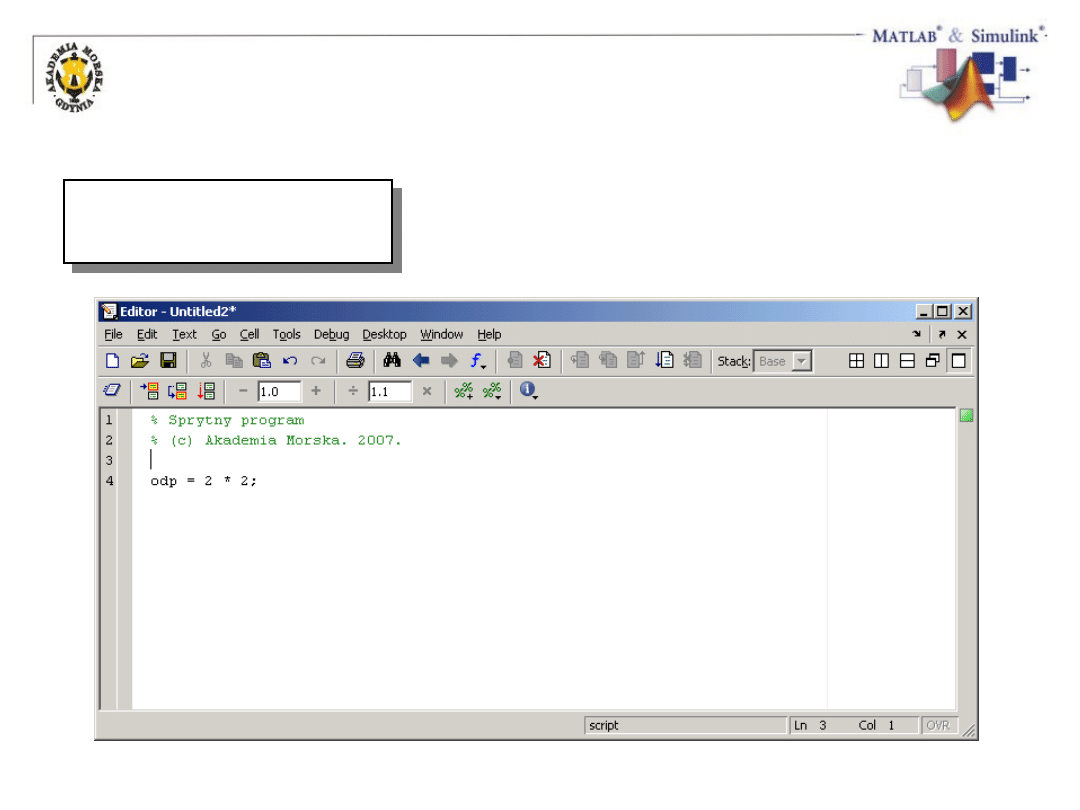
Edycja skryptu

>> edit
>> edit nazwa.ext

38

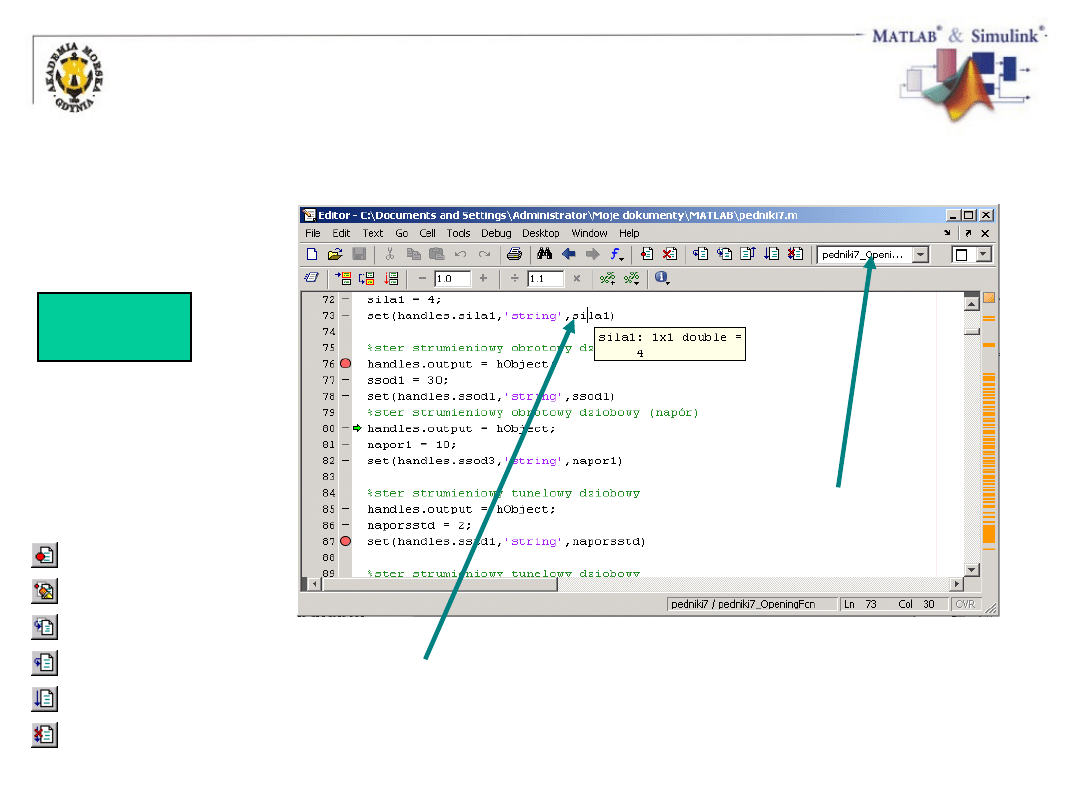
Debuggowanie skryptu

Ustaw pułapkę
Usuń pułapki
Krok do funkcji
Krok w funkcji
Kontynuuj
Wyjście

Obsługa stosu

Kursor nad
zmienną = wartość

K

>>

39

W następnych odcinkach...

•Funkcje I/O
•Grafika 2D i 3D
•Podstawy „Handle Graphics”
•Przykłady zastosowań

•SIMULINK