Małgorzata Dzida
I. Wstęp teoretyczny
Celem ćwiczenia przeprowadzanego przez studentów było zbadanie temperaturowej
zależności oporu przewodników dla 3 różnych pierwiastków oraz oporu zastępczego
szeregowego i równoległego połączenia oporników. Wiadomości teoretyczne, które były
wykorzystywane w ćwiczeniu to:
Opór elektryczny – inaczej zwany rezystancją. Jest to wielkość, która charakteryzuje
zależność pomiędzy natężeniem a napięciem prądu elektrycznego w obwodach prądu
stałego. Opór oznacza się umownie literą R a jednostką oporu w układzie Si jest Ω.
Pierwsze prawo Ohma – nazwa wywodzi się od nazwiska uczonego (
Georga Simona Ohm
a),
który odkrył prawidłowość taką, że: Natężenie prądu płynącego przez przewodnik jest
proporcjonalne do napięcia między końcami przewodnika
= ∙
Drugie prawo Ohma – w drugim prawie brana jest pod uwagę geometria przewodnika.
Mianowicie jego długość, przekrój poprzeczny oraz właściwości materiału z którego został
wykonany. Matematycznie wyrażane jest wzorem:
=
Gdzie:
l - długość przewodnika
S – przekról poprzeczny
− stała materiałowa
R – opór właściwy
Pierwsze prawo Kirchhoffa – mówi ono, że suma natężeń prądów wpływających do węzła i
z
niego
wypływających
jest
równa
0.
= 0
Drugie prawo Kirchhoffa - Według tego prawa suma wartości chwilowych sił
elektromotorycznych w układzie równa się sumie wartości chwilowych spadków napięć na
opornikach danego obwodu.
=
Oporniki można połączyć ze sobą w dwojaki sposób
1. Szeregowo:
Połączenie takie charakteryzuje
się tym, że koniec pierwszego opornika (w naszym przypadku R
1
) jest bezpośrednio
połączony z początkiem kolejnego opornika (R
2
).
Ich rezystancja zastępcza jest sumą poszczególnych oporów.
R
z
= R
1
+ R
2
+ R
3
2
.
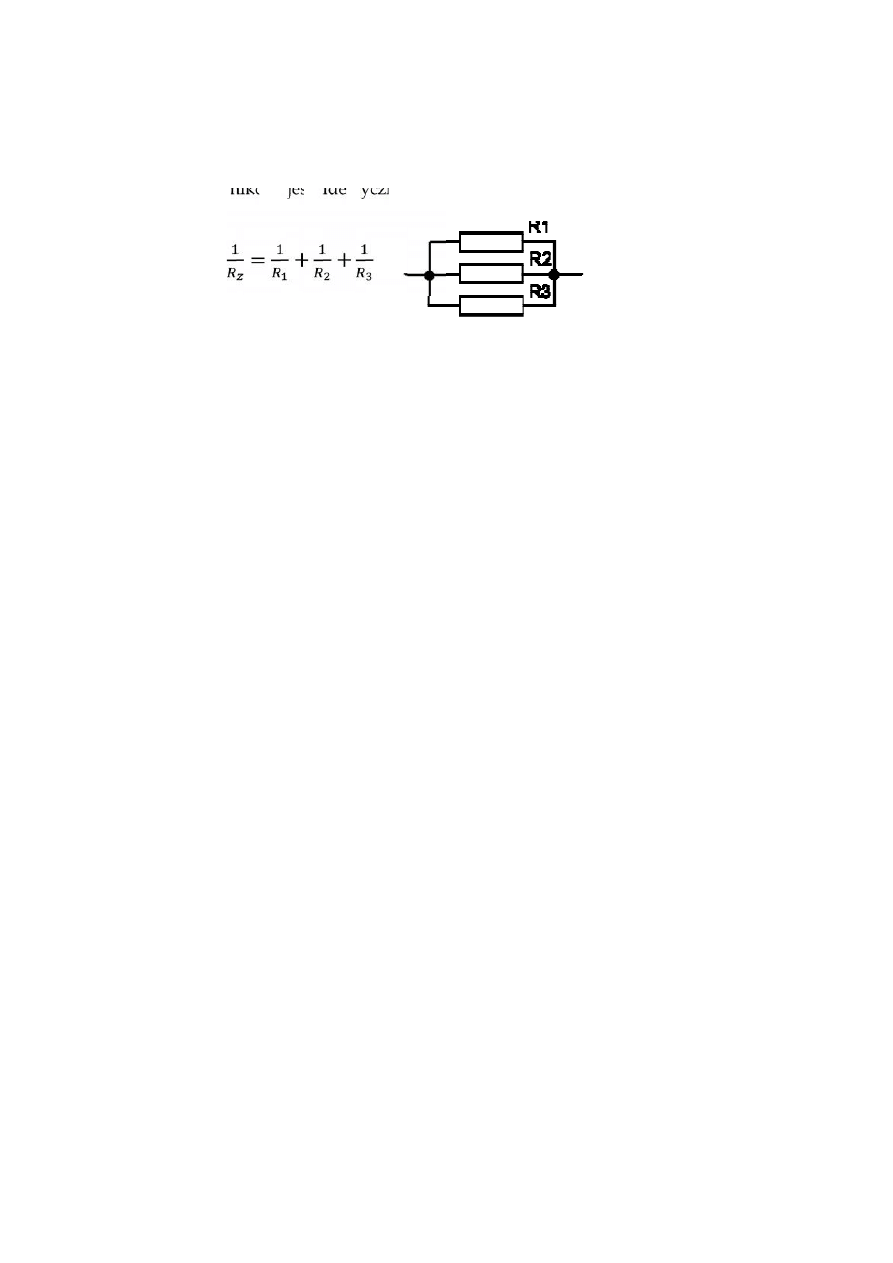
Równolegle: W przypadku takiego połączenie następuje spadek napięcia, który na
każdym z oporników jest identyczny i jest równy spadkowi napięcia na rezystancji
zastępczej R
z
Matematycznie:
= + +
Pasmowa teoria przewodnictwa ciał stałych:
Wyróżniamy: izolatory, półprzewodniki i przewodniki. Po krótce omówię każdy z nich.
Izolatory – W swojej budowie najwyżej położone pasmo zwane pasmem przewodnictwa
materiały takie mają całkowicie wyplenione. Żeby przewodzenie prądu w takim materiale
było możliwe, to elektron musiałby wskoczyć na wyżej położony poziom w pasie
przewodnictwa. W izolatorach jednak jest to niemożliwe ze względu na zbyt dużą odległość
pomiędzy pasmem przewodnictwa a pasmem walencyjnym. Przerwa jest za duża i elektron
nie pokona takiej bariery energetycznej.
Półprzewodniki – w swojej budowie bardzo podobne są do izolatorów z tą jedynie różnicą,
że przerwa energetyczna jest mniejsza. Gdy w układzie temperatura zaczyna wzrastać,
elektrony mogą uzyskać energię, która pozwoli im pokonać barierę przerwy energetycznej i
przejdą na wyższy poziom – pasma przewodnictwa. W materiale takim zacznie płynąć prąd
elektryczny.
Przewodniki – Są to substancje, które bardzo dobrze przewodzą prąd elektryczny.
Charakteryzują się tym, że pasmo przewodnictwa jest tylko częściowo wypełnione i przerwa
energetyczna nie jest duża, więc elektrony mogą swobodnie przejść do wyższego stanu.
Opór elektryczny zmienia się wraz z wartością temperatury z tego powodu, że przewodniki
mają wokół siebie bardzo dużo elektronów, które stanowią gaz elektronowy. Są one
względem siebie w nieustannym ruchu gdy brak zewnętrznego źródła pola elektrycznego.
Możemy wytworzyć jednak dodatkową składową prędkości tych elektronów. Dokonać tego
można wytwarzając różnicę potencjałów. W jej wyniku gaz elektronowy dryfuje i zaczyna
płynąć prąd. Gdy zwiększamy energię (w postaci temperatury) rosną amplitudy drgań
atomów sieci krystalicznej wokół położeń równowagi. Powoduje to, że maleje średnia droga
swobodna elektronów (częściej się ze sobą zderzają) a w konsekwencji opór właściwy rośnie.
Przewodnictwo przewodników przy wzroście temperatury maleje (opór wzrasta) – Pt, Ni, a
półprzewodników i dielektryków rośnie (opór maleje) – C. Dzieje się tak dlatego, że jak
napisano wyżej rośnie amplituda drgań atomów w sieci krystalicznej, co powoduje, że w
przypadku przewodnika utrudniają one ruch swobodnych elektronów, (przewodnictwo
maleje) natomiast w przypadku dielektryka ułatwiają oderwanie się elektronów
walencyjnych (przewodnictwo rośnie).
Zależność oporu i oporu właściwego od temperatury:
−
=
( − )
=
+
( − )
=
−
( − )
Gdzie:
– opór właściwy w temperaturze T
– opór właściwy w temperaturze
– temperaturowy współczynnik oporu właściwego
T – temperatura dla której badamy wartość oporu
– opór opór przewodnika w temperaturze T
– opór początkowy, wartość określana dla konkretnej temperatury początkowej
( )
α to temperaturowy współczynnik oporu właściwego, który jest wielkością, która
dla każdego materiału przyjmuje inne wartości. Dla niklu i platyny jest on dodatni i
wynosi odpowiednio: 0,006 [ ] i 0,003 [ ]. Natomiast dla węgla współczynnik ten
przyjmuje wartość ujemną i wynosi -0,0005 [ ].
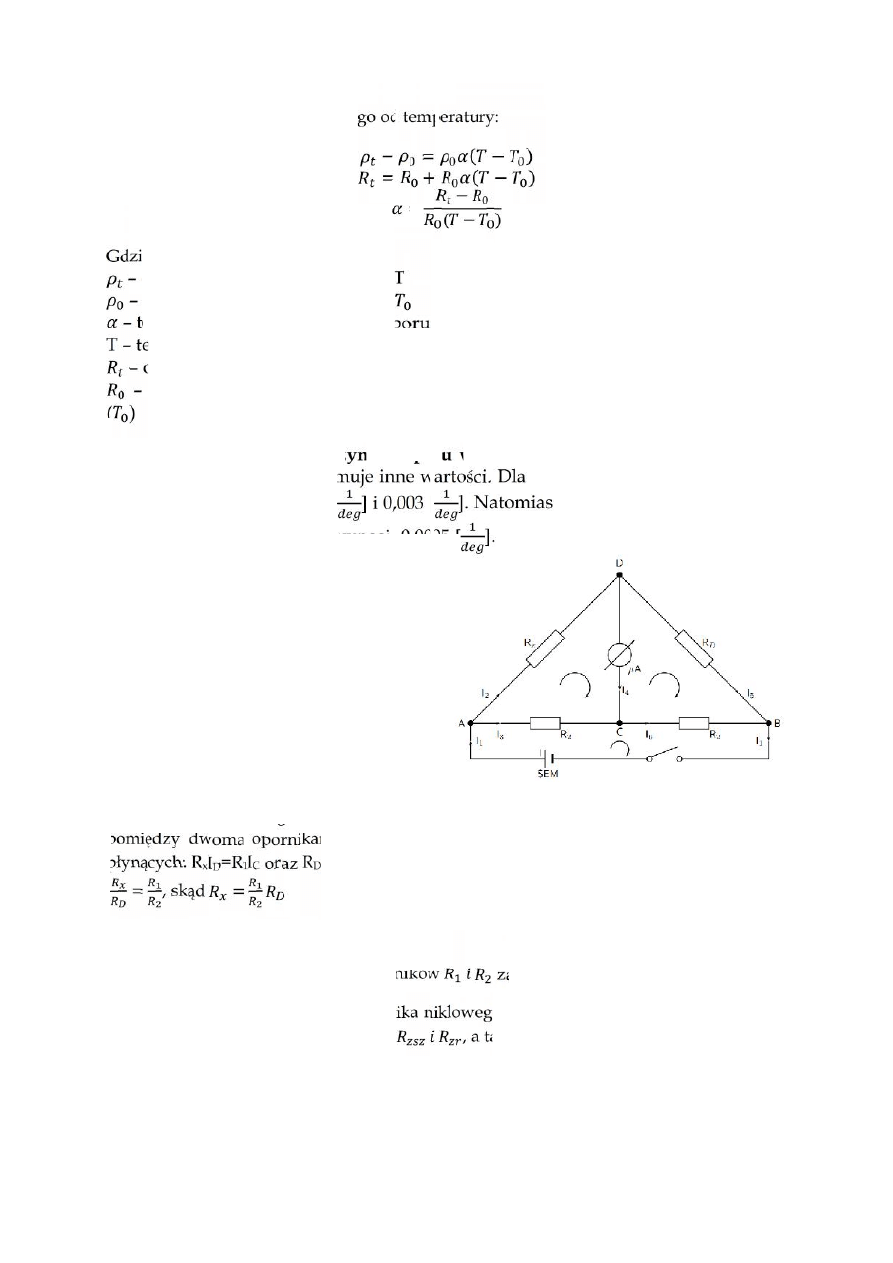
W ćwiczeniu zbudować należało układ
zwany mostkiem Wheatestone’a.
Układ taki zbudowany jest z:
- źródła napięcia
- 4 oporników
- mikroamperomierza
Znane są opory 3 oporników co pozwala nam
obliczyć opór 4-go opornika.
Gdy mostek jest zrównoważony, przed
odcinek CD nie płynie prąd. Tak więc natężenie prądu I
1
=I
5
=I
D
oraz I
3
=I
6
=I
C
. Jeśli
skorzystamy z drugiego prawa Kirchhoffa, po przekształceniach otrzymamy zależność
pomiędzy dwoma opornikami połączonymi równoległe i natężeniami prądów przez nie
płynących: R
x
I
D
=R
1
I
C
oraz R
D
I
D
=R
2
I
C.
Po kolejnych przekształceniach dochodzimy do postaci
= , skąd
=
Przebieg ćwiczenia:
1. Wyznaczono wartość oporu dla oporników
za pomocą omomierza
2. Zmierzono wartość oporu dla opornika niklowego i platynowego za pomocą omomierza
w temperaturze 28,5 °C. Zmierzono też
, a także R
c
.
3. Własnoręcznie zbudowano mostek Wheatestone’a i podłączono go do źródła napięcia 1,5
V.
4. Układ ogrzewano od temperatury 28,5 °C. do 90 °C.
5. Gdy obwód był otwarty, ustawiono na opornicy dekadowej spodziewaną wartość oporu
(wyznaczonych na podstawie wcześniejszych pomiarów za pomocą omomierza) dla
poszczególnych oporników. Następnie zamykano obwód kluczem, zmieniano wartość
oporu na opornicy dekadowej tak, aby wskazówka mikroamperomierza była jak najbliższa
położeniu równowagi (0 A), czyli prąd nie płynął. Za pomocą termometru odczytywano
temperaturę, w jakiej ustalono dany opór opornicy dekadowej. Niepewność termometru jest
równa najmniejsze podziałce skali. Powtarzano czynności przedstawione w tym punkcie dla
poszczególnych oporników przy różnych temperaturach.
6. Po osiągnięciu przez układ maksymalnej temperatury 90 °C układ stopniowo ochładzano i
ponownie zapisywano zmiany oporu dla poszczególnych oporników.
7. Po zakończeniu pomiarów układ rozmontowano.
Opracowanie wyników:
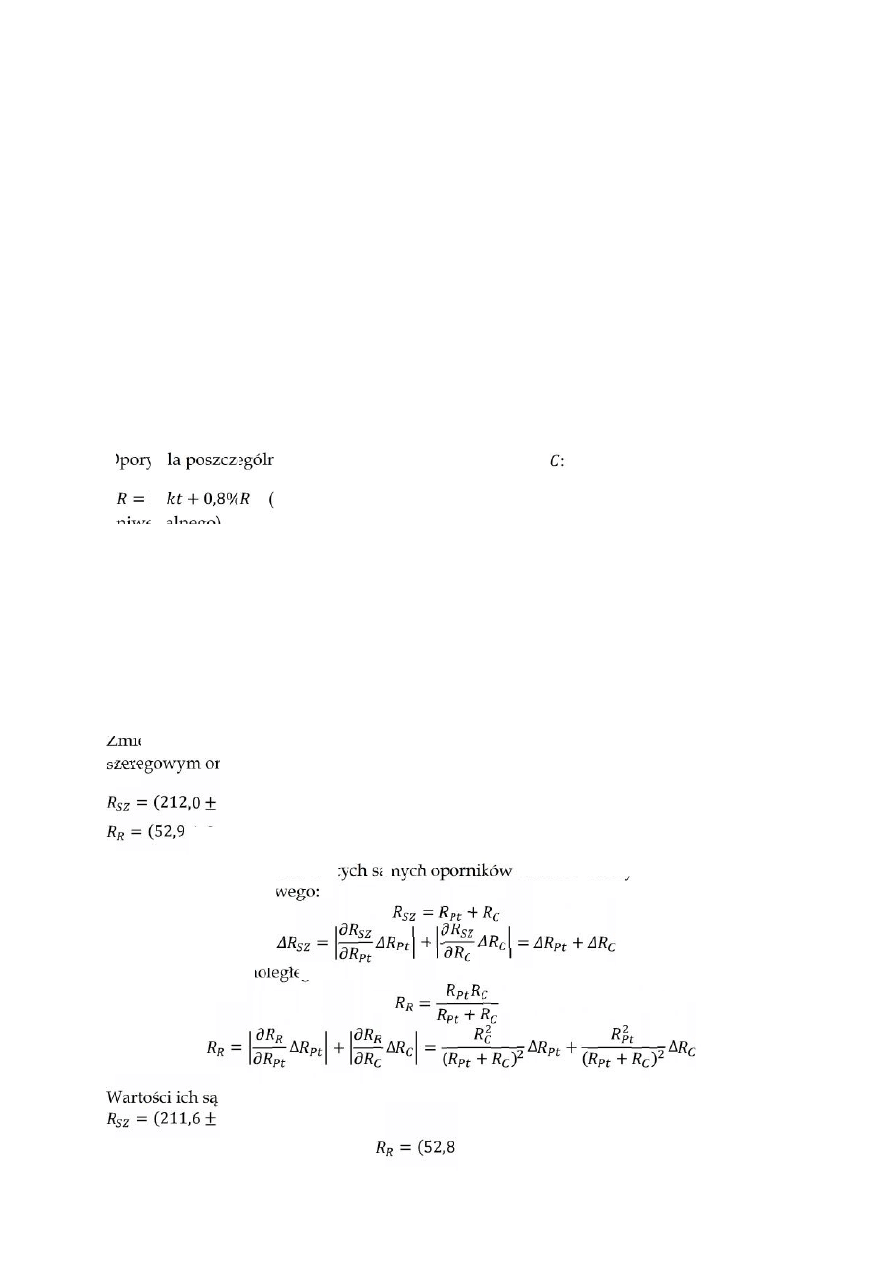
Opory dla poszczególnych oporników w temperaturze 28,5 ° :
∆ = 00 + 0,8%
(niepewność dla pomiarów mierzonych za pomocą miernika
uniwersalnego)
R
Ni
=117,3 Ω
∆R
Ni
=1,1 Ω
R
Ni
=(117,3 ± 1,1) Ω
R
Pt
=110,8 Ω
∆R
Pt
=1,0 Ω
R
Pt
=(110,8±1,0)Ω
R
C
=100,8 Ω
∆R
C
=0,9 Ω
R
C
=(100,8±0,9)Ω
R
zsz
=211,6 Ω
∆R
zsz
=2,7 Ω
R
zsz
=(211,6 ± 2,7) Ω
R
zr
=52,9 Ω
∆R
zr
=0,6 Ω
R
zr
=(52,9 ± 0,6) Ω
R
1
=10,4 Ω
∆R
1
=0,2 Ω
R
1
=(10,4 ± 0,2) Ω
R
2
=10,0 Ω
∆R
2
=0,2 Ω
R
2
=(10,0 ± 0,2) Ω
Zmierzono wartości oporu dla dla opornika węglowego i platynowego przy połączeniu
szeregowym oraz równoległym. Wynosiły one odpowiednio:
= (212,0 ± 2,7) Ω
= (52,9 ± 0,6) Ω
Wartość teoretyczną oporu dla tych samych oporników obliczono korzystając ze wzorów:
Dla połączenia szeregowego:
=
+
=
+
=
+
Dla połączenia równoległego:
=
+
Δ
=
Δ
+
Δ
= ( + ) ∆ + ( + ) ∆
Wartości ich są równe:
= (211,6 ± 1,9) Ω
= (52,8 ± 0,5) Ω
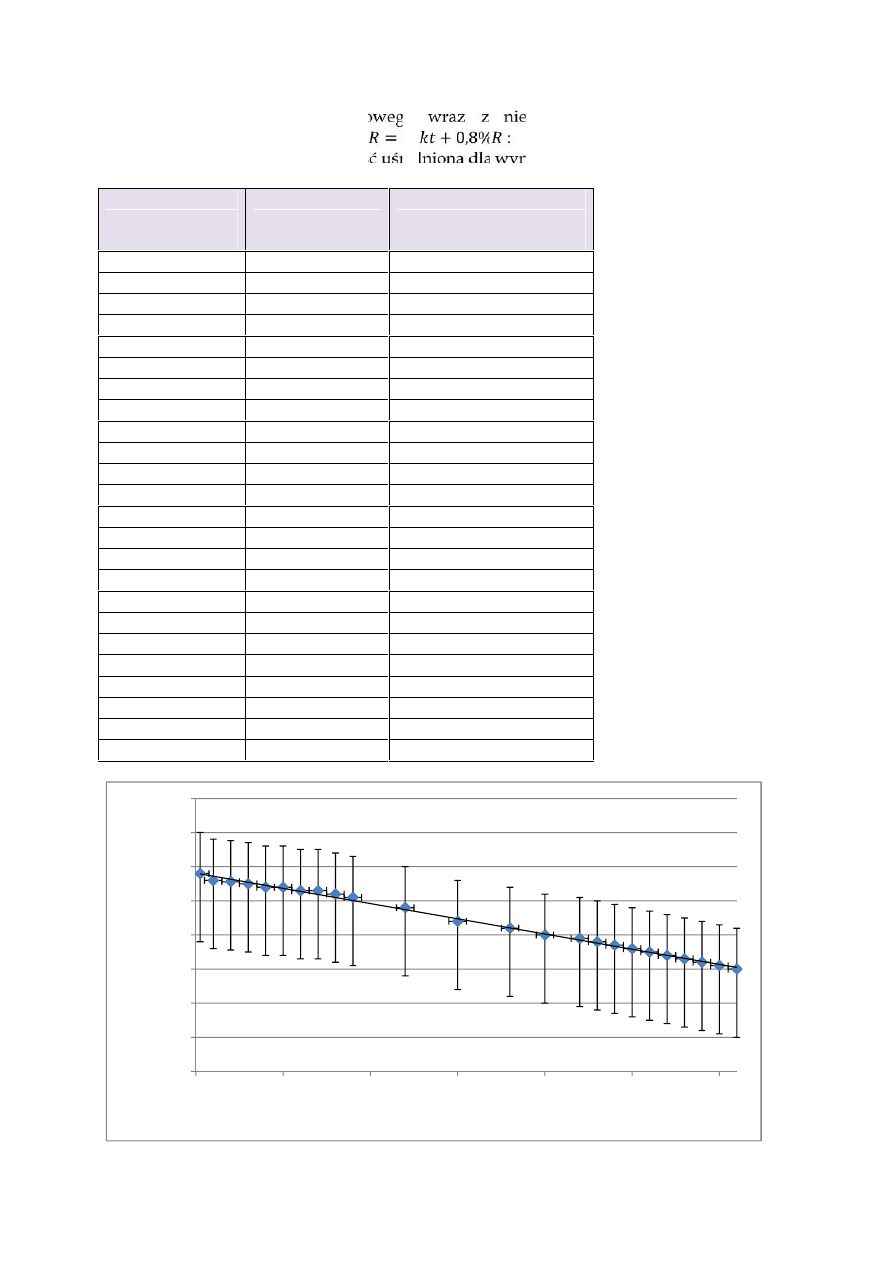
Wartości oporu opornika węglowego wraz z niepewnością mierzone miernikiem
elektronicznym za pomocą wzoru ∆ = 00 + 0,8% :
Temperatura występuje jako wartość uśredniona dla wyników z ogrzewania i ochładzania.
temperatura
T
[°C]
(∆T=1 °C)
opór
opornika
węglowego R
C
[Ω]
niepewność
oporu
opornika
węglowego ∆R
C
[Ω]
28,5
100,9
0,6045
30
100,8
0,6040
32
100,78
0,6039
34
100,75
0,6038
36
100,7
0,6035
38
100,7
0,6035
40
100,65
0,6033
42
100,65
0,6033
44
100,6
0,6030
46
100,55
0,6028
52
100,4
0,6020
58
100,2
0,6010
64
100,1
0,6005
68
100
0,6000
72
99,95
0,5998
74
99,9
0,5995
76
99,85
0,5993
78
99,8
0,5990
80
99,75
0,5988
82
99,7
0,5985
84
99,65
0,5983
86
99,6
0,5980
88
99,55
0,5978
90
99,5
0,5975
y = -0,0223x + 101,53
R² = 0,9963
98
98,5
99
99,5
100
100,5
101
101,5
102
28
38
48
58
68
78
88
R[
Ω
]
T[
°C]
Przy liczeniu oporu i jego niepewności dla oporników niklowego i platynowego posłużono
się wzorami:
=
Δ
=
Δ
+
Δ
+
Δ
=
∆
+
∆ +
∆
W tabelach podobnie jak w przypadku opornika węglowego dla oporu przyjęto
wartość uśrednioną dla pomiarów z ogrzewania jak i ochładzania.
temperatura T [°C]
(∆T=1 °C)
opór
opornika
niklowego R
Ni
[Ω]
niepewność oporu opornika
niklowego ∆R
Ni
[Ω]
28,5
120,64
5,83
30
121,68
5,87
32
122,72
5,92
34
124,80
5,99
36
125,84
6,04
38
128,96
6,16
40
129,48
6,18
42
130,00
6,21
44
131,04
6,25
46
133,64
6,35
52
135,20
6,41
58
136,24
6,45
64
136,76
6,47
68
138,32
6,54
72
139,36
6,58
74
140,40
6,62
76
140,40
6,62
78
142,48
6,70
80
143,52
6,74
82
145,60
6,83
84
146,64
6,87
86
147,68
6,91
88
148,72
6,95
90
149,76
5,83
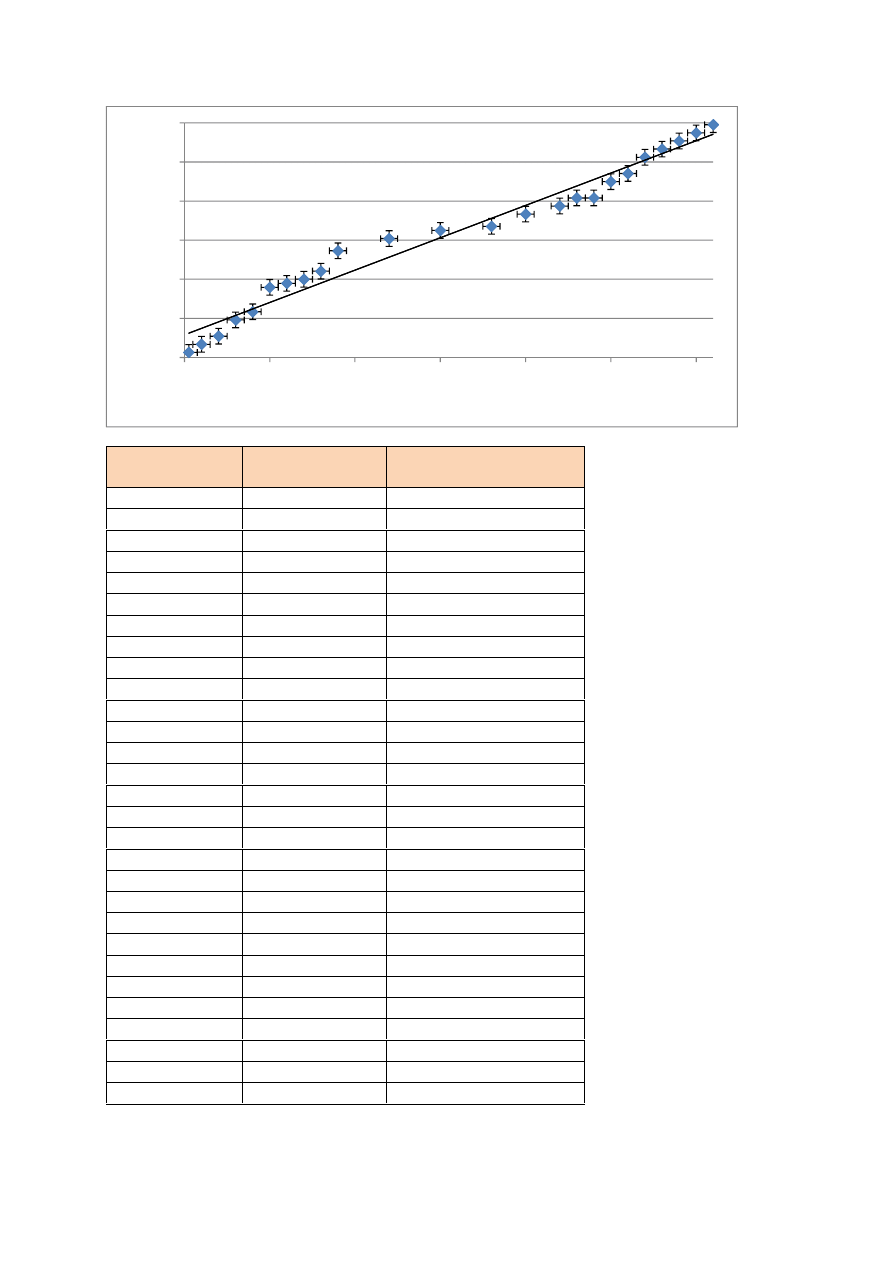
temperatura T [°C]
(∆T=1 °C)
opór opornika
platynowego R
Pt
[Ω]
niepewność oporu opornika
platynowego ∆R
Pt
[Ω]
34
113,36
5,54
36
113,36
5,54
38
114,40
5,59
40
115,44
5,63
42
116,48
5,67
44
116,48
5,67
46
117,52
5,71
48
118,56
5,75
50
119,08
5,77
52
118,56
5,75
54
119,60
5,79
56
121,16
5,85
58
120,64
5,83
60
122,72
5,92
62
122,72
5,92
64
123,76
5,96
66
123,76
5,96
68
125,84
6,04
70
125,84
6,04
72
127,92
6,12
74
127,92
6,12
76
129,48
6,18
78
130,00
6,21
80
130,52
6,23
82
131,04
6,25
84
132,08
6,29
86
133,12
6,33
88
134,16
6,37
90
135,20
6,41
y = 0,4137x + 111,31
R² = 0,9673
120
125
130
135
140
145
150
28
38
48
58
68
78
88
R[
Ω
]
T[
°C]
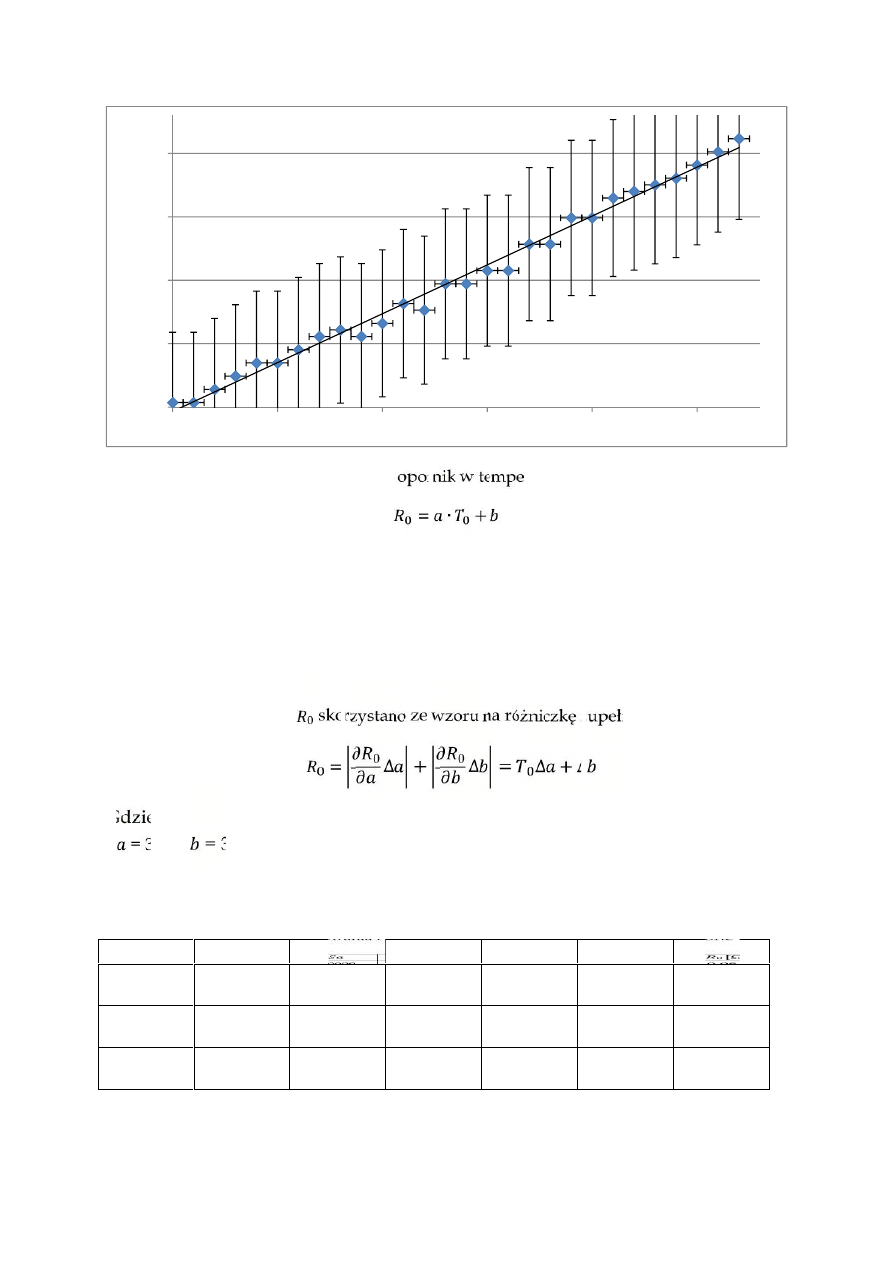
Opór który charakteryzuje odpowiedni opornik w temperaturze 20 ⁰C wyraża się wzorem:
= ∙
+
Gdzie: a i b to współczynniki prostej otrzymane za pomocą regresji liniowej. Wykresy i
obliczone współczynniki zostały w programie MsExcel i w sprawozdaniu pominięto te
obliczenia w celu poprawienia przejrzystości tekstu.
Wartości niepewności dla a i b to S
a
i S
b
.
Aby obliczyć niepewność
skorzystano ze wzoru na różniczkę zupełną a mianowicie:
∆
=
0
Δ +
0
Δ =
0
∆ + ∆
Gdzie
∆ = 3S
a
i
∆ = 3S
b
Wyniki pomiarów dla ogrzewania i ochładzania biorąc pod uwagę uśrednione
wartości wyników:
a
b
Sb
R
o
[Ω]
∆
0
[Ω]
Opornik
węglowy
-0,02
0,0009
101,53
0,06
101,13
0,08
Opornik
niklowy
0,41
0,06
111,31
3,30
119,51
4,50
Opornik
platynowy
0,39
0,021
99,37
0,44
107,17
0,86
y = 0,3854x + 99,546
R² = 0,9915
113,00
118,00
123,00
128,00
133,00
34
44
54
64
74
84
R[
Ω
]
T[
°C]
Przekształcając wzór na temperaturowy współczynnik oporu otrzymujemy równanie:
= ( − ) + 1
=
+ ( −
)
Tak więc: =
; =
−
Obliczone ze wzoru współczynniki ‘b’ regresji liniowej.
b
c
=101,13 − (−0,0002 ∙ 101,13 ∙ 20) = 101,53
b
Pt
=107,17−(0,0043 ∙ 107,17 ∙ 20) = 97,95
b
Ni
=119,51 − (0,0034 ∙ 119,51 ∙ 20) = 111,38
Czyli temperaturowy współczynnik oporu wynosi =
Niepewność tego współczynnika obliczona metodą różniczki zupełnej wynosi:
Δ =
Δ +
Δ
=
1
Δ +
Δ
[ ]
∆
Opornik
niklowy
0,0034
0,0005
Opornik
platynowy
0,0043
0,0002
Opornik
węglowy
-0,0002
0,000009
IV. Podsumowanie
Opory zastępcze połączenia szeregowego i równoległego oporników niklowego i
platynowego są zgodne z oporami zastępczymi teoretycznymi w granicach ich niepewności.
Dla połączenia szeregowego wartość teoretyczna to: