2010 06 Szkoła konstruktorów klasa III

Czerwiec 2010

Elektronika dla Wszystkich

Policz 172

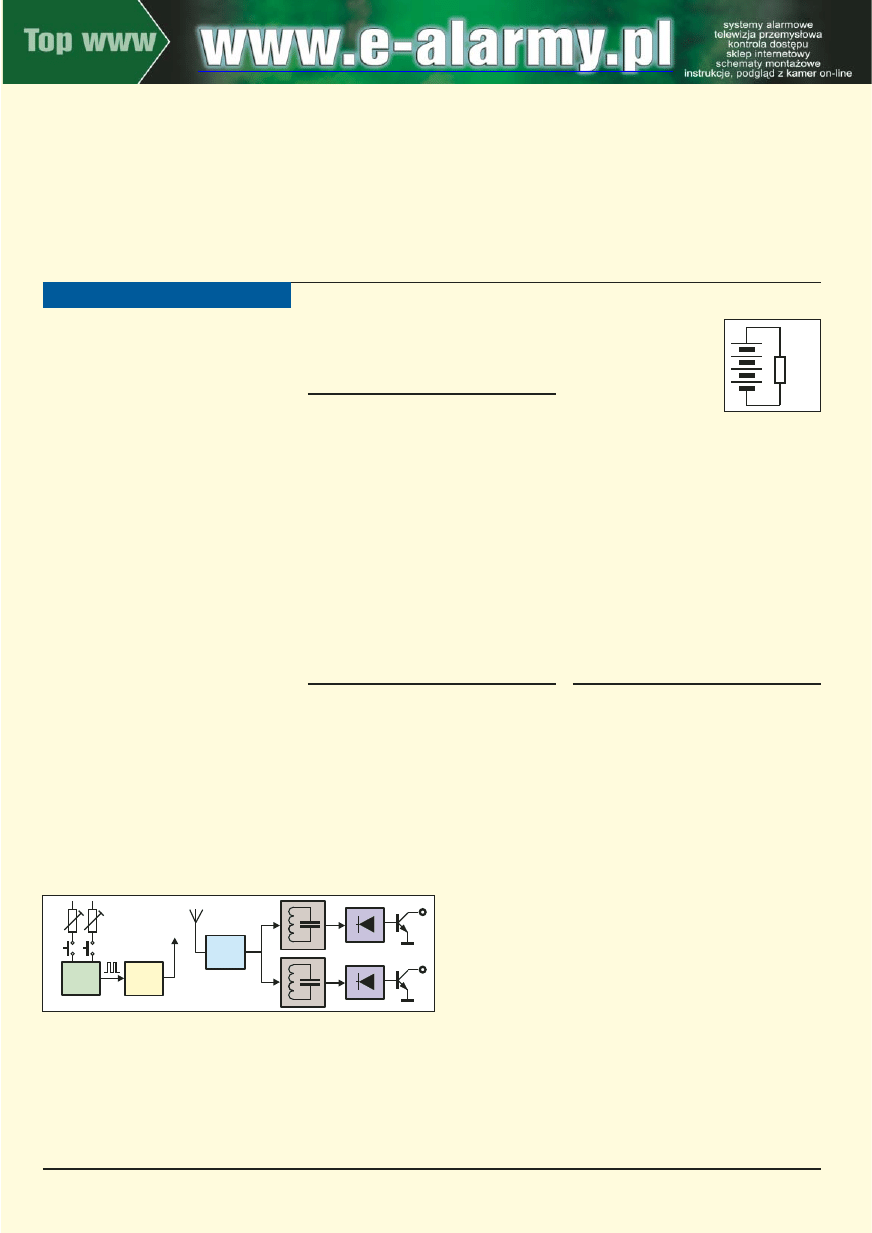
Przymierzamy się do budowy nietypowego,
eksperymentalnego zdalnego sterowania z
wykorzystaniem modułów radiowych 433MHz.
Posiadane moduły umożliwiają przesyłanie syg-
nałów o częstotliwości do 5kHz. W naszym
systemie potrzebne są tylko dwa rozkazy. W
nadajniku pracowałby generator przebiegu pro-
stokątnego, który po naciśnięciu przycisku dałby
przebiegi o jednej z potrzebnych częstotliwości
f

lub f

. Zastanawiamy się, czy w odbiorniku

nie wykorzystać dwóch obwodów rezonanso-
wych nastrojonych na te dwie częstotliwości,
według ogólnej idei z rysunku A. Zakładamy,
że częstotliwości tych obwodów f

, f

będą

leżeć w zakresie 1...5kHz. Chcemy wykorzy-
stać gotowe dławiki i popularne kondensatory
MKT. Gotowi jesteśmy przeprowadzić liczne
próby, sprawdzić różne konfiguracje układowe
i sprawdzić doświadczalnie, czy taka koncepcja
się sprawdzi. Jednak nawet do wstępnych prób
potrzebne są elementy LC, które trzeba kupić.
W ramach zadania 172 należy:
- zaproponować wartości częstotliwości f

, f

- obliczyć, jakie dławiki i kondensatory nale-
ży w tym celu zakupić.

Jak zawsze, bardzo proszę, żeby nadsyłane

rozwiązania były możliwie krótkie. Praca powin-
na zawierać zwięzły opis przebiegu obliczeń.

Nagrodami będą kity AVT lub książki, a

najaktywniejsi uczestnicy są okresowo nagra-
dzani bezpłatnymi prenumeratami EdW lub
innego wybranego czasopisma AVT. Wszystkie
rozwiązania należy nadsyłać w terminie 60 dni
od ukazania się tego numeru EdW. Powinny

one mieć dopisek

Policz172 (na kopercie,

a w tytule maila dodatkowo nazwisko, np.:
Policz172Jankowski). Z uwagi na specyfikę
zadania, bardzo proszę o podawanie swoje-
go wieku oraz miejsca nauki czy pracy. W
e-mailach podawajcie też od razu swój adres
pocztowy.

Zapraszam do rozwiązania tego zadania

zarówno doświadczonych, jak i początkujących

elektroników, którzy nie potrafią przeanalizo-
wać wszystkich subtelności układu. Można też
jeszcze nadsyłać rozwiązania zadania Policz171
z poprzedniego miesiąca.

Rozwiązanie zadania

Policz 167

W EdW 1/2010 przedstawione było zadanie
Policz167, które brzmiało: Mamy urządzenie
zasilane z czterech baterii jednorazowych, alka-
licznych paluszków AA. Średnio pobiera ono
moc 0,36W (

rysunek B).

W ramach zadania Policz167 należało:
- obliczyć, a raczej oszacować czas pracy z

jednego kompletu baterii.

Wprawdzie zadanie było o tyle trudniejsze,

że trzeba było zdobyć dodatkowe informacje o
pojemności alkalicznych paluszków AA (LR6),
jednak uczestnicy dobrze sobie z tym poradzili.
W Internecie można bez trudu znaleźć potrzeb-
ne informacje o pojemności. Efektem jest duża
liczba uczestników tego zadania.

Podstawowe obliczenia

Problem polegał na tym, że nie ma jednej
jedynie słusznej wartości pojemności baterii
alkalicznych. Producenci podają różne war-
tości, przeważnie w zakresie od 2000mAh do
3000mAh. Można było ostrożnie przyjąć, że
pojemność takiej baterii wynosi na przykład
2000mAh, czyli 2Ah. Do obliczeń trzeba też
było przyjąć wartość napięcia baterii – mogło to
być napięcie nominalne, czyli 1,5V. Pomnożenie
tych dwóch wartości daje ilość energii zawartej
w jednej baterii:

E = 2Ah * 1,5V =
3VAh = 3Wh

My mamy zestaw

czterech takich bate-
rii, więc sumaryczna
ilość zawartej w nich
energii to 12Wh.

W zadaniu było

podane, że średnia moc, czyli średni pobór ener-
gii, wynosi 0,36W.

Wystarczy podzielić ilość energii przez moc,

by otrzymać czas pracy:
t = 12Wh / 0,36W = 33,3h

Baterie starczą na 33 godziny, czyli jedną

dobę i dziewięć godzin.

Większość uczestników liczyła nieco ina-

czej. Rysunek B sugeruje, że ogniwa są połą-

czone szeregowo, więc
ich napięcie się sumuje.
W najprostszym przypad-
ku można było przyjąć,
że napięcie w obwodzie
wynosi 4*1,5V=6V, co
przy mocy 0,36W=360mW daje prąd
I = 360mW / 6V = 60mA

Teraz wystarczyło podzielić

pojemność ogniwa przez prąd, by otrzymać
czas pracy. Dla pojemności 2000mAh wynik
jest oczywiście taki sam:
t = 2000mAh / 60mA = 33,3h

Poszczególni uczestnicy przyjęli różne

wartości pojemności ogniwa alkalicznego, od
1800mAh do 2890mAh i obliczone przez nich
mniejsze lub większe czasy pracy odpowiadały
tak przyjętej wartości. Takie proste obliczenia
pozwalały oszacować czas pracy z bardzo małą
dokładnością, niemniej były jak najbardziej
prawidłowym i wystarczającym rozwiązaniem
postawionego zadania.

Dla dociekliwych

W omawianym przypadku dokładne obliczenia
były praktycznie niemożliwe, i to z kilku powo-
dów. Warto mieć wyobrażenie o wchodzących
tu w grę zależnościach i wątpliwościach, by
nie trzymać się kurczowo wzorów i informacji
handlowych. Otóż na uzyskiwaną pojemność
mają duży wpływ rozwiązania technologiczne,
wykorzystywane przy produkcji baterii. Baterie
dobrych firm mają znacząco lepsze właści-
wości od wielu znacznie tańszych baterii nie-
markowych (ale czasem bywa też odwrotnie).
Dokładniejsza analiza mogłaby wykazać, że
korzystniejsze ekonomicznie jest wykorzysty-
wanie trochę gorszych, ale dużo tańszych baterii
niemarkowych niż drogich wyrobów znanych
firm, reklamujących się w telewizji. Ale to
zupełnie inny temat. Dla nas ważny jest fakt, że
nieużywane baterie alkaliczne różnych wytwór-
ców mogą mieć znacząco różną pojemność.

Pojemność baterii. Jeden z uczestników

napisał: Według angielskiej Wikipedii pojem-
ność alkalicznych baterii AA, czyli LR6, wynosi
od 1700 do 3000mAh.

Ale to nie jest cała prawda o bateriach:

pojemność zależy nie tylko od producenta, ale
też od prądu rozładowania i od temperatury
pracy. W materiałach reklamowych podawa-
na jest pojemność przy małym albo bardzo

Trzecia klasa Szkoły Konstruktorów

cia i będą statyczne, realizowane za pomo-
cą woltomierza i amperomierza, to wszystko
może się zgadzać i może się wydawać, że
układ uwzględnia obecność rezystora R8 i dzia-
ła świetnie. Wady można wykryć dopiero za
pomocą oscyloskopu, zmieniając gwałtownie
prąd obciążenia. Wtedy okaże się, iż parametry
dynamiczne takiego zasilacza są wręcz fatalne.
A to może się zemścić w wielu praktycznych
zastosowaniach. Niestety, analizowany układ
został zaprojektowany przez kogoś, kto nie

czuje problemów związanych z zasilaczami, a
w omawianym układzie z rysunku B technika
cyfrowa nie jest w stanie wyeliminować wad i
błędów części analogowej.

Ogólnie biorąc, zadanie Co tu nie gra?

numer 167 okazało się trudne. Napłynęło
mniej niż zwykle rozwiązań. Wygląda na to, że
część uczestników nie przeanalizowała dokład-
nie działania tranzystora, współpracującego z
układem LM317. Owszem, część uczestników
słusznie podkreślała, że wadą jest umieszczenie

rezystora pomiaru prądu R8, jednak nie poja-
wiły się prawidłowe propozycje poprawy. Jak
wspomniałem, tymi kwestiami zajmiemy się
szeroko w cyklu Kuchnia Konstruktora. A na
razie podsumowując zadanie Co to nie gra? 167
informuję, że upominki otrzymują:
Andrzej Telszewski

– Banie,

Rafał Miąskiewicz

– Kawęczyn,

Jan Łocki

– Wrocław.

Wszystkich uczestników dopisuję do listy

kandydatów na bezpłatne prenumeraty.

generator

moduł

nadawczy

odbiorczy

0,36W

Rys. B

Rys. A

worldmags & avaxhome

Szkoła Konstruktorów

Elektronika dla Wszystkich

Czerwiec 2010

małym prądzie rozładowania. Bateria, która
rzeczywiście przy małych prądach, rzędu
miliamperów, ma pojemność 3000mAh, po
włożeniu do aparatu fotograficznego, który
pobiera dużo prądu, może mieć pojemność
tylko 1000mAh, a nawet mniej. Jeszcze gorzej
będzie w niskich temperaturach. Pojemność
zależy też od tego, czy bateria jest rozładowy-
wana w sposób ciągły, czy też jest wykorzy-
stywana okresowo i może „odpocząć”.

Producenci niezbyt chętnie informują o

takich faktach w materiałach reklamowych, nie-
mniej odpowiednie dane zawarte są w kartach
katalogowych ich baterii. Wiele cennych infor-
macji na ten temat można znaleźć w pliku:
http://data.energizer.com/PDFs/alkaline_app-
man.pdf

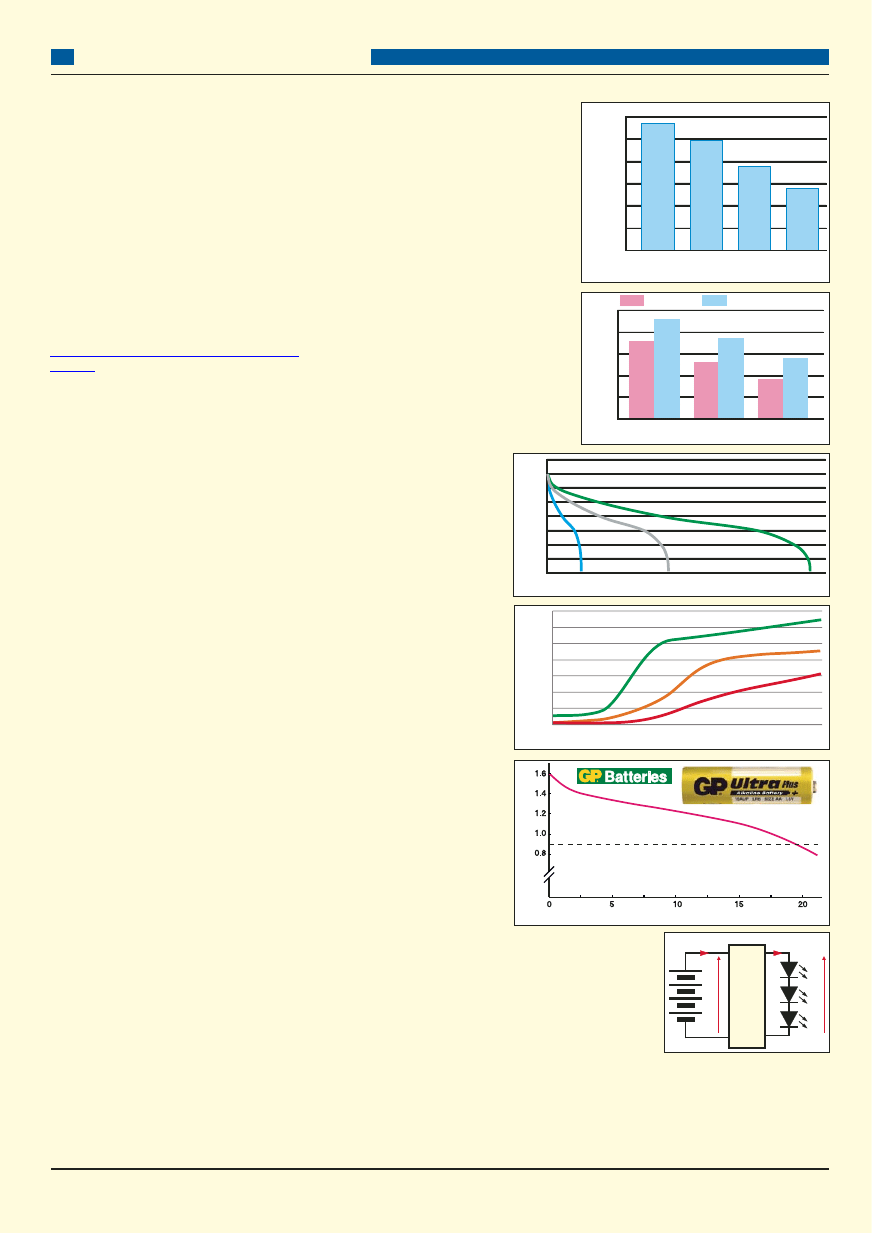
I tak rysunek C przedstawia zależność

pojemności od prądu rozładowania. Problem
ten w niewielkim stopniu dotyczy analizowa-
nego zadania, ponieważ prąd 60mA dla baterii
AA (LR6) to nie jest duży prąd, który znacząco
obniżyłby pojemność. Warto też wiedzieć, że
uzyskana pojemność zależy też w pewnym
stopniu od napięcia końcowego rozładowania.
Inna będzie zmierzona pojemność przy napięciu
końcowym 1,1V/ogniowo, a inna, większa, przy
napięciu końcowym 0,8V/ogniwo. Rysunek D
pokazuje korzystny wpływ pracy przerywanej.
W zadaniu nic na ten temat nie było powiedzia-
ne, możemy przyjąć, że chodzi o rozładowanie
ciągłe. Rysunek E przedstawia wpływ niskich
temperatur na pojemność baterii. Jeszcze jaśniej
pokazuje ten katastrofalny wręcz wpływ rysu-
nek F – w niskich temperaturach i przy dużych
prądach pojemność baterii jest bliska zeru.
Temperatura ma wpływ także na samorozłado-
wanie, ale odwrotny – czym niższa temperatura,
tym mniejsza samoczynna utrata pojemności. W
zadaniu nie było wzmianki o temperaturze, więc
możemy założyć, że chodzi o temperaturę poko-
jową i przyjąć dużą pojemność baterii 2000mAh
lub nawet trochę więcej.

Napięcie baterii. Podczas obliczeń trzeba

było przyjąć jakieś napięcie baterii. Niektórzy
nie poprzestali na nominalnej wartości 1,5V,
tylko analizowali przebieg napięcia podczas
rozładowania. Przykład krzywej rozładowania
pokazany jest na rysunku G. Ci dociekliwi
uczestnicy zwracali uwagę na fakt, że średnie
napięcie podczas pracy baterii na pewno nie jest
równe 1,5V i przyjęli mniejsze wartości.

Pobór prądu – właściwości obciążenia.

Fakt, że w baterii napięcie zmienia się w czasie
rozładowywania, wzbudził u niektórych pytania
o pobór prądu. Prosty rachunek pokazuje, że
moc 0,36W przy napięciu czterech baterii rów-
nym 6V oznacza prąd 60mA, ale przy napięciu
4V (1V/ogniwo) – 90mA. I niektórzy uczestnicy
przyjmowali takie zwiększone wartości prądu.

Czy jednak przy napięciu 1V/ogniwo pobór

prądu wzrośnie do 90mA? Czy zmniejszenie
napięcia może spowodować wzrost prądu? Czy
to ma sens i czy nie przeczy logice?

Nie sposób odpowiedzieć na to pytanie,

ponieważ w zadaniu nie było żadnych informa-

cji o tym, czym jest obciążenie. Wprawdzie na
rysunku B narysowany był rezystor, jednak w
zadaniu było wyraźnie powiedziane, że Mamy
urządzenie zasilane z czterech baterii (...). A
jeśli jest to urządzenie, to wbrew pozorom
możliwe jest, że przy zmniejszaniu się napię-
cia, prąd będzie wzrastał. I wcale nie trzeba
doszukiwać się tu jakiejś ujemnej rezystancji.
Taka sytuacja będzie miała miejsce na przy-
kład przy zastosowaniu przetwornicy impulso-
wej DC/DC do sterowania diod LED, jak na
rysunku H. Inteligentna przetwornica będzie
niezależnie od napięcia zasilania utrzymywać
niezmienne napięcie U

LED

i prąd I

LED

diod, a to

oznacza niezmienną moc na wyjściu przetwor-
nicy. Przetwornica ma wysoką i praktycznie
niezmienną sprawność. A to oznacza, że pobór
mocy z baterii (U

BAT

* I

BAT

) będzie stały, nie-

zależnie od napięcia baterii, czyli tak, jak w
postawionym zadaniu. Wtedy przy zmniejsza-
niu napięcia wyczerpującej się baterii pobierany
z niej prąd będzie wzrastał.

Inna sytuacja miałaby miejsce,

gdyby obciążeniem było źródło prą-
dowe, na przykład według rysunku
J. Wtedy pobór prądu będzie nie-
zmienny, praktycznie niezależny od
napięcia zasilania.

Jeszcze inna sytuacja będzie

przy obciążeniu o charakterze czy-
sto rezystancyjnym – wtedy prąd
będzie malał, proporcjonalnie do
zmniejszania się napięcia baterii. A
jeszcze inna sytuacja wystąpiłaby,
gdyby obciążeniem była klasycz-
na żarówka. Wolframowe włókno
żarówki ma znaczny dodatni współ-
czynnik cieplny. Przy zmniejszaniu
napięcia zasilającego, rezystancja
włókna będzie się zmniejszać, co
spowoduje mniejsze zmiany prądu,
niż w układzie z rezystorem. Na
rysunku K pokazane są przykła-
dowe charakterystyki prądowo-
-napięciowe wspomnianych rodza-
jów obciążenia. Podkreślam, że w
zadaniu nie było żadnej wzmian-
ki na temat charakteru obciążenia,
więc można było przyjąć dowolny
z omówionych przypadków.

A jeśli chodzi o charakterystyki

baterii przy obciążeniu o różnym
charakterze, to poszczególni producenci podają
informacje w różny sposób. W nielicznych kar-
tach katalogowych można znaleźć informacje o
pracy przy niezmiennej mocy (constant power).
Takie charakterystyki pokazane są na rysunku
L. Dane zgadzają się z naszymi wcześniejszymi
obliczeniami, bo podane w zadaniu 360mW
dotyczy 4 baterii, a więc na jedną przypadka
90mW. Najczęściej w kartach katalogowych
baterii podawane są wykresy rozładowania przy
niezmiennej rezystancji obciążenia. Przykład
masz na rysunku M. Gdy obliczymy, że nasze
obciążenie przy mocy 360mW, napięciu 6V,
prądzie 60mA ma 100

Ω i gdy uwzględnimy,

że na jedną
baterię przy-
pada jedna
czwarta tej
o p o r n o ś c i ,
czyli 25

Ω,

to znów potwierdzą się nasze wcześniejsze
obliczenia.

W katalogach dość często podawany jest

czas pracy przy niezmiennym prądzie. Przykład
masz na rysunku N. Znów zielona charak-
terystyka dotycząca „paluszków” LR6 (AA)

500

1000

1500

2000

3000

25mA

100mA 250mA 500mA

Pojemność

(mAh)

Prąd rozładowania

bateria AA/LR6

Pojemność (mAh) przy 21 C rozładowanie do 0.8V

500

1000

1500

2000

2500

250mA

1000mA

500mA

rozładowanie

ciągłe

rozładowanie

ciągłe

rozładowanie przerywane

10s praca / 90s przerwa

rozładowanie przerywane

10s praca / 90s przerwa

Pojemność

(mAh)

)

Prąd rozładowania

bateria AA/LR6

-20 C

0 C

-20 C

0.8

0.9

1.0

1.1

1.2

1.3

1.4

1.5

1.6

Czas (godziny - h)

Rozładowanie ciągłe 250mA

bateria AA/LR6

ię

500

1000

1500

2000

2500

3000

3500

-40

-20

25 mA

250 mA

1000 mA

Temperatura ( C)

Pojemno

ść

bateria AA/LR6

Hours

oltage

(V)

BAT

LED

Rys. D

Rys. E

Rys. F

Rys. G

Rys. H

Rys. C

worldmags & avaxhome

Szkoła Konstruktorów

Czerwiec 2010

Elektronika dla Wszystkich

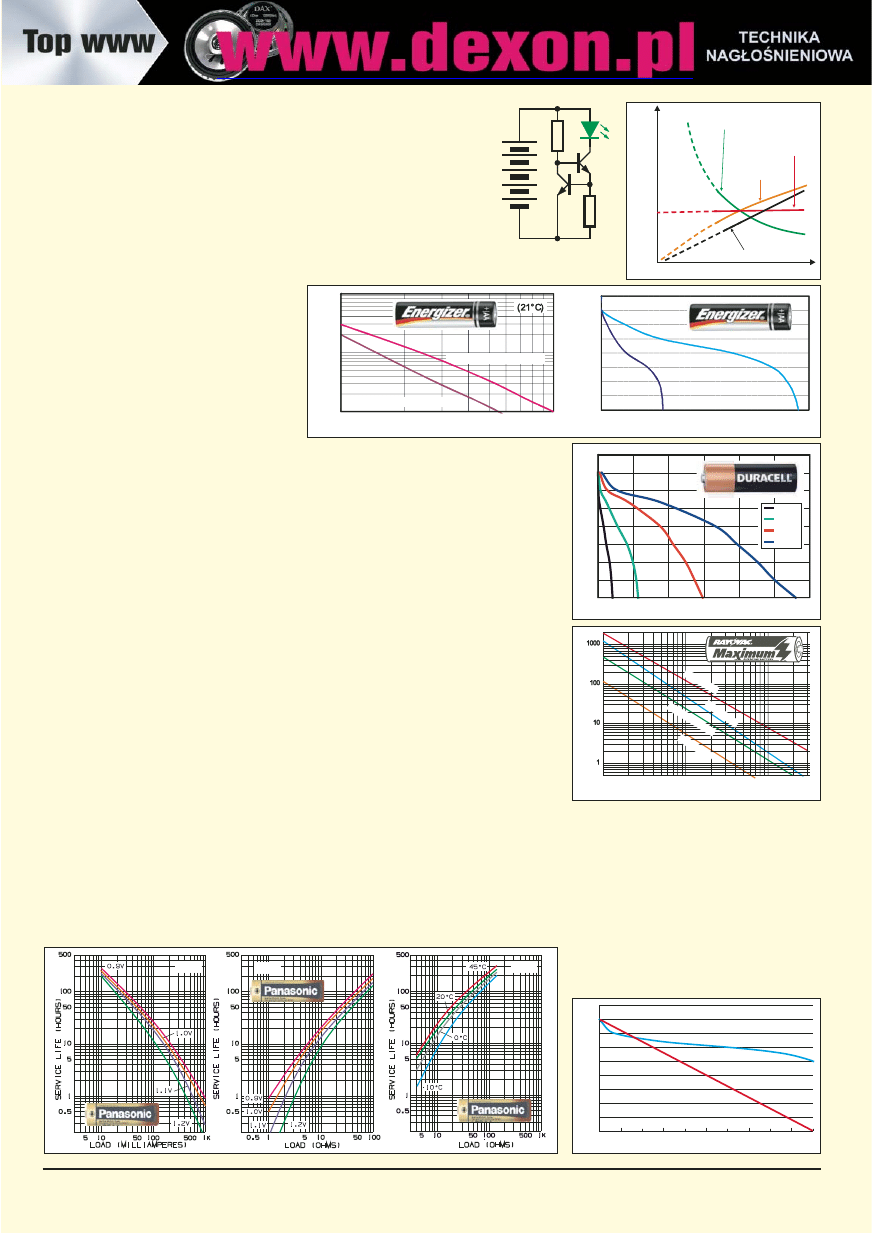
potwierdza nasze wcześniejsze obliczenia.
Warto też porównać krzywe rozładowania przy
stałym prądzie obciążenia i przy stałej rezystan-
cji obciążenia, jeśli producent podaje takie dane
– przykład na rysunku O.

Niektórzy Koledzy odszukali i porównali

parametry kilku baterii różnych producentów.
Ale to też nie daje kompletnego obrazu, ponie-
waż często jeden producent oferuje baterie alka-
liczne danej wielkości o różnych parametrach.

Zdecydowana większość uczestników obli-

czyła prąd pracy, a potem dzieląc pojemność
przez prąd, obliczała czas pracy. Tylko nieliczni
liczyli inaczej.

Dwóch młodych „przeliczyło” pojemność

baterii wyrażaną w miliamperogodzinach na
pojemność kondensatora. Teoretycznie można
obliczyć, w kondensatorze o jakiej pojemności
przy danym napięciu można zgromadzić tyle
samo energii, co w baterii. Przykładowo w bate-
rii o pojemności 2Ah 1,5V zawartych jest 3Wh
energii, co w przeliczeniu na watosekundy, czyli
dżule, daje 10800Ws=10800J. Po przekształce-
niu wzoru E = 0,5CU

można obliczyć pojem-

ność kondensatora, który naładowany do napię-
cia 1,5V zawierałby taką samą ilość energii:
C = 2*10800J / (1,5)

C = 21600 / 2,25
C = 9600F

Musiałby to być zestaw ultrakondensatorów

o łącznej pojemności 9600 faradów. Jednak nie
jest to właściwa droga nie tylko ze względu na
niepraktycznie wielką pojemność (choć obecnie
możliwą do zrealizowania). W kondensatorze
rozładowywanym niezmiennym prądem napię-
cie liniowo zmniejsza się do zera. Natomiast
bateria nie jest kondensatorem, tylko chemicz-
nym źródłem prądu i w pierwszym przybliżeniu
uznajemy, że napięcie podczas pracy jest nie-
zmienne. W rzeczywistości zmienia się według
krzywej, jednak na pewno zachowuje się zupeł-
nie inaczej niż rozładowywany kondensator,
jak pokazuje rysunek P. Dlatego nie należy
przeprowadzać takich analogii.

Dwóch uczestników wspomniało o rezy-

stancji wewnętrznej baterii. W tym przypadku
można ją było spokojnie pominąć, ponieważ
dla ogniw AA jest ona mniejsza niż 1 om, więc
przy prądzie rzędu 60mA nie odgrywa istotnego
znaczenia.

Jeden z Czytelników napisał, że zadania

rozwiązać się nie da, bo jest za mało

danych. W dalszej części maila
przedstawił jednak sensowne rozu-
mowanie i prawidłowo oszacował
czas pracy na około 30 godzin.

Opinia, że zadania rozwiązać

się nie da, jest charakterystyczna
dla typowo szkolnego, niepraktycz-
nego podejścia. Owszem, nie spo-
sób przeprowadzić precyzyjnych
obliczeń, ale nawet gdyby można
było, to nie miałyby one sensu. Trzeba spojrzeć

na problem ze strony praktycznej,

tak jak to bywa w życiu. Istotnie, nie mamy
wszystkich szczegółów, ale chcemy
mieć orientację, co do przybliżone-
go czasu pracy. Kolejny raz podkreślam, że w
życiu i w elektronice bardzo często mamy takie
właśnie sytuacje i takie potrzeby. I trzeba się
z nimi zmierzyć. Natomiast wielu nauczycieli
szkolnych nie uczy takiego praktycznego podej-
ścia, tylko przyzwyczaja uczniów do sztywnych
i suchych formułek. Potem tak ukształtowani
młodzi ludzie mają kłopoty z rozwiązaniem
rzeczywistych problemów technicznych, które
napotkają. Stwierdzają, że brakuje danych i
wzorów. A tymczasem często dane i wzory nie
są konieczne, a zdecydowanie bar-
dziej potrzebny jest zdrowy chłopski
rozum. Ja celowo dobieram tak zadania Policz,
żeby pokazać występujące w elektronice zależ-
ności i problemy. Celowo też dzielę rozwiązanie
na dwie części – podstawową i rozszerzoną.
W praktyce zazwyczaj wystarczy rozwiązanie
uproszczone, natomiast szersza wiedza o szcze-
gółach jest potrzebna konstruktorom, rozszerza
bowiem horyzonty i pozwala uniknąć wielu
poważniejszych czy drobniejszych błędów.

Jeśli chodzi o zadanie 167, to wszystkie

rozwiązania, z wyjątkiem jednego, mogę uznać
za prawidłowe. Jednocześnie podkreślam, że
nie było dwóch odpowiedzi jednakowych.

Szacowany przez uczestników czas pracy bate-
rii to 19 do 100 godzin. Gratuluję wszystkim
uczestnikom, którzy spróbowali zmierzyć się z
tym zadaniem! Upominki za zadanie Policz167
otrzymują:
Piotr Wachulec – Piotrków Trybunalski,
Łukasz Uszko – Ubiad,
Przemysław Smoliński – Sieradz.

Wszystkich uczestników dopisuję do listy

kandydatów na bezpłatne prenumeraty.

BAT

rezystor

żarówka

źródło prądowe

przetwornicaDC/DC

100

300

200

600

1000

Czas

pracy

(h)

)

Czas pracy (h)

0.8

0.9

1.0

1.1

1.2

1.3

1.4

1.5

1.6

Napięcie

(V)

ię

)

100 mW

250 mW

Obciążenie (mW)

napięcie końcowe 1,2V

napięcie końcowe 0,9V

21°C (70°F)

0.8

0.9

1.1

1.2

1.3

1.4

1.5

1.6

100

120

Czas pracy [h]

Napięcie

[V]

ię

]

3.9 OHM

10 OHM

24 OHM

43 OHM

Prąd [mA]

Czas

pracy

[h]

]

100

1000

3000

300

813=

LR20

814=

LR1

815=

LR06

=AA

824=

LR03

0.0

0.2

0.4

0.6

0.8

1.0

1.2

1.4

1.6

1.8

100

Napięcie

[V]

ię

]

Stopień rozładowania [%]

kondensator

bateria

Rys. J

Rys. K

Rys. L

Rys. M

Rys. N

Rys. O

Rys. P

worldmags & avaxhome