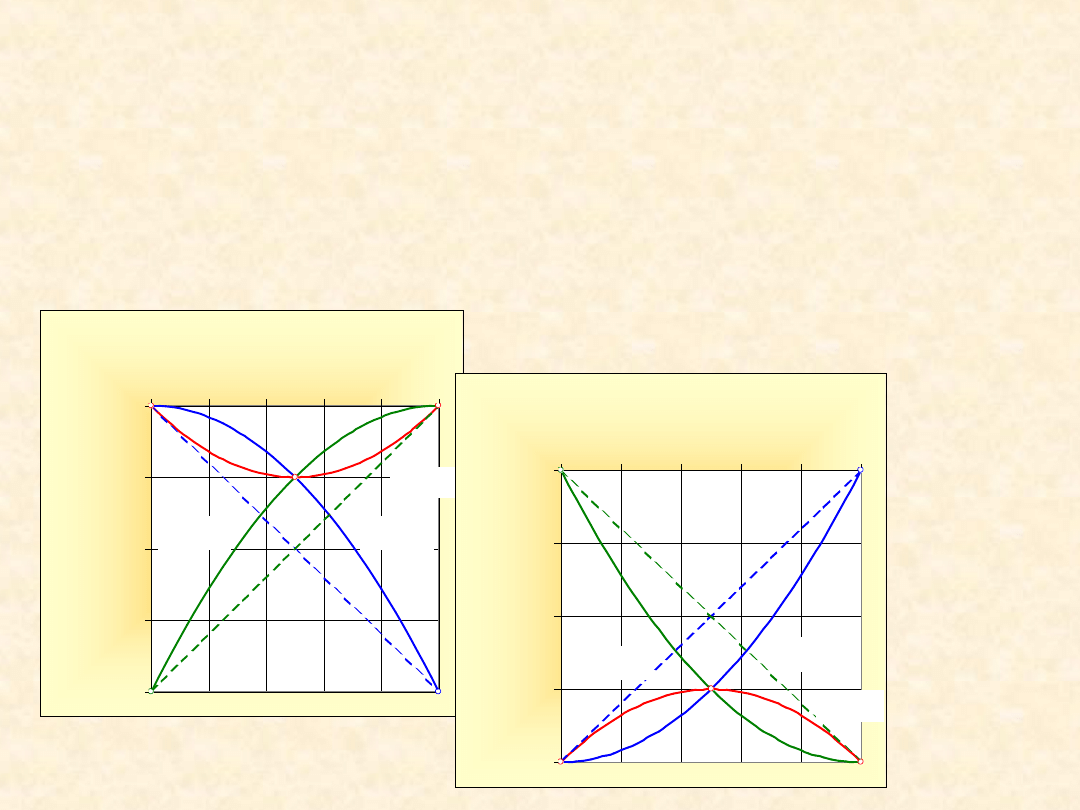
1

Fazy

wieloskładnikowe -

roztwory (a)

Waldemar Ufnalski

Wprowadzenie do termodynamiki

chemicznej

Wykład 10a

-1,00

-0,75

-0,50

-0,25

0,00

0,0

0,2

0,4

0,6

0,8

1,0

x

B

Y

E

/R

T

G

E

/RT



A

E

/RT



B

E

/RT

A

B

0,00

0,25

0,50

0,75

1,00

0,0

0,2

0,4

0,6

0,8

1,0

x

B

Y

E

/R

T

G

E

/RT



A

E

/RT



B

E

/RT

A

B

2

10.1. Opis

termodynamiczny

roztworu

Wykład 10a

3

Wielkości molowe
cząstkowe ...

Układ badany:

faza otwarta wieloskładnikowe jed -

norodna mogąca wymieniać materię z otoczeniem

dn

i

n

1

...

n

k

T,
P





k

n

n

n

P

T

Z

,

,

,

,

,



2

1

(1
)

















k

i

i

k

k

m

n

n

n

n

P

T

Z

x

x

x

P

T

Z

1

2

1

1

2

1

,

,

,

,

,

,

,

,

,

,





(2
)







k

j

j

i

i

n

n

x

1

(3
)

4



































k

i

i

i

n

n

T

n

n

P

dn

Z

dP

P

Z

dT

T

Z

dZ

k

k

1

1

1





,

,













i

j

n

P

T

i

k

i

n

Z

x

x

P

T

Z



















,

,

,

,

,





1

1



Wielkości molowe
cząstkowe ...

Różniczka zupełna ekstensywnej funkcji Z:

(4
)
(5
)



















































k

i

i

n

P

T

i

n

n

T

n

n

P

dn

n

Z

dP

P

Z

dT

T

Z

dZ

i

j

k

k

1

1

1

,

,

,

,

















Wielkość (funkcja) molowa cząstkowa:

(6
)

5

Wielkości molowe
cząstkowe ...

Funkcje jednorodne stopnia m:

(7
)

(8
)



Twierdzenie Eulera:

(9
)









k

m

k

y

y

y

f

a

ay

ay

ay

f





,

,

,

,

2

1

2

1



























k

i

y

i

i

k

i

j

y

f

y

y

y

y

mf

1

2

1







,

,

Ekstensywne
funkcje stanu są
funkcjami
jednorodnymi 1 -
go stopnia
względem ilości
składników.



1







k

i

i

i

Z

n

Z

T,P = const

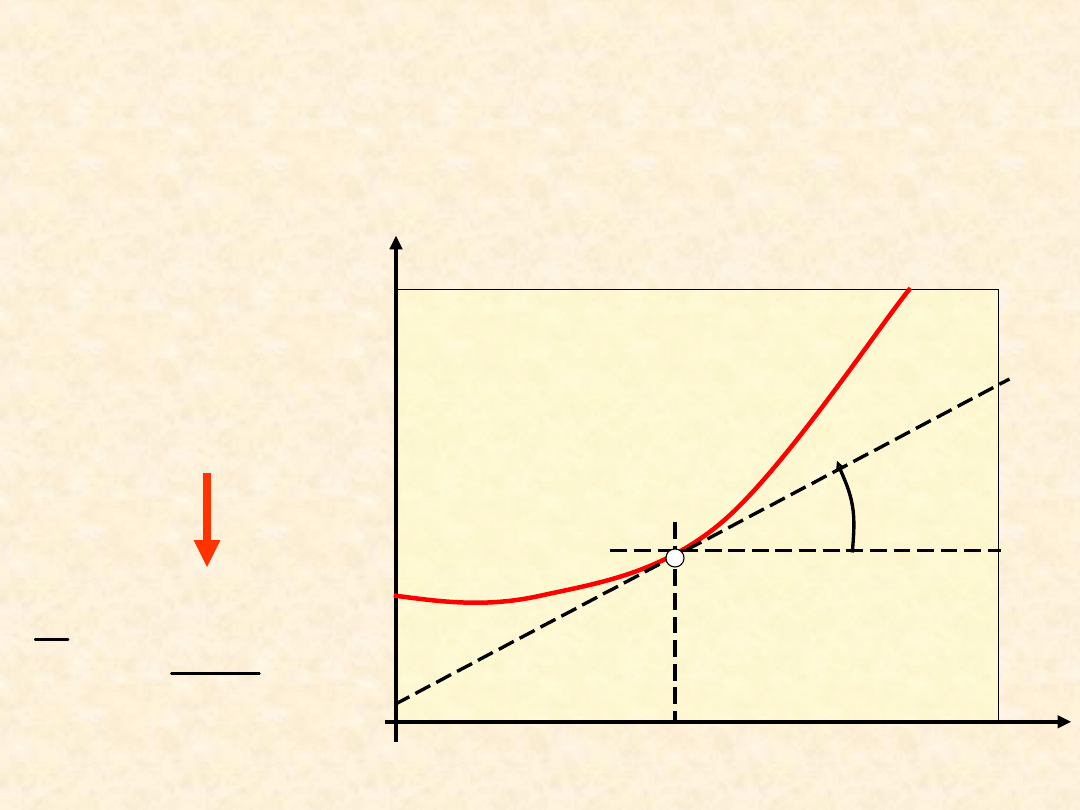
6

Wielkości molowe
cząstkowe ...

Sens fizyczny:

udział wnoszony przez 1 mol

składnika do funkcji stanu roztworu (np.
objętości, energii wewnętrznej, ...itd.)

Wyznaczani

e zgodnie z

definicją:

Y

n

B



i

j

n

P

T

i

i

n

Z

Z

















,

,





7

Wielkości molowe
cząstkowe ...

Relacje T, P = const

(1
1)

(1
0)



Relacja Gibbsa - Duhema

(12
)









k

i

i

i

dn

Z

dZ

1

1







k

i

i

i

Z

n

Z











k

i

i

i

k

i

i

i

dn

Z

Z

d

n

dZ

1

1

+

0

=

1





k

i

i

i

Z

d

n

8

Wielkości molowe
cząstkowe ...

Wniosek:

Zmiany wielkości molowych cząstkowych

w funkcji składu roztworu są od siebie zależne.

(12
a)

0

=

1





k

i

i

i

Z

d

n

0

=

1





k

i

i

i

Z

d

x

0

1























j

l

n

j

i

k

i

i

n

Z

n





0

1





















j

i

k

i

i

x

Z

x





(12
d)

(12
c)

(12
b)

Relacje Gibbsa - Duhema (T,P = const):

9

Wielkości molowe
cząstkowe ...

(13
a)

Układ dwuskładnikowy (T, P = const):



  

 

0

1







B

B

B

B

A

B

x

Z

d

x

x

Z

d

x





 

 

0

1







B

B

B

B

B

B

A

B

dx

x

Z

d

x

dx

x

Z

d

x

 





 

B

B

A

B

B

B

B

B

dx

x

Z

d

x

x

dx

x

Z

d







1

(13
b)

(13
d)

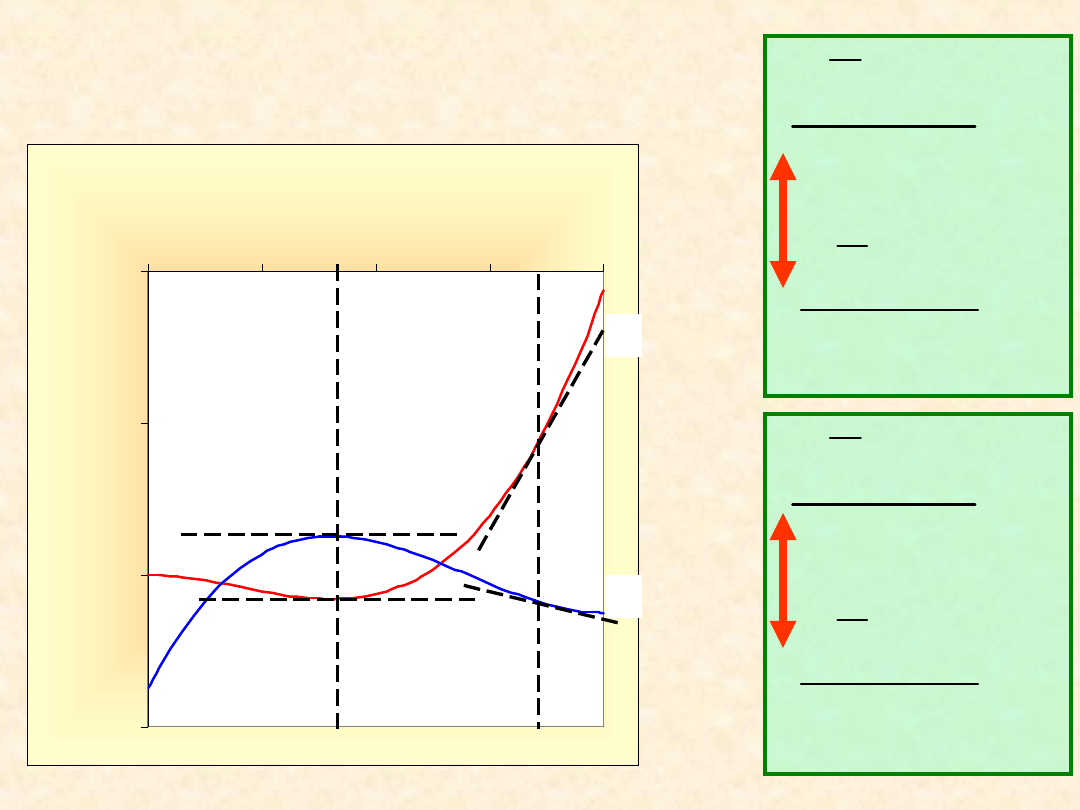
10

3,0

5,0

7,0

9,0

0,0

0,3

0,5

0,8

1,0

x

B

Z

i

Z

A

Z

B

Wielkości molowe
cząstkowe ...

Układ dwuskładnikowy (T, P = const):

 

0



B

B

B

dx

x

Z

d

 

0



B

B

A

dx

x

Z

d

 

0



B

B

B

dx

x

Z

d

 

0



B

B

A

dx

x

Z

d

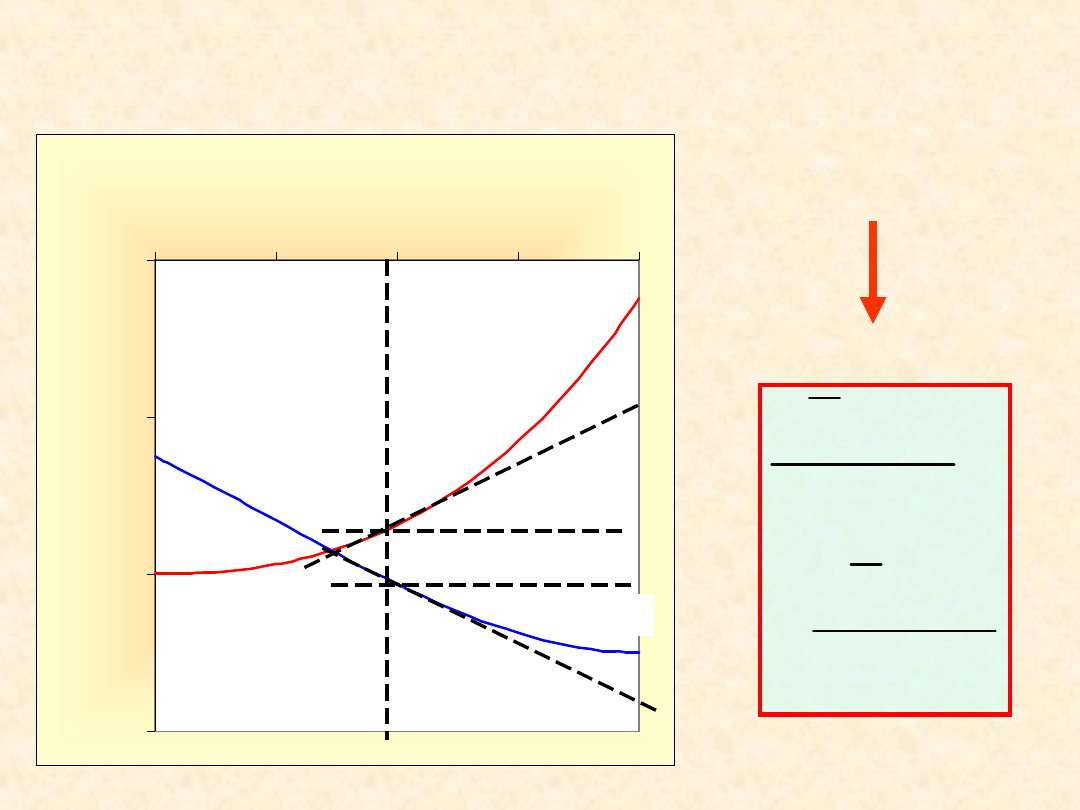
11

Wielkości molowe
cząstkowe ...

Układ dwuskładnikowy (T, P = const):

4,0

5,0

6,0

7,0

0,0

0,3

0,5

0,8

1,0

x

B

Z

i

Z

A

Z

B





x

B

= 1/2

 

 

B

B

A

B

B

B

dx

x

Z

d

dx

x

Z

d





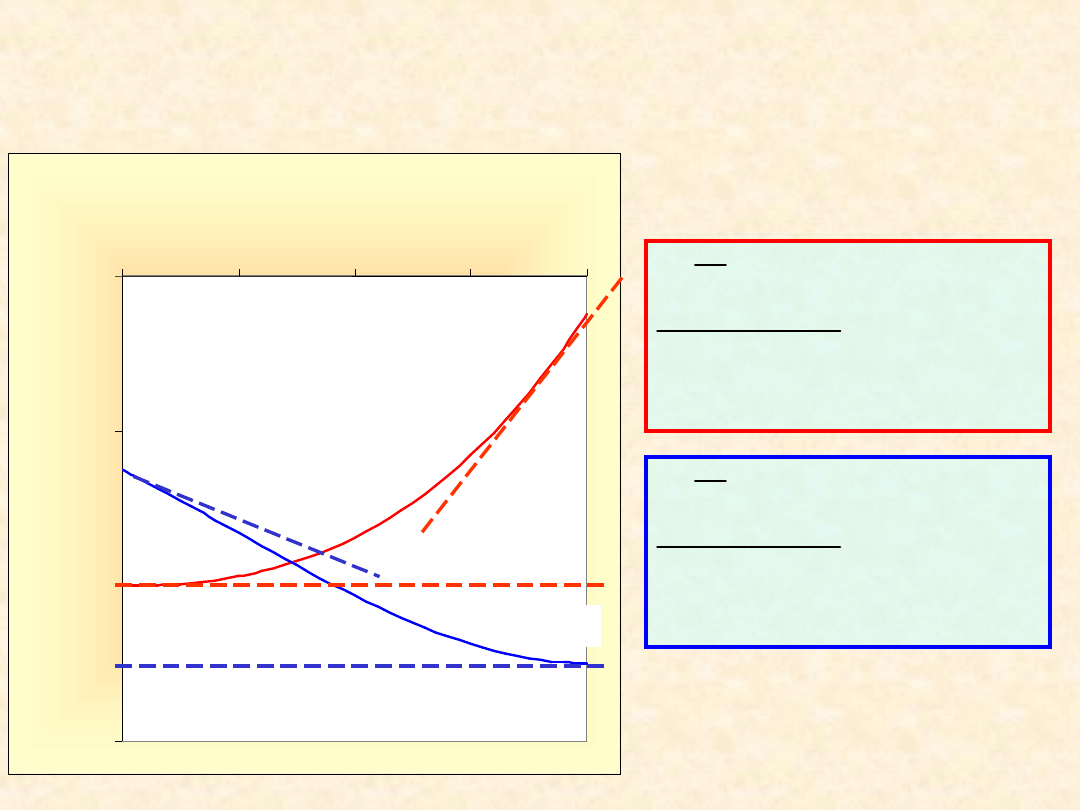
12

Wielkości molowe
cząstkowe ...

Układ dwuskładnikowy (T, P = const):

4,0

5,0

6,0

7,0

0,0

0,3

0,5

0,8

1,0

x

B

Z

i

Z

A

Z

B

 

0

1











B

X

B

B

B

dx

x

Z

d

 

0

0











B

X

B

B

A

dx

x

Z

d

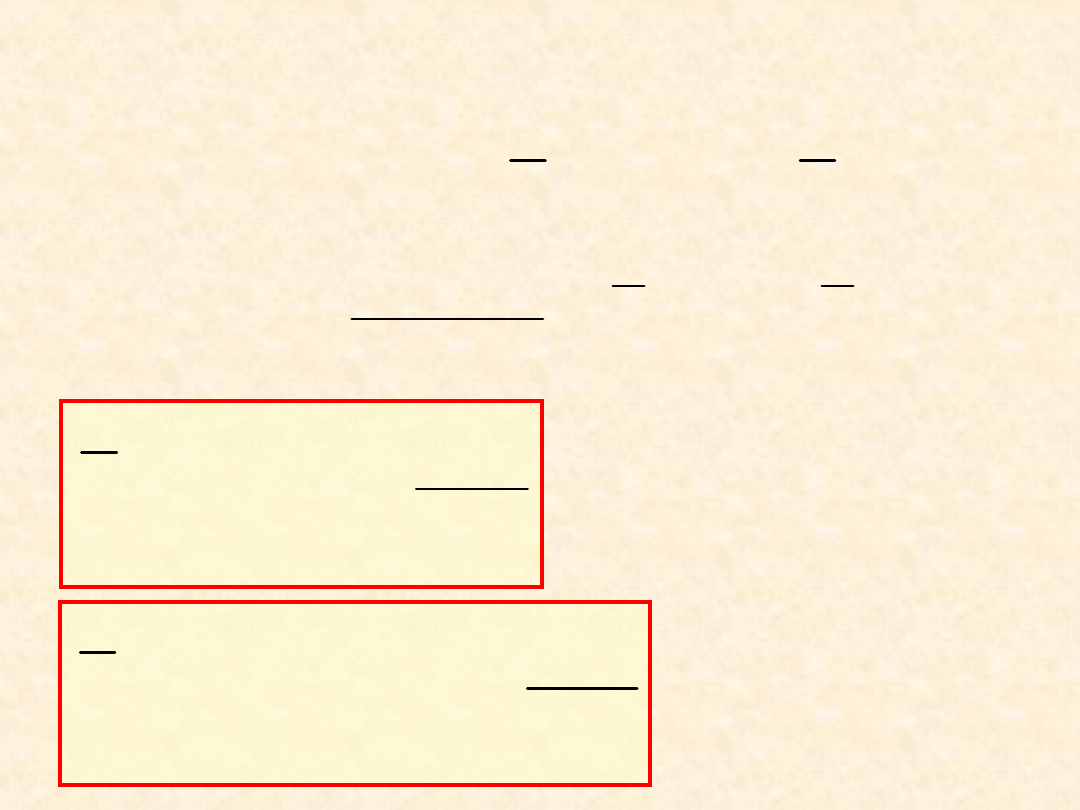
13

Wielkości molowe
cząstkowe ...

Wyznaczanie w układzie dwuskładnikowym ...

  

  

 

B

B

B

B

A

B

B

m

x

Z

x

x

Z

x

x

Z





 1

 

 

 

B

A

B

B

B

B

m

x

Z

x

Z

dx

x

dZ





B

m

B

m

A

dx

dZ

x

Z

Z









B

m

B

m

B

dx

dZ

x

Z

Z







1

(1
4)
(1
5)

(1
6)

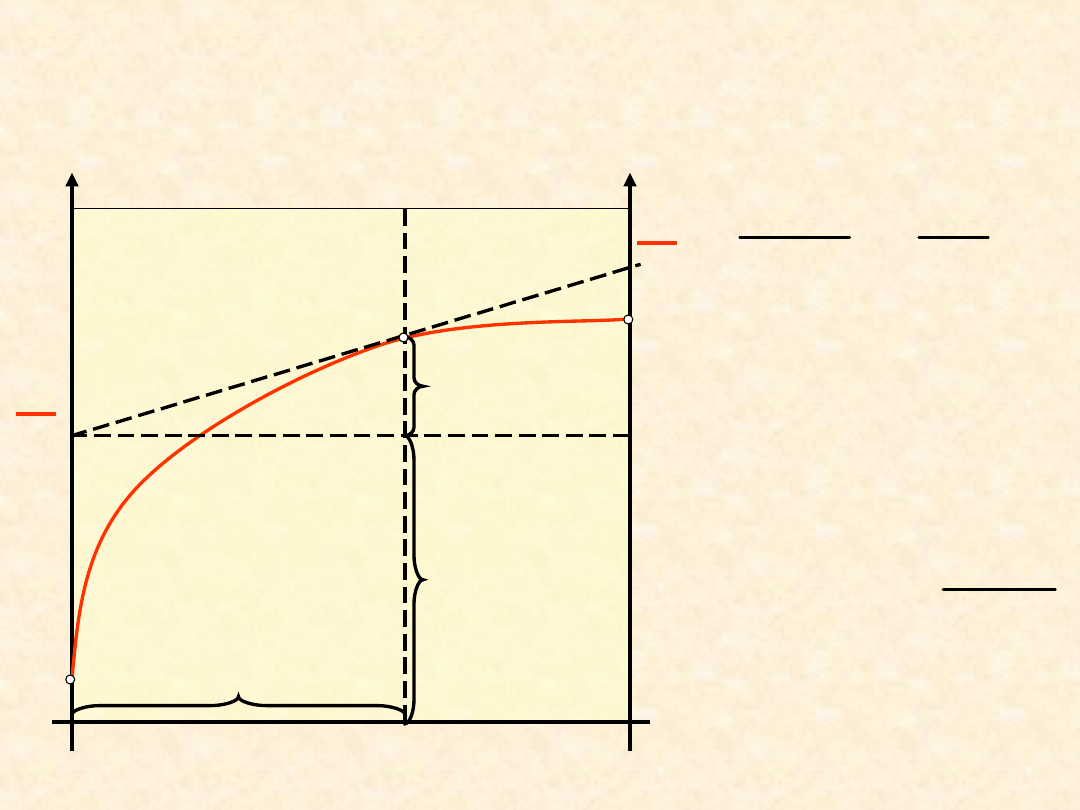
14

Wielkości molowe
cząstkowe ...

Wyznaczanie w układzie dwuskładnikowym

B

B

m

x

a

dx

dZ



B

m

B

m

m

dx

dZ

x

Z

a

Z

h









Z

m

x

B

B

A

a

x

B

h



Z

B

Z

A

15

Wielkości molowe
cząstkowe ...

Relacje:

takie same jak między funkcjami

molowymi substancji czystych.

i

i

i

S

T

H

G





i

x

P

i

S

T

G

















,





i

x

T

i

V

P

G















,





i

j

k

k

i

j

n

P

T

n

n

P

i

n

n

P

n

P

T

i

T

Z

n

n

Z

T



























































,

,

,

,

,

,

,

,





1

1

















(1
7)



Wobec:

.....

16

Wielkości molowe cząstkowe -

potencjał chemiczny ...

(1
8)







k

n

n

n

P

T

G

,

,

,

,

,



2

1





k

n

n

n

V

T

F

,

,

,

,

,



2

1

,

















































k

i

i

n

P

T

i

n

n

T

n

n

P

dn

n

G

dP

P

G

dT

T

G

dG

i

j

k

k

1

1

1

,

,

,

,

















..
.

















































k

i

i

n

V

T

i

n

n

T

n

n

V

dn

n

F

dV

V

F

dT

T

F

dF

i

j

k

k

1

1

1

,

,

,

,

















..
.

17





i

j

i

j

i

j

i

j

n

P

S

i

n

V

S

i

n

V

T

i

n

P

T

i

k

i

n

H

n

U

n

F

n

G

x

x

P

T

































































,

,

,

,

,

,

,

,

,

,

,



















=

1

1



Wielkości molowe cząstkowe -

potencjał chemiczny ...

(1
9)

..
.



























k

i

i

n

P

T

i

dn

n

G

VdP

SdT

dG

i

j

1

,

,

































k

i

i

n

V

T

i

dn

n

F

PdV

SdT

dF

i

j

1

,

,





Można wykazać ogólnie:

Potencjał
chemiczny
składnika

18

10.2. Funkcje mieszania

i funkcje nadmiarowe

Wykład 10a

19

Funkcje mieszania

(T,P

=const)

...

(2
0)











k

i

i

i

k

P

T

Z

n

Z

n

n

n

1

2

1

moli

skladniki

Czyste

,

,

,

*

*















k

i

k

i

i

k

x

x

P

T

Z

n

Z

n

n

n

1

1

1

2

1

moli

Roztwor





,

,

,

,

,

















































k

i

i

k

i

i

k

i

i

i

k

i

k

i

i

M

P

T

Z

x

x

P

T

Z

n

P

T

Z

n

x

x

P

T

Z

n

Z

Z

Z

1

1

1

1

1

1

1

,

,

,

,

,

,

,

,

*

*

*





Funkcja
mieszania

20





























k

i

i

k

i

i

k

i

i

M

M

m

P

T

Z

x

x

P

T

Z

x

n

Z

Z

1

1

1

1

,

,

,

,

*



Funkcje mieszania

(T,P

=const)

...

(2
1)

Molowa funkcja mieszania:

Relacje:

takie same jak między funkcjami

molowymi substancji czystych.



M

m

x

P

M

m

S

T

G

















,





M

m

x

T

M

m

V

P

G















,





M

m

M

m

M

m

TS

H

G





..
.

(2
2)

21

Funkcje mieszania ...

Wyznaczanie w układzie dwuskładnikowym ...

(2
3)

  

  





 





*

*

B

B

B

B

A

B

A

B

B

M

m

Z

x

Z

x

Z

x

Z

x

x

Z









 1



B

M

m

B

M

m

A

A

dx

dZ

x

Z

Z

Z







*





B

M

m

B

M

m

B

B

dx

dZ

x

Z

Z

Z









1

*

22

Funkcje mieszania;

wyznaczanie w

układzie

dwuskładnikowym

Z

M

m

x

B

B

A

Z

B

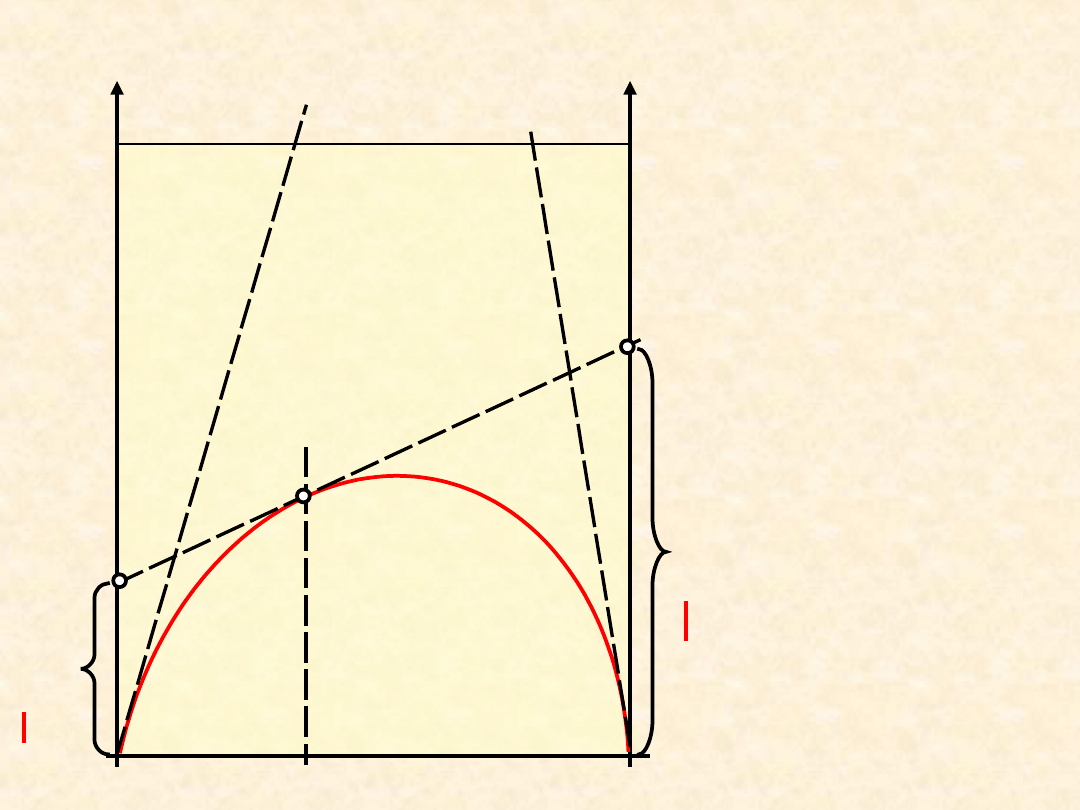
(x

B

)-

Z

* B

Z

A

(x

B

)-

Z

* A

23

Funkcje mieszania-

definicja

roztworu

doskonałego...

(24a/
b)



Dla gazów doskonałych - model molekularny







k

i

i

i

M

dosk

m

x

x

RT

G

1

ln

)

(









k

i

i

i

M

dosk

m

x

x

R

S

1

ln

)

(

lub

Zależność (24a) lub (24b) przyjmuje się
arbitralnie jako termodynamiczną
definicję roztworu doskonałego

24

Funkcje mieszania-

roztwór

doskonały...

(25)

























k

i

i

i

x

P

M

dosk

m

M

dosk

m

x

x

R

T

G

S

1

ln

.

)

(

)

(





0







M

dosk

m

M

dosk

m

M

dosk

m

TS

G

H

)

(

)

(

)

(

0



















x

T

M

dosk

m

M

dosk

m

P

G

V

.

)

(

)

(





0







M

dosk

m

M

dosk

m

M

dosk

m

PV

H

U

)

(

)

(

)

(

0



















x

P

M

dosk

m

M

dosk

P

T

H

C

.

)

(

)

(





25

Funkcje mieszania-

funkcje molowe

cząstkowe składników roztworu
doskonałego...

(26)

i

i

dosk

i

dosk

i

x

RT

G

ln

*

)

(

,

)

(

,











i

i

m

dosk

i

x

R

S

S

ln

*

,

)

(

,





;

;

;

;

*

,

)

(

,

,

*

,

)

(

,

*

,

)

(

,

*

,

)

(

,

i

P

dosk

i

P

i

m

dosk

i

i

m

dosk

i

i

m

dosk

i

C

C

U

U

V

V

H

H









26

Nadmiarowe funkcje
mieszania...

(27)















































k

i

E

i

i

k

i

dosk

i

i

i

k

i

i

dosk

i

i

k

i

i

i

i

M

dosk

m

M

m

E

Z

x

Z

Z

x

Z

Z

x

Z

Z

x

Z

Z

Z

1

1

1

1

)

(

,

*

)

(

,

*

)

(

Definicja:

27

Nadmiarowe funkcje
mieszania...

(2
8)

Relacje...









k

i

i

i

M

m

E

x

x

RT

G

G

1

ln









k

i

i

i

M

m

E

x

x

R

S

S

1

ln

M

m

P

E

P

M

m

E

M

m

E

M

m

E

C

C

U

U

V

V

H

H

,

;

;

;









28

Relacje:

takie same jak między funkcjami

molowymi substancji czystych.

Nadmiarowe funkcje
mieszania...



E

x

P

E

S

T

G

















,





E

x

T

E

V

P

G















,





E

E

E

TS

H

G





(2
9)

..
.

)

(

, dosk

i

i

E

i

Z

Z

Z





(3
0)

29

Wyznaczanie w układzie dwuskładnikowym ...

Nadmiarowe funkcje
mieszania...

  

  

 





 

 







  

 

B

E

B

B

B

E

A

B

B

dosk

B

B

B

B

B

dosk

A

B

A

B

B

E

x

Z

x

x

Z

x

x

Z

x

Z

x

x

Z

x

Z

x

x

Z

















1

1

)

(

,

)

(

,



(3
1)

B

E

B

E

E

A

dosk

A

A

dx

dZ

x

Z

Z

Z

Z









)

(

,





B

E

B

E

E

B

dosk

B

B

dx

dZ

x

Z

Z

Z

Z











1

)

(

,

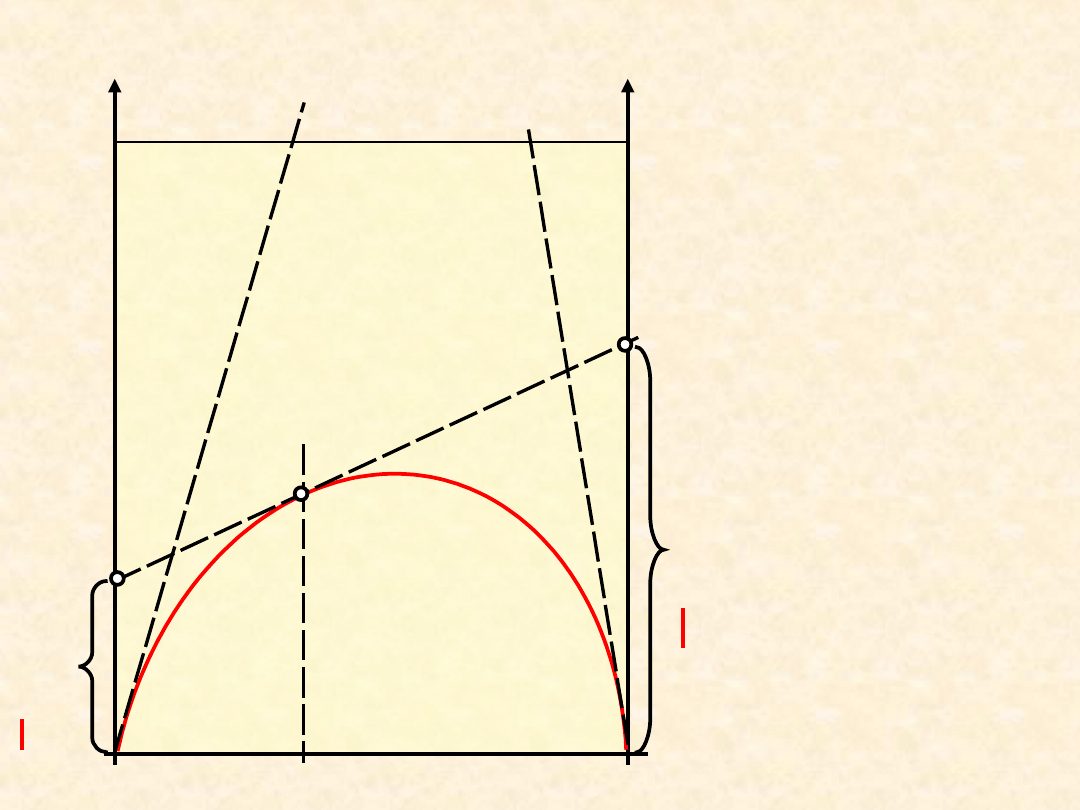
30

Z

E

x

B

B

A

Z

B

E

(x

B

)

Z

A

E

(x

B

)

Nadmiarowe funkcje mieszania;

wyznaczanie

w układzie

dwuskładnikowym

31

Liczba jest istotą wszystkich rzeczy.

Pitagoras, (ok. 572 –474 p.n.e.),

matematyk i filozof grecki.

Logika jest anatomią myślenia.

John Lockie (1632-1704)

filozof angielski