1
Fazy
wieloskładnikowe -
roztwory (b)
Waldemar Ufnalski
Wprowadzenie do termodynamiki
chemicznej
Wykład 10b
0
50
100
150
0,00
0,25
0,50
0,75
1,00
x
B
Z
E
/(
J/
m
o
l)
C
6
H
6
CCl
4
H
E
G
E
TS
E
-2000
-1500
-1000
-500
0
0,00
0,25
0,50
0,75
1,00
x
B
Z
E
/(
J/
m
o
l)
1,4-dioksan
Chloroform
G
E
H
E
TS
E
2
10.3. Roztwory
(mieszaniny) gazów
Wykład 10b
3
RT
n
V
P
k
i
i
dosk
dosk
1
)
(
)
(
Pojęcia i wzory
podstawowe ...
Ciśnienie cząstkowe składnika (też w
mieszaninie rzeczywistej):
(1
)
(2
)
(3
a)
P
y
P
i
i
k
i
i
k
i
i
P
P
y
P
1
1
Równanie stanu roztworu doskonałego
gazów doskonałych:
RT
V
P
dosk
m
dosk
)
(
,
)
(
(3
b)
4
Pojęcia i wzory
podstawowe ...
Prawo Daltona :
(4
)
(5
)
(6
)
Roztwór doskonały gazów doskonałych...
k
i
dosk
i
k
i
dosk
i
dosk
P
V
RT
n
P
1
1
)
(
,
)
(
)
(
RT
n
V
P
i
dosk
dosk
i
)
(
)
(
,
i
k
i
i
i
dosk
dosk
i
y
n
n
P
P
1
)
(
)
(
,
5
T
B
y
T
B
y
y
T
B
y
y
y
T
B
m
22
2
2
12
2
1
11
2
1
2
1
2
,
Roztwory gazów
rzeczywistych ...
Model mieszania losowego (random mixing):
prawdopodobieństwo kontaktu między drobinami
jest proporcjonalne do iloczynu ich ilości.
(7
)
(8a
)
(8
b)
Wirialne równanie stanu...
1
1
k
m
m
y
y
T
B
P
RT
V
,
,
k
i
k
j
j
i
j
i
k
m
T
B
y
y
y
y
T
B
1
1
1
1
,
,
,
Roztwór dwuskładnikowy:
6
Roztwory gazów
rzeczywistych ...
(9
)
(1
0)
Sześcienne równania stanu - przybliżone
obliczenia za pomocą parametrów
pseudokrytycznych
(W. B Kay).
Lepsze przybliżenie za pomocą reguł mieszania
(Lorentza - Berthelota); np. dla równana VdW:
;
;
;
,
)
(
,
)
(
,
)
(
k
i
i
k
i
m
k
k
i
i
k
i
m
k
k
i
i
k
i
m
k
V
y
V
P
y
P
T
y
T
1
1
1
2
1
k
i
i
i
a
y
a
k
i
i
i
b
y
b
1
7
Roztwory gazów
rzeczywistych ...
(1
1)
(1
3)
Współczynnik lotności składnika roztworu gazowego
i
GD
dosk
i
P
RTd
d
ln
)
(
,
i
i
f
RTd
d
ln
P
y
y
y
P
T
f
P
y
y
P
T
f
y
y
P
T
i
k
i
i
k
i
k
i
1
1
1
1
1
1
,
,
,
,
,
,
,
,
,
(1
2)
1
0
P
const
y
T
i
P
,
lim
(1
4)
8
Roztwory gazów
rzeczywistych ...
(1
7)
(1
5)
Współczynnik lotności składnika - sens fizyczny:
(1
6)
RT
P
T
y
y
P
T
y
y
P
T
GD
i
k
i
k
i
,
,
,
,
,
,
,
ln
*
1
1
1
1
Współczynnik lotności składnika - obliczanie:
const
y
T
dP
P
RT
V
RTd
i
i
,
ln
P
k
i
k
i
dP
P
RT
y
y
P
T
V
y
y
P
T
RT
0
1
1
1
1
,
,
,
,
,
,
,
ln
Niezbędne jest równanie stanu
roztworu gazowego.
9
Roztwory gazów
rzeczywistych ...
Współczynnik lotności składnika - oszacowanie:
Reguła Lewisa - Randalla:
cząstkowy
współczyn - nik lotności składnika
mieszaniny jest niezależny od jej składu i
równy współczynnikowi lotności czystego
składnika w tych samych warunkach
ciśnienia i temperatury.
Założenie:
objętość molowa cząstkowa każdego
składnika jest równa jego objętości molowej, tzn.
w procesie mieszania gazów rzeczywistych zostaje
zachowana addytywność objętości (V
M
= 0).
10
10.4. Roztwory
nieelektrolitów -
aktywność i układy
odniesienia
Wykład 10b
11
Aktywność i współczynnik
aktywności ...
Pojęcie...
(1
8)
Potencjał chemiczny składnika
roztworu doskonałego:
Ogólna definicja doskonałości roztworu
G.N. Lewis i M. Randall (1923)
i
i
i
dosk
i
x
RT
P
T
x
P
T
ln
,
,
,
*
)
(
,
const
P
T
x
RTd
d
i
dosk
i
,
ln
)
(
,
const
P
T
a
RTd
d
i
i
,
ln
Ogólna definicja aktywności składnika roztworu
(1
9)
12
Aktywność i współczynnik
aktywności ...
(2
1)
Sens fizyczny aktywności
Współczynnik aktywności
(2
0)
1
1
k
i
i
x
x
P
T
a
a
,
,
,
i
k
i
k
i
x
x
x
P
T
a
x
x
P
T
1
1
1
1
,
,
,
,
,
,
Składnik
„ i” w
roztworze
Składnik
„ i” w
roztworze
T,P =
const
i
i
i
i
i
i
i
i
x
x
RT
a
a
RT
ln
ln
(2
2)
13
Aktywność i współczynnik
aktywności ...
Układ odniesienia aktywności
•Definiuje się stan
standardowy składnika
-
skład - nikowi w stanie standardowym przypisuje
się równe jedności wartości aktywności (a
o
=1) i
współczynni - ka aktywności.
•Wybiera się sposób wyrażania składu roztworu
(ułamek molowy, molalność (ewentualnie
molowość).
14
Aktywność i współczynnik
aktywności ...
Symetryczny układ odniesienia aktywności ...
Wybór stanu standardowego:
Czysty składnik
w danych warunkach temperatury i ciśnienia
•Skład wyrażany ułamkiem molowym
1
1
1
1
1
1
k
i
i
o
i
k
i
o
i
k
i
x
x
P
T
x
RT
P
T
x
x
P
T
a
RT
P
T
x
x
P
T
,
,
,
ln
,
,
,
,
ln
,
,
,
,
1
1
i
x
i
a
lim
1
1
i
x
i
lim
RT
dosk
i
i
i
)
(
,
ln
(24a
)
(2
3)
(24b
)
(2
5)
15
Aktywność i współczynnik
aktywności ...
Symetryczny układ odniesienia aktywności ...
Relacje:
(26
)
(2
7)
(2
8)
k
i
i
i
M
m
a
x
RT
G
1
ln
k
i
i
i
E
x
RT
G
1
ln
i
E
i
RT
ln
Klasyfikacja odchyleń od doskonałości - znak G
E
:
G
E
> 0 odchylenia dodatnie
G
E
< 0 odchylenia ujemne
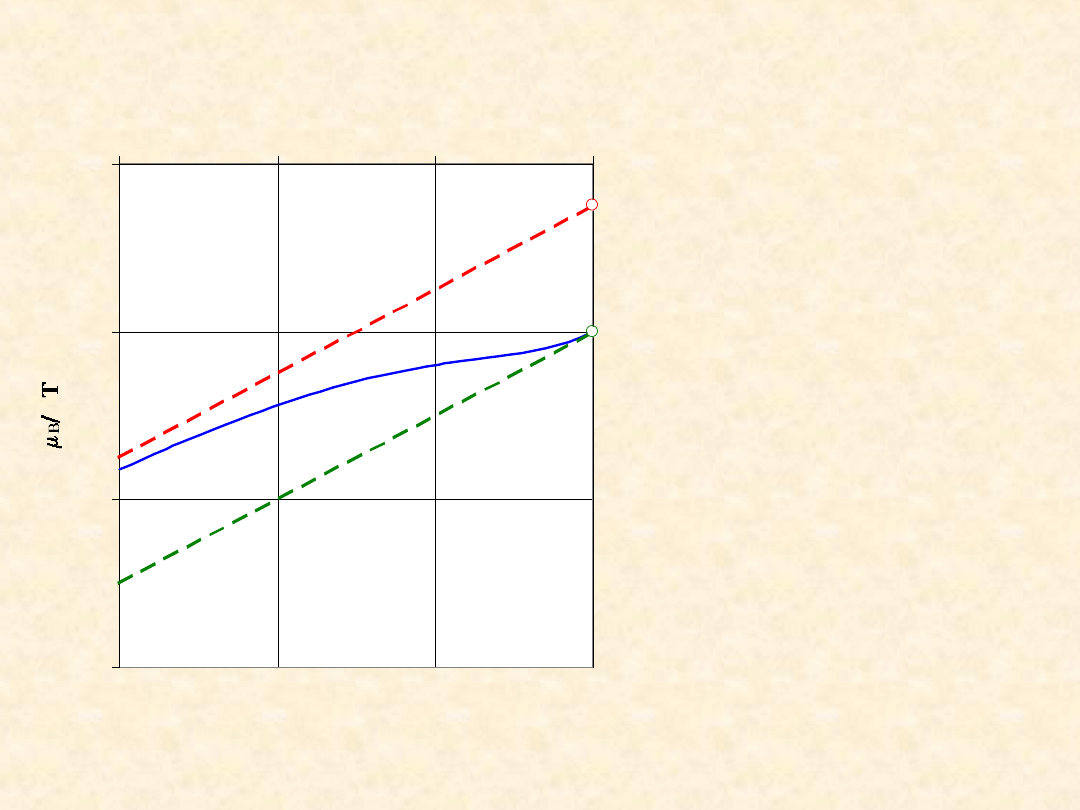
16
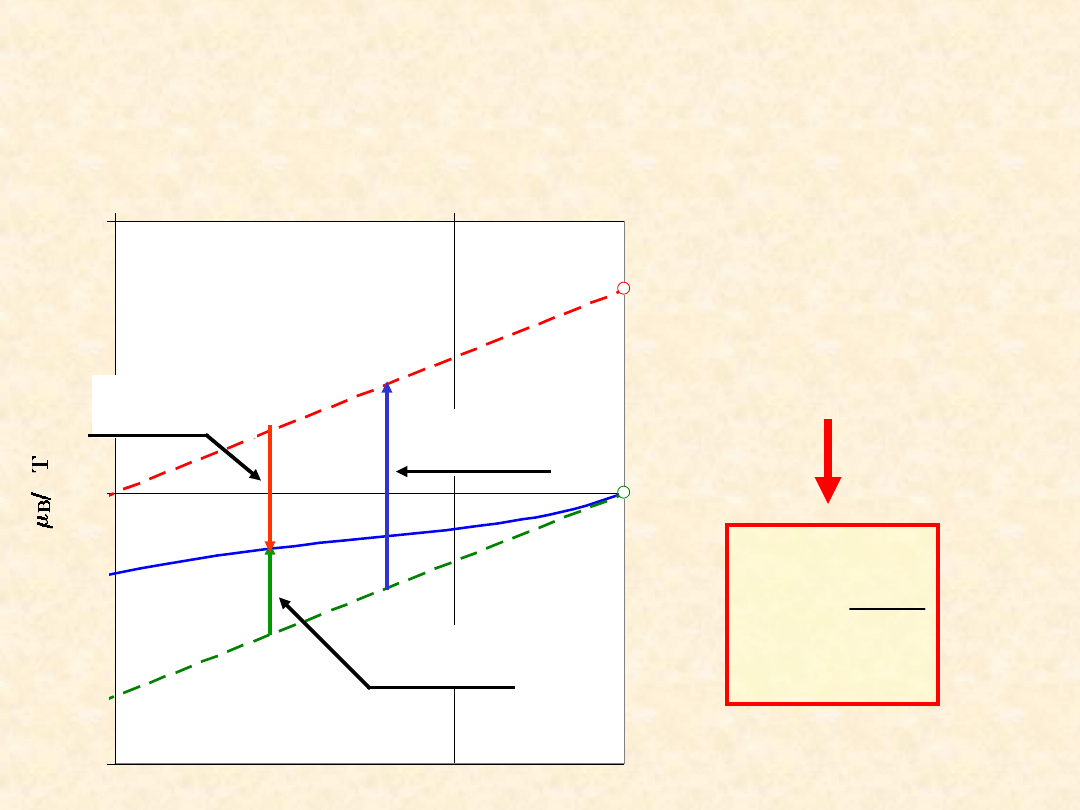
Aktywność - roztwory
rozcieńczone ...
Zależność potencjału chemicznego składnika
od jego ułamka molowego
*
B
o
B
ˆ
-4
-2
0
2
-3
-2
-1
0
ln x
B
R
17
Aktywność - roztwory
rozcieńczone ...
x
A
> 0,9
A - rozpuszczalnik; B - substancja rozpuszczona
A
A
A
A
x
RT
P
T
x
P
T
ln
,
,
,
*
(2
9)
A
A
A
B
A
x
RT
dx
d
dx
d
Wobec relacji Gibbsa - Duhema
0
B
B
B
B
A
A
dx
d
x
dx
d
x
B
A
B
A
B
B
dx
d
x
x
dx
d
2
2
x
RTd
d
ln
B
o
B
B
B
x
RTd
P
T
x
P
T
ln
,
ˆ
,
,
(
(3
0)
18
Aktywność - roztwory
rozcieńczone ...
x
A
> 0,9
A - rozpuszczalnik; B - substancja rozpuszczona
A
A
A
A
x
RT
P
T
x
P
T
ln
,
,
,
*
(2
9)
Doskonałość w sensie prawa Raoult’a
B
o
B
B
B
x
RTd
P
T
x
P
T
ln
,
ˆ
,
,
(
(3
0)
x
B
< 0,1
Doskonałość w sensie prawa Henry’ego
B
o
B
B
B
a
RT
P
T
x
P
T
ˆ
ln
,
ˆ
,
,
B
B
B
B
B
x
x
P
T
a
x
P
T
,
,
ˆ
,
,
ˆ
1
0
i
x
i
ˆ
lim
(3
1)
(3
1)
(3
2)
19
Aktywność - roztwory
rozcieńczone ...
Związek między
współczynnikam
i aktywności
*
B
o
B
ˆ
-2
0
2
-2
-1
ln x
B
R
B
RT
ln
B
RT
ˆ
ln
B
RT
ln
i
i
i
ln
ln
ˆ
ln
i
i
i
ˆ
(3
2)
20
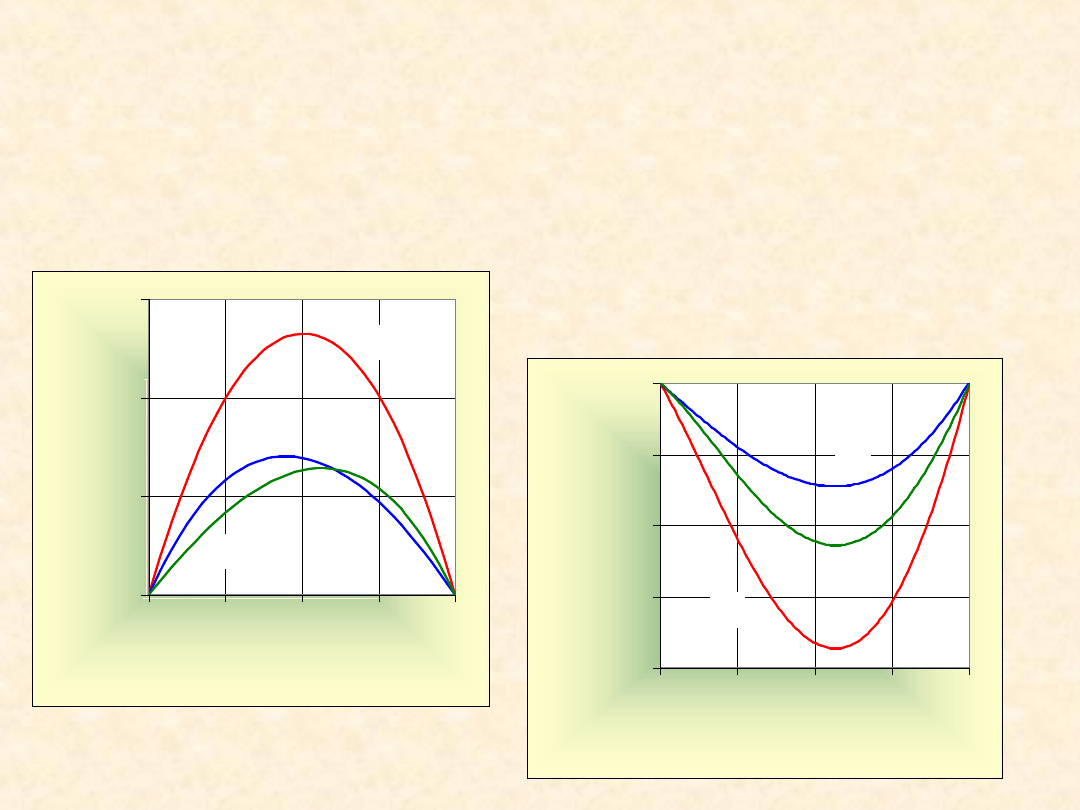
10.5. Roztwory
nieelektrolitów -
wybrane modele i
korelacje
Wykład 10b
21
Model roztworu prostego...
Definicja:
Relacje:
(3
3)
(3
4)
(3
5)
B
B
B
A
B
E
x
x
P
T
g
x
x
P
T
g
x
P
T
G
1
,
,
,
,
2
B
E
A
x
P
T
g ,
2
A
E
B
x
P
T
g ,
2
B
A
x
RT
P
T
g ,
exp
2
A
B
x
RT
P
T
g ,
exp
Układ dwuskładnikowy...
22
Model roztworu prostego...
Relacje:
(3
6)
P
B
A
E
T
P
T
g
P
T
s
x
x
P
T
s
S
,
,
,
gdzie
P
T
Ts
P
T
g
P
T
x
x
P
T
h
H
B
A
E
,
,
,
,
h
gdzie
T
B
A
E
P
P
T
g
P
T
v
x
x
P
T
v
V
,
,
,
gdzie
P
B
A
E
P
T
P
T
h
P
T
x
x
P
T
c
C
,
,
,
c
gdzie
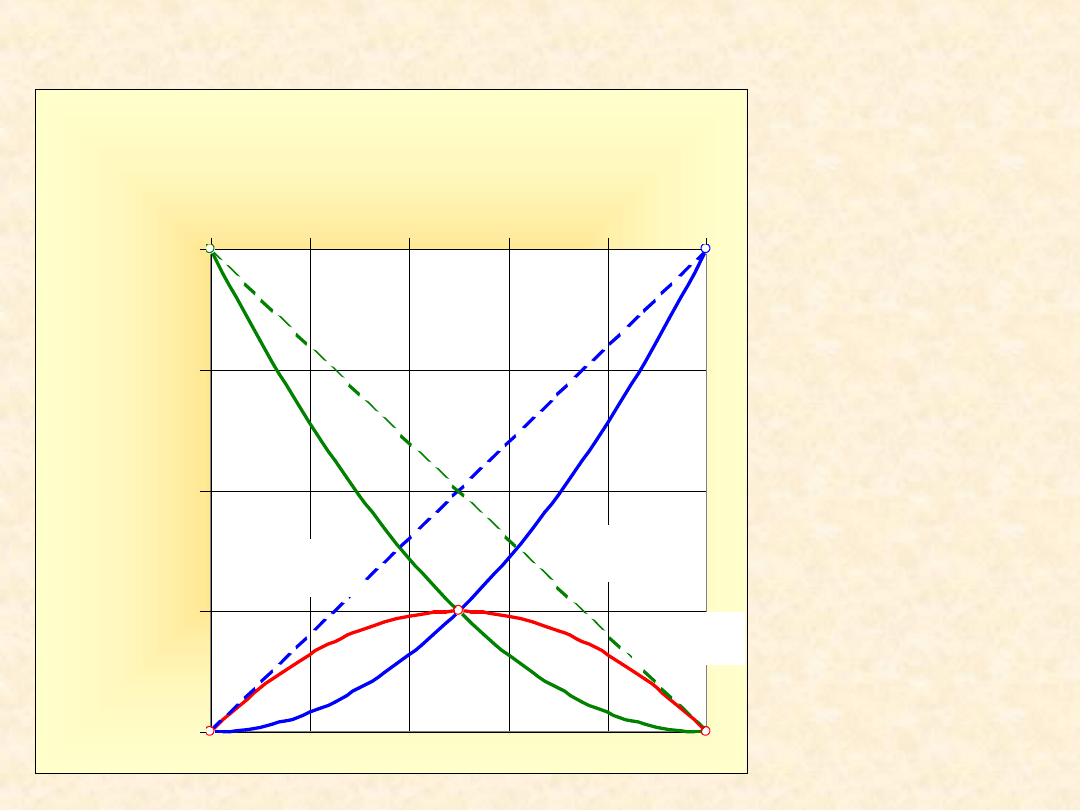
Parabole symetryczne względem x
B
= x
A
=1/2
23
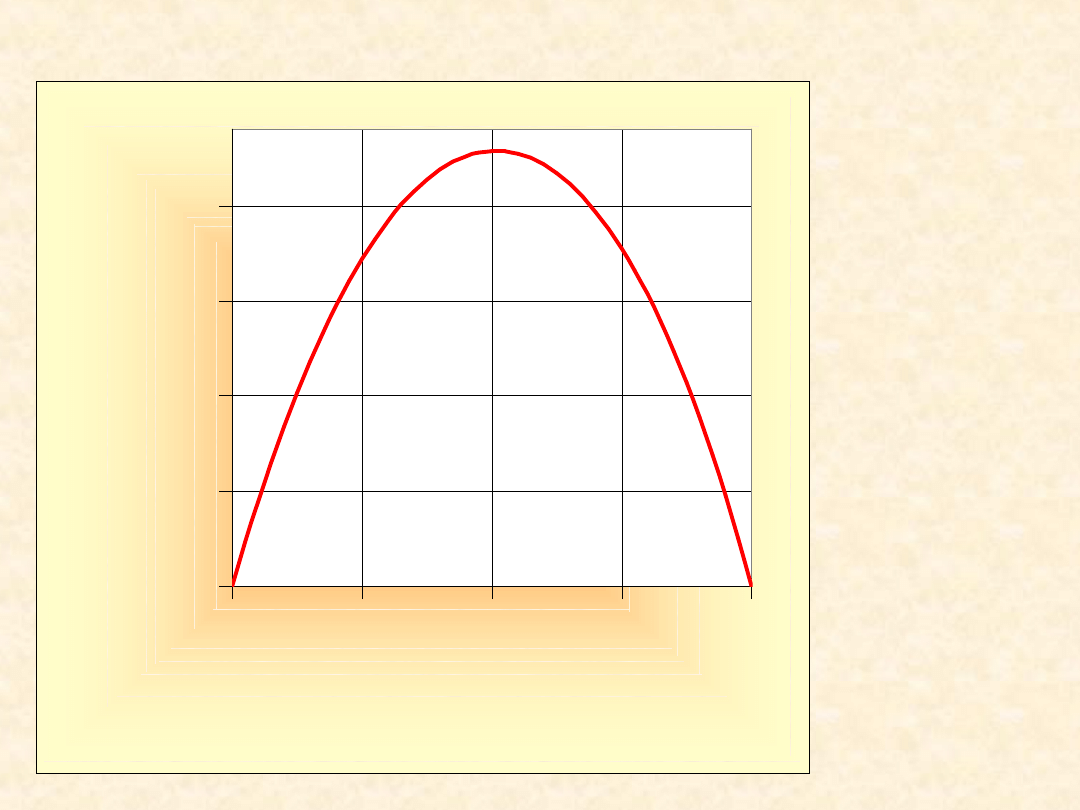
Model roztworu prostego...
g =
1,00
0,00
0,25
0,50
0,75
1,00
0,0
0,2
0,4
0,6
0,8
1,0
x
B
Y
E
/R
T
G
E
/RT
A
E
/RT
B
E
/RT
A
B
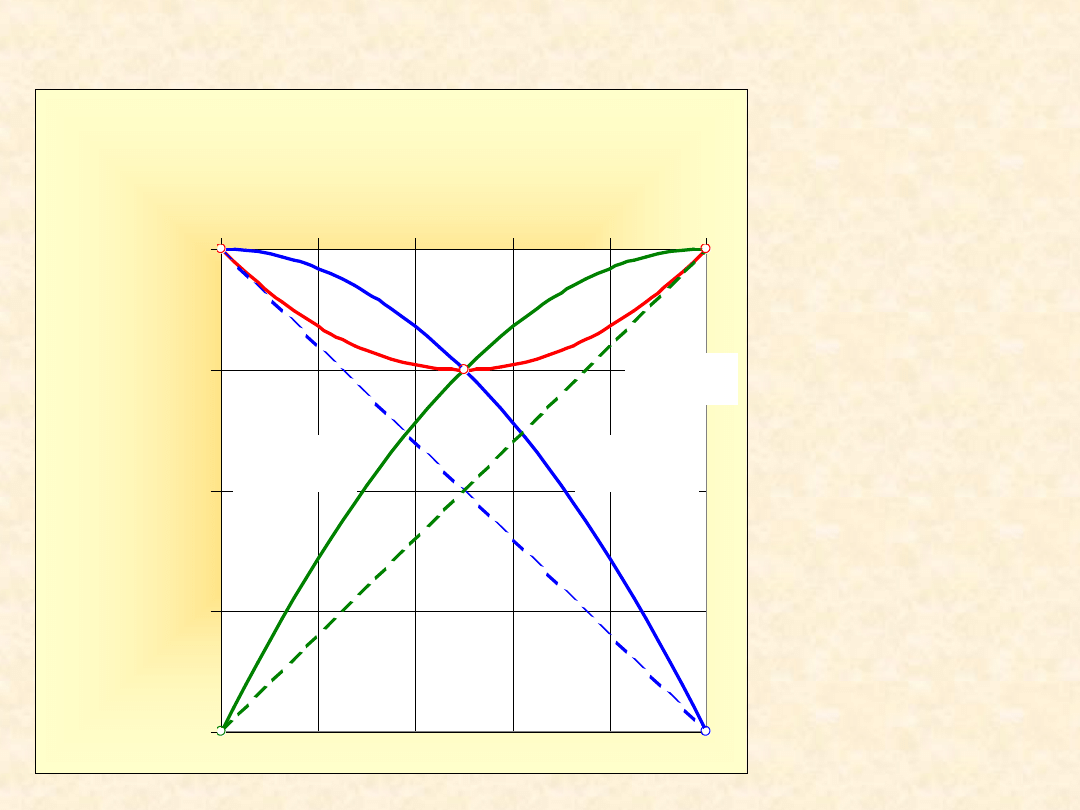
24
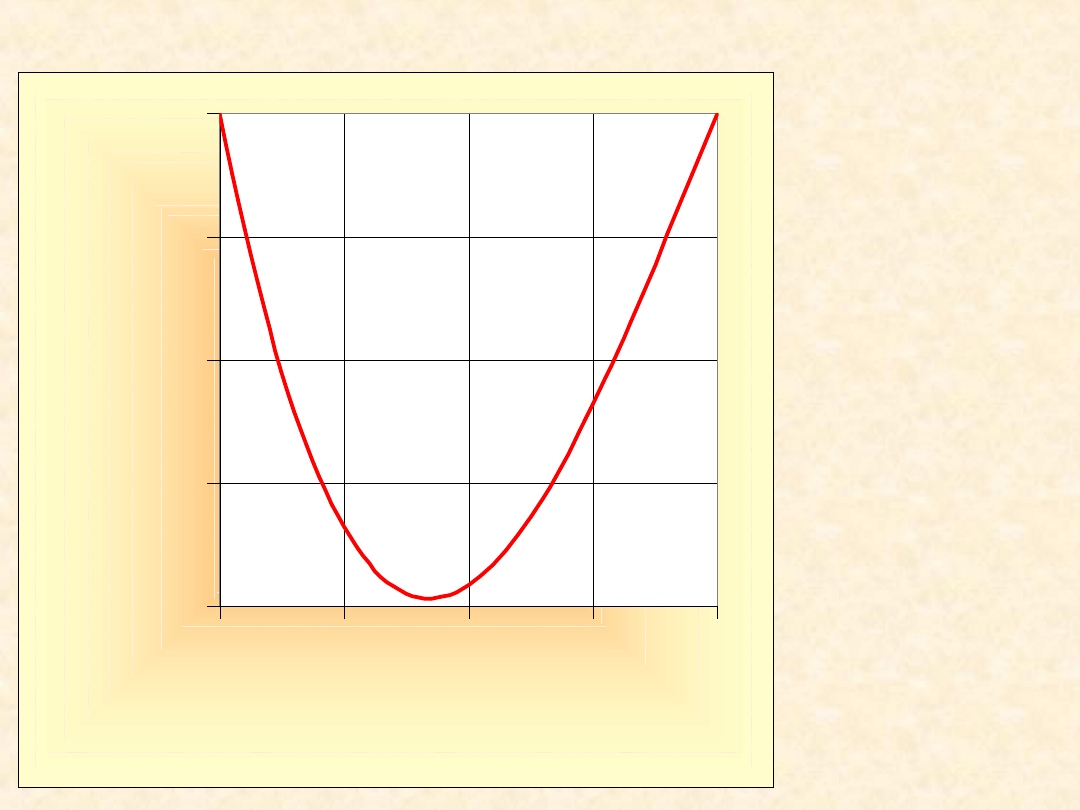
Model roztworu prostego...
g =
-1,00
-1,00
-0,75
-0,50
-0,25
0,00
0,0
0,2
0,4
0,6
0,8
1,0
x
B
Y
E
/R
T
G
E
/RT
A
E
/RT
B
E
/RT
A
B
25
Uzasadnienie molekularne...
•Drobiny składników są niepolarne, mają
symetrię kulistą i zbliżone do siebie rozmiary
(promienie).
•Energia oddziaływań między dwiema drobinami
zależy wyłącznie od odległości między środkami
ich mas i dla każdej pary drobin może być
opisana funkcją w postaci
gdzie
0
jest funkcją uniwersalną dla wszystkich
par drobin, natomiast f
i,j
oraz g
i,j
- stałymi
indywidual - nymi dla każdej pary drobin
Model roztworu prostego...
j
i
j
i
j
i
j
i
j
i
g
r
f
r
,
,
,
,
,
0
26
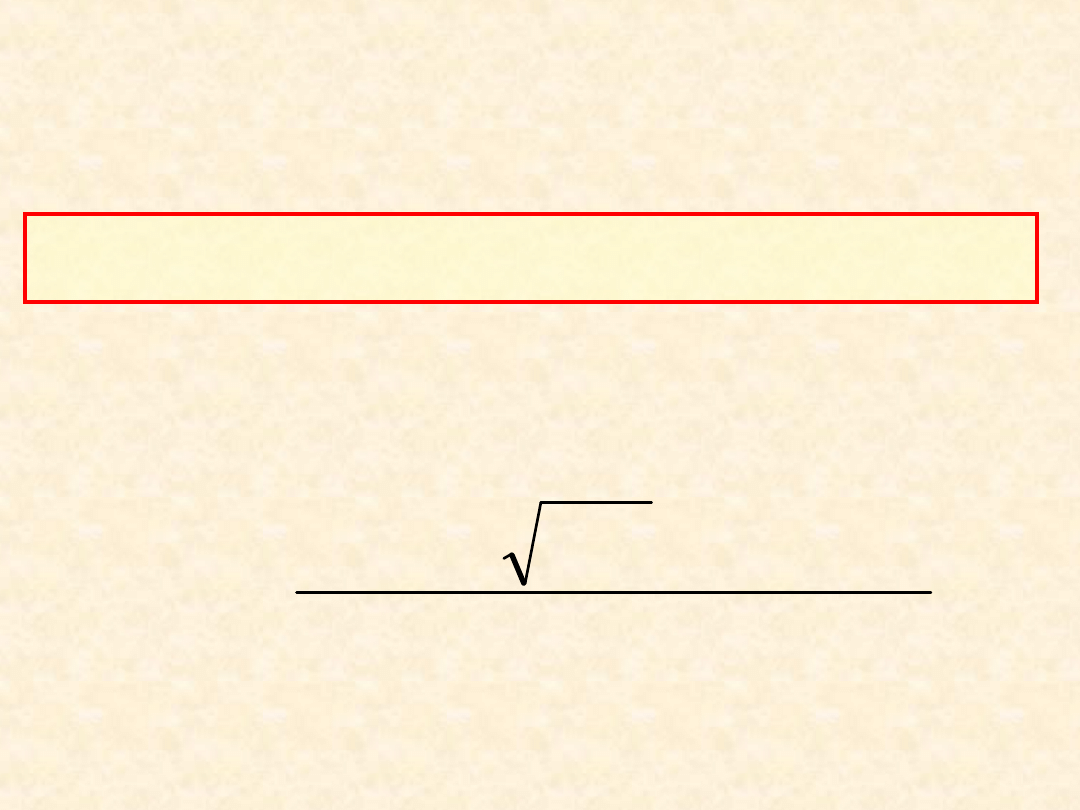
Uzasadnienie molekularne...
•Zgodnie z przyjętym modelem
molekularnym różna od zera wartość
współczynnika g(T,P) wynika z różnych
energii oddziaływań między identycznymi
(
11
,
22
) oraz różnymi (
12
) drobinami:
Model roztworu prostego...
12
22
11
2
g
(3
6)
27
Założenie:
niedoskonałość roztworu wynika wynika
wyłącznie z efektu energetycznego (entalpowego)
Model roztworu regularnego...
(3
7)
;
;
;
0
0
0
E
E
E
E
E
U
H
G
V
S
Założenie:
czyste ciecze oraz roztwór
spełniają równanie van der Waalsa; stosuje
się regułę mieszania Lorentza - Berthelota
*
*
1
1
1
1
2
2
2
2
1
2
1
2
1
1
2
V
x
V
x
x
a
x
x
a
a
x
a
E
koh
Energia kohezji roztworu: udział oddziaływań między -
cząsteczkowych w energii wewnętrznej roztworu
(3
8)
28
Model roztworu regularnego...
(3
9)
Energia kohezji czystych składników:
(4
0)
*
,
*
,
2
2
2
1
1
1
oraz
V
a
E
V
a
E
koh
koh
Nadmiarowa energia Gibbsa mieszania:
koh
koh
koh
M
E
E
E
x
E
x
E
U
U
G
,
,
2
2
1
1
*
*
*
*
2
2
2
1
1
1
1
1
1
1
2
2
2
2
1
2
1
2
1
1
2
V
a
x
V
a
x
V
x
V
x
x
a
x
x
a
a
x
a
G
E
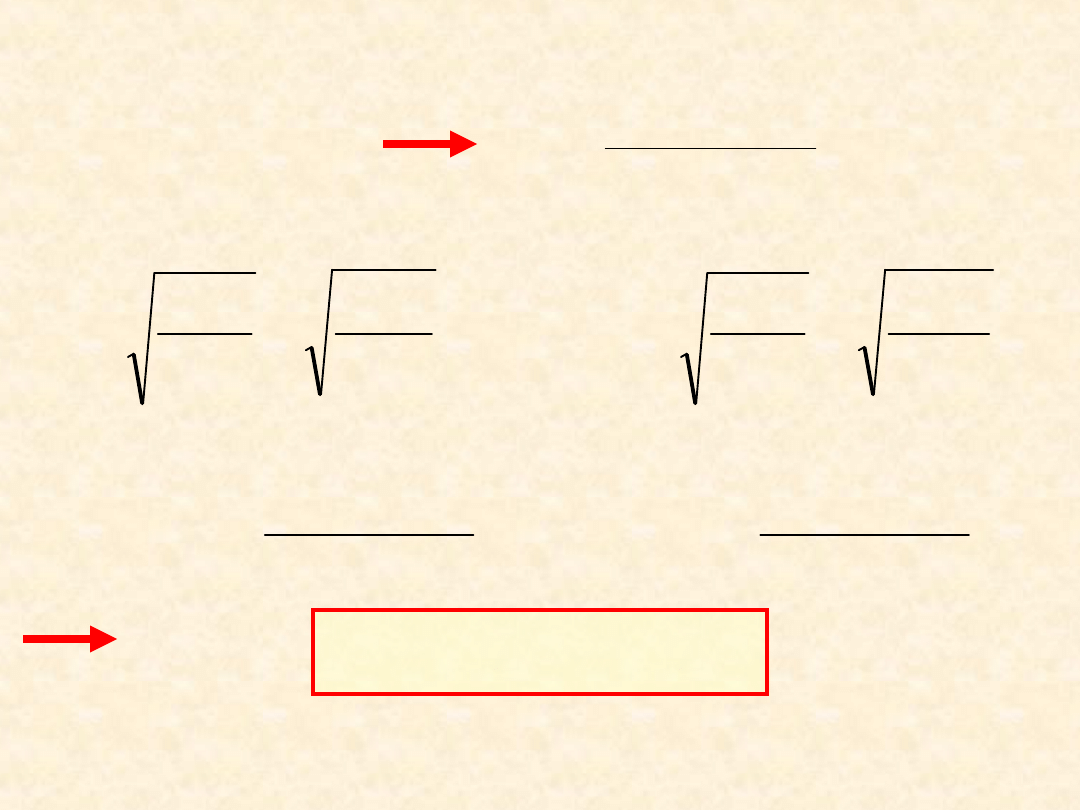
29
Model roztworu regularnego...
(4
1)
(4
2)
Nadmiarowa energia
Gibbsa mieszania:
2
1
2
2
2
1
1
2
1
2
1
*
*
*
*
V
x
V
x
V
V
x
x
G
E
oraz
2
2
1
1
2
2
2
2
2
1
1
1
1
1
*
*
*
*
*
*
V
x
V
x
V
x
V
x
V
x
V
x
oraz
2
2
2
2
2
2
1
1
2
1
1
1
*
,
*
*
,
*
V
E
V
a
V
E
V
a
koh
koh
Parametry rozpuszczalności:
Pozorne ułamki objętościowe:
(4
3)
2
1
2
2
1
m
E
V
G
*
*
2
2
1
1
V
x
V
x
V
m
(4
4)
(4
5)
30
Model roztworu regularnego...
(4
6)
Nadmiarowe potencjały chemiczne składników:
Wyznaczanie parametrów rozpuszczalności (42) -
na podstawie objętości molowej i energii
parowania (pomiar gęstości i entalpii parowania).
(4
7)
2
1
2
2
1
2
2
2
2
1
2
2
2
1
1
1
*
*
ln
ln
V
RT
V
RT
E
E
RT
H
U
E
par
par
koh
*
*
31
Model roztworu regularnego...
•charakter półilościowy
• służy do oszacowania właściwości
termodynamicz - nych roztworu na
podstawie właściwości czystych składników
•dopuszcza wyłącznie dodatnie odchylenia
od dos - konałości (G
E
> 0)
•jest stosowany do przewidywania i
wyjaśniania roz- puszczalności substancji
organicznych w rozpusz - czalnikach jedno-
i wieloskładnikowych.
•należy go stosować do substancji
niepolarnych, zbu- dowanych z niewielkich
drobin o symetrii zbliżonej do sferycznej
32
Założenie:
niedoskonałość roztworu wynika
wynika wyłącznie z efektu entropowego
Model roztworu atermalnego...
(4
8)
;
;
;
0
0
0
E
E
E
E
TS
G
V
H
Model siatkowy roztworu:
CH
3
H
2
C
HC OH
H
3
C
Cl CH
3
CH
3
OH
33
Model roztworu atermalnego...
(4
9)
Entropia mieszania N
1
+ N
2
drobin
(1 - zajmuje 1 węzeł; 2 - r węzłów):
2
1
2
2
2
1
1
1
rN
N
rN
N
rN
N
N
N
R
S
M
ln
ln
Założenie:
*
2
V
r
1
2
2
1
1
1
1
2
2
1
1
1
1
1
2
1
1
1
1
2
1
1
*
*
*
*
*
*
*
*
*
V
x
V
x
V
x
V
N
V
N
V
N
V
rN
V
N
V
N
rN
N
N
2
2
2
1
1
2
2
2
2
1
1
2
2
1
2
1
1
1
2
2
1
2
*
*
*
*
*
*
*
*
*
V
x
V
x
V
x
V
N
V
N
V
N
V
rN
V
N
V
rN
rN
N
rN
1/2
- pozorne ułamki objętościowe - wzór (43)
34
Model roztworu atermalnego...
(5
0)
Wobec:
2
2
1
1
ln
ln
x
x
R
S
M
m
2
1
2
2
2
1
1
1
rx
x
rx
x
rx
x
x
x
R
S
M
m
ln
ln
2
2
1
1
x
x
x
x
R
S
id
m
ln
ln
2
2
2
1
1
1
x
x
x
x
R
S
E
ln
ln
2
1
2
2
1
1
1
rx
x
r
x
rx
x
x
R
S
M
m
ln
ln
(5
1)
35
Model roztworu atermalnego...
(5
2)
(5
3)
2
2
2
1
1
1
x
x
x
x
RT
G
E
ln
ln
2
1
2
2
1
1
1
rx
x
r
x
rx
x
x
RT
G
E
ln
ln
2
1
2
2
1
1
1
1
1
rx
x
x
r
rx
x
RT
RT
E
ln
ln
2
1
1
2
1
2
2
1
rx
x
x
r
rx
x
r
RT
RT
E
ln
ln
36
•charakter półilościowy
• służy do oszacowania właściwości
termodynamicz - nych roztworu na
podstawie właściwości czystych składników
•dopuszcza wyłącznie ujemne odchylenia
od dosko - nałości (G
E
< 0)
•jest stosowany do przewidywania i
wyjaśniania roz- puszczalności polimerów w
rozpuszczalnikach niepolarnych.
•należy go stosować do substancji
niepolarnych, zbu- dowanych z drobin o
budowie liniowej różniących się znacznie
rozmiarami.
Model roztworu atermalnego...
37
10.6. Roztwory ciekłe
nieelektrolitów -
przegląd i interpretacja
jakościowa zależności
doświadczalnych
Wykład 10b
38
Nadmiarowa objętość
mieszania ...
0,00
0,25
0,50
0,75
1,00
0,00
0,25
0,50
0,75
1,00
x
B
V
E
/(
cm
3
/m
o
l)
C
6
H
6
C
6
HF
5
T= 298,2
K
39
Nadmiarowa objętość
mieszania ...
-0,60
-0,40
-0,20
0,00
0,00
0,25
0,50
0,75
1,00
x
B
V
E
/(
cm
3
/m
o
l)
1,4-dioksan
o-toluidyna
T= 298,2
K
40
Nadmiarowa objętość
mieszania ...
T= 298,2
K
-0,10
0,00
0,10
0,20
0,00
0,25
0,50
0,75
1,00
x
B
V
E
/(
cm
3
/m
o
l)
C
6
H
11
OH
C
6
H
12
41
Nadmiarowa entalpia
mieszania ...
T= 298,2
K
0
25
50
75
100
0,00
0,25
0,50
0,75
1,00
x
B
H
E
/(
J/
m
o
l)
C
6
H
6
CCl
4
42
Nadmiarowa entalpia
mieszania ...
T= 298,2
K
-200
-150
-100
-50
0
0,00
0,25
0,50
0,75
1,00
x
B
H
E
/(
J/
m
o
l)
CHCl
3
furan
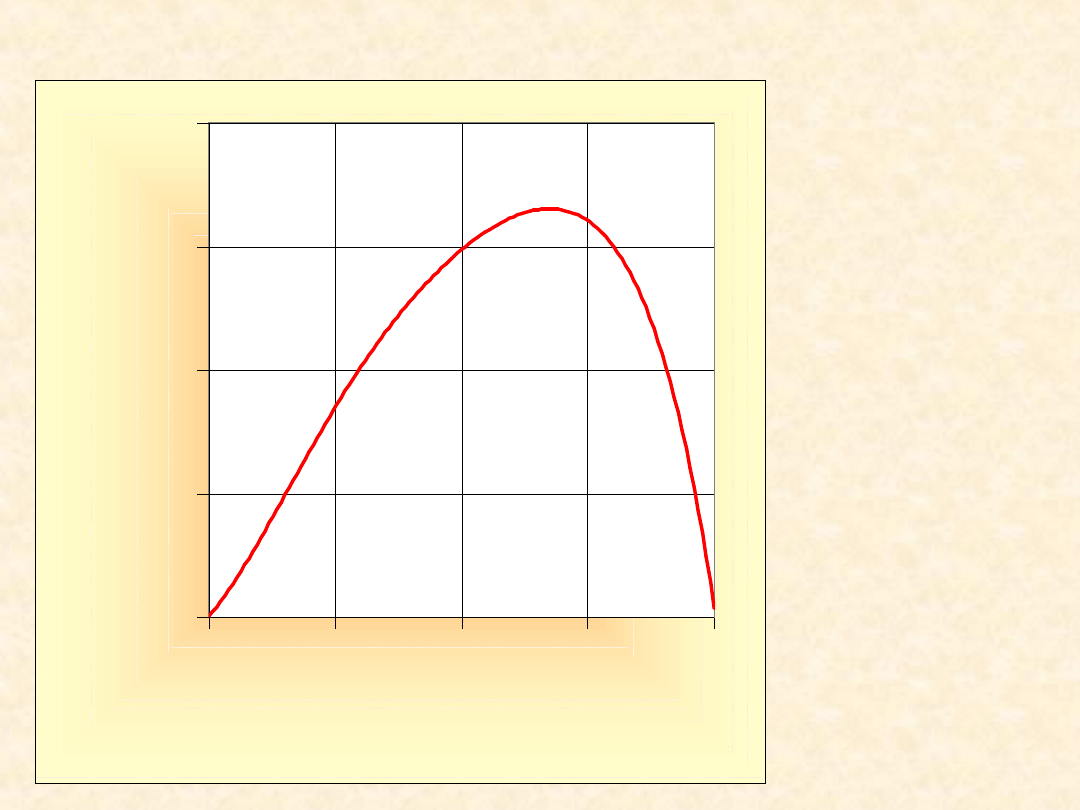
43
Nadmiarowa entalpia
mieszania ...
T= 298,2
K
0
200
400
600
800
0,00
0,25
0,50
0,75
1,00
x
B
H
E
/(
J/
m
o
l)
C
6
H
12
C
6
H
11
OH
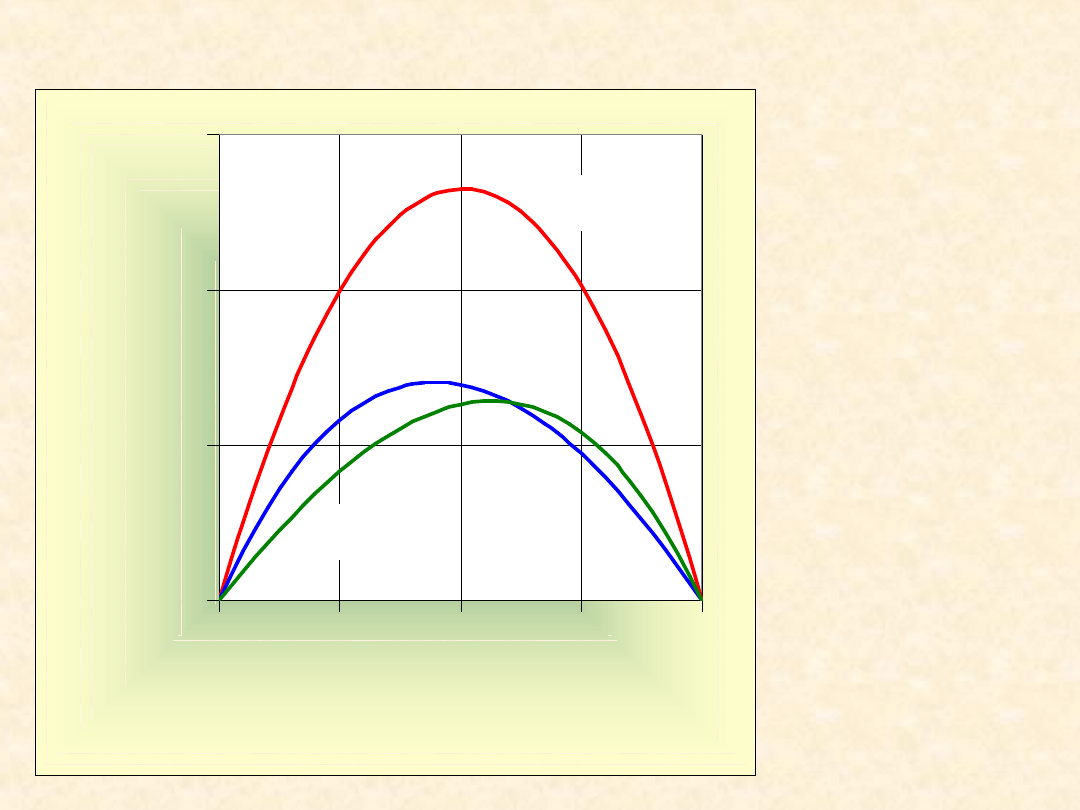
44
Nadmiarowe funkcje
mieszania ...
T= 318,2
K
0
50
100
150
0,00
0,25
0,50
0,75
1,00
x
B
Z
E
/(
J/
m
o
l)
C
6
H
6
CCl
4
H
E
G
E
TS
E
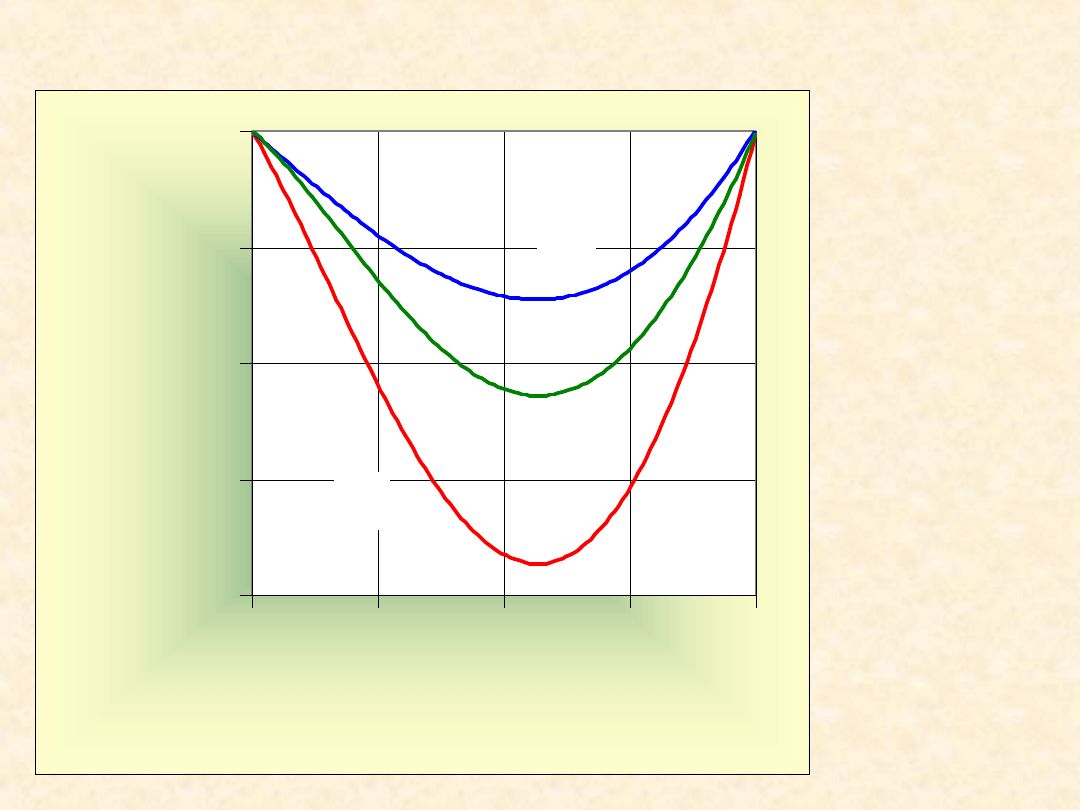
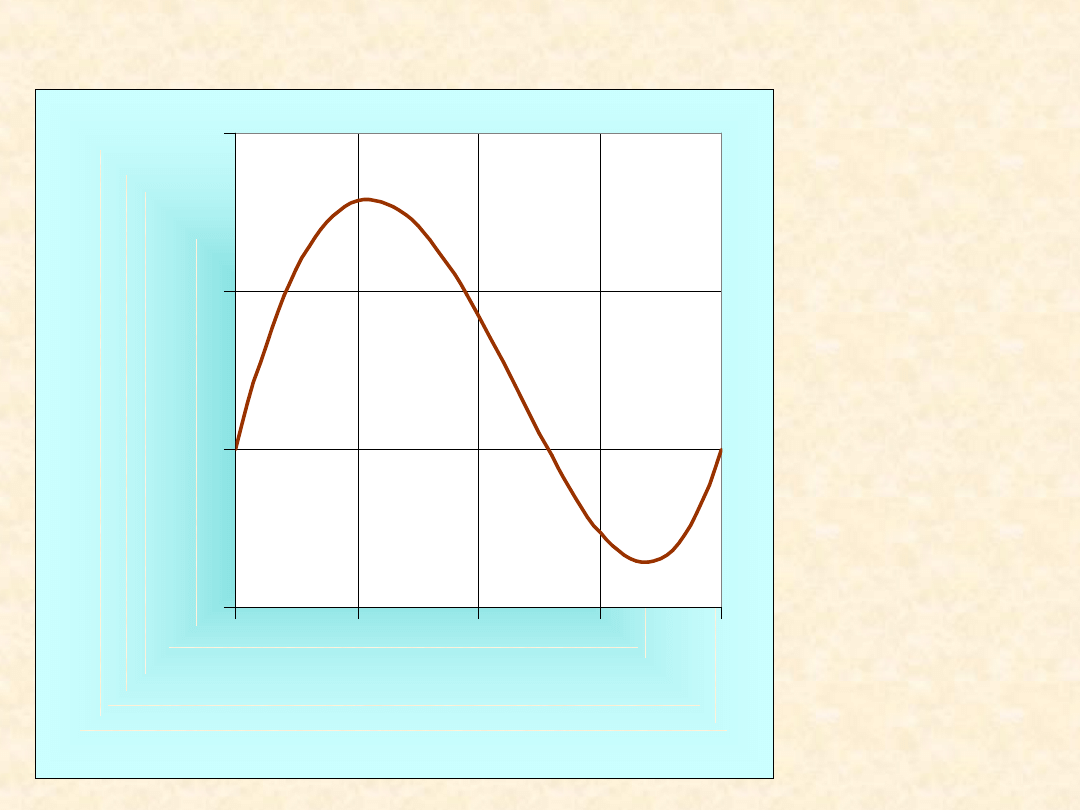
45
Nadmiarowe funkcje
mieszania ...
T= 323,2
K
-2000
-1500
-1000
-500
0
0,00
0,25
0,50
0,75
1,00
x
B
Z
E
/(
J/
m
o
l)
1,4-dioksan
Chloroform
G
E
H
E
TS
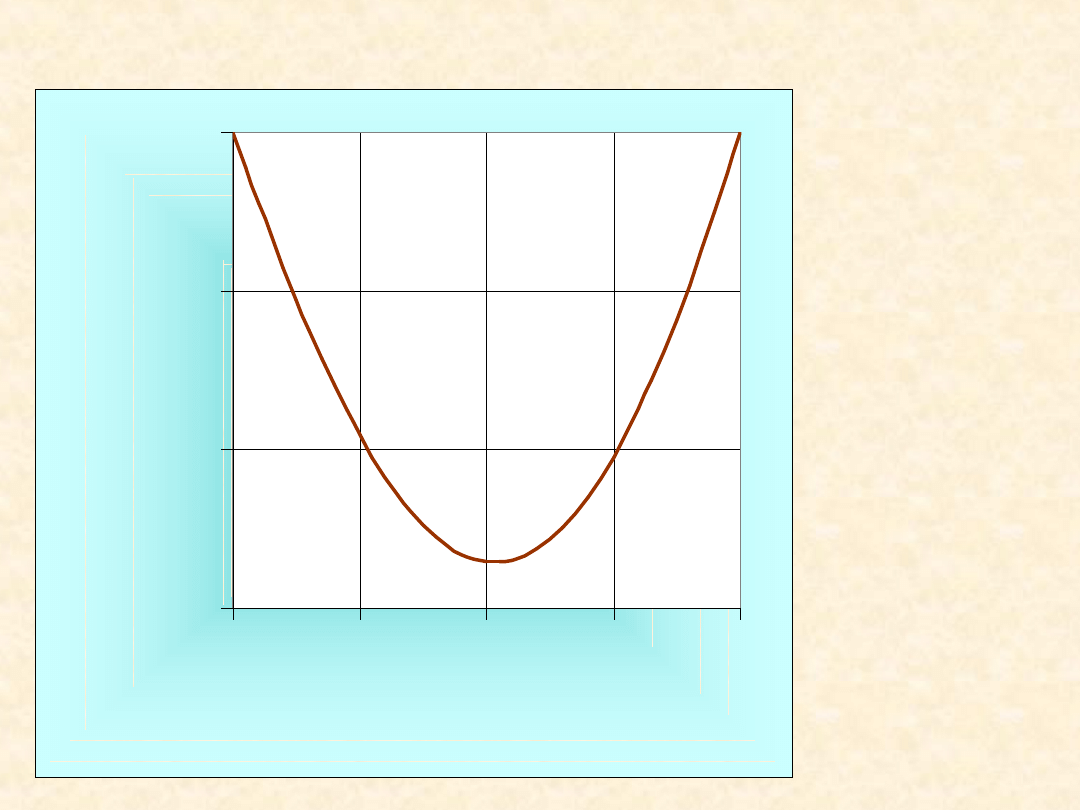
E
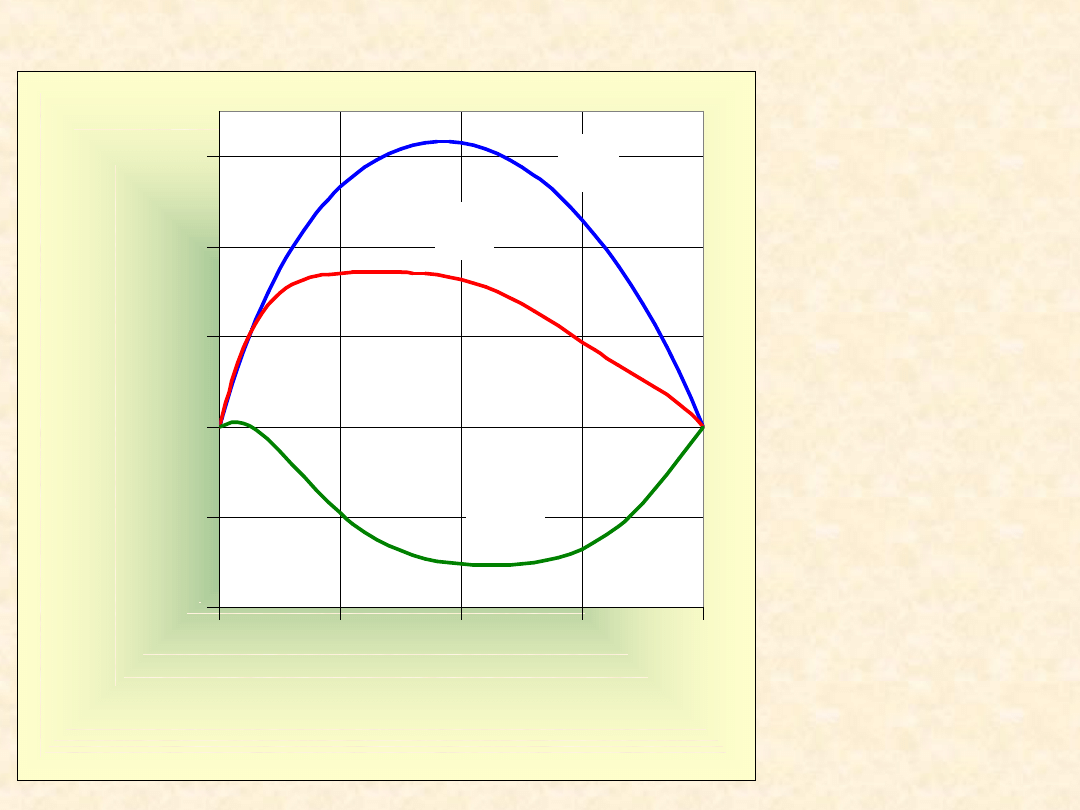
46
Nadmiarowe funkcje
mieszania ...
T= 298,2
K
-800
-400
0
400
800
1200
0,00
0,25
0,50
0,75
1,00
x
B
Z
E
/(
J/
m
o
l)
benzen
metanol
G
E
H
E
TS
E
47
Prawdziwa wiedza – to znajomość
przyczyn.
Franciszek Bacon (1561 – 1626)
angielski mąż stanu i filozof