Amper [A]

Definicja 1 A - prąd o natężeniu 1 A, jest to stały prąd

elektryczny, który płynąc w dwóch równoległych,

prostoliniowych, nieskończenie długich przewodach o

znikomo małym przekroju kołowym, umieszczonych w

próżni w odległości 1 m od siebie, spowodowałby

wzajemne oddziaływanie przewodów na siebie z siłą
równą

2 x 10

-7

[N]

na każdy metr długości przewodu.

Do definicyjnego wyznaczenia jednostki służy waga prądowa. Dokładnością ustępuje

jednak kalibratorom prądu i w praktyce jest przez nie wyparta.

Jeśli przepływający przez dany przekrój prąd ma

natężenie 1 A, oznacza to, że w ciągu 1 s przepływa 1 C

ładunku,

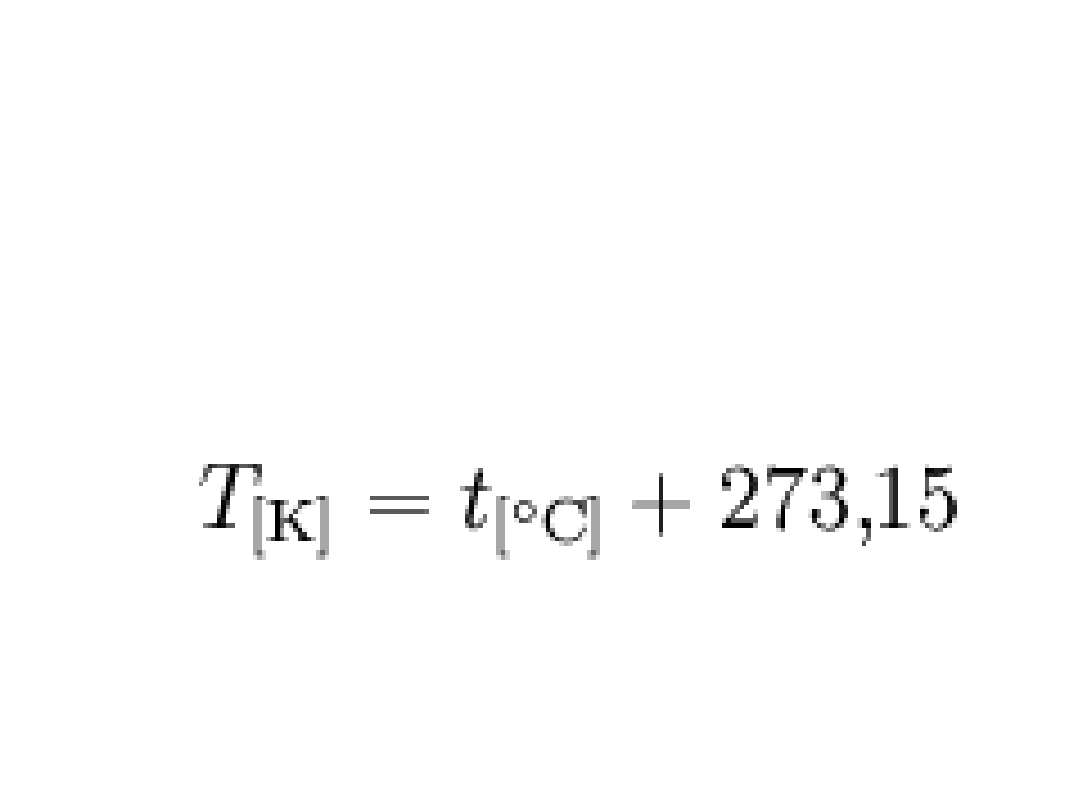
kelwin [K]

kelwin - jednostka temperatury w

układzie SI równa 1/273,16
temperatury termodynamicznej
punktu potrójnego wody, oznaczana
[K]

kandela (świeca)

jednostka światłości źródła światła; jednostka

podstawowa w układzie SI, oznaczana [cd].

Jest to światłość, z jaką świeci w określonym

kierunku źródło emitujące promieniowanie

monochromatyczne o częstotliwości 5,4·1014

Hz, i wydajności energetycznej w tym

kierunku równej (1/683) [W/srd].

Kandela to również światłość 1/600000 m²

ciała doskonale czarnego w temperaturze

krzepnięcia platyny pod ciśnieniem 1

atmosfery fizycznej.

mol [mol]

Mol – podstawowa w układzie SI jednostka liczności materii,

oznaczana [mol].

Jeden mol jest to liczba indywiduów chemicznych (np. atomów,

cząsteczek, jonów, elektronów itp.) równa liczbie atomów zawartych

w 12 gramach izotopu węgla C12 (przy założeniu, że węgiel jest w

stanie niezwiązanym chemicznie, w spoczynku, a jego atomy nie

znajdują się w stanie wzbudzenia). W jednym molu znajduje się

6,02214179±0,00000030 · 10

23

cząstek.

Liczba ta jest nazywana stałą Avogadra[2]. Mol jest szczególnie

istotny dla pojęcia masy molowej, która ma duże znaczenie

praktyczne dla ilościowego doboru składników reakcji chemicznych.

lumen [lm]

- jednostka miary strumienia

świetlnego w układzie SI (jednostka
pochodna układu SI)

1 lm = 1 [cd·sr]
Jest to strumień świetlny wysłany w

jednostkowy kąt bryłowy (steradian)
przez izotropowe punktowe źródło
światła o światłości jednej kandeli
umieszczone w wierzchołku tego kąta

Luks [lx]

- jednostka natężenia oświetlenia E w

układzie SI (Jednostka pochodna układu
SI)

1 lx = 1 cd·sr / m

2

Luks określany jest jako oświetlenie wywołane przez

równomiernie rozłożony strumień świetlny o wartości
równej 1 lumen (lm) padający na powierzchnię 1m

2

, a

więc:

1 lx = 1 lm / m

2

.

Po latach szczególna teoria

względności Einsteina oprze

się na dwóch postulatach

 

- ruch bezwzględny nie może być

wykryty ;

- szybkość światła jest niezależna od

ruchu źródła

czego Galileusz i Newton nie

wiedzieli.

Często w ramach postulatów szczególnej teorii względności

mówimy także o zasadzie kosmologicznej która mówi, że nie
ma wyróżnionego punktu w przestrzeni co jest innym
sformułowaniem zasady (1)

Oddziaływania
fundamentalne

są odpowiedzialne za siły działające pomiędzy
cząstkami.

Elektromagnetyczne
Słabe

Silne jądrowe
Silne kolorowe

Elektryczne
magnetyczne

Podstawowe oddziaływania:

1. Grawitacyjne

2. Elektrosłabe

3

.

Silne

Dla opisu zjawisk fizycznych byłoby najlepiej,
gdyby istniało tylko jedno oddziaływanie,
zawierające w sobie wszystkie do tej pory
wymienione.

Jesteśmy blisko Teorii Wszystkiego - unifikacji
oddziaływań słabych, elektromagnetycznych i
silnych.

KINEMATYKA -dział mechaniki, który podaje opis
przestrzenno-czasowych właściwości ruchu

DYNAMIKA - badanie ruchu z uwzględnieniem jego
przyczyn, zajmuje się

zobacz: R. Kulessa UJ Wykłady z Fizyki

http://users.uj.edu.pl/~kulessa

Układy
odniesienia

Jakieś zdarzenie fizyczne w określonym miejscu
definiujemy przez podanie dokładnej
informacji o miejscu i czasie, w którym to
nastąpiło podając jednocześnie układ
odniesienia.

Z

A

B

1

r

2

r

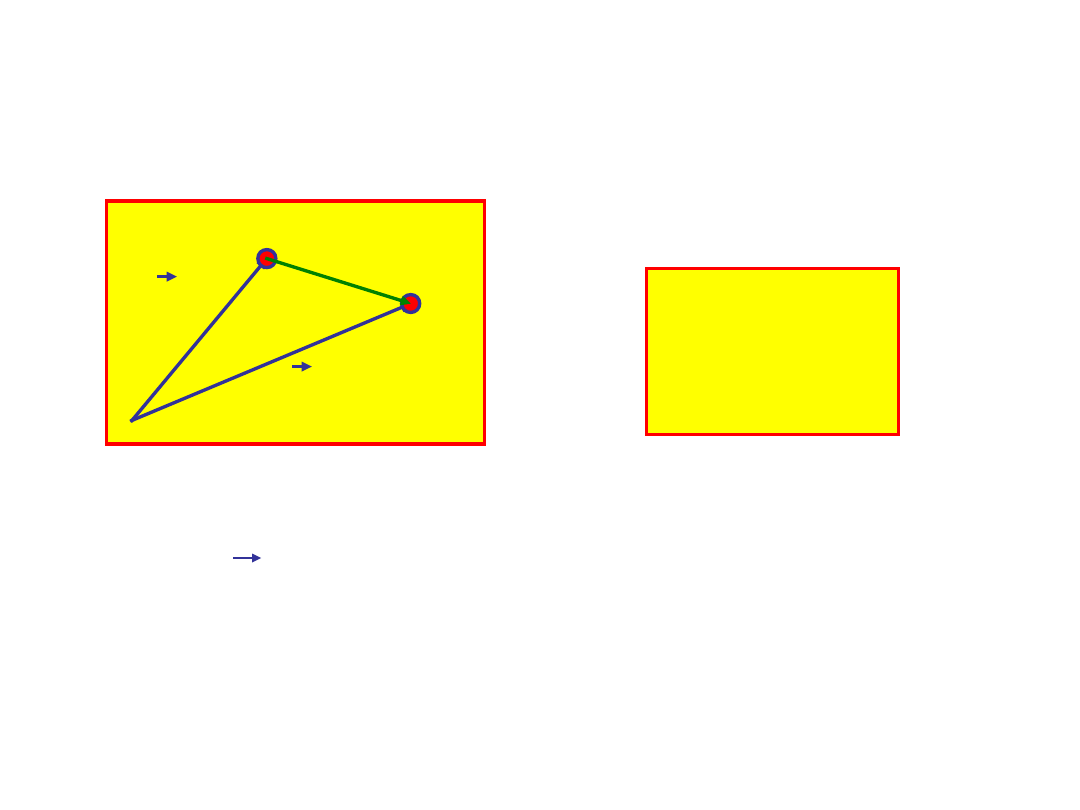
Aby opisać dwa zdarzenia obserwator musi
zarejestrować miejsce i czas każdego z nich w
danym układzie.

i

f

r

i

t

i

r

f

t

f

Jeśli obserwator
zarejestruje
miejsce zdarzeń i i f,
oraz ich czasy t

i

i t

f

, to

równania

i

f

i

f

t

t

t

r

r

r



















określają wektor przesunięcia dla tych
zdarzeń, oraz przedział czasowy pomiędzy
nimi.
Wektor r określa odległość między

zdarzeniami i i f, oraz kierunek od i do f.

Okazuje się, że wektor przesunięcia może
być taki sam dla kilku różnych
obserwatorów umiejscowionych w
różnych miejscach

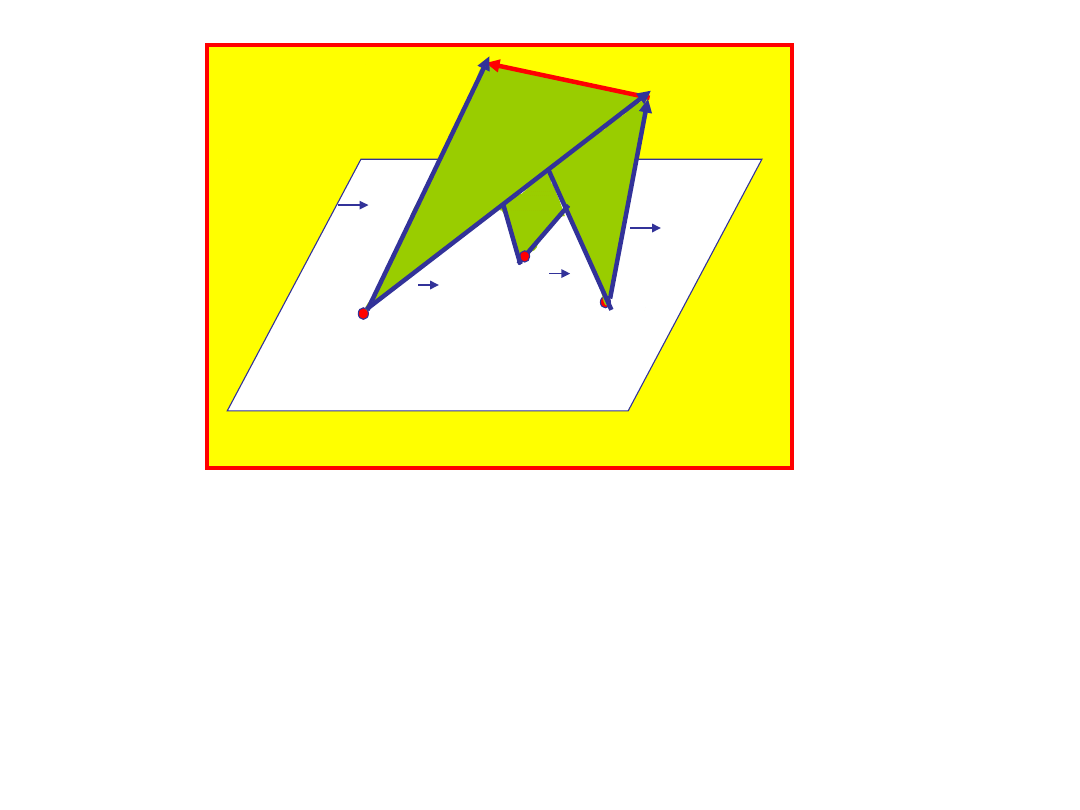
Jeśli mamy trzech obserwatorów, których
względna pozycja się nie zmienia, każdy z nich
określi zdarzenie

i

i

f

przez inne wektory to

przesunięcie

od punktu i do f będzie dla

wszystkich obserwatorów takie same.
Również

czas jaki upłynie od zdarzenia i do f

będzie dla

wszystkich obserwatorów taki sam

.

A

B

C

r

iA

r

fA

r

iB

r

fB

i

f

Układ odniesienia nazywamy inercjalnym,
jeżeli porusza się on ruchem jednostajnym po
linii prostej albo pozostaje w spoczynku
względem innego układu inercyjnego.
Układ taki jest de facto definiowany przez
podanie transformacji Galileusza a także w I
Zasadzie dynamiki Newtona. Takie
definiowanie jest zaledwie wewnętrznie spójne
i fizycy długo poszukiwali absolutnego układu
odniesienia aby w końcu stwierdzić, że go nie
ma! : )

Ruch punktu (i nie tylko) może być opisany w
różnych układach
współrzędnych, np. Kartezjańskim, walcowym,
biegunowym, sferycznym.
Obserwator jest (zwykle) umieszczony w początku
układu współrzędnych.

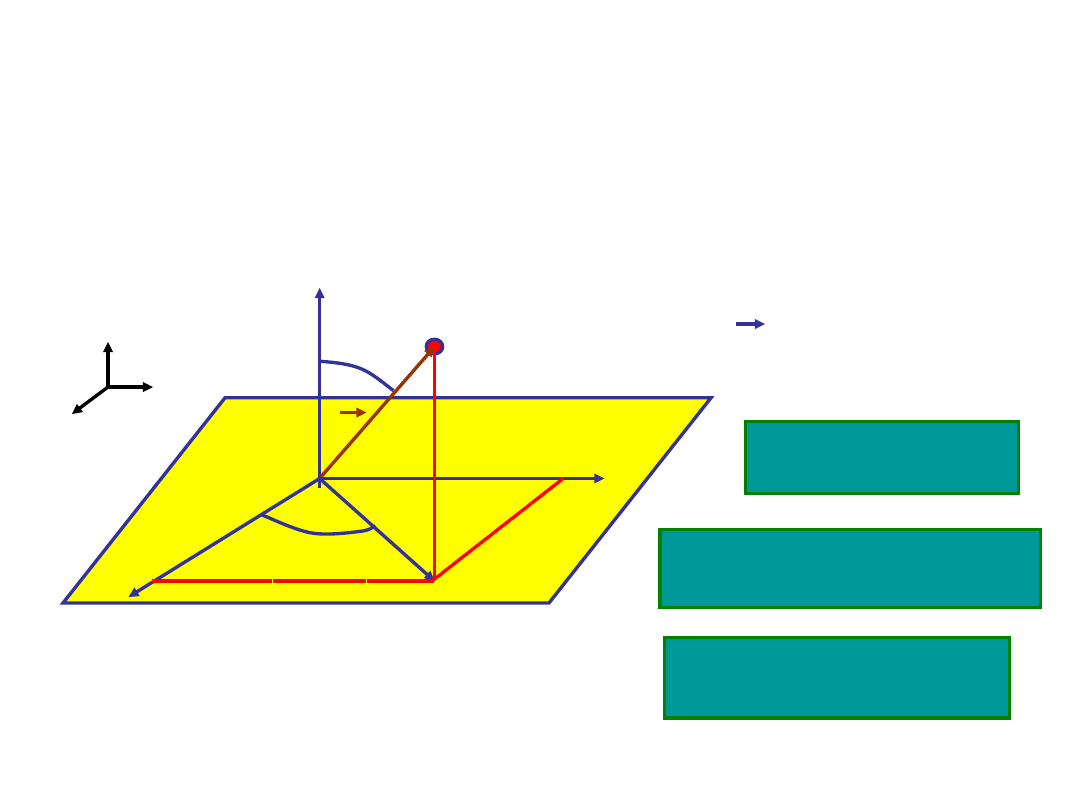
Układy współrzędnych

Jeżeli chcemy podać położenie punktu to
możemy to uczynić definiując tzw.

wektor

położenia

(wektor wodzący)

, w różnych

układach współrzędnych

z

x

y





r

P

y

x

z

Promień
wodzący
r możemy
podać w
różny sposób:

z

y

x

r















k

z

z

j

y

y

i

x

x

ˆ

,ˆ

,ˆ













k

z

j

y

i

x

r

ˆ

ˆ

ˆ









k

j

i

ˆ

,

ˆ

,

ˆ

oznaczają
wektory jednostkowe
poszczególnych osi.

ˆk

ˆi

ˆj

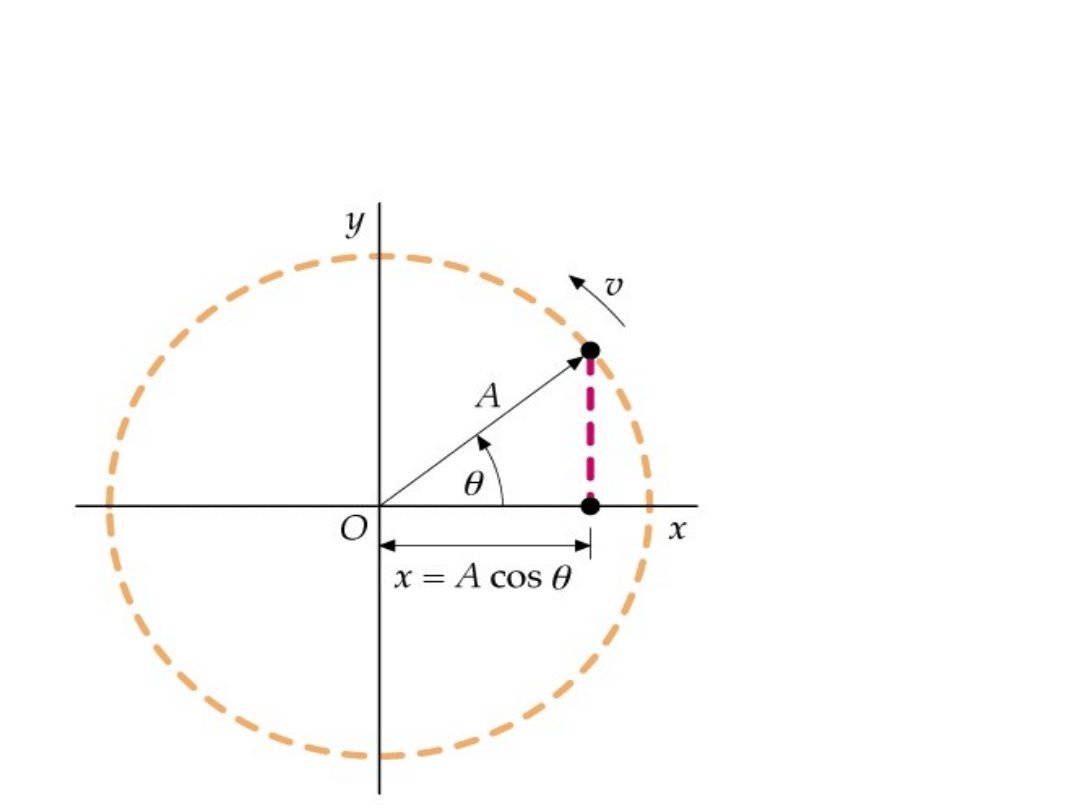
Współrz

ę

dne biegunowe

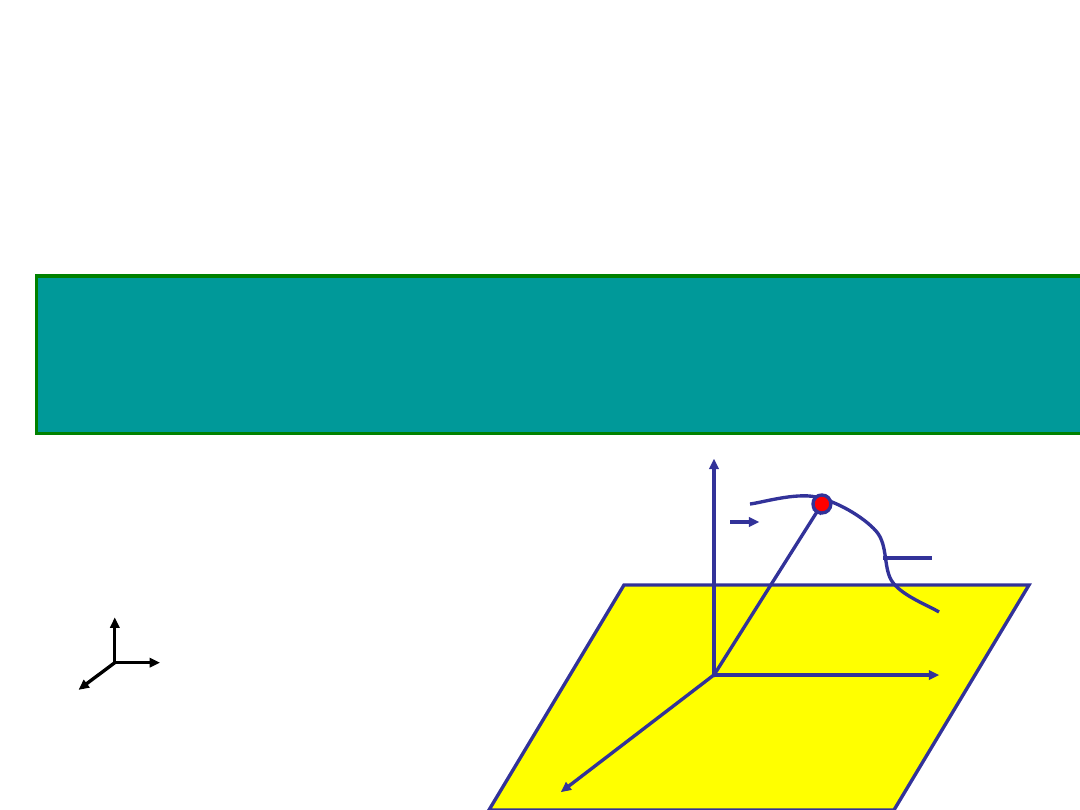
Jeżeli położenie punktu zmienia się w czasie to w

układzie współrzędnych prostokątnych możemy to opisać

w następujący sposób

)

)

(

ˆ

)

(

ˆ

)

(

ˆ

)

(

t

z

k

t

y

j

t

x

i

t

r









ˆk

ˆi

ˆj

Zakładamy, że układ jest prawoskrętny
ale może nie być : )

tor ruchu

x

y

r(t)

P(x(t),y(t),z(t))

Wersory możemy również zapisywać na różne
sposoby. W trakcie tego wykładu używać
będziemy wersji drugiej, czyli i z daszkiem.

x, y i z są współrzędnymi kartezjańskimi.
Współrzędne punktu P możemy również
zapisać we współrzędnych sferycznych.

k

k

i

z

j

j

i

y

i

i

i

x

z

y

x

ˆ

ˆ

ˆ

ˆ

ˆ

ˆ

0

0

0









































cos

sin

sin

cos

sin

r

z

r

y

r

x







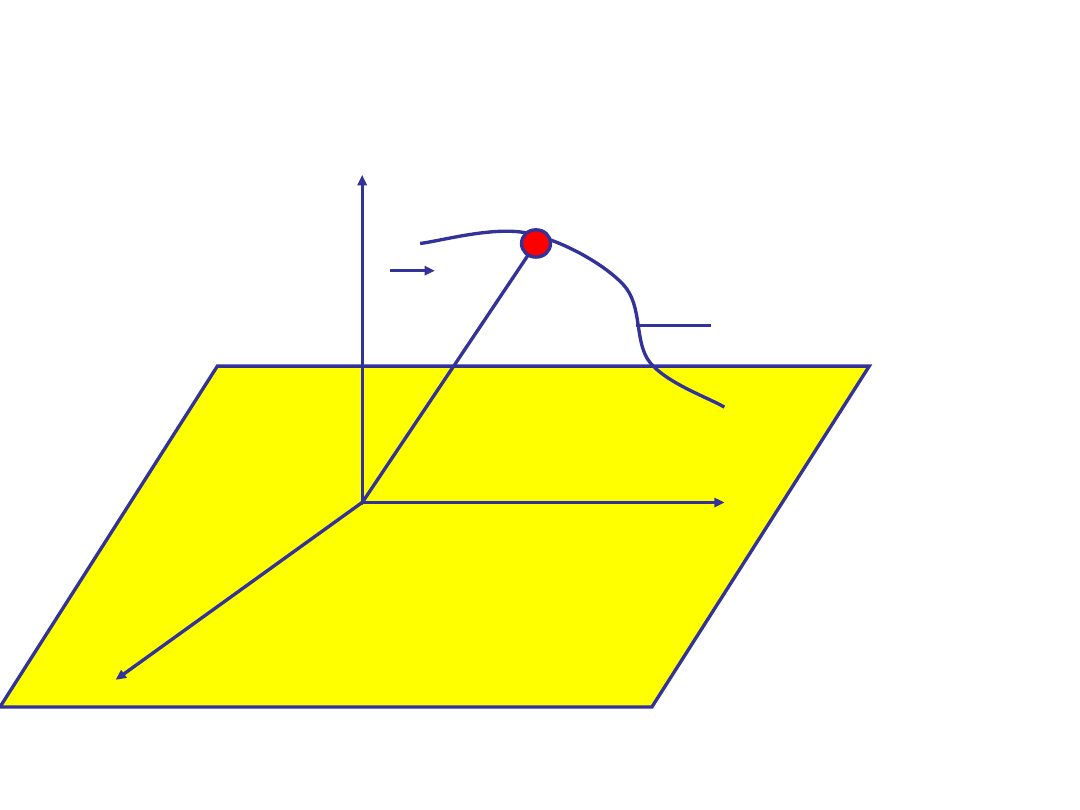
W zależności od tego, czy tor jest linią krzywą
czy prostą, mówimy o

ruchu krzywoliniowym

lub

prostoliniowym.

P(x(t),y(t),z(t))

z

tor

x

y

r(t)

.

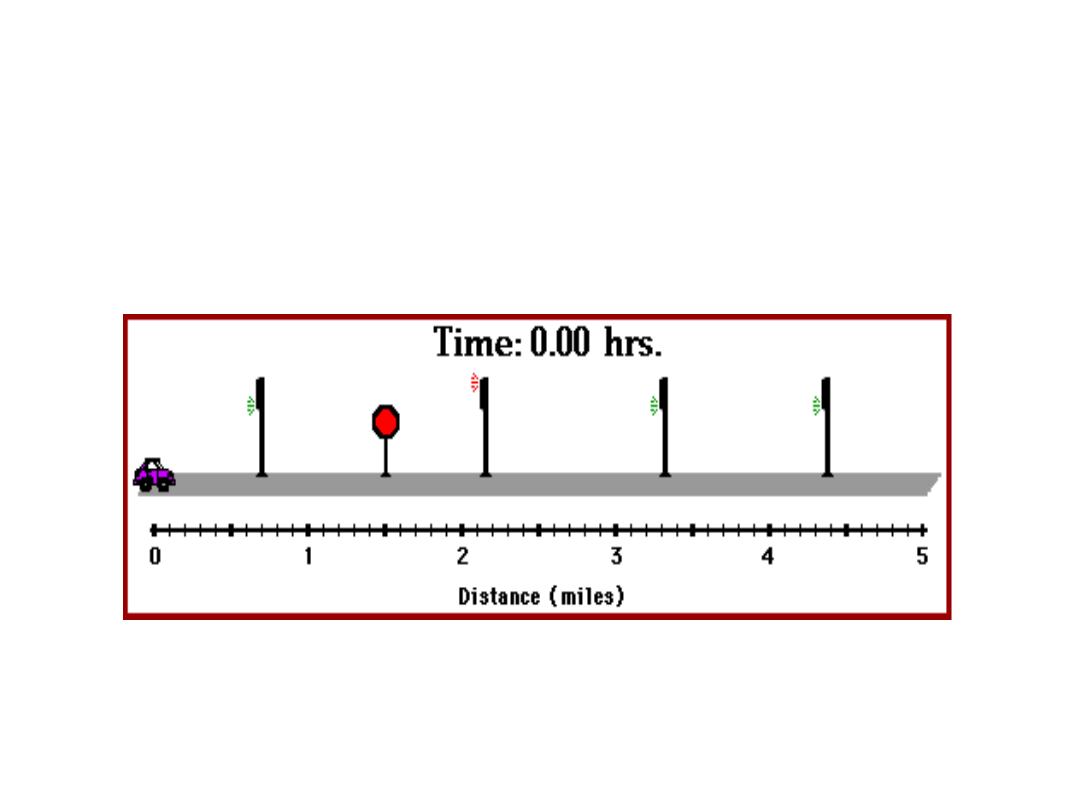
Przykładem ruchu dla którego celowe jest
określenie prędkości średniej jest ruch
samochodu w mieście. Nie zawsze „zielona
fala” umożliwia ruch samochodu ze stałą
prędkością.
Powyższa animacja pokazuje taką sytuację.

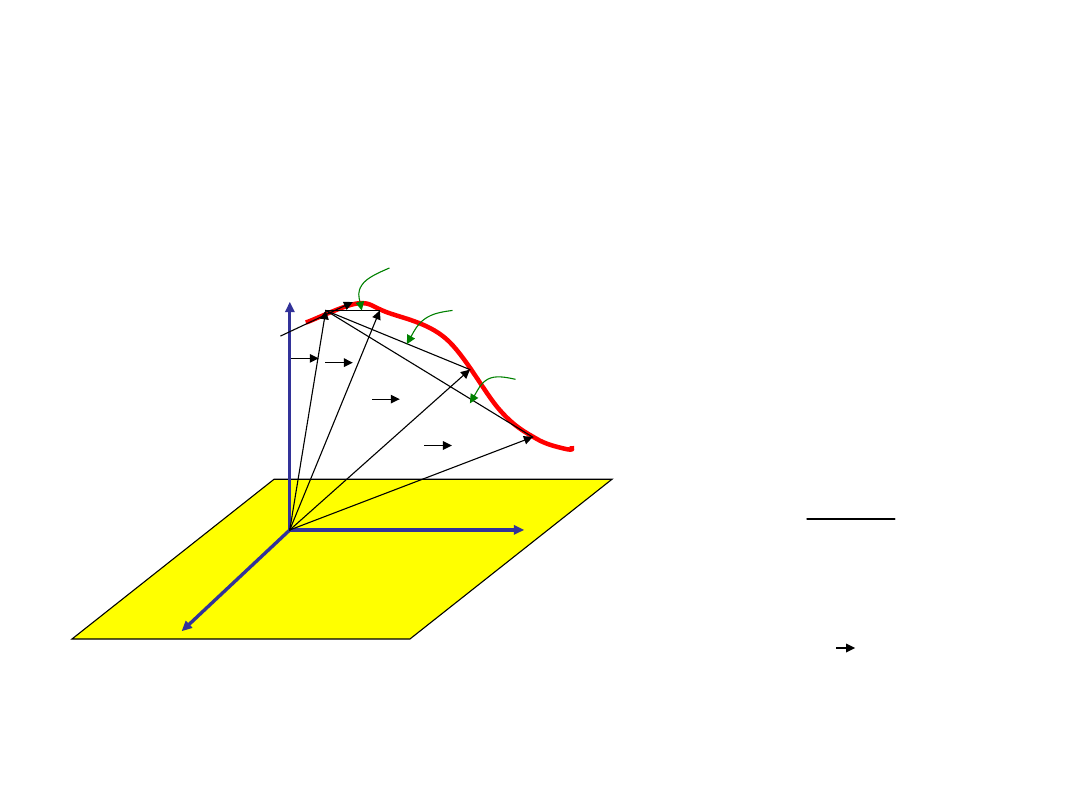
Prędkość i przyśpieszenie

jako pochodna

wektora położenia

Interesuje nas prędkość jakiegoś ciała w
konkretnym punkcie P. W jaki sposób możemy ją
obliczyć?

r

1

r

2

r

3

P

1

P

2

P

3

P

x

y

z

r

r

1

r

3

r

2

t

1

Zacznijmy skracać odstępy
czasu w których określamy
położenie ciała.
Każdorazowo konstruujemy
wektor prędkości średniej

Gdy skracamy
nieograniczenie

odstęp czasu t  0, wartość bezwzględna wektora

r / t dąży do

pewnej wartości granicznej.

n

n

n

t

r











v

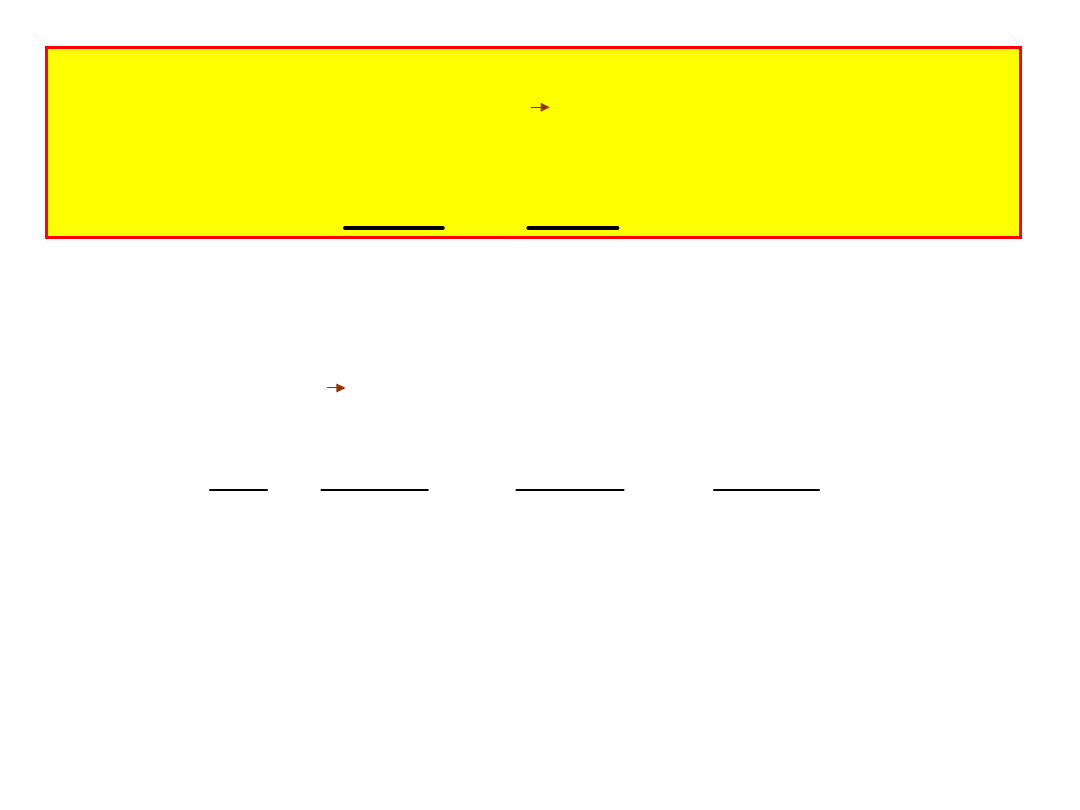
Wektor, do którego dąży wektor prędkości
średniej gdy
t

n

 0 nazywamy prędkością v ciała w punkcie

P.

Ponieważ wektor r ma trzy składowe możemy
napisać

Wektor prędkości został rozłożony na trzy
składowe:

Kierunek tego wektora dąży do kierunku stycznej do toru w punkcie P.

i

dt

t

dz

i

dt

t

dy

i

dt

t

dx

dt

r

d

y

x

ˆ

)

(

ˆ

)

(

ˆ

)

(

v













z

z

y

y

x

x

i

i

i

ˆ

v

ˆ

v

ˆ

v

v









dt

r

d

t

r

t



















0

lim

v

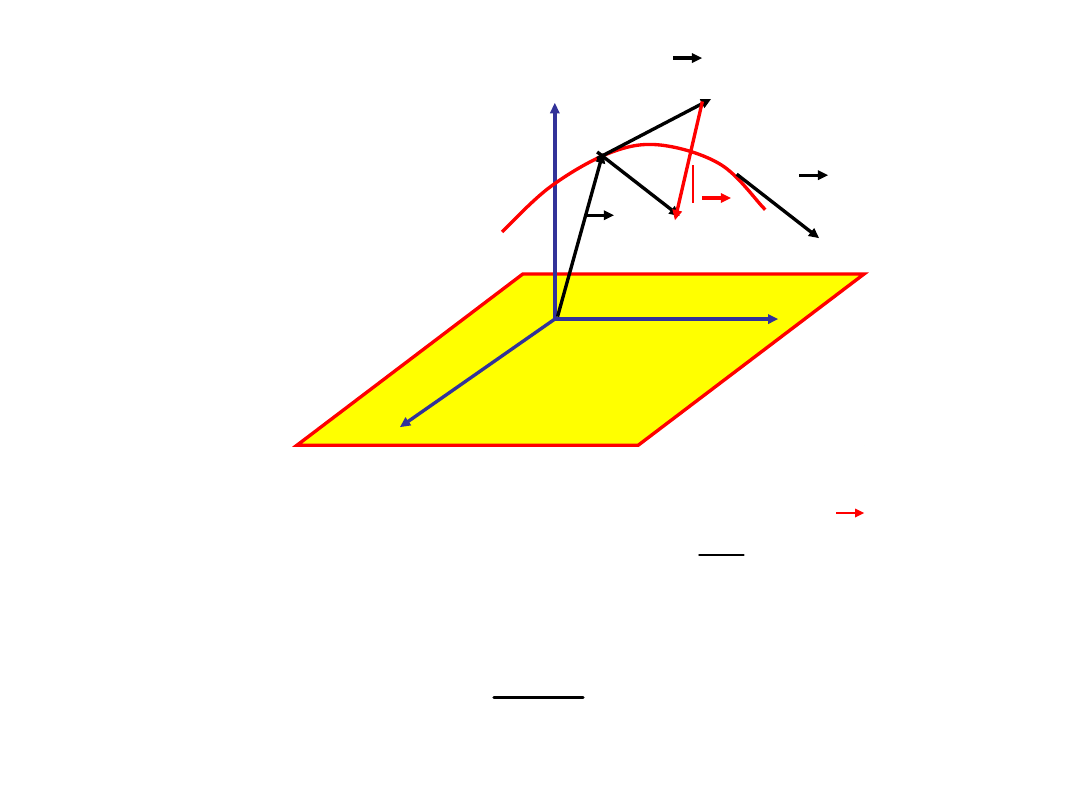
z

v

1

x

y

tor

P

1

P

2

v

2



v

r

1

Z rysunku widzimy, że w stosunku do
punktu P

1

w punkcie P

2

nastąpiła zmiana

prędkości

w czasie t.

Średnie

przyśpieszenie definiujemy jako

:

v



t

a

śr







v



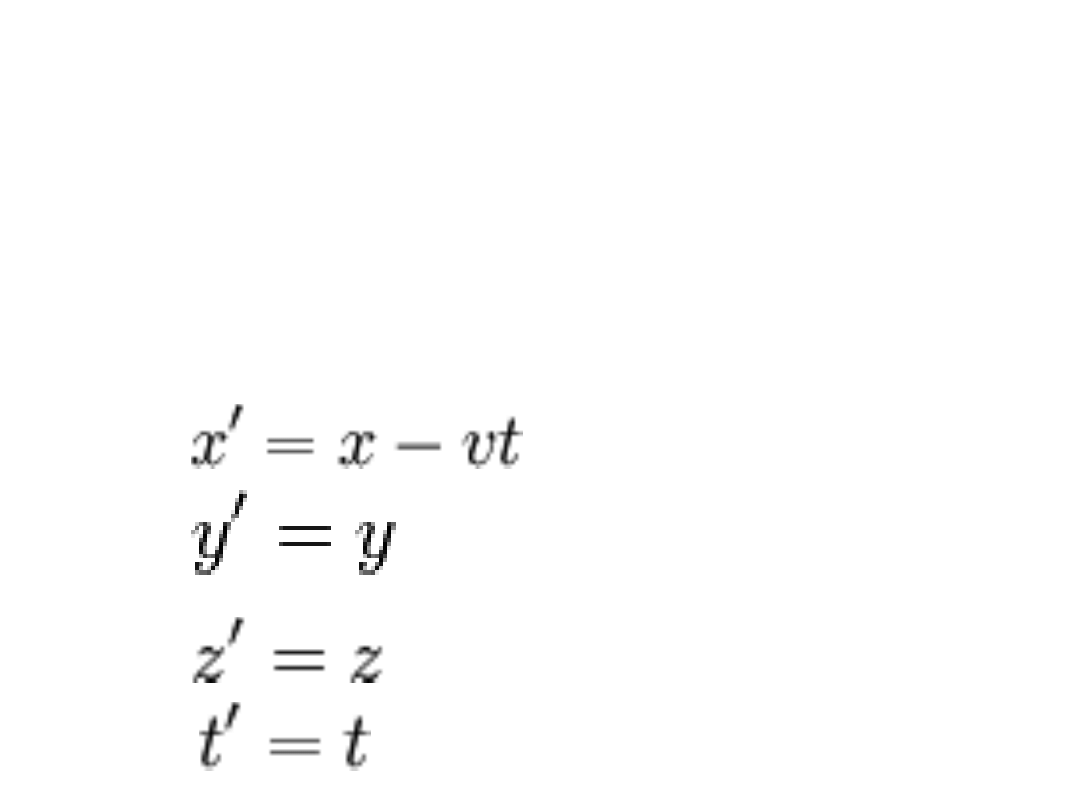
Transformacja

Galileusza

Jeżeli przyjmiemy, że zdarzenie w układzie inercjalnym A opisane

jest współrzędnymi czasoprzestrzennymi (x,y,z,t), a w układzie

inercjalnym B przemieszczającym się z prędkością v w kierunku

osi x, są to odpowiednio (x',y',z',t'), to transformacja

współrzędnych będzie opisana układem równań:

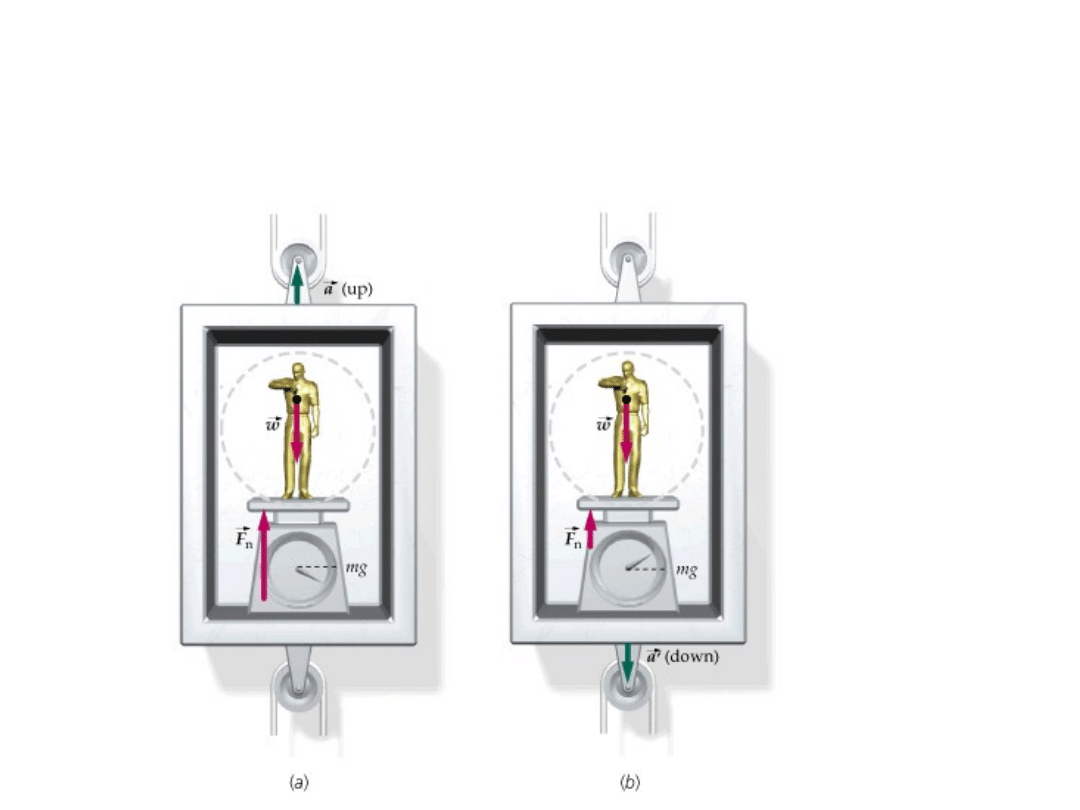
Winda jako układ inercyjny i

nieinercyjny

Winda jest układem
nieinercyjnym
a nawet inercyjnym
Klasyk

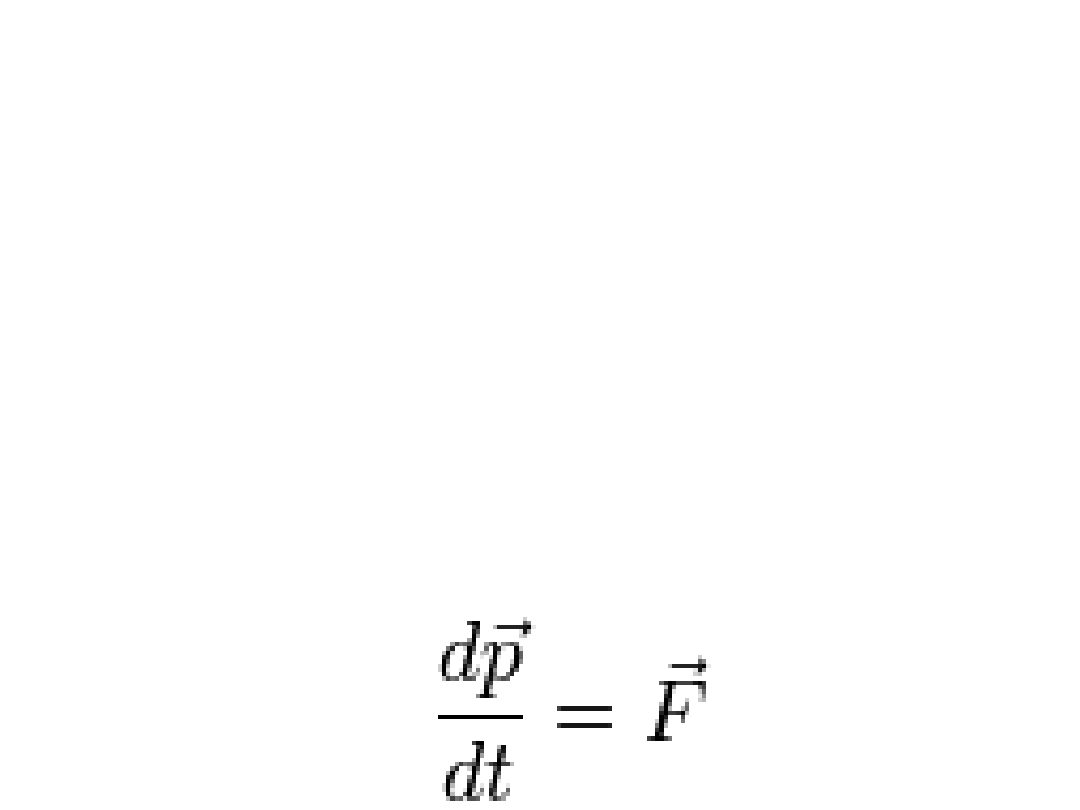
II Zasada Dynamiki

Newtona

• Lex II. Mutationem motus

proportionalem esse vi motrici
impressae, et fieri secundum lineam
rectam qua vis illa imprimitur.

’’Zmiana ruchu jest proporcjonalna do

przyłożonej siły poruszającej i odbywa
się w kierunku prostej, wzdłuż której
siła jest przyłożona.’’

• W wersji zwanej uogólnioną (uogólniona druga zasada dynamiki),

Jeśli na spoczywające
ciało nie działa żadna
siła to pozostaje ono w
spoczynku. Jeśli ciało
porusza się ruchem
jednostajnym, ze stałą
prędkością, to w tym
stanie ruchu będzie
pozostawać dopóki nie
zacznie na nie działać
siła zewnętrzna.

a

m

F













m

F

a

F

AB

= - F

BA

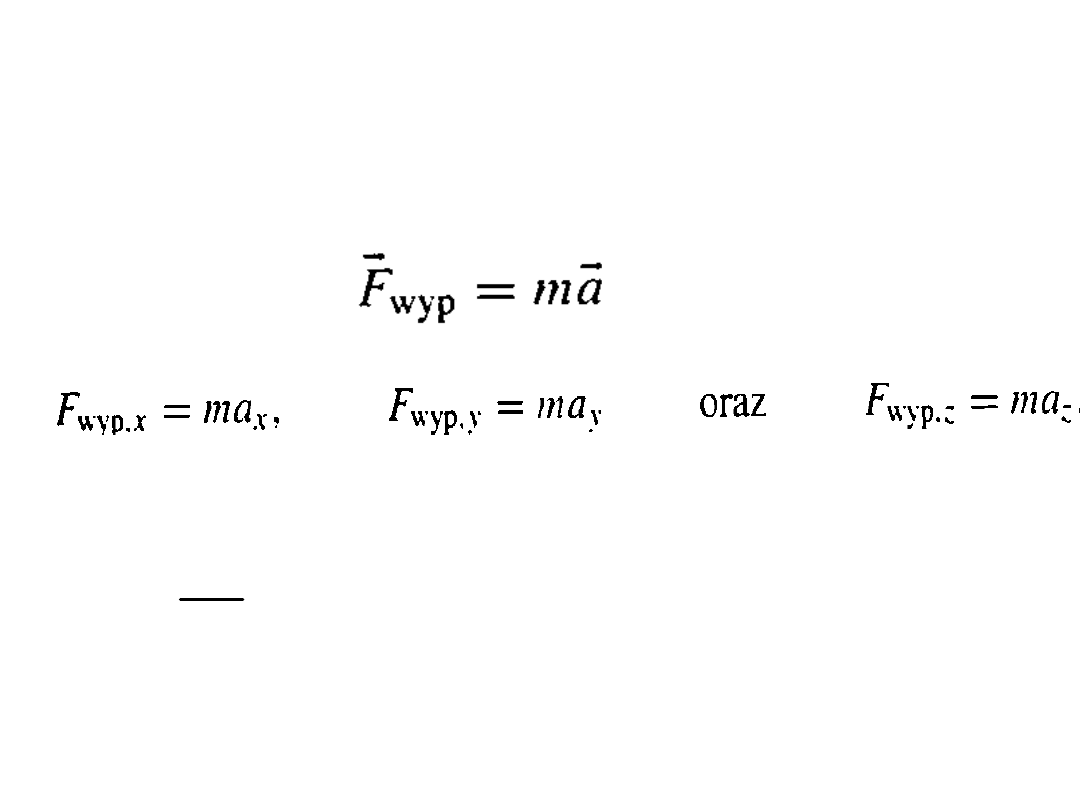
II Zasada dynamiki

Newtona

Stąd

a

m

F













m

F

a



 F

F











a

m

F

F







Stąd

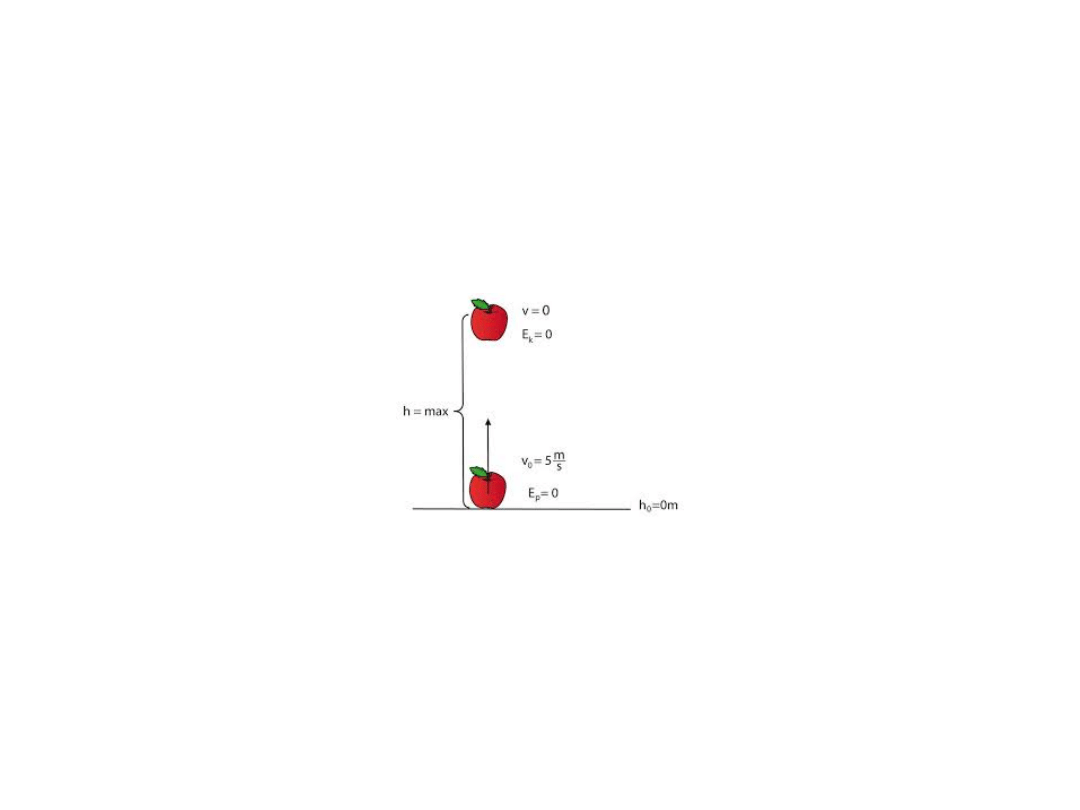
III Zasada Dynamiki

Lex III. Actioni contrariam semper et aequalem esse

reactionem; sive corporum duorum actiones in se mutuo

semper esse aequales et in partes contrarias dirigi.

F

AB

= - F

BA

Względem każdego działania istnieje przeciwdziałanie zwrócone

przeciwnie i równe, to jest wzajemne działania dwóch ciał są

zawsze równe i zwrócone przeciwnie.

III Zasada dynamiki, słuszna tylko w mechanice nierelatywistycznej, zwana jest

zasadą akcji i reakcji. Zasada ta zakłada, że oddziaływania rozchodzą się w

przestrzeni z nieskończoną prędkością. Doświadczenia wskazują, że wszystkie

oddziaływania rozchodzą się ze skończoną prędkością nieprzewyższającą

prędkości światła. Zgodnie ze współczesnymi poglądami w zasadach dynamiki

należy rozumieć: ciało – punkt materialny, ruch – ruch względem układu

odniesienia będącego układem inercjalnym. Zasady dynamiki mają swoje

wersje także dla ruchu obrotowego (punktu i bryły) oraz mogą być stosowane

w układach nieinercjalnych po uwzględnieniu sił bezwładności

.

Prawo powszechnego
ciążenia
Siła grawitacji

Według Newtona prawo powszechnego ciążenia
w układzie inercjalnym można podać w postaci;

gdzie G jest stałą grawitacji i

G=6.67·10

-11

Nm

2

/kg

2

.

m

1

i m

2

są masami dwóch ciał oddziałujących, ich masy

grawitacyjne. Są one źródłem

pola

grawitacyjnego.

W fizyce mówimy o polu wówczas, gdy
każdemu punktowi danej przestrzeni
możemy przyporządkować pewną wartość
jakiejś wielkości fizycznej – skalar, wektor
lub tensor.

Przykłady pól skalarnych i wektorowych wielkości podane są na następnej
stronie

r

r

r

m

m

G

F





2

2

1







Siłę, która nadaje ciału przyśpieszenie
ziemskie g, nazywamy ciężarem. F = m g

Z drugiej strony przyspieszenie
to stosunek siły do masy

Tylko wtedy, gdy masa grawitacyjna jest równa
bezwładnej wszystkie ciała w polu ziemskim mają
to samo przyśpieszenie.

I tak właśnie jest nie tylko na Ziemi

Masa grawitacyjna i masa bezwładna

B

C

B

m

m

g

m

F

g





Zasady zachowania w Fizyce

Zasady zachowania występujące w fizyce są to prawa określające
stałość pewnych parametrów charakteryzujących układ fizyczny.
Do najważniejszych należą zasady zachowania:

energii,
pędu,
krętu,
ładunku elektrycznego,
liczby barionowej,
liczb leptonowych,
parzystości kombinowanej CPT.

Zasady zachowania wynikają (

twierdzenie

Noether

) z

niezmienniczości równań opisujących stan układu względem
pewnych transformacji.

istnieją różne rodzaje energii:

-grawitacyjna,

-kinetyczna,

-elektryczna,

-magnetyczna,

-potencjalna,

-chemiczna,

-jądrowa,

-energia promieniowania, i inne.

energię kinetyczną istniejącą zawsze przy
ruchu ciał, oraz o energię potencjalną ściśle
związanej z działaniem sił.

Zasada zachowania energii

W mechanice klasycznej obowiązują zasady
zachowania;

energii, pędu i momentu pędu

.

Te trzy zasady można traktować jako
konsekwencje pewnych symetrii.

Zasada zachowania energii

wynika więc z

niezmienniczości
względem przesunięcia w czasie. Inaczej
mówiąc, jeżeli w każdej chwili czasu

zasada

wariacyjna najmniejszego działania,

oraz

równania ruchu opisujące układ nie zmieniają
się , to energia układu w tych chwilach jest
taka sama.

Moc

Pracę i energią mierzy się w tych samych
jednostkach. Bardzo często interesuje nas
zdolność wykonywania pracy przez pewne
urządzenia w ciągu określonego czasu.
Definiujemy wtedy

moc,

jako pracę wykonaną

w jednostce czasu.





dW d

P

F dr

F v

dt

dt







 

r

r

r

r

Jednostką mocy jest jeden wat.

1W = 1J/s = [kg·m

2

·s

-3

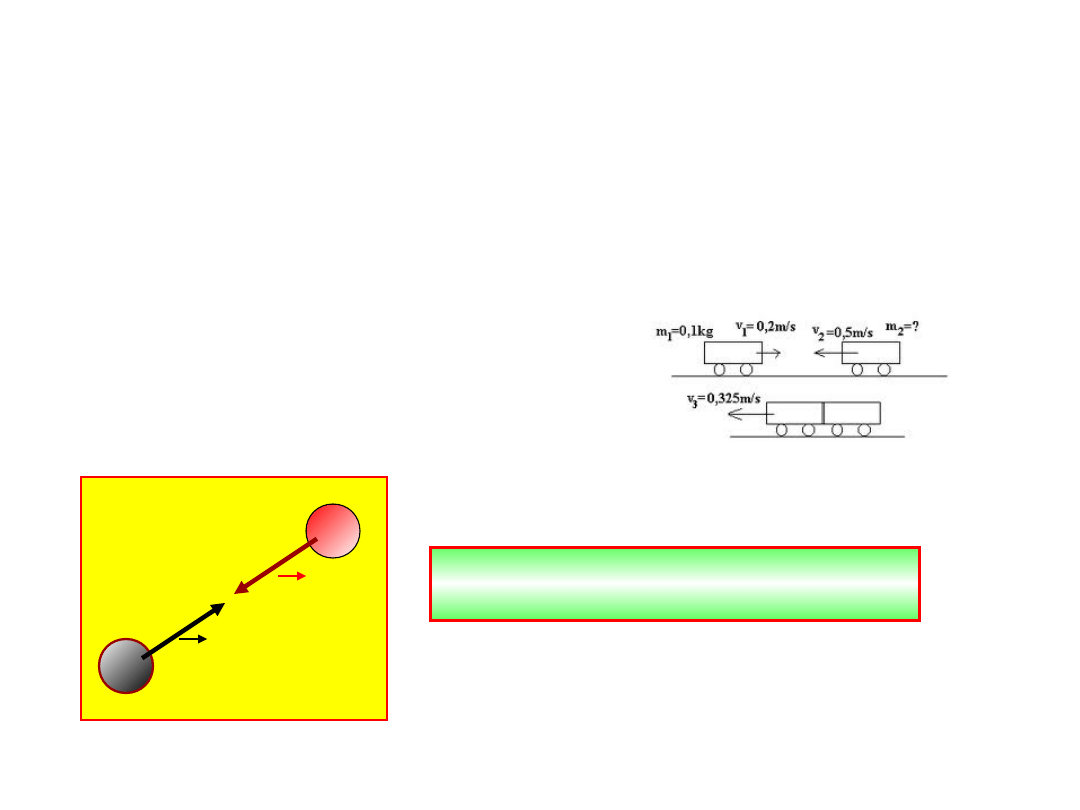
Zasada zachowania pędu

korzystając z 3 zasady dynamiki Newtona
znajdziemy dodatkową regułę dotyczącą
oddziaływania pomiędzy ciałami, która
podobnie jak zasada zachowania energii jest
ważna dla wszystkich sił niezależnie od tego,
czy siły te szczegółowo znamy czy nie.

zasada akcji i reakcji

F

2

1

F

12

Wiemy, że,

12

21

12

21

0

F

F

F

F









r

r

r

r

Zasadę akcji i reakcji da się uogólnić
na wiele ciał.

Suma wszystkich sił działających pomiędzy
tymi ciałami jest równa zero.
Siły takie nazywamy

siłami wewnętrznymi

i ich

suma jest równa 0, gdyż siły te się znoszą
parami.

F

2

1

F

32

F

13

F

31

F

23

F

12

1

0

N

ik

i k

i k

F

 







r

Z zasady tej ważnej tylko
dla sił wewnętrznych
znajdziemy regułę.

1 1

2 2

12

21

(

)

(

)

0

d mv

d mv

F

F

dt

dt









r

r

Przez całkowanie tego równania otrzymujemy;

1 1

2 2

mv mv

p const



 

r

r

r

Całkowity pęd p układu dwóch ciał nie
zmienia się pod wpływem działania sił
wewnętrznych

.

Równanie to możemy uogólnić dla układu

N

ciał oddziaływujących tylko przez siły
wewnętrzne.

1

N

i i

i

mv

p const



 



r

r

Równanie

to

stanowi zapis

zasady

zachowania pędu

dla układu N izolowanych ciał.

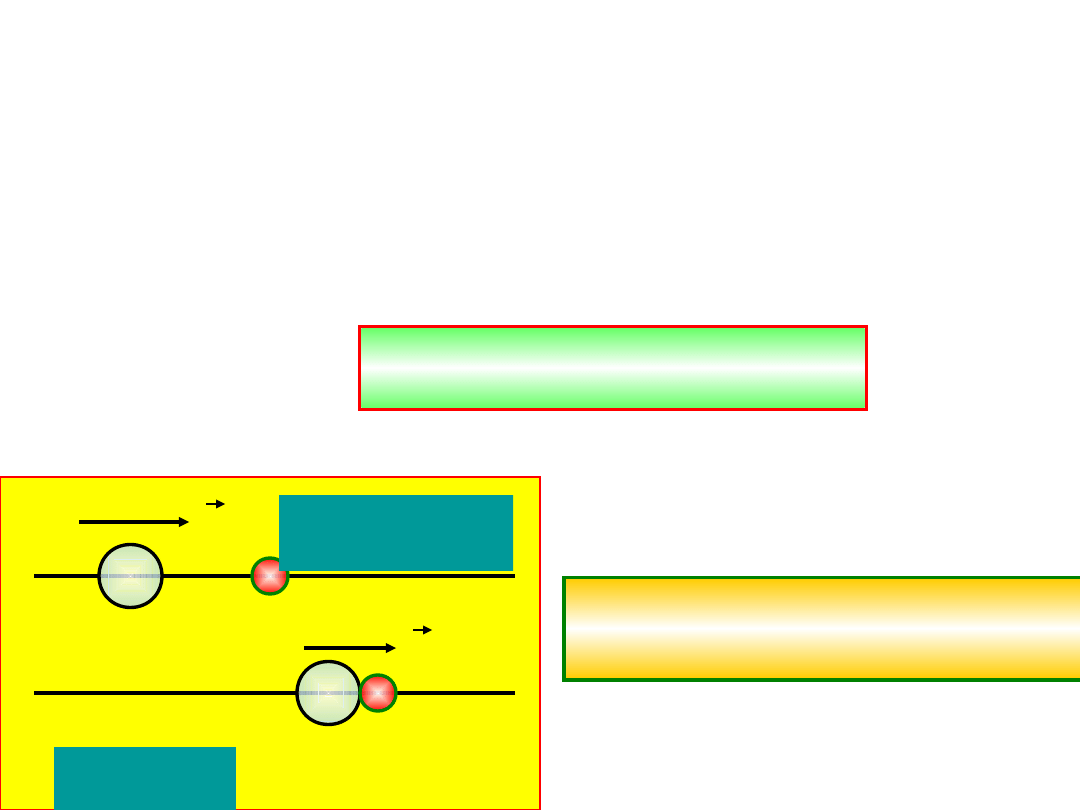
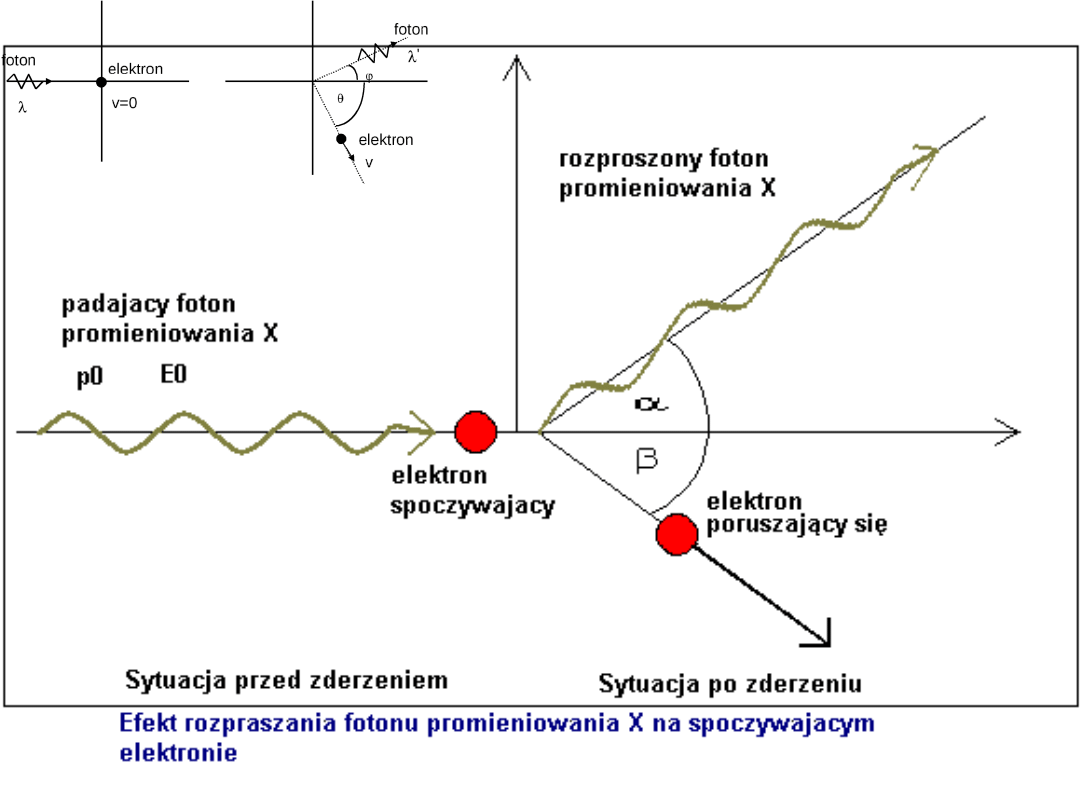
Zderzenia ciał Zasada

zachowania pędu

W czasie zderzenia działają przez krótki okres czasu pomiędzy

partnerami zderzenia siły. Siły wewnętrzne w czasie zderzenia są
zdecydowanie silniejsze od sił zewnętrznych.

Zasada zachowania pędu i

energii zastosowana

do sytuacji przed i po zderzeniu, często pozwala

nam przewidzieć efekt końcowy zderzenia

.

'

'

1 1

2 2

1 1

2 2

mv mv

mv mv







r

r

r

r

m

1

m

2

m

1

+

m

2

v

1

v

1

’

przed
zderzeniem

po
zderzeniu

Zderzenie niesprężyste gdy kulki
po zderzeniu są razem

2

'

1 1

1

1

0 (

)

mv

m m v

 



r

r

Zderzenie sprężyste

A poniżej niesprężyste

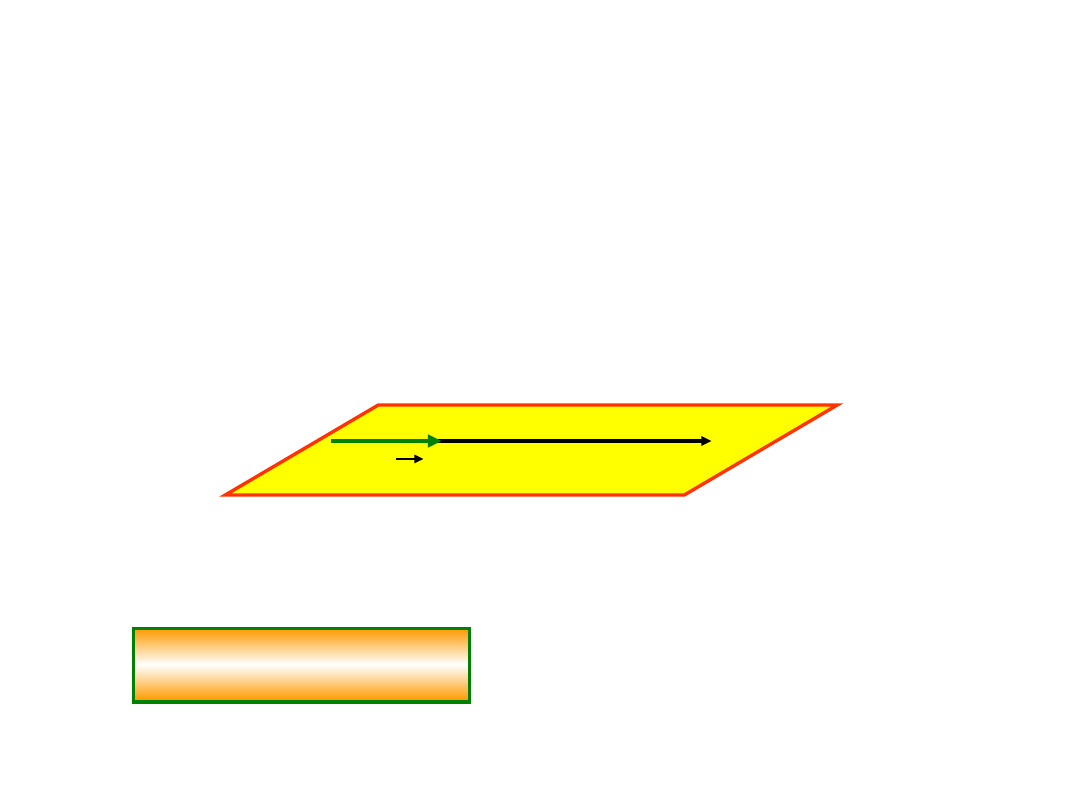
Ruch prostoliniowy

Jeżeli tor ruchu ciała jest linią prostą, to
zawsze możemy tak dobrać układ
współrzędnych, aby jedna z jego osi
pokrywała się z torem. Zwykle wybiera się oś
x.

x

r

x

i

t

x

t

x

t

r

ˆ

)

(

)

(

)

(











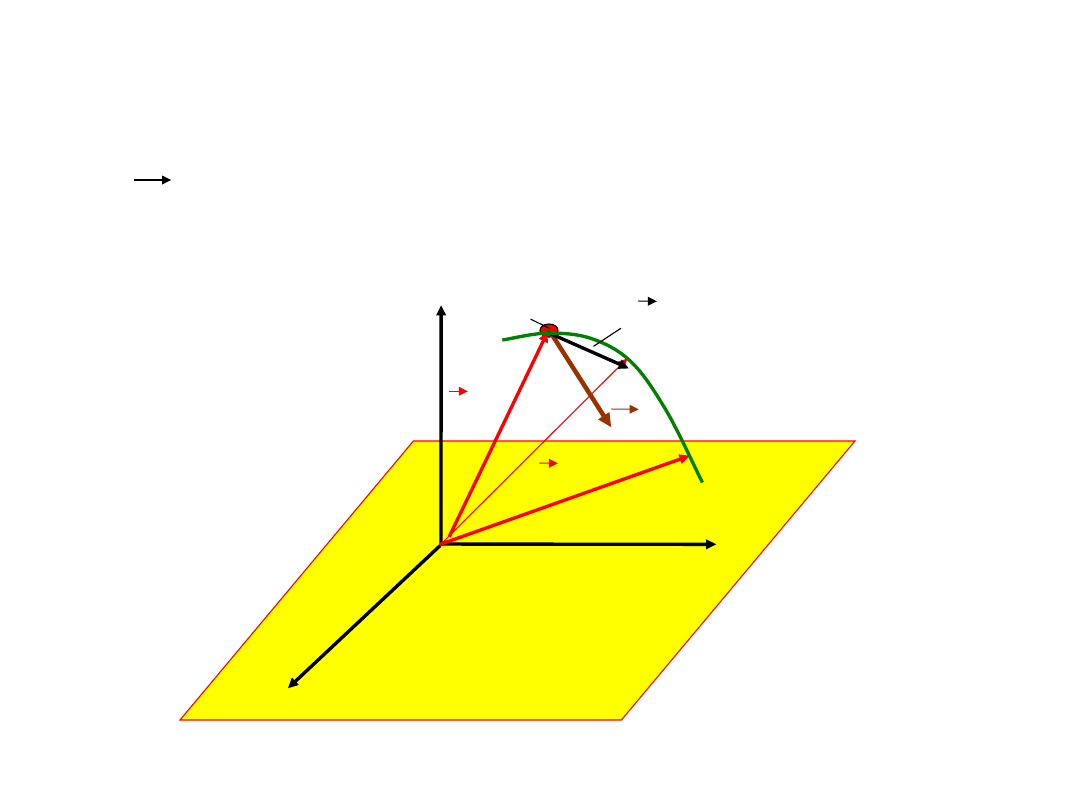
Energia kinetyczna i potencjalna

Rozważmy ciało o masie m znajdujące się pod
działaniem siły F(r). Zadajmy sobie pytanie,
czy istnieje jakaś wielkość fizyczna, która się
w trakcie ruchu nie zmienia

x

y

z

A

B

dr

r(t)

r(t

0

)

F

m

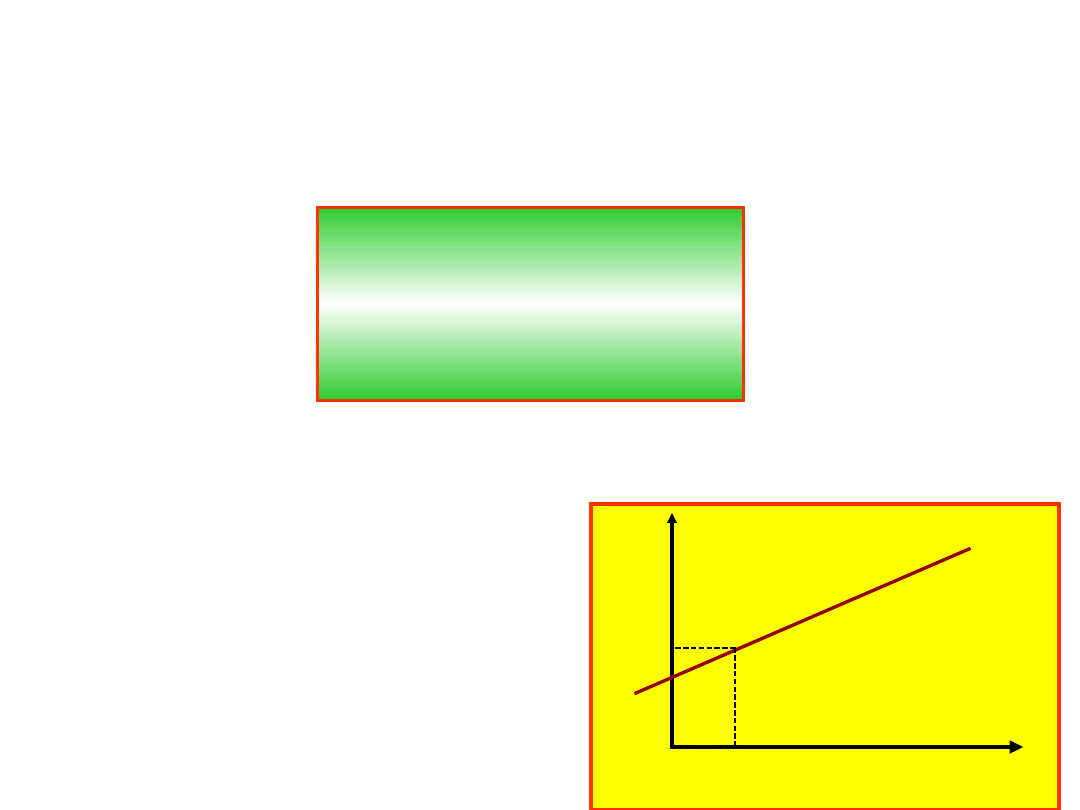
Ruch jednostajny

Ruch jednostajny, jest to taki ruch, w którym
prędkość jest stała, v=const.

)

(

)

(

0

0

0

0

0

0

t

t

v

x

x

t

t

v

dt

v

dt

v

x

x

t

t

t

t





















.

x jest przebytą przez ciało drogą, którą zwykle
oznaczaliśmy przez s.
Wykres drogi od czasu

ma więc postać:

s

t

x=x

0

+

v(t

-t

0

)

t

0

x

0

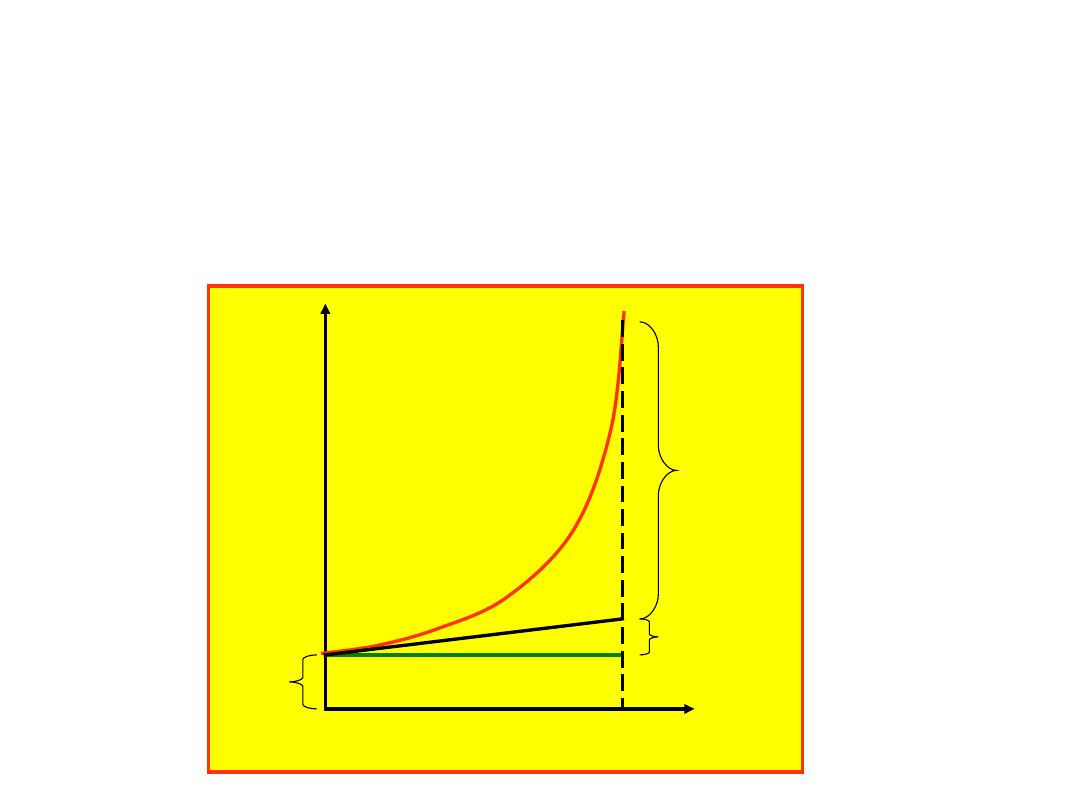
t

s=x

x

0

v

0

t

1/2at

2

Narysujmy drogę
którą ciało przebywa w czasie t
przy założeniu, że t

o

= 0.

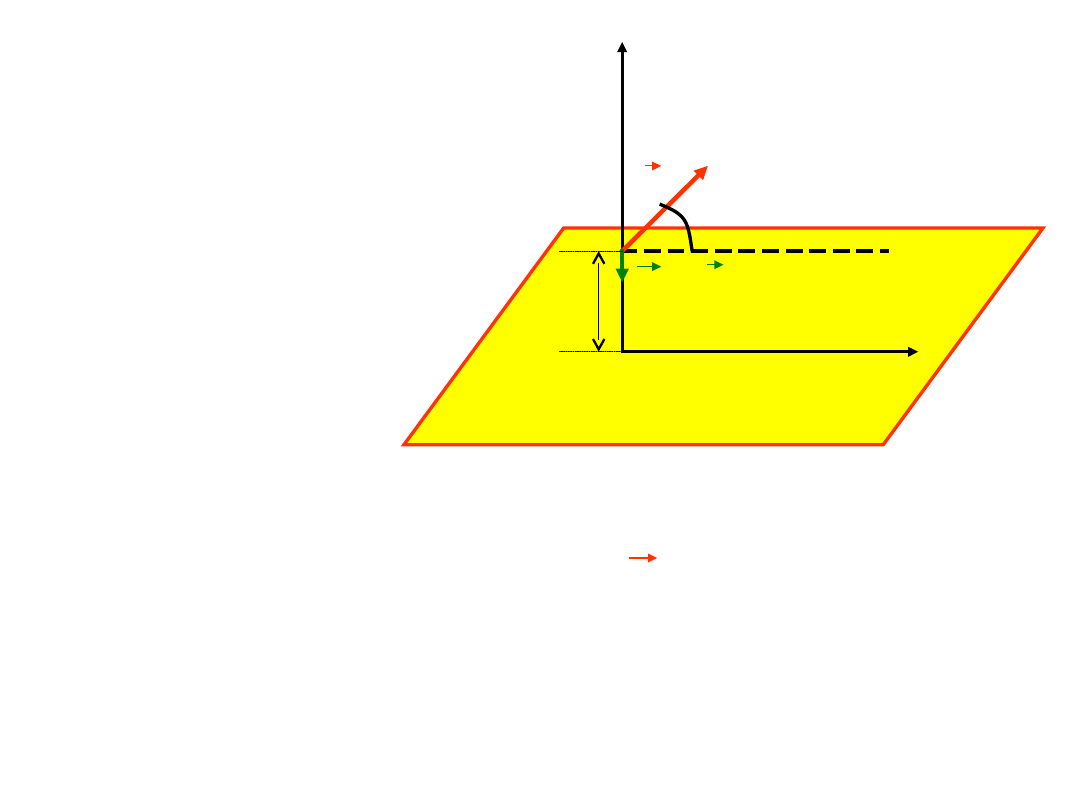
x

y

g = -g i

y

v

0

h



W polu ciężkości na wysokości h
wyrzucamy pod kątem  do poziomu z

prędkością

v

0

jakieś ciało.

Możemy tu rozróżnić następujące przypadki:

Rozważmy
następujący ruch.

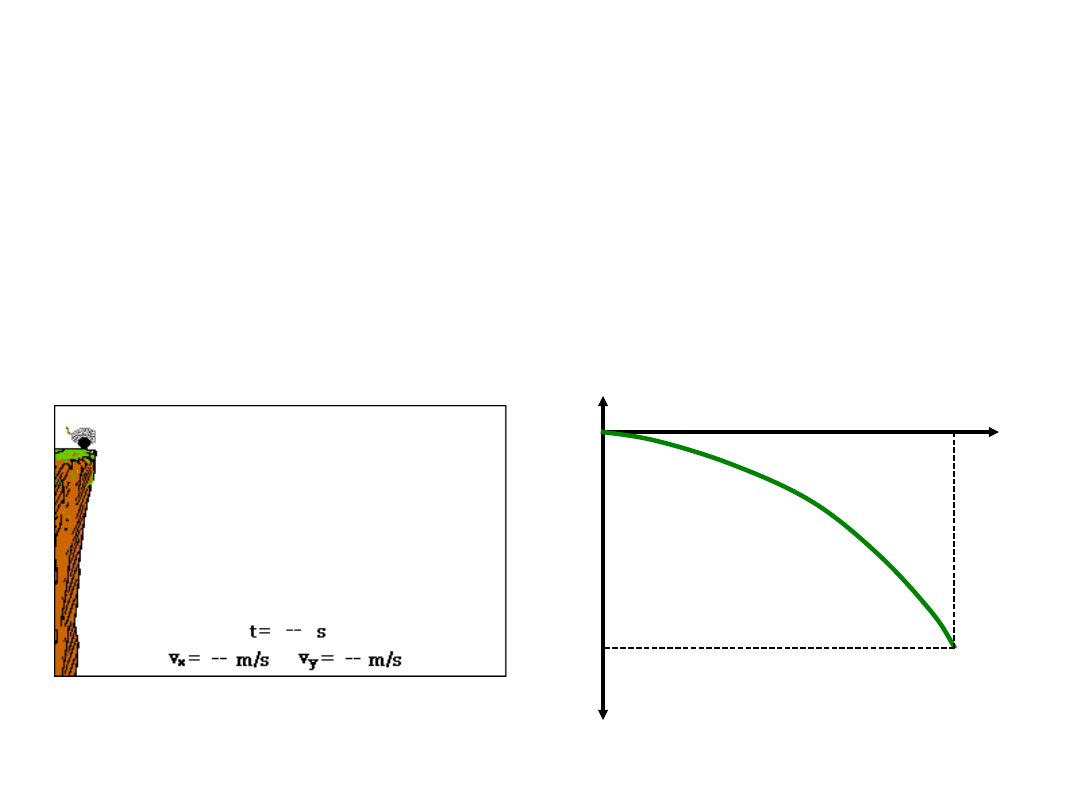
Rzut poziomy

Kula armatnia została wystrzelona poziomo ze
stałą prędkością v

0x

=100 m/s. Kula spadła na

ziemię w odległości 1200 m od miejsca
wystrzelenia . Jaka jest długość drogi pionowej
jaką przebyła kula przy zaniedbaniu oporu
powietrza.

x

y

x = 1200 m

y = ?

Zasada superpozycji
ruchów

Zauważmy, że rozważaliśmy ruch

poziomy

niezależnie od ruchu

pionowego

aby wyznaczyć

czas lotu kamienia.

Ruch pionowy jest spadkiem swobodnym, dla którego
mamy:

v

0y

= 0

oraz

a

y

=-g =-9.81 m/s

2

.

Z równania (2.9a) dla ruchu w kierunku osi y mamy

y = -1/2 g t

2

= -1/2 · 9.81 m/s · (12m)

2

= 706.32 m

Zauważmy, że rozważaliśmy ruch

pionowy

niezależnie od ruchu

poziomego

aby wyznaczyć

wysokość spadku kamienia.

Niezależność tych dwóch ruchów implikuje, że pocisk
przy

v

0x

= 0

w czasie

12 s

spadnie o

706.32 m

.

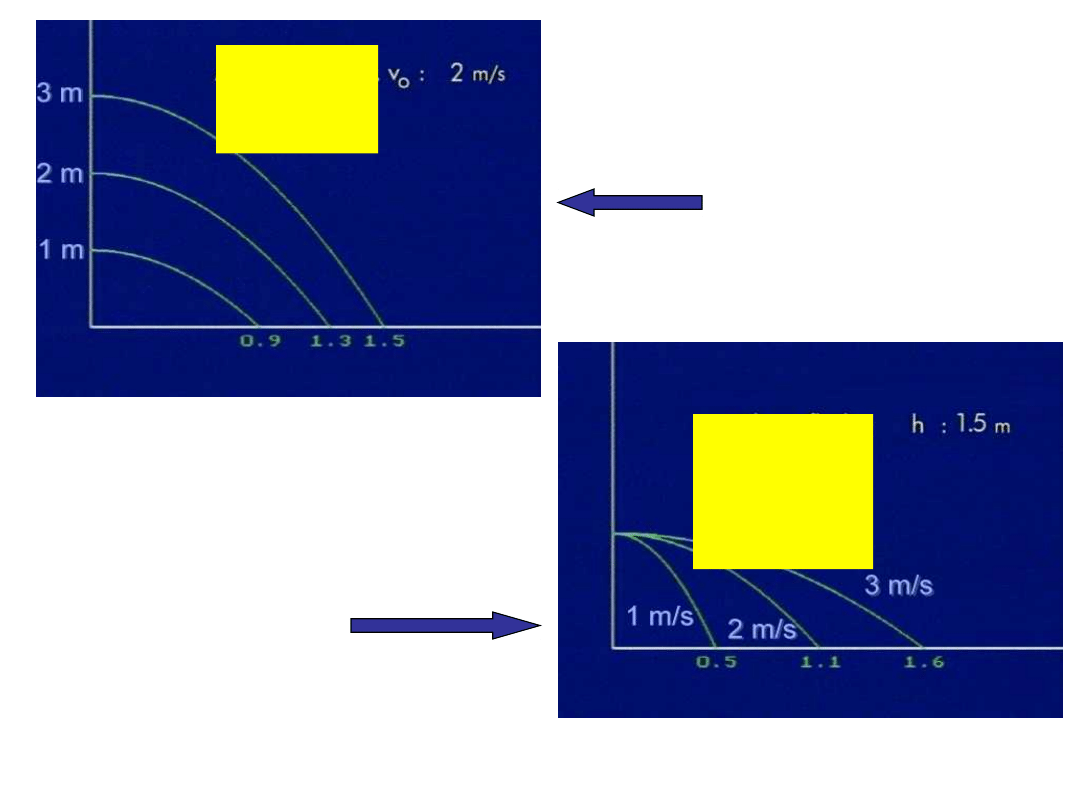
Prędkość
początko
wa

Wysokoś
ć
początko
wa

Ta sama prędkość
początkowa z
różnych wysokości

Ta sama wysokość,
różne prędkości
początkowe

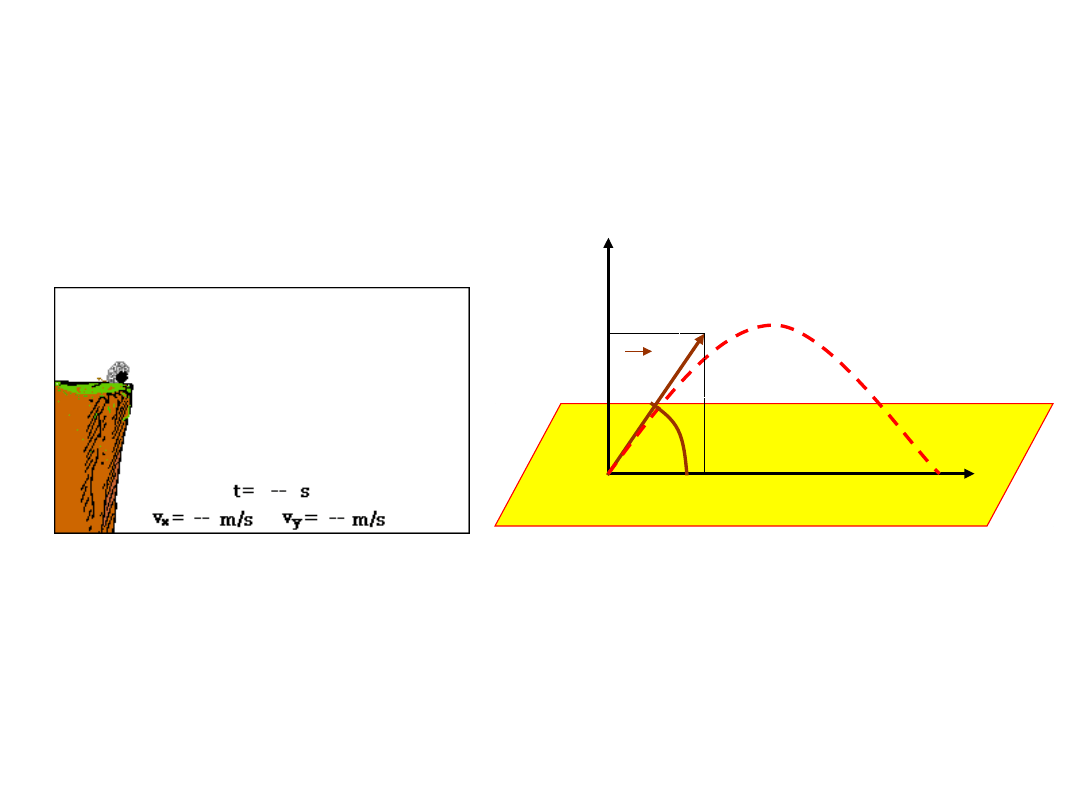
Rzut
ukośny

Jest to przypadek, dla którego:

h = 0 lub h  0, 0 <  < 90

0

, v

0

 0.

y

x

v

0



Składowe prędkości
początkowej
wynoszą:





sin

v

v

cos

v

v

0

0

0

0





y

x

Rzut ukośny charakteryzują

następujące wielkości:

1. Zasięg rzutu,
2. Maksymalna wysokość

Zasięg rzutu otrzymamy

licząc odległość

poziomą x dla y=0.

Równanie to ma dwa
rozwiązania:

2

0

0

2

1

v

)

(

v

)

(

t

g

t

t

y

t

t

x

y

x











0

cos

v

2

2

2

2

0







x

g

tg

x









2

sin

v

cos

v

2

0

2

0

2

2

0

2

max

1

g

g

tg

x

x

x











Maksymalną wysokość rzutu otrzymamy
licząc maksimum funkcji przedstawiającej
równanie toru, czyli dla dy/dx=0.

0

cos

2

2

2

2

0





x

v

g

tg





Otrzymujemy
więc:

max

2

0

2

1

2

sin

2

x

g

v

x







.

Podstawiając wyrażenie na x do równania
(2.13), otrzymujemy na maksymalną
wysokość poruszającego się rzutem ukośnym
wartość:



2

2

0

max

sin

2g

v

y



.

Widzimy z podanych wzorów, że zarówno
maksymalny zasięg rzutu jak i maksymalna
wysokość rzutu zależą od wartości i kierunku
prędkości początkowej.

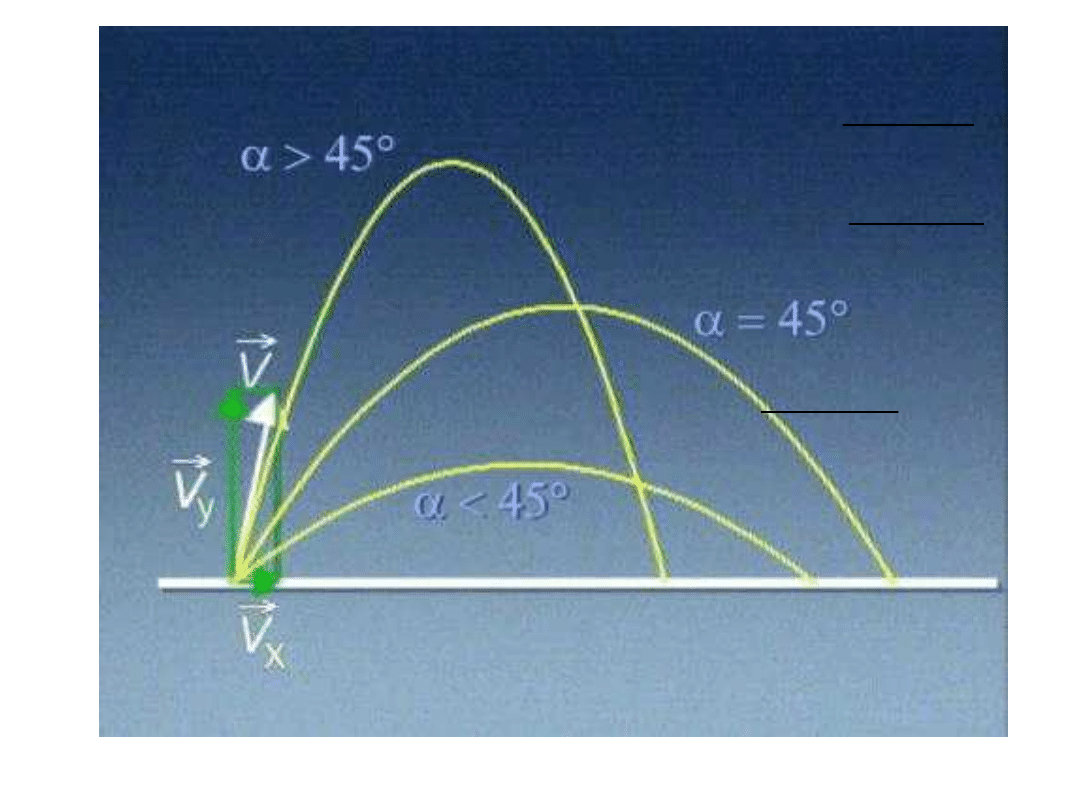
Wysokość rz.:

g

v

y

2

sin

2

2

0

max





Zasięg rz.:

g

v

x



2

sin

2

0

max



Tor ruchu

przedstawia

przesunięta parabola

g

y

2

sin

v

2

2
0

max





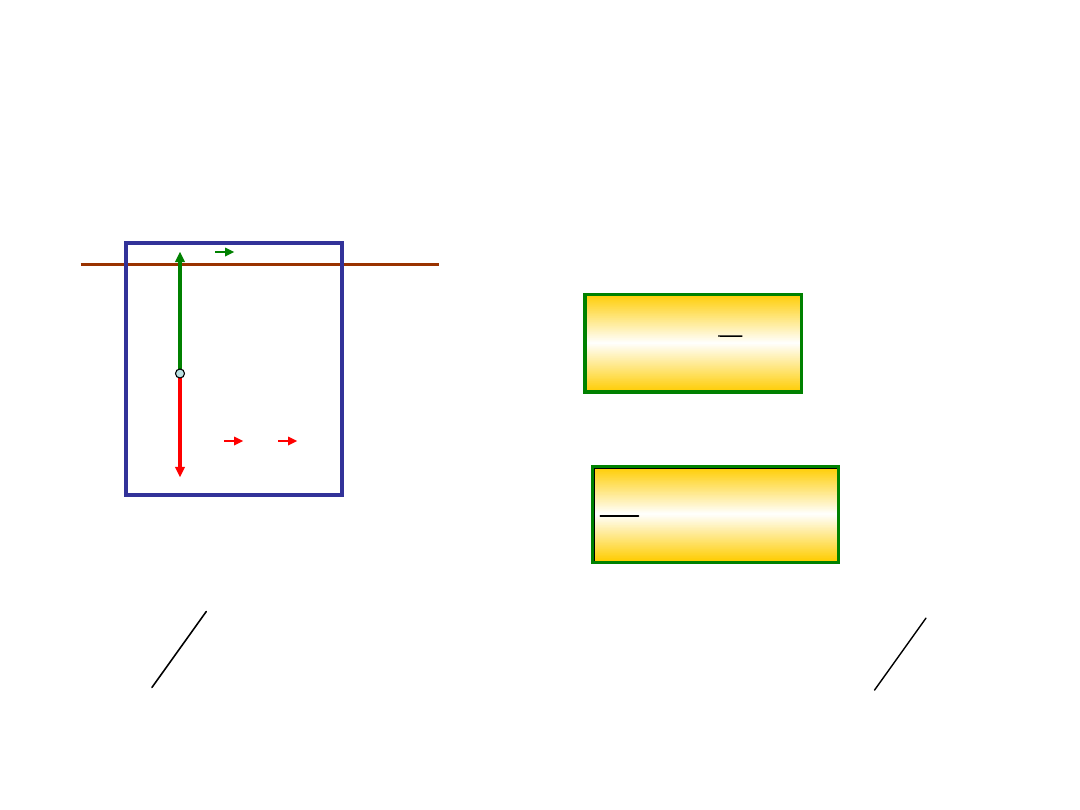
Należy jeszcze wspomnieć o szczególnym
przypadku rzutu ukośnego, a mianowicie

rzutu pod kątem  = 90

0

z prędkością

początkową v

0

. Taki przypadek nazywamy

rzutem pionowym

.

v

0

v = g
t

Przebywana w czasie t
droga wynosi:

2

0

2

1

gt

t

v

s





Maksymalną wysokość
uzyskamy z warunku

0

0







gt

v

dt

ds

.

Czas ruchu ciała do maksymalnej wysokości h
wynosi więc:
, a uzyskana maksymalna wysokość
.

g

v

t

0



g

v

h

2

2

0



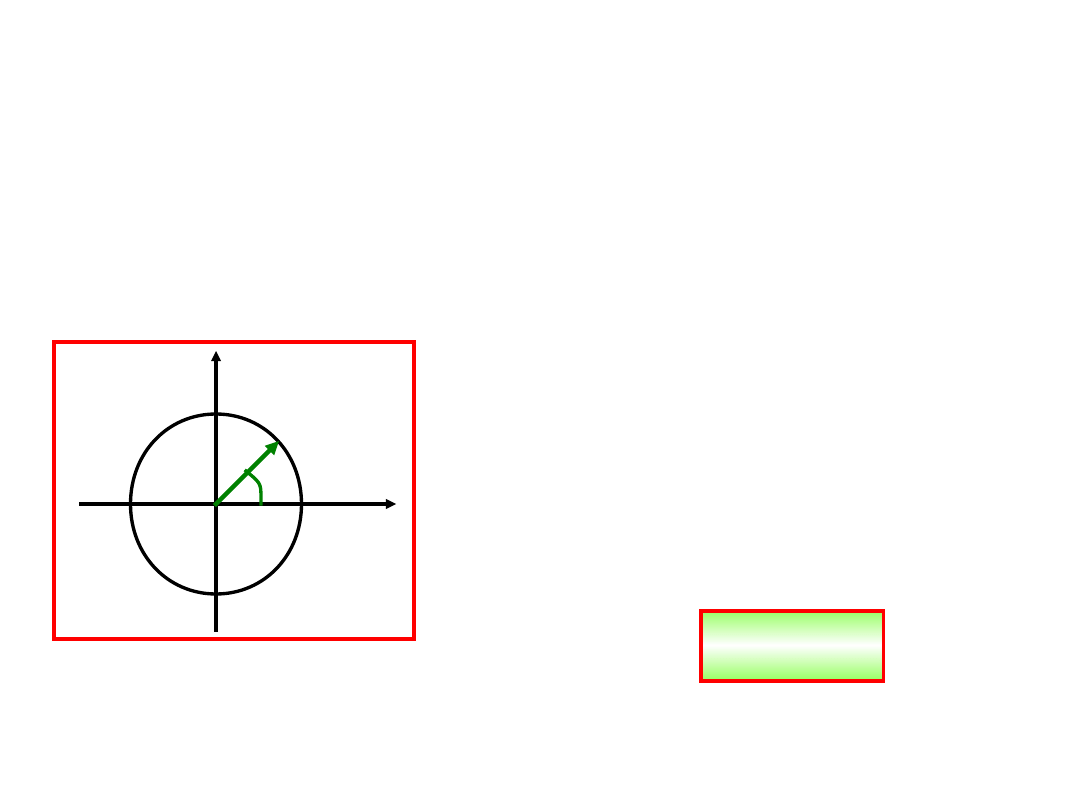
Ruch jednostajny po
okregu

Początek układu współrzędnych wybieramy w środku
koła, po którym odbywa się ruch. Położenie punktu
na na kole możemy podać jednoznacznie przez
podanie kąta biegunowego  i odległości r od

początku układu.

y

x

r



s

Ruch ciała określony jest
przez funkcję

 = (t),

definiująca tzw. drogę
kątową.

Jeśli przez s oznaczymy
drogę, którą ciało przebyło
po okręgu w czasie gdy
przebyło ono drogę kątową
, to

r

s







(2.15)

Różniczkując to równanie obustronnie,
otrzymujemy;

.

Pod wpływem działania siły F ciało zmienia w czasie dt swój pęd,

dp F dt

 

r

r

oraz położenie

dr v dt

 

r r

Eliminując z tych równań dt otrzymujemy;

0

v dp F dr

 

 

r

r r

r

To ostatnie równanie możemy napisać jako:

0

p dp

F dr

m





 

r

r

r

r

Wykorzystując fakt, że

(

)

2

d p p

dp p p dp

p dp

     



r r

r r

r r

r

Możemy równanie (4.4) zapisać jako;

B

A

W

F dr







r

r

.

Z równania tego widzimy również, że praca
może być wykonana tylko przez składową siły
styczną do drogi.

Policzmy dla przykładu jaką pracę musimy
wykonać wydłużając sprężynę z położenia
równowagi o x. Zgodnie z prawem Hooke’a
sprężyna sprzeciwia się rozciąganiu z siłą
F=-cx. Wobec tego

2

0

0

2

x

x

c

W

Fdx

c xdx

x











Praca ta jest ujemna, gdyż sprężyna nie
wykonuje pracy, tylko ją podejmuje.

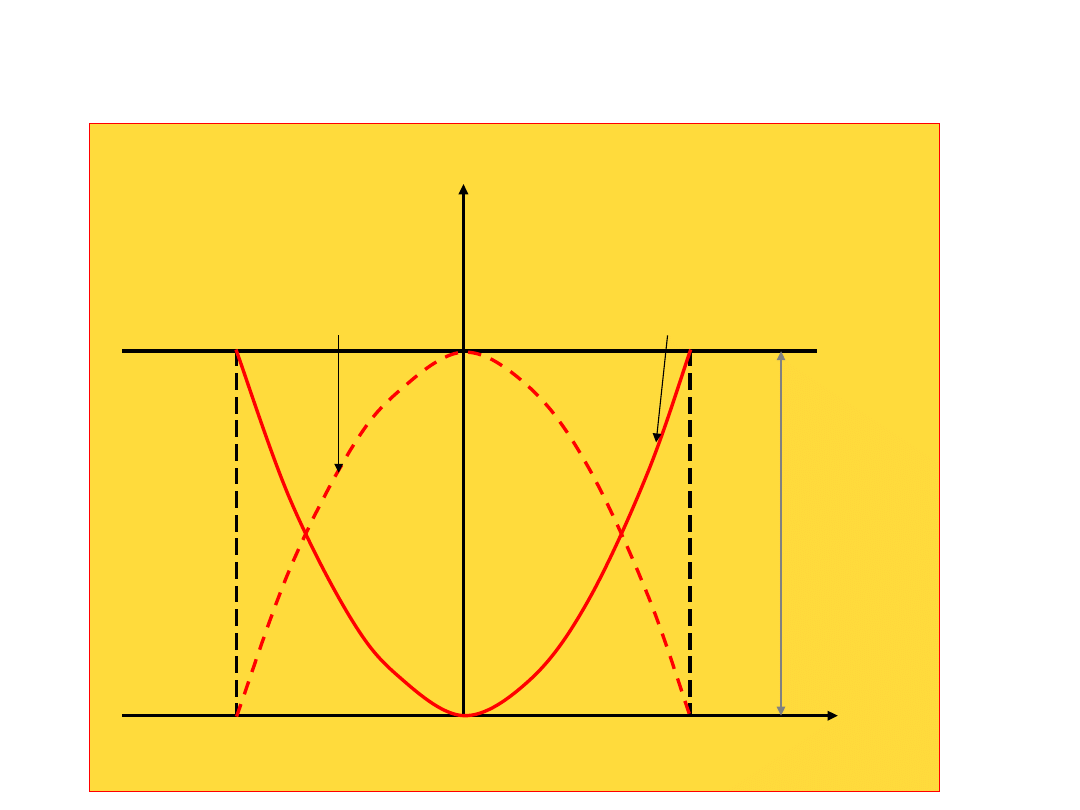
energia

x

E

k

=E-E

p

E

kmax

=E

E

p

=c/2x

1

2

E

p

=c/2x

2

E

pmax

E

k

=0

-x

1

x

1

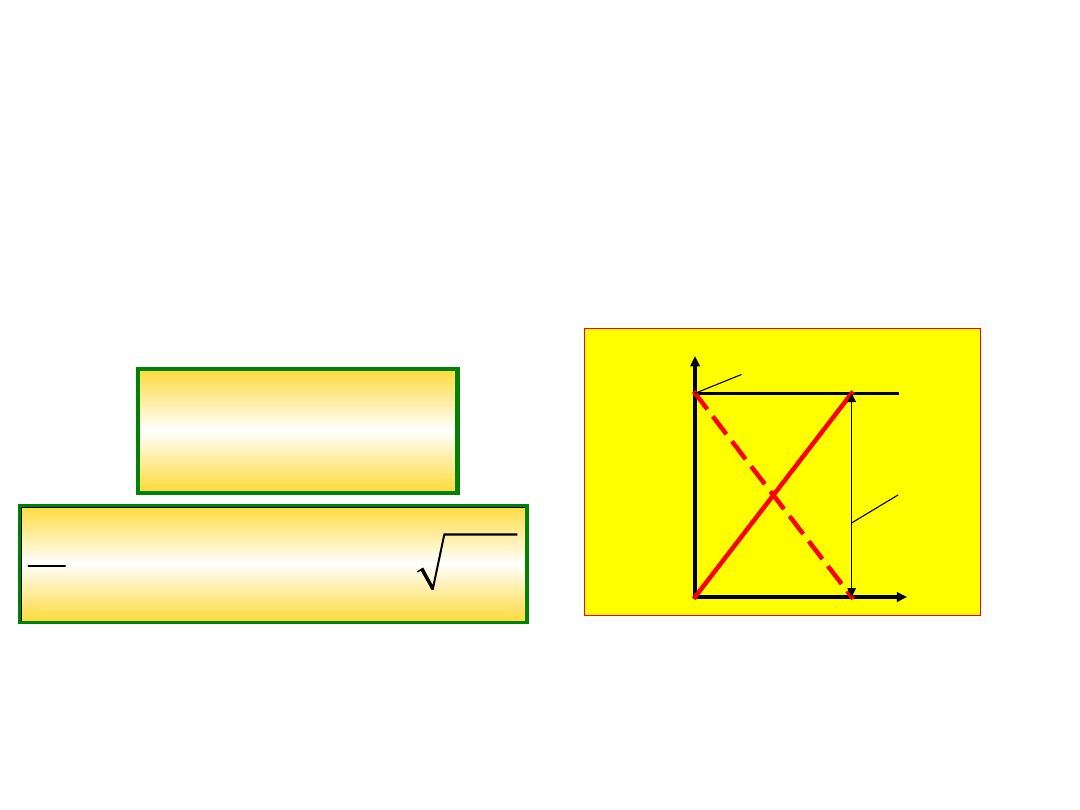
Praca i energia potencjalna
przy podnoszeniu ciężaru

Jeśli podniesiemy masę

m

wbrew sile

grawitacji na wysokość

h

(niewielkiej

względem promienia Ziemi), wymaga to
wykonania pracy zwiększającą energię
potencjalną masy m ;

p

E

mgh



Jeśli pozwolimy masie

m

spaść z wysokości

h

,

wzrasta jej prędkość, a tym samym energia
kinetyczna, równocześnie spada energia
potencjalna masy m. Jednak sumaryczna
energia pozostaje niezmieniona.

Energia

h

E

k

E

p

E=mg
h

E

pmax

=E

kin

2

2

2

m

v

mgh

v

gh







Siły zachowawcze i niezachowawcze

Ogólnie dzielimy siły na dwie klasy, siły
zachowawcze i siły niezachowawcze.
Rozróżnienie pomiędzy nimi jest oparte na
wielkości pracy jaką siła wykonuje na drodze
zamkniętej.
Siły zachowawcze są to takie siły dla których
praca po drodze zamkniętej jest równa zero.

0

F ds

 



r r

�

Siły tarcia są siłami niezachowawczymi.
Ogólnie biorąc siłami niezachowawczymi są
siły zależne od czasu i siły zależne od
prędkości.
Należy podkreślić, że suma energii
potencjalnej i kinetycznej jest stała tylko dla
sił zachowawczych.

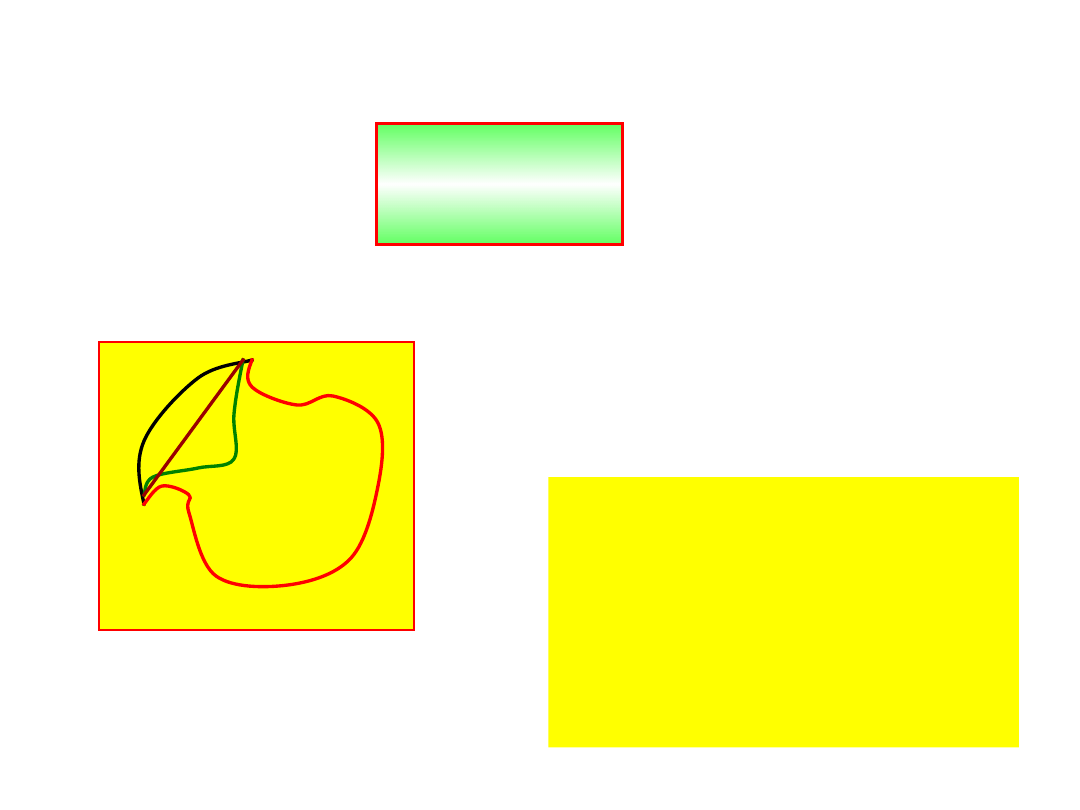
Zależy od drogi. Możemy więc podać inną
definicję siły zachowawczej

B

A

F ds const

 



r r

niezależnie od drogi pomiędzy A i B.

B

A

Siły są zachowawcze,
jeśli w czasie ruchu
pod wpływem tych sił
spełniona jest

zasada

zachowania energii
mechanicznej.

Możemy również
stwierdzić, że

Tak jest w polu sił zachowawczych
Czyli polu potencjalnym

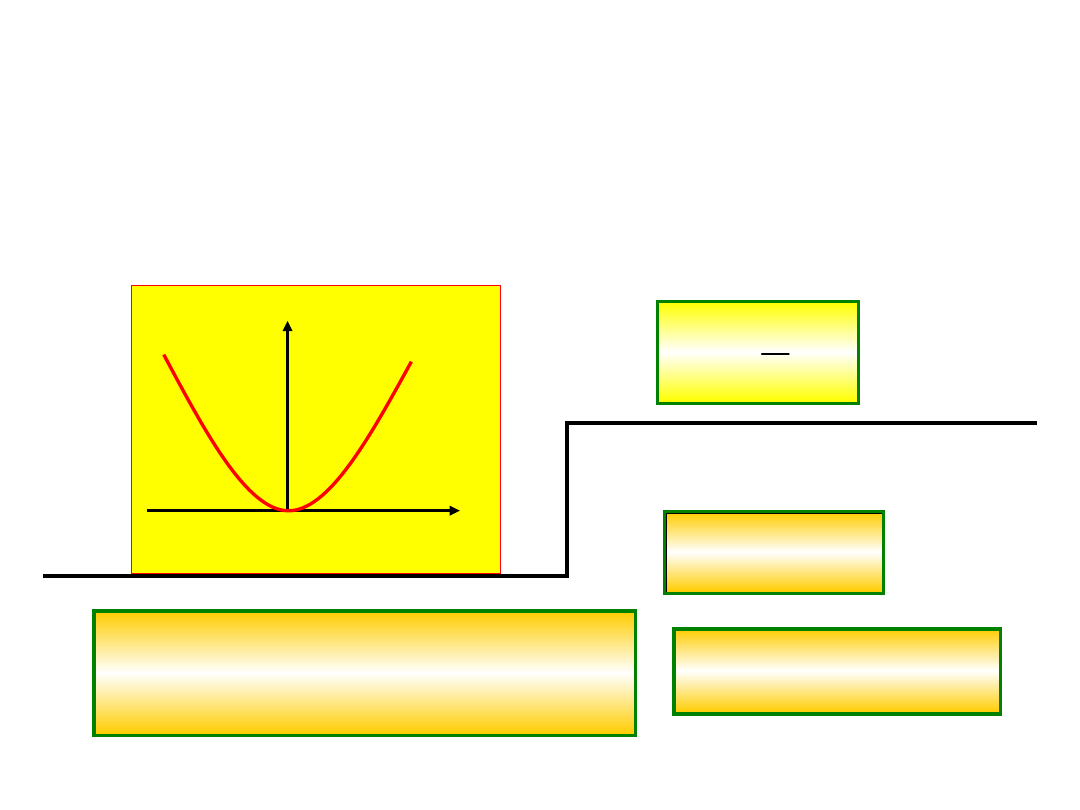
Przykłady energii potencjalnych sił
zachowawczych

1. Energia potencjalna sprężyny

2

1

2

p

E

cx



E

p

x

2. Energia Potencjalna stałej siły

ˆ

x

F

mgi



r

0

ˆ ˆ

(

)

x

p

x

x

E

mgi i dx

mgx











( )

p

E x

mgx



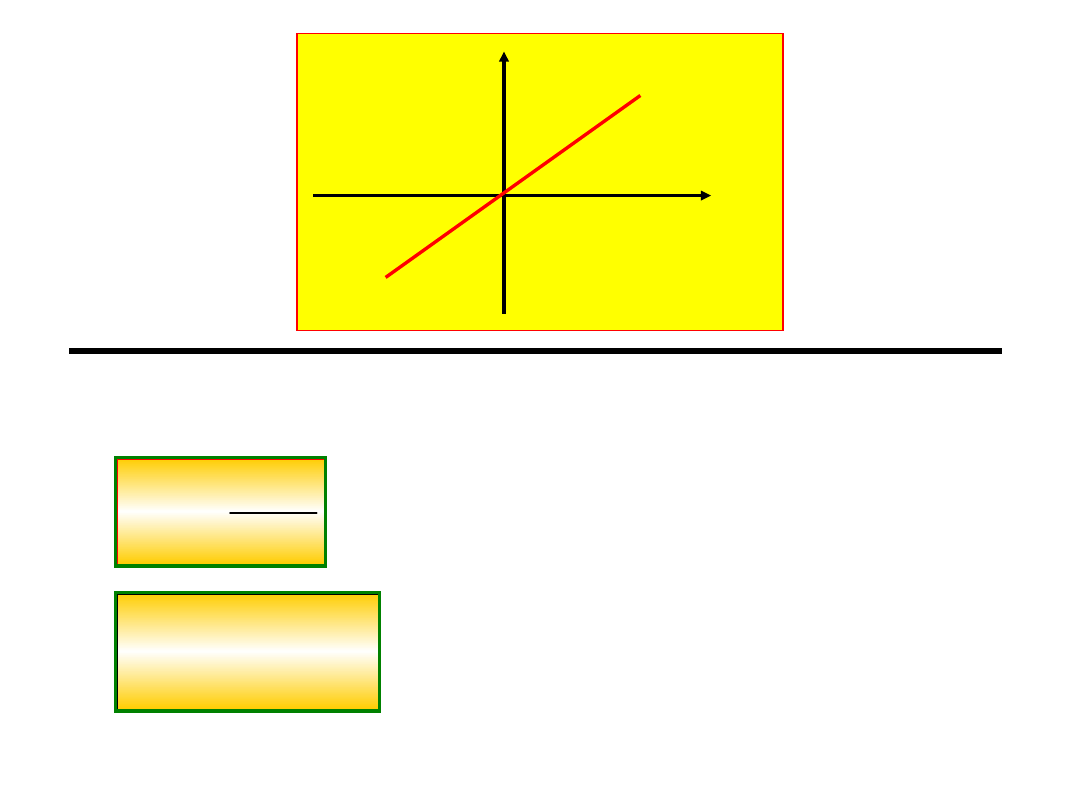
E

p

x

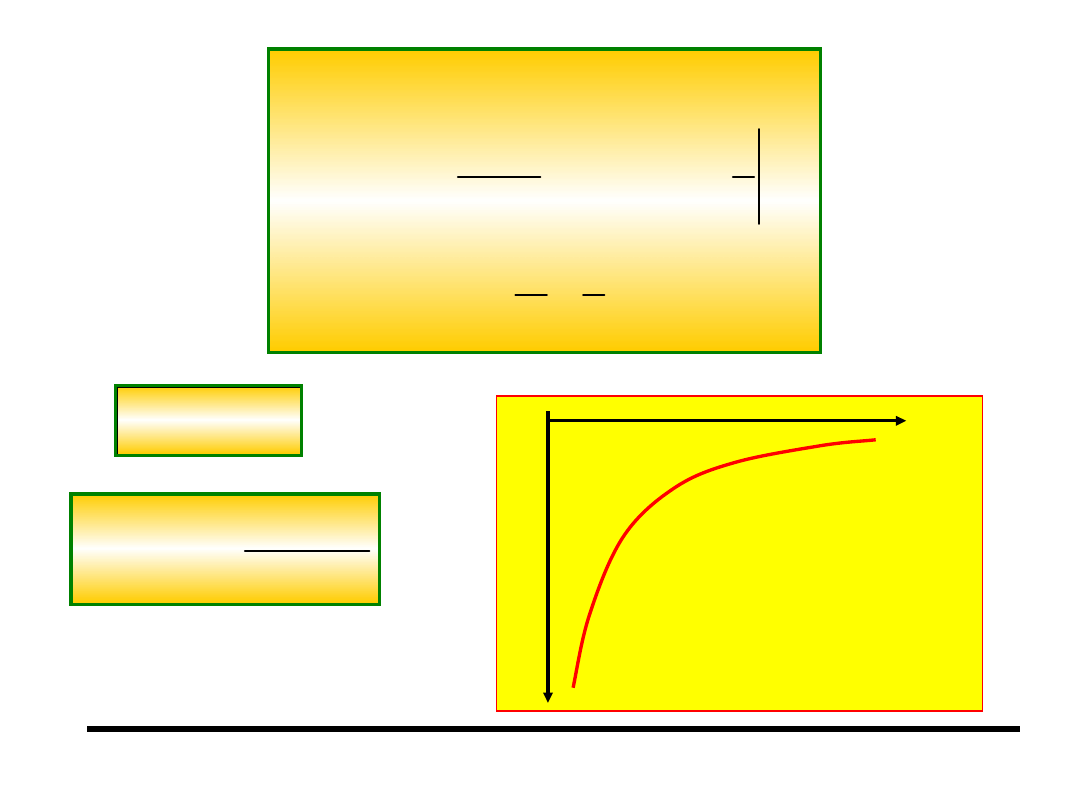
3 Energia potencjalna uniwersalnej siły
grawitacji

1 2

2

mm

F G

r



r jest odległością masy m

1

od

masy m

2

.

0

r

p

r

E

F ds









r

r

Załóżmy, że liczymy zmianę energii
przy przesunięciu masy m

2

z

nieskończoności do r.

1 2

1 2

2

1 2

( )

( )

1

1 1

p

p

p

r

r

E

E r

E

mm

G

dr Gmm

r

r

Gmm

r











 



























( ) 0

p

E  

1 2

( )

p

Gmm

E r

r



r

E

p

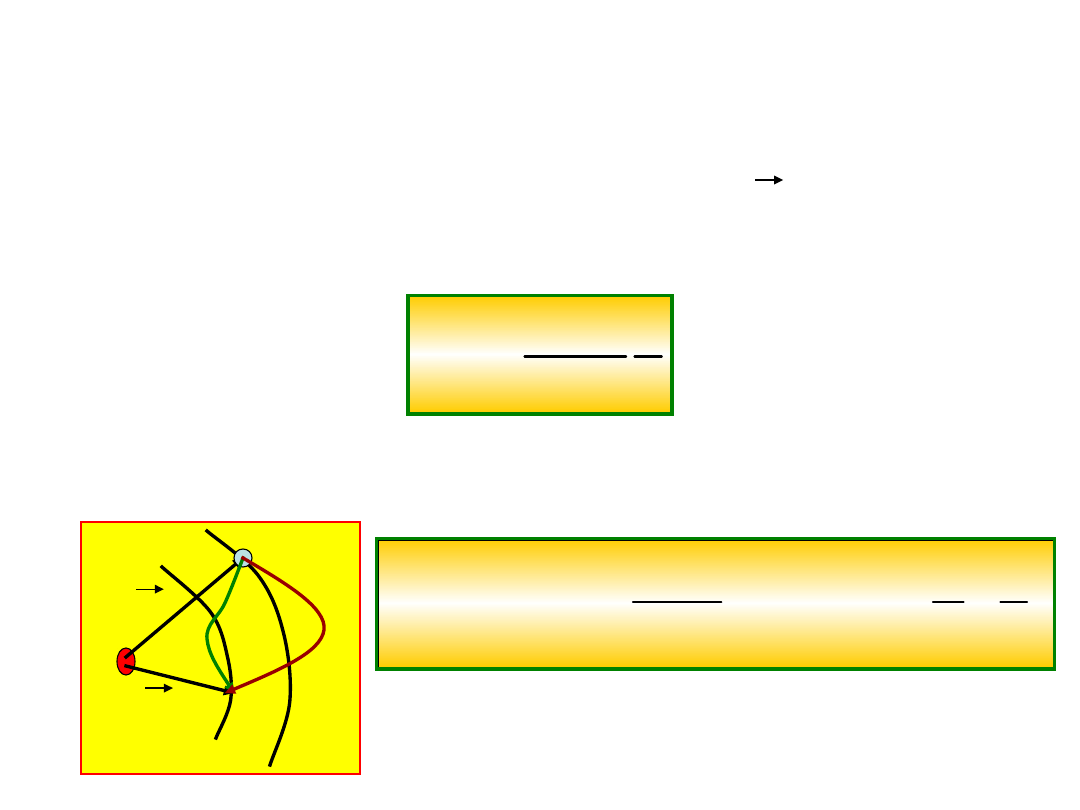
Praca i energia potencjalna dla sił
elektrostatycznych

Pomiędzy dwoma ładunkami q

1

i q

2

umieszczonymi w odległości r od siebie działa
wzdłuż wektora r siła elektrostatyczna zgodnie z
prawem Coulomba,

1

2

2

q q r

F k

r

r





r

r

Jaką pracę wykona ta siła, jeśli ładunek q

2

przesuniemy z punktu P

1

do punktu P

2

.

2

2

1

1

1

2

1 2

2

2

1

1 1

r

r

r

r

q q

W

Fdr

k

dr

kqq

r

r

r



























q

1

q

2

P

2

P

1

r

1

r

2

.

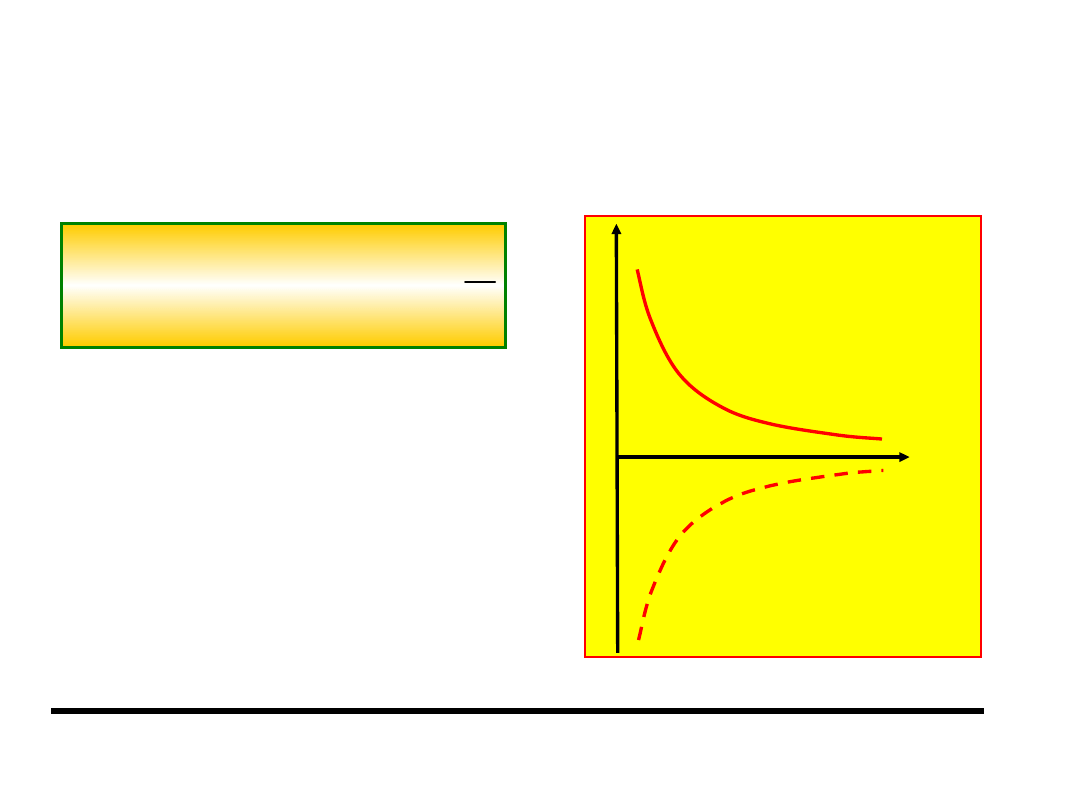
Oznacza to, że energia potencjalna E

p

= -W

zależy tylko od r

1

i r

2

. Często interesuje nas

pytanie jaką prace należy wykonać, aby
ładunek z nieskończoności przesunąć do
punktu P

2.

2

2

1 2

2

1

P

r

E

W

F dr kqq

r











r

E

p

q

1

·q

2

> 0

q

1

·q

2

< 0

przyciąganie

odpychanie

Kształt energii
potencjalnej
oddziaływania
elektrostatycznego
jest opisany taką samą
funkcją f(r) jak dla
oddziaływania
grawitacyjnego. Może
ona jednak być
również dodatnia, czyli
odpychająca.

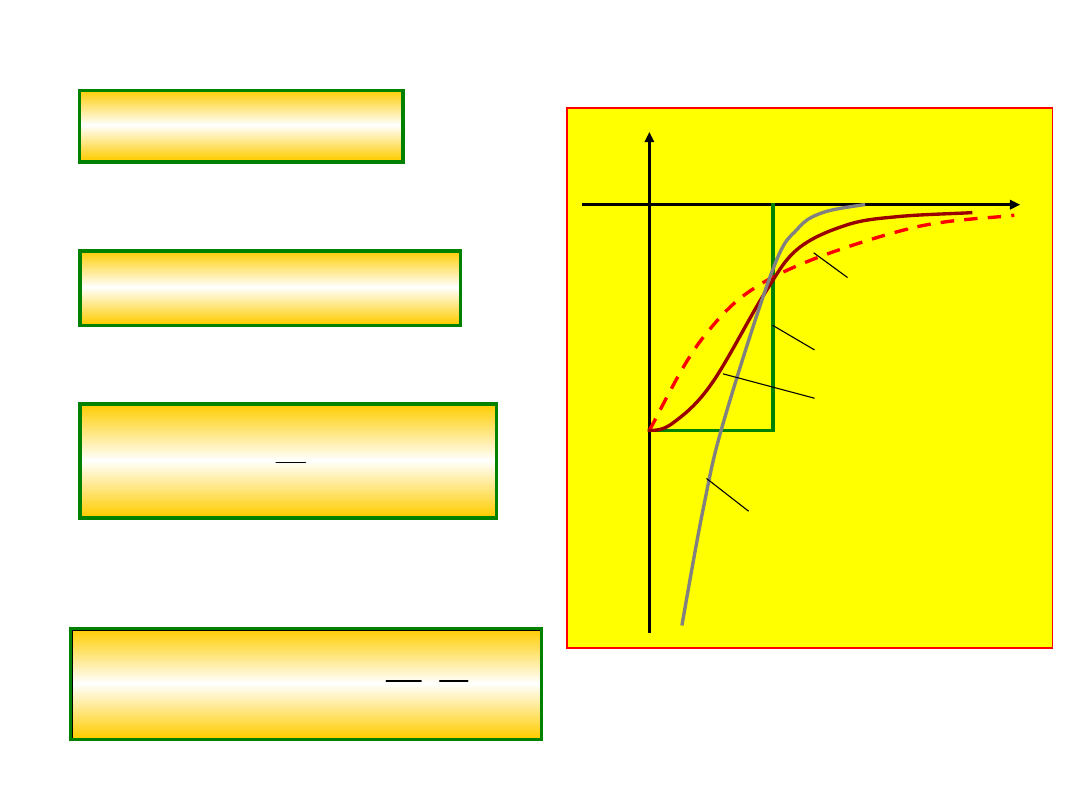
2. Potencjał wykładniczy

0

0

( )

exp( / )

p

E r

V

r r





3. Potencjał Gaussa

2

2

0

0

( )

exp(

/ )

p

E r

V

r r





0

0

0

( )

( )exp( / )

p

r

E r

V

r r

r





4. Potencjał Yukawy

5. Potencjał
oscylatora
harmonicznego

2

2

0

0

2

0

0

( )

(

)

(

1)

p

V r

E r

r r

r r

 





E

p

(r)/V

0

r/r

0

p. Yukawy

p. Gaussa

p. jamy prostokątnej

p. wykładniczy

Jak wyglądają te potencjały?

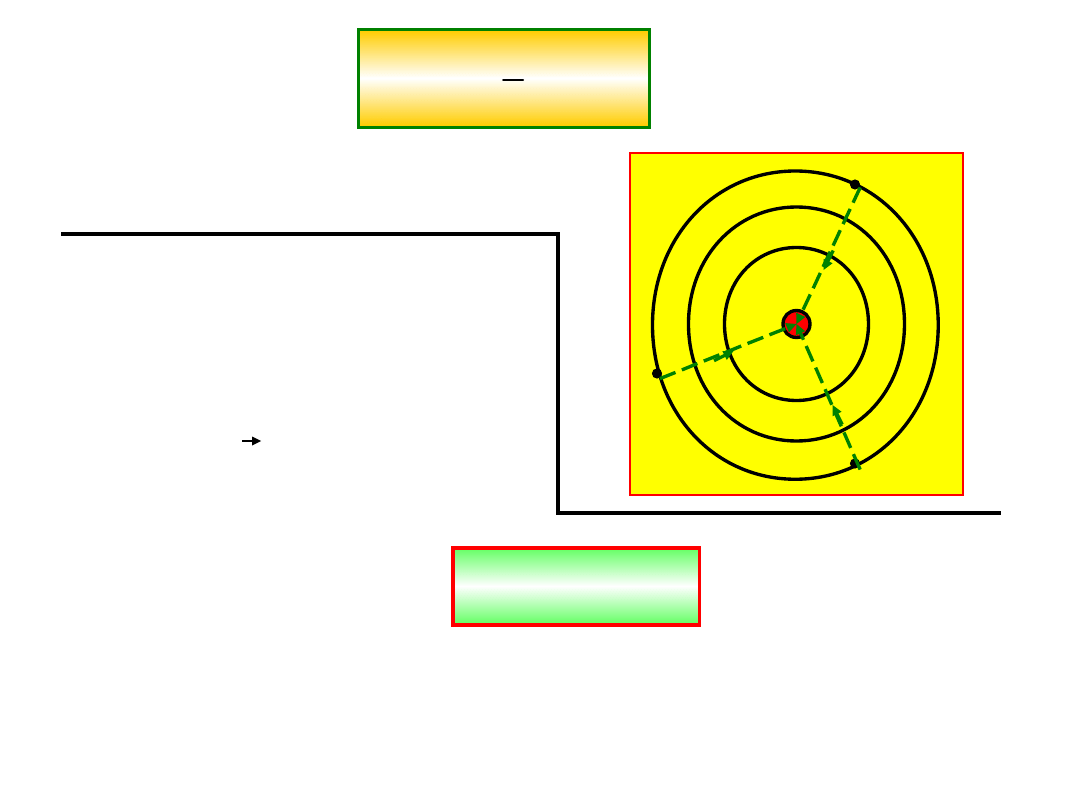
1

p

E

k

const

r

  

,

są powierzchniami kul.

W jaki sposób można
policzyć
wielkość siły
działającej na elektron
w dowolnym miejscu.
Jeśli przesuniemy
elektron o dr, to
energia potencjalna
zmieni się o

p

dE

F dr

 

r r

Jeśli przesuniemy elektron po powierzchni
ekwipotencjalnej,
dE

p

= 0, czyli nie została wykonana praca.

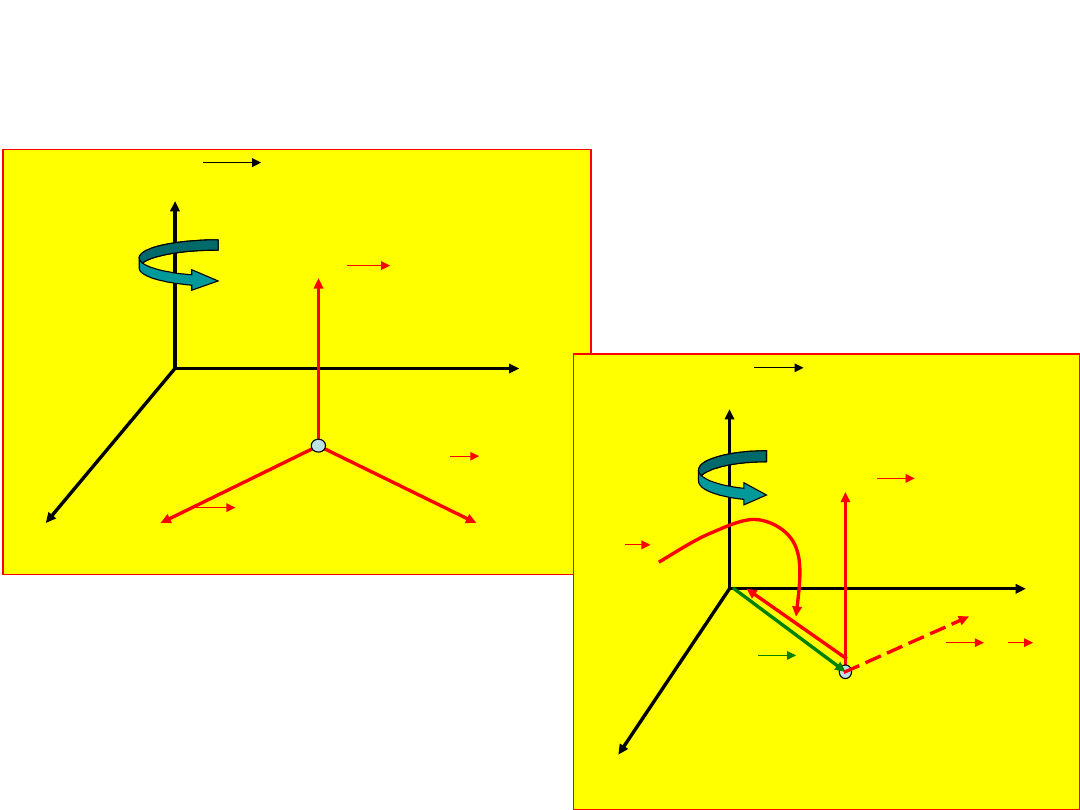
Dynamika bryły sztywnej



x

’

y

’



P

a

C

v

’



x

’

y

’



P

’

 x r

’

a

d

Reinhard Kulessa

69

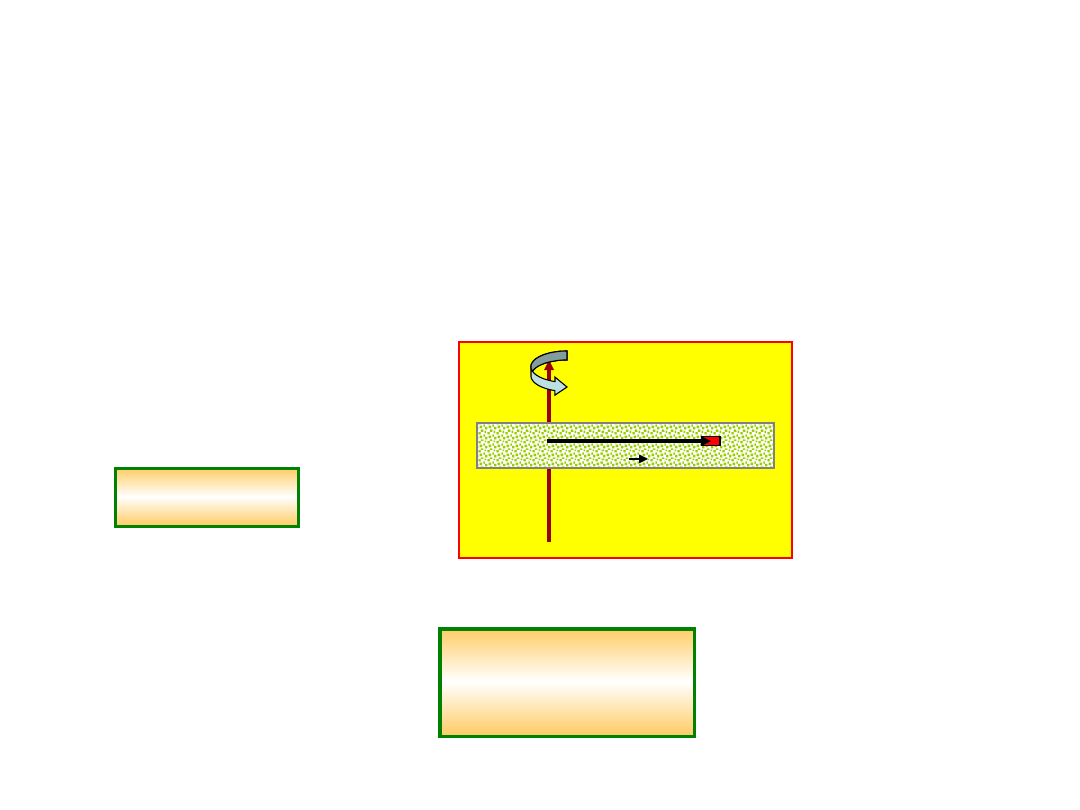
Moment pędu bryły sztywnej

- Moment bezwładności

Rotujące ciało sztywne charakteryzuje się tym,
że wszystkie jego części poruszają się ze stałą
prędkością kątową wokół osi obrotu.
Weźmy płytę płaskorównoległą i rozważmy jej
obrót dookoła osi prostopadłej.



r

j

m

j

Pamiętamy, że

v

r



 

r

r r

.

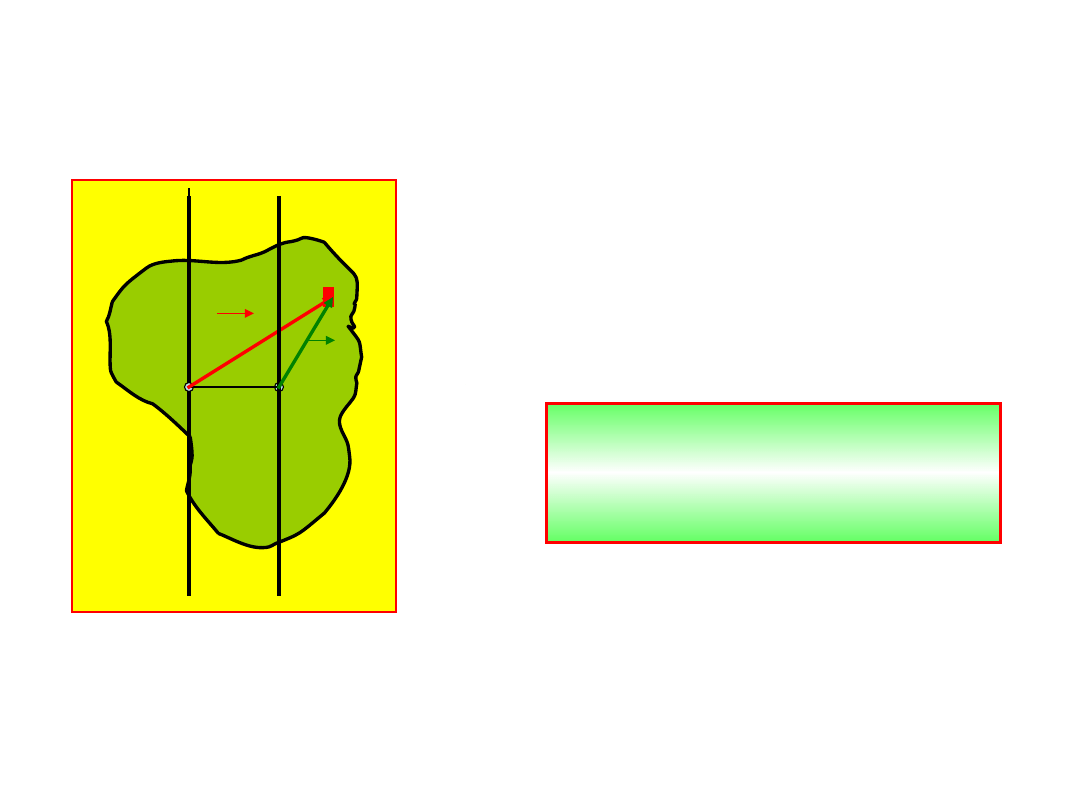
Pamiętamy, że dla każdego układu cząstek
definicja momentu pędu jest następująca:

1

(

)

N

i

i

i

i

L

m r v









r

r r

Reinhard Kulessa

70

Twierdzenie Steinera

W ogólnym przypadku ciągłego rozkładu masy,
moment bezwładności musimy liczyć
przechodząc od sumowania do całkowania.

2

2

I

r dm

r dV











5.15)

.

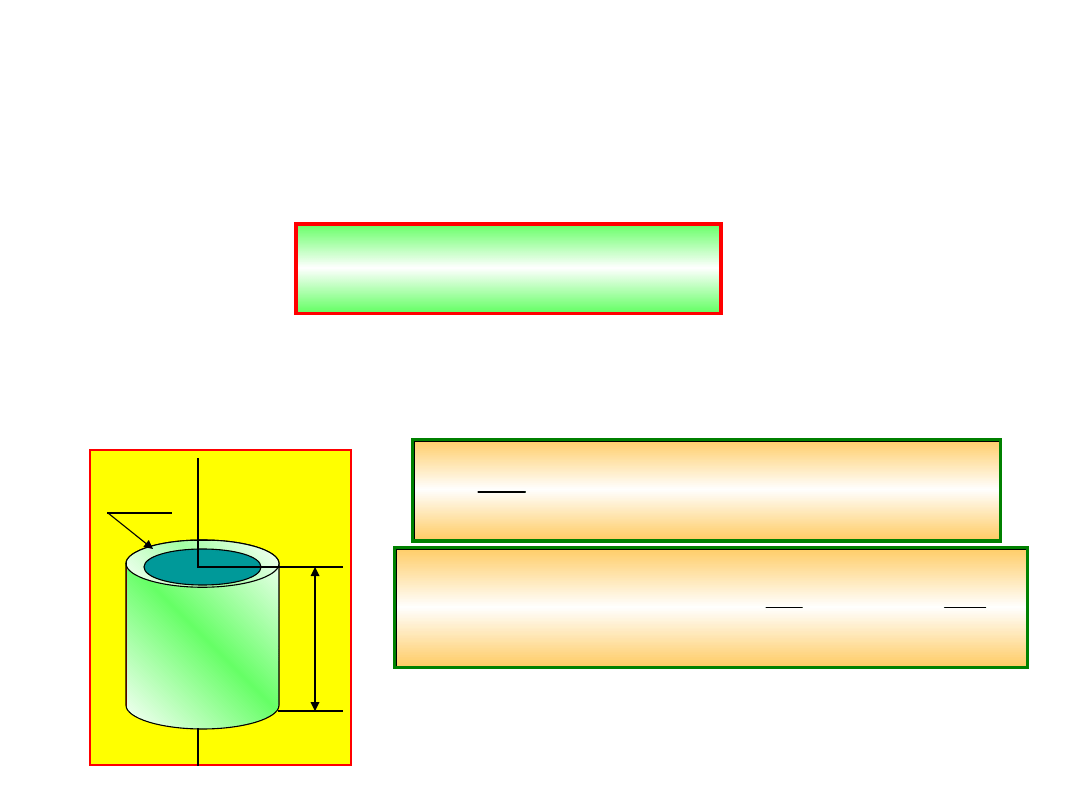
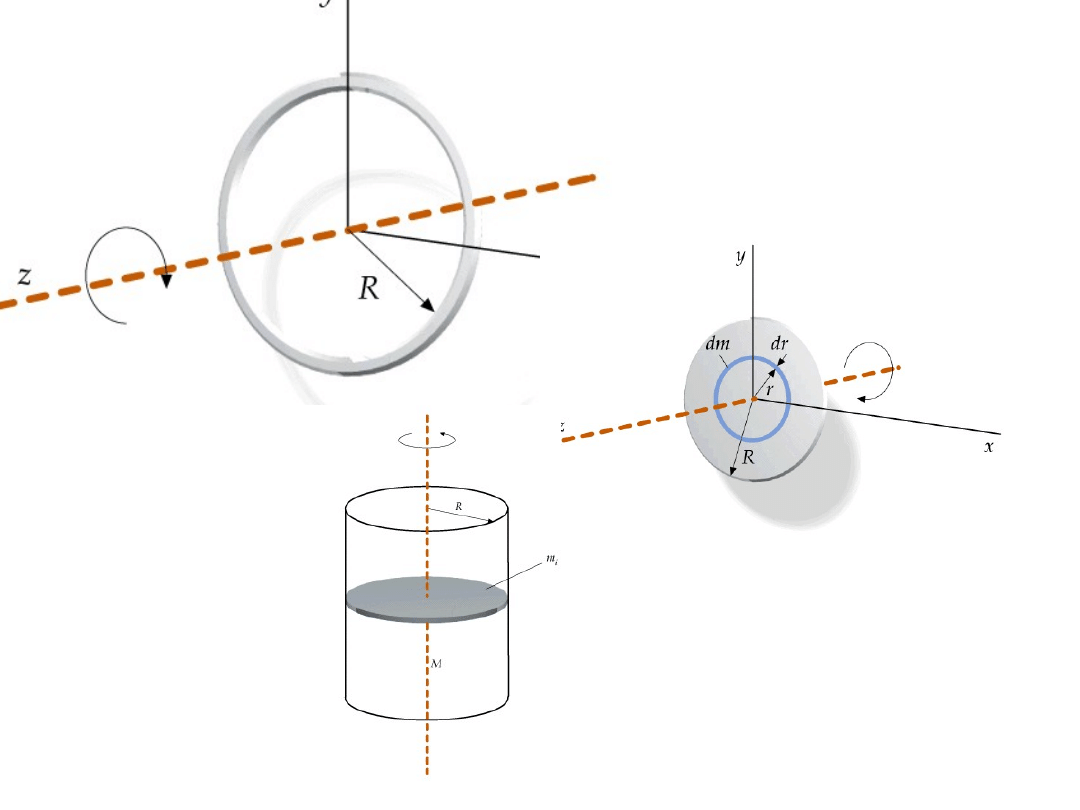
Obliczmy dla przykładu moment bezwładności
pełnego walca względem jego osi.

r

0

l

dr

2

dm

const dm

dV

l

r dr

dV





 







 



0

4

2

2

0

0

0

2

2

4

2

r

r

M

I

r l

rdr

l

I

r

 

 











Masa walca jest równa

M =



r

0

2

l.

Reinhard Kulessa

71

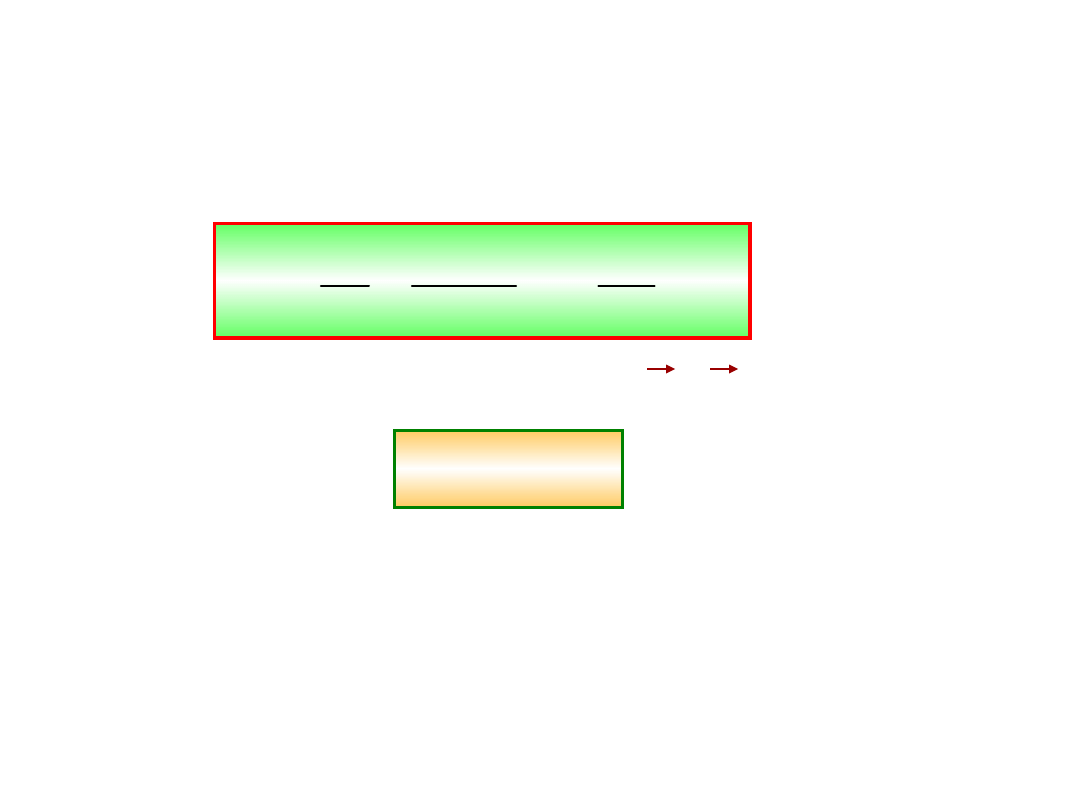
Moment bezwładności bryły względem osi
przechodzącej przez środek masy ciała jest
związany z momentem bezwładności względem
dowolnej osi.

O

S

h

R

i

R

iS

2

S

I I

Mh

 

.

Zależność podaje

twierdzenie Steinera.

Dynamika ruchu bryły sztywnej – druga
zasada

Pamiętamy z wzoru (5.3), że moment pędu
może zostać zmieniony tylko przez działanie
zewnętrznego momentu siły.

( )

z

dL d I

d

M

I

I

dt

dt

dt











 



r

r

r

r

r

W przypadku braku sił zewnętrznych

L

i

= L

f

i

wtedy

i

i

f

I

I







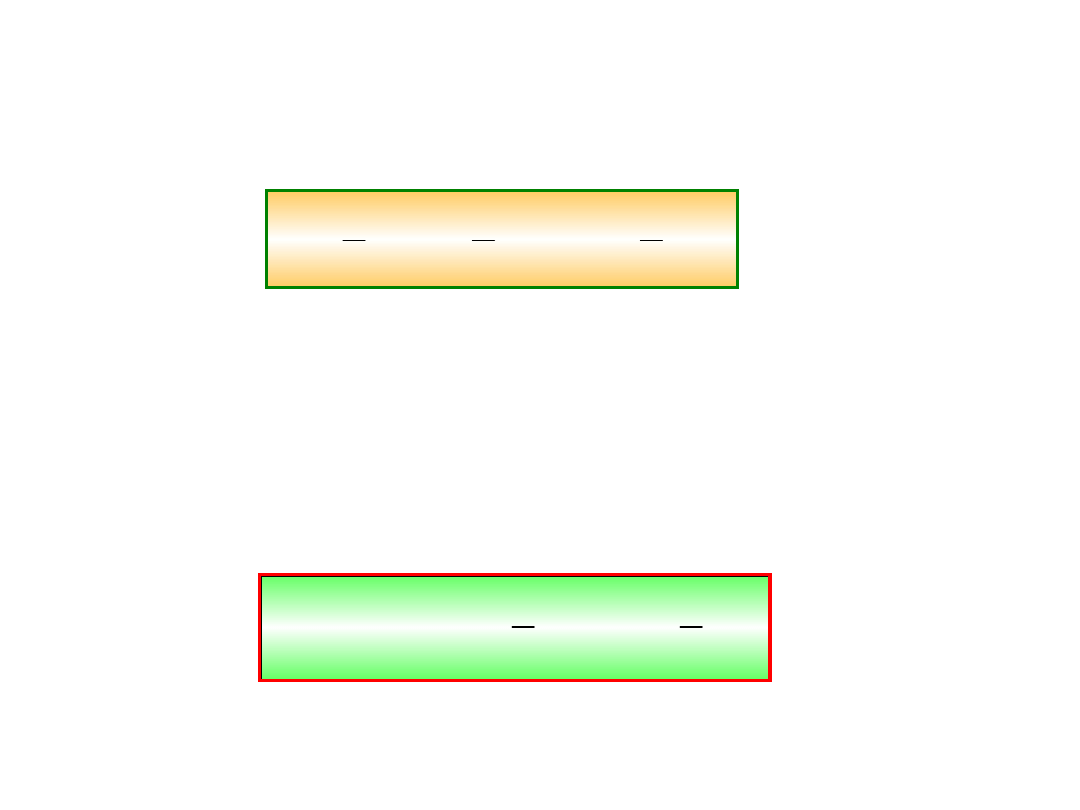
Rozważmy sobie jako przykład

wahadło fizyczne

.

Reinhard Kulessa

73

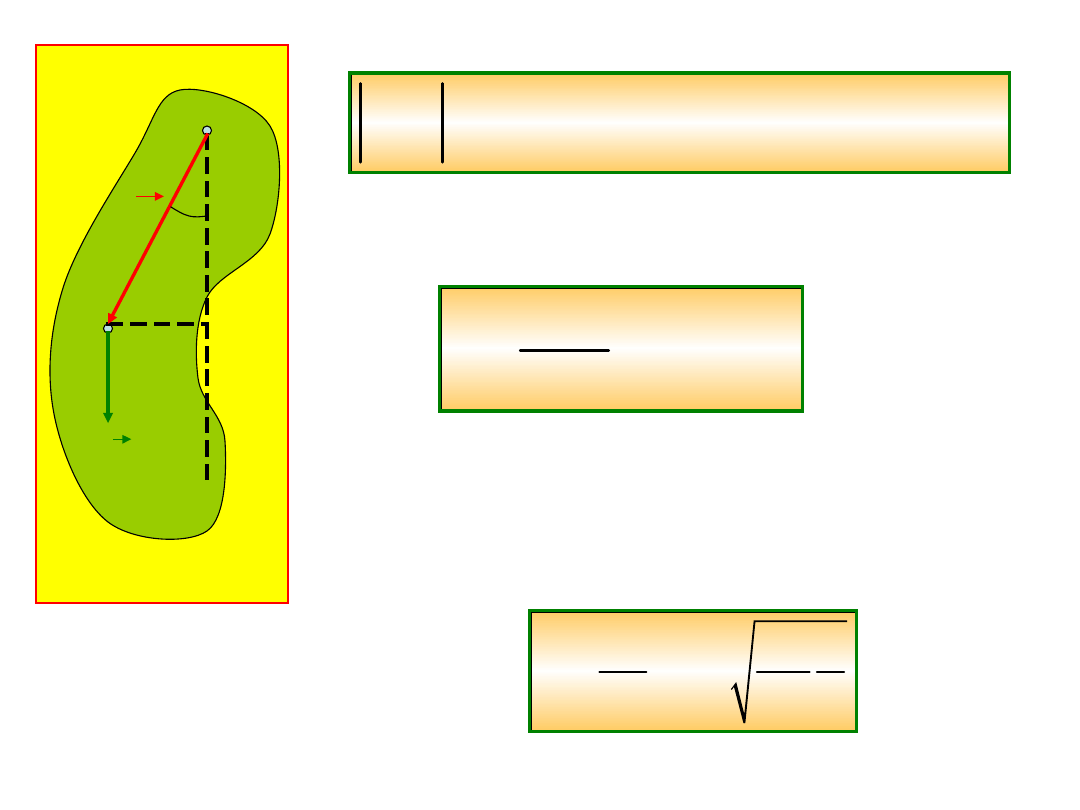
r

Mg

O

S



rsin

sin

O

M

Mgr

L I

I









 



r

&

& &&

Mamy więc równanie

sin

0

Mgr

I











&&

.

Dla małych wychyleń sin  

, wtedy
otrzymujemy równanie
oscylatora harmonicznego z


2

=Mgr/I, z rozwiązaniem

2

1

2

I

T

Mr g











.

Reinhard Kulessa

74

Energia kinetyczna bryły
sztywnej

2

2

2

2

1

1

1

2

2

2

i

i i

i i

i

E

mv

mr

I











Sumując po wszystkich punktach otrzymujemy;

2

2

2

1

1

1

1

2

2

N

N

kin

i

i i

i

i

E

E

mr

I



















.

Reinhard Kulessa

75

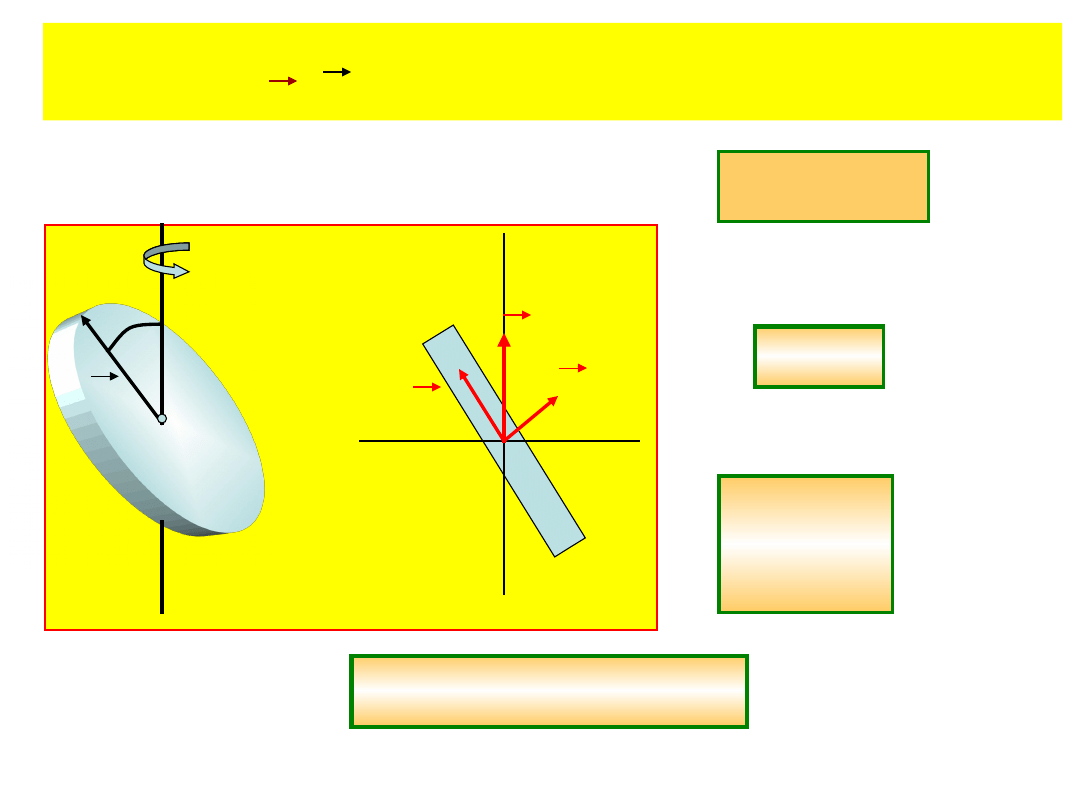
Tylko w przypadku rotacji względem osi
głównych momentu bezwładności

  L .

r



o
ś









 

Rozważmy ogólny przypadek.

 









P

r

r

r

Pamiętamy, że

L I





r

r

.

Zachodzi więc;

||

|| ||

L

I

L

I

w

w

^

^ ^

=

=

r

r

r

,

||

|| ||

L L L

I

I

w

w

^

^ ^

= +

=

+

r

r

r

r

r

.

Reinhard Kulessa

76

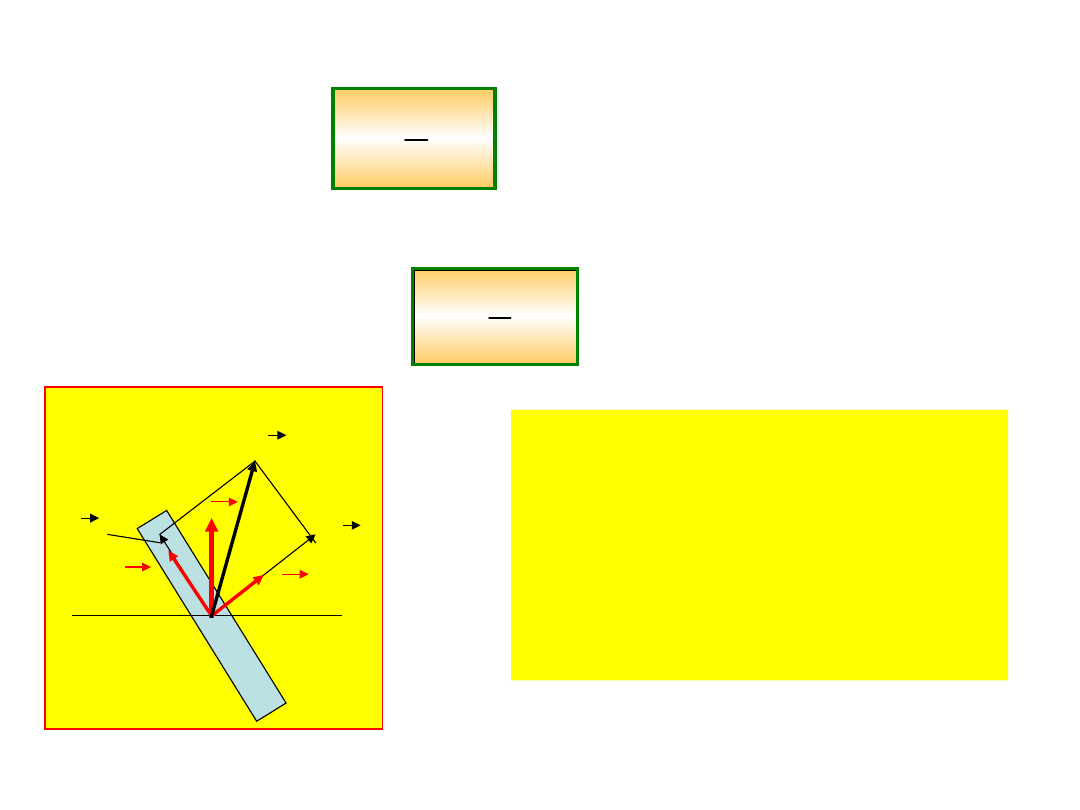
Moment bezwładności względem osi
równoległej do osi do

dysku jest równy , gdzie r jest
promieniem

dysku, a względem osi do niej prostopadłej,
czyli leżącej

wzdłuż średnicy dysku .

2

||

1
2

I

mr

=

2

1

4

I

mr













 

I





 

I







L

Widzimy, że przy
obrocie względem
dowolnej osi
moment pędu nie jest
równoległy do
prędkości kątowej.

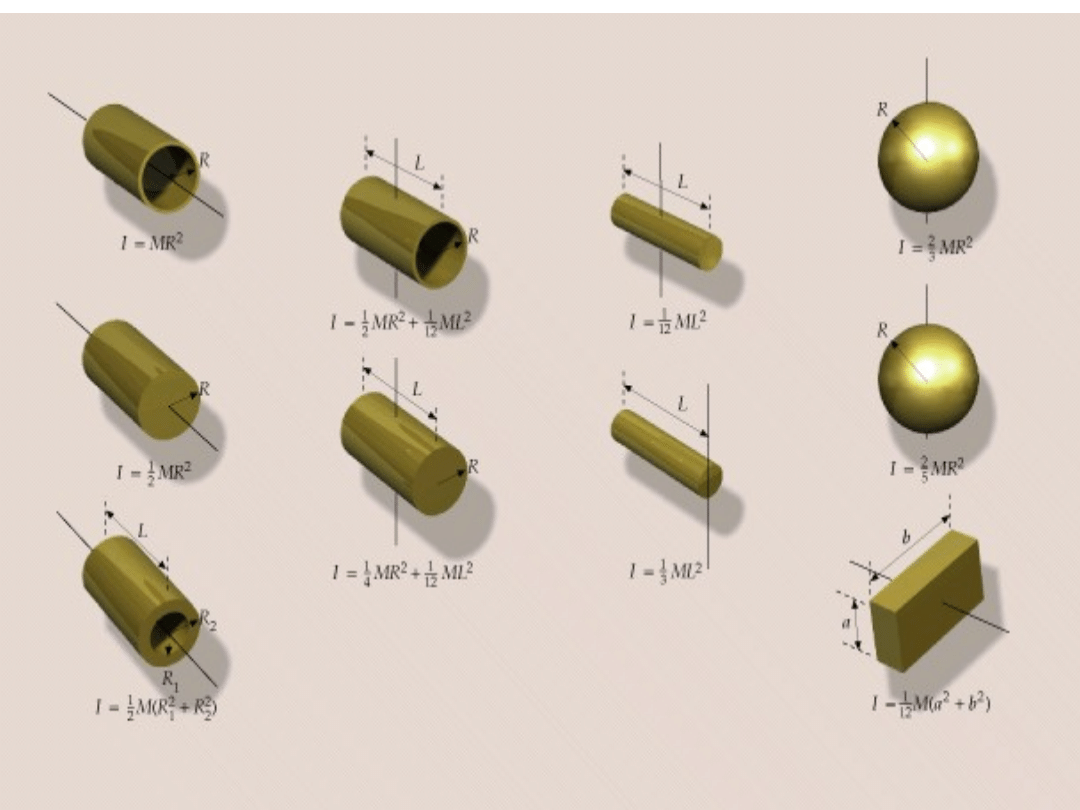
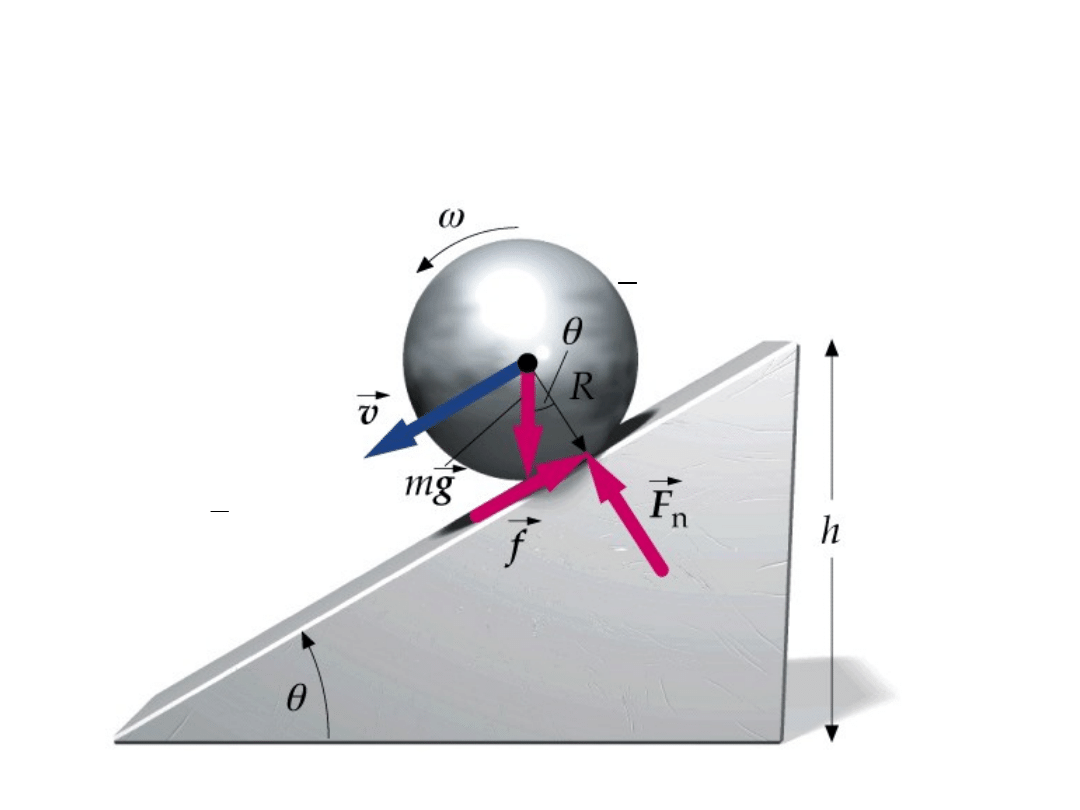
Jak staczać się po równi

pochyłej

2

cm

R

m

5

2

I 

sinθ

g

7

5

a

cm



Przy tej samej wadze

decyduje rozkład masy

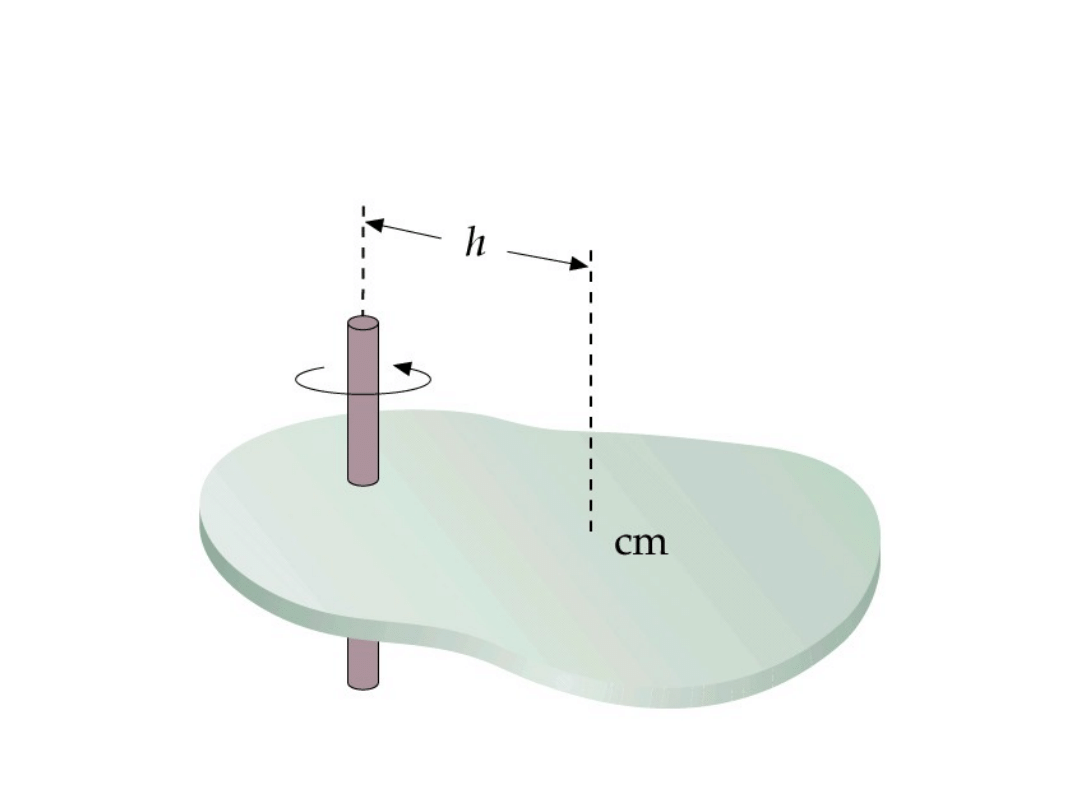
2

h

M

cm

I

I





Twierdzenie Steinera

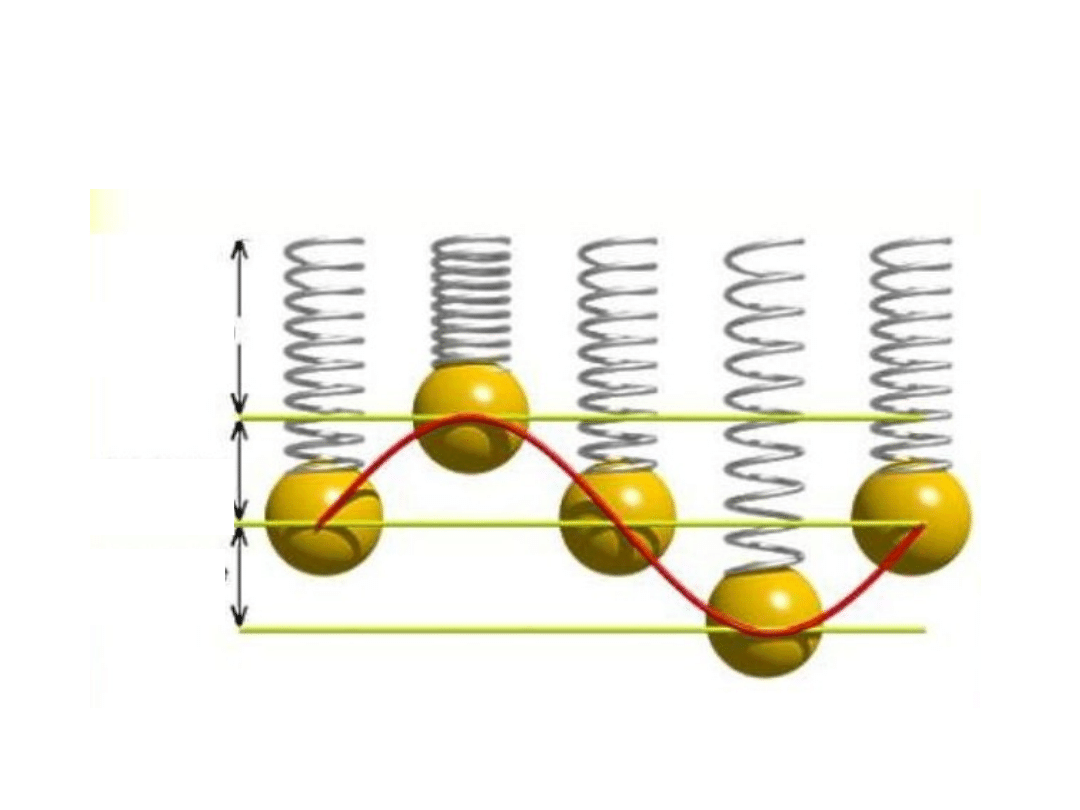
Drgania i fale w ośrodkach

sprężystych.

Drgania i fale w ośrodkach
sprężystych.
Oscylator harmoniczny, drgania
cząsteczek, 2h
Zastosowanie rach. różniczkowego i
operatorowego w zagadnieniach fizyki
2h
Elementy akustyki. Propagacja fal 1h

Amplitu
da

Amplitu
da

Minimu
m

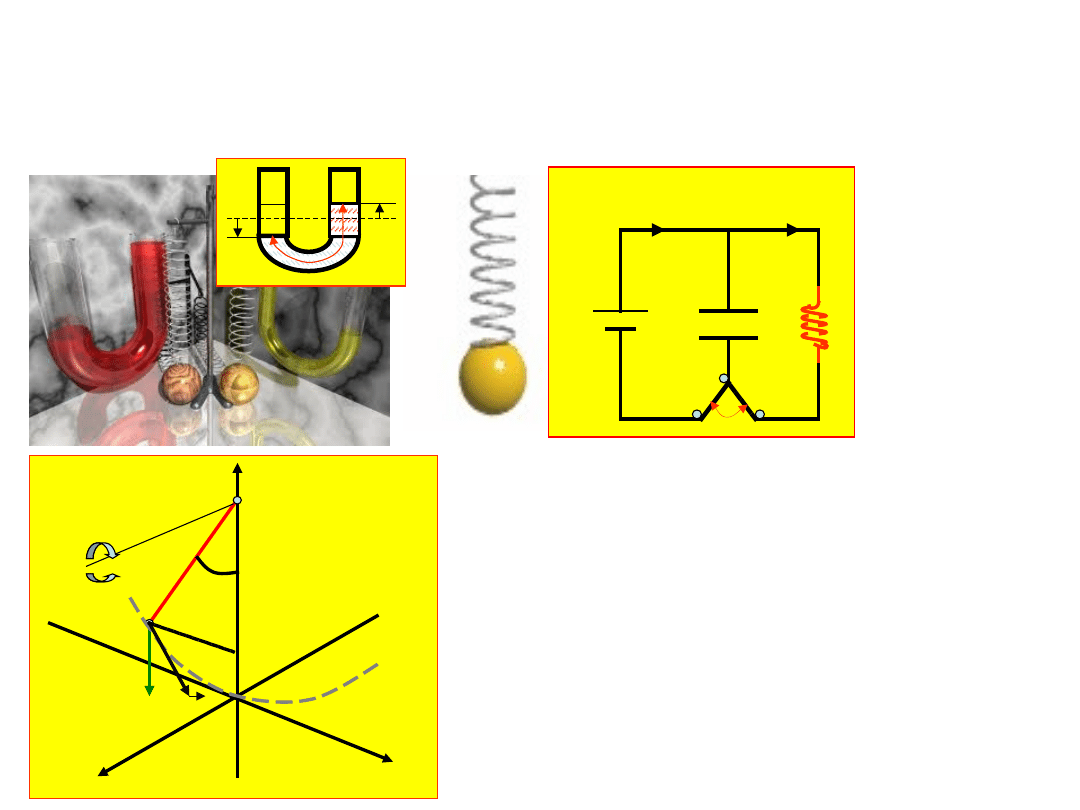
Ruch drgający - Oscylatory

x

y

z

l

mg

p



lsin



y

y

l

L

C

I

U

0

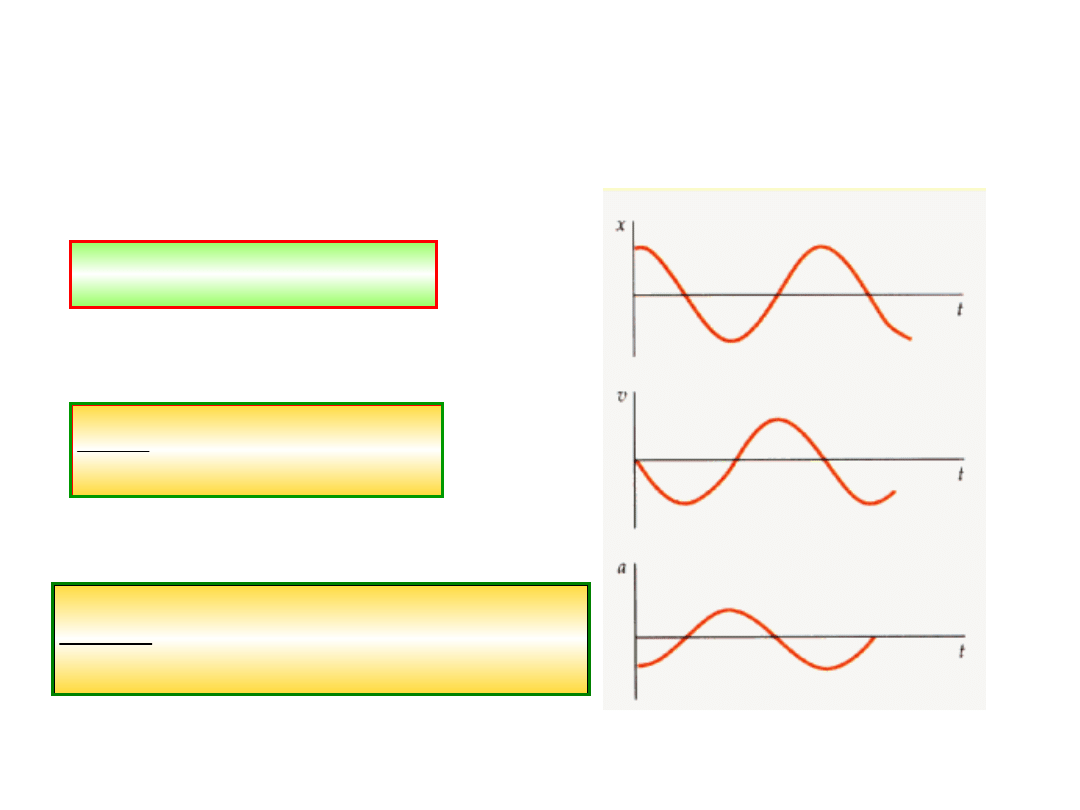
Opis matematyczny ruchu
harmonicznego.

)

cos(

)

(

0









t

A

t

x

Prędkość wynosi:

)

sin(

)

(

0













t

A

dt

t

dx

Przyśpieszenie wynosi:

x

t

A

dt

t

x

d

2

0

2

2

2

)

cos(

)

(



















Oscylator harmoniczny
tłumiony

Jeżeli uwzględnimy oprócz siły napędzającej
oscylator harmoniczny również siły oporu np.
proporcjonalne do prędkości, to równanie
oscylatora przyjmuje postać;

2

2

0

d x

dx

m

Cx

dt

dt









Po wprowadzeniu oznaczeń
otrzymujemy równanie;

2

0

1

C

m

m











2

2

0

2

1

0

d x

dx

x

dt

dt











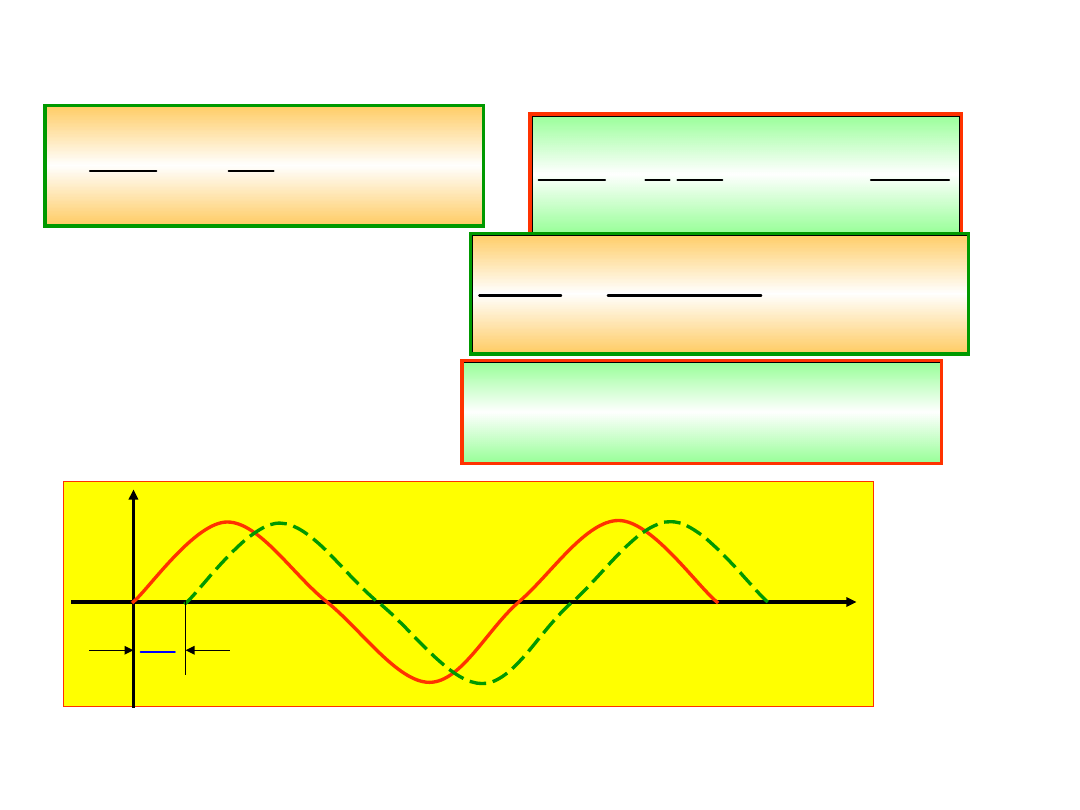
Rozwiązaniem jest funkcja

0

( )

sin

t

x t

x e

t









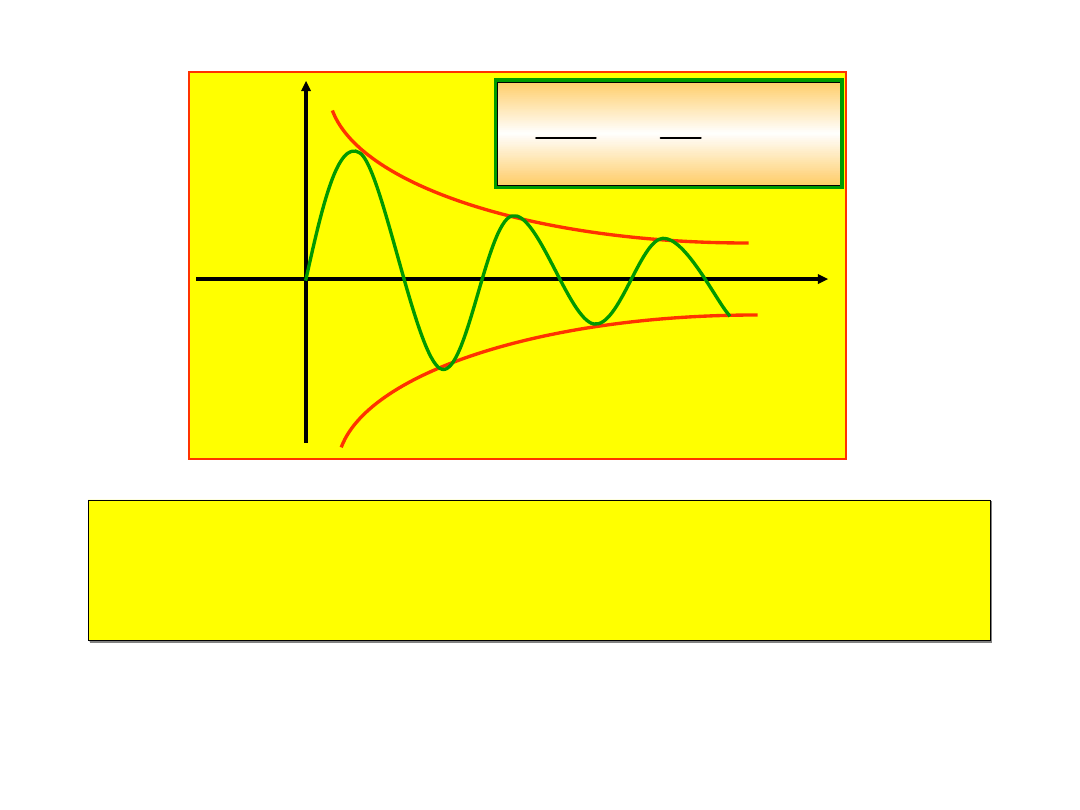
15.12.2008

Reinhard Kulessa

86

t

x(t)

Czas relaksacji jest to czas po którym
amplituda drgań maleje do 1/e wartości
początkowej.

Czas relaksacji jest to czas po którym
amplituda drgań maleje do 1/e wartości
początkowej.

2

2

0

d x

dx

m

Cx

dt

dt









15.12.2008

Reinhard Kulessa

87

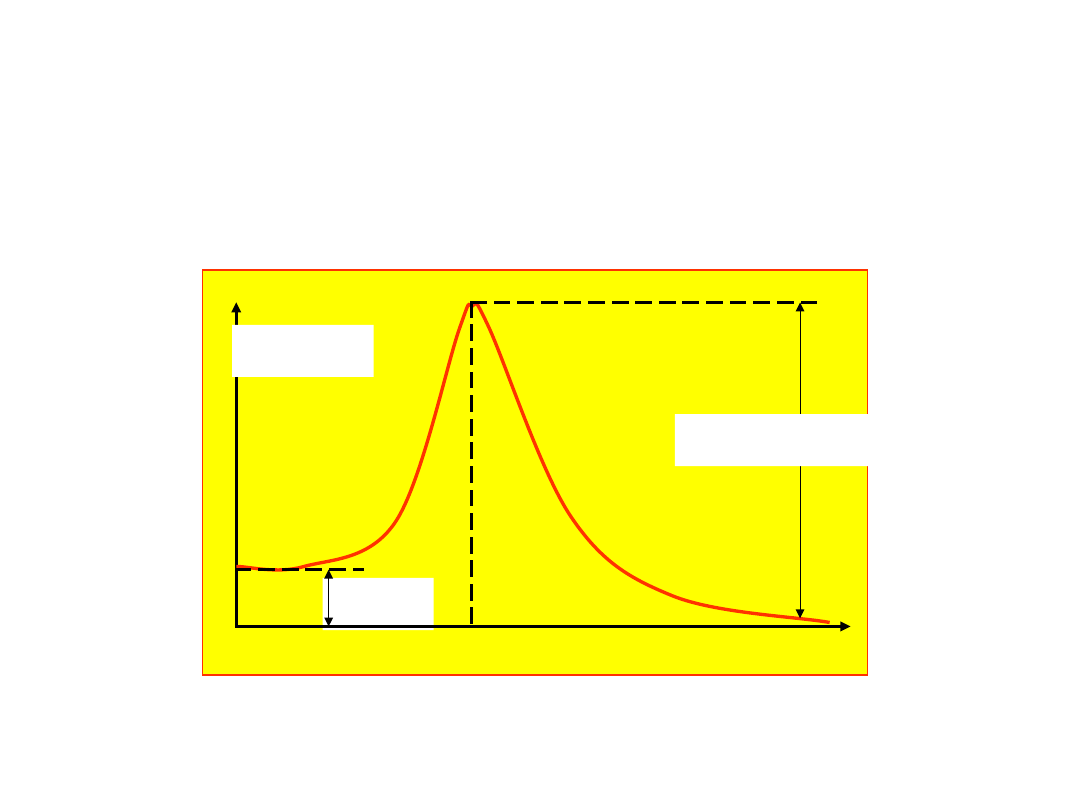
Drgania wymuszone oscylatora

2

2

( )

d x

dx

m

Cx F t

dt

dt









2

2

0

2

1

( )

d x

dx

F t

x

dt

dt

m











0

0

sin

( )

sin

F

t

F t

t

m

m











.

0

sin(

)

x x

t

 





F(t)

x(t)

ω



t

Jeśli siła zmienia się
sinusoidalnie

To rozwiązaniem będzie przebieg
Sinusoidalny. (zazwyczaj
przesuniety w fazie

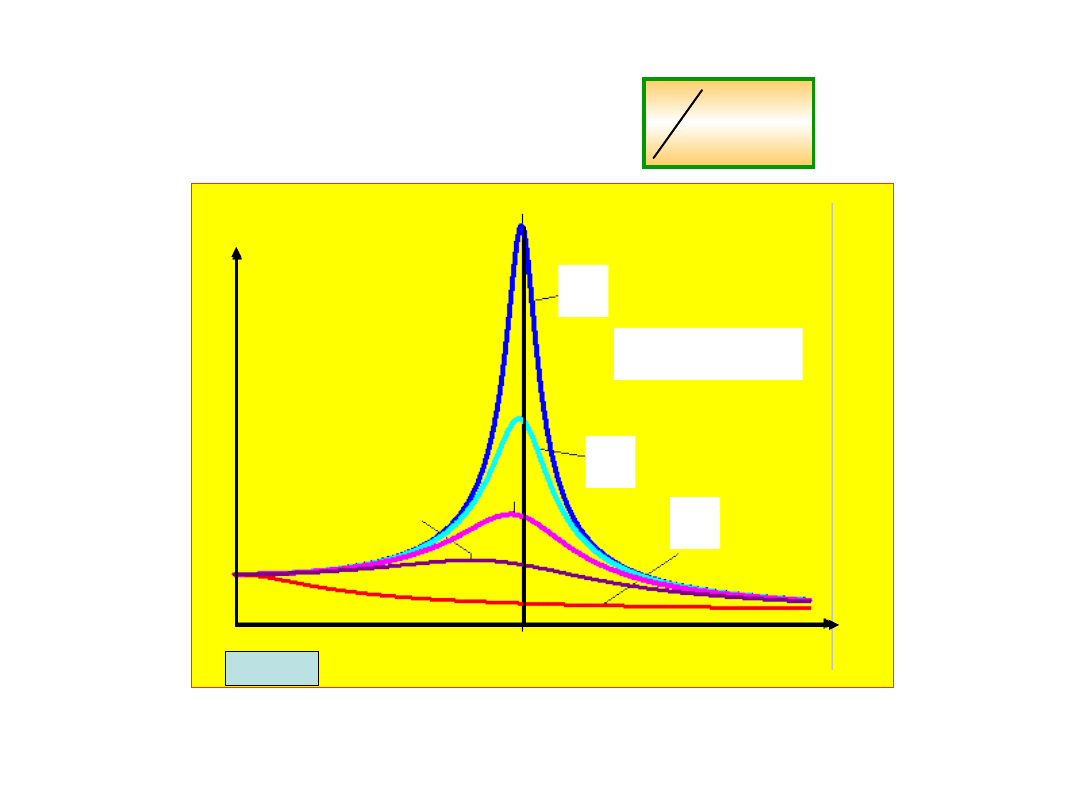
Zjawisko
rezonansu

Amplituda i częstość drgań wymuszonych
zależy od częstości siły wymuszającej.
Zależność tą pokazuje poniższy rysunek.



0

/

0

2





0

x

0

()

x

max



0

/

0



0

>>1

Dla częstości  = 

0

amplituda jest

maksymalna.

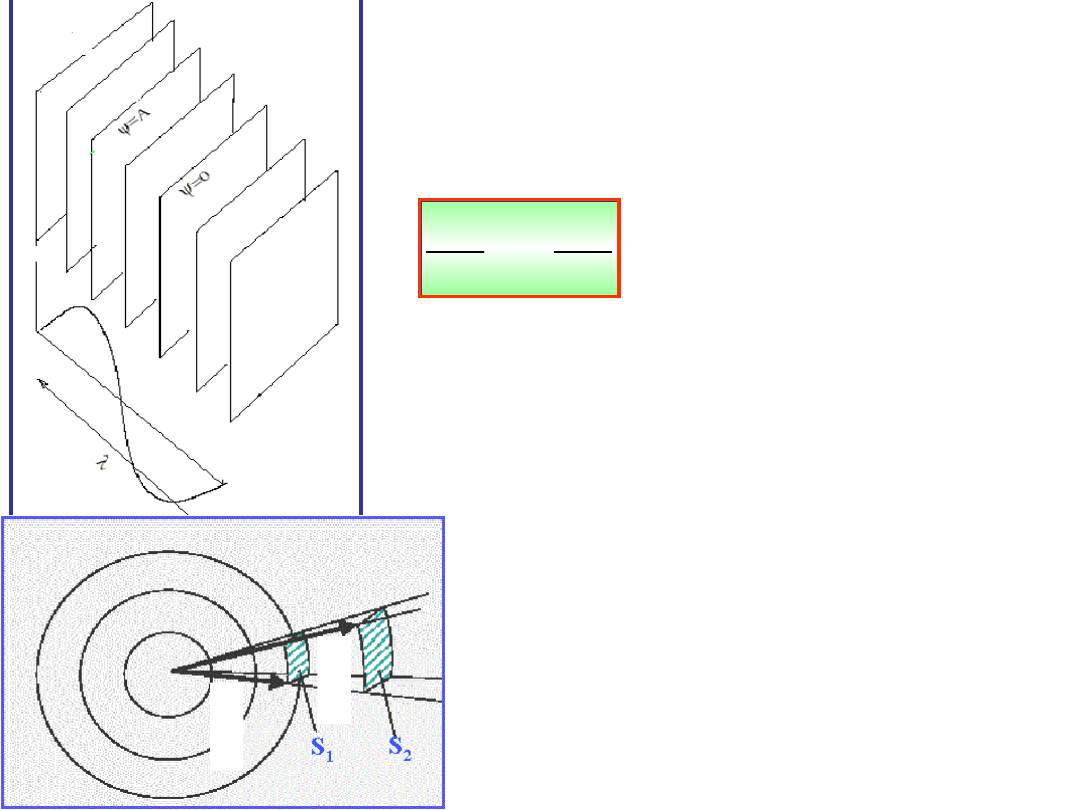
Zobaczmy w jaki sposób zmienia się krzywa
rezonansowa dla różnych parametrów
tłumienia

2

1

2









0



x

0

()



r



1



2



3



1

< 

2

< 

3

Fale –równanie

falowe



=

0



=

- A

2

2

2

2

2

v

t

x















r

1

r

2

13-01-2009

Reinhard Kulessa

91

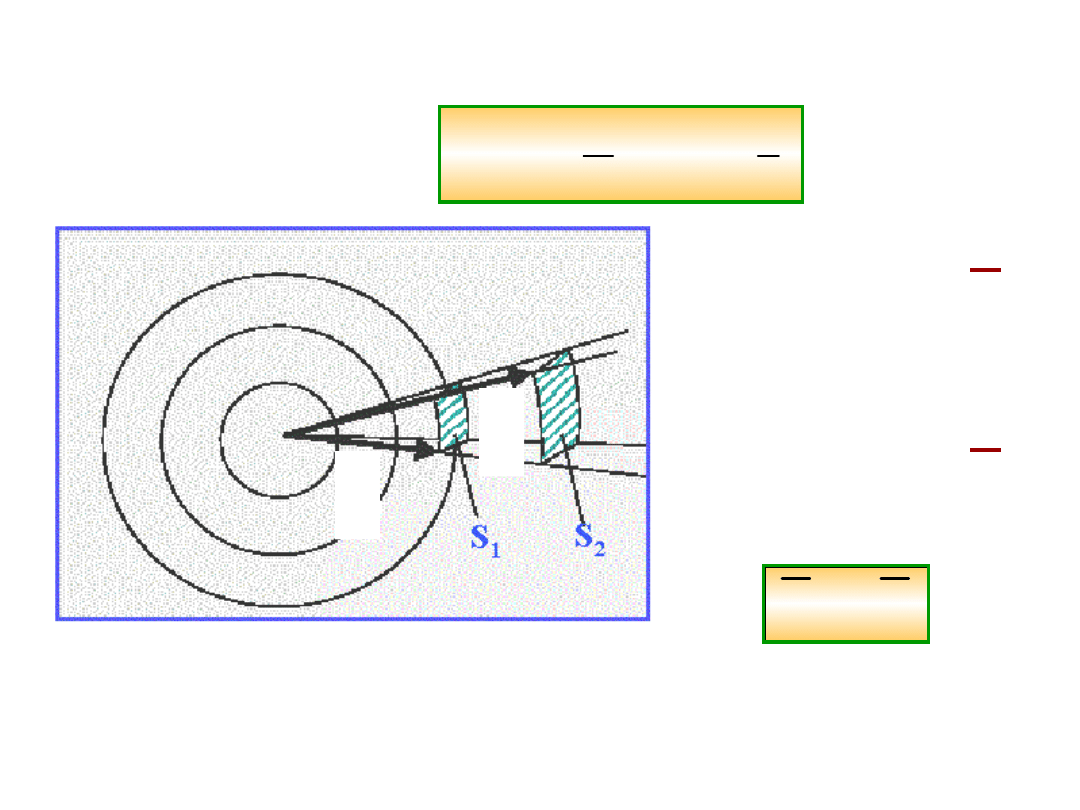
Wróćmy do problemu rozchodzenia się fal
kulistych.

r

1

r

2

Rozpatrzmy falę:

( , )

sin (

)

A

r

r t

t

r

v









Średnia gęstość
strumienia mocy
fali

P

1

przechodzącej
przez
powierzchnię

S

1

jest w ośrodku bez
absorbcji równa
średniej gęstości
strumienia mocy
fali

P

2

przechodzącej
przez
powierzchnię

S

2

.

Czyli

1

2

P

P



.

Natężenie fali spada więc z rosnącą
odległością r.

Elektryczność. Fale

Elektryczność.

Podstawowe pomiary

elektryczne

Układ RLC,

http://www.edw.com.pl/ea/wstep.ht
ml

podstawowe definicje:
1.Amper, Wolt
2.Opór, pojemnośc, indukcyjnośc
3.Prawo Ohma, Prawa Kirhoffa
4.Prawa Nortona i Thevenina

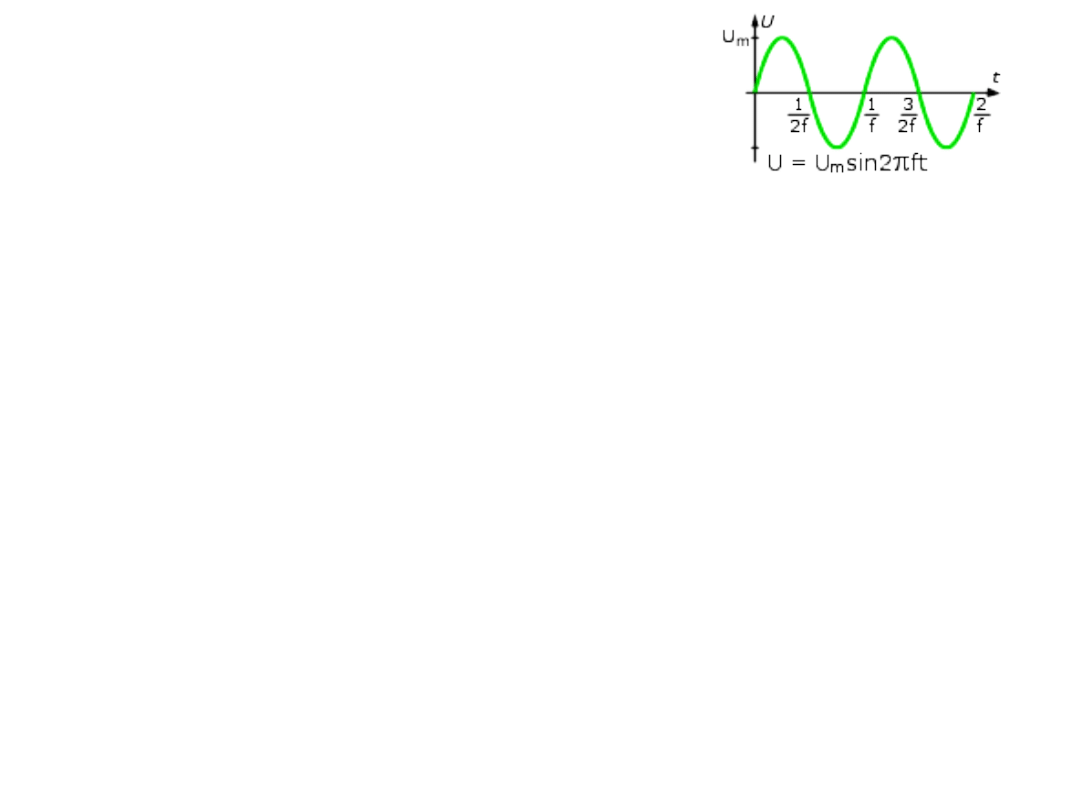
Sygnał sinusoidalny U(t) = Umsin( ω t),
gdzie:
Um - amplituda,
ω=2πf,
f - częstotliwość wyrażona w hercach (Hz),
t - czas w sekundach.
 Falę sinusoidalną opisują dwa parametry amplituda
i częstotliwość (dotyczy to również innych sygnałów).
Czasami zamiast amplitudy używa się pojęcia wartości
skutecznej Usk czy też wartości międzyszczytowej Upp.
Wartość skuteczna jest równa Usk=0,707*Um,
wartość międzyszczytowa jest równa Upp=2Um.
Przykładem wartości skutecznej sygnału sinusoidalnego
może być znana wszystkim wartość 230V napięcia
o częstotliwości 50Hz w gnieździe sieciowym, jakie
znajduje się w każdym mieszkaniu. Amplituda tego
napięcia wynosi 325V, a wartość międzyszczytowa 650V.

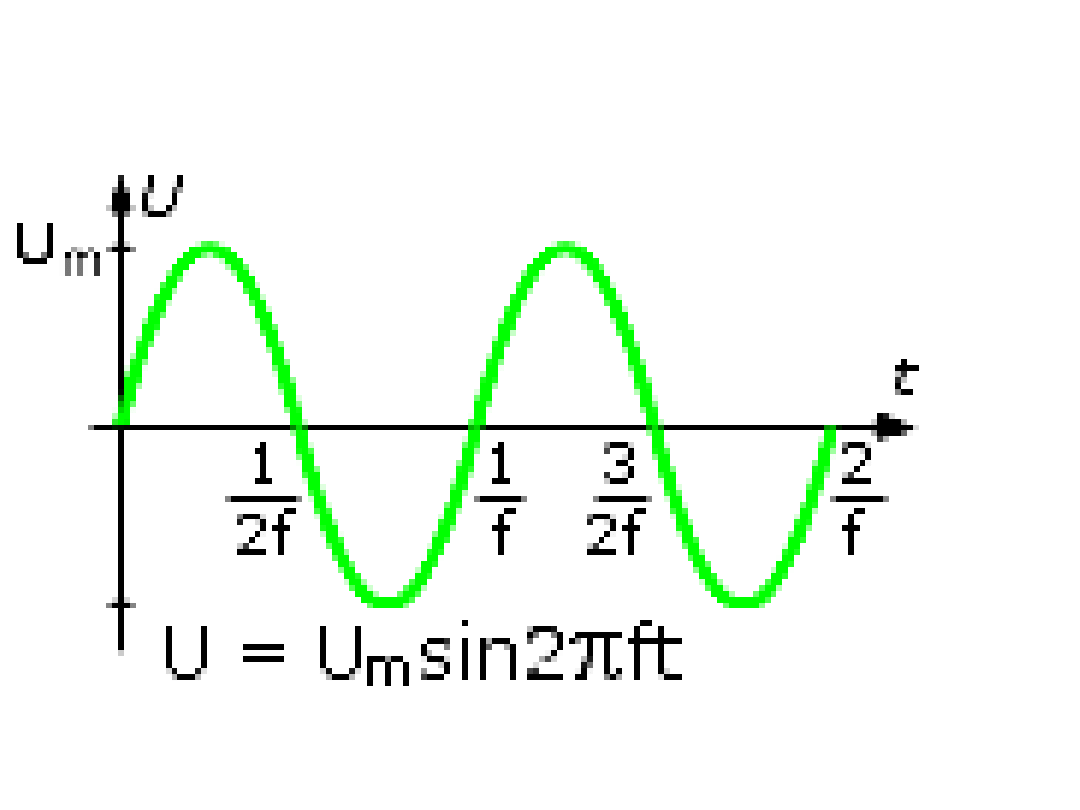
Przebieg napięcia w

sieci

+325V

-
325
V

10ms

10ms

10ms

10
ms

---------------20ms
--------------

230V
(220V)

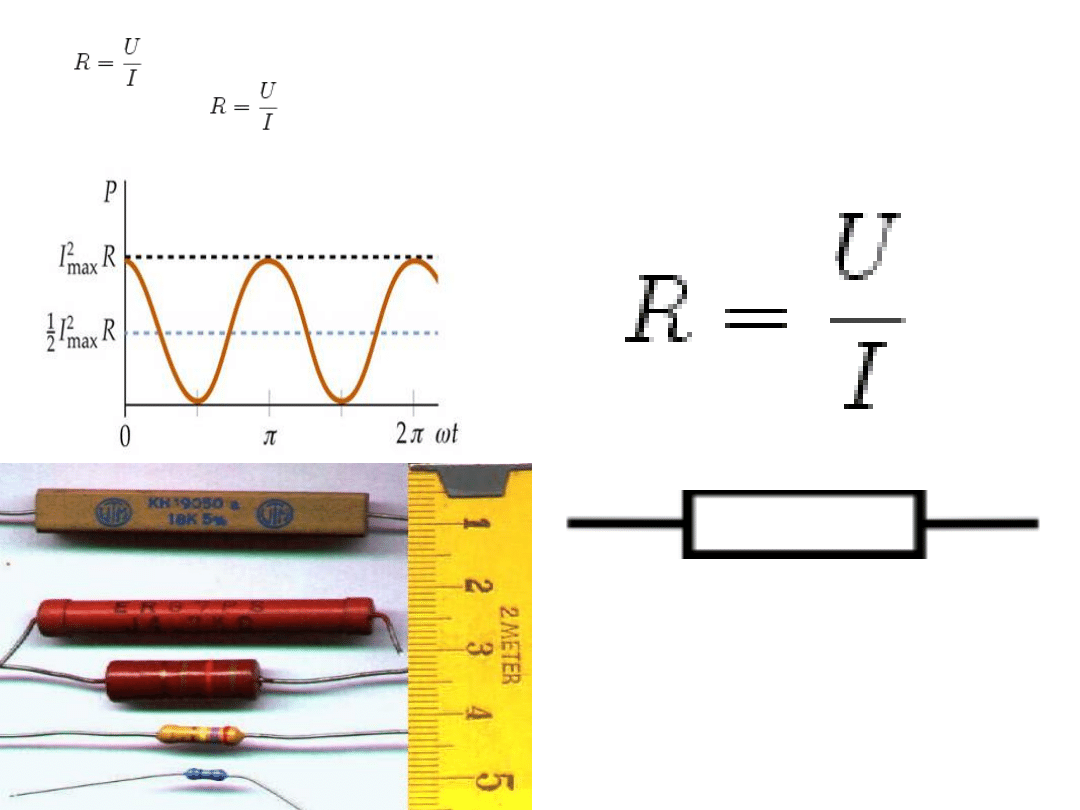
Oporność

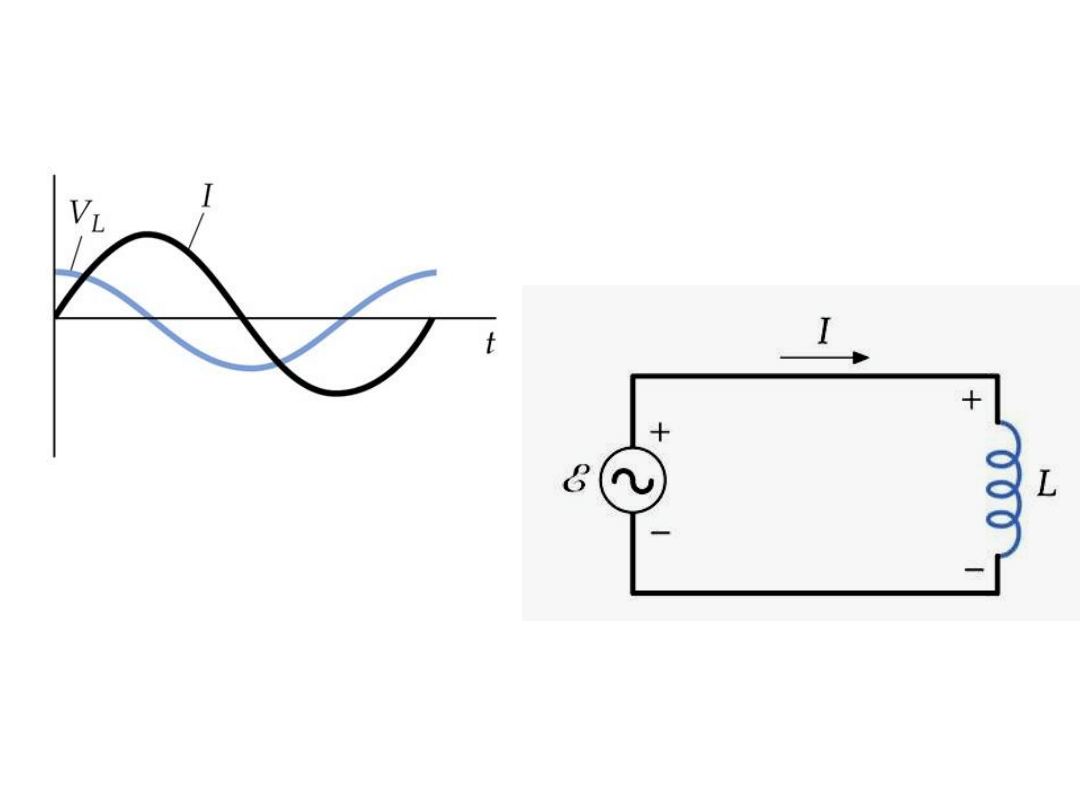
Indukcyjność

i(t) = u(t) : jωL

i(t) =

I

cos(ωt – φ)

Napięcie wyprzedza prąd o ¼ T
czyli o π/2

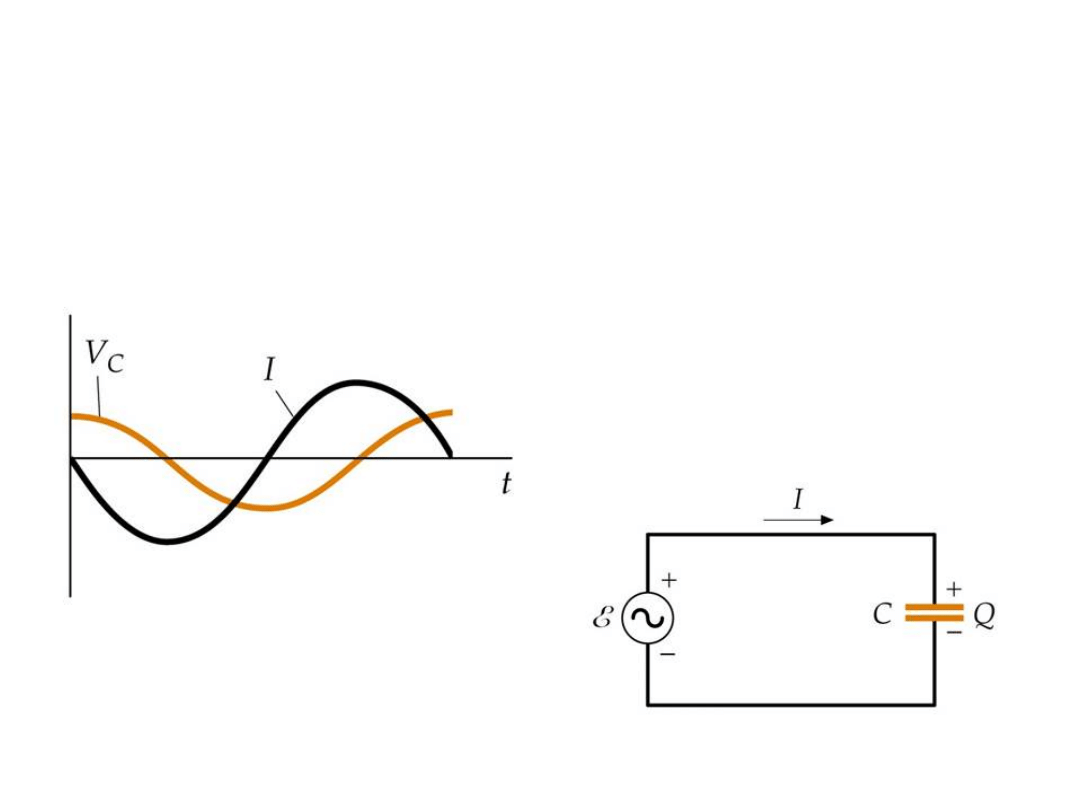
POJEMNOŚĆ

i(t) = u(t) jωC i(t) = I cos(ωt + φ)

Prąd wyprzedza napięcie o ¼ T czyli o π/2

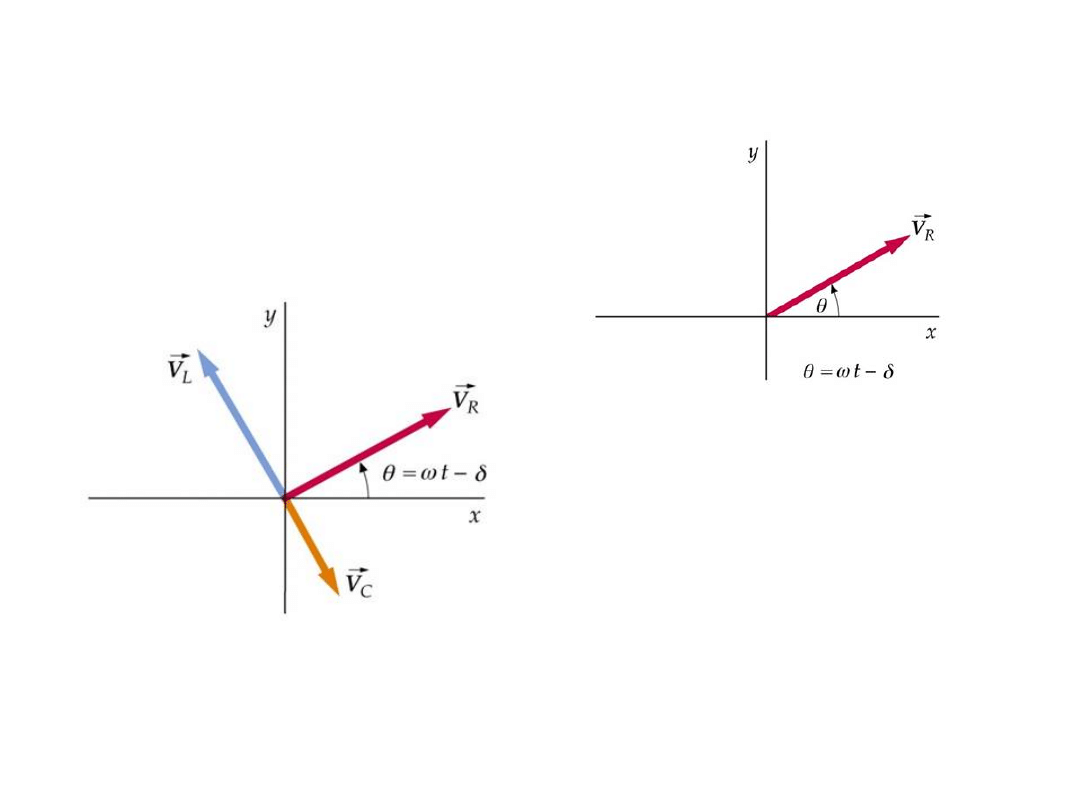
WSKAZY i wskazy

wiruj

ą

ce

Napięcie na indukcyjności wyprzedza napięcie
na pojemności o π/2.
Wskaz napięcia jest przesunięty o kąt θ w
stosunku do fazy prądu, którą zazwyczaj przyj-
mujemy za zerową
Można tak kombinować jeżeli pominiemy
zmiany czasowe, (sinusoidalne) co jest
Interpretowane jako wiowanie wskazów.
Aby nie dostać oczopląsu wirowanie pomujamy

To dla Orłów

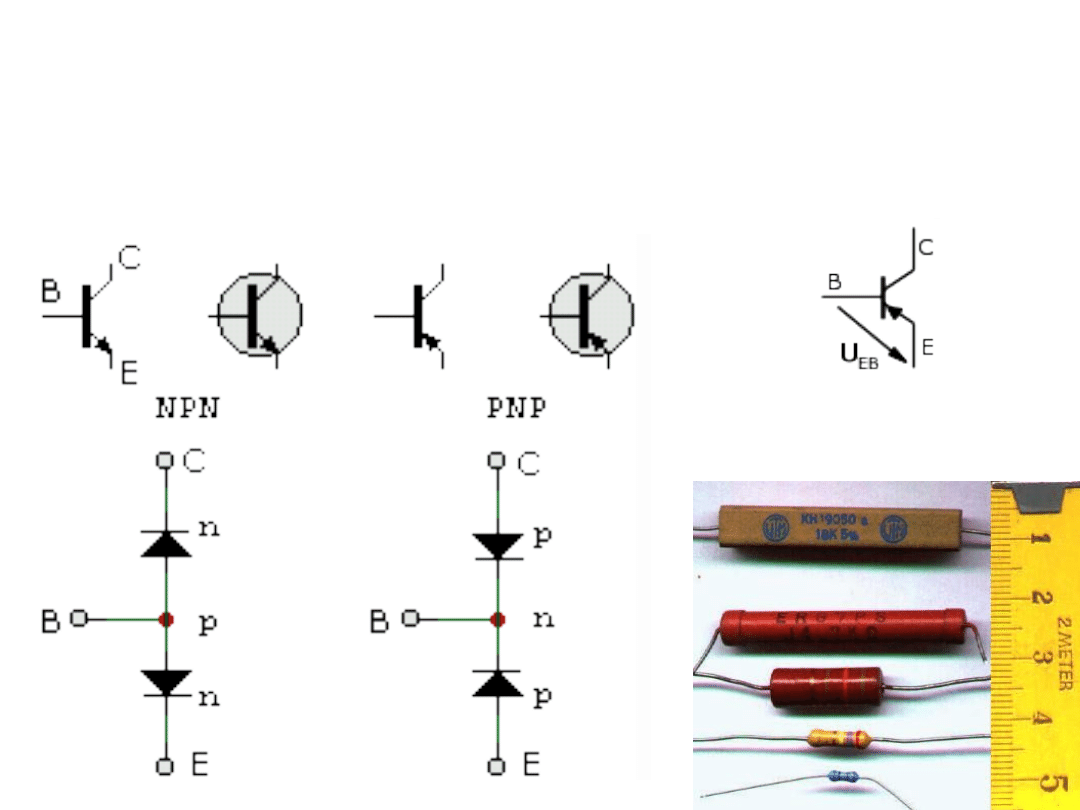
ELEMENTY AKTYWNE i

PASYWNE my uczymy si

ę

RLC

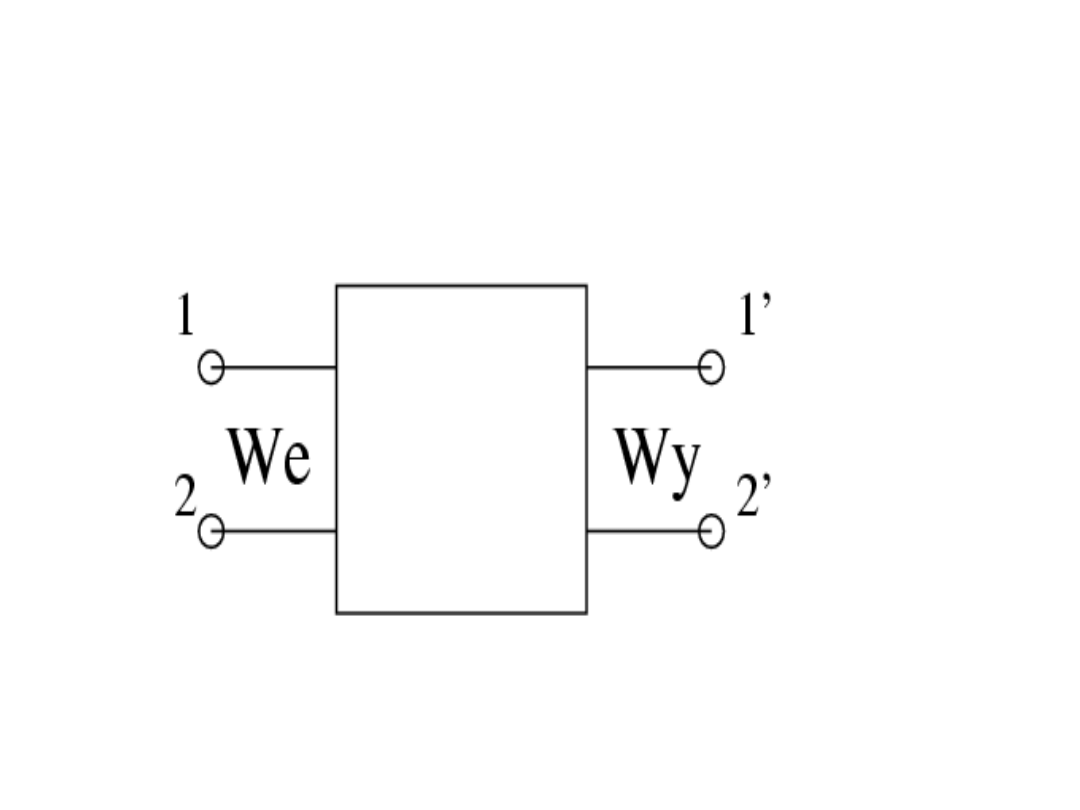
CZWÓRNIK DWÓNIK

CZARNA SKRZYNKA

K(jω)

U

1

(t

)

U

2

(

t)

To pojęcie z cybernetyki dotyczy nie tylko układów elektronicznych. Jeżeli np. „na wejściu”
wzrośnie akcyza na paliwo to na wyjściu spadną obroty firm i dochody z podatków a potem

upadnie Rząd.

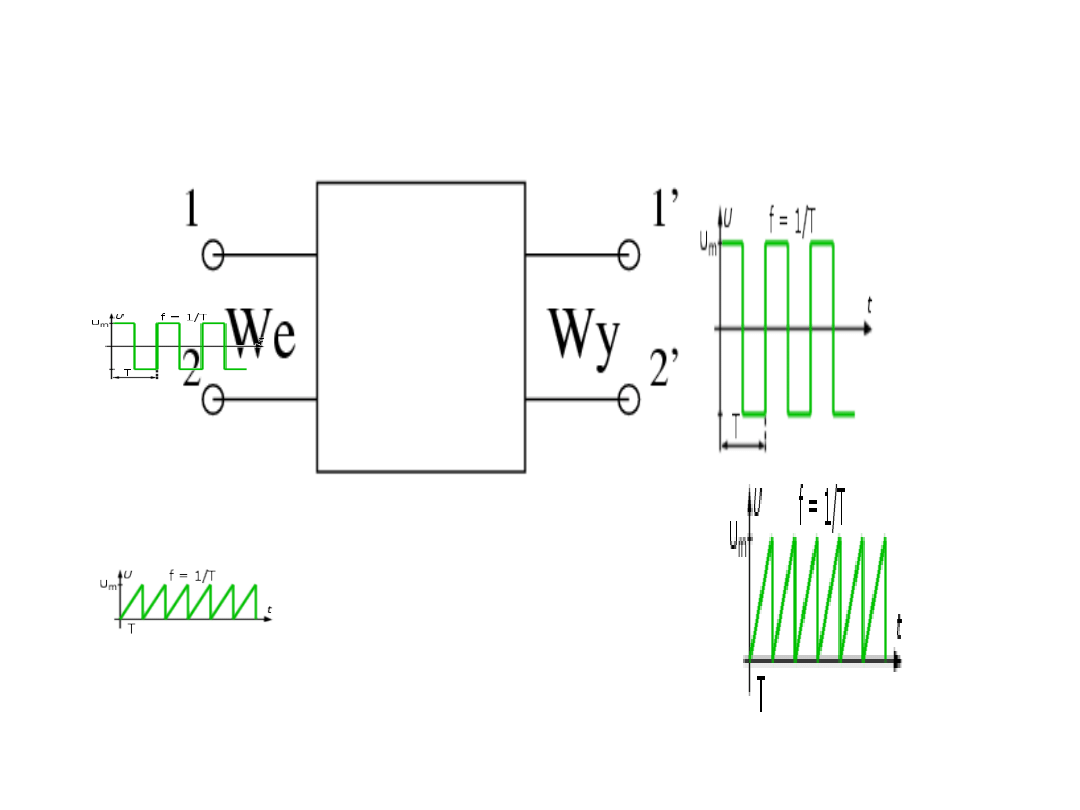
CZWÓRNIK DWÓNIK

CZARNA SKRZYNKA

K(jω)

U

1

(t)

U

2

(t)

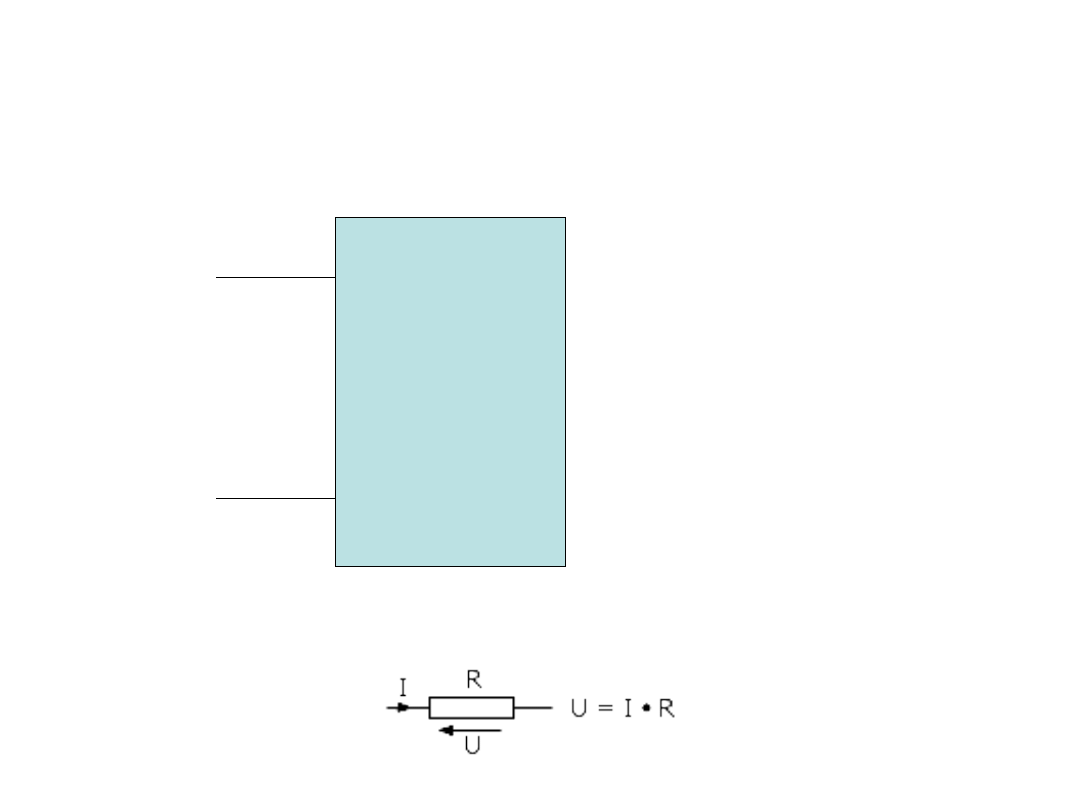
DWÓJNIK

i(t)

u(t)

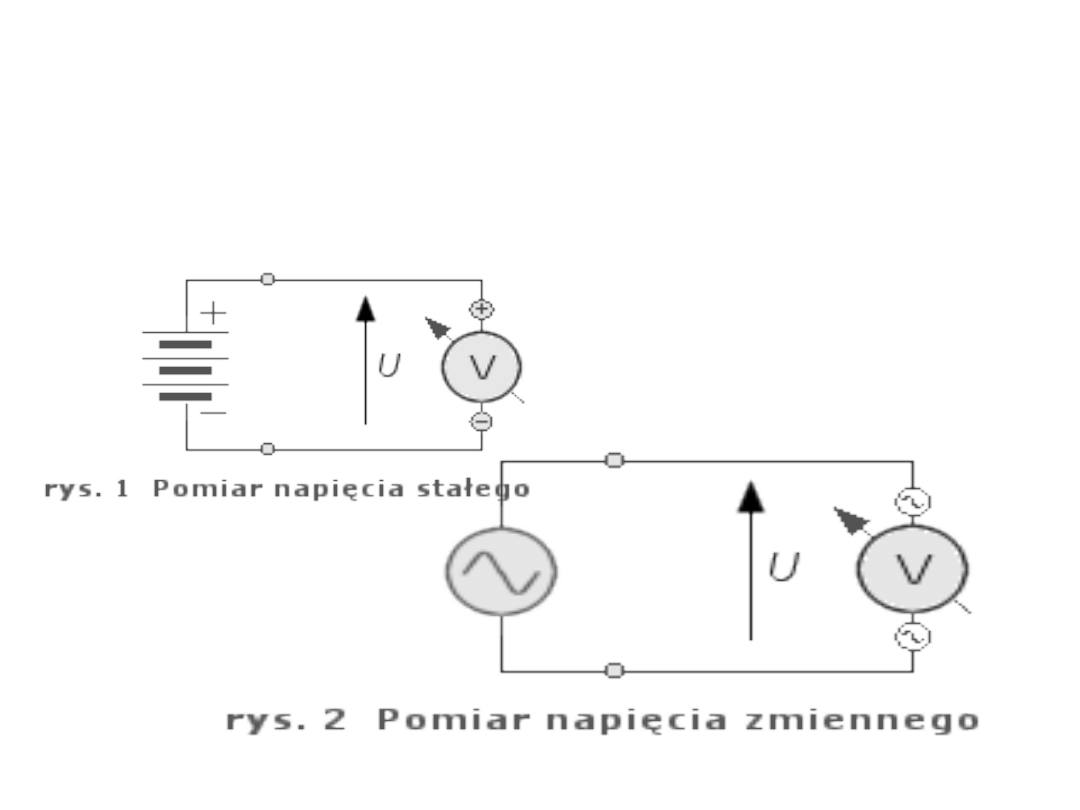
Pomiar Napięcia

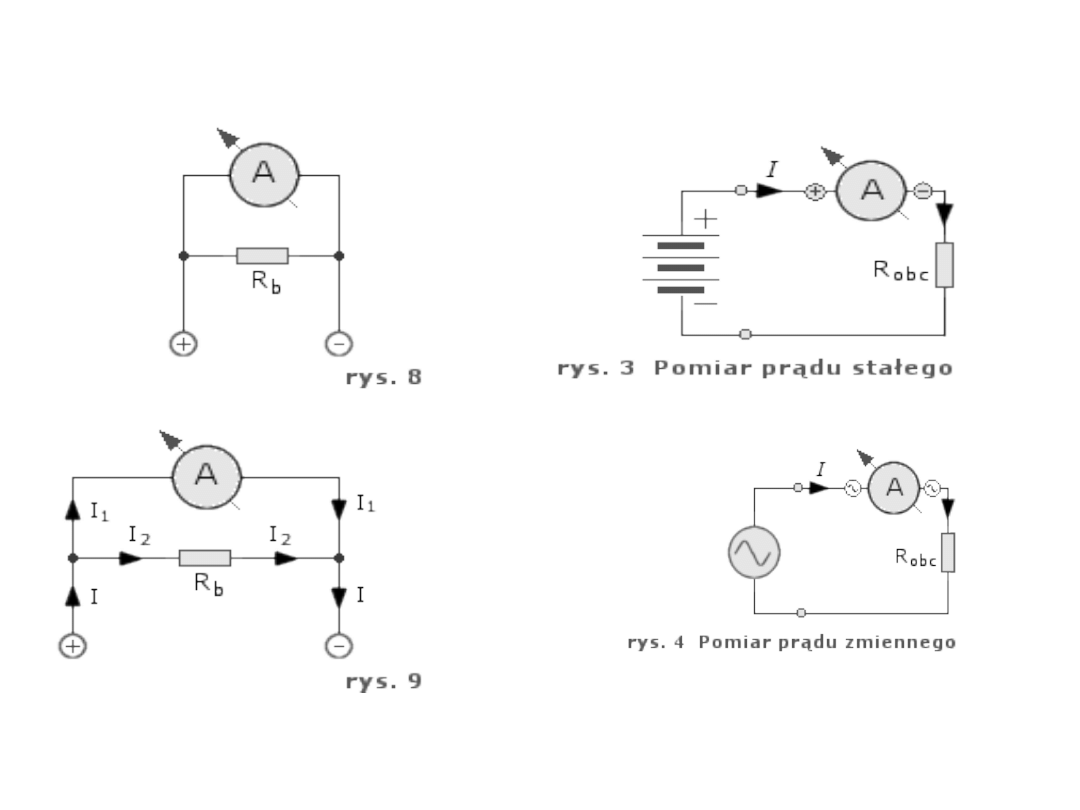
Pomiar prądu

Zastosowanie „bocznika” zwieksza
Zakres amperomierza

Wstawienie amperomierza zwiększ
opór
w obwodzie i miernik wskazuje
mniejszy prąd

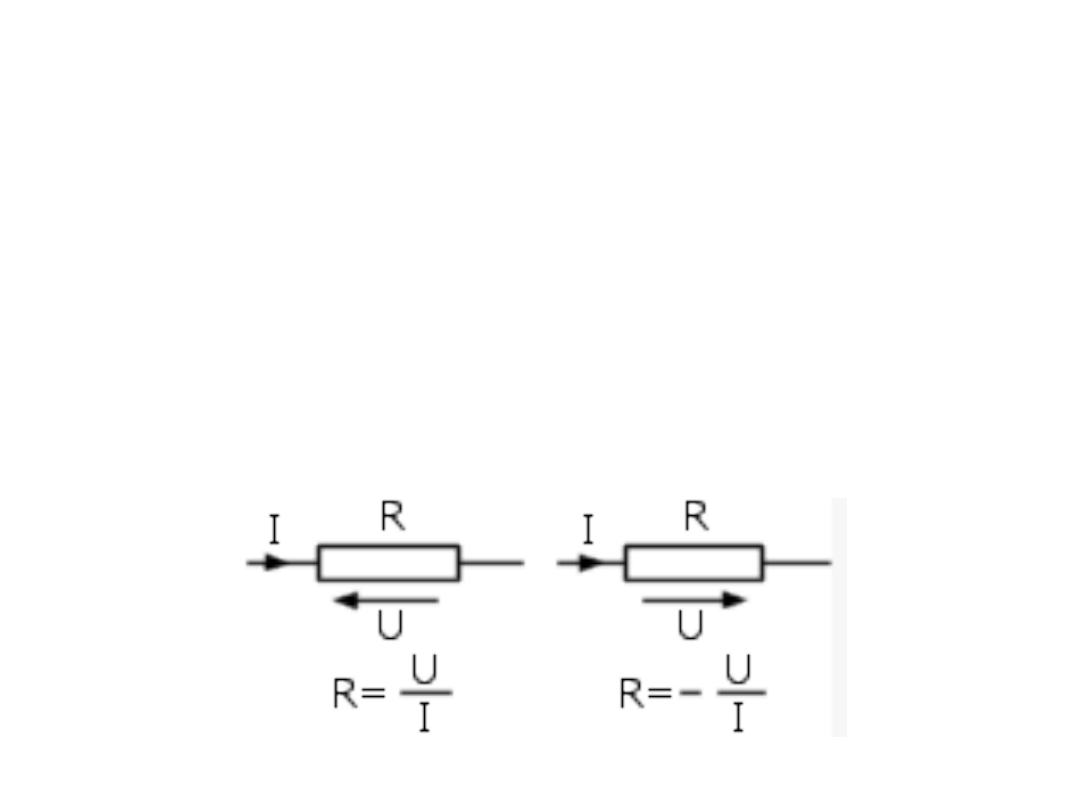
Prąd, opór, Prawo

Ohma

Prąd wyraża szybkość przepływu ładunku elektrycznego obok
pewnego punktu. Jednostką miary jest 1A (amper). Można więc
powiedzieć, że prąd jednego ampera jest równy przepływowi ładunku
jednego kulomba na sekundę

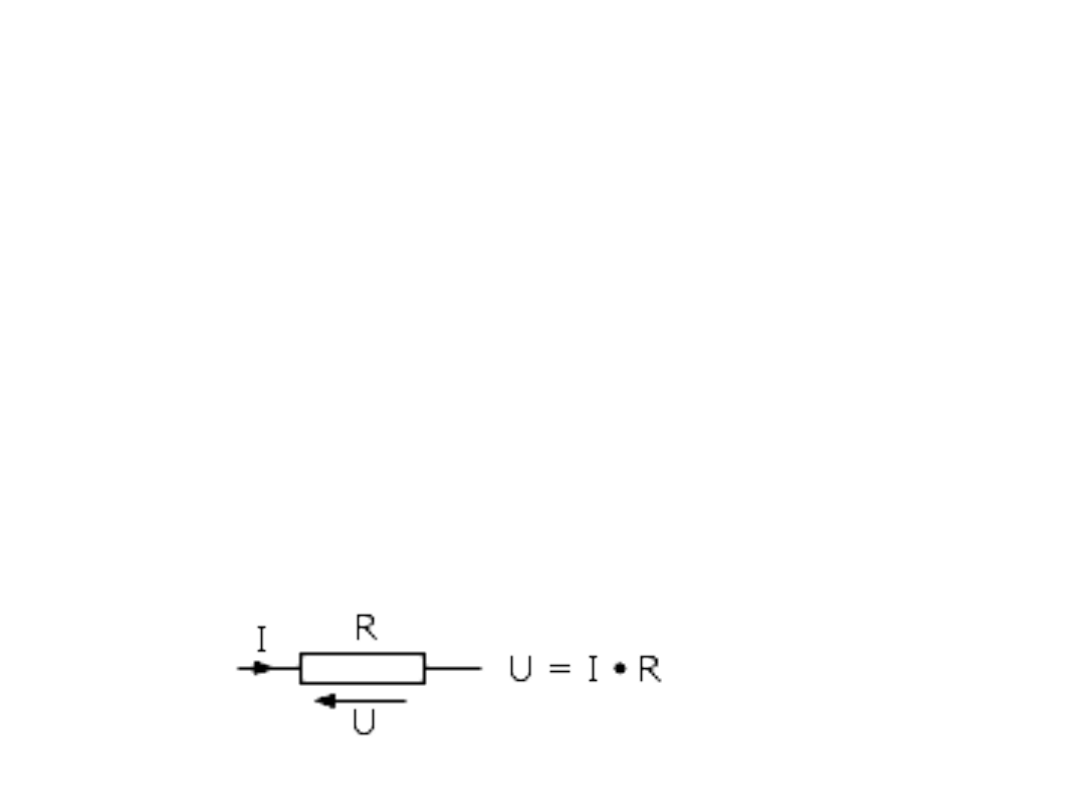
Nie do końca wiadomo czy napięcie

zależy od prądu czy prąd od napięcia
ale zakładamy zależność liniową

Prawo Ohma mówi, że napięcie U na końcach przewodnika, przez
który płynie prąd o natężeniu I jest iloczynem natężenia prądu
i rezystancji R tego przewodnika, czyli U = I 

*

R       Jest to prawo,

z którego będziesz wielokrotnie korzystał, gdy będziesz musiał
obliczyć prąd lub napięcie czy też wyliczyć właściwą dla danego
układu wartość rezystora.

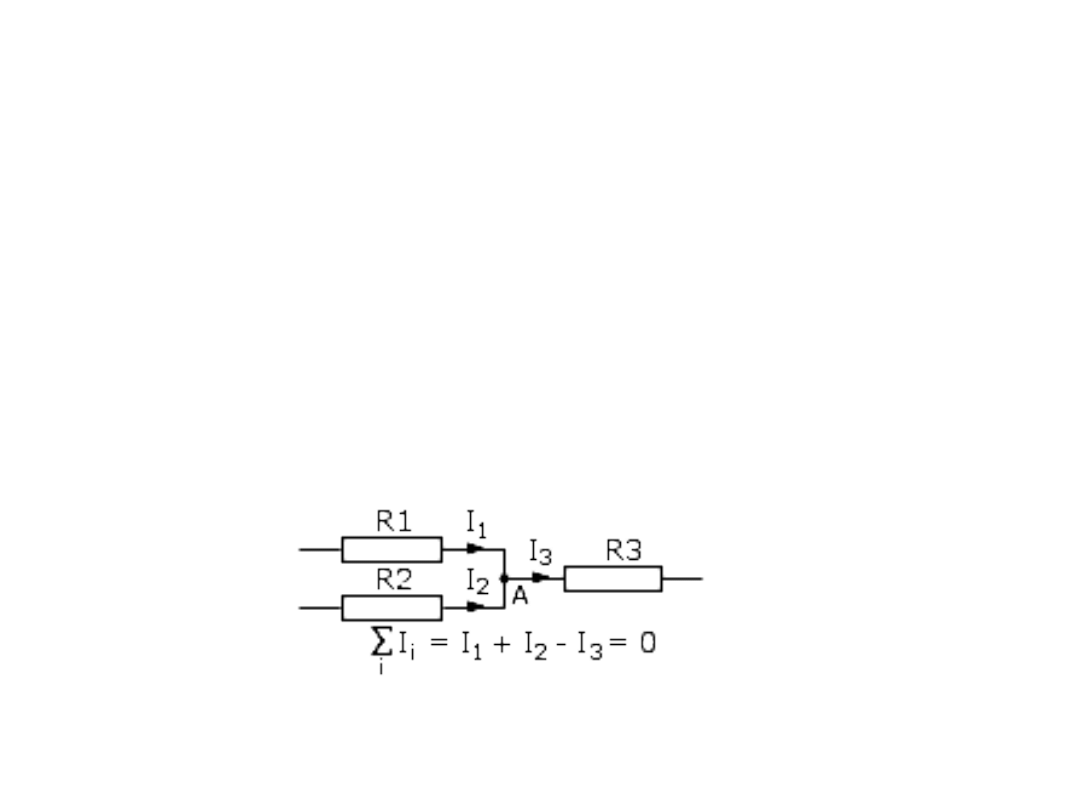
Prawa Kirchoffa

Pierwsze prawo Kirchhoffa mówi, że suma prądów wpływających
do węzła jest równa sumie prądów wypływających z niego lub
inaczej, że suma wszystkich prądów w węźle jest równa zeru
   Prądy wpływające do węzła mają znak dodatni, a wypływające
znak ujemny.
   Przykładem węzła jest punkt A na rysunku. Prądy I1, I2 są
dodatnie, a I3 ujemny.

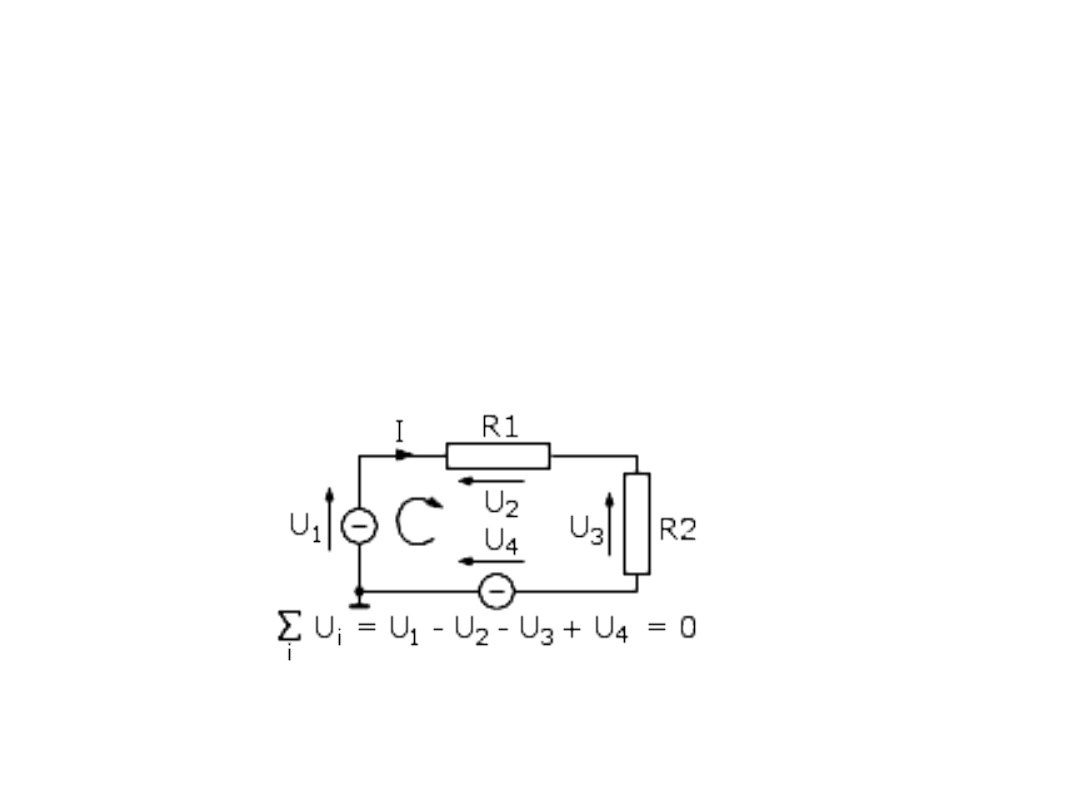
Drugie prawo Kirchhoffa mówi, że w obwodzie zamkniętym
(oczku) suma wszystkich napięć jest równa zeru
   Napięcia, których zwrot strzałki jest zgodny z obiegiem oczka są
dodatnie, a te, których zwrot jest przeciwny są ujemne. Obieg oczka
przyjmuje się zgodnie z zaznaczoną okrągłą strzałką wewnątrz
obwodu.
   Zgodnie z tymi założeniami napięcia U1 i U4 są dodatnie, a U2
i U3 ujemne.

Mierniki

magnetyczne

zawsze mierzą tak

na prawdę prąd

A mierniki cyfrowe ????

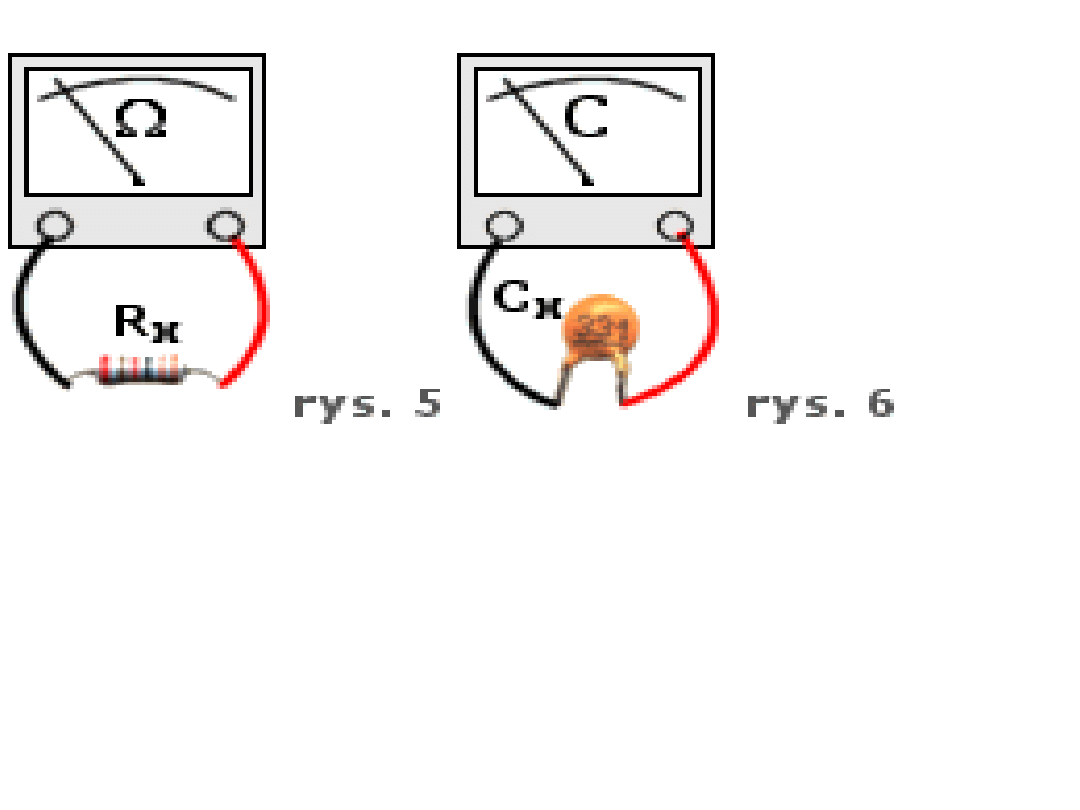
Pomiar rezystancji - R - tą wielkość mierzymy omomierzem.
Pomiaru dokonujemy bezpośrednio na elemencie (rezystorze) -
pamiętać należy, że pomiar rezystora wlutowanego w płytkę razem z
innymi elementami może dawać wskazania odbiegające od
faktycznej wartości (rys. 5).
Pomiar pojemności - C - tą wielkość mierzymy miernikiem
pojemności. Pomiaru dokonujemy bezpośrednio na elemencie -
kondensatorze (rys. 6)

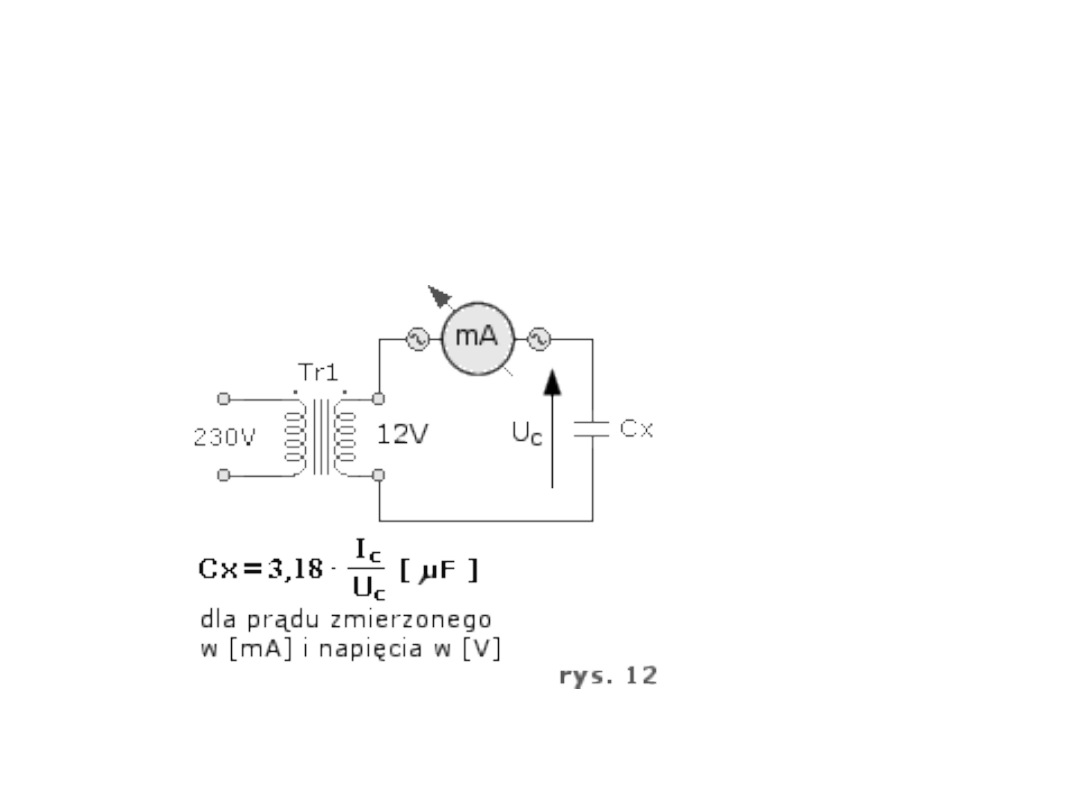
Pomiar pojemności

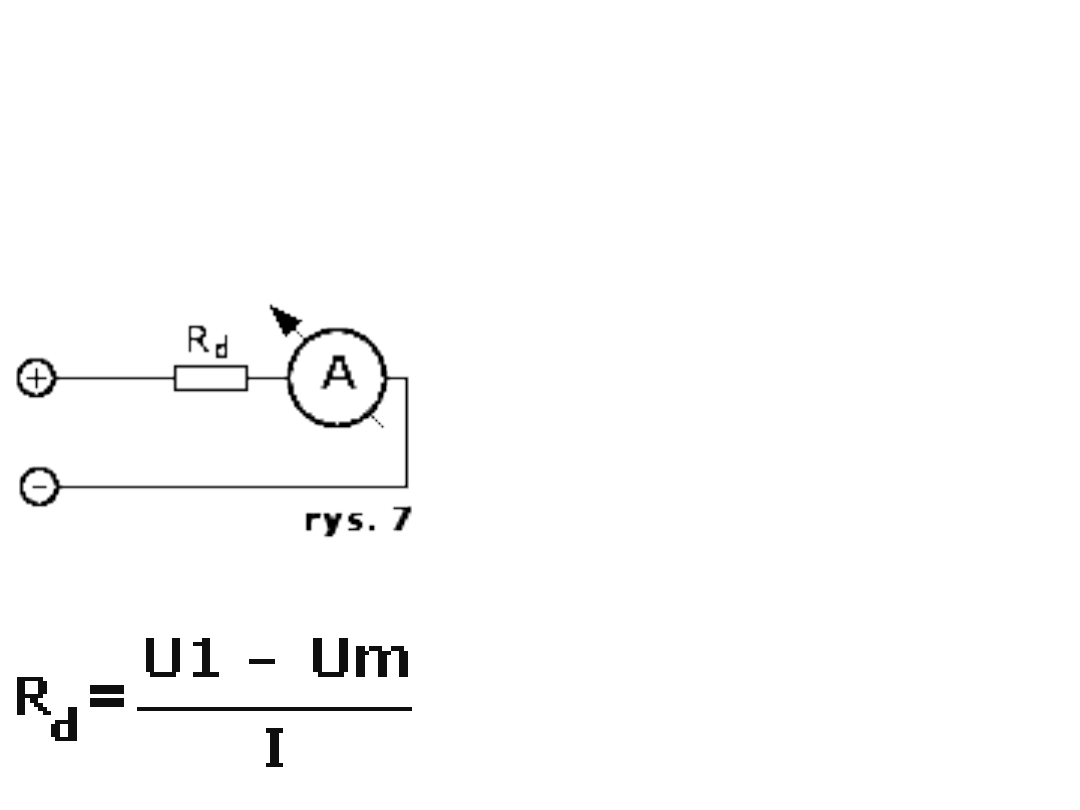
Pomiar napięcia -
Woltomierz

R

d

- oporność

opornika
dodatkowego;

U

1

- napięcie

mierzone;

U

m

- spadek napięcia

na

ustroju;

I - prąd

amperomierza

OPORNOŚĆ i

OPORNIKI

•

 Szeregowe i równoległe łączenie rezystorów.

Z prawa Ohma, które można zapisać R=U/I,

wynikają następujące właściwości rezystorów:

- rezystancja zastępcza dwóch rezystorów

połączonych szeregowo (rys. 2.3) wynosi:

• R=R1+R2
•

czyli przez szeregowe połączenie rezystorów

zawsze otrzymuje się większą rezystancję,

rys. 2.3 - rezystancja zastępcza dwóch rezystorów

połączonych równolegle (rys 2.4) wynosi:

 

                   

                     

    

 

        

         

   

 

        

         

      

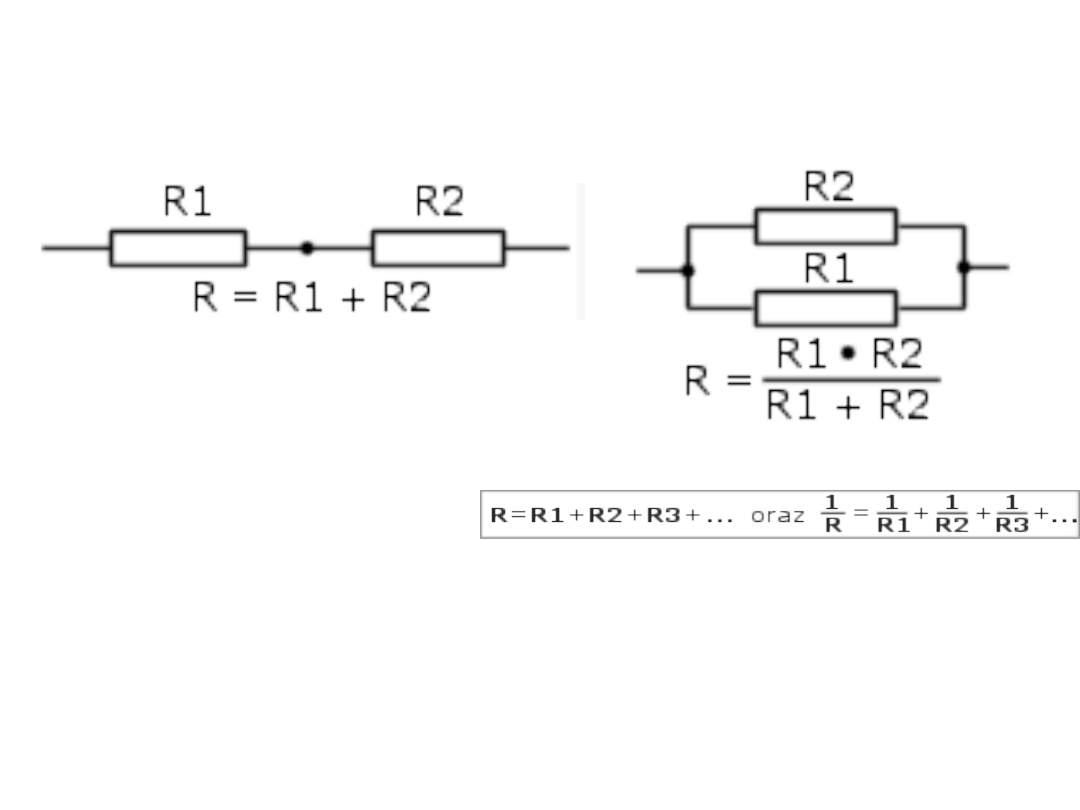
Połączenie szeregowe i

równoległe

2

.

3

                                                      

                                    

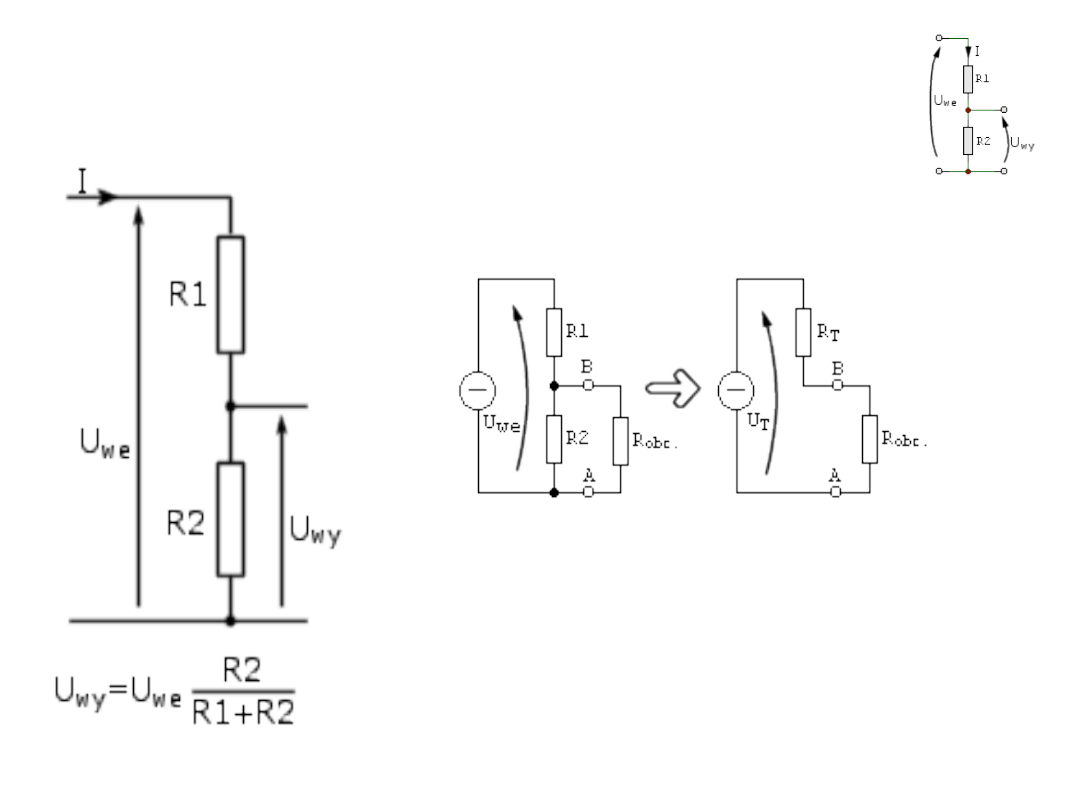
Dzielniki napięcia

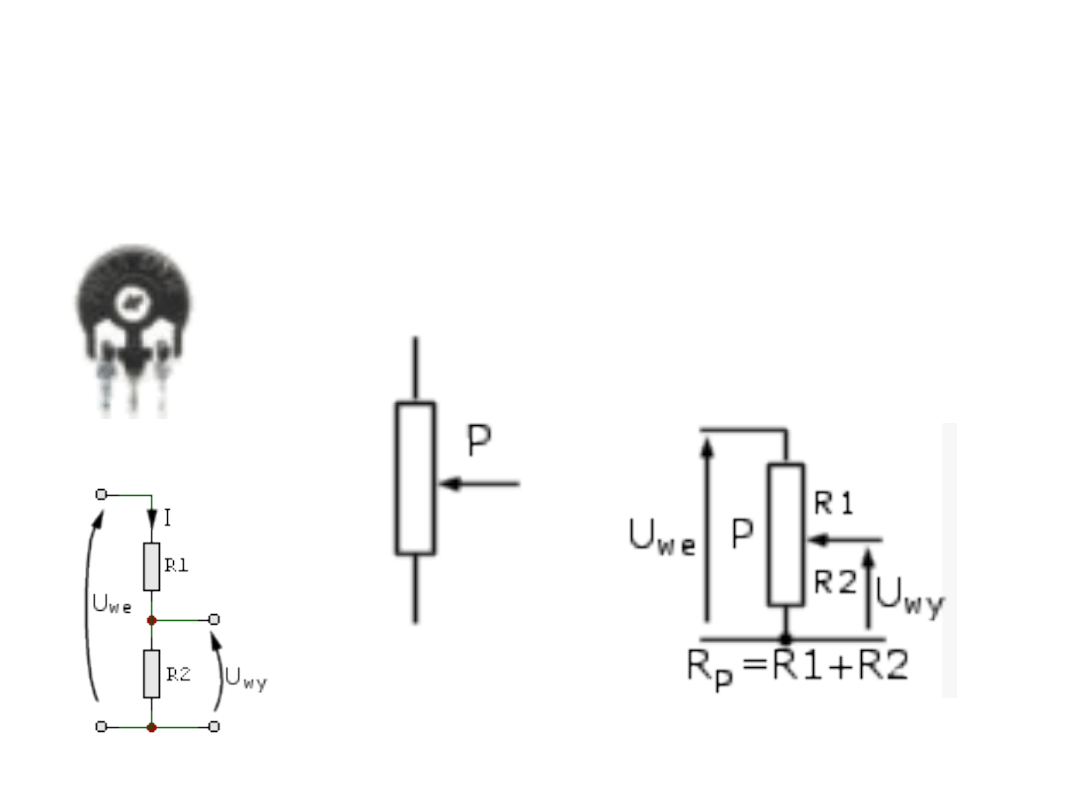
Dzielniki -

potencjometry

 

           

 

          

 

rys. 2.7

rys. 2.8

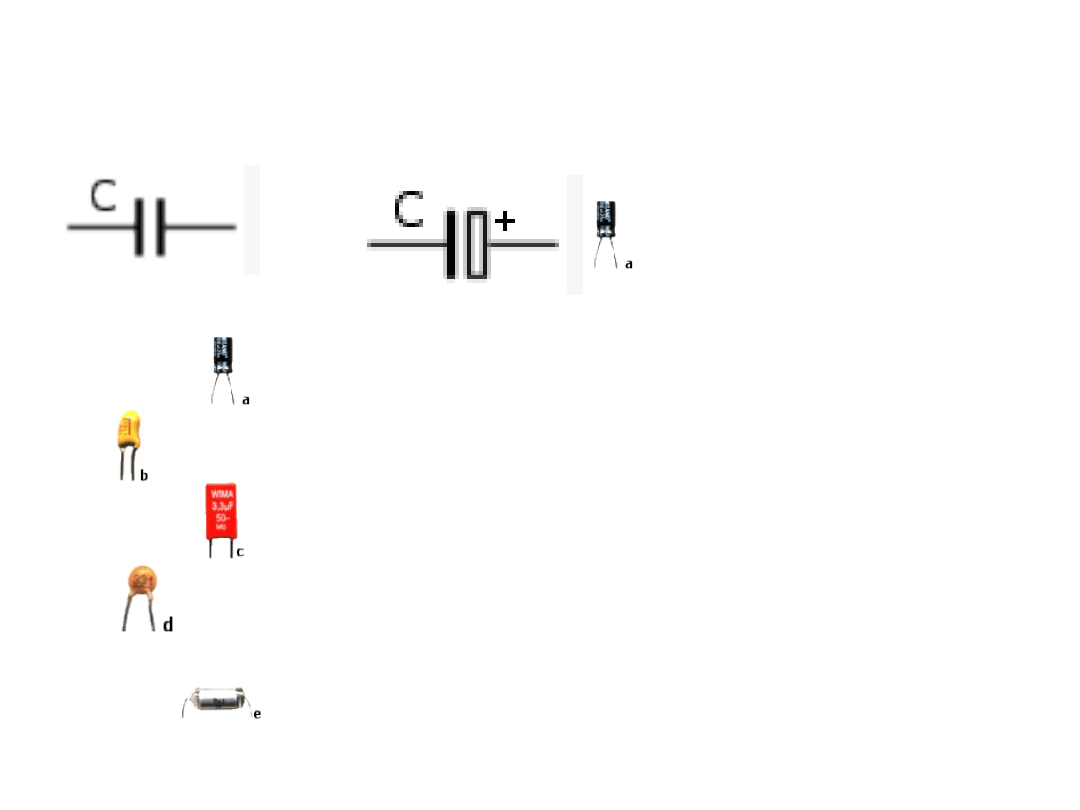
Pojemność -

kondensator

  Kondensator jest

elementem nieco

bardziej

skomplikowanym niż

rezystor, gdyż prąd

płynący przez niego

nie jest wprost

proporcjonalny do

napięcia lecz do

szybkości jego zmian

i dlatego można

napisać:

I = dQ/dt Q = C U

I = C dU/dt

Z tego wzoru (jeśli

czegośnie rozumiesz

to zajrzyj do działu

trochę matematyki)

Zdjęcia przedstawiają
kondensatory:
a) elektrolityczny,

b) tantalowy,

c) poliestrowy,

d) ceramiczny,

e) styrofleksowy

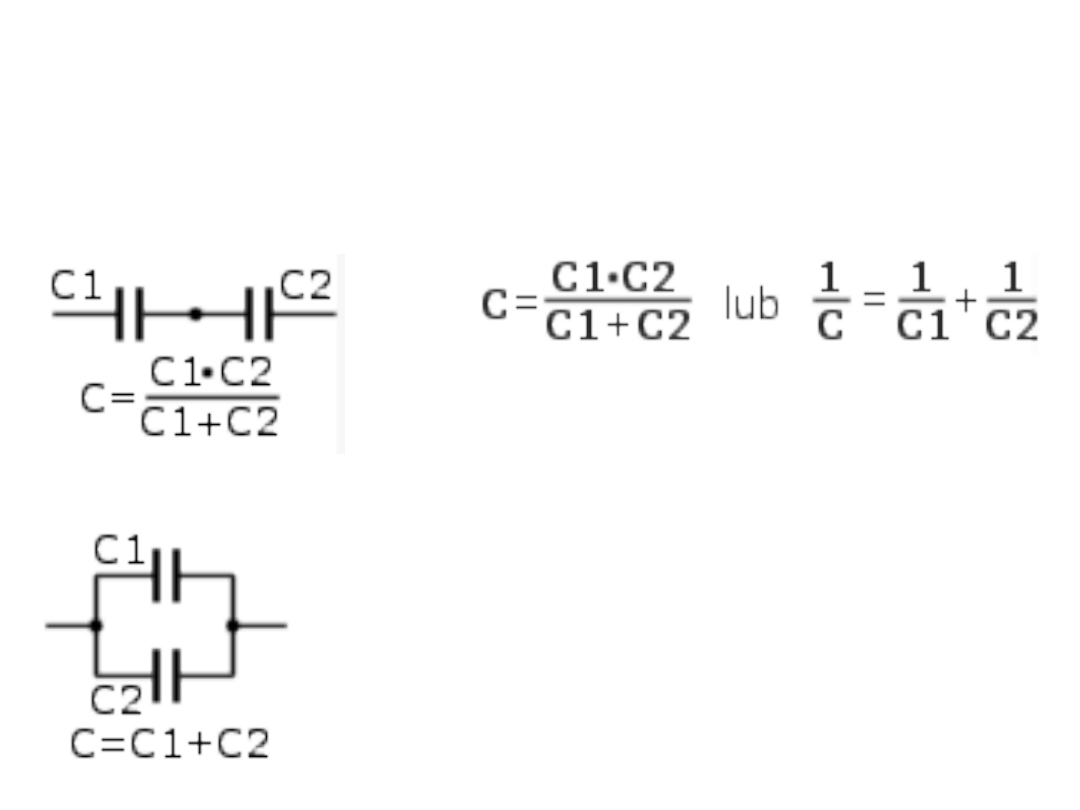
Łączenie

pojemności

szeregowe

równole
głe

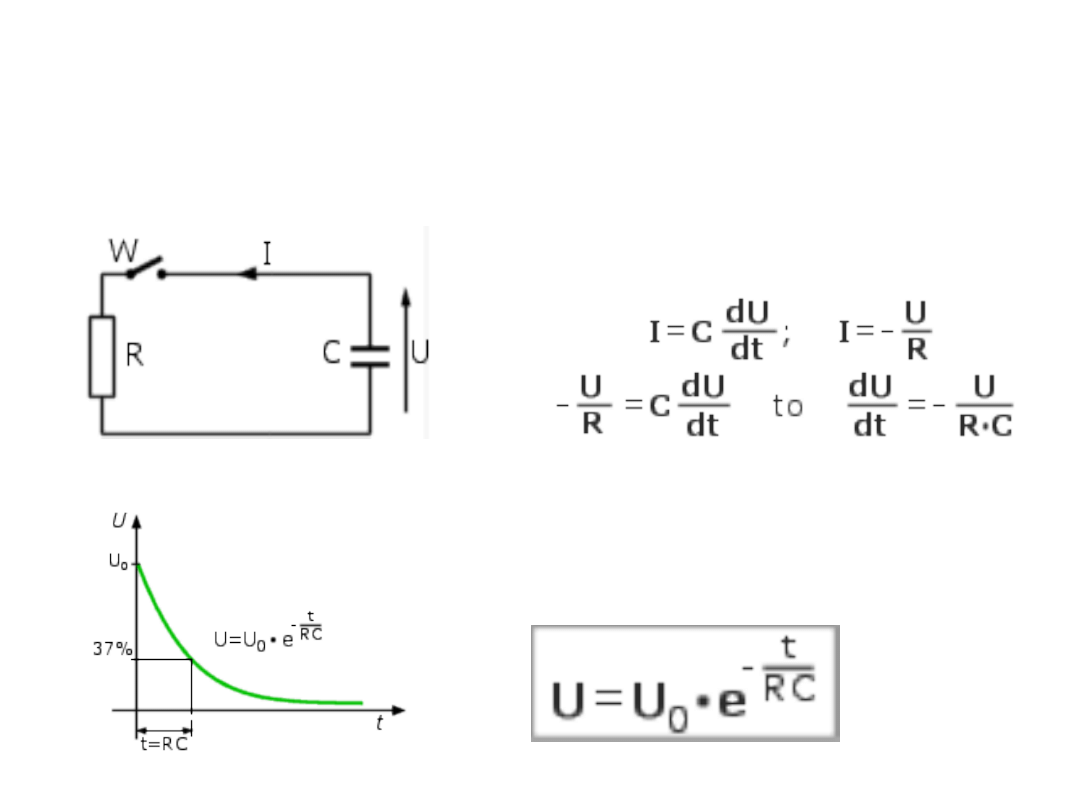
Rozładowanie

kondensatora

 

                                                

           

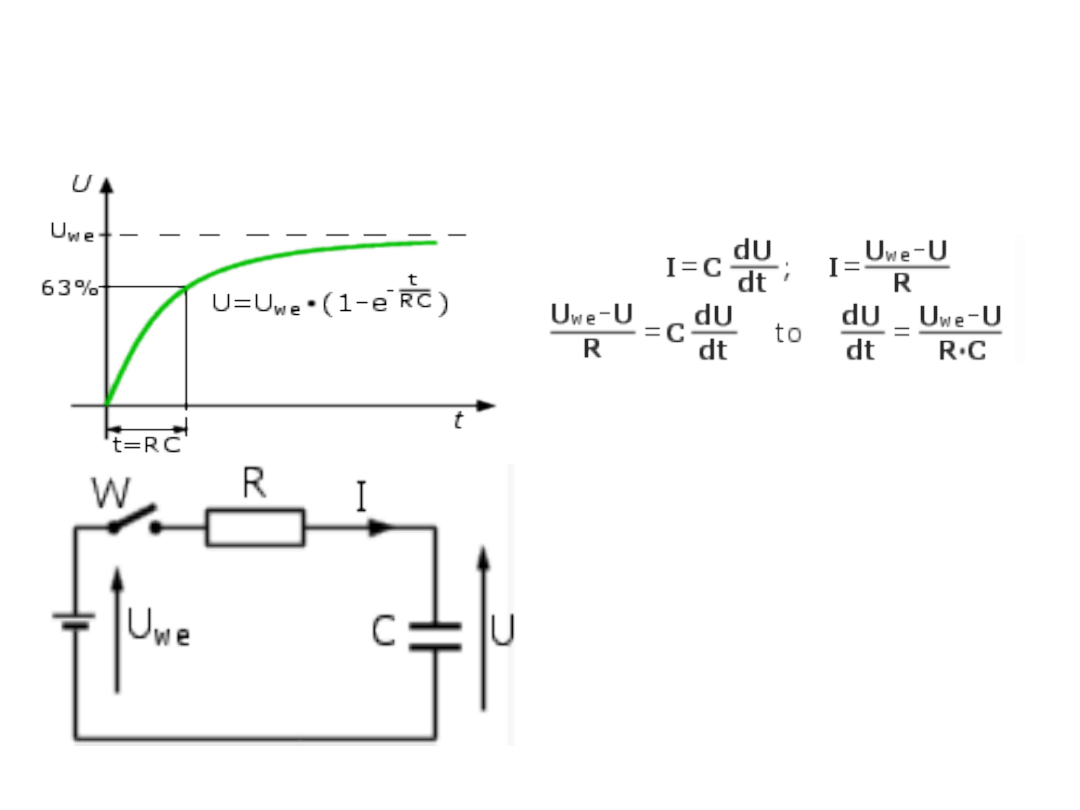
Ładowanie

kondensatora

Ładowanie kondensatora w układzie

RC. Na rys. 2.15 pokazany jest układ,
w którym po zamknięciu wyłącznika
w w chwili

t=0,

rozpocznie

się

ładowanie kondensatora C poprzez
rezystor R. Kondensator C będzie
ładowany prądem I z baterii o napięciu
U

we

. Można to zapisać w postaci

równań:

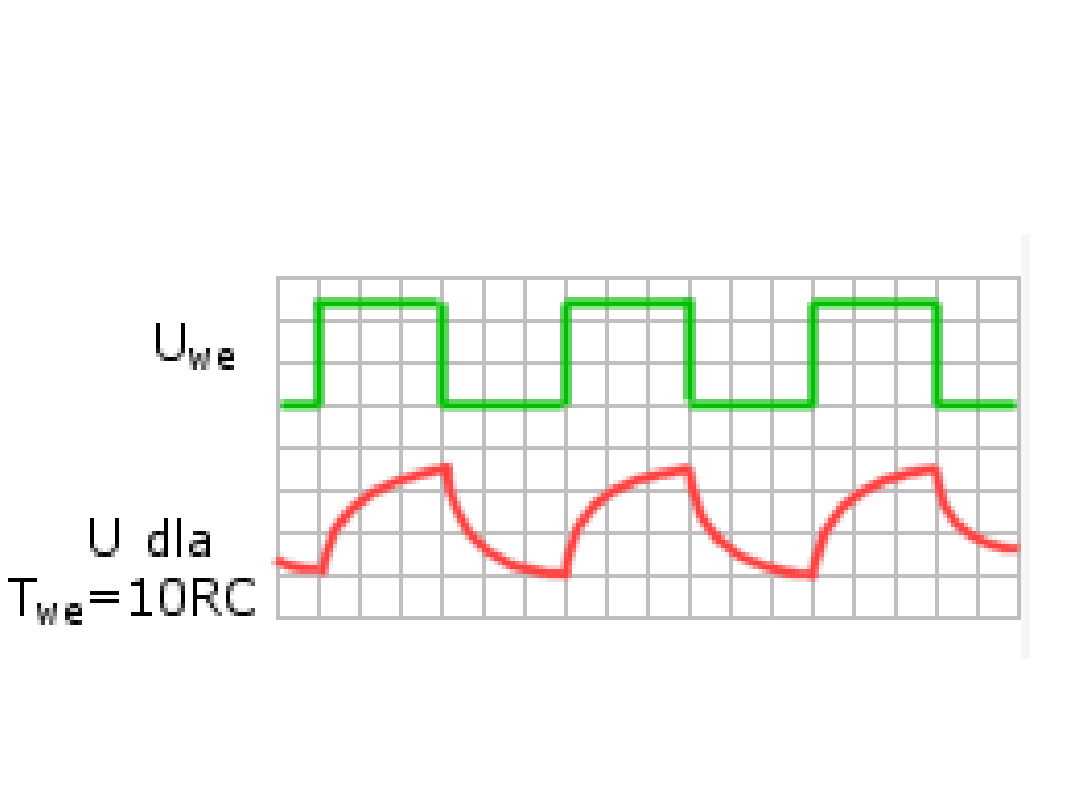
Zniekształcenia

sygnału

Zniekształcenie sygnału prostokątnego jest spowodowane istnieniem pojemności
(tutaj szkodliwej) a pojemność lubi się ładować co trwa. Czas ładowania τ = RC

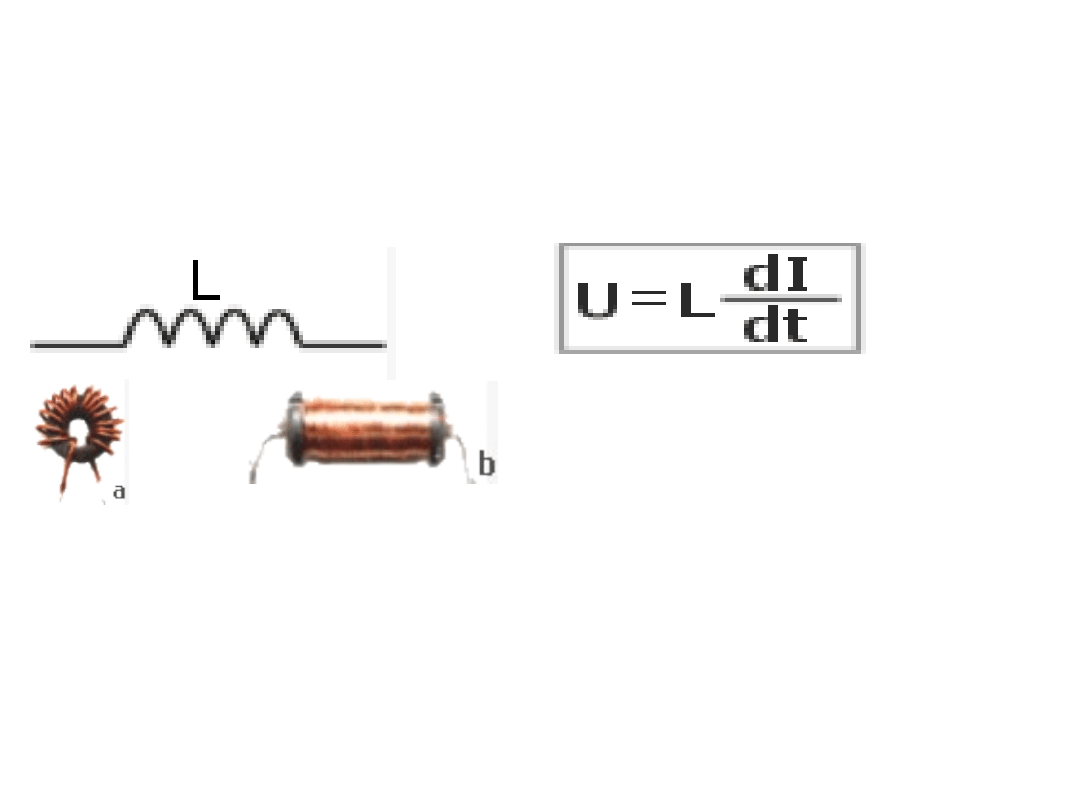
Indukcyjność

(cewka)

r
y

s
.

2

.
1
8

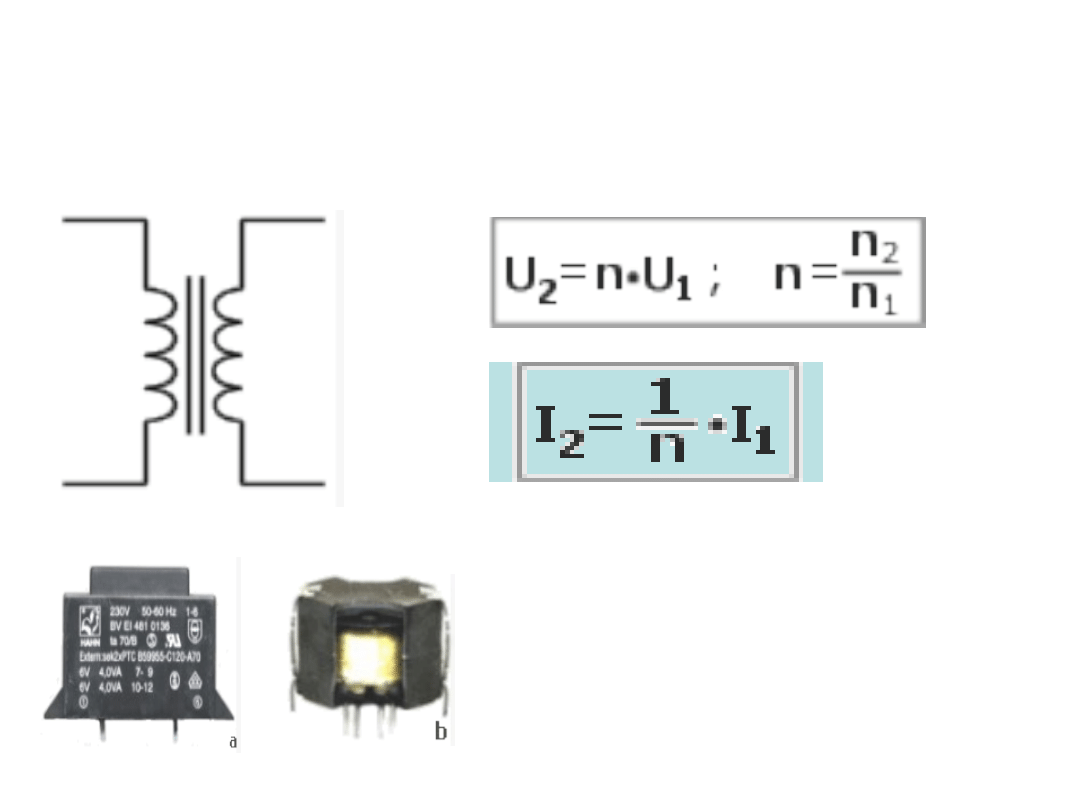
Transformator

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                                    

BEZPIECZNIKI

przeciążeniowe - przerywają obwód
elektryczny po przekroczeniu w
przewodzie określonego natężenia
prądu.
przeciwprzepięciowe - chonią
urządzenia przed przepięciami
występujacymi w sieci.
przeciw asymetrii - chroniące
urządzenia wielofazowe przed
zanikiem jednej z faz prądu
trójfazowego.
przeciwporażeniowe - chroniące
obsługę urządzeń przed porażeniem
prądem elektrycznym; coraz częściej
stosuje się bezpieczniki
różnicowo-prądowe

Wyłącznik różnicowo-prądowy (RCD) jest
to urządzenie służące do ochrony przed
porażeniem przez dotyk pośredni jak i
bezpośredni.

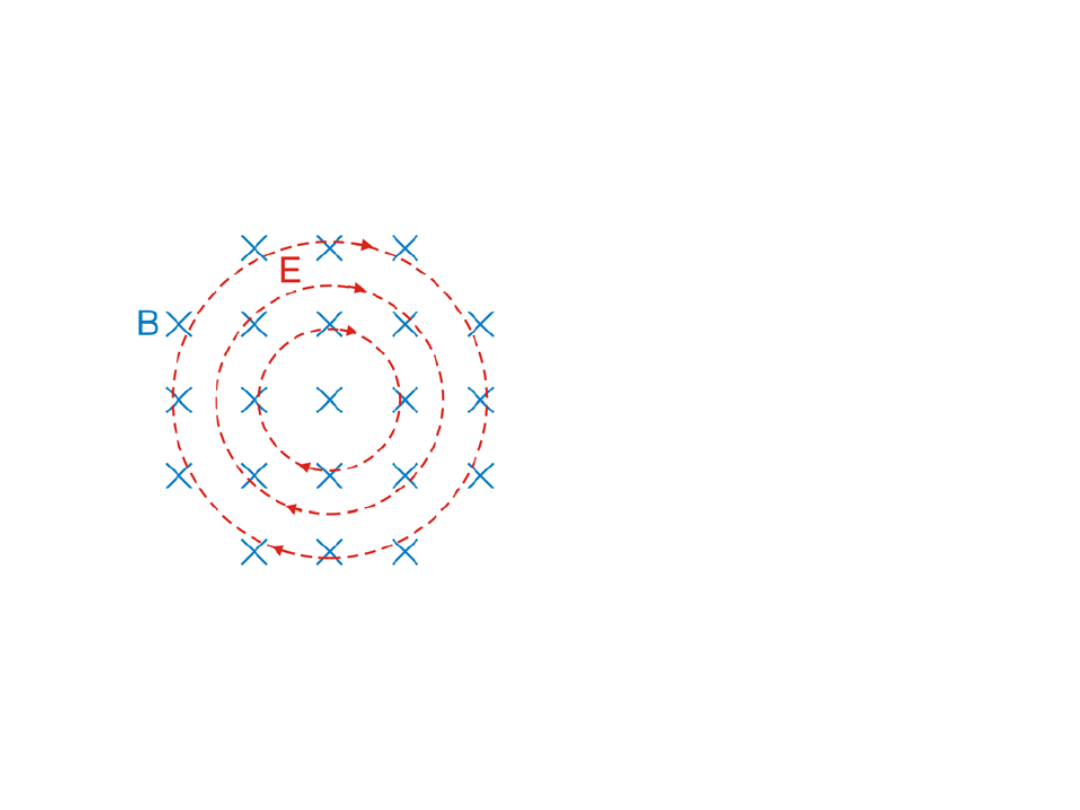
Indukowane pole

elektryczne

127

Zmianom pola
magnetycznego
towarzyszy zawsze
powstawanie pola
elektrycznego.

Jeżeli w obszarze zmieniającego się pola
magnetycznego nie ma przewodnika kołowego to nie
będziemy obserwować przepływu prądu, ale
indukowane pole elektryczne nadal istnieje. Jeżeli
znajdzie się tam przewodnik kołowy to zaindukowane
na skutek
Zmian wektora B pole elektryczne E spowoduje
przepływ ładunków

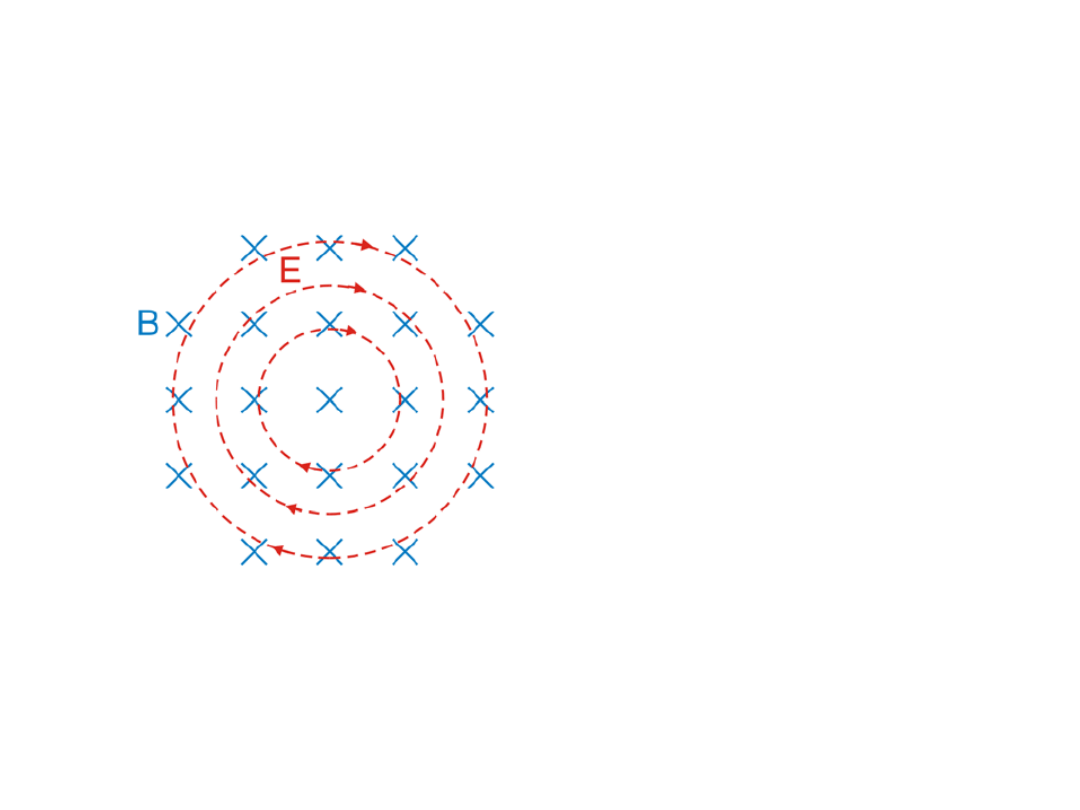
Indukowane pole

elektryczne

/

128

Linie sił pola
elektrycznego
indukowanego przez
zmienne pole
magnetyczne mają
kształt koncentrycznych
okręgów czyli w
odróżnieniu od linii sił
pola pochodzącego od
ładunków elektrycznych
są liniami zamkniętymi!

Indukowane pola elektryczne są związane ze
zmianą strumienia magnetycznego a nie z
ładunkami elektrycznymi.

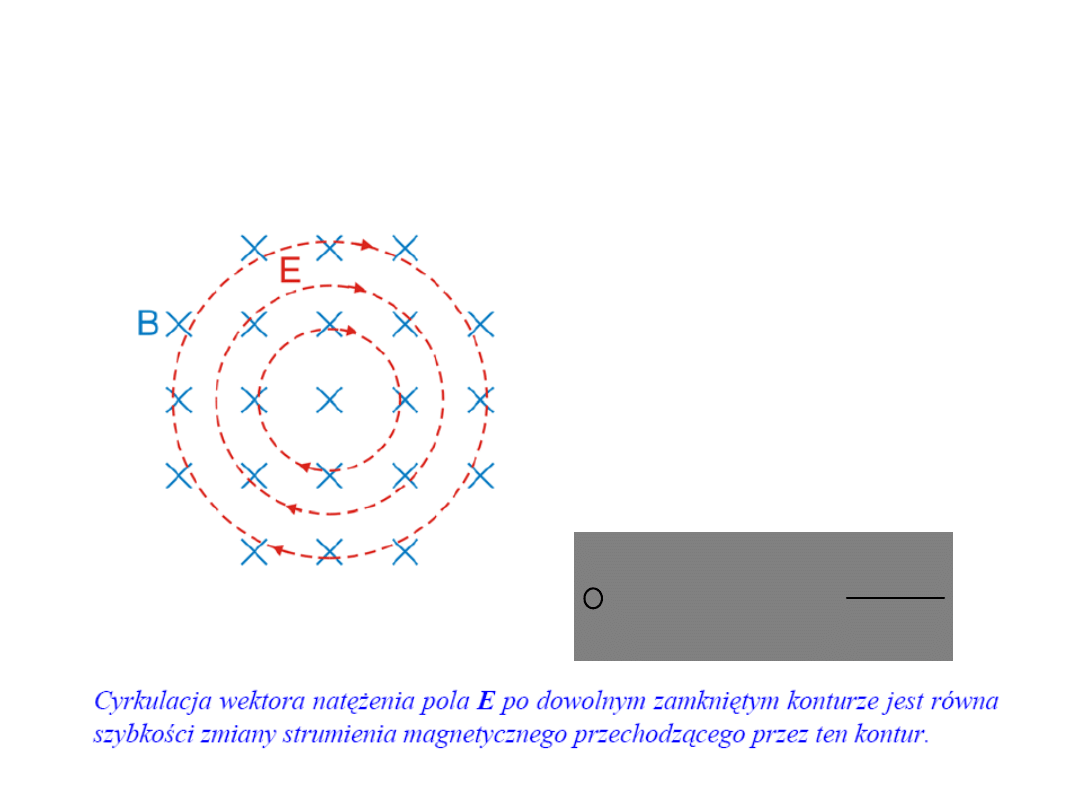
Indukowane pole

elektryczne

129

Indukowane pole
elektryczne nazywamy w
takim przypadku
wirowym polem
elektrycznym.

Stąd uogólnione prawo
indukcji Faradaya:











dt

d

Edl

B



Indukowane pole

magnetyczne

130

Zmieniające się pole
elektryczne wytwarza
zmienne pole
magnetyczne.

Stąd uogólnione prawo
Ampera:









I

dt

d

Bdl

E

0

0

0







Pole magnetyczne może być wytwarzane zarówno
przez przepływ prądu (prawo Ampera) jak i przez
zmienne pole elektryczne.

Fale elektromagnetyczne

131

Piotr Słoma CMF http://cmf.p.lodz.pl/psloma/

Prawo Gaussa dla pola elektrycznego

 
 

Ładunek wytwarza pole elektryczne o indukcji odwrotnie

proporcjonalnej do kwadratu odległości. Źródłem pola
elektrostatycznego są ładunki elektryczne – zaczynają się w nich i
kończą linie sił tego pola.







q

S

d

D





Prawo Gaussa dla pola magnetycznego

 
 

W przyrodzie nie istnieją magnetyczne odpowiedniki

ładunków elektrycznych. Linie sił pola magnetycznego są
krzywymi zamkniętymi.







0

S

d

B





Fale elektromagnetyczne

132

Piotr Słoma CMF http://cmf.p.lodz.pl/psloma/

Fale elektromagnetyczne

133

Piotr Słoma CMF http://cmf.p.lodz.pl/psloma/

Równania Maxwella opisują cały kompleks zjawisk elektromagnetycznych w

skali makroskopowej (teoria Maxwella nie obejmuje mikropól atomowych

i cząsteczkowych – poprawnie opisuje je dopiero tzw. elektrodynamika

kwantowa) ujmując w postaci jednolitej teorii wszelkie prawidłowości

zaobserwowane wcześniej i wszelkie równania, którymi opisywano

zjawiska elektryczne i magnetyczne.

Na podstawie tych równań można wykazać zarówno istnienie fal

elektromagnetycznych, jak i określić ich prędkość, która równa jest

prędkości światła. W ten sposób Maxwell pierwszy pokazał, że światło ma

naturę fali elektromagnetycznej. Istnienie fal elektromagnetycznych

zostało eksperymentalnie potwierdzone przez Hertza w 1890 roku.

Fale elektromagnetyczne

Fala elektromagnetyczna polega na rozchodzeniu się w

przestrzeni zaburzenia w postaci drgań wektorów

natężenia pola elektrycznego i magnetycznego.

Oba wektory są prostopadłe zarówno do siebie wzajemnie

jak i do kierunku rozchodzenia się fali (fala poprzeczna),

są ponadto przesunięte w fazie o /2.

134

Fale elektromagnetyczne -

właściwości

135