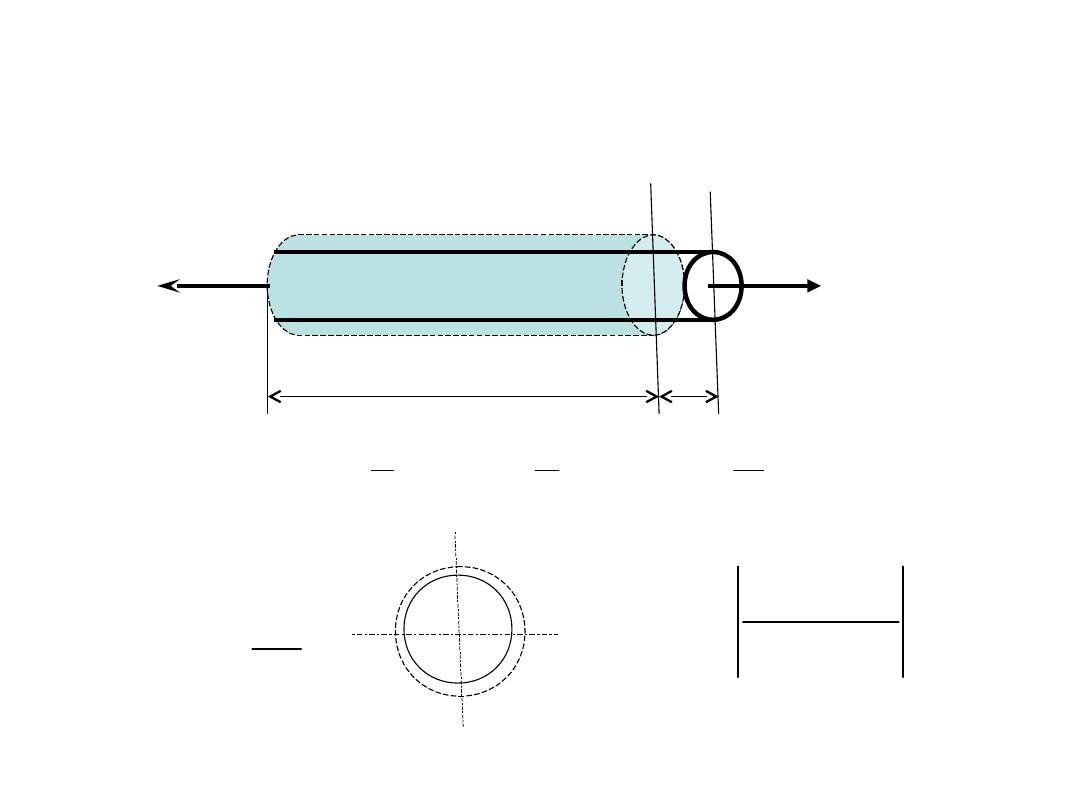
Stałe sprężyste

• Moduł Younga E

l

l

;

A

F

;

E

wzdl

















l

Δl

F

F

Liczba Poissona 

wzdl

poprzeczne









d

d

poprzeczne







0,3

stali

dla

5

,

0

0











Próby wytrzymałościowe

1) Próba rozciągania

F

F

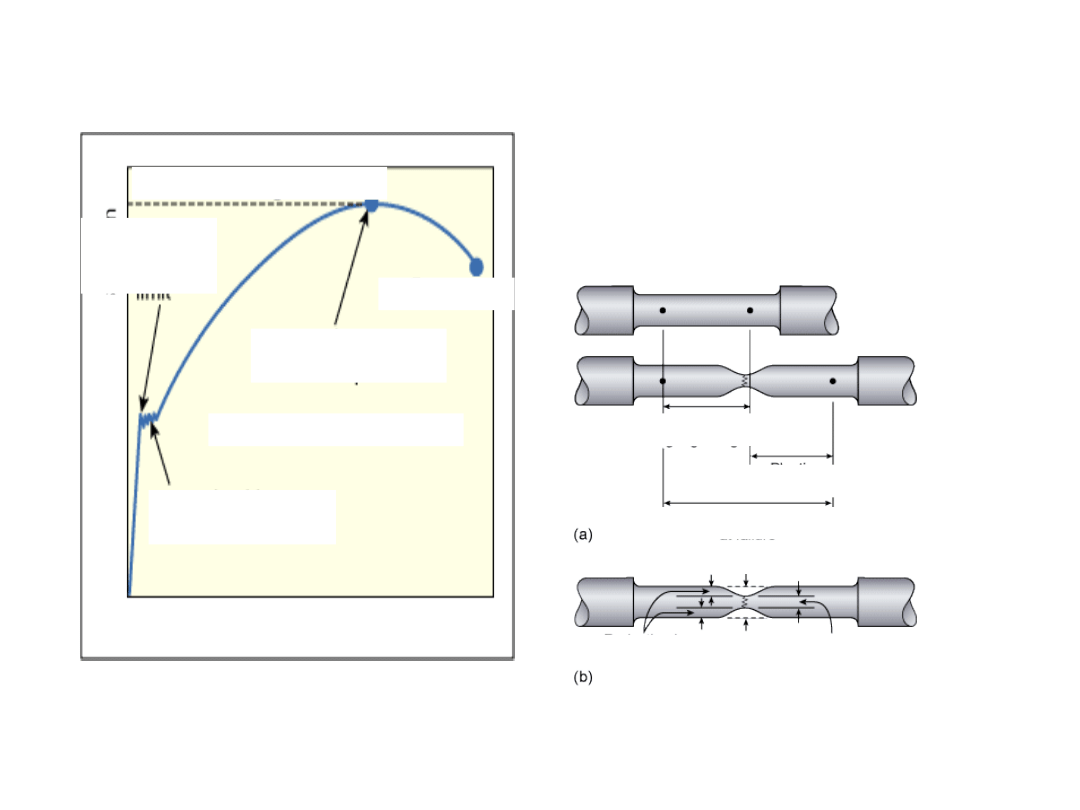
Pierwotna długość

Długość po zerwaniu

Odkształcenie trwałe

średnica początkowa

Średnica po zerwaniu

Zmiana średnicy

Wydłużenie próbki Δl

Siła maksymalna

zerwanie

„miękka” (ciągliwa) stal

pojawia się tzw.
„szyjka”

płynięcie
materiału

koniec
zakresu
sprężystego

si

ła

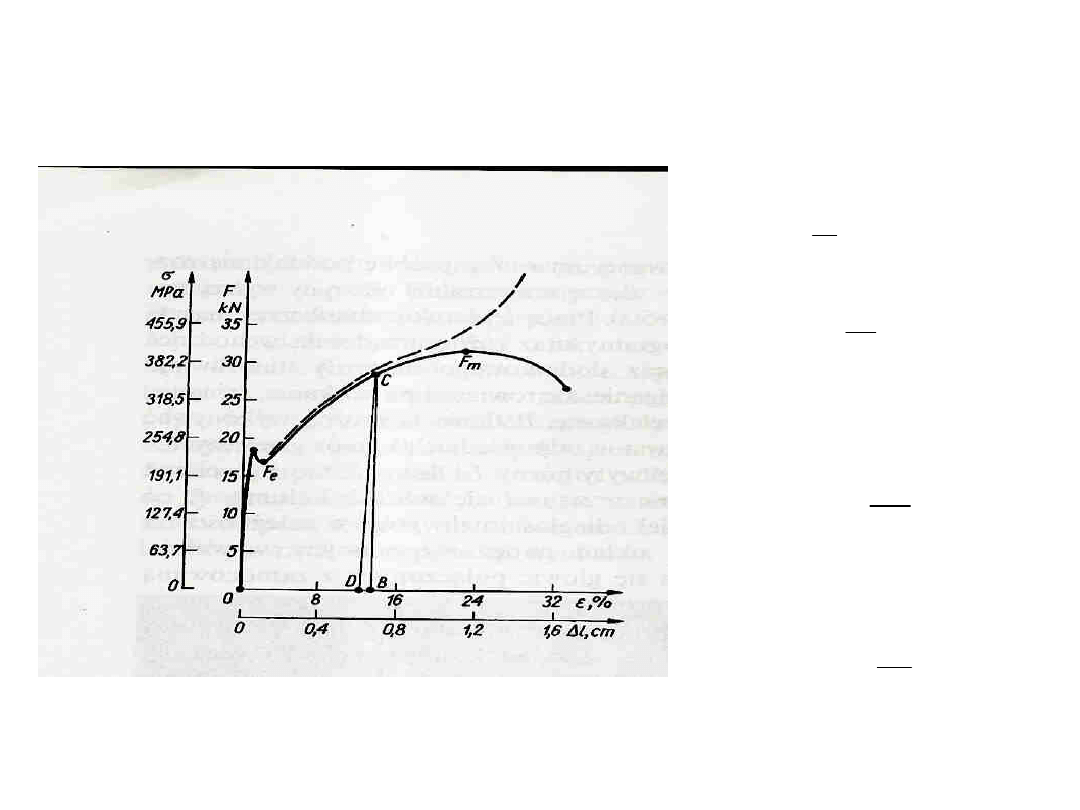
Wykres rozciągania stali miękkiej

l

l

;

A

F

wzdl











A

F

R

m

m



Wytrzymałość na rozciąganie

Wyraźna granica plastyczności

A

F

R

e

e



A – pole poczatkowego przekroju
L – długość poczatkowa

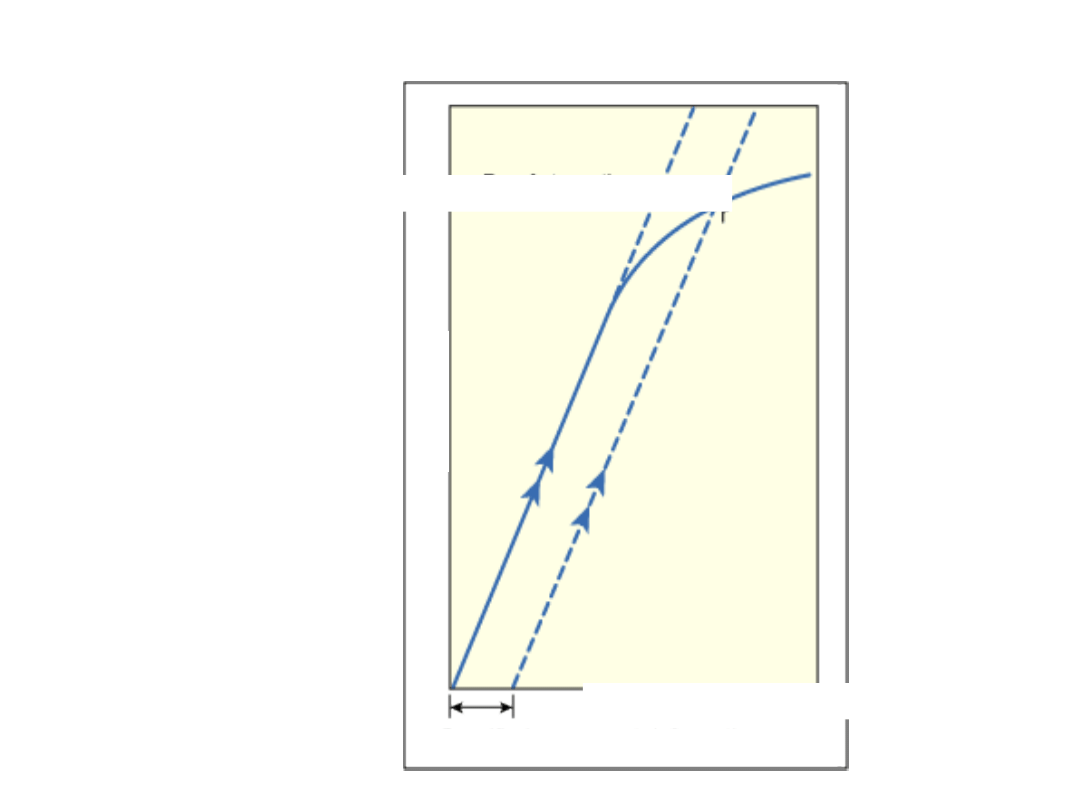
Odkształcenie względne ε %

0,2%

Umowna granica plastyczności

N

a

p

rę

że

n

ie

R

e0,2

–

umowna
granica
plastycznosci

Materiały „kruche”

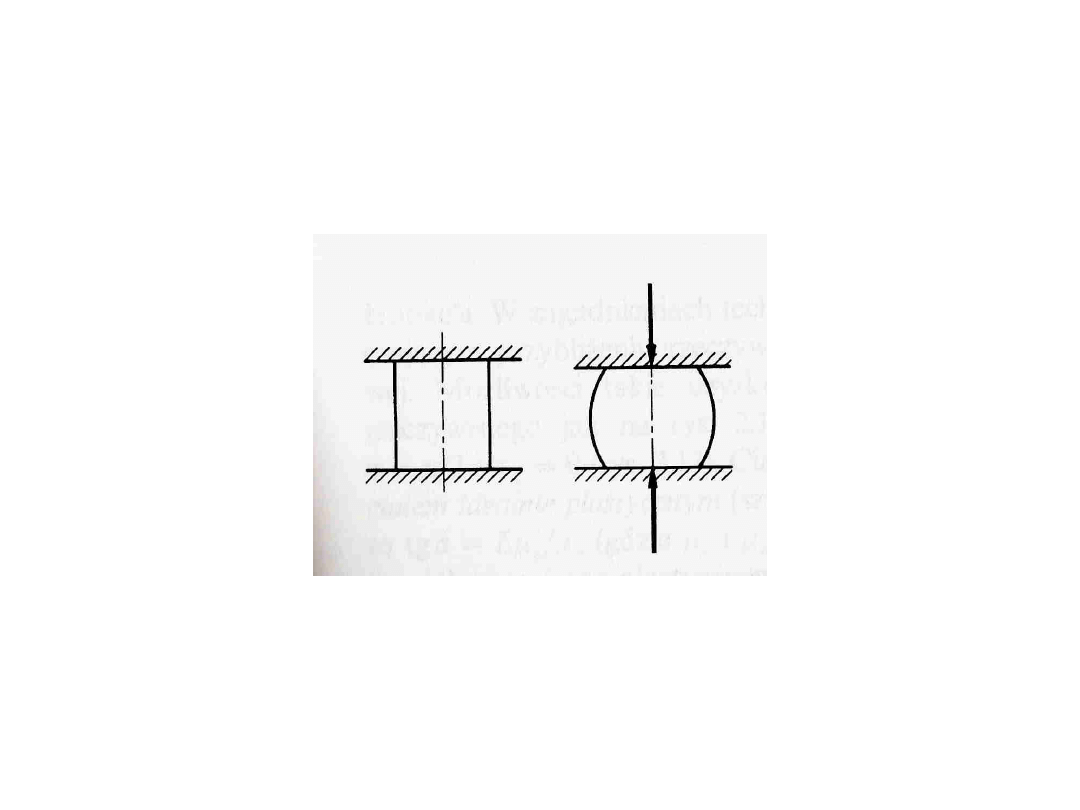
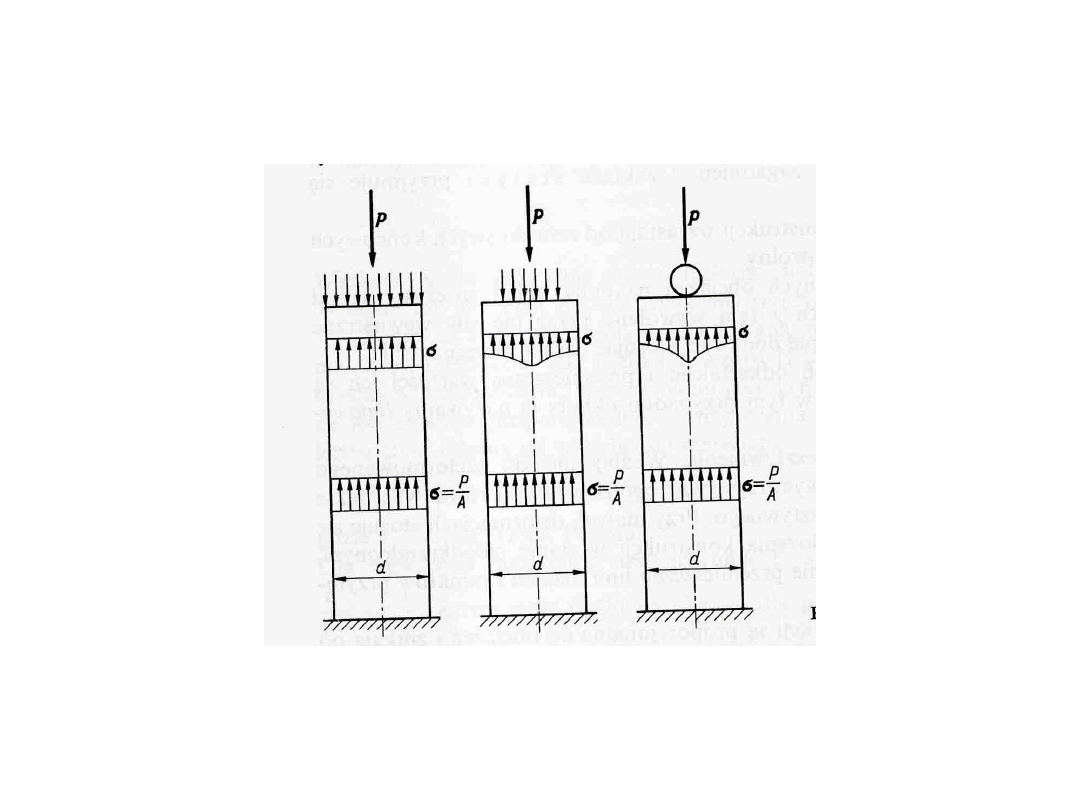
Próby ściskania

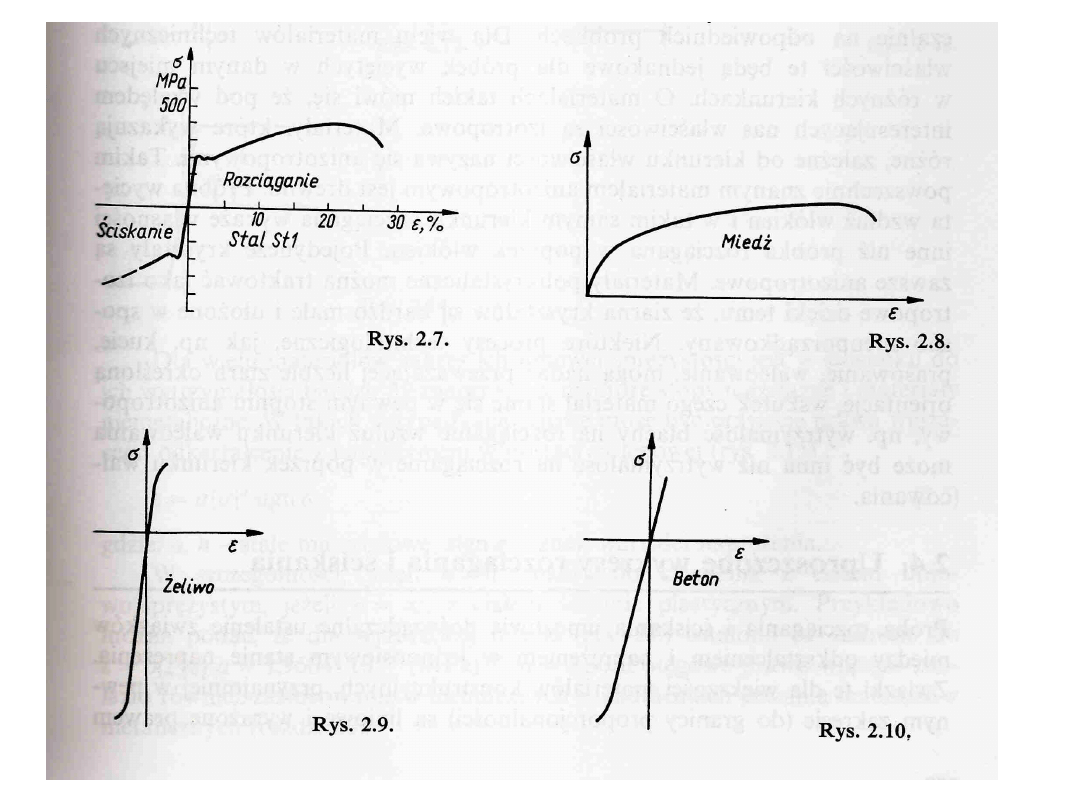
Wytrzymałość na ściskanie
- R

c

Dla stali R

c

=R

m

Dla żeliwa R

c

=5-10

R

m

Dla betonu R

c

=10-kilkadziesiąt R

m

Naprężenia dopuszczalne

n

k

zne

niebezpiec

dop





n – współczynnik bezpieczeństwa n>1

zne

niebezpiec



????

2

e

dop

1

m

dop

n

R

k

n

R

k





dop

max

k





Warunek wytrzymałościowy

Zasada de Saint – Venanta – układy równoważne

Zasada superpozycji

P

P

a

a

P

a

a

P

2a

=

+

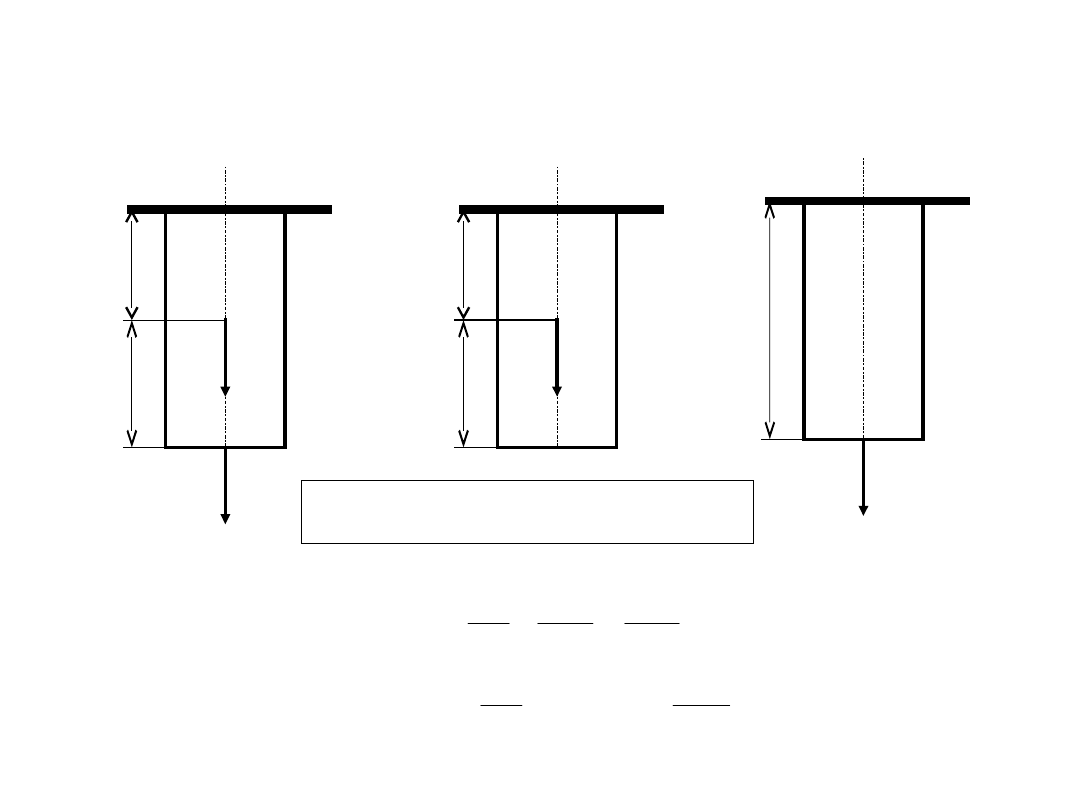
Przykład
Pręt utwierdzony o stałym polu przekroju poprzecznego A i module Younga E

2

1

2

1





















Przykład obliczeń
wydłużenie

2

1

2

1

l

l

l

EA

a

2

P

l

;

EA

Pa

l

EA

Pa

3

EA

Pa

2

EA

Pa

l



























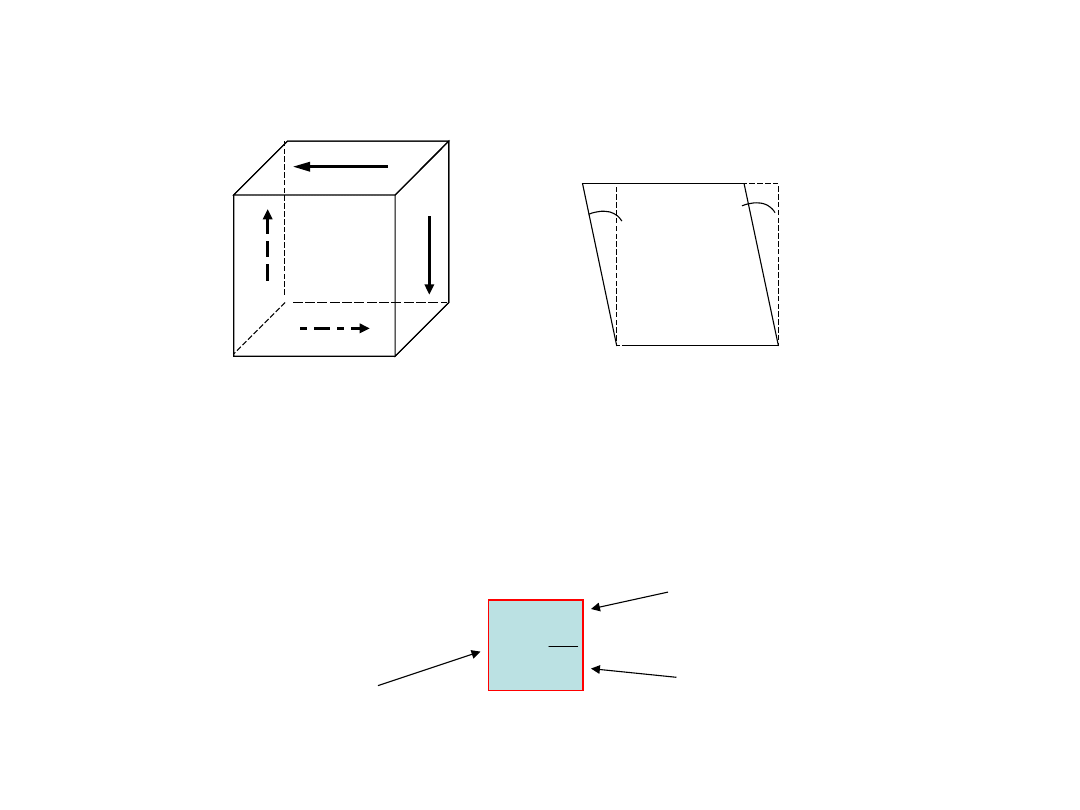
Czyste ścinanie

G





















- naprężenie styczne

 -

kąt odkształcenia postaciowego

Prawo Hooke’a dla ścinania

(rad)

(MPa)

(MPa)

Stała sprężysta G – moduł odkształcenia postaciowego (moduł Kirchhoffa)

)

1

(

2

E

G







Stała sprężysta E – moduł Younga

Stała sprężysta  – liczba Poissona

Dls stali G=8·10

4

MPa

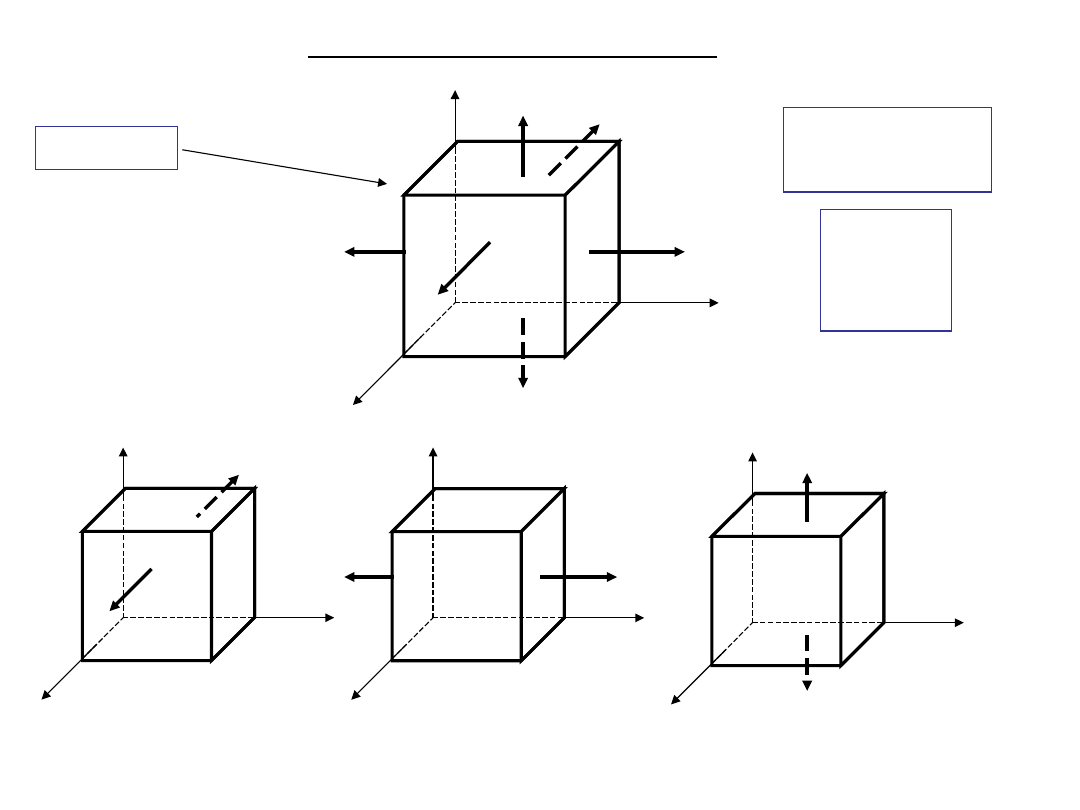
Uogólnione prawo Hooke’a

x

y

z



x



x



z



y



y



z

x

y

z



x



x

x

y

z



y



y

x

y

z



z



z

+

+

„I”

„II”

„III”

Znane E,



Dane



x

, 

y

,



z

,



x

=?



y

=?



z

=?

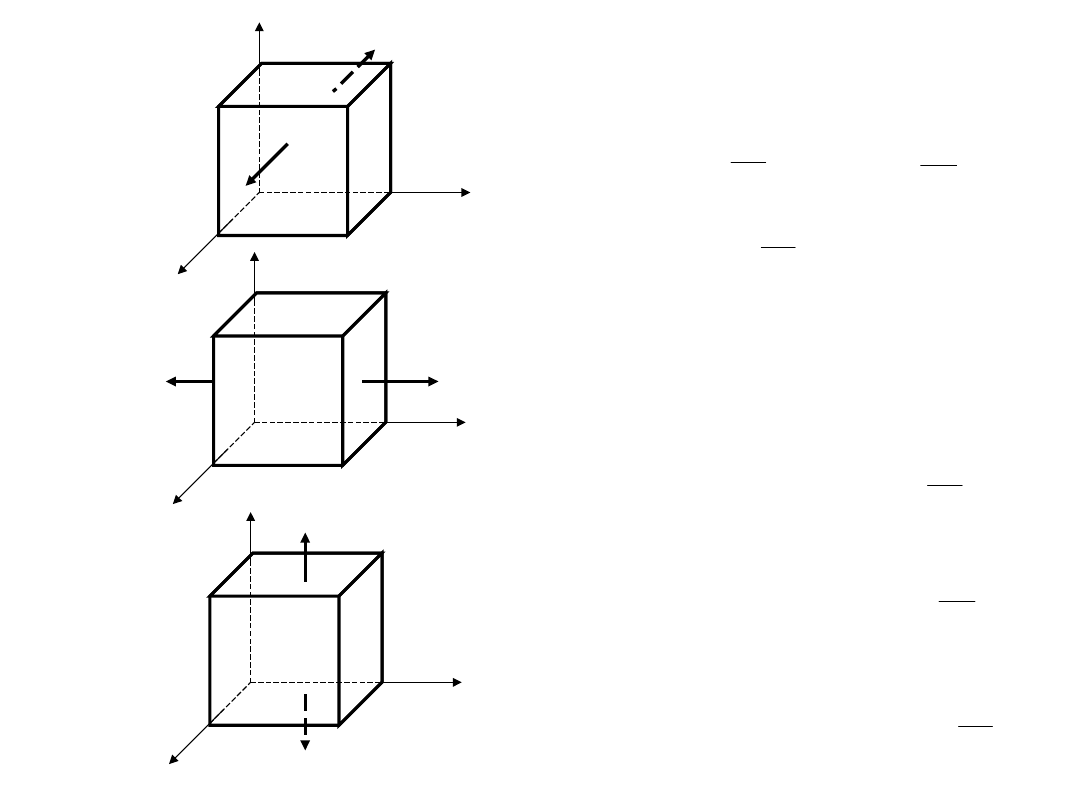
„I”

x

y

z



x



x

Zgodnie z prawem Hooke’a

dla jednokierunkowego rozciągania

x

y

z



y



y

x

y

z



z



z

„III”

„II”

E

x

"

I

"

x







E

y

"

II

"

y







E

z

"

III

"

z







Odkształcenia w kierunkach poprzecznych

do

kierunku rozciągania

Dla stanu „I”

E

x

"

I

"

x

"

I

"

z

"

I

"

y





















E

y

"

II

"

y

"

II

"

z

"

II

"

x





















Dla stanu „II”

Dla stanu „III”

E

z

"

III

"

z

"

III

"

y

"

III

"

x





















Zgodnie z zasadą superpozycji

"

III

"

"

II

"

"

I

"















W takim razie

E

E

E

E

E

E

E

E

E

y

x

z

z

x

z

y

y

z

y

x

x























































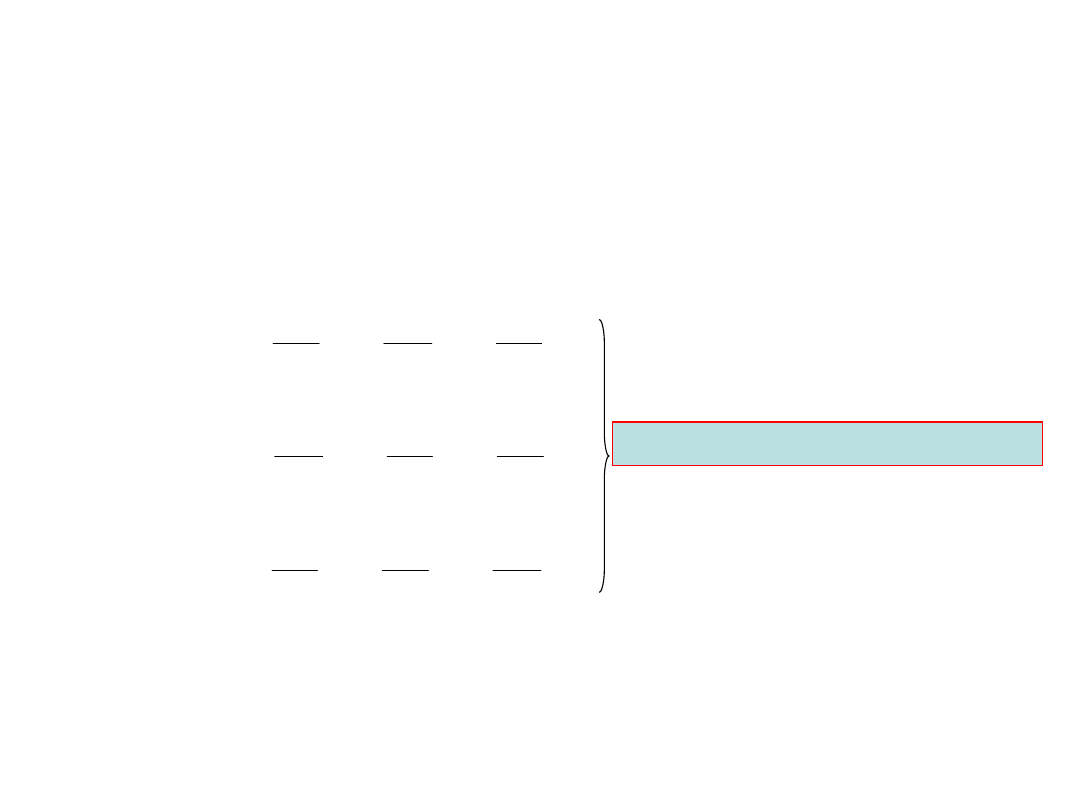
Uogólnione prawo Hooke’a

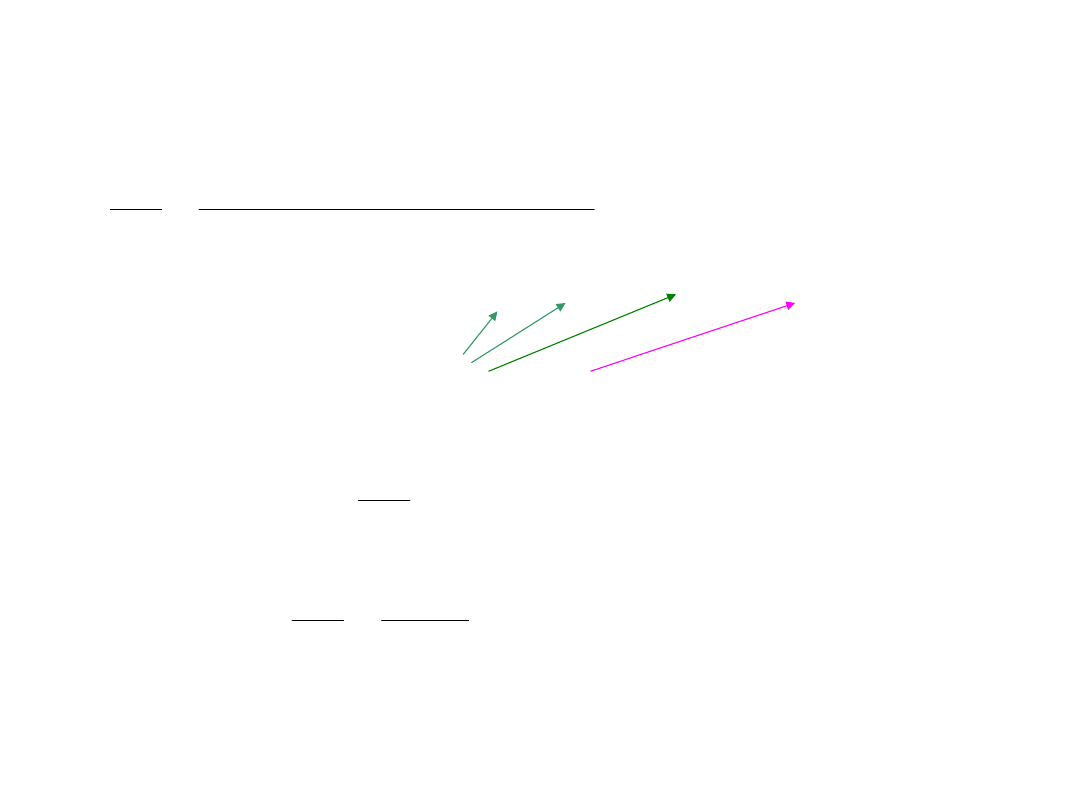
Względna zmiana objętości sześcianu o boku równym 1

1

1

1

1

)

1

)(

1

)(

1

(

V

V

z

y

x

z

y

z

x

y

x

z

y

x

z

y

x































































Po pominięciu wielkości małych drugiego i trzeciego rzędu

z

y

x

V

V















)

(

E

2

1

V

V

z

y

x



















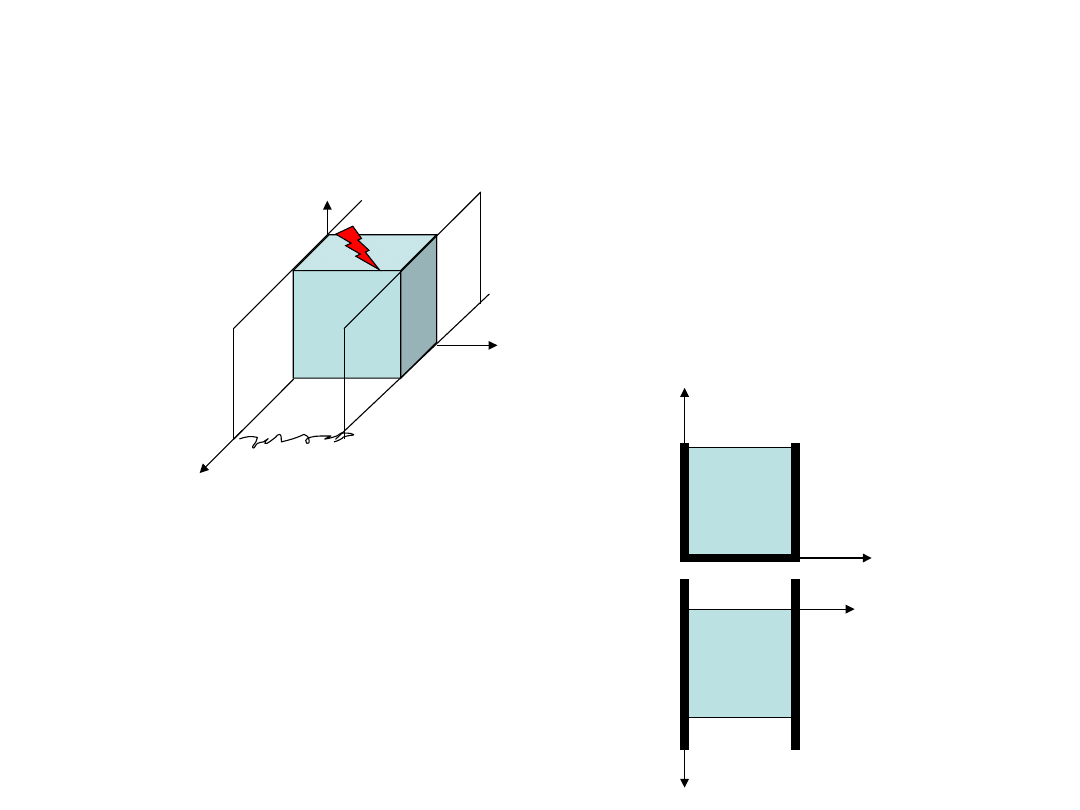
Sześcian o boku a wstawiono (bez luzu i bez wcisku) do nieodkształcalnego rowka
o szerokości a i następnie ogrzano o ΔT. Obliczyć względną zmianę objętości sześcianu,
jeśli znane są E,

, 

- współczynnik rozszerzalności liniowej.

Przykład

x

z

y

ΔT

x

z

y

y

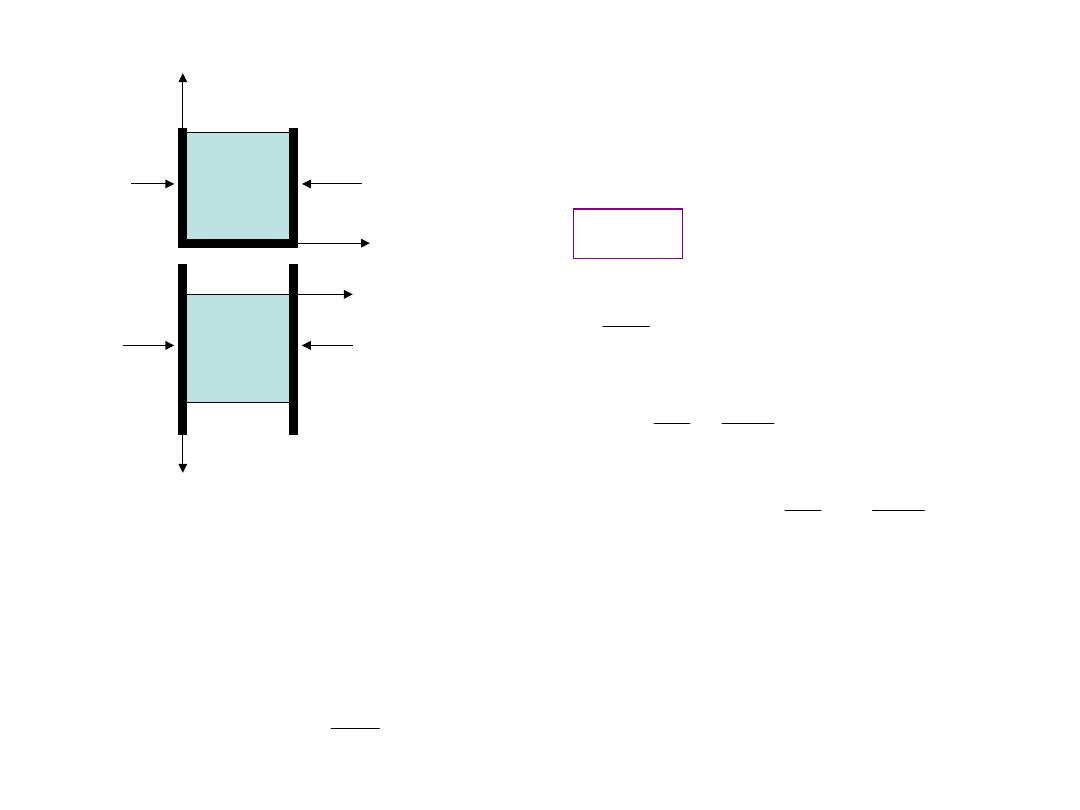
x

z

y

y

T

a

a

a

a

t

z

t

y

t

x

























Odkształcenia termiczne

0

a

y





R

R

R

R

T

E

a

a

0

a

y

t

y

mech

y

y





























0

;

a

R

z

x

2

y















;

E

a

R

E

;

E

a

R

E

2

y

mech

z

mech

x

2

y

mech

y





























T

)

1

(

2

V

V











