Politechnika Lubelska
Katedra Sieci Elektrycznych i
Zabezpieczeń

Dr hab. inż. Piotr Kacejko, prof. PL

Zwarcia - przykłady obliczeń

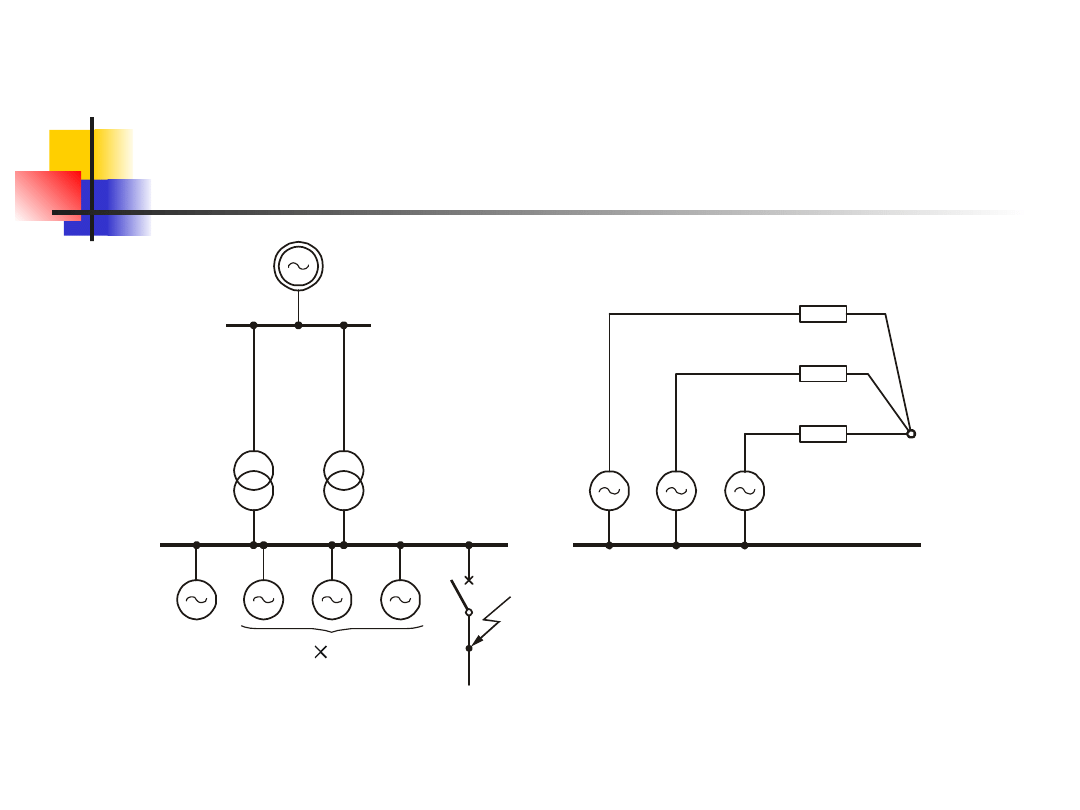
Dla podanej sieci należy wyznaczyć
charakterystyczne prądy podczas trwania
zwarcia w punkcie F. Przyjąć czas trwania zwarcia
t

K

=0,1s.

a )

T 1

T 2

L 1

L 2

Q

b )

F

M 1

3 M 2

Z

M 1

Z

M 2

Z

G

F

Schemat do przykładu: a) analizowanej sieci;
b) zastępczy zredukowany sieci składowej zgodnej

Dane elementów sieci:

System zastępczy 110 kV:

1

,

0

/

MVA;

2750

Q

Q

"

KQ





X

R

S

Linie kablowe L1,L2: parametry jednostkowe

km.

85

,

4

/km;

0,1

x

/km;

1

,

0

L

L











l

r

Transformatory T1,T2:

%

6

,

0

%;

11

kV/kV;

115/6,6

MVA;

16

Kr

K

r

rT









u

u

t

S

Silnik Ml

.

2

biegunów

par

liczba

;

4

/

;

97

,

0

;

86

,

0

cos

kV;

6

MW;

5

rM

LR

1

M

1

1

rM

1

rM













p

I

I

U

P

M





Silnik M2 (3 szt.):

.

1

biegunów

par

liczba

;

5

,

5

/

;

94

,

0

;

83

,

0

cos

kV;

6

MW;

1

rM

LR

r

2

2

rM

2

rM













p

I

I

U

P

M





Reaktancje elementów sieci i prąd początkowy I”

K



































016

,

0

115

6,6

2750

110

1,1

2

2

2

HV

rT

LV

rT

"

KQ

2

rQ

'

Q

U

U

S

cU

X





0016

,

0

'

Q

R

(metoda IEC zezwala na przyjęcie

Q

Q

1

,

0 X

R 

przy braku innych danych —

dotyczy to sieci o napięciu poniżej 35 kV, powyżej można przyjmować

0

Q



R

)







































































01

,

0

16

6

,

6

100

0,6

100

285

,

0

16

6

,

6

100

5

,

10

100

0016

.

0

0016

,

0

115

6

,

6

1

,

0

85

,

4

2

rT

2

LV

rT

K

1

T

2

rT

2

LV

rT

K

1

T

'

2

L

'

L1

2

2

HV

rT

LV

rT

'

2

L

'

1

L

S

U

u

R

S

U

u

X

R

R

U

U

x

l

X

X

R

L

Reaktancje elementów sieci i prąd początkowy I”

K

























16

,

0

285

,

0

0016

,

0

2

1

016

,

0

2

1

1

T

'

1

L

'

Q

KS

X

X

X

X

























0074

,

0

01

,

0

0016

,

0

2

1

0016

,

0

2

1

1

T

'

1

L

'

Q

KS

R

R

R

R

kA

8

,

23

16

,

0

3

6

1

,

1

3

KS

"

KS











X

cU

I

n

"

2

KM

"

1

KM

"

KS

"

K

I

I

I

I







Reaktancje elementów sieci i prąd początkowy I”

K













5

,

1

6

6

4

1

/

1

2

1

M

2

M

M

1

M

r

r

r

LR

S

U

I

I

Z

MVA

6

97

,

0

86

,

0

5

cos

1

M

1

M

1

M

1

M















r

r

P

S

















705

,

1

28

,

1

6

5

,

5

3

1

3

1

2

2

M

2

M

M

2

M

r

r

r

LR

S

U

/I

I

Z

MVA

28

,

1

cos

2

M

2

M

2

M

2

M











r

r

P

S

Reaktancje elementów sieci i prąd początkowy I”

K

kA

23

,

2

705

,

1

3

6

1

,

1

3

kA

54

,

2

5

,

1

3

6

1

,

1

3

2

M

"

2

KM

1

M

"

1

KM





















Z

cU

I

Z

cU

I

n

n

kA

6

,

28

23

,

2

54

,

2

8

,

23

"

KM2

"

KM1

"

KS

"

K















I

I

I

I

Prąd wyłączeniowy I

B

Dla sieci zewnętrznej, w której nie ma wyróżnionych żadnych źródeł można
zgodnie z IEC 60909 przyjąć, że I

BS

= I”

KS

czyli pominąć efekt zanikania.

"

2

KM

2

M

2

M

2

BM

"

1

KM

1

M

1

M

1

BM

I

q

I

I

q

I









współczynnik

s

1

,

0

czasu t

dla

K













72

,

0

/

32

,

0

exp

72

,

0

62

,

0

80

,

0

/

32

,

0

exp

72

,

0

62

,

0

2

"

2

2

M

1

"

1

K

M1

















rM

KM

rM

M

I

I

I

I





Prąd wyłączeniowy I

B

57

,

0

0

,

1

ln

12

,

0

57

,

0

ln

12

,

0

57

,

0

67

,

0

5

,

2

ln

12

,

0

57

,

0

ln

12

,

0

57

,

0

2

M

2

M

1

M

1

M





















m

q

m

q

kA

91

,

0

41

,

0

57

,

0

72

,

0

kA

38

,

1

536

,

0

67

,

0

8

,

0

"

2

KM

"

2

KM

2

BM

"

1

KM

"

1

KM

1

BM

















I

I

I

I

I

I

kA

1

,

26

91

,

0

38

,

1

8

,

23

2

BM

BM1

BS

B















I

I

I

I

Współczynniki q dla t

K

= 0,1s

Ustalony prąd zwarcia I

K

kA

8

,

23

"

KS

K



I

I

Prąd udarowy i

p

0462

,

0

16

,

0

0074

,

0

S

S





X

R









kA

75

,

62

8

,

23

87

,

1

2

2

87

,

1

0462

,

0

3

exp

98

,

0

02

,

1

3

exp

98

,

0

02

,

1

"

KS

pS

S

S





























I

i

X

R

s

s





2

pM

1

pM

pS

p

i

i

i

i







Prąd udarowy i

p

kA

53

,

5

2

kA

26

,

6

54

,

2

75

,

1

2

2

"

2

KM

2

M

2

pM

"

1

KM

1

M

1

pM















I

i

I

i





kA

54

,

74

53

,

5

26

,

6

75

,

62

2

pM

1

pM

p

p















i

I

i

i

S

Dla obydwu silników m≥1 MW, zatem R

M

/X

M

=0,1

Składowa nieokresowa (aperiodyczna) prądu
zwarcia i

dc





Q

K

"

KQ

dcQ

exp

2

/T

-t

I

i







1

Q

Q

Q

/

2





X

fR

T



:

- zewnętrzna sieć zasilająca

s;

069

,

0

)

0462

,

0

50

2

(

1

aS













T

- silniki M1, M2





M

2

M

1

1

M

s

032

,

0

1

,

0

50

2

a

a

a

T

T

T

















(dla silników indukcyjnych

MW

1

gdy

,

1

,

0

/





m

X

R

).

























kA

14

,

0

032

,

0

/

1

,

0

exp

24

,

2

2

/

exp

2

kA

16

,

0

032

,

0

/

1

,

0

exp

54

,

2

2

/

exp

2

kA

88

,

7

069

,

0

/

1

,

0

exp

8

,

23

2

/

exp

2

M

K

"

2

KM

2

dcM

M

K

"

1

KM

1

dcM

S

K

"

KS

dcS











































a

a

a

T

t

I

i

T

t

I

i

T

t

I

i

kA

18

,

8

14

,

0

16

,

0

88

,

7

2

dcM

1

dcM

dcS

dc















i

i

i

i

Dla czasu t

K

=0,1s

Składowa nieokresowa (aperiodyczna) prądu
zwarcia i

dc

2

2

B

asym

B

dc

i

I

I





kA

35

,

27

18

,

8

1

,

26

2

2

asym

B







I

Prąd zwarciowy wyłączeniowy
niesymetryczny

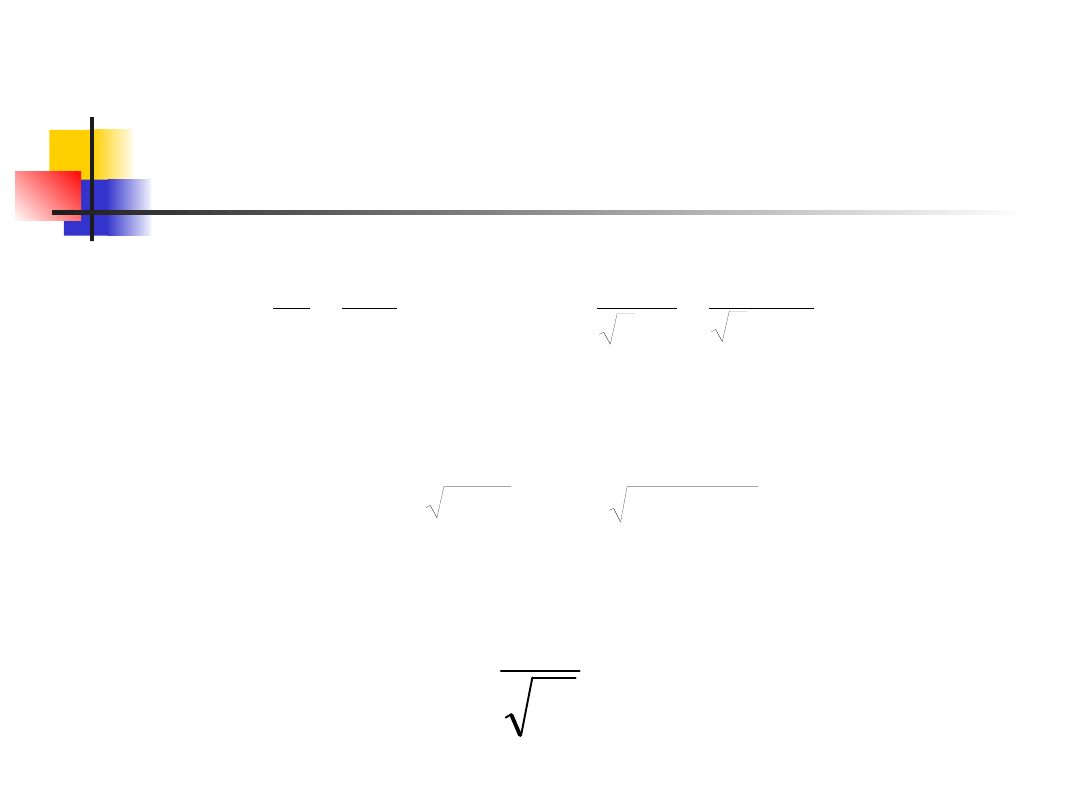
Zwarciowy prąd cieplny I

th

81

,

1

8

,

23

2

54

,

74

2

2

,

1

8

,

23

6

,

28

"

K

p

K

"

K















I

i

I

I





Charakterystyczne parametry dla

K

t = 0,1 s wynoszą m = 0,58, n = 0,98, czyli

kA

7

,

35

98

,

0

58

,

0

6

,

28

"

K

th













n

m

I

I

K

1

thr

th

1

t

I

I



