Systemy informatyczne

zarządzania

W.
Bartkiewicz

Wykład 8. Systemy Wspomagania Decyzji

•

Omawiane w wcześniej kategorie systemów informatycznych

koncentrują się przede wszystkim na zaspokajaniu potrzeb

informacyjnych decydentów, usprawniając prace związane z

ewidencją

i

przetwarzaniem

danych

transakcyjnych

przedsiębiorstwa.

•

Kolejny krok na drodze informatycznego wspomagania procesu

zarządzania związany jest ze wspomaganiem samego procesu

podejmowania

decyzji,

z

wykorzystaniem

Systemów

Wspomagania Decyzji (DSS – Decision Support Systems).

•

Systemy Wspomagania Decyzji są zorganizowanym zbiorem

ludzi, procedur, baz danych i urządzeń wykorzystywanych w celu

wspomagania podejmowania decyzji na wszystkich etapach tego

procesu, poczynając od rozpoznania czyli zdefiniowania

problemu

i zaklasyfikowania

go

do

określonej

grupy

standardowej, następnie poprzez wybór odpowiednich danych

stworzenie i analizę modelu informacyjnego opisującego

rzeczywistość, dalej pomagając w generowaniu wariantów

dopuszczalnych rozwiązań oraz w wyborze najlepszego

rozwiązania.

Pojęcie systemu DSS

•

DSS stosowane są w sytuacji gdy podjęcie decyzji jest zadaniem

skomplikowanym, gdy mamy do czynienia z problemami słabo

ustrukturalizowanymi. Systemy te skupiają więc uwagę na

wspomaganiu, a nie automatyzacji decyzji. Tym samym ich

celem jest podnoszenie skuteczności a nie sprawności

zarządzania.

•

W szczególności DSS pozwalają na realizację następujących

zadań:

– wyszukiwanie danych jednostkowych, czyli wyodrębnionych ze

zbiorów danych,

– swobodny dostęp do danych oraz ich analizę przyczynowo-

skutkową,

– dostarczanie danych zbiorczych wcześniej zdefiniowanych,
– przygotowywanie projektów możliwych decyzji,
– przedstawienie konsekwencji (ocenę) proponowanych decyzji przy

wykorzystaniu modeli obliczeniowych i symulacyjnych: "co - jeżeli?",

– określanie danych problemu niezbędnych do realizacji określonego

celu: wykonywanie analiz sterowanych celami

– wybranie wariantu decyzji na podstawie zadanych kryteriów.

Pojęcie systemu DSS

• Analizując zadania DSS, możemy powiedzieć, że są to systemy

informatyczne, które wspomagają decydentów w słabo
ustrukturalizowanym

środowisku

decyzyjnym

przy

wykorzystaniu analitycznych modeli decyzyjnych z dostępem do
baz danych.

• Biorąc pod uwagę powyższe cele Systemów Wspomagania

Decyzji, możemy sformułować kilka cech tej klasy systemów:

– Zakres zastosowań. DSS koncentrują się wspomaganiu

rozwiązywania rzeczywiście powstających problemów decyzyjnych.
Są wyspecjalizowane w kierunku i tylko w kierunku podejmowania
ściśle określonych decyzji.

– DSS koncentruje się więc na konkretnym problemie, w

przeciwieństwie np. do systemów MIS, dostarczających informacji
wspomagających kompleksowo proces zarządzania daną dziedziną.

– W konsekwencji DSS wspiera przede wszystkim pojedynczych

decydentów i niewielkie grupy, a dopiero w dalszej kolejności całą
organizację.

Cechy DSS

– Konieczność

wykonywania

skomplikowanych,

wyrafinowanych

analiz

i

porównań,

przy

wykorzystaniu

zaawansowanych

pakietów

oprogramowania. Zadania stawiane DSS wymagają
zwykle zastosowania znacznie bardziej skomplikowanych
algorytmów działania niż w przypadku tradycyjnie
rozumianego przetwarzania danych.

– W związku z tym tworzone są one często w

specjalistycznych

środowiskach

programistycznych

dostarczających odpowiednich procedur obliczeniowych
(takich jak np. SAS, Matlab, czy nawet w prostszych
przypadkach MS Excel).

– DSS może również stanowić platformę integrującą dla

samodzielnych zewnętrznych programów analitycznych.

Cechy DSS

– Możliwość przetwarzania dużych ilości danych. DSS nie jest

systemem przetwarzania danych masowych w tradycyjnym tego
słowa znaczeniu.

– Wiele z nich jednak wyposażonych jest w możliwości

przeszukiwania obszernych baz danych, co pozwala na integrację
tradycyjnego

przetwarzania

danych

z

metodami

badań

operacyjnych, ułatwiając kadrze menedżerskiej stosowanie
ilościowych technik zarządzania.

– Należy ponadto zwrócić uwagę, że możliwości gromadzenia

obszernych zbiorów danych oferowane przez współczesną
technologię informatyczną nie do końca idą w parze z
możliwościami ich interpretacji i wykorzystania. Fakt ten
uznawany jest obecnie za jedno z najistotniejszych „wąskich
gardeł” w procesie rozwoju cywilizacyjnego.

– DSS wyspecjalizowane w analizie dużych zbiorów danych,

określane jako systemy „eksploracji danych” (data mining)
stanowią jedną z najbujniej rozwijających się dziedzin informatyki.

Cechy DSS

– Pobieranie i przetwarzanie danych z różnych źródeł.

Niektóre dane mogą rezydować w bazach danych na
komputerach osobistych, kolejne mogą być ulokowane w
innych systemach operacyjnych lub sieciowych.

– Dane mogą być przechowywane również w arkuszach

kalkulacyjnych, lub innych specyficznych formatach,
związanych z np. oprogramowaniem analitycznym.

– DSS powinien mieć możliwości, pozwalające na integrację

danych z jak największej liczby źródeł.

Cechy DSS

– Tworzenie raportów i elastyczność prezentacyjna. Jedną z

przyczyn powstania DSS był fakt, że systemy transakcyjne i
systemy informatyczne zarządzania nie były dostatecznie
elastyczne do zaspokojenia wszystkich potrzeb informacyjnych
i problemów decydentów. Wyjściami z tego typu systemów są
zwykle drukowane raporty o ustalonej strukturze i formacie.

– W przypadku Systemów Wspomagania Decyzji menedżerowie

mogą otrzymać informację, jakiej potrzebują, w formacie
dostosowanym do ich indywidualnych wymagań.

– DSS opierają się przede wszystkim na interakcyjnych raportach

na ekranie komputera, pozwalających na nawiązanie dialogu z
użytkownika z systemem i współprace z nim w trybie on-line.

– W zależności od preferencji osoby rozwiązującej problem

wyjście może być prezentowane oczywiście również w formie
drukowanej, ale zasadniczo DSS są zorientowane ekranowo.

Cechy DSS

– Orientacja tekstowa i graficzna. Sposób prezentacji

informacji wyjściowych w DSS mogą zwykle jest bardzo
elastyczny. Obejmuje on zarówno w format tekstowy, jak i
graficzny (a coraz częściej również multimedialny).
Współczesne DSS mogą tworzyć informacje tekstowe,
tabelaryczne, wykresy liniowe, kołowe, linie trendu, itd.

– Stosowanie elastycznej techniki prezentacyjnej pozwala

decydentom na lepsze zrozumienie sytuacji i łatwiejszą
interpretację wyników działania systemu.

– Elastyczność i adaptacyjność. Systemy Wspomagania

Decyzji dostosowują się do zmian, jakie zachodzą w
otoczeniu decydenta, umożliwiając indywidualne podejście
do problemu decyzyjnego.

– Użytkownik często ma możliwość ingerencji w strukturę

wewnętrzną DSS i konfigurowania jej w zależności od swoich
indywidualnych potrzeb i uwarunkowań sytuacji decyzyjnej.

Cechy DSS

• Oczywiście nie wszystkie Systemy Wspomagania Decyzji

odpowiadają

wszystkim

wyżej

wymienionym

charakterystykom. Ponieważ tworzone są one na potrzeby
konkretnych

problemów

decyzyjnych,

stopień

ich

zaawansowania zależy w dużym stopniu od samego
problemu jak i potrzeb decydenta.

• W wielu przypadkach Systemy Wspomagania Decyzji mają

mniejszy

zakres,

posiadając

jedynie

wybrane

z

wymienionych właściwości. Przy budowie lub wyborze
gotowego DSS zyski z jego właściwości powinny być w
równowadze z kosztami systemu, jego złożonością i
stopniem kontroli nad nim.

• Wyrafinowany DSS może być bardzo skomplikowany,

podczas gdy inny, zaimplementowany np. w postaci
modelu w arkuszu kalkulacyjnym może być bardzo prosty.

Cechy DSS

• Systemy Wspomagania Decyzji tworzone są z myślą o

rozwiązywaniu konkretnych indywidualnych problemów. W

związku z tym trudno jest mówić o jakimś uniwersalnym

jednolitym wzorcu ich budowy. DSS mają silnie zróżnicowaną

strukturę wewnętrzną, w zależności od problemu dla którego

zostały one stworzone, oraz preferencji użytkownika odnośnie

działania systemu.

• Tym niemniej możemy wyróżnić pewien ramowy schemat ich

budowy,

obejmujący

zwykle

kilka

standardowych

podsystemów:

– Baza danych zawiera aktualne dane dotyczące działalności

organizacji i jej otoczenia. Z tego powodu możemy czasami

mówić o bazie danych wewnętrznych i zewnętrznych organizacji.

Dane wewnętrzne pochodzą przede wszystkim z baz danych

transakcyjnych oraz innych systemów informatycznych. Dane

zewnętrzne pochodzą zwykle od otoczenia gospodarczo-

politycznego organizacji. Działanie DSS w sposób kluczowy

zależy od jakości danych, tak więc powinny być one uważnie

kontrolowane.

Struktura DSS

– Baza modeli składa się z wielu modułów, z których każdy

zawiera opis odpowiednich zachowań związanych z daną sytuacją

decyzyjną. Modele te wspierają podejmowanie decyzji na różnych

poziomach zarządzania w zakresie różnych funkcji kierowniczych

i w różnych dziedzinach działalności obiektu. Z tego powodu

ważne jest zapewnienie szczególnie dla tego elementu DSS

możliwości ciągłej modyfikacji i rozbudowy. Ta część systemu

decyduje bowiem o rzeczywistych możliwościach całego systemu.

– Podsystem symulacyjno-decyzyjny na podstawie żądań

użytkownika oraz istniejących danych dokonuje wyboru

kombinacji modeli niezbędnych do rozwiązania zadania, wyboru

danych wejściowych dla tych modeli, oraz wykonuje z ich pomocą

niezbędne obliczenia. Zauważmy że przepływy informacyjne tego

podsystemu z bazą danych mają charakter dwukierunkowy. Może

on nie tylko pobierać dane wejściowe, ale również zapisywać w

bazie danych informacje będące wynikiem działania DSS.

Podobnie w przypadku bazy modeli podsystem symulacyjno-

decyzyjny może również modyfikować modele pod katem

konkretnego problemu oraz istniejących danych (np. poprzez

reestymację ich parametrów) zapisując zmiany w bazie modeli.

Struktura DSS

– Interfejs użytkownika (menedżer dialogu) ma zapewnić

wysoki komfort obsługi. Pozwala decydentowi na łatwy
dostęp i manipulowanie DSS. Steruje pracą modułu
symulacyjno-decyzyjnego, oraz przekazuje użytkownikowi
otrzymane od niego wyniki obliczeń. Użytkownik musi
otrzymywać to czego zażąda w możliwie różnorodnej
formie, a system musi być przygotowany na żądania
niestandardowe. Nowoczesne interfejsy mają za zadanie
jak największe uproszczenie sposobu komunikacji z
systemem, poprzez komunikację graficzną, multimedialną,
z wykorzystaniem powszechnie stosowanej terminologii
biznesowej, a nawet przy użyciu języka naturalnego.

Struktura DSS

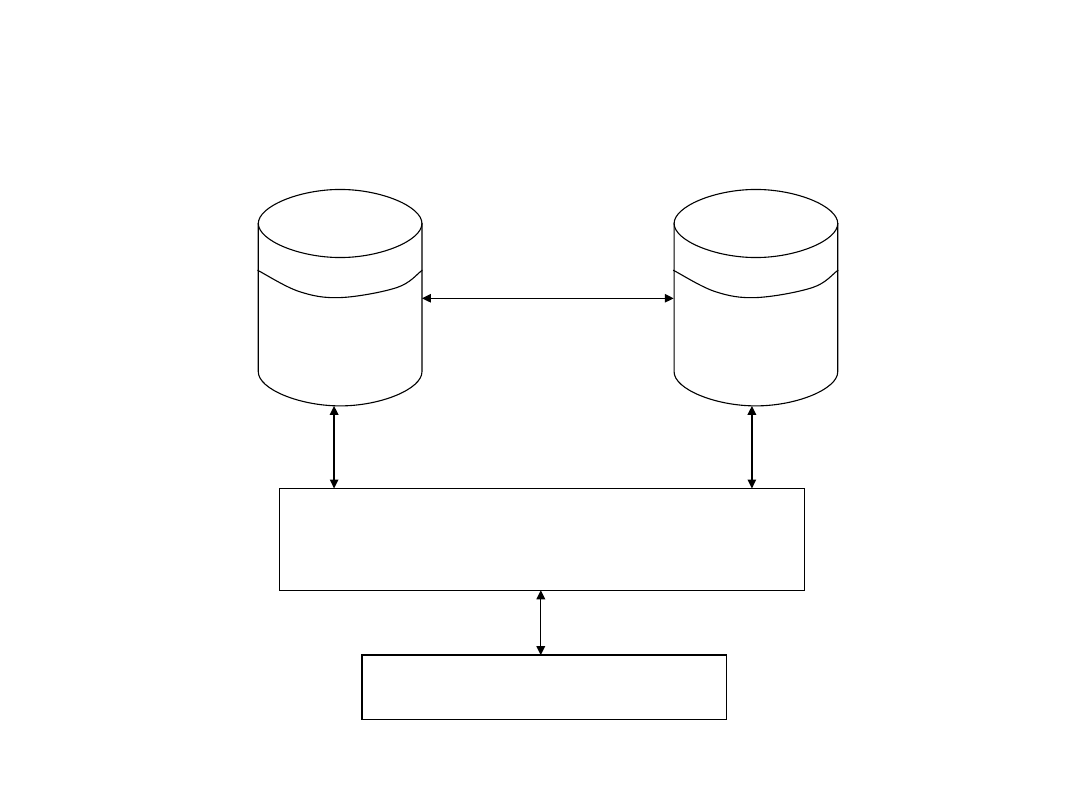
Struktura DSS

Podsystem symulacyjno-

-decyzyjny

Interfejs użytkownika

Baza

danych

Baza

modeli

• Jak mogliśmy to zaobserwować w poprzednim punkcie jądrem

Systemu Wspomagania Decyzji, decydującym o jego

możliwościach są modele przechowywane w bazie modeli.

Scharakteryzujemy więc teraz ten element DSS nieco

dokładniej.

• Modelem nazywamy abstrakcję (czyli świadome i celowe

uproszczone

odwzorowanie)

określonego

fragmentu

rzeczywistości. Przydatność modelu warunkowana jest przez

następujące warunki:

– Konstrukcji modelu musi towarzyszyć świadomość celu w jakim

został on stworzony.

– Model powinien odzwierciedlać wszystkie istotne z punktu

widzenia celu elementy rzeczywistości, ich własności oraz relacje

między nimi i ich własnościami.

– Model powinien być wewnętrznie zgodny i zgodny z

informacjami, które były podstawą jego konstrukcji.

– Model

powinien

uwzględniać

relacje

między

realnym

fragmentem rzeczywistości, a jego otoczeniem.

Modele

• Biorąc pod uwagę wybraną formę reprezentacji rzeczywistości

możemy mówić o modelach:

– fizycznych (w skład których zaliczymy przede wszystkim różnego

rodzaju prototypy urządzeń mechanicznych, elektronicznych itp.),

– graficznych (reprezentujących modelowane aspekty problemu z

wykorzystaniem różnego rodzaju diagramów i innych form

obrazkowych),

– matematycznych.

• Z punktu widzenia możliwości wykorzystania modelu przez

systemy informatyczne, największe nasze zainteresowanie budzi

oczywiście ta ostatnia grupa. Istnieje przy tym cały szereg metod

reprezentacji

świata

rzeczywistego

przez

programy

komputerowe, wśród których wyróżnić można dwa podstawowe

podejścia:

– numeryczne – wykorzystujące do opisu stanu modelowanego wycinka

rzeczywistości równania i formuły matematyczne,

– symboliczne (logiczne) – opisujące rzeczywistość w postaci zestawów

umownych symboli oraz zależności logicznych między nimi.

Modele

• Podział ten nie ma oczywiście charakteru ostrego. W

zasadzie

można

powiedzieć,

że

każdy

program

komputerowy

stanowi

model

rzeczywistości,

wykorzystujący do jej opisu zarówno aparat matematyczny,

jak i logiczny. W zależności od przewagi udziału każdego z

nich możemy zakwalifikować go do którejś z grup.

• Jako przykłady krańcowych przypadków możemy z jednej

strony wymienić tu z jednej skomplikowane modele

matematyczne

wymagające

zastosowania

złożonych

algorytmów numerycznych, zaś z drugiej strony systemy

oparte na inżynierii wiedzy.

• Mówiąc o reprezentacji rzeczywistości w postaci systemu

informatycznego należy wskazać tu na dwa podstawowe

elementy modelowane w komputerze: stan rzeczywistości

reprezentowany z wykorzystaniem danych, oraz dynamikę

zmian stanu (zachowanie) rzeczywistości reprezentowaną

w postaci algorytmu.

Modele

• Ze względu na stopień naszej wiedzy o reprezentowanym

fragmencie

rzeczywistości,

możemy

mówić

o

następujących rodzajach modeli:

– modele algorytmiczne. Są to tzw. „silne” modele, z

silnymi

założeniami

i

bez

parametrów

wolnych

(szacowanych na podstawie danych).

– Wymagają one dogłębnego zrozumienia natury

problemu i istnienia wiedzy o sposobie jego

rozwiązania,

pozwalającej

na

wyspecyfikowanie

równań lub algorytmów opisujących zachowanie

modelowanego systemu.

– Stanowią one niewątpliwie najefektywniejszą metodologię

rozwiązania problemu.

– Zwykle jednak stosowane mogą być jedynie w przypadku

systemów stosunkowo prostych, dla których możliwe jest

precyzyjne

zrozumienie

i

opisanie

modelowanych

fenomenów.

Modele

– modele dedukcyjne. Stosowane są w przypadku problemów,

dla których nie jesteśmy w stanie zbudować precyzyjnej

specyfikacji matematycznej lub algorytmicznej (logicznej).

– Możemy tym niemniej na podstawie bezpośredniej obserwacji

systemu wykryć pewne stałe wzorce jego zachowania.

Pozwala to na określenie przez modelującego pewnych

ogólnych zasad opisujących dynamikę systemu.

– Typowymi

przykładami

zastosowania

rozumowania

dedukcyjnego są systemy ekspertowe oraz wnioskowanie

statystyczne.

– W pierwszym przypadku modelujący wraz z „ekspertem”

tworzy bazę wiedzy opisującą zachowanie systemu w postaci

szeregu reguł logicznych o niewielkiej liczbie parametrów

wolnych.

– Systemy wnioskowania statystycznego dla odmiany, takie jak

regresja liniowa, czynią silne założenia odnośnie natury

związku

między

zmiennymi,

pozwalając

oszacowanie

parametrów wolnych na podstawie zaobserwowanych danych.

Modele

– modele indukcyjne. W miarę jak wzrasta złożoność

systemu,

możliwość

bezpośredniego,

precyzyjnego

określenia pewnych stałych wzorców jego zachowania

zwykle maleje.

– Powiązania między zmiennymi stają się niejawne, nie

można poczynić niemal żadnych założeń odnośnie ich

natury.

– Problemy tego typu rozwiązywane mogą być przy

wykorzystaniu nieparametrycznych metod, takich jak sieci

neuronowe,

nieparametryczna

regresja,

adaptacyjne

systemy rozmyte czy też algorytmy genetyczne.

– Metody te w procesie analizy danych pozwalają na

określenie nie tylko wartości parametrów, ale również

kształtu odwzorowania między zmiennymi.

Modele

– modele indukcyjne. W miarę jak wzrasta złożoność systemu,

możliwość bezpośredniego, precyzyjnego określenia pewnych

stałych wzorców jego zachowania zwykle maleje.

– Powiązania między zmiennymi stają się niejawne, nie można

poczynić niemal żadnych założeń odnośnie ich natury.

– Problemy tego typu rozwiązywane mogą być przy

wykorzystaniu nieparametrycznych metod, takich jak sieci

neuronowe, nieparametryczna regresja, adaptacyjne systemy

rozmyte czy też algorytmy genetyczne.

– Metody te w procesie analizy danych pozwalają na określenie

nie tylko wartości parametrów, ale również kształtu

odwzorowania między zmiennymi.

• Jak

więc

widzimy,

w

miarę

wzrostu

złożoności

modelowanego problemu nasz stopień jego poznania a

priori zwykle maleje i ciężar przesuwa się w kierunku

analizy wzorców jego zachowania na podstawie obserwacji.

Modele

• Systemy Wspomagania Decyzji obejmują zwykle wobec tego

nie tylko modele wspomagające sam proces decyzyjny, ale

również modele analityczne identyfikujące pewne istotne

zmienne i fakty występujące w badanym problemie oraz

porządkujące zebrana wiedzę o zależnościach między nimi.

• Tak więc z tego punktu widzenia modele wykorzystywane

przez DSS ogólnie podzielić możemy na następujące

kategorie:

– Modele objaśniające – w których odwzorowujemy związki i

logiczne powiązania między własnościami modelowanych

obiektów i na ich podstawie przedstawiamy wynikające z nich

wnioski.

– Ich celem jest zdobycie wiedzy o samych obiektach, czyli

zmiennych, faktach czy procesach mających wpływ na

podejmowaną decyzję.

– Typowymi przykładami tej klasy modeli mogą być różnego

rodzaju modele finansowe, kalkulacji kosztów, prognostyczne,

identyfikacji systemów, itd.

Modele

– Modele weryfikujące – w których, nie ingerując we

własności

modelowanych

obiektów,

dokonujemy

uporządkowania informacji o badanej rzeczywistości.

– Modele te związane są zwykle z różnorodnymi technikami

analitycznymi i diagnostycznymi, takimi jak między innymi

analiza zależności między zmiennymi (korelacji), analiza

skupień, klasyfikacja, itp.

– Na przykład analiza skupień w danych dotyczących

sprzedaży, pozwala na stworzenie modelu rynku, opartego

na rozłącznych (lub nie) segmentach. Diagnostyka

natomiast polega na analizie wnętrza modelu, w celu

wykrycia przyczyn występowania takich, a nie innych

zjawisk.

– Modele decyzyjne – na podstawie których chcemy

wyznaczyć w modelu nowe obiekty, lub wskazać zamiany w

obiektach istniejących, tak, aby spełniały one cel zawarty w

naszym problemie.

Modele

•

Modele finansowe dostarczają narzędzi do analiz finansowych

takich wielkości jak strumienie pieniądza, stopy zwrotu i innych

elementów analiz finansowo-ekonomicznych.

•

Ogólnie modele tego typu podzielić można na dwie podstawowe

grupy:

– Modele bilansowe sensu stricto, czyli modele bilansu, rachunku

wyników,

rachunku

inwestycyjnego

i

analiz

finansowo-

ekonomicznych,

a

także

proste

modele

arytmetyczne

wykorzystywane przy planowaniu, kontroli i ocenie uzyskiwanych

wyników.

Wykorzystują

one

przede

wszystkim

metody

matematyczne algebraiczne, a bardzo rzadko również rachunku

różniczkowego i całkowego.

– Modele przepływów międzyoperacyjnych, międzywyrobowych,

międzyzakładowych,

międzybranżowych

i

międzygałęziowych

wykorzystywane w planowaniu. Wykorzystują one przede wszystkim

statyczną analizę input-output oraz metody algebraiczne.

•

Modele bilansowe wykorzystywane są przede wszystkim w

jednoetapowych dobrze ustrukturalizowanych problemach

decyzyjnych deterministycznych (decyzji podejmowanych w

warunkach pewności), oraz do wyznaczania wartości istotnych

zmiennych w modelach innych klas.

Modele finansowe

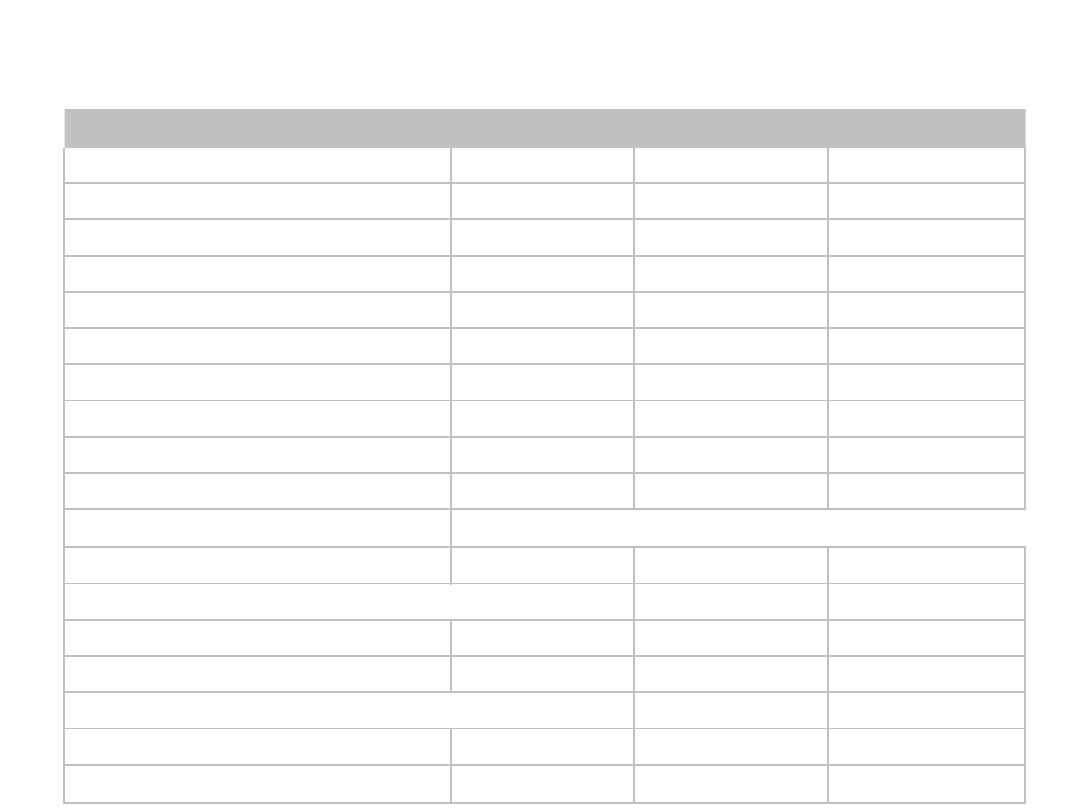
Modele finansowe

Charakterystyka

J ednostka

WX Supermon 2

Konstrix A12

Koszt nabycia

zł

30 000,00 zł

62 000,00 zł

Okres użytkowania

rok

6

6

Wartość likwidacyjna

zł

- zł

8 000,00 zł

Zdolność produkcyjna

szt./rok

8000

10000

Pensje obsługi

zł/rok

5 000,00 zł

5 000,00 zł

Wynagrodzenia

zł/rok

25 000,00 zł

11 000,00 zł

Inne koszty stałe

zł/rok

5 000,00 zł

6 000,00 zł

Materiały

zł/rok

40 000,00 zł

48 000,00 zł

Inne koszty zmienne

zł/rok

3 000,00 zł

3 000,00 zł

Kalkulacyjna stopa procentowa

%

10%

10%

Koszty zmienne

68 000,00 zł

62 000,00 zł

Koszty zmienne znormalizowane

68 000,00 zł

49 600,00 zł

Koszty stałe

Amortyzacja

5000

9000

Odsetki

1 500,00 zł

3 500,00 zł

Koszty zmienne znormalizowane

68 000,00 zł

49 600,00 zł

Koszty stałe razem

16 500,00 zł

23 500,00 zł

Łączne koszty

84 500,00 zł

73 100,00 zł

(Analiza kosztów)

•

W przypadku modeli optymalizacyjnych, zakładamy, że celem

budowy modelu jest znalezienie rozwiązania, optymalnego pod

względem pewnego zadanego kryterium (lub kryteriów).

Warunki definiujące tego typu cel nazywamy warunkami

kierunkowymi.

•

Warunki kierunkowe w modelach optymalizacyjnych nazywamy

kryteriami, lub funkcjami celu. Typowym przypadkiem

warunku

kierunkowego

w

systemach

informacyjnych

zarządzania jest minimalizacja kosztów lub maksymalizacja

zysku.

•

Jako funkcje celu wykorzystywane mogą być również pochodne

tych wielkości, przede wszystkim różnego rodzaju wskaźniki

(takie jak np. wewnętrzna stopa zwrotu).

•

W rzeczywistych warunkach dopuszczalne są jedynie pewne

rozwiązania, spełniające określone warunki. Warunki te

nazywamy ograniczeniami. Typowymi przykładami ograniczeń

przy podejmowaniu decyzji z zakresu zarządzania, są wielkości

zasobów z których może korzystać organizacja przy realizacji

celu.

Modele optymalizacyjne

•

W przypadku modeli optymalizacyjnych, zakładamy, że celem

budowy modelu jest znalezienie rozwiązania, optymalnego pod

względem pewnego zadanego kryterium (lub kryteriów).

Warunki definiujące tego typu cel nazywamy warunkami

kierunkowymi.

•

Warunki kierunkowe w modelach optymalizacyjnych nazywamy

kryteriami, lub funkcjami celu. Typowym przypadkiem

warunku

kierunkowego

w

systemach

informacyjnych

zarządzania jest minimalizacja kosztów lub maksymalizacja

zysku.

•

Jako funkcje celu wykorzystywane mogą być również pochodne

tych wielkości, przede wszystkim różnego rodzaju wskaźniki

(takie jak np. wewnętrzna stopa zwrotu).

•

W rzeczywistych warunkach dopuszczalne są jedynie pewne

rozwiązania, spełniające określone warunki. Warunki te

nazywamy ograniczeniami. Typowymi przykładami ograniczeń

przy podejmowaniu decyzji z zakresu zarządzania, są wielkości

zasobów z których może korzystać organizacja przy realizacji

celu.

Modele optymalizacyjne

• W modelach jednokryterialnych wyróżniany jest tylko

jeden warunek kierunkowy. Tak więc mają one tylko jedną
określoną funkcję celu, dla której należy wyznaczyć
maksimum lub minimum. W ogólnym przypadku mają one
strukturę:

gdzie są funkcjami wielu zmiennych
definiującymi odpowiednio funkcję celu oraz ograniczenia.

Optymalizacja

jednokryterialna

M

M

C

C

C











)

(

...

)

(

max

)

(

2

2

1

x

x

x

R

R

C

C

n

M



:

,...,

1

• Tak więc kryterium, np. zysk może być funkcją wielu

zmiennych, powiedzmy różnego rodzaju nakładów:

produkcyjnych, reklamowych. itp. Interesuje nas

znalezienie takiej kombinacji nakładów, dla których zysk

jest jak największy.

• Musi być on przy tym zrealizowany przy pewnych

ograniczeniach, dla przykładu łączna wartość wszystkich

nakładów nie powinna przekraczać pewnej określonej z

góry kwoty.

Optymalizacja

jednokryterialna

• W praktyce ekonomicznej często zdarza się, że wszystkie

funkcje , tzn. C

1

, ..., C

M

zarówno funkcja celu i funkcje

ograniczeń, mają charakter liniowy. W takim przypadku
znalezienie maksymalnej wartości funkcji celu wiąże się
z

rozwiązaniem

tzw.

zadania

programowania

liniowego.

• Jest

to

jedna

z

najważniejszych

klas

modeli

optymalizacyjnych, dla której ponadto istnieje algorytm
pozwalający efektywnie wyznaczyć dokładny punkt
ekstremum funkcji celu w skończonej liczbie kroków.
Algorytm ten nazywany jest algorytmem simpleks.

• W przypadku jeśli rozwiązanie zadania programowania

liniowego musi być znalezione w dziedzinie liczb
całkowitych,

mówimy

o

programowaniu

całkowitoliczbowym.

Optymalizacja

jednokryterialna

• W przypadku nieliniowych funkcji celu i funkcji

definiujących ograniczenia nie ma już takich prostych
algorytmów rozwiązania jak algorytm simpleks (lub
algorytmy od niego pochodne).

• Szukanie ekstremum funkcji staje się wówczas procesem

iteracyjnym, wymagającym często wielu kroków i
pozwalającym

na

znalezienie

jedynie

wyniku

przybliżonego.

• Skomplikowana powierzchnia funkcji celu może mieć

ponadto charakter wielomodalny, tzn. może istnieć
wiele jej lokalnych ekstremów.

• Do najważniejszych ogólnych klas metod znajdowania

ekstremum funkcji celu należą:

Optymalizacja

jednokryterialna

• Metody enumeratywne.

– Związane są one z sytuacją gdy zbiór wszystkich rozwiązań

problemu spełniających ograniczenia jest skończony (i
ponadto niezbyt duży).

– Jeśli potrafimy dla każdej alternatywy decyzyjnej obliczyć

wartość funkcji celu, to wybierając rozwiązanie o wartości
maksymalnej rozwiązujemy zadanie.

– Rozważmy następujący przykład: Celem naszym jest wybór

wariantu inwestowania o maksymalnej stopie zwrotu. Po
analizie ofert inwestycyjnych, okazało się, że nasze
ograniczenia (dotyczące np. wielkości zaangażowanego
kapitału, zabezpieczeń, strategii inwestowania, itp.)
spełniają trzy z nich. Po obliczeniu stopy zwrotu, okazało
się, że mają one odpowiednio wartości: 13.5%, 12.9%,
14.1%. Decyzją optymalną będzie oczywiście wybór
wariantu trzeciego.

Optymalizacja

jednokryterialna

• Metody losowe.

– Możliwość zastosowania metod enumeratywnych jest

oczywiście na ogół ograniczona.

– Inne metody rozwiązywania zadań optymalizacyjnych mają

charakter iteracyjny.

– Rozpoczyna się od pewnego rozwiązania początkowego,

poprawiając je w każdym kroku algorytmu poprzez wybór
rozwiązania lepszego pod względem wartości kryterium.

– W metodach losowych wybór kolejnego rozwiązania

odbywa się na chybił trafił w określonym sąsiedztwie
rozwiązania poprzedniego lub poprzez określone analizy
probabilistyczne (metody pseudolosowe).

– Przykładem algorytmu tego typu może być wyżarzanie

wykładnicze.

Optymalizacja

jednokryterialna

• Metody gradientowe.

– Wiadomym jest, że w punkcie ekstremum pochodna funkcji

celu (dla funkcji wielu zmiennych nazywana gradientem)
musi być równa 0. Jeśli wobec tego da się rozwiązać
równanie (bądź raczej układ równań) wyznaczające miejsce
zerowe pochodnej, będzie oznaczać to znalezienie
rozwiązania optymalnego.

– Niestety zastosowanie tego typu metod jest ograniczone do

pewnych niewielkich klas problemów (np. znajdowanie
minimum kwadratowej funkcji błędu w zagadnieniu regresji
liniowej może być dokonane przez rozwiązanie układu
równań normalnych, wyznaczającego miejsce zerowe
pochodnej funkcji błędu).

– Pojawia się tu również problem z ograniczeniami.

Optymalizacja

jednokryterialna

• Metody gradientowe c.d.

– Znana jest również zależność, ze znak pochodnej wskazuje na to czy

funkcja maleje czy rośnie.

– W przypadku wielowymiarowym oznacza to, że poruszanie się w

kierunku przeciwnym do gradientu funkcji celu oznacza zbliżanie się
do jej minimum.

– Większość metod gradientowych ma więc charakter iteracyjny.

Kolejne przybliżenia rozwiązania wyznaczane są w kierunku
przeciwnym do gradientu funkcji celu, pod warunkiem, że spełnia ono
ograniczenia.

– Do tej kategorii należą np. takie podstawowe algorytmy minimalizacji

funkcji jak metoda najszybszego spadku, czy też sprzężonych
gradientów.

• Metody heurystyczne.

– Są to metody iteracyjne, wyznaczające kolejne przybliżenia

rozwiązania, poprzez heurystyczne przekształcenia rozwiązań
poprzednich. Np. algorytmy genetyczne wykorzystują heurystykę, że
połączenie dwu dobrych rozwiązań może zaowocować czymś jeszcze
lepszym.

Optymalizacja

jednokryterialna

• Nieco innymi przykładami zadań optymalizacyjnych są zadania

optymalizacji kombinatorycznej, łączą one problematykę

znajdowania ekstremum funkcji celu z teorią grafów.

• Wymienić

tu

możemy

przykładowo

zagadnienia

harmonogramowania, czy też optymalizacji sieciowej,

takie jak optymalizacja sieci dystrybucji, tras przejazdów,

analiza przedsięwzięcia, itp.

• Modele optymalizacyjne stosowane są najczęściej w

jednoetapowych problemach decyzyjnych, w warunkach

pewności. Łączone są one często z modelami finansowymi

pozwalającymi

na

wyznaczenie

istotnych

parametrów

optymalizacji.

• Niektóre metody wykorzystywane są jednak również w

decyzjach wieloetapowych, np. programowanie dynamiczne,

czy też metody analizy sieciowej (PERT, CPM).

• Dla niektórych modeli optymalizacyjnych istnieją również

wersje stochastyczne, stosowane w warunkach ryzyka.

Optymalizacja

jednokryterialna

• W praktyce zarządzania często możemy spotkać decyzje,

które nie mają jednego kryterium celu.

• Jeśli rozważamy dla przykładu decyzje inwestycyjne, to

bez wątpienia jednym z celów menedżera jest
maksymalizacja zysku, ale również należy wziąć pod
uwagę inne kryteria, np. minimalizacja ryzyka.

• Modele decyzyjne w których bierzemy pod uwagę wiele

celów nazywamy wielokryterialnymi. W ogólnym
przypadku mają one strukturę:

Optymalizacja

wielokryterialna

Gdzie C

1

, ..., C

K

: R

n

 R są funkcjami definiującymi K

funkcji celu podlegających optymalizacji, C

K+1

, ..., C

M

: R

n

 R są funkcjami ograniczeń.

Optymalizacja

wielokryterialna

M

M

K

K

K

x

C

x

C

x

C

x

C

















)

(

...

)

(

max

)

(

...

max

)

(

1

1

1

• Rozwiązania

dopuszczalne

optymalne

pod

względem

wszystkich kryteriów, nazywamy idealnymi.

• Należy jednak powiedzieć, że zadanie decyzyjne optymalizacji

wielokryterialnej rzadko posiada rozwiązanie idealne.
Kryteria mogą być ze sobą w dużej mierze sprzeczne (np. jak
najniższa cena i jak najwyższa jakość wybieranego towaru),
ponadto zwykle rozwiązanie idealne znajduje się poza
obszarem dopuszczalnym wyznaczanym przez ograniczenia.

• W większości wypadków w modelach wielokryterialnych

musimy więc zadowolić się wyznaczeniem rozwiązania
niezdominowanego, tzn. takiego, dla którego nie ma
rozwiązań

dopuszczalnych

o

wartościach

wszystkich

kryteriów bardziej zbliżonych do rozwiązania idealnego, czyli
jest ono w obszarze dopuszczalnym optymalne pod kątem
choćby jednego kryterium.

Optymalizacja

wielokryterialna

• Rozwiązań niezdominowanych może jednak istnieć wiele.

Powstaje więc pytanie, które z niech powinniśmy
wybrać?

• Problem jest w zasadzie nierozstrzygalny, jeśli

przyjmiemy, ze wszystkie kryteria są równie ważne dla
decydenta. Jedynym rozwiązaniem jest wyartykułowanie
przez niego pewnych preferencji (np. w formie wag)
odnoszących się do istotności poszczególnych kryteriów.

• Pozwala to na scalenie wartości kryteriów w jedną

funkcję, nazywaną zwykle użytecznością rozwiązania.
Problem optymalizacyjny może być już wtedy rozwiązany
metodami

wykorzystywanymi

w

optymalizacji

jednokryterialnej, poprzez maksymalizację użyteczności.

Optymalizacja

wielokryterialna

• Problem modelowania preferencji decydenta nie jest

oczywiście zadaniem prostym.

• Istnieje cały szereg modeli wielokryterialnych, związanych z

wyznaczaniem wag poszczególnych kryteriów w ogólnej
użyteczności (agregacja liniowa), jak również innymi
sposobami agregacji kryteriów.

• Przykładem może być tu nieliniowe modelowanie funkcji

użyteczności z wykorzystaniem sieci neuronowych.

• Preferencje decydenta modelowane są zazwyczaj na bazie tzw.

macierzy preferencji, w której zbiera się wyniki porównania
parami istotności poszczególnych kryteriów. Na podstawie
analizy macierzy preferencji wyznaczane są wagi kryteriów.

• Wagi zazwyczaj dobierane są metodą najmniejszych

kwadratów, lub z użyciem metody AHP (Adaptive Hierarchical
Process) Saaty’ego.

Optymalizacja

wielokryterialna

• Omawiane

w

poprzednim

punkcie

modele

optymalizacyjne zakładają możliwość wyspecyfikowania
jasno określonej funkcji celu (bądź wielu funkcji celów)
pod kątem których menedżer ocenia różne opcje
decyzyjne prowadzące do rozwiązania problemu.

• Jednak już w przypadku modeli wielokryterialnych

napotkaliśmy na poważne problemy z tego rodzaju
założeniem. Nietrudno więc wyobrazić sobie sytuację, w
której funkcja celu jest niemożliwym do jawnego
sprecyzowania zagmatwanym zlepkiem różnych
kryteriów.

• Ponadto decyzja niekoniecznie musi być związana z

optymalizacją celów. Często wystarczy nam osiągnięcie
pewnego satysfakcjonującego stanu.

Klasyfikacja

• Zastanówmy się dla przykładu nad decyzjami kredytowymi

w bankach.

– Oczywiście mamy w ich przypadku do wyboru dwie

podstawowe alternatywy: przyjąć wniosek lub go odrzucić.

– Czasami mogą w grę wchodzić również dodatkowe opcje, takie

jak konsultacja z przełożonym, dokładniejsze przebadanie
sytuacji wnioskodawcy, itp. ale dla uproszczenia pominiemy je
w dalszych rozważaniach.

– Celem decyzji o przyznaniu kredytu jest oczywiście osiągnięcie

określonych zysków przy jak najmniejszym ryzyku.

– Analizując wniosek kredytowy nie korzystamy jednak w sposób

jawny z funkcji celu wyliczając ją dla każdej z alternatyw i
znajdując jej ekstremum.

– Po prostu na podstawie parametrów wniosku, takich jak kwota

kredytu,

dochody

wnioskodawcy,

zabezpieczenia,

itp.

wybieramy jedną ze wspomnianych wyżej decyzji.

Klasyfikacja

• W przypadku decyzji kredytowej możemy więc mówić o

klasyfikowaniu wniosków kredytowych na podstawie wartości
pewnych istotnych zmiennych (atrybutów) do jednej z dwu
(lub ogólnie pewnej skończonej liczby) grup odpowiadających
poszczególnym alternatywom decyzyjnym.

• Podobnych sytuacji decyzyjnych możemy wymienić tu bardzo

wiele:

– w grze giełdowej na podstawie cen, indeksów i wskaźników

giełdowych podejmowane są decyzje transakcyjne typu
sprzedaj, kup, wstrzymaj się;

– na podstawie informacji o kliencie i jego historii zakupów

podejmowane są decyzje o podjęciu w stosunku do niego akcji
marketingowej lub nie;

– rozpoznając stan przedsiębiorstwa na podstawie jego

wskaźników ekonomicznych podejmujemy decyzję o tym czy jest
ono zagrożone bankructwem lub nie, czy ma szanse rozwoju czy
grozi mu stagnacja, itp.

Klasyfikacja

• Ogólnie mówiąc zadanie klasyfikacji polega więc na

znalezieniu odwzorowania (tzw. klasyfikatora):

Gdzie C = {C

1

, ..., C

n

} jest skończonym zbiorem klas

odpowiadających

poszczególnym

alternatywom

decyzyjnym, zaś zbiór X  R

p

przestrze-nią atrybutów

których wartości decydują o wyniku klasyfikacji.
Odwzorowanie klasyfikujące f

c

dzieli więc przestrzeń X

na n obszarów decyzyjnych grupujących wzorce
atrybutów należące do jednej kategorii.

Klasyfikacja

f R

X

C

c

p

:

 

• W przypadku zagadnień klasyfikacji liczba i same

alternatywy decyzyjne muszą być znane i określone z
góry.

• Aby zbudować model niezbędne jest jednak zbudowanie

odwzorowania klasyfikującego f

c

, które wybierze dla

danego zestawu atrybutów wejściowych odpowiadającą
mu alternatywę decyzyjną czyli klasę do której należy
dany wzorzec wejściowy.

• Często klasyfikator f

c

dla danego wzorca wejściowego

określa

rozkład

prawdopodobieństwa

jego

przynależności do poszczególnych klas. Znając rozkład
prawdopodobieństwa, łatwo można wybrać konkretną
klasę, kierując się choćby regułą maksymalnego
prawdopodobieństwa.

Klasyfikacja

• Klasyfikatory budowane są zazwyczaj na podstawie

zgromadzonych danych. W tym celu należy mieć
zdefiniowanych reprezentantów każdej klasy w postaci:

– jednego wzorca idealnego tzw. centroidu, lub
– zestawu danych o których wiemy, że należą do tej klasy.

• Przykładowo jeśli zgromadziliśmy dwa zestawy danych

dotyczących

wniosków

kredytowych:

tych

które

zakończyły się pomyślną spłatą kredytu, oraz tych w
przypadku których należności okazały się nieściągalne,
możemy wykorzystując metody statystycznej analizy
danych zbudować klasyfikator, który dla nowych
wniosków określi decyzję jaką należy w stosunku do nich
podjąć.

Klasyfikacja

• Istnieje cały szereg rozmaitych podejść do budowy

klasyfikatorów,

wykorzystujących

różne

formalizmy

matematyczne i opierających się często na zupełnie
odmiennych koncepcjach budowy.

• Do najważniejszych metodologii wykorzystywanych w tego

typu zadaniach należą: analiza dyskryminacyjna, korzystająca
z klasycznych modeli statystycznych regresji liniowej,
klasyfikacja Bayesowska (tzw. naiwny Bayes lub metoda k-
najbliższych sąsiadów), czy też sieci neuronowe.

• Inne podejścia stosowane do budowy klasyfikatora polegają

na określeniu symbolicznych reguł klasyfikujących, które w
sposób jawny definiują wartości (lub przedziały wartości)
atrybutów dla których należy wybrać określoną alternatywę
decyzyjną.

• Reguły te mogą być zapisane w formie klasycznych reguł

wnioskowania lub w postaci tzw. drzewa decyzyjnego.

Klasyfikacja

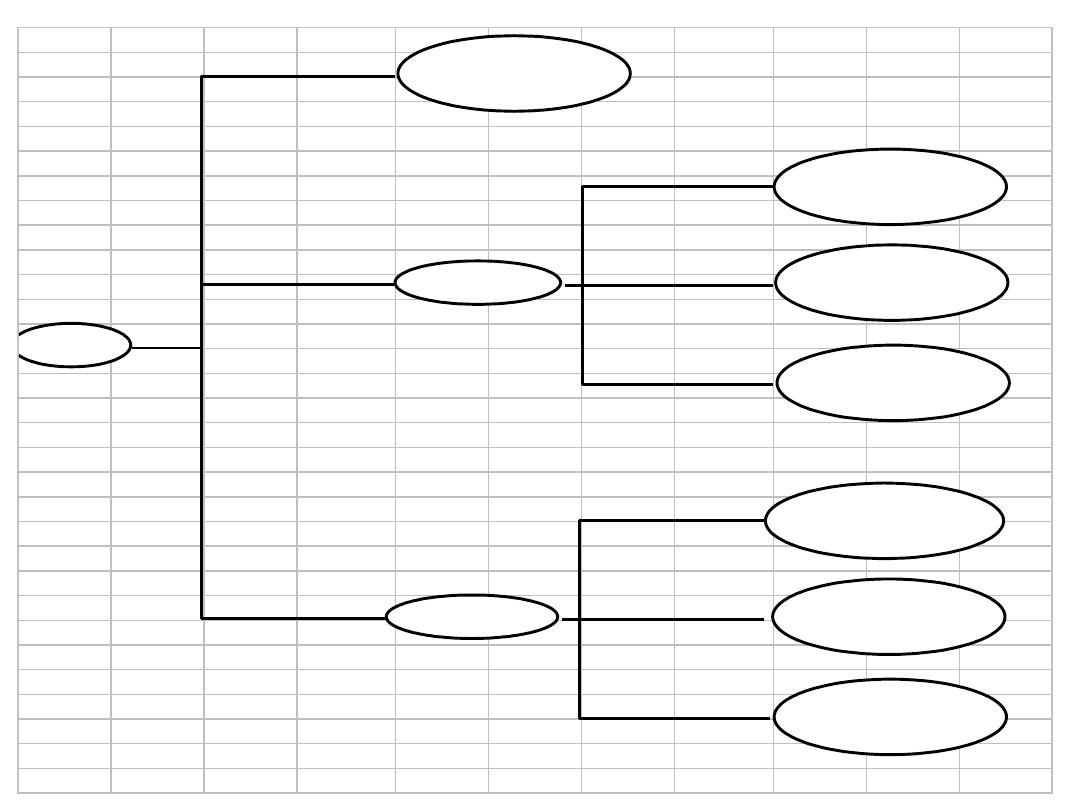
FAŁSZ

FAŁSZ

PRAWDA

FAŁSZ

PRAWDA

FAŁSZ

FAŁSZ

FAŁSZ

FAŁSZ

Wartość

niska

średnia

Nieruchomość -

słaba

wysoka

Lokalizacja

Nieruchomość -

średnia

zła

dobra

znakomita

Nieruchomość -

średnia

Nieruchomość -

dobra

Lokalizacja

Nieruchomość -

średnia

zła

dobra

znakomita

Nieruchomość -

dobra

Nieruchomość -

dobra

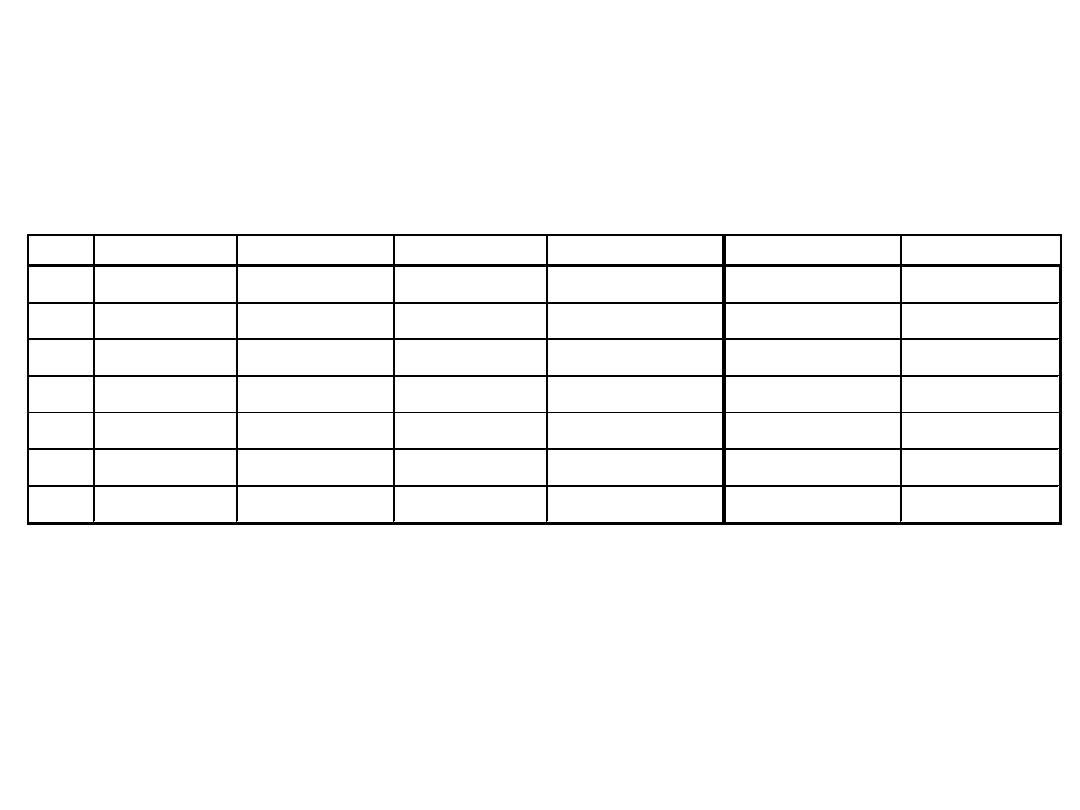
Klasyfikacja

Nr.

Zmienna

Wartość

Zmienna

Wartość

Zmienna

Wartość

1

Wartość

niska

Nieruchomość

słaba

2

Lokalizacja zła

Wartość

średnia

Nieruchomość

średnia

3 Lokalizacja

zła

Wartość

wysoka

Nieruchomość

średnia

4 Lokalizacja

dobra

Wartość

średnia

Nieruchomość

średnia

5 Lokalizacja

dobra

Wartość

wysoka

Nieruchomość

dobra

6 Lokalizacja

znakomita

Wartość

średnia

Nieruchomość

średnia

7 Lokalizacja

znakomita

Wartość

wysoka

Nieruchomość

dobra

JEŻELI Lokalizacja=‘zła’ I Wartość = ‘średnia’
TO

Nieruchomość = ‘średnia’

• Reguły klasyfikacyjne mogą być opracowywane na

podstawie

wiedzy

eksperta

lub

doświadczonego

operatora zajmującego się danym problemem, ale
również często generowane są na podstawie danych.

•

Do

najważniejszych

metod

określania

reguł

klasyfikacyjnych na podstawie danych należą:

– indukcyjne metody uczenia maszynowego (algorytmy CART,

C4.5),

– algorytmy

genetyczne

(tzw.

genetyczne

systemy

klasyfikujące),

– metody generowania reguł z wykorzystaniem sieci

neuronowych.

Klasyfikacja

• Modele klasyfikujące stosowane mogą być nie tylko w

przypadku decyzji podejmowanych w warunkach pewności
ale dają często możliwość określenia niepewności (ryzyka)
klasyfikacji.

• Klasyfikator zamiast wybierać konkretną klasę ze zbioru

może wspomagać decydenta poprzez określenie rozkładu
prawdopodobieństwa wyboru każdej z nich.

– Tak więc np. dla konkretnego nowego wniosku kredytowego,

zamiast kategorycznie stwierdzać czy przyznać kredyt czy też
odmówić jego udzielenia, klasyfikator może określić rozkład
prawdopodobieństwa: przyznać z prawdopodobieństwem 0.8,
odrzucić z prawdopodobieństwem 0,2.

• Klasyfikatory, zwłaszcza oparte na regułach klasyfikujących,

mogą mieć również charakter rozmyty. O metodach
rozmytych dokładniej będziemy mówili w dalszej części
wykładu.

Klasyfikacja

• Modele klasyfikujące wymagają znajomości z góry

opisów kategorii (alternatyw decyzyjnych) w postaci ich
centroidów lub zbiorów przykładów (danych należących
do klasy).

• Zdarza się jednak, że założenia te nie są spełnione. Na

podstawie analizy zależności występujących w danych
zebranych o badanym zagadnieniu klasy muszą zostać
określone bez wcześniejszej znajomości ich opisów.
Proces ten nazywamy analizą skupień (grupowaniem).

• Celem analizy skupień jest więc wykrycie w danych

jednorodnych podgrup, do których należą wzorce
podobne do siebie. Wzorce wyraźnie różniące się między
sobą powinny natomiast zostać zaliczone do różnych
podgrup.

Analiza skupień

(grupowanie)

Analiza skupień

(grupowanie)

• Typowe zastosowania analizy skupień to:

– Segmentacja rynku – wykrywanie w zbiorze klientów

jednorodnych podgrup (segmentów rynkowych), do których
kierowane będą różne działania marketingowe.

– Podział przedsiębiorstw opisanych przez wskaźniki

gospodarcze na jednorodne podgrupy, odpowiadające
różnym poziomom bezpieczeństwa przedsiębiorstwa.

– Wykrycie w danych giełdowych jednorodnych wzorców

zachowania inwestorów, prowadzących do identyfikacji
zachowania całego rynku lub konkretnego waloru.

– Redukcja wymiarowości danych, poprzez zgrupowanie

danych podobnych pod względem wybranych cech, które
będą mogły zostać pominięte w dalszej analizie.

– Wizualizacja danych wielowymiarowych w postaci „map”

podobieństwa w przestrzeni dwu- lub trójwymiarowej.

Analiza skupień

(grupowanie)

•

Większość algorytmów grupowania danych opiera się na jednym

z dwu najważniejszych podejść :

– Grupowanie hierarchiczne (hierarchical clustering).
– Grupowanie podziałowe (partitional clustering).

•

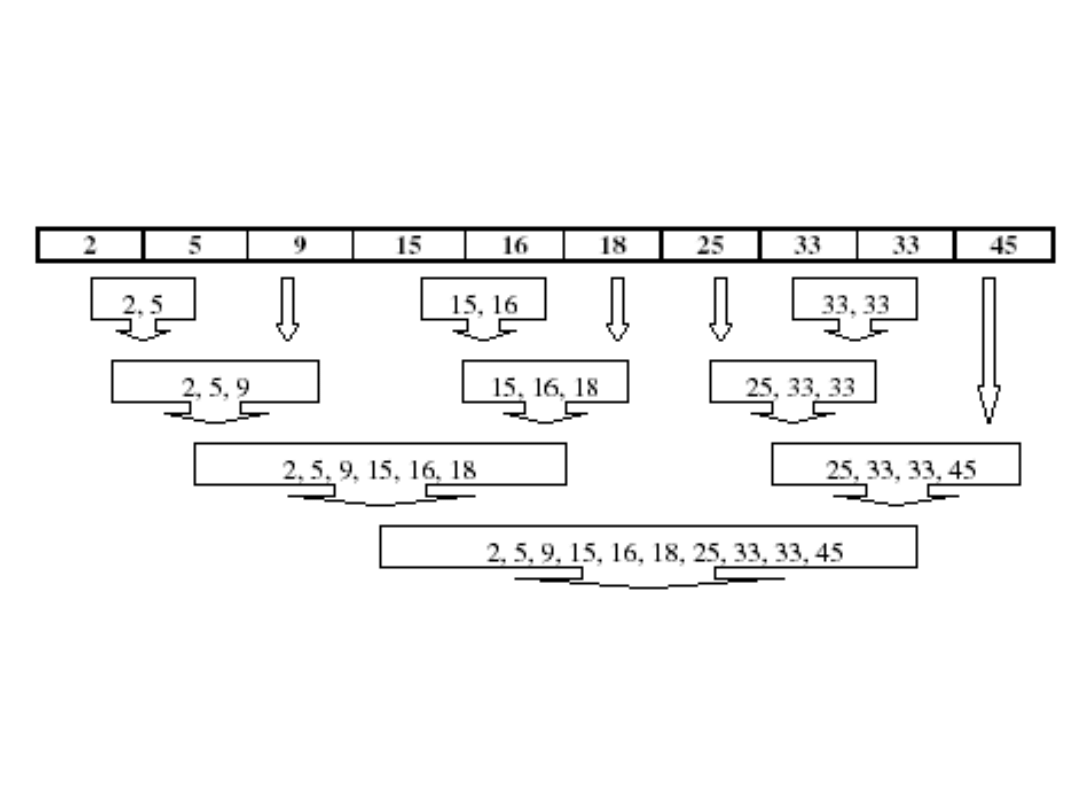
Grupowanie hierarchiczne organizuje dane w drzewiastą

strukturę coraz bardziej zagnieżdżonych skupień, poprzez

rekurencyjne rozdzielanie (metody rozdziałowe) lub łączenie

(metody aglomeracyjne) skupień.

– Metody grupowania aglomeracyjnego (agglomerative clustering)

rozpoczynają od niewielkich skupień (często jednoelementowych).

W kolejnych krokach skupienia najbliższe łączone są w nowe,

większe grupy, redukując w ten sposób liczbę skupień. Algorytm

kończy się z chwilą osiągnięcia jednego skupienia, obejmującego

cały zbiór danych.

– Metody

grupowania

rozdziałowego

(divisive

clustering)

rozpoczynają od jednego wielkiego skupienia. W każdym kroku

najbardziej niepodobne wzorce danych przenoszone są do nowych

skupień, aż do chwili rozdzielenia danych na drobne,

jednoelementowe grupy.

– Metody aglomeracyjne wykorzystywane są znacznie częściej.

Analiza skupień

(grupowanie)

Analiza skupień

(grupowanie)

• W grupowaniu podziałowym próbujemy uzyskać podział

zbioru danych na grupy, który minimalizuje ich
zróżnicowanie

wewnętrzne,

lub

maksymalizuje

zróżnicowanie między skupieniami. Metody te nie mają
charakteru hierarchicznego, ponieważ ich wynikiem są
grupy danych na tym samym poziomie podziału.

• Do najważniejszych podejść do grupowania podziałowego

należą algorytm c-środków, algorytm Kohonena.

Analiza skupień

(grupowanie)

• Analiza powinowactwa polega na badaniu atrybutów lub

cech, które „współwystępują razem”. Metody analizy
powinowactwa, nazywane również „analizą koszyków
rynkowych” poszukują powiązań (asocjacji) między tymi
atrybutami, tj. reguł opisujących związek między dwoma
lub więcej atrybutami.

• Reguły asocjacyjne przyjmują formę „Jeżeli poprzednik to

konkluzja” wraz z miarami tzw. wsparcia i ufności reguły.

– Jeśli dla przykładu w pewnym supermarkecie stwierdzono,

że na 1000 klientów w czwartkową noc 200 kupiło
serwetki, a spośród nich 50 kupiło również piwo, to reguła
asocjacyjna miałaby postać: „Jeżeli kupowane są serwetki
to kupowane jest piwo” ze wsparciem 50/1000 = 5% i
ufnością 50/200 = 25%.

Reguły asocjacyjne

• Przykładami zastosowań analizy asocjacji mogą być:

– Badanie proporcji abonentów sieci telefonii komórkowej,

którzy

pozytywnie

odpowiedzieli

na

różne

oferty

promocyjne.

– Badanie proporcji dzieci, którym rodzice często czytali na

głos do dzieci dobrze czytających.

– Określanie, które towary sprzedawane są razem, a które

prawie nigdy nie są sprzedawane razem.

– Analiza które strony webowe odwiedzane są przez tych

samych użytkowników.

– Określanie jakie dokumenty powinna zaproponować

wyszukiwarka

użytkownikowi,

który

wykazał

zainteresowanie określonym ich zestawem.

Reguły asocjacyjne

• Zadanie określenia reguł asocjacyjnych na podstawie

zbioru danych, odbywa się zwykle w dwu następujących
fazach:

– Wykrywanie

zbiorów

często

współwystępujących

elementów (frequent itemsets), tj. zbiorów atrybutów, które
występują z częstością (wsparciem) większym od pewnego
założonego progu.

– Generowanie

na

podstawie

tych

zbiorów

reguł

asocjacyjnych, które mają ufność powyżej pewnego
założonego progu.

• Najważniejszym algorytmem służącym do tworzenia

reguł asocjacyjnych jest tzw. algorytm A priori.

Reguły asocjacyjne

• Modele analizy decyzyjnej możemy uznać za połączenie

modeli klasyfikacyjnych i optymalizacyjnych. Wymagają one

analizy kolejnych alternatyw decyzyjnych oraz wpływających

na nie czynników z wykorzystaniem drzewa decyzyjnego.

• Poszczególne alternatywy określają zyski/straty jakie są z

nimi związane, analiza wpływu czynników zewnętrznych

dostarcza prawdopodobieństw realizacji poszczególnych

opcji.

• Wyboru alternatywy decyzyjnej, dokonuje się korzystając z

reguły maksymalnej wartości oczekiwanej zysku.

• Przykład: Przedsiębiorstwo sadownicze rozważa problem

ubezpieczenia sadu przed skutkami wymrożenia. Koszt

ubezpieczenia wynosi 5000 zł. Koszt ewentualnej szkody

powstałej wskutek wymrożenia sadu oszacowany został na

40000 zł. Na podstawie prognoz długoterminowych i opinii

górali prawdopodobieństwo łagodnej zimy, która nie

spowoduje szkód ocenia się na 0,8.

Analiza decyzyjna

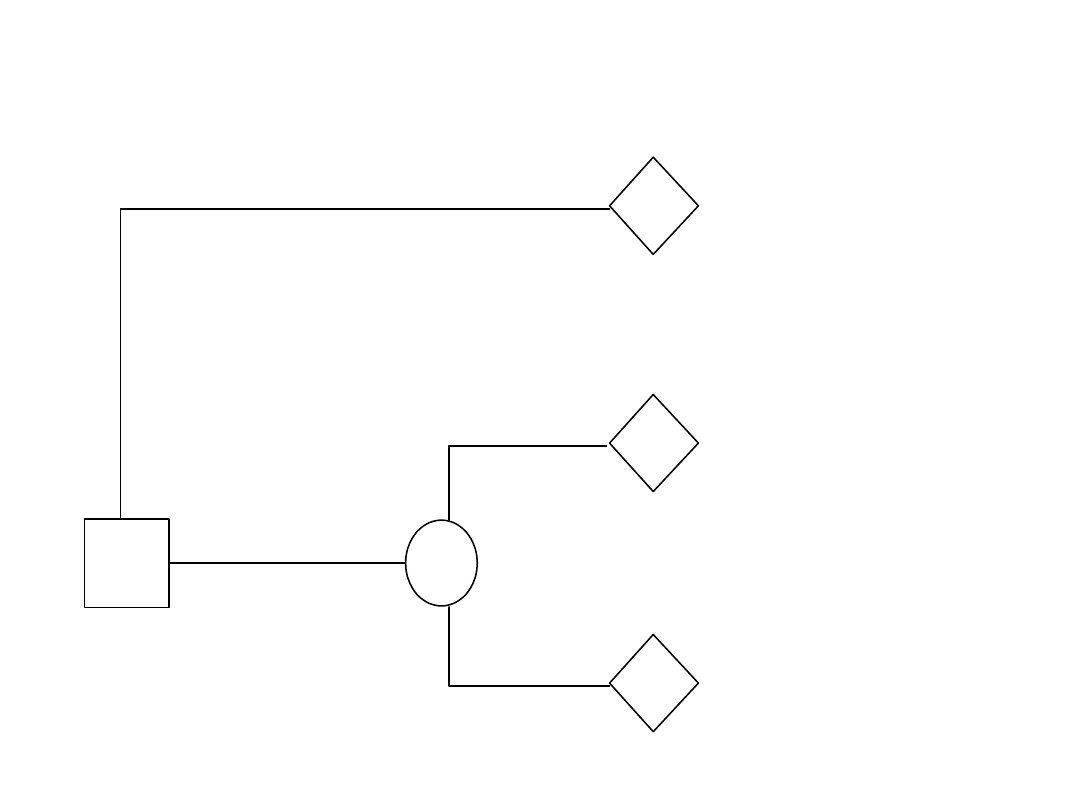
Analiza decyzyjna

Ubezpieczenie

r2: pośredni

5 000 zł

-

5 000 zł

-

r1: najlepszy

Brak

-

zł

ubezpieczenia

0,8

r1*p+r3*(1-p)

8 000 zł

-

r3: najgorszy

40 000 zł

-

0,2

Nie wymrozi

Wymrozi

D

X

R

R

R

• Modele prognostyczne pełnią istotną rolę w procesie

podejmowania

decyzji,

pozwalając

na

uzyskanie

oszacowań wartości (lub rozkładów prawdopodobieństw)
istotnych zmiennych wpływających na wybór alternatywy
decyzyjnej.

• Tworząc prognozę staramy się zwykle przy użyciu różnych

metod zbudować model badanego zjawiska, który pozwoli
nam określić wartości zmiennej wyjściowej na podstawie
znanych nam faktów z teraźniejszości lub przeszłości.

• O prognozach mówimy w przypadku gdy naszym celem

jest świadome i naukowe przewidywanie przyszłości.

• W sytuacji gdy zbliżone metody stosowane są do

określenia nie znanych bezpośrednio zjawisk w
teraźniejszości mówimy o identyfikacji systemów.

Modele prognostyczne i

identyfikacji systemów

• Modele analizy i prognozowania szeregów czasowych,

zwane również modelami ekstrapolacji prostej.

– Opierają się na analizie chronologicznej sekwencji obserwacji

prognozowanej zmiennej (lub prognozowanych zmiennych).

– Ich celem jest wykrycie zależności i korelacji między jej pomiarami

w różnych momentach czasowych.

– Zidentyfikowane wzorce zachowania prognozowanej zmiennej są

następnie wykorzystywane w teraźniejszości lub ekstrapolowane w

przyszłość.

– Tak więc zakładają one, że jedynymi czynnikami wpływającymi na

prognozowaną zmienną są jej przeszłe wartości, oraz czas.

– Prognoza może być sporządzana na następny okres, bezpośrednio

po chwili dla której mamy ostatnią obserwację, lub na kilka

okresów do przodu (najczęściej metodą krokową, poprzez

iteracyjne działanie modelu).

– Do najważniejszych modeli szeregów czasowych należą: metody

średniej ruchomej i wygładzania wykładniczego, analityczne i

adaptacyjne modele tendencji rozwojowej, modele składowej

periodycznej, modele Boxa-Jenkinsa (ARMA, ARIMA i różnego

rodzaju warianty) oraz łańcuchy Markowa.

Modele prognostyczne i

identyfikacji systemów

• Modele przyczynowe.

– Zakładają one, że zachowania prognozowanej zmiennej

(nazywanej również zmienną zależną, objaśnianą) może być

objaśnione przez zachowanie zbioru innych zmiennych

(zmiennych niezależnych, objaśniających).

– Celem modelu przyczynowego jest więc identyfikacja zależności

między zmiennymi i wykorzystanie jej do celów prognostycznych.

– U podstaw modeli przyczynowych leży analiza statystyczna, ale

często w powiązaniu z teorią modelowanych zjawisk. Ta ostatnia

zwykle stosowana jest do doboru postaci analitycznej modelu i

zmiennych objaśniających (identyfikacja strukturalna modelu).

Poprzez analizę danych statystycznych z przeszłości szacowane

natomiast

zwykle

są

parametry

modelu

(identyfikacja

parametryczna).

– Niekiedy spotkać można sytuację, kiedy teoria nie daje podstaw

do budowy modelu przyczynowego, natomiast badania

empiryczne

wykazują

związek

między

rozpatrywanymi

zmiennymi, co umożliwia zbudowanie prognozy wyłącznie w

oparciu o analizę danych historycznych. Tego typu modele

nazywamy symptomatycznymi.

Modele prognostyczne i

identyfikacji systemów

• Modele przyczynowe.

– Do

najważniejszych

i

najczęściej

stosowanych

prognostycznych modeli przyczynowych należą liniowe
modele statystyczne (regresji liniowej i krzywoliniowej),
oraz modele nieliniowe, takie jak regresja nieliniowa, sieci
neuronowe, lub systemy z logika rozmytą.

– W przypadku prognoz jakościowych, wymienić możemy

modele klasyfikacyjne (klasyfikatory), sieci neuronowe i
systemy ekspertowe.

Modele prognostyczne i

identyfikacji systemów

• Metody prognozy przez analogię.

– Służą one do przewidywania przyszłości określonej zmiennej

na podstawie danych o zmiennych podobnych, co do których
istnieją zbyt słabe podstawy, aby przypuszczać, że są one
przyczynowo powiązane ze zmienną prognozowaną.

– Istota zmiennych uwzględnianych w badaniu może być bądź

taka sama (np. liczba klientów w supermarketach w kinach
w Warszawie i w Łodzi) bądź różna (np. wydatki reklamowe
przedsiębiorstwa i liczba kooperantów).

• Metody heurystyczne.

– Polegają one na wykorzystaniu opinii ekspertów, opartej na

ich intuicji i doświadczeniu.

– Istotną cechą tych metod jest położenie nacisku na

połączenie w procesie prognozowania myślenia świadomego
(systematycznego) i intuicyjnego (nieświadomego kojarzenia
i porządkowania informacji).

Modele prognostyczne i

identyfikacji systemów

• Metody heurystyczne.

– Ekspert buduje model myślowy prognozowanego wycinka

rzeczywistości, starając się uwzględnić fakty zarówno już

znane, jak i przeczuwane, ilościowe i jakościowe. Dokonuje

eksperymentów na modelu, starając się odgadnąć czynniki,

które mogą wpłynąć na zmianę prognozowanego zjawiska.

– W procesie prognozowania występuje zazwyczaj wielu

ekspertów. Ich opinie analizowane są przez organizatora

badania, który w celu uzyskania prognozy stosuje zwykle

regułę najwyższego prawdopodobieństwa (tzn. prognozą jest

opinia najczęstsza) lub jej zmodyfikowane wersje (np. prognozą

może być opinia najczęstsza, po odrzuceniu opinii skrajnych).

– Metody heurystyczne wykorzystywane są do prognozowania

nowych zdarzeń np. nowych odkryć naukowych, technologii,

czy potrzeb ludzi, a także do przewidywania zmian

dotychczasowych zależności i prawidłowości.

– Do grupy tej zaliczyć możemy takie metody jak burza mózgów,

metoda delficka, analiza wpływów krzyżowych, czy znacznie

bardziej sformalizowane systemy ekspertowe.

Modele prognostyczne i

identyfikacji systemów

• Teoria gier stosowana jest do wspomagania decyzji w

sytuacjach konfliktowych i niepewnych. Stosowana może być

do analizy wielu decyzji mikro i makroekonomicznych.

• Możemy mówić o różnych rodzajach gier:

– Gry z naturą – w których gracz gra przeciwko pewnym

obiektywnym sytuacjom losowym, wykorzystując informacje

probabilistyczną o pewnych stanach natury.

– Gry dwuosobowe – w których uczestniczy dwu graczy. Możemy

mówić o następujących rodzajach gier dwuosobowych:

• Gry o sumie zero, w których zysk jednego z graczy równy jest

stracie drugiego. W związku z tym gra ma charakter

konkurencyjny, nie ma możliwości współpracy między

graczami.

• Gry o sumie dowolnej, w których warunek równości zysków i

strat obu graczy nie zachodzi. Ich interesy nie są całkiem

przeciwne - możliwe jest, że dzięki współpracy mogą obaj

zyskać. Oczywiście porozumienie obu graczy może być

niedozwolone (gry niekooperacyjne) lub dopuszczalne (gry

kooperacyjne).

– Gry wieloosobowe – kooperacyjne i niekooperacyjne.

Teoria gier

• W punktach poprzednich koncentrowaliśmy się przede

wszystkim na modelach matematycznych. Obok nich
istotną funkcję w Systemach Wspomagania Decyzji
pełnią modele o charakterze graficznym.

• Pakiety tego rodzaju umożliwiają wyświetlanie, ale

również

interakcyjne

tworzenie

różnego

rodzaju

diagramów i wykresów prezentujących dane i informacje.

• Modele graficzne mają często kluczowy charakter,

ponieważ wizualizacja ułatwia decydentom postrzeganie
danych zbiorczych oraz zależności miedzy danymi.

Modele graficzne