KONSTRUKCJE BETONOWE 1b

KONSTRUKCJE BETONOWE 1b

KONSTRUKCJE BETONOWE 1b

KONSTRUKCJE BETONOWE 1b

WYKŁAD nr2

PŁYTY

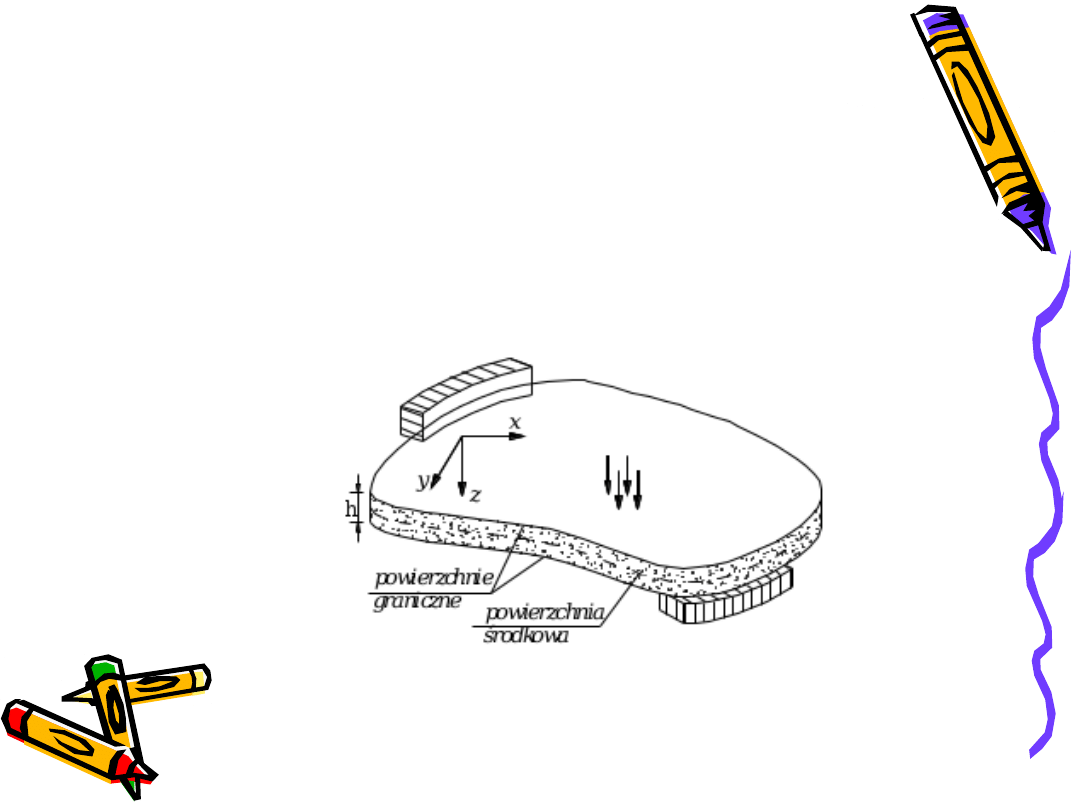
Płytą

nazywamy bryłę materialną, której jeden z wymiarów (grubość) jest

dużo mniejszy od pozostałych, obciążoną prostopadle do płaszczyzny środkowej.

Płyta jest płytą cienką, jeżeli jej grubość nie przekracza 1/10 dłuższej rozpiętości.
.

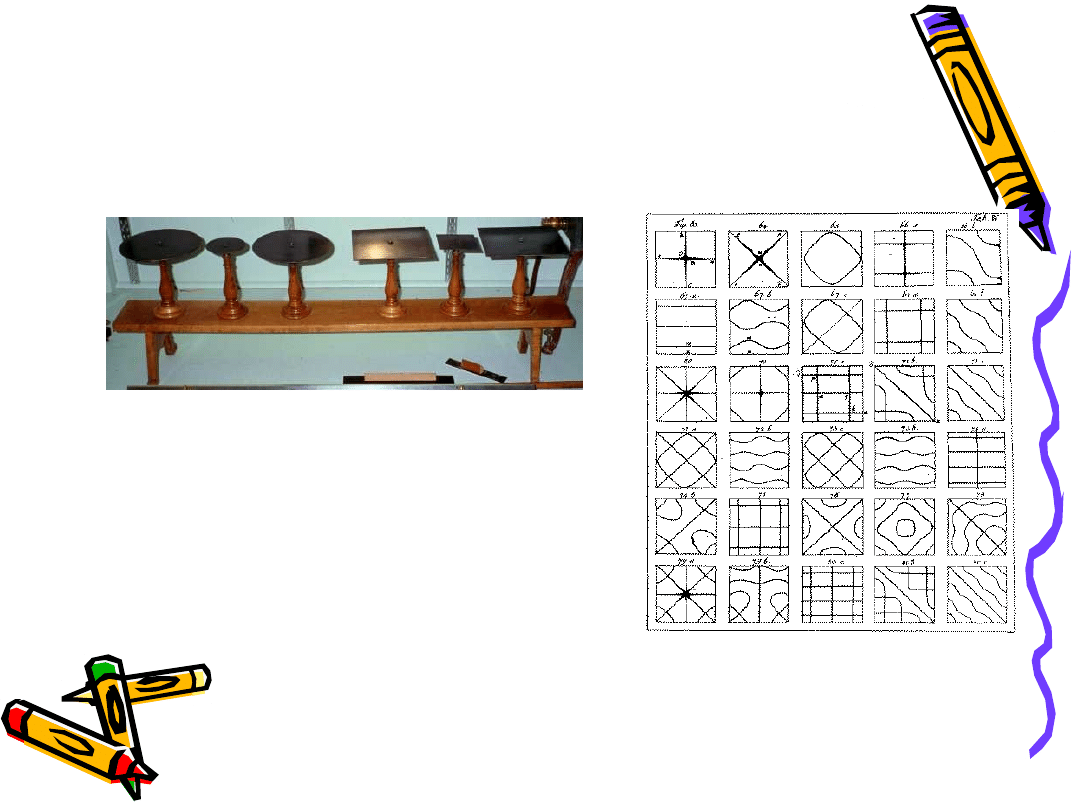
Historyczne początki rozwoju teorii płyt

Pierwsze teoretyczne opisy pracy płyty pojawiły się w końcu XVIII w.
W 1787 roku fizyk E.F.F.Chladni opublikował wyniki doświadczenia.

W 1789 J.Bernoulli roku bazując na
powyższym doświadczeniu przedstawił
Petersburskiej Akademii pracę, w której
przedstawił

równanie

różniczkowe

amplitudy drgań.

M.S.Germain, J.L.Lagrange,
S.D.Poisson, L.M.H.Navier,
A.Cauchy. G.Kirchhoff (1820-
1829)
.

Teoria G.Kirchhoffa (1850) oparta na dwóch hipotezach
kinematycznej
i statycznej do dnia dzisiejszego jest podstawą teorii płyt
cienkich.

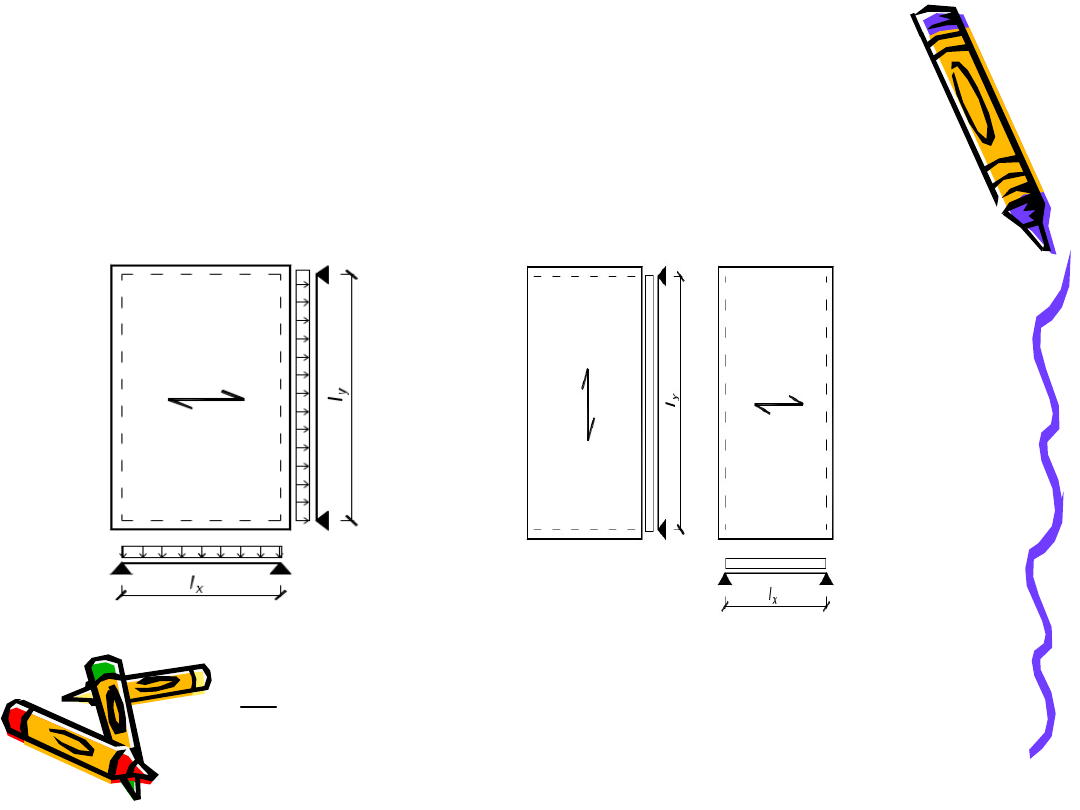
PŁYTY JEDNOKIERUNKOWO ZBROJONE

.

2



x

y

l

l

Sposób podparcia Wymiary Rodzaj
obciążenia

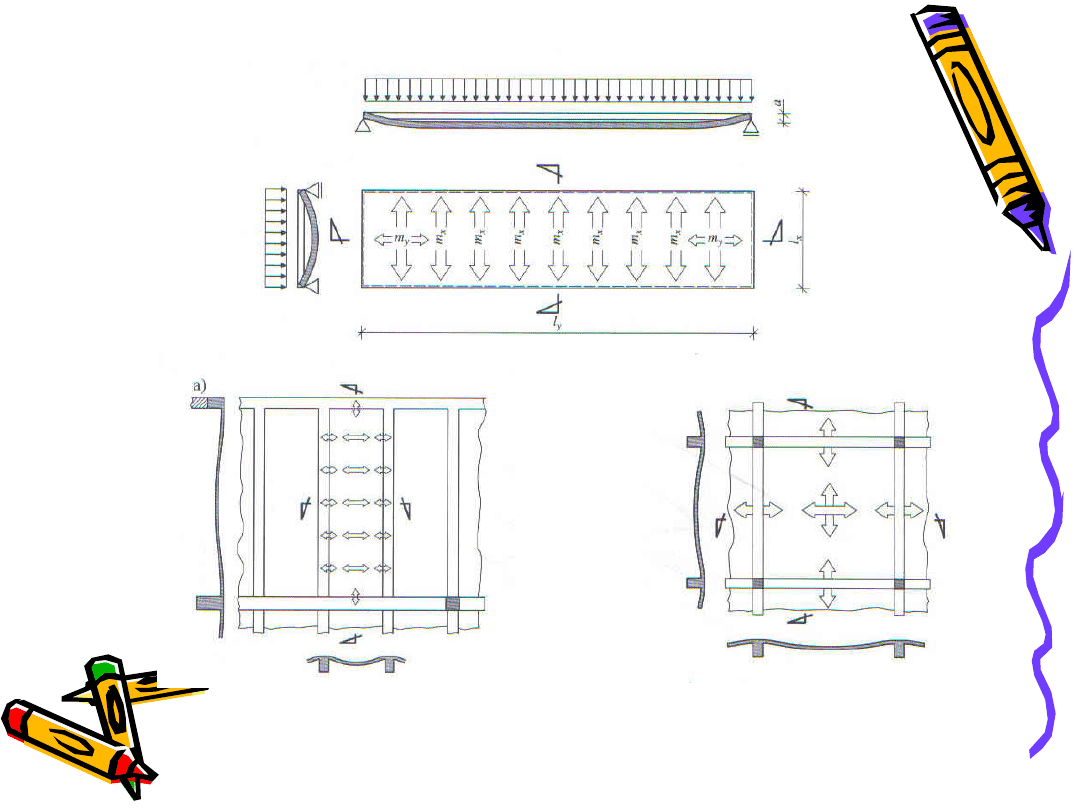
Płyta pracująca jednokierunkowoPłyta pracująca dwukierunkowo

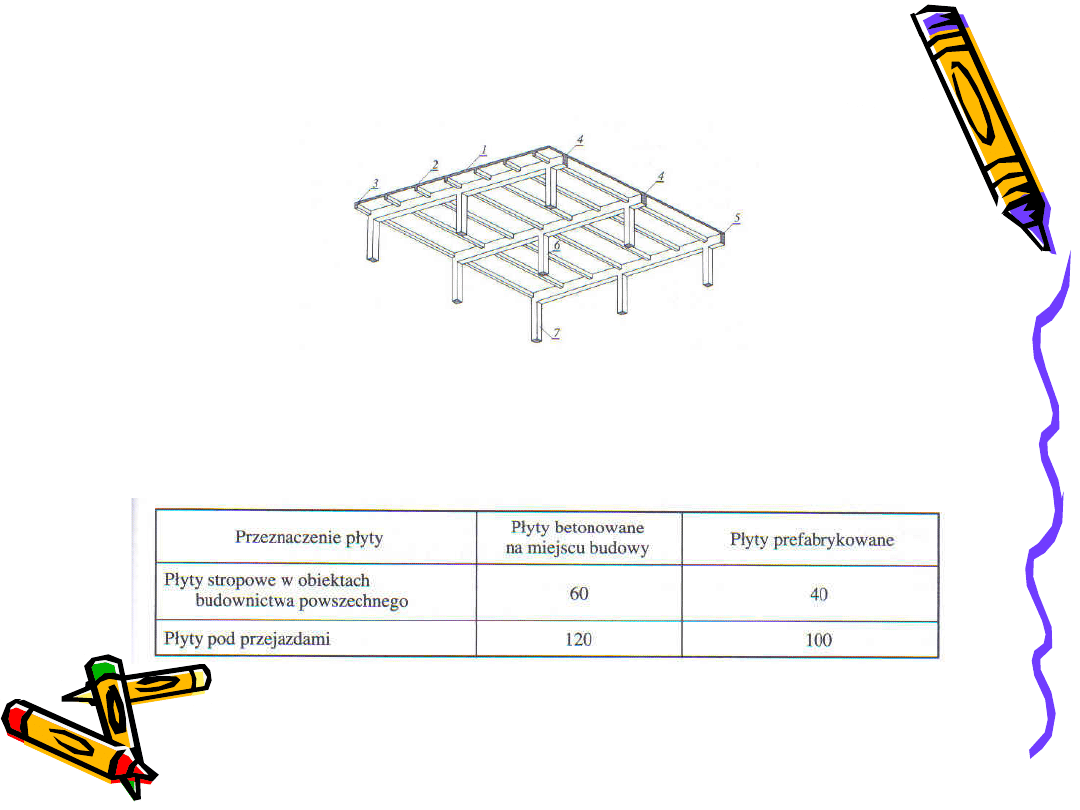
STROPY PŁYTOWO-BELKOWE

Szerokość płyty od 1,8 do 3,5 m

Minimalne grubości płyty w mm

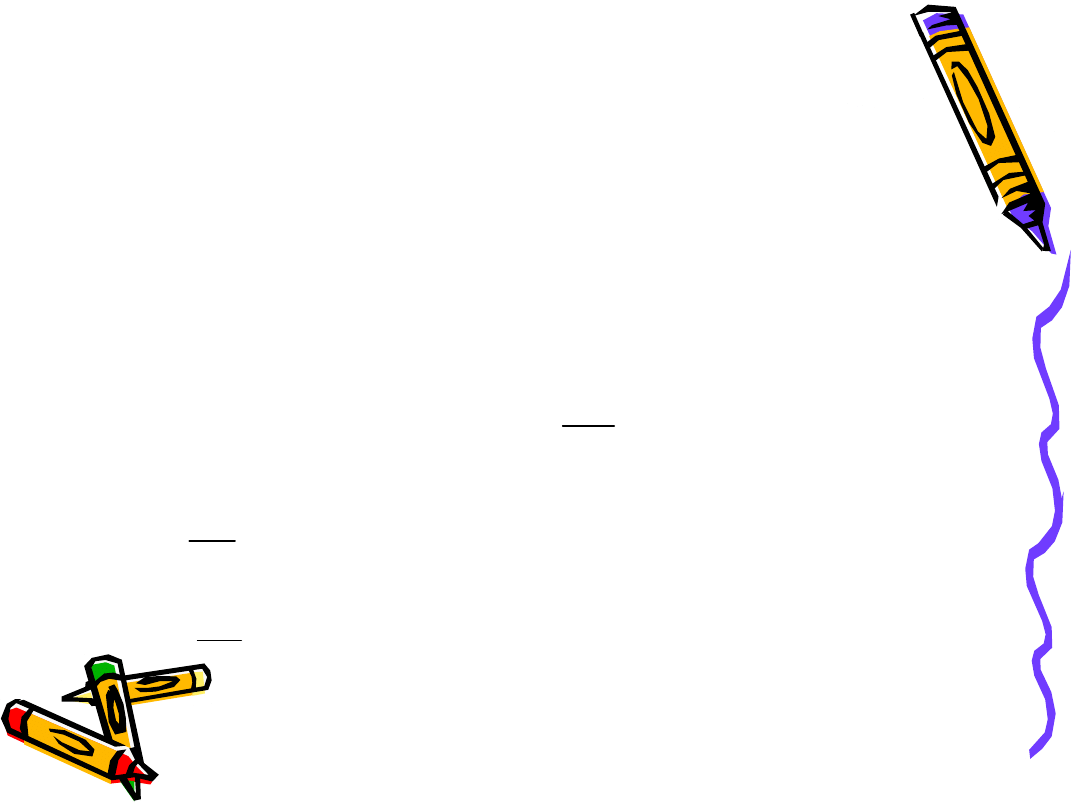
• Stopniowanie grubości płyty co 10 mm.
• Dla h≥120 mm stopniowanie co 20 mm.
• Grubość płyty nie może być mniejsza niż wynika to z warunku

prawidłowego otulenia betonem zbrojenia (PN-B-0324, pkt.
8.1.1.2 Otulenie prętów zbrojeniowych) i z warunku odpowiedniej
ochrony

przeciwpożarowej

(instrukcja

ITB

409/2005

Projektowanie elementów żelbetowych i murowych z uwagi na
odporność ogniową).

• Grubość płyty powinna w miejscu maksymalnego zagęszczenia

zbrojenia mieścić się w granicach









MPa

w

f

f

f

bd

A

cd

yd

cd

s

012

,

0

007

,

0





40



d

l

ef

50



d

l

ef

- płyty swobodnie podparte

- płyty ciągłe

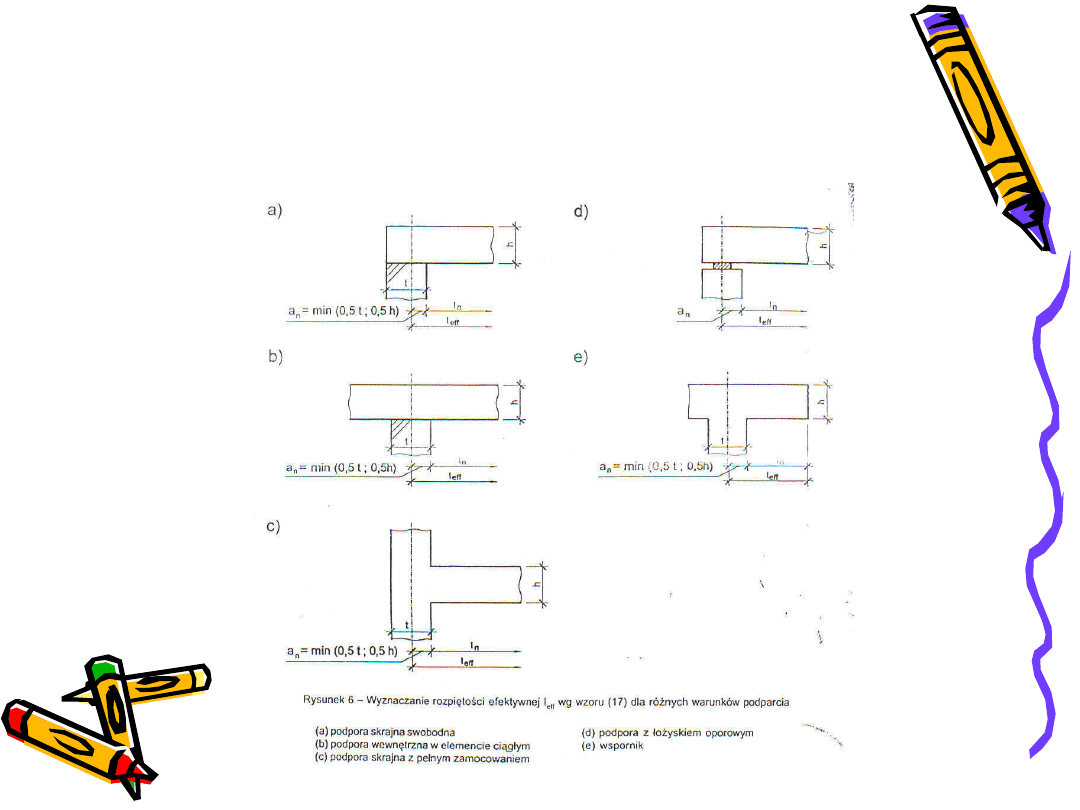
2

1

a

i

a

n

l

2

1

a

a

l

l

n

ef







- rozpiętość w świetle podpór

- wartości a

n

określone

dla sąsiednich podpór

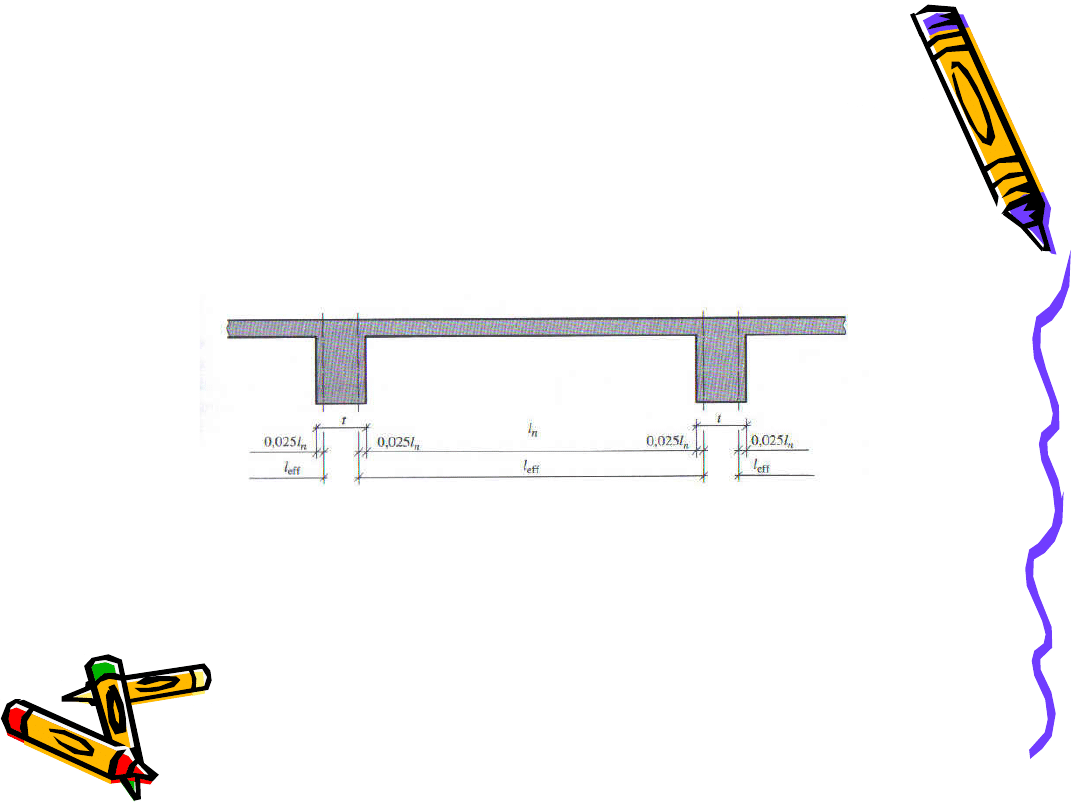
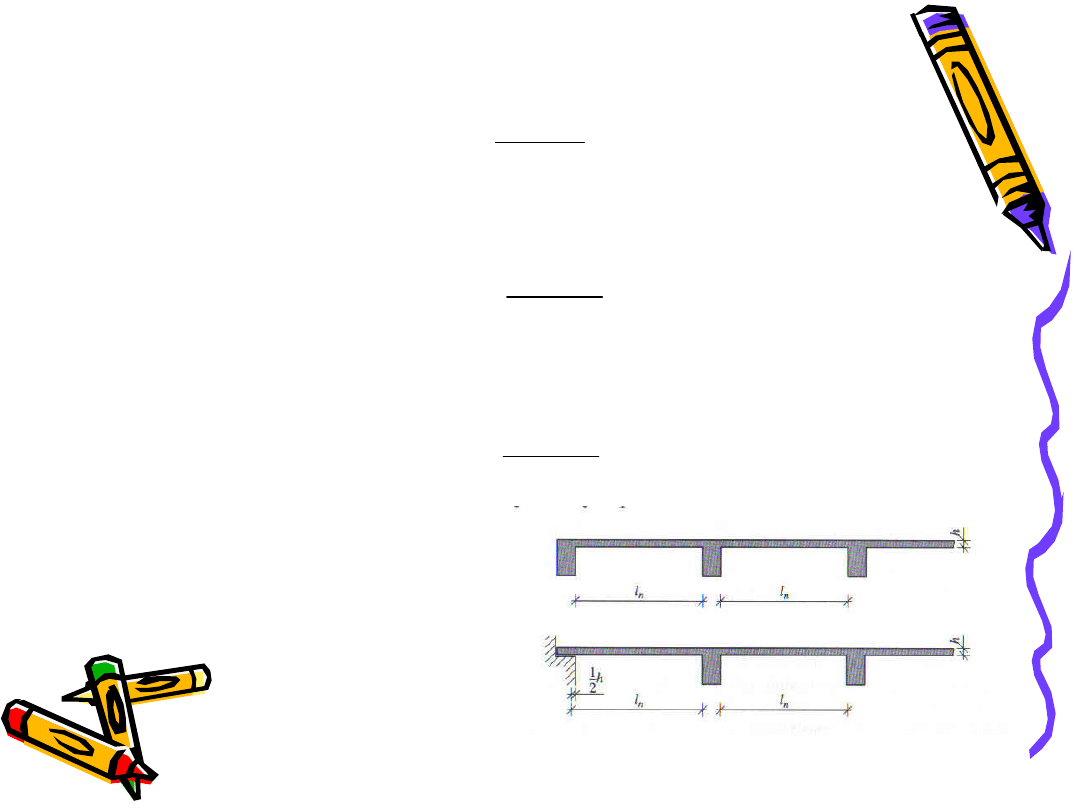
Jeżeli szerokość podpory t przekracza 1/20 rozpiętości
przęsła w świetle l

n

, to za punkt podparcia należy przyjąć

punkt w odległości 0,025 ln od krawędzi podpory

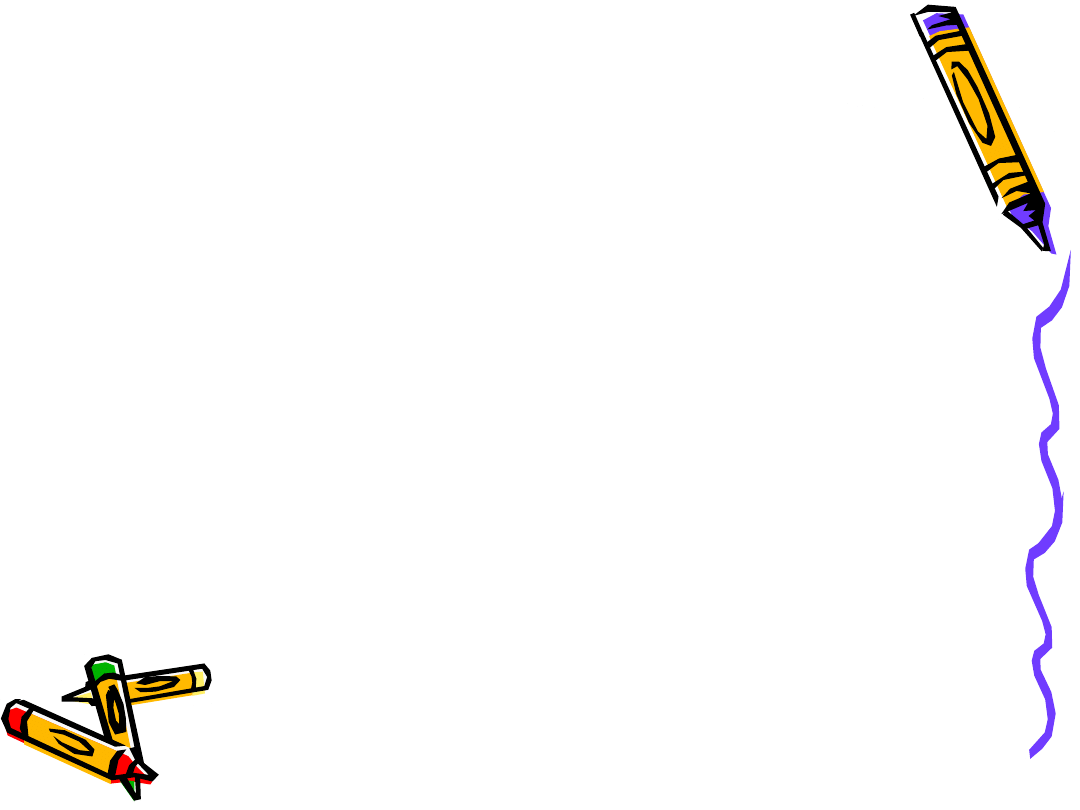
OBLICZENIA

W obliczeniach przyjmuje się model obliczeniowy
konstrukcji, który jest pewną idealizacją konstrukcji
rzeczywistej i jej zachowania.
Metody obliczeniowe:
• teoria sprężystości
założenia:

- liniowa zależność miedzy naprężeniem i

odkształceniem

- średnie wartości modułu sprężystości
- brak zarysowań przekrojów poprzecznych

• analiza liniowo - sprężysta z ograniczoną redystrybucją
(metoda
plastycznego wyrównywania momentów)

założenia jak w analizie sprężystej z wyłączeniem

węzłów,
w których przewidziano redystrybucję
momentów, która
prowadzi do liniowych zmian momentów w
pozostałej części
elementu
-

•

teoria plastyczności (teoria nośności granicznej)

Podstawy teorii stworzył K.W. Johansen formułując metodę linii załomów.
Linia załomów tworzy siatkę, dzieląc płytę na płaty, które traktowane są
jako sztywne, połączone plastycznym zawiasem, płyt przekształca się
w mechanizm. Zakłada się, że odkształcenia płyty są małe, mechanizm
zniszczenia nie zmienia się w procesie odkształcenia.

Obraz zarysowania płyty pracującej
dwukierunkowo

Model płyty w stanie
granicznym

• modele nieliniowe
Przyjmuje się w każdym przekroju sztywność zgodną z jego
kształtem,
zbrojeniem i aktualnym poziomem wytężenia.
Charakterystyki materiałów określają sztywność
przekroju w sposób
zbliżony do rzeczywistego

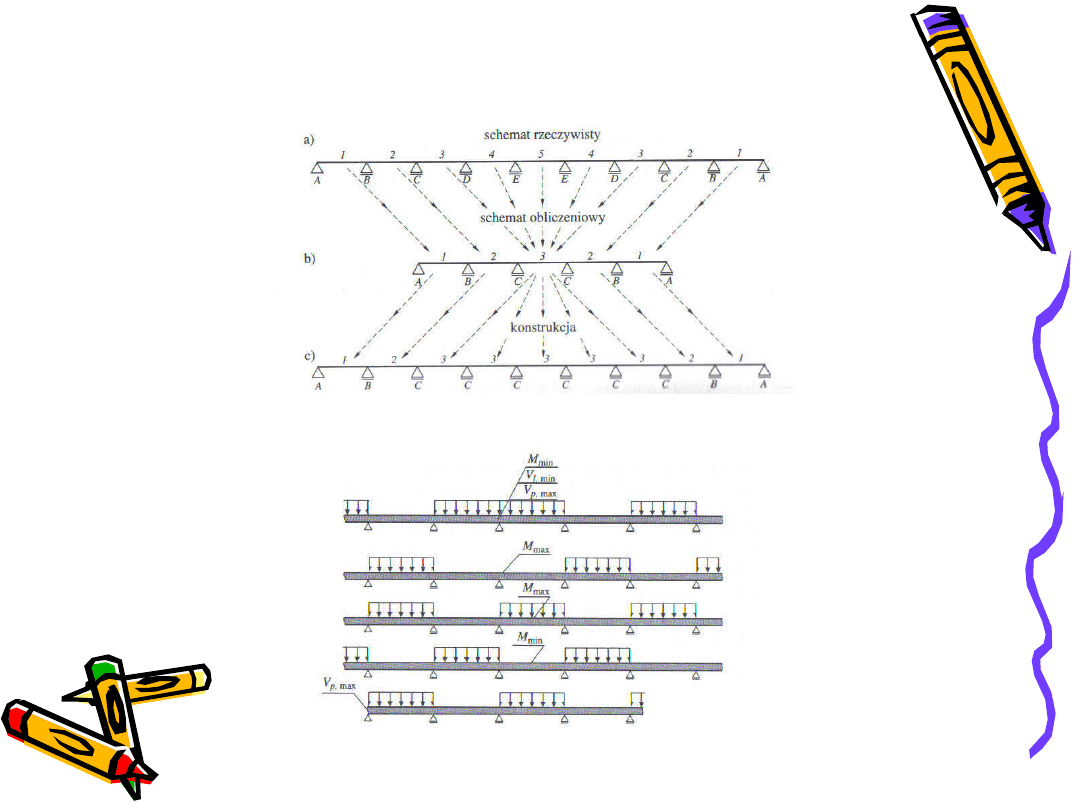
Zamiana rzeczywistego schematu konstrukcji na schemat obliczeniowy

Przykładowy schemat ustawienia obciążeń zmiennych

OBLICZANIE STATYCZNE PŁYT

jednokierunkowo zbrojonych

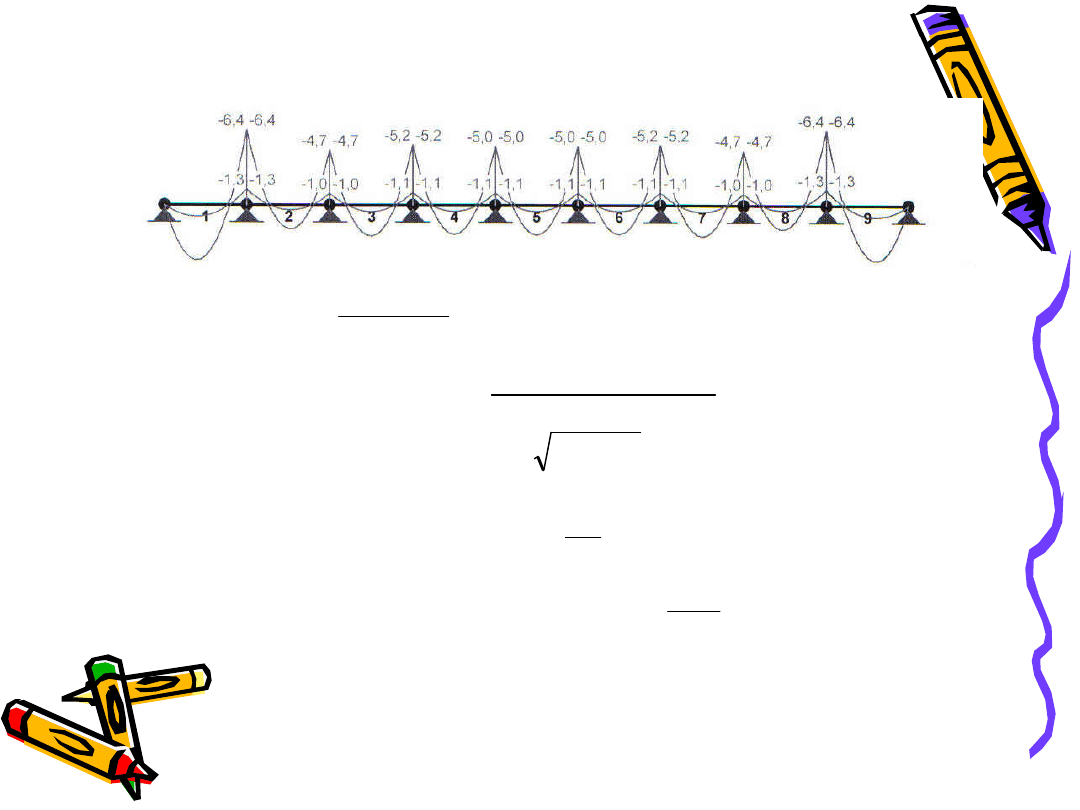
cd

sd

cc

f

d

b

M

S

2



m

b 1



/m

cm

3,954

A

/m

m

3,954x10

210

13,3

08x

0,078x1x0,

A

f

f

bd

ξ

A

2002)

:

03264

-

B

-

PN

(tabl.9

0,62

ξ

0,078

ξ

2S

1

1

ξ

0,075

x13,3x10

1x0,08

6,4

S

2

s1

2

4

s1

yd

cd

ef

s1

lim

ef,

ef

cc

ef

3

2

cc



























Dane;
Beton C30/25, fcd=13,3MPa
Stal A-I, fyd=210 MPa
Msd=6,4 kNm
h=0,1 m

Dla klasy ekspozycji XO
d=0,08 m

Teoria sprężystości

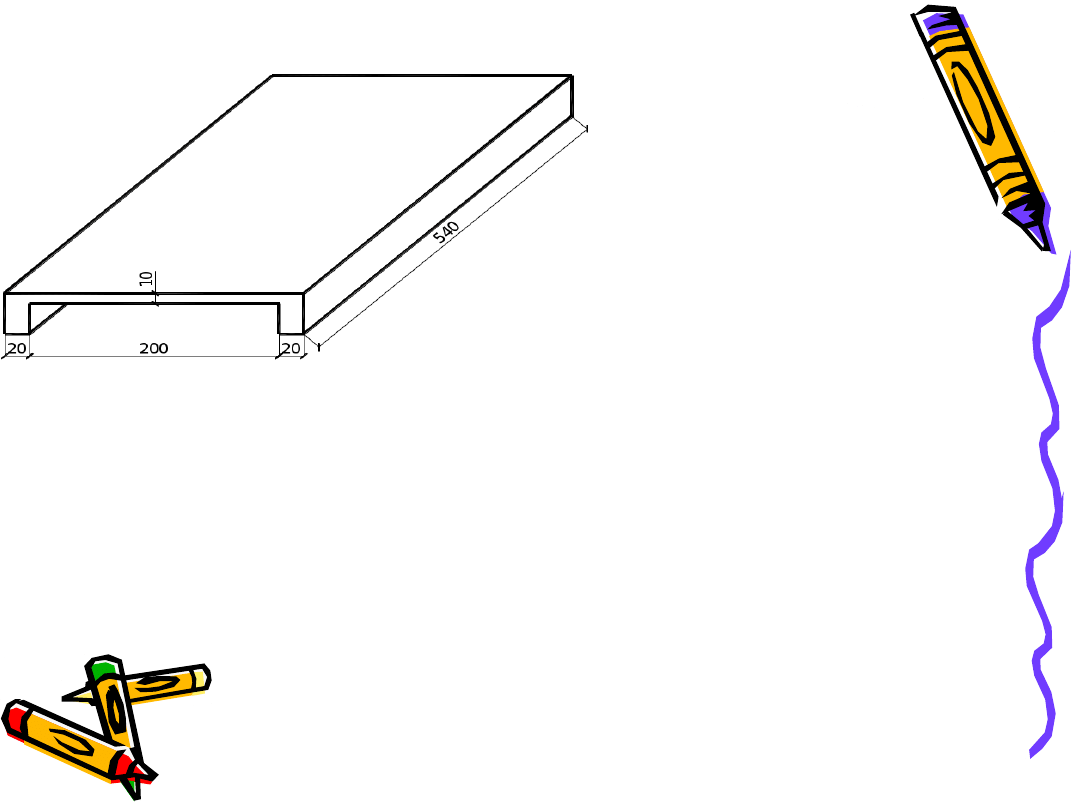
Przykład nr 2
Zaprojektuj płytę
żelbetową
Dane;
Beton C30/25,
f

cd

=13,3MPa,

g

b

=25 kN/m

3

,

Stal A-I, f

yd

=210 MPa,

h=0,1 m,
p=7 kN/m

2.

Dla klasy ekspozycji XO
d=0,1 – 0,02= 0,08 m
ly/lx=5,4/2,4=2,25>2 Płyta jednokierunkowo
zbrojona
l

ef

= l

n

+a

1

+a

2

a

n

= min(0,5h;0,5t)

a

n

= min(0,5x0,1;0,5x0,2) = min(0,05;0,1)

l

ef

= 2+2x0,05 = 2,1 m

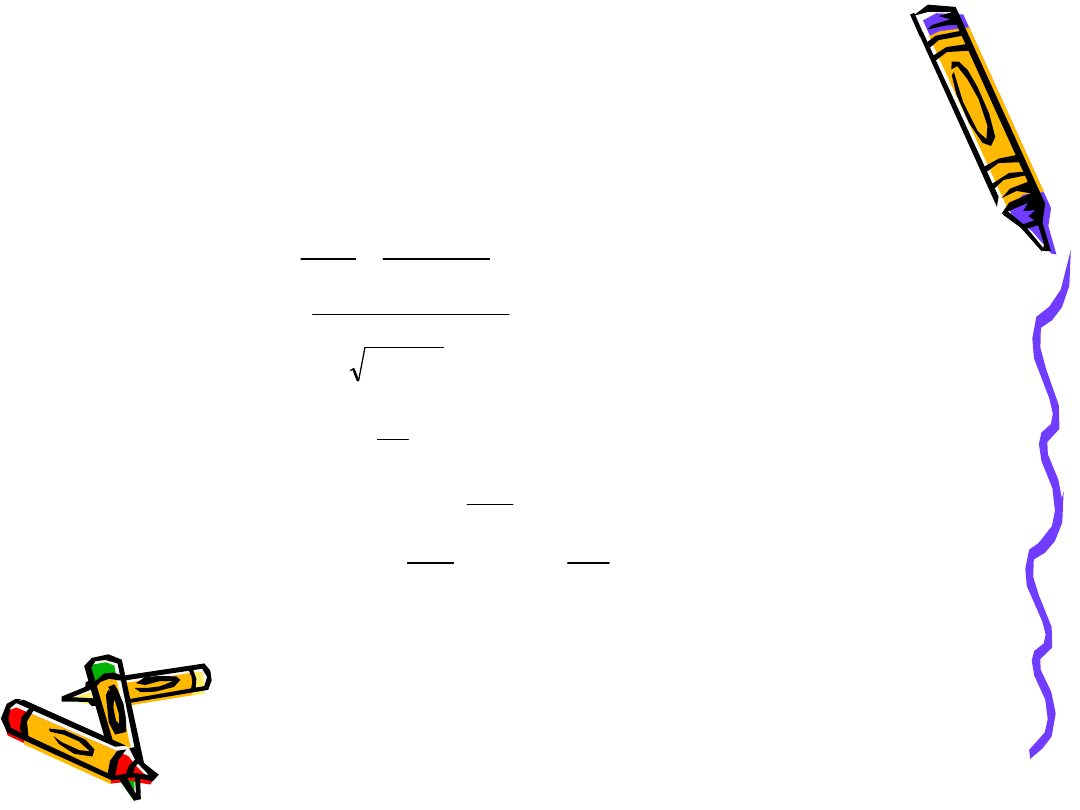
/m

cm

3,93

cm

10

co

6/8

przyj.

/m

cm

3,8

A

A

/m

m

3,8x10

210

13,3

08x

0,075x1x0,

A

f

f

bd

ξ

A

2002)

:

03264

-

B

-

PN

(tabl.9

0,62

ξ

0,075

ξ

2S

1

1

ξ

0,072

x13,3x10

1x0,08

6,15

S

8

gl

M

2

2

s1

min

s1,

2

4

s1

yd

cd

ef

s1

lim

ef,

ef

cc

ef

3

2

cc

ef

2









































































2

4

2

4

2

10

04

,

1

08

,

0

1

013

,

0

0013

,

0

10

9

,

1

08

,

0

1

240

2

,

2

26

,

0

26

,

0

/

15

,

6

8

1

,

2

15

,

11

m

bd

m

bd

f

f

m

kNm

x

yk

ctm

p

d

=7x1,2=8,4 kN/m

2

q

d

=0,1x25x1,1=2,75 kN/m

2

g=8,4+2,75=11,15 kN/m

2

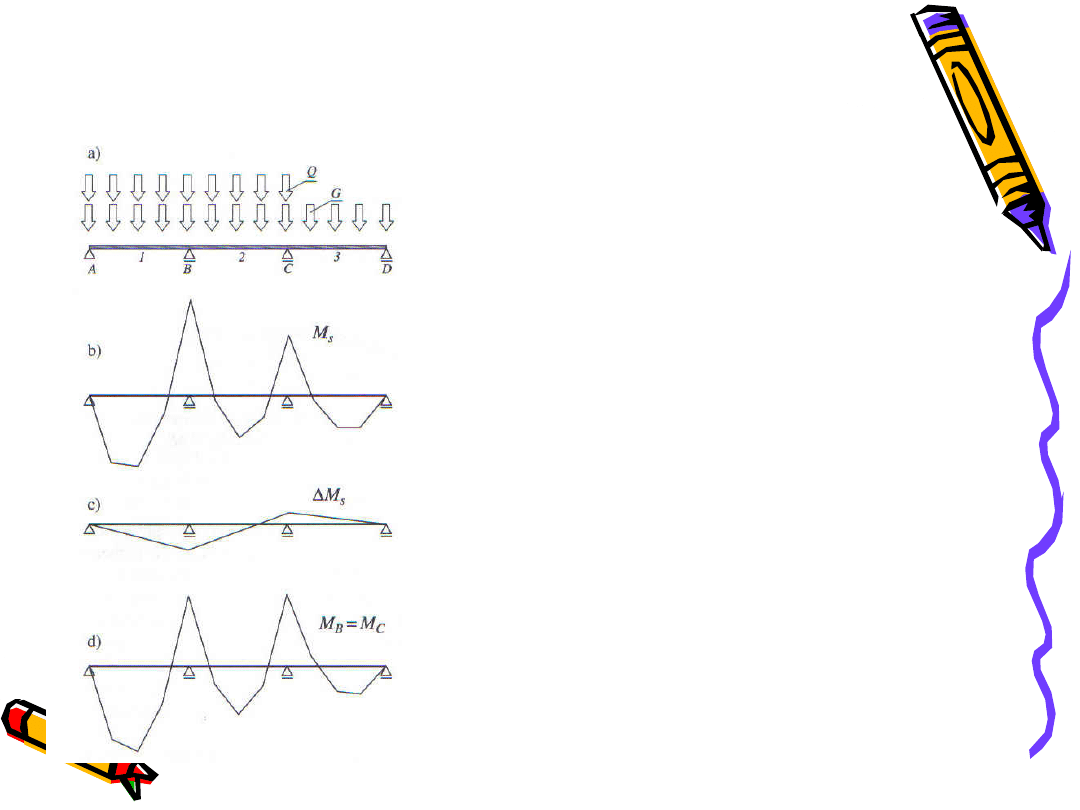
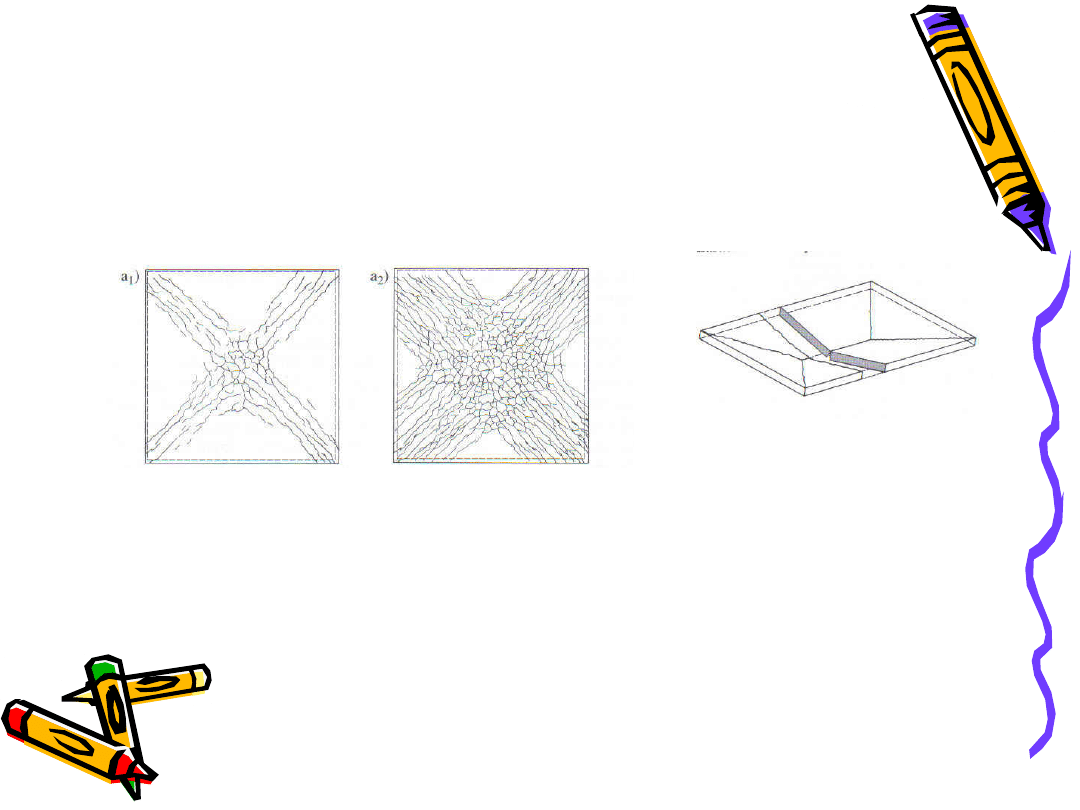
Metoda plastycznego wyrównywania

momentu

Dla dowolnego obciążenia (a) ustrój
rozwiązuje się przyjmując pracę sprężystą
(b). Wprowadza się dodatkowe momenty
podporowe DM , dowolnego znaku, o
ograniczonej

wartości.

Dodatkowe

momenty podporowe powodują powstanie
dodatkowych liniowo zmienne momentów
(c).

Są

to

momenty

wyrównania

plastycznego.

Ostateczny

wynik

po

redystrybucji

to

zsumowanie

tych

momentów z pierwotnym wykresem (d).
Norma żąda, aby w przypadku płyt
momenty po wyrównaniu M

w

nie różnił się

od momentu dla rozwiązania sprężystego
M

s

o więcej niż 30%

M

w

≤ (0±0,3) M

s

Metodę można stosować dla płyt jednokierunkowo zbrojonych jeżeli
a)M

p

/M

g

≤ 2

M

p

-moment od obciążenia użytkowego

M

g

– moment od obciążenia stałego

b) Płyty ciągle są monolitycznie połączone z belkami
c) Zbrojenie płyty żelbetowej jest wykonane ze stali klasy od A-0 do
A-III
d) Przekroje płyty są tak dobrane, że ξ

ef

≤ 0,7ξ

ef,lim

Jeżeli rozpiętość poszczególnych przęseł nie różni się więcej niż o
20%, momenty zginające można obliczać za pomocą wzorów
• w przęśle skrajnym





11

2

1

n

l

q

g

M





• W przęsłach wewnętrznych





16

2

2

n

l

q

g

M





• Na pierwszej podporze wewnętrznej





11

2

1

n

l

q

g

M







• Na pozostałych podporach wewnętrznych





16

2

2

n

l

q

g

M







l

n

– rozpiętość w świetle

g – obciążenie stałe
q – obciążenie zmienne

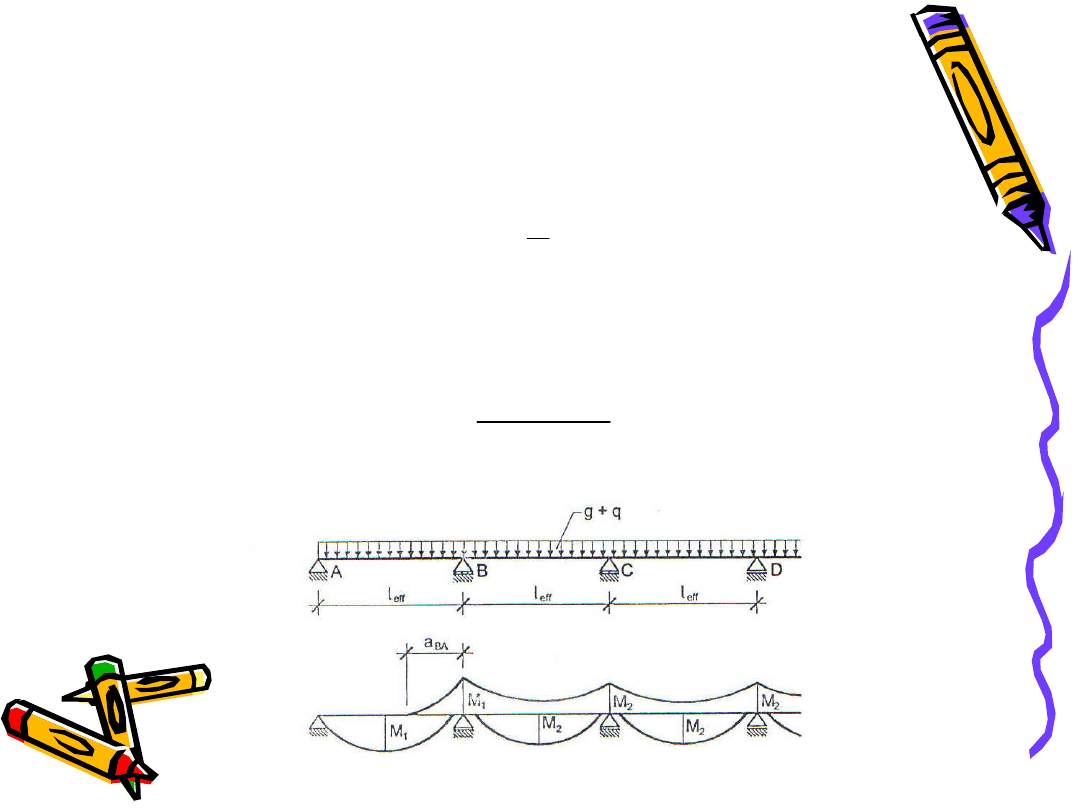
• Wartości momentów minimalnych w przęsłach pośrednich

należy obliczać przy przyjęciu wartości momentów
podporowych wyznaczonych jak wyżej zakładając, że
przęsła obciążone są zstępczym obciążeniem o wartości

4

q

g

q

p





• Zasięg w prześle skrajnym momentu podporowego na

podporze przedskrajnej wyznacza się ze wzoru





p

ef

BA

q

l

q

g

a

8





Głębokość oparcia płyt na podporze powinna zapewniać
właściwe zakotwienie zbrojenia i powinna być nie mniejsza
niż:
• 80 mm przy oparciu na murze, ścianie z betonu lekkiego
lub zwykłego klasy B15,
• 60 mm przy oparciu na ścianie z betonu zwykłego klasy
wyższej
niż B15,
• 40 mm przy oparciu na stalowych belkach.
Głębokość oparcia prefabrykowanych płyt zbrojonych
powinna być nie mniejsza niż 40 mm.

KONSTRUKCA PŁYT

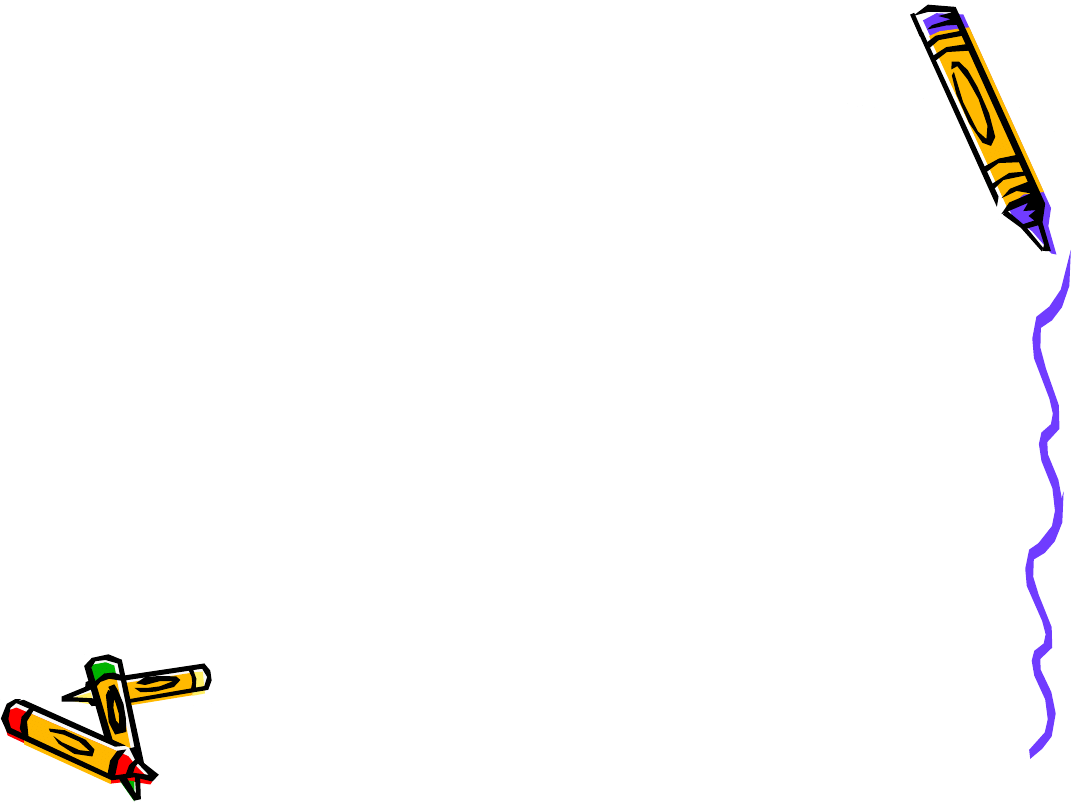
Zbrojenie główne

Średnica prętów zbrojenia głównego powinna być nie mniejsza niż
4,5 mm.

Największe rozstawy prętów zbrojeniowych w miejscu występowania
max momentów i obciążeń skupionych nie powinna być większy niż:
• 120 mm – dla płyt o h≤100 mm,
• 1,2 h – dla płyt o h>100 mm,
• Max rozstaw prętów głównych nie powinien być większy niż 25 cm.

Do podpory należy doprowadzić nie mniej niż 1/3 zbrojenia
przęsłowego
i przynajmniej trzy pręty na 1 m długości.

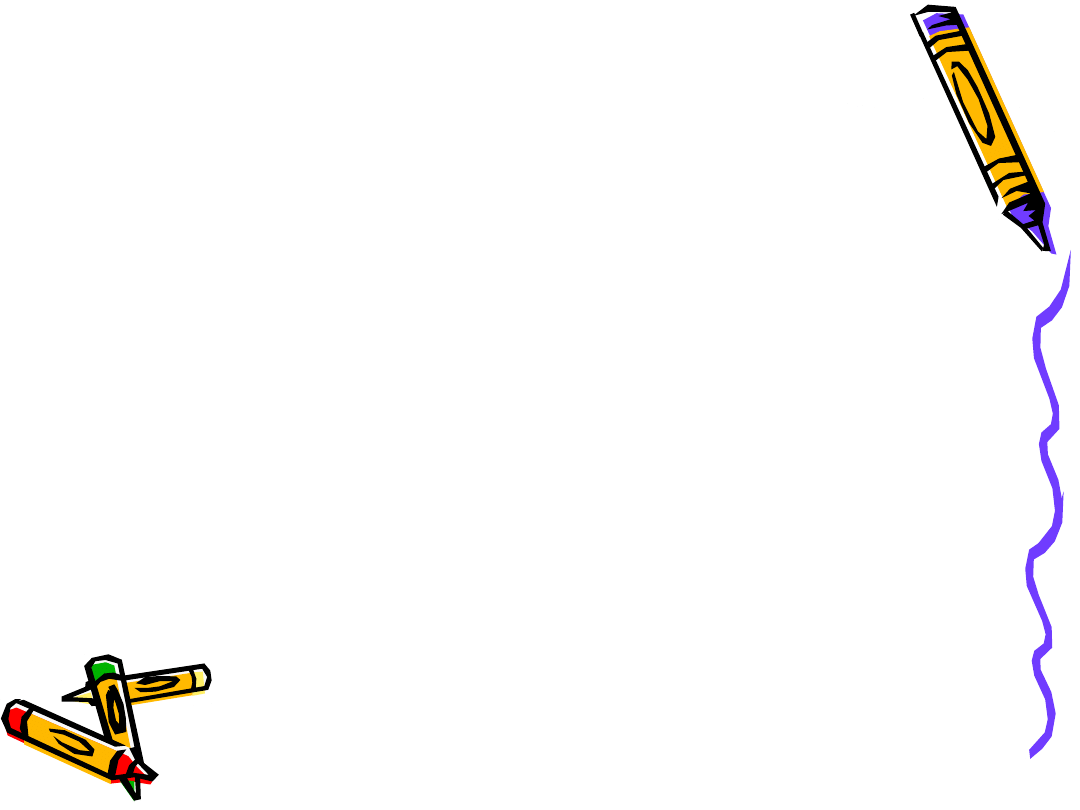
Zbrojenie rozdzielcze

umieszcza się prostopadle do zbrojenia

głównego.
Zadanie:
• rozkłada równomiernie obciążenie od sił skupionych,
• przeciwdziała odkształceniom skurczowym,
• ułatwia montaż dzięki polaczeniu z prętami głównymi.

Średnica prętów rozdzielczych nie mniej niż 4,5 mm.
Rozstaw prętów rozdzielczych nie powinien przekraczać 300mm oraz
łączyna nośność nie powinna być mniejsza niż:
• 1/10 nośności zbrojenia głównego przy obciążeniu równomiernym,
• 1/4 nośności zbrojenia głównego, gdy momenty zginające wywołane
obciążeniami skupionymi są nie większe niż 50% momentów
całkowitych.
W przeciwnym przypadku zbrojenie prostopadłe do zbrojenia
głównego
należy obliczyć.

Połączenie płyty z podciągiem

Połączenie płyty z wieńcem Połączenie płyty z podciągiem

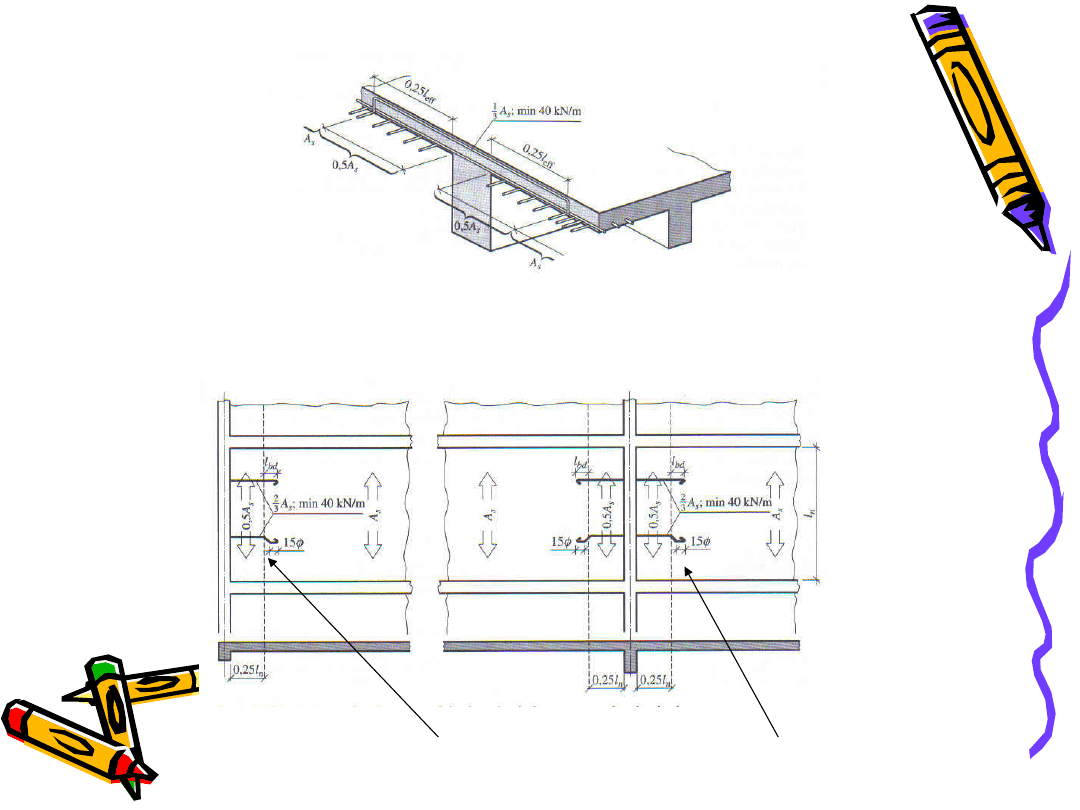
Zakotwienie prętów na podporze

Kotwienie wkładek na podporze

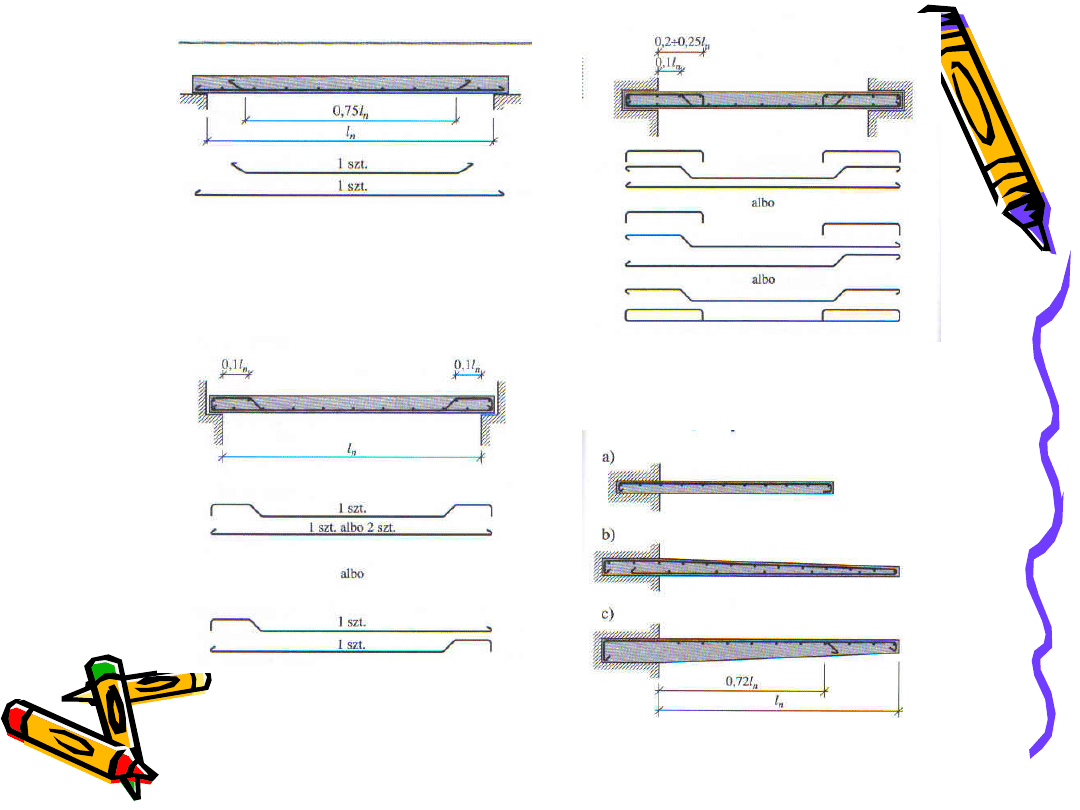
Zbrojenie płyty jednoprzęsłowej

swobodnie podpartej

Zbrojenie płyty jednoprzęsłowej

częściowo zamocowanej na podporze

Zbrojenie płyty jednoprzęsłowej

zamocowanej na podporze

Zbrojenie wsporników

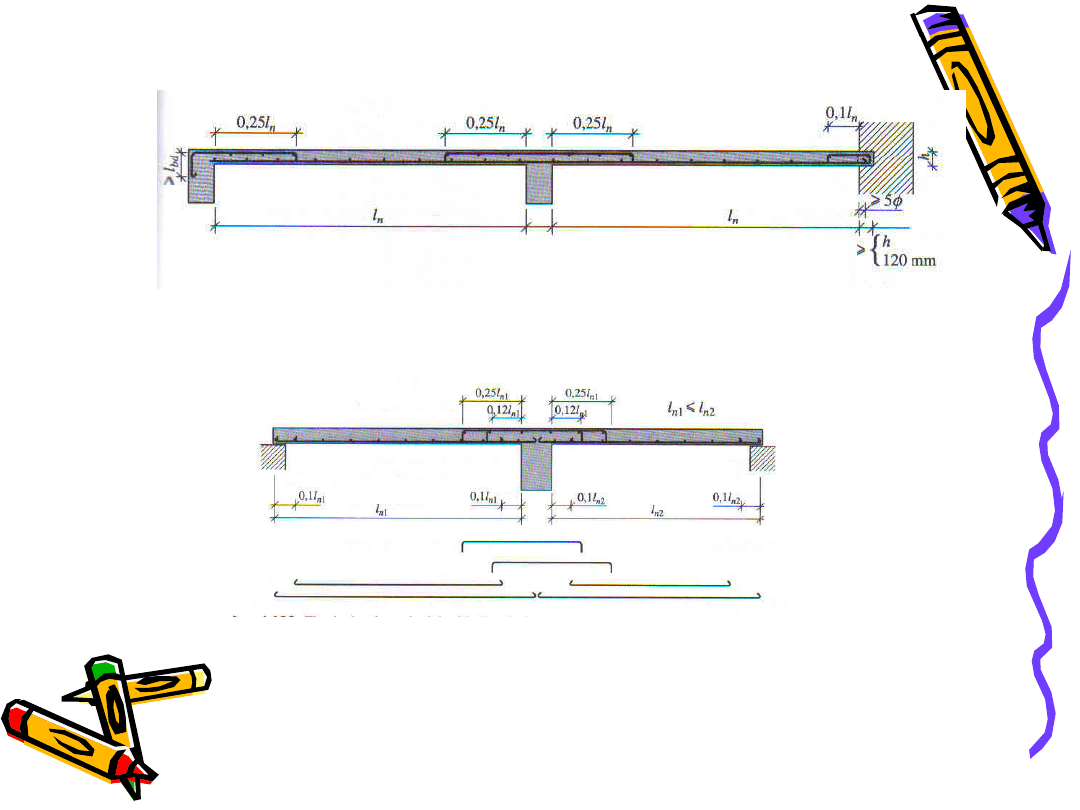
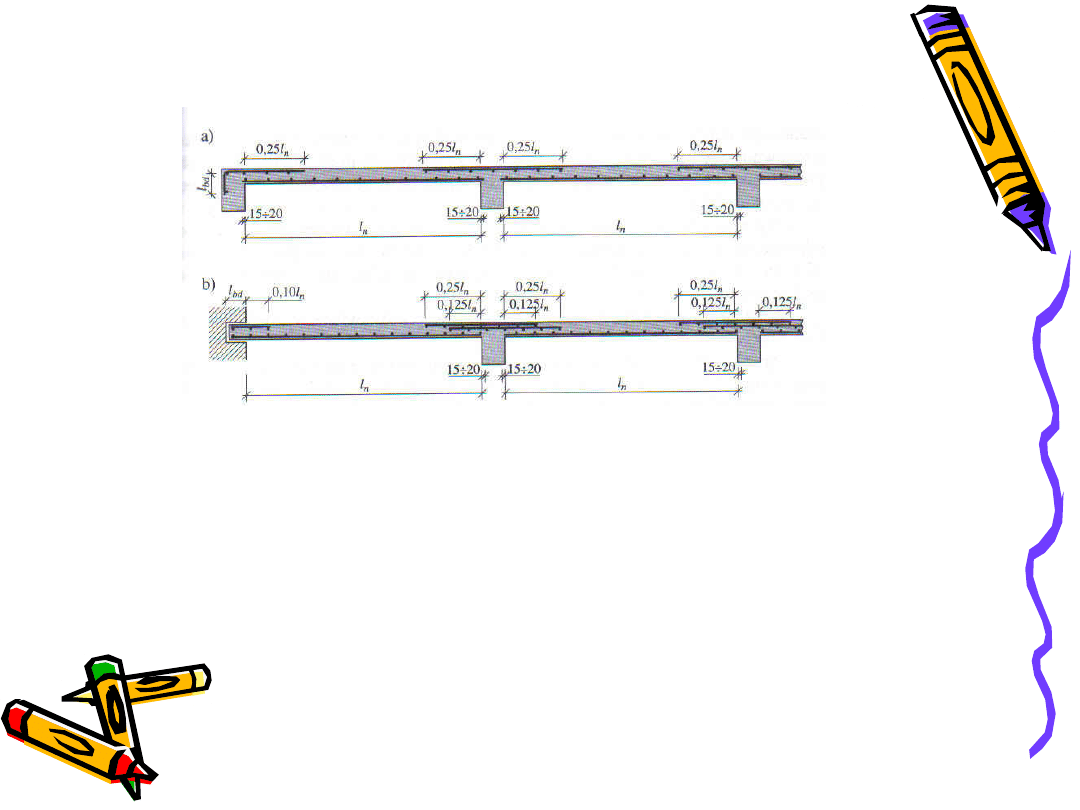
Zbrojenie płyty ciągłej wkładkami nieodginanymi o stałej intensywności

Zbrojenie płyty ciągłej wkładkami nieodginanymi o zmiennej intensywności

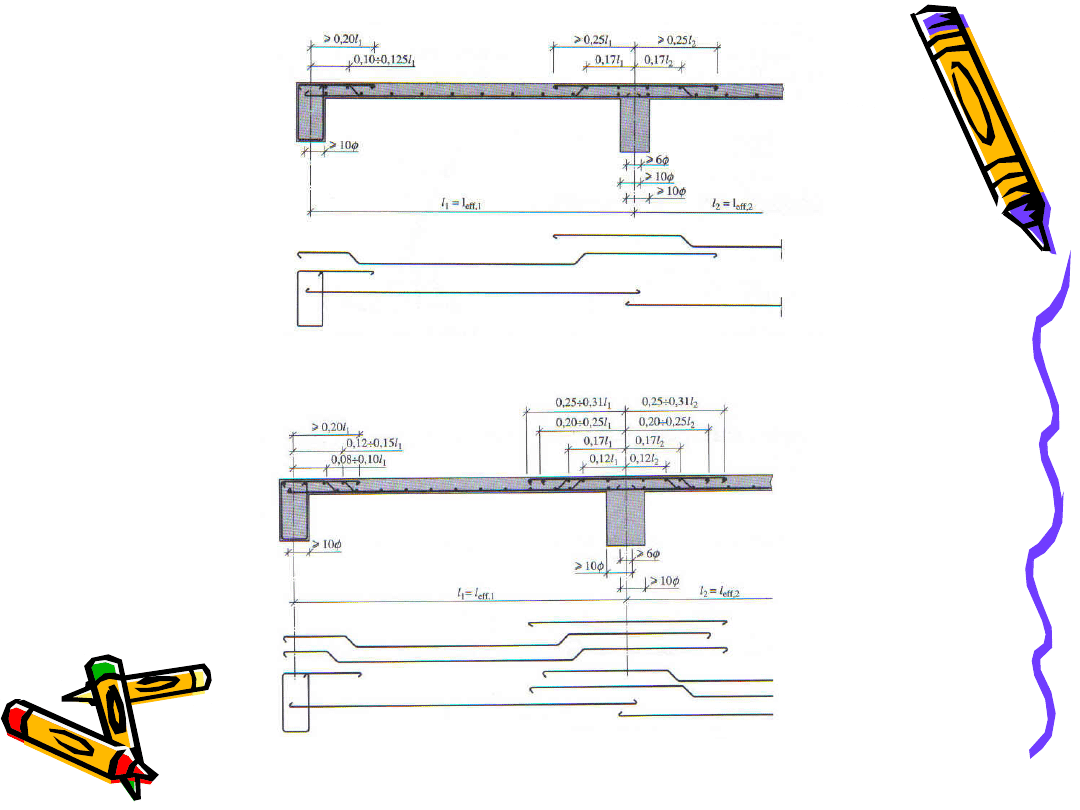
Zbrojenie płyty ciągłej wkładkami odginanymi w jednej warstwie

Zbrojenie płyty ciągłej wkładkami odginanymi w dwóch warstwach

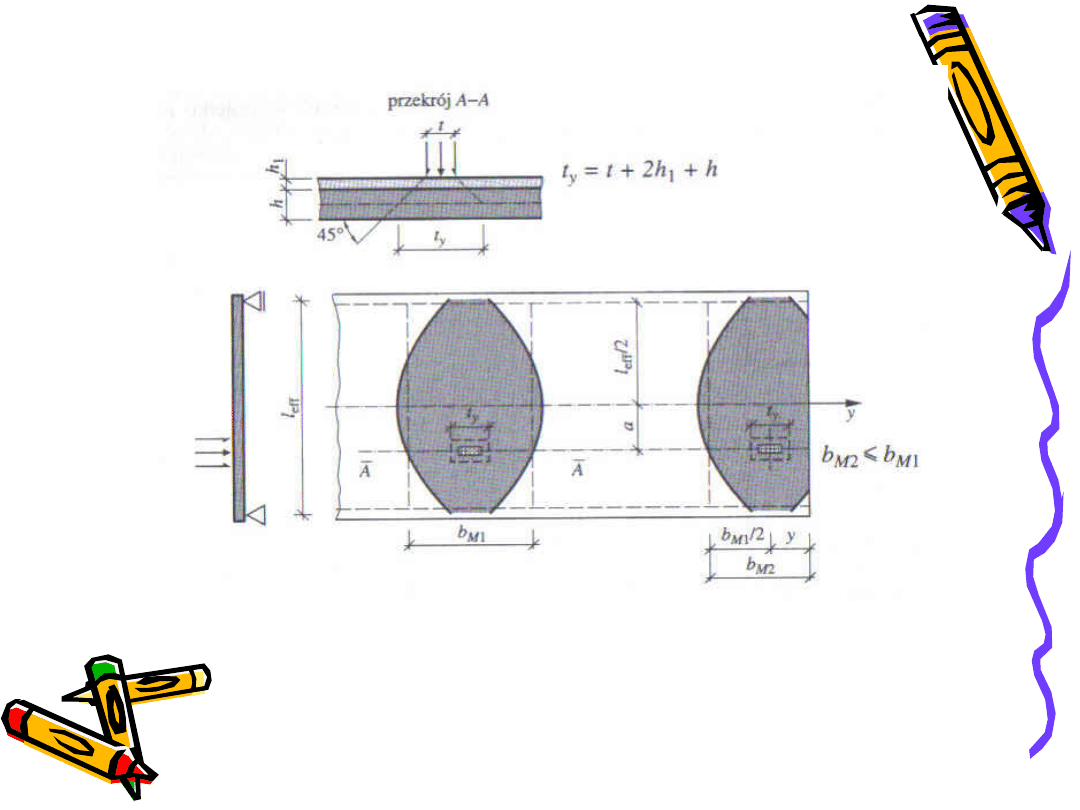
t – szerokość powierzchni, na którą oddziałuje

obciążenie skupione

h

1

– grubość warstwy leżącej na płycie

h – grubość płyty





















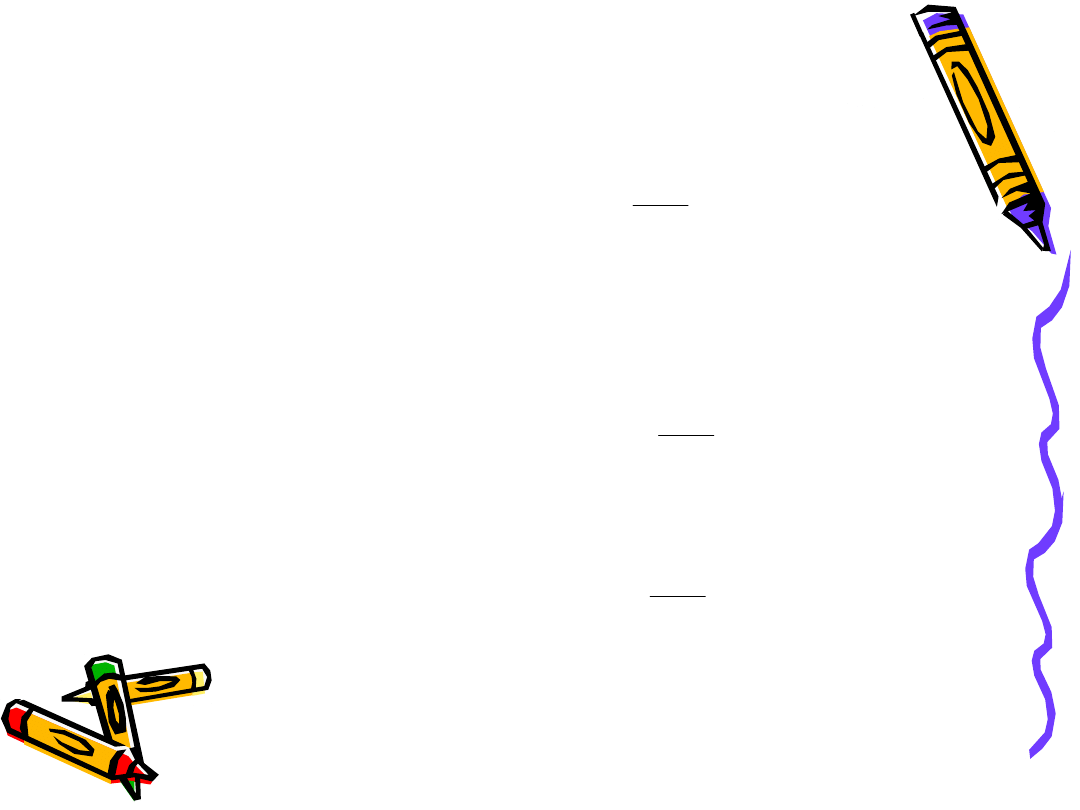
ef

ef

y

M

l

a

l

t

b

2

1

1

4

75

,

0

h

h

t

t

y

y







1

1

2





















ef

ef

y

M

l

a

l

t

b

2

1

1

4

5

,

0

Dla płyty zamocowanej jednej podporze i opartej swobodnie
na drugiej oraz dla przęseł skrajnych płyt ciągłych

Dla płyty swobodnie podpartej

Dla płyty zamocowanej na podporach oraz dla środkowych
przęseł płyt ciągłych





















ef

ef

y

M

l

a

l

t

b

2

1

1

4

625

,

0

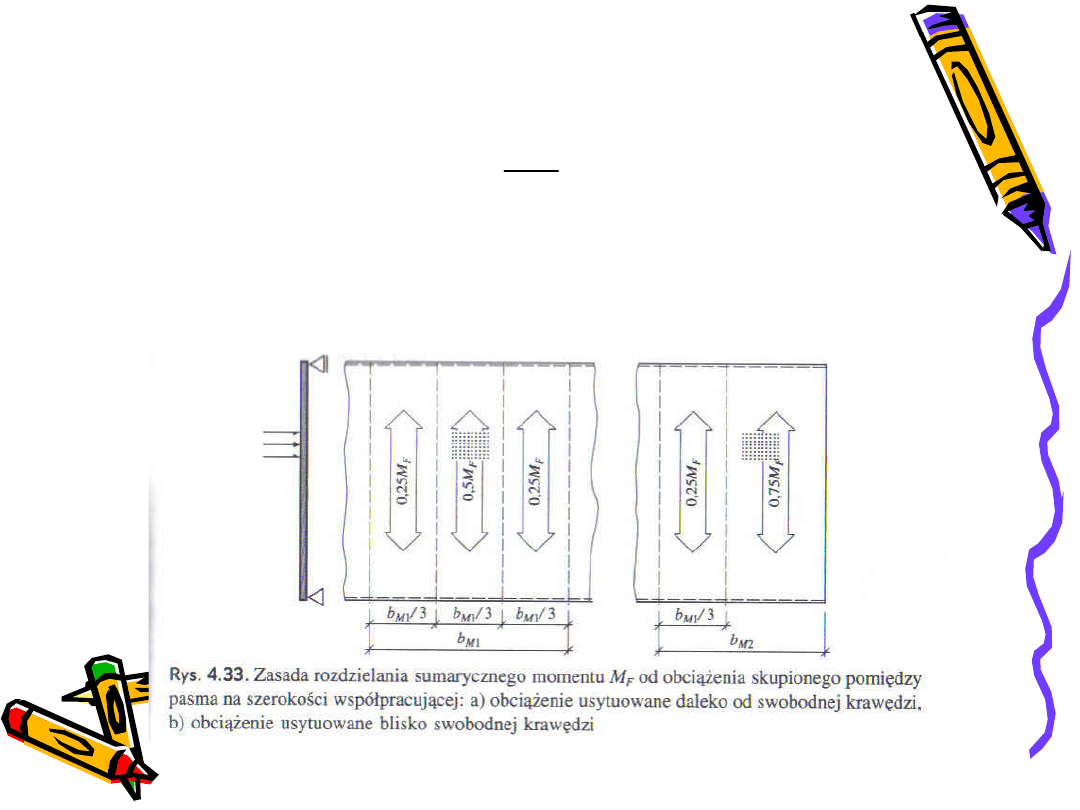
2

1

M

b

y 

Szerokość określa się jako b

M2

Jeżeli odległość obciążenia y od krawędzi swobodnej jest
mniejsza niż b

M1

/2

1

2

5

,

0

M

M

b

y

b





Pytania na egzamin

5.

Kiedy płytę projektujemy jako płytę jednokierunkowo
zbrojoną.

6.

Zadanie - przykład 2.

7.

Konstrukcja płyt.

8.

Zbrojenie płyt jednoprzęsłowych.

9.

Zbrojenie płyty ciągłej jednokierunkowo zbrojonej.