4. STRATY
OBJĘTOŚCIOWE
Straty objętościowe w układzie hydraulicznym to straty występujące w elementach tego
układu. Natomiast strata objętościowa w elemencie hydraulicznym występuje w różnego
rodzaju szczelinach. Rodzaj szczeliny i jej położenie w elemencie hydraulicznym decydują
między innymi o wartości straty objętościowej.
Szczelinowe straty objętościowe wyznacza się wychodząc z podstawowego równania
przepływu Naviera-Stokesa oraz z równania ciągłości przepływu.
Równanie Naviera-Stokesa zapisuje się w postaci ogólnej jako:
,
(4.1)
oraz równanie ciągłości przepływu w postaci (4.2):
.
(4.2)
W przypadku stosowania układu współrzędnych prostokątnych równanie (4.1) można rozpisać:
,
(4.3)
,
(4.4)
.
(4.5)
p
grad
1
v
grad
div
v
grad
v
t
v
0
v
div
x
p
1
z
x
y
x
x
x
z
x
z
y
x
y
x
x
x
t
x
2
2
2
2
2
2
y
p
1
z
y
y
y
x
y
z
y
z
y
y
y
x
y
x
t
y
2
2
2
2
2
2
z
p
1
z
z
y
z
x
z
z
z
z
y
z
y
x
z
x
t
z
2
2
2
2
2
2
Natomiast równanie (4.2) w zapisie szczegółowym w układzie współrzędnych prostokątnych
przedstawia się następująco:
.
(4.6)
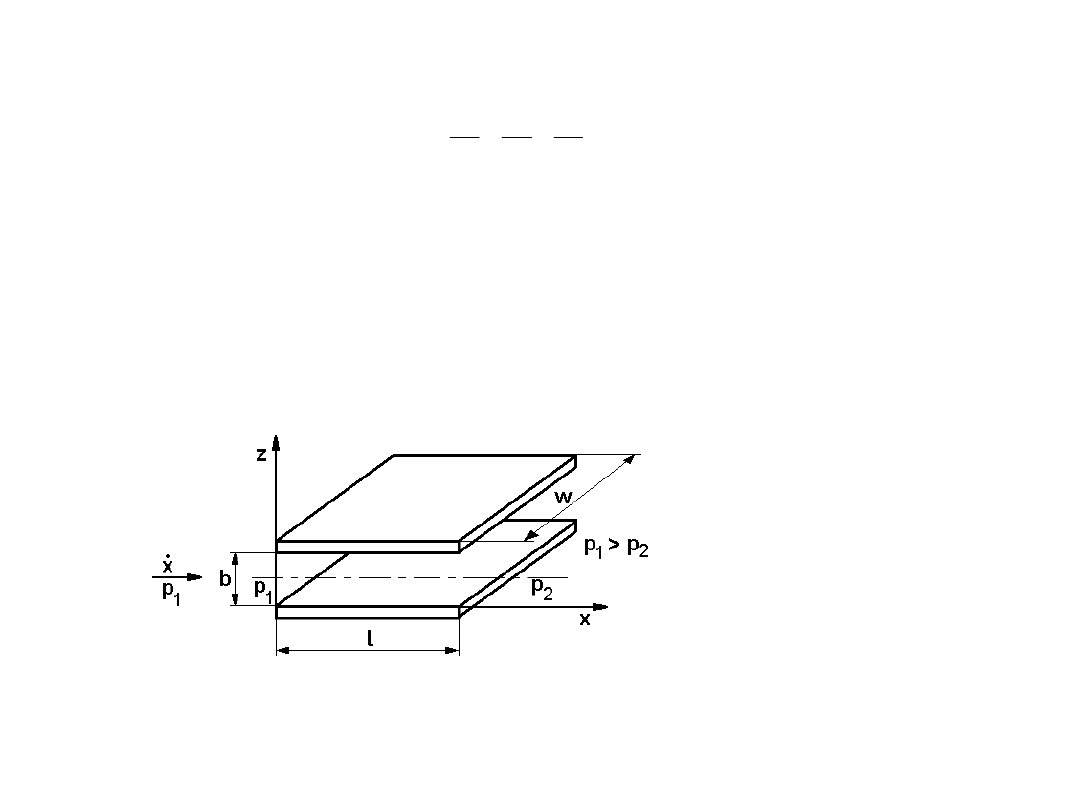
4.1.1. Szczelina płaska o nieruchomych ściankach
Ciecz przepływa między nieruchomymi równoległymi ściankami odległymi od siebie o
wartość b. W celu wyznaczenia prędkości przepływu i natężenia przepływu cieczy korzystamy
z równań (4.3, 4.4, 4.5, 4.6), rys.4.1.
Rys. 4.1. Szczelina płaska o nieruchomych
ściankach
4.1. Szczeliny o nieruchomych
ściankach
0
z
z
y
y
x
x

Stałe całkowania C
1
i C
2
wyznacza się z warunków brzegowych zakładając, że dla z = 0 i z =
b prędkość przepływu równa jest zeru, a więc:
C
2
= 0 , , .
Przyjmujemy w tym przypadku prędkość i zmienność , a więc równania
powyższe przyjmą postać:
,
(4.7)
, , .
Z powyższych zależności wynika, że ciśnienie w tym przypadku zależy tylko od zmiennej x, a
pochodna:
.
Rozwiązując równanie (4.7) otrzyma się:
,
.
(4.8)
x
p
1
z
x
0
2
2
0
y
p
0
z
p
0
x
x
const
x
p
2
2
z
x
dx
dp
1
2
1
2
C
z
C
z
dx
dp
2
1
x
0
y
z
,
x
f
x
x
b
C
b
dx
dp
2
1
0
1
2
b
dx
dp
2
1
C
1

Ostatecznie prędkość w przekroju przepływu wyniesie:
.
(4.9)
Rozkład prędkości w przekroju poprzecznym szczeliny jest paraboliczny. Maksymalna
prędkość występuje w płaszczyźnie osiowej szczeliny, a więc dla z = b/2, i wynosi:
.
(4.10)
Natężenie przepływu przez przekrój poprzeczny szczeliny płaskiej wyznacza się jako:
,
(4.11)
Wprowadzając równanie (4.9) do równania (4.11) otrzyma się
bz
z
dx
dp
2
1
x
2
4
b
dx
dp
2
1
x
2
max
b
0
dz
w
x
Q
b
0
2
b
0
2
dz
bz
z
dx
dp
2
w
dz
w
bz
z
dx
dp
2
1
Q
w
b
dx
dp
12
1
Q
3
Przyjmując, że ciśnienie w szczelinie maleje liniowo ze wzrostem długości szczeliny l ,
otrzymuje się:
l
p
p
dx
dp
2
1

a zatem ostatecznie: .
(4.12)
Średnia prędkość przepływu w szczelinie wyniesie:
Q = v · A = v · b · w
,
,
.
(4.13)
l
12
w
b
p
Q
3
w
b
v
l
12
w
b
p
3
l
12
b
p
v
2
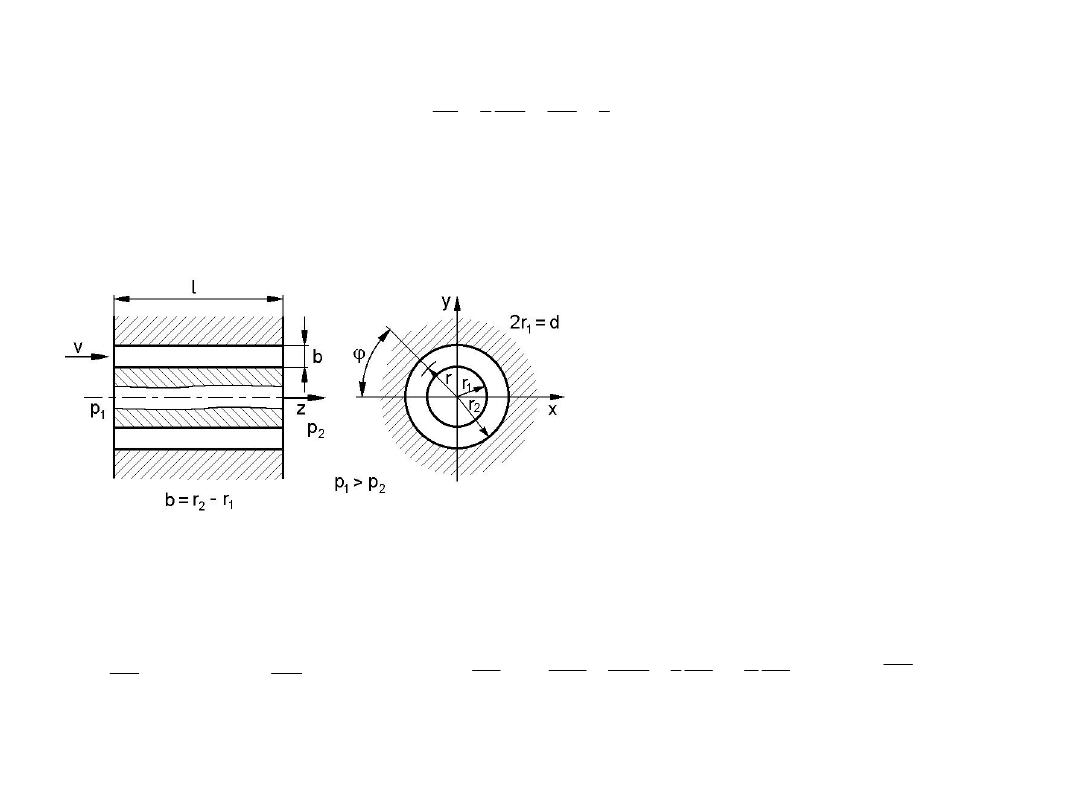
4.1.2. Szczelina pierścieniowa centryczna
Wyznaczenie natężenia przepływu w szczelinie pierścieniowej wymaga zapisu równania (4.1)
Naviera-Stokesa w układzie współrzędnych cylindrycznych. Równanie to przedstawia się
następująco:
,
(4.14)
,
(4.15)
,
(4.16)
r
p
1
r
r
r
2
r
r
r
1
z
r
r
r
1
r
r
r
z
r
z
r
r
r
r
r
t
r
2
2
2
2
2
2
2
2
2
2
p
r
1
r
r
r
2
r
r
1
z
r
1
r
r
r
z
z
r
r
r
t
2
2
2
2
2
2
2
2
2
2
z
p
1
r
z
r
1
z
z
z
r
1
r
z
z
z
z
z
r
r
z
r
t
z
2
2
2
2
2
2
2
oraz równanie ciągłości przepływu:
.
(4.17)
W przypadku szczeliny pierścieniowej jak na rys.4.2 składowe prędkości cieczy , prędkość
cieczy
występuje w kierunku osi z, a więc:
.
Rys. 4.2. Szczelina pierścieniowa centryczna
0
r
0
r
r
z
z
r
1
r
r
z
,
r
f
z
Z równań (4.14, 4.15, 4.16) wynika więc,
że:
0
r
p
0
p
z
p
1
r
z
r
1
z
z
r
z
z
z
z
2
2
2
2
0
z
z

Po uporządkowaniu otrzyma się:
.
(4.18)
Z równań tych wynika, że prędkość przepływu cieczy w kierunku z zależy jedynie od
promienia r, a ciśnienie jest funkcją tylko odciętej z. Równanie (4.18) można przedstawić w
postaci następującej:
,
,
,
,
.
(4.19)
W tym przypadku ścianki szczeliny pierścieniowej są nieruchome, a więc dla promieni
r = r
1
i r = r
2
prędkość przepływu równa jest . Wprowadzając warunki brzegowe do
równania
(4.19) otrzyma się:
0
z
z
p
1
r
z
r
r
z
2
2
0
dz
dp
1
dr
z
d
r
dr
d
r
dz
dp
r
dr
z
d
r
dr
d
1
2
C
dz
dp
2
r
dr
z
d
r
r
1
C
r
dz
dp
2
1
dr
z
d
1
2
1
2
C
r
ln
C
r
dz
dp
4
1
z
2
1
1
2
1
C
r
ln
C
r
dz
dp
4
1
0
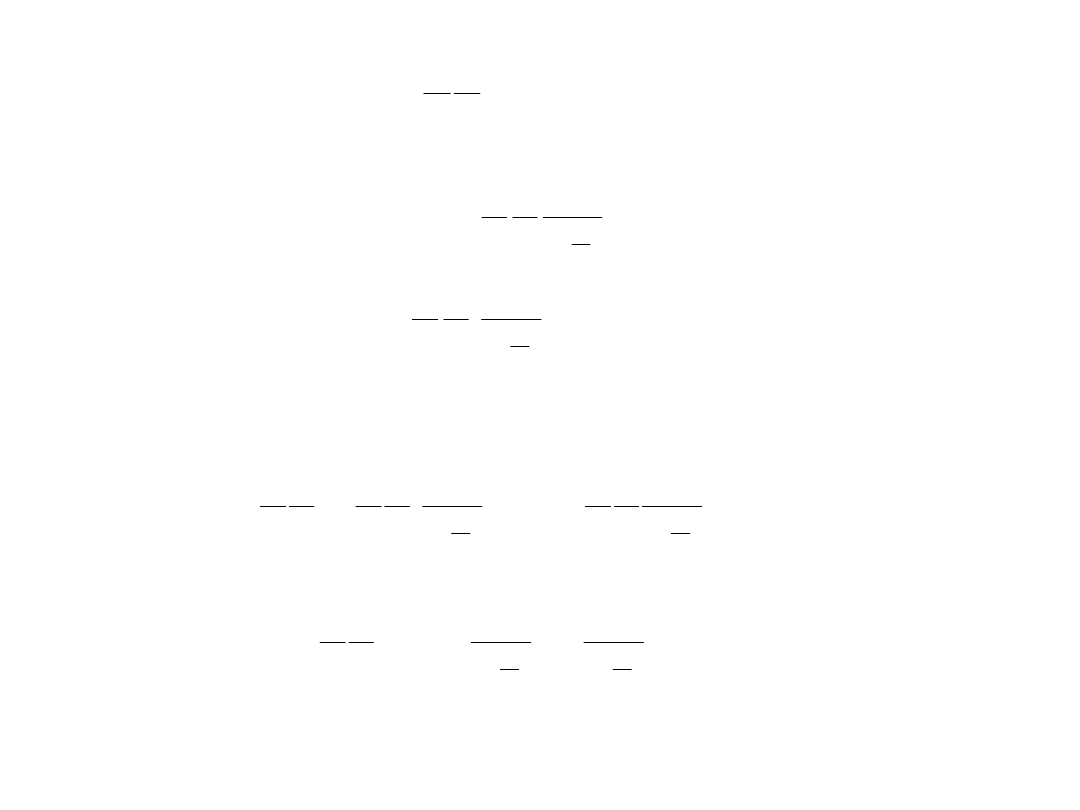
2
2
1
2
2
C
r
ln
C
r
dz
dp
4
1
0
Z powyższych równań otrzymujemy stałe całkowania C1 i C2 :
,
(4.20)
.
(4.21)
Wstawiając stałe całkowania (4.20) i (4.21) do równania (4.19) otrzyma się:
,
,
1
2
2
1
2
2
1
r
r
ln
r
r
dz
dp
4
1
C
2
1
1
1
2
2
1
2
2
2
r
r
ln
r
r
ln
r
r
dz
dp
4
1
C
r
ln
r
r
ln
r
r
dz
dp
4
1
r
r
ln
r
r
ln
r
r
dz
dp
4
1
r
dz
dp
4
1
z
1
2
2
1
2
2
2
1
1
1
2
2
1
2
2
2
r
ln
r
r
ln
r
r
r
ln
r
r
ln
r
r
r
r
dz
dp
4
1
z
1
2
2
1
2
2
1
1
2
2
1
2
2
2
1
2
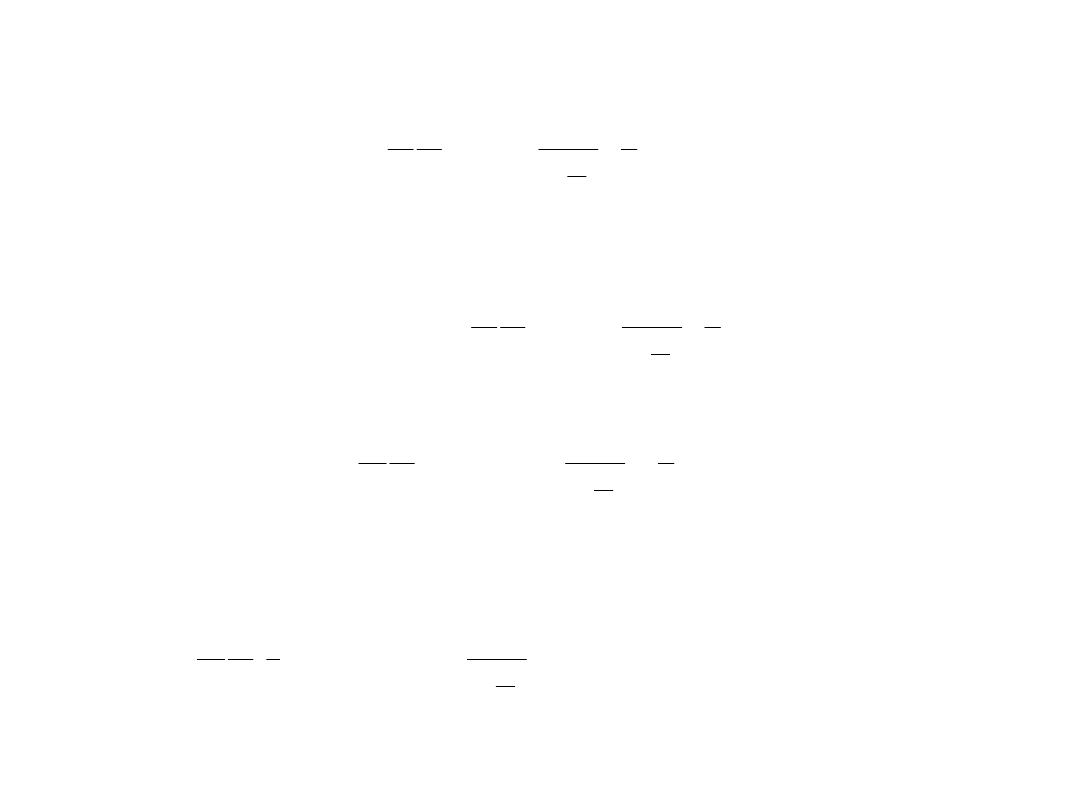
a więc ostatecznie prędkość w szczelinie pierścieniowej wyniesie:
.
(4.22)
1
1
2
2
1
2
2
2
1
2
r
r
ln
r
r
ln
r
r
r
r
dz
dp
4
1
z
Natężenie przepływu w tej szczelinie wyniesie:
,
.
Otrzymuje się ostatecznie:
.
(4.23)
dr
r
r
ln
r
r
ln
r
r
r
r
dz
dp
4
1
r
2
dr
z
r
2
Q
1
1
2
2
1
2
2
2
1
2
r
r
1
r
r
1
2
1
2
1
2
1
2
1
2
1
r
r
r
r
r
r
1
1
2
2
1
2
2
2
1
2
1
dr
r
r
ln
r
r
ln
r
r
dr
r
dr
r
dz
dp
2
r
Q
1
1
2
1
2
1
1
2
2
1
2
2
1
2
2
1
2
2
1
3
1
3
2
1
r
ln
r
r
r
r
r
ln
r
r
ln
r
r
r
ln
r
r
r
r
r
r
r
3
1
dz
dp
2
r
Q

W przypadku gdy różnica wymiarów r
2
–r
1
jest mała w stosunku do promienia r
1
, równania
(4.22) i (4.23) dają się uprościć. Wprowadzając oznaczenia grubości szczeliny b = r
2
- r
1
i r
– r
1
= y oraz rozwijając w szereg wyrażenie stosunku logarytmów w równaniu (4.22) można
zależność (4.22) przedstawić według równania (4.24):
,
,
.
Po przekształceniach otrzyma się:
. (4.24)
1
1
1
1
1
2
1
r
2
b
r
2
y
1
b
y
r
b
1
ln
r
y
1
ln
r
r
ln
r
r
ln
1
r
2
1
2
2
2
1
2
r
2
b
2
y
1
b
y
r
r
r
r
dz
dp
4
1
z
1
1
1
1
2
1
2
r
2
b
r
2
y
1
b
y
b
r
2
b
y
r
2
y
dz
dp
4
1
z
y
b
by
r
2
1
by
2
y
2
dz
dp
4
1
z
2
2
1
2
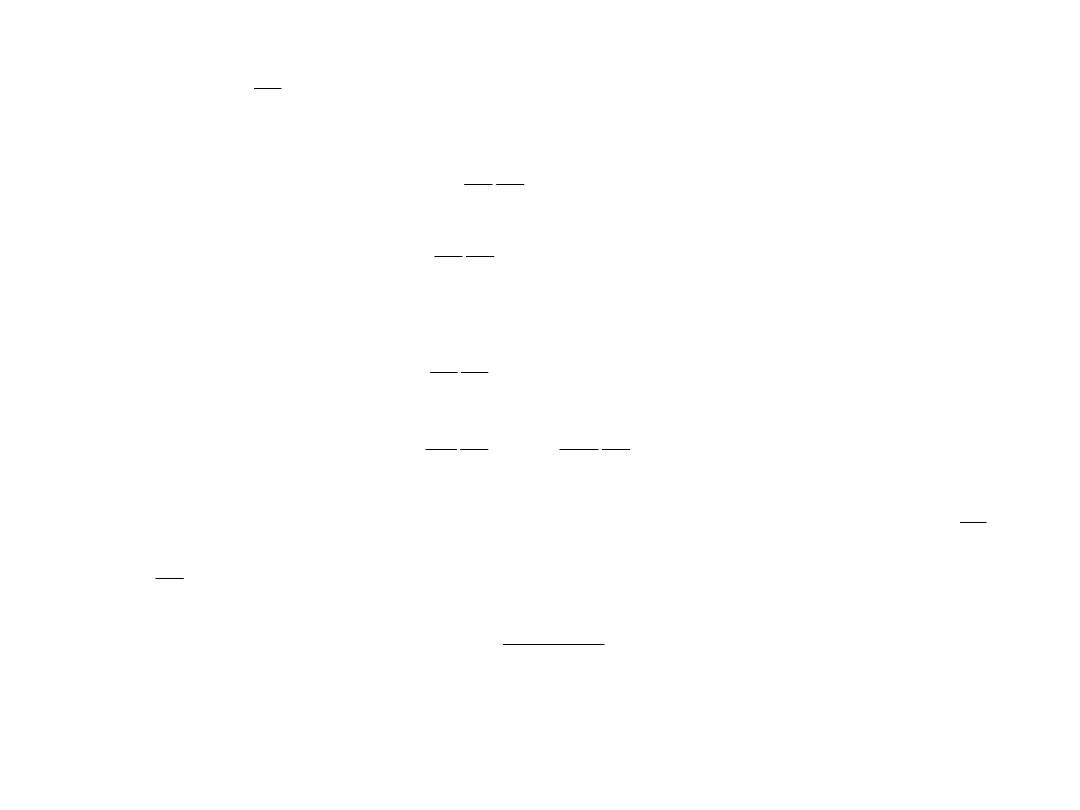
Porównując wyrażenie z dwoma pierwszymi członami z równania (4.24) można
stwierdzić,
że jest ono znacznie mniejsze i może być pominięte, a więc przybliżona postać prędkości
opisana jest związkiem (4.25):
,
(4.25)
lub
.
Natężenie przepływu w tym przypadku wyniesie:
,
.
(4.26)
Przyjmując rozkład liniowy spadku ciśnienia na długości szczeliny l można wprowadzić w
miejsce
wyrażenie , a równanie (4.26) przedstawi się w postaci:
.
(4.27)
y
b
by
r
2
1
2
2
1
z
by
y
dz
dp
2
1
z
2
1
2
r
r
r
r
dz
dp
2
1
z
b
0
1
b
2
dy
r
2
y
y
dz
dp
2
1
Q
3
3
1
b
dz
dp
12
d
b
dz
dp
6
r
Q
dz
dp
l
p
l
12
b
p
d
Q
3
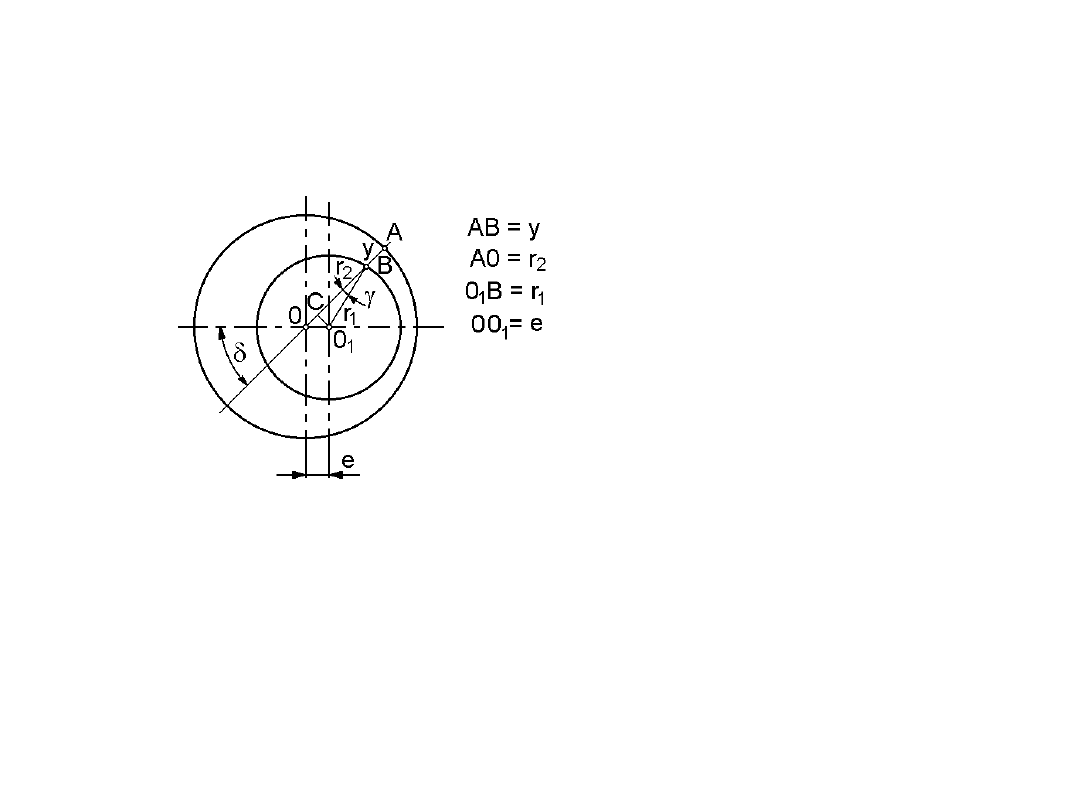
4.1.3. Szczelina pierścieniowa niecentryczna
Przypadek szczeliny pierścieniowej centrycznej jest praktycznie mało prawdopodobny. W
rzeczywistości spotyka się raczej szczeliny pierścieniowe niecentryczne. Oznaczać to będzie,
że grubość szczeliny y (rys.4.3) zmienia się na obwodzie szczeliny.
Wychodząc z oznaczeń na rys. 4.3 można ustalić funkcję grubości szczeliny niecentrycznej
y jako:
.
(4.28)
Zakładając małe wartości mimośrodu e, kąt
jest bliski zeru, a więc cos
1. Zatem
równanie (4.28) napisać można w postaci:
Rys. 4.3. Szczelina
pierścieniowa
niecentryczna
cos
e
cos
r
r
y
1
2
cos
e
r
r
y
1
2
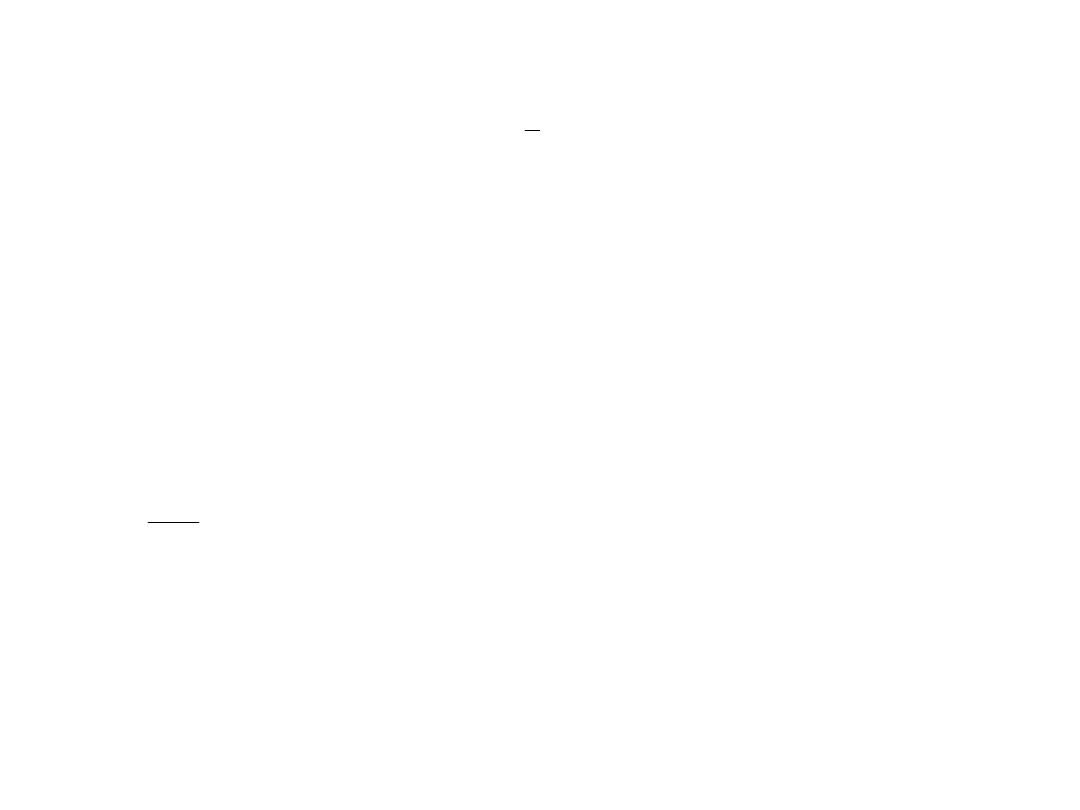
Wprowadzając oznaczenie na grubość szczeliny centrycznej b = r
2
– r
1
, y wyniesie:
.
(4.29)
Stosunek mimośrodu e do grubości b oznacza się przez
stanowiącym tzw. mimośrodowość
względną szczeliny pierścieniowej niecentrycznej. Jeśli
= 0 oznacza to, że szczelina
pierścieniowa jest centryczna, natomiast
= 1 wyznacza wartość maksymalnej
mimośrodowości e równej grubości szczeliny b.
Równanie (4.29) można zatem zapisać w postaci:
.
(4.30)
Korzystając z równania (4.12) na natężenie przepływu w szczelinie płaskiej i przyjmując, że w
szczelinie pierścieniowej niecentrycznej zmienia się grubość szczeliny y i szerokość w,
elementarne natężenie przepływu określić można związkiem:
,
(4.31)
gdzie: , a d
w
= r
1
d
.
l
12
p
e
d
r
y
e
dQ
1
3
cos
b
e
1
b
y
cos
1
b
y
Wstawiając do równania (4.31) zależność (4.30) otrzyma się:
.
d
r
cos
1
b
e
dQ
1
3
3

Stąd natężenie przepływu cieczy określić można jako:
,
otrzymując ostatecznie:
.
Po wprowadzeniu oznaczeń zastępczych natężenie przepływu w szczelinie pierścieniowej
niecentrycznej wynosi:
.
(4.32)
Porównując równanie (4.27) i (4.32) na natężenie przepływu w szczelinie pierścieniowej
centrycznej
i niecentrycznej można stwierdzić, że wystąpienie mimośrodowości powiększa wpływ
czynnika
razy.
Dla maksymalnej wartości mimośrodowości względnej, tj. = 1 natężenie przepływu w tej
szczelinie wzrośnie aż 2,5 raza w stosunku do wypływu w szczelinie centrycznej.
2
0
3
2
2
1
3
d
cos
cos
3
cos
3
1
r
b
e
Q
2
3
1
5
,
1
1
e
b
r
2
Q
2
3
5
,
1
1
l
12
b
p
d
Q
2
5
,
1
1
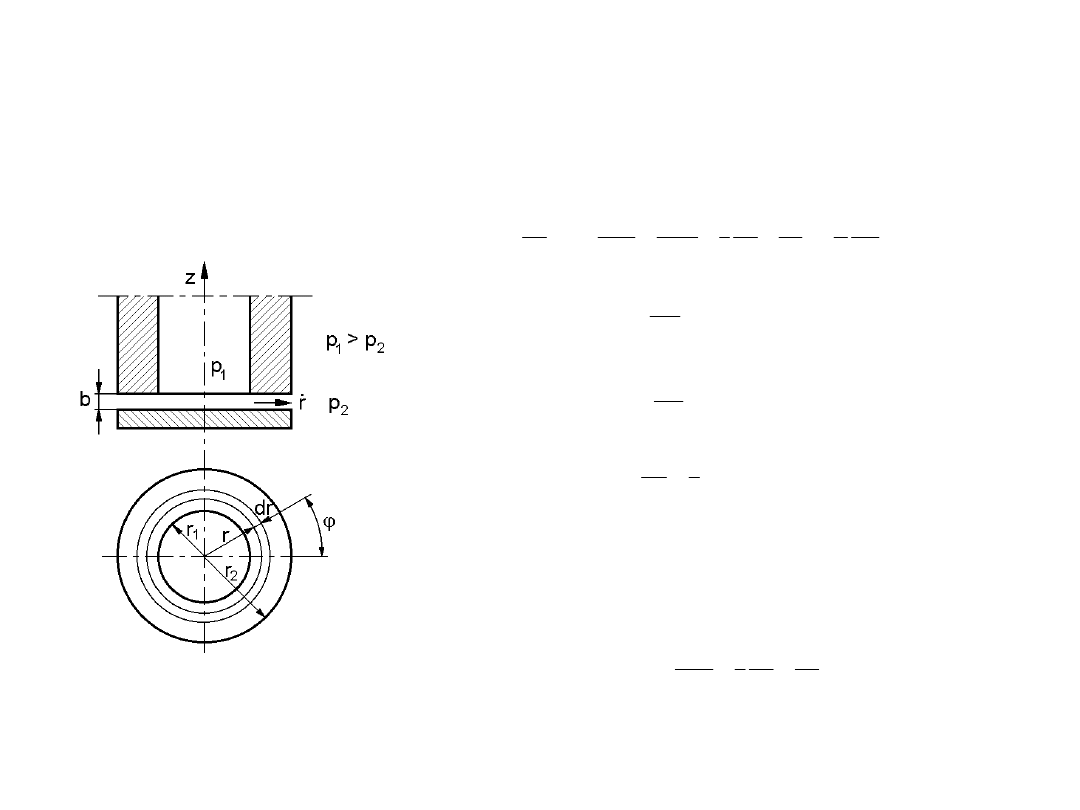
4.1.4. Szczelina pierścieniowa czołowa
Niech w szczelinie czołowej przedstawionej na rys.4.4 na wejściu od wnętrza panuje ciśnienie
p
1
, a na wyjściu ciśnienie p
2
. Stosując równanie Naviera-Stokesa (4.14), (4.15), (4.16) i
ciągłości przepływu (4.17) oraz zakładając, że , i , otrzyma się:
Rys. 4.4. Szczelina pierścieniowa
czołowa
0
z
z
,
r
f
r
r
p
1
r
r
r
r
r
1
z
r
r
r
r
r
r
2
2
2
2
2
0
p
0
z
p
0
r
r
r
r
Obliczając pochodną równania (4.36) otrzymuje się
wyrażenie:
0
r
r
r
r
r
1
r
r
2
2
2
4.33
4.34
4.35
4.36

Zakładając dodatkowo, że wyrażenie jest znacznie mniejsze od ,
powyższe równanie
można przedstawić w postaci uproszczonej:
,
a więc po scałkowaniu otrzyma się prędkość przepływu cieczy w kierunku promieniowym :
.
(4.37)
Wprowadzając warunki brzegowe zakładając, że dla z = 0, i z = b, ,
otrzymamy:
C
2
= 0 ,
,
.
r
r
r
2
2
z
r
2
2
z
r
dr
dp
1
2
1
2
C
z
C
2
z
dr
dp
1
r
r
0
r
0
r
b
C
b
dr
dp
2
1
C
1
2
b
dr
dp
2
1
C
1
Ostatecznie równanie (4.37) przedstawia się w postaci:
.
(4.38)
bz
z
dr
dp
2
1
r
2

Natężenie przepływu w szczelinie pierścieniowej czołowej określa się z wyrażenia:
,
,
.
(4.39)
Zakładając stałe natężenie przepływu cieczy w szczelinie i określoną jej konstrukcję można
wyznaczyć rozkład ciśnienia w tej szczelinie po przekształceniu równania (4.39):
,
b
0
b
0
2
b
0
dz
bz
z
dr
dp
2
1
r
2
dz
r
r
2
b
r
2
dz
r
b
1
Q
b
0
3
3
2
2
b
3
b
dr
dp
r
dz
bz
z
dr
dp
r
Q
dr
dp
b
6
r
Q
3
Q
b
1
r
6
dr
dp
3
a więc:
,
,
czyli:
,
.
(4.40)
r
r
3
p
p
1
1
r
dr
Q
b
6
dp
1
3
1
r
ln
r
ln
Q
b
6
p
p
1
3
1
r
r
ln
Q
b
6
p
p
1
3
1
r
r
ln
Q
b
6
p
p

Rozkład ciśnienia w szczelinie pierścieniowej czołowej jest logarytmiczny z promieniem r.
Wprowadzając do równania (4.40) promień r = r
2
a p = p
2
otrzyma się:
,
a więc:
.
(4.41)
1
2
3
2
1
r
r
ln
Q
b
6
p
p
1
2
3
r
r
ln
6
p
b
Q
We wszystkich rozpatrywanych dotąd przypadkach szczelin ścianki ograniczające były
nieruchome. Znacznie częściej spotyka się szczeliny utworzone przez jedną ściankę stałą a
drugą ruchomą lub o jednej ściance poruszającej się względem drugiej. Straty objętościowe
w tych przypadkach zależeć będą również od prędkości ruchu ścianek oraz zwrotu tej
prędkości w stosunku do zwrotu prędkości cieczy.
4.2. Szczeliny o ruchomych
ściankach
4.2.1. Szczelina płaska z ruchomą ścianką
Rozkład prędkości przepływu cieczy w szczelinie oraz natężenie przepływu określa się
zgodnie z rys.4.5 z wykorzystaniem równania (4.8) wyprowadzonego dla szczeliny o
nieruchomej ściance.
2
1
2
C
z
C
z
dx
dp
2
1
x
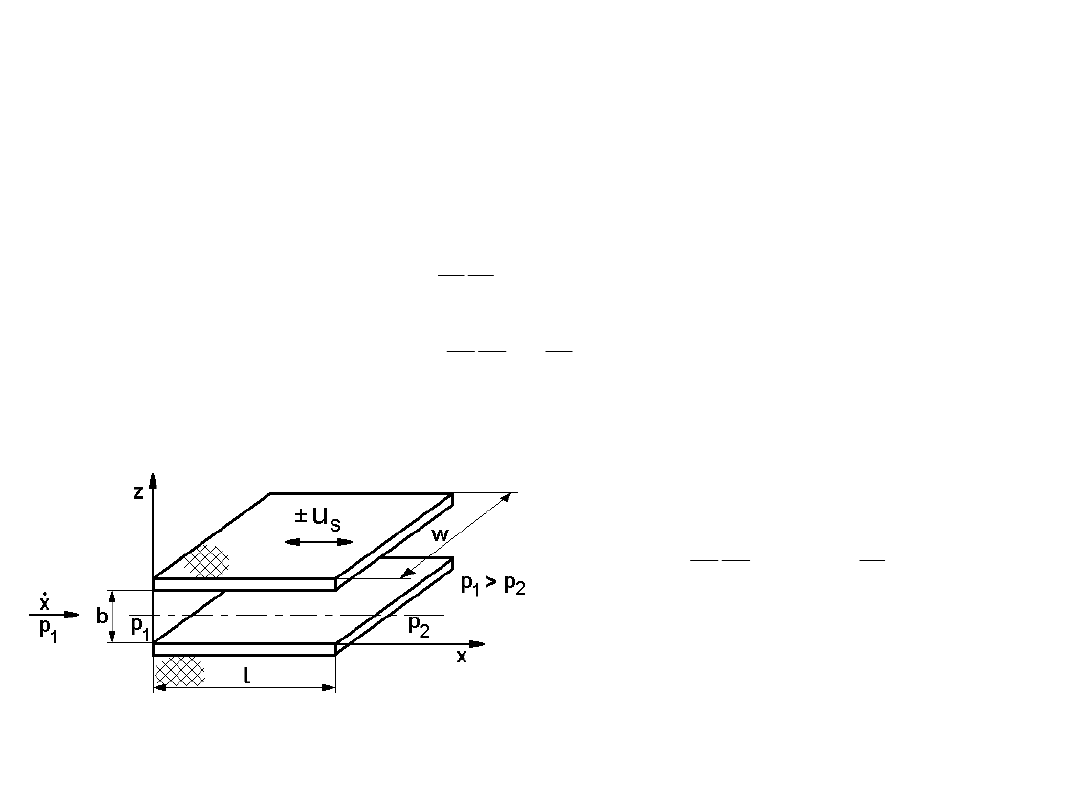
Jeżeli jedna ze ścian porusza się z prędkością u
s
, to warunki brzegowe dla wyznaczania
stałych całkowania wynoszą:
z = 0
z = b ,
a więc:
C
2
= 0
,
.
Rys. 4.5. Szczelina płaska o ruchomej
ściance
Ostatecznie rozkład prędkości przepływu
cieczy w szczelinie przedstawia równanie
(4.42):
.
(4.42)
z
b
u
bz
z
dx
dp
2
1
x
s
2
0
x
s
u
x
b
C
b
dx
dp
2
1
u
1
2
s
b
u
b
dx
dp
2
1
C
s
1
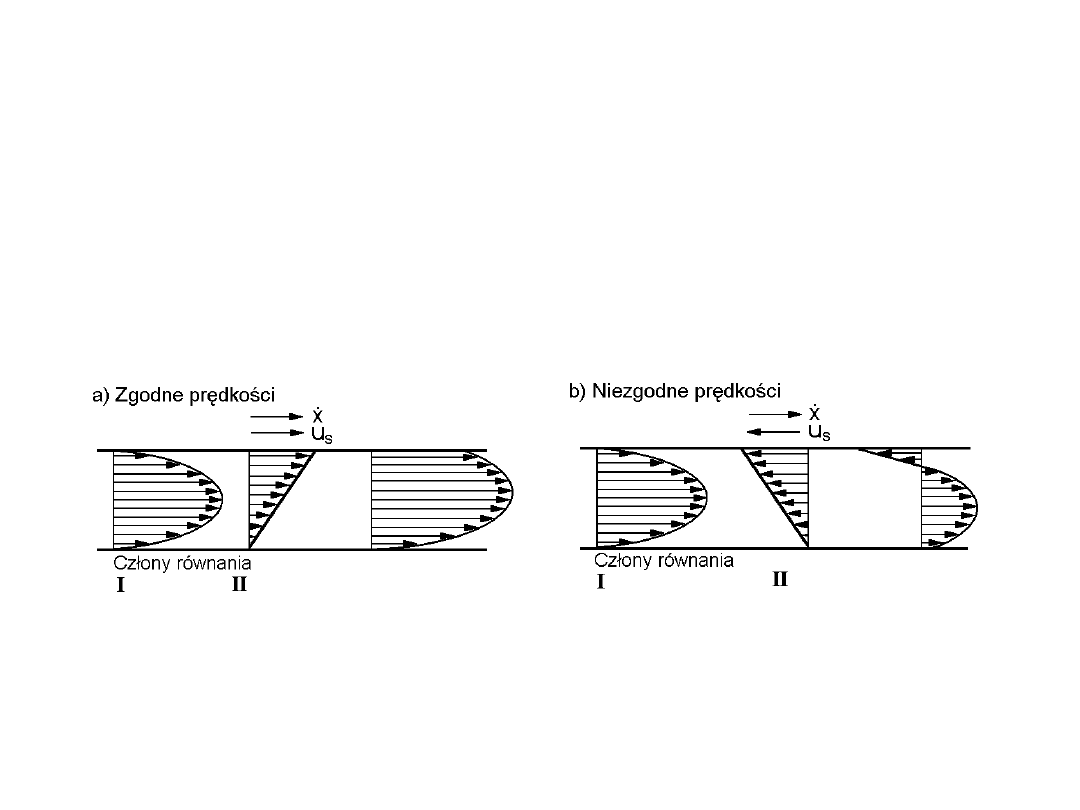
Rozkład prędkości w przekroju szczeliny (rys.4.6) jest złożony i zależny od zwrotów prędkości
ruchu ścianek i przepływu cieczy . Jeżeli prędkość ścianki u
s
ma zwrot zgodny z kierunkiem
spadku ciśnienia, czyli ze zwrotem prędkości cieczy, to drugi człon w równaniu (4.42) posiada
znak dodatni, a rozkład prędkości wypadkowej według rys. 4.6 a. W przeciwnym przypadku w
równaniu (4.42) wystąpi znak minus, a rozkład prędkości wypadkowej przedstawia rys. 4.6 b.
Natężenie przepływu cieczy przez szczelinę daje się obliczyć jako:
(4.43)
b
0
dz
w
x
Q
x
Rys. 4.6. Rozkład prędkości przepływu w szczelinie płaskiej o ruchomej
ściance
Wprowadzając wyrażenie (4.42) do równania (4.43) i po scałkowaniu otrzyma się
ostatecznie:
,
a po podstawieniu:
,
wyznacza się natężenie przepływu cieczy w szczelinach płaskich o ruchomej ściance:
.
(4.44)
4.2.2. Szczelina pierścieniowa centryczna o ruchomej ściance
w
2
b
u
w
b
dx
dp
2
1
Q
s
3
l
p
dx
dp
2
w
b
u
l
12
w
b
p
Q
s
3
Rys. 4.7. Szczelina pierścieniowa
centryczna
o ruchomej ściance
Prędkość przepływu cieczy oraz
natężenie przepływu cieczy dla
szczeliny pierścieniowej centrycznej o
ruchomej ściance wyznacza się na
podstawie rys.4.7.

Wykorzystując zależność (4.19) dla szczeliny o nieruchomych ściankach:
,
i przyjmując warunki brzegowe:
dla r = r
1
dla r = r
2
wyznacza się stałe całkowania C
1
i C
2
:
,
.
Wprowadzając stałe całkowania do powyższego równania otrzyma się:
.
(4.45)
2
1
2
C
r
ln
C
r
dz
dp
4
1
z
s
u
z
0
z
1
2
s
1
2
2
1
2
2
1
r
r
ln
u
r
r
ln
r
r
dz
dp
4
1
C
1
2
1
s
2
1
1
1
2
2
1
2
2
2
r
r
ln
r
ln
1
u
r
r
ln
r
r
ln
r
r
dz
dp
4
1
C
1
2
1
s
1
2
1
2
1
2
2
2
1
2
r
r
ln
r
r
ln
1
u
r
r
ln
r
r
ln
r
r
r
r
dz
dp
4
1
z
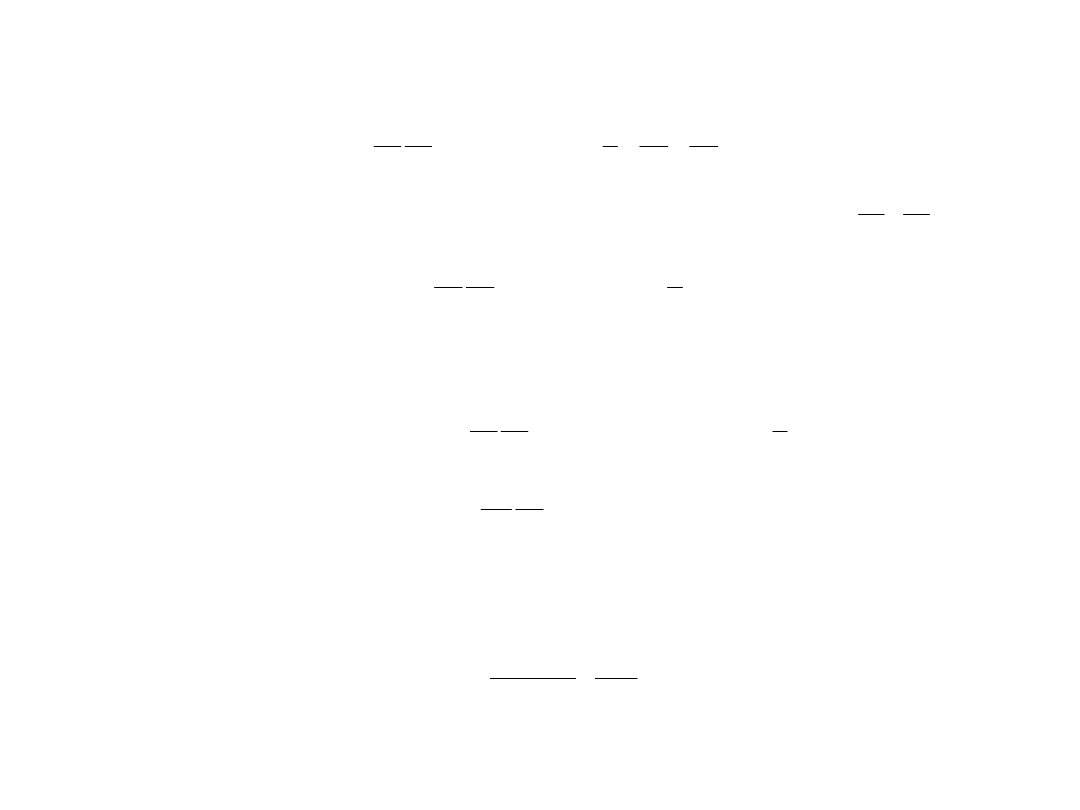
Przekształcając równanie (4.45) analogicznie do równania (4.24) otrzymuje się:
.
Zakładając jednak, że y i b są znacznie mniejsze od średnicy 2r
1
= d, i po pominięciu
otrzyma się ostatecznie:
.
(4.46)
Natężenie przepływu cieczy w tym przypadku zostanie określone jako:
,
.
(4.47)
Zakładając rozkład liniowy ciśnienia na długości szczeliny l oraz wprowadzając w równaniu
(4.47) w miejsce promienia r
1
d/2 otrzyma się ostateczną zależność na natężenie przepływu:
.
(4.48)
1
1
s
2
r
2
b
r
2
y
b
y
1
u
by
y
dz
dp
2
1
z
1
1
r
2
b
r
2
y
b
y
1
u
by
y
dz
dp
2
1
z
s
2
b
0
b
0
s
1
2
b
0
1
1
dy
b
y
1
u
r
2
dy
by
y
dz
dp
2
1
r
2
dy
r
2
z
Q
b
u
r
b
dz
dp
6
r
Q
s
1
3
1
s
3
u
2
db
l
12
b
p
d
Q
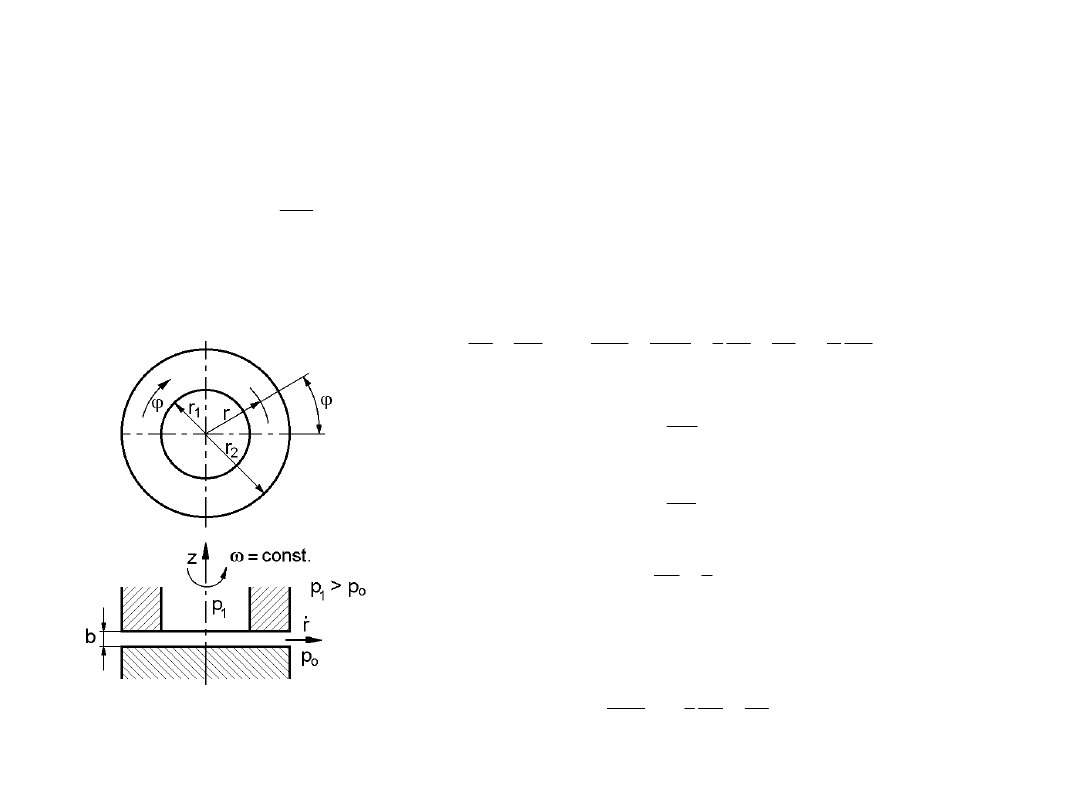
4.2.3. Szczelina pierścieniowa czołowa z obrotową ścianką
W szczelinie pierścieniowej czołowej z obrotową ścianką o stałej prędkości = const.
Ciśnienie na wlocie wynosi p
1
, a na wylocie p
o
(rys.4.8). Zgodnie ze schematem rys. 4.8
można ustalić, że prędkość przepływu w kierunku promieniowym r jest funkcją promienia i
wysokości szczeliny oraz prędkość
obwodowa równa jest . Natomiast prędkość cieczy w kierunku osi z równa jest zero.
Przyjmując powyższe ustalenia i wprowadzając je do równania Naviera-Stokesa i
uwzględniając równanie ciągłości przepływu otrzymuje się:
,
(4.49)
z
,
r
f
r
z
b
r
r
p
1
r
r
r
r
r
1
z
r
r
r
r
r
r
r
2
2
2
2
2
2
Rys. 4.8. Szczelina pierścieniowa
czołowa o obrotowej
ściance
,
(4.50)
,
(4.51)
.
(4.52)
Z równania (4.52) otrzyma się:
.
(4.53)
0
p
0
z
p
0
r
r
r
r
2
2
2
r
r
r
r
r
1
r
r
Wprowadzając wyrażenie (4.53) do równania (4.49) uzyskuje się:
.
(4.54)
Podstawiając do równania (4.54) wartość prędkości obwodowej otrzyma się:
.
(4.55)
Pomijając człon jako znacznie mniejszy od pozostałych, wyrażenie (4.55) przyjmie
postać:
.
(4.56)
Po podwójnym całkowaniu równania (4.56) uzyskuje się zależność na prędkość promienia :
.
(4.57)
Stałe całkowania C
1
i C
2
wyznacza się z warunków brzegowych; dla rozpatrywanego
przypadku przyjmuje się:
z = 0; ;
(4.58)
z = b; ;
oraz
r = r
1
; p = p
1
(4.59)
r =r
2
; p = p
o
dr
dp
1
z
r
r
r
r
r
2
2
2
dr
dp
1
z
r
r
b
z
r
r
r
2
2
2
2
2
r
r
r
dr
dp
1
z
r
r
b
z
2
2
2
2
2
2
1
4
2
2
2
C
z
C
z
b
12
r
z
dr
dp
2
1
r
0
r
0
0
r
r
Po podstawieniu warunków brzegowych (4.58) otrzyma się stałe całkowania w postaci:
,
oraz
C
2
= 0
.
Wprowadzając stałe całkowania do równania (4.57) uzyskuje się ostateczną postać na
prędkość promieniową w szczelinie:
,
(4.60)
Średnia prędkość przepływu cieczy w szczelinie w kierunku promieniowym wyniesie:
,
(4.61)
a więc po podstawieniu:
.
Rozwiązując powyższą równość otrzymamy ostatecznie postać v
r
:
.
(4.62)
Natężenie przepływu cieczy w szczelinie czołowej wyniesie:
.
(4.63)
b
dr
dp
2
1
12
r
b
C
2
1
2
4
2
2
b
z
bz
12
r
bz
z
dr
dp
2
1
r
b
0
r
dz
r
b
1
v
b
0
2
4
2
2
r
dz
b
z
bz
12
r
bz
z
dr
dp
2
1
b
1
v
10
b
r
dr
dp
12
b
v
2
2
2
r
r
v
b
r
2
Q

Wprowadzając związek za średnią prędkość v
r
z równania (4.62) do równania (4.63) uzyskuje
się postać na objętościowe natężenie przepływu:
.
(4.64)
Zakładając stałe natężenie przepływu w szczelinie ustalić można rozkład ciśnienia w
szczelinie czołowej:
.
Przekształcając wyrażenie z rozdzieleniem zmiennych mamy:
,
,
a więc:
.
(4.65)
Z równania (4.65) wyznacza się związek na natężenie przepływu cieczy w szczelinie:
.
(4.66)
20
b
r
dr
dp
6
b
r
Q
3
2
2
3
3
3
2
2
b
r
6
Q
20
b
r
dr
dp
2
1
0
1
r
r
3
3
2
2
p
p
dr
b
r
6
Q
20
b
r
dp
1
2
3
2
1
2
2
2
1
o
r
r
ln
b
Q
6
r
r
20
3
p
p
2
1
2
2
2
1
2
3
o
1
r
r
20
3
r
r
ln
b
Q
6
p
p
p
2
1
2
2
2
1
2
3
r
r
20
3
p
r
r
ln
6
b
Q
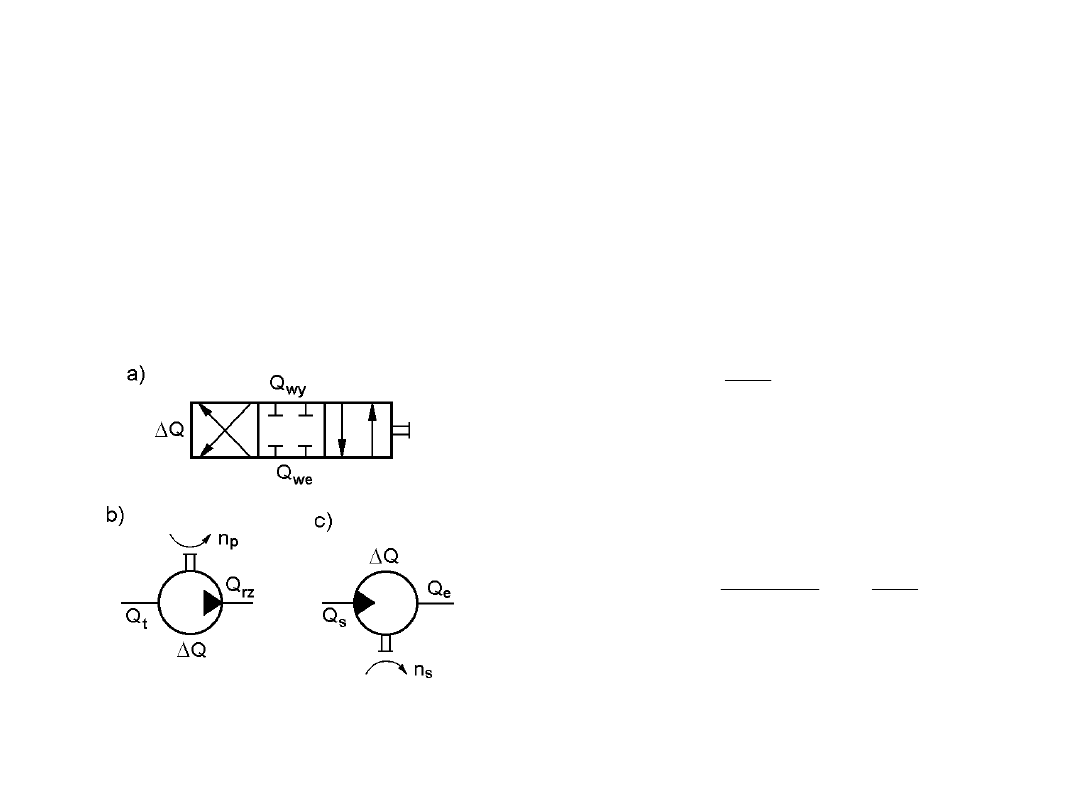
Zakładając, że całkowita strata
objętościowa w elemencie hydraulicznym
wynosi Q, związek (4.67) można
przedstawić w postaci:
.
(4.68)
Porównując związek (4.41) z powyższym równaniem można określić wpływ prędkości kątowej
lub też wpływ obrotu ścianki w szczelinie czołowej na natężenie wypływu cieczy.
Wprowadzenie zatem obrotu ścianki powiększa natężenie wypływu tym więcej, im prędkość
kątowa oraz różnica kwadratów promieni ograniczających szczelinę jest większa.
Straty objętościowe określone dla poszczególnych węzłów konstrukcyjnych elementów
hydraulicznych pozwalają na wyznaczenie całkowitych strat objętościowych elementu, a w
konsekwencji jego sprawności objętościowej. Zgodnie z oznaczeniami na rys. 4.9 sprawność
objętościową elementu hydraulicznego można określić według wzoru (4.67):
.
(4.67)
4.3. Sprawność objętościowa elementów
hydraulicznych
Rys. 4.9. Elementy hydrauliczne z oznaczeniem
wielkości do
obliczania strat objętościowych: a) rozdzielacz
czterodrogowy, trójpołożeniowy,b) pompa
wyporowa,
c) silnik wyporowy
we
wy
v
Q
Q
we
we
we
v
Q
Q
1
Q
Q
Q

Strata objętościowa węzła konstrukcyjnego w elemencie hydraulicznym jest określona
zależnie od rodzaju szczeliny według ogólnego związku:
.
(4.69)
Współczynnik proporcjonalności X jest związany z konstrukcją szczeliny i wynosi dla
przykładu szczelin o nieruchomych ściankach:
X
p
Q
str
- szczelina płaska
- szczelina o przekroju kołowym
- szczelina pierścieniowa centryczna
- szczelina pierścieniowa
niecentryczna
- szczelina pierścieniowa czołowa
l
12
w
b
X
3
1
l
128
d
X
4
2
l
12
b
d
X
3
3
2
3
4
5
,
1
1
l
12
b
d
X
1
2
3
5
r
r
ln
6
b
X

Całkowitą zatem stratę objętościową w elemencie hydraulicznym Q można wyznaczyć jako
sumę strat natężeń wypływu cieczy przez wszystkie szczeliny (węzły konstrukcyjne):
. (4.70)
Wprowadzając do równania (4.70) wyrażenie (4.69) otrzyma się postać na całkowitą stratę
objętościową w elemencie hydraulicznym:
. (4.71)
Sprawność objętościowa elementu hydraulicznego może zatem zostać określona według wzoru:
. (4.72)
Sprawność objętościowa elementu, jak to wynika z równania (4.72), zwiększa się ze wzrostem
natężenia na zasilaniu elementu oraz ze wzrostem lepkości cieczy roboczej. Wzrost różnicy
ciśnień, a więc wzrost obciążenia w układzie prowadzi do obniżenia sprawności objętościowej
elementu hydraulicznego. Wymiary i liczba szczelin w elemencie hydraulicznym prowadzić
mogą do znacznych zmian w wartościach sprawności.
str
Q
Q
n
1
i
i
X
p
Q
we
n
1
i
i
v
Q
X
p
1

Sprawność objętościowa elementu, jak to wynika z równania (4.72), zwiększa się ze wzrostem
natężenia na zasilaniu elementu oraz ze wzrostem lepkości cieczy roboczej. Wzrost różnicy
ciśnień, a więc wzrost obciążenia w układzie prowadzi do obniżenia sprawności objętościowej
elementu hydraulicznego. Wymiary i liczba szczelin w elemencie hydraulicznym prowadzić
mogą do znacznych zmian w wartościach sprawności.
Sprawność objętościowa pompy lub silnika wyporowego zależy od strat wewnętrznych w tych
elementach. Straty objętościowe w pompie wyporowej lub silnika mogą być ogólnie podzielone
na dwie grupy, a mianowicie na straty związane z lepkością dynamiczną cieczy oraz związane z
gęstością cieczy (4.73):
.
(4.73)
Straty całkowite objętościowe Q w pompie lub silniku hydraulicznym można więc przedstawić
jako:
,
(4.74)
gdzie: q – wydajność (chłonność) właściwa;
1
- lepkość dynamiczna cieczy na wejściu do
pompy (silnika);
1
- gęstość cieczy na wejściu do pompy (silnika); C
- współczynnik strat objętościowych
powodowanych lepkością cieczy; c
r
- współczynnik strat objętościowych powodowanych
gęstością
cieczy.
Q
Q
Q
3 2
1
r
1
q
p
2
c
q
2
p
C
Q
Korzystając z wzoru (4.68) sprawność objętościową pompy wyporowej można zdefiniować
jako:
,
(4.75)
t
rz
vp
Q
Q
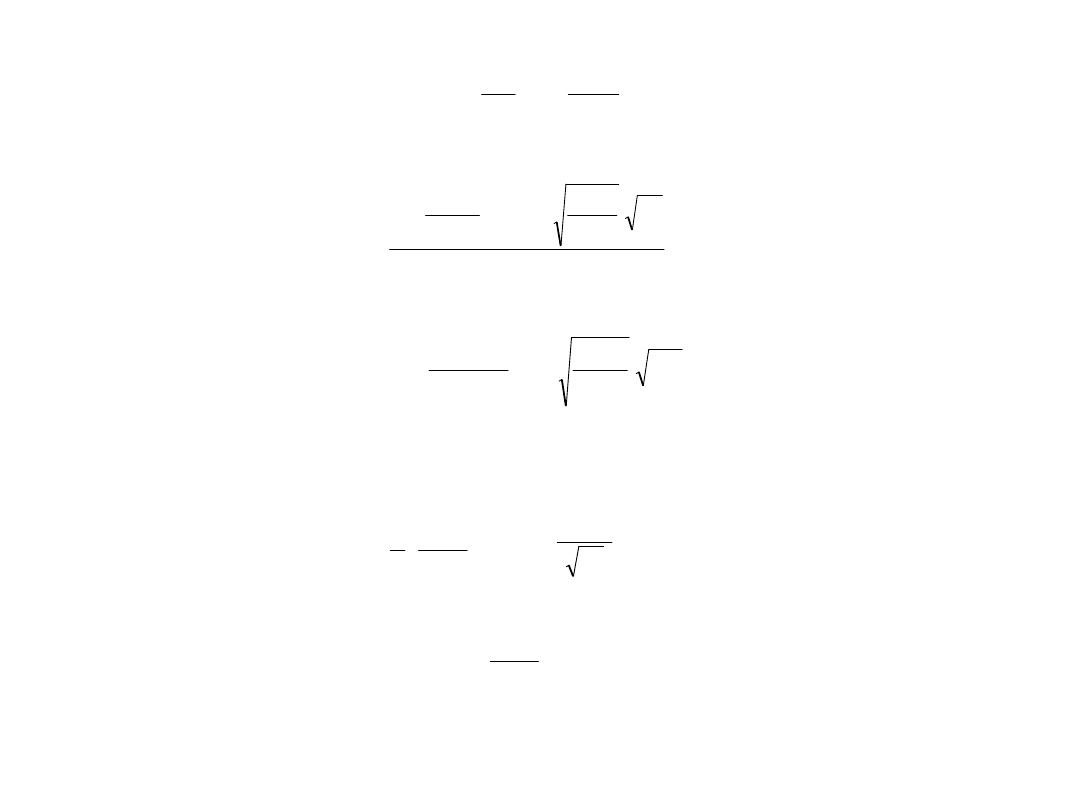
oraz przekształcając zgodnie z oznaczeniami na rys. 4.9 otrzyma się:
.
(4.76)
Wprowadzając do równania (4.76) zależność (4.74) uzyska się:
,
a po uporządkowaniu ostateczną postać:
.
(4.77)
Współczynniki strat objętościowych c
i c
r
zależą od wymiarów szczelin oraz wydajności
(chłonności) właściwej; można je ogólnie zapisać jako:
i ,
Y
i
– wielkość charakterystyczna dla szczelin: np.: dla szczeliny płaskiej wynosi:
.
A
sz
– powierzchnia szczelin związana ze stratą objętościową członu gęstości cieczy.
p
t
vp
q
n
Q
1
Q
Q
1
p
3 2
p
p
1
p
rp
p
p
1
p
p
vp
q
n
q
p
2
c
q
2
p
c
1
3
1
p
2
p
p
1
p
rp
p
1
p
p
p
vp
q
n
p
2
c
n
2
p
c
1
q
Y
6
c
n
1
i
i
3
2
sz
r
q
A
c
2
w
b
Y
3
i
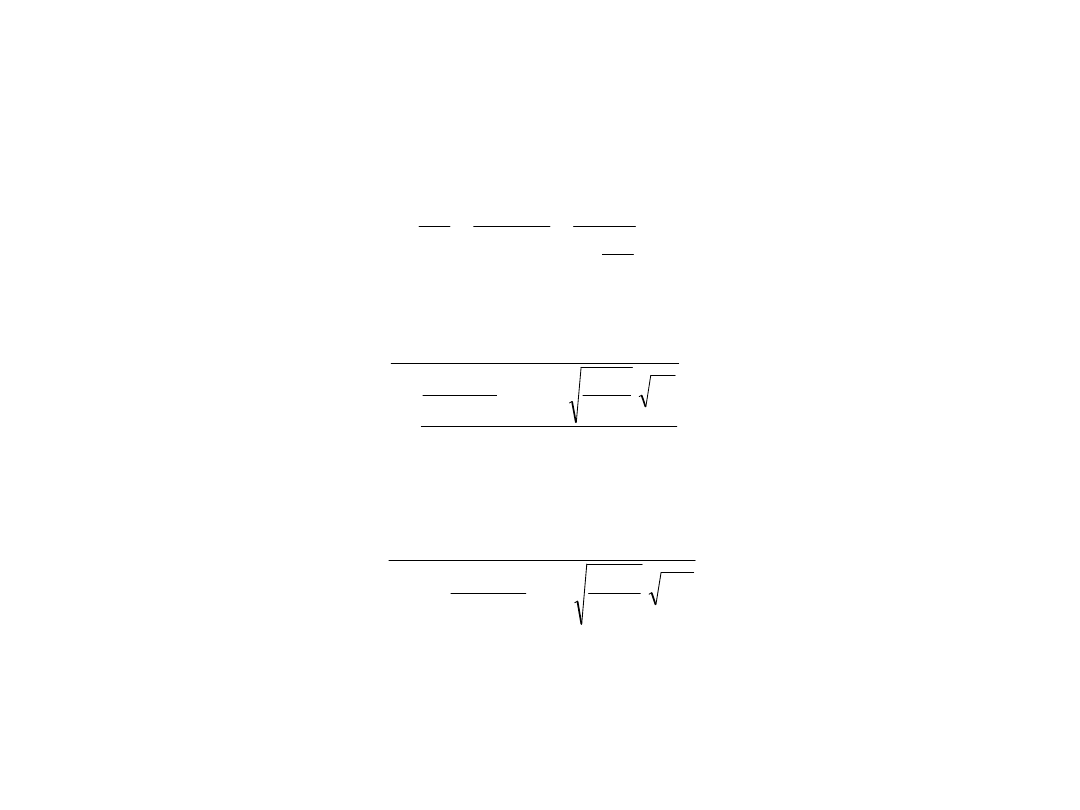
Jak wynika z równania (4.77), sprawność objętościowa pompy wyporowej jest tym większa, im
prędkość obrotowa wałka pompy jest większa. Wzrost lepkości i gęstości cieczy na wejściu do
pompy prowadzi do podniesienia sprawności objętościowej. Istotne zwiększenie sprawności
objętościowej można uzyskać w przypadku jednostek wyporowych o większych wydajnościach
właściwych. Wzrost różnicy ciśnień bądź też ciśnienia tłoczenia pompy prowadzić może do
obniżenia jej sprawności objętościowej.
Sprawność objętościowa silnika hydraulicznego zgodnie z oznaczeniami na rys. 4.9 może zostać
zdefiniowana jako:
.
(4.78)
Wprowadzając do równania (4.78) wyrażenie na straty całkowite Q według równości (4.74)
otrzyma się:
.
Po przekształceniu powyższej zależności uzyska się wyrażenie na sprawność objętościową
silnika hydraulicznego:
.
(4.79)
Sprawność objętościowa silnika hydraulicznego według wzoru (4.79) jest tym większa, im
lepkość cieczy, gęstość cieczy oraz prędkość obrotowa są większe. Wzrost obciążenia silnika
hydraulicznego prowadzi do obniżenia sprawności objętościowej. Wzrost chłonności właściwej
silnika hydraulicznego może poprawić wartość sprawności objętościowej.
t
t
t
s
e
vs
Q
Q
1
1
Q
Q
Q
Q
Q
s
3 2
s
s
1
s
rs
s
s
1
s
s
vs
q
n
q
q
p
2
c
q
2
p
c
1
1
3
1
s
2
s
s
1
s
rs
s
s
1
s
s
vs
q
n
p
2
c
n
2
p
c
1
1
6.3. Rozkład temperatury w
szczelinach
Wpływ lepkości cieczy na rozkład temperatury cieczy w szczelinach przeprowadza się przy
pominięciu wpływu temperatury na lepkość. Rozważania przykładowe pokazano dla szczeliny
o przekroju kołowym (rys.6.9) i szczeliny płaskiej o nieruchomych ściankach (rys. 6.10).
6.3.1. Rozkład temperatury w szczelinie o przekroju kołowym
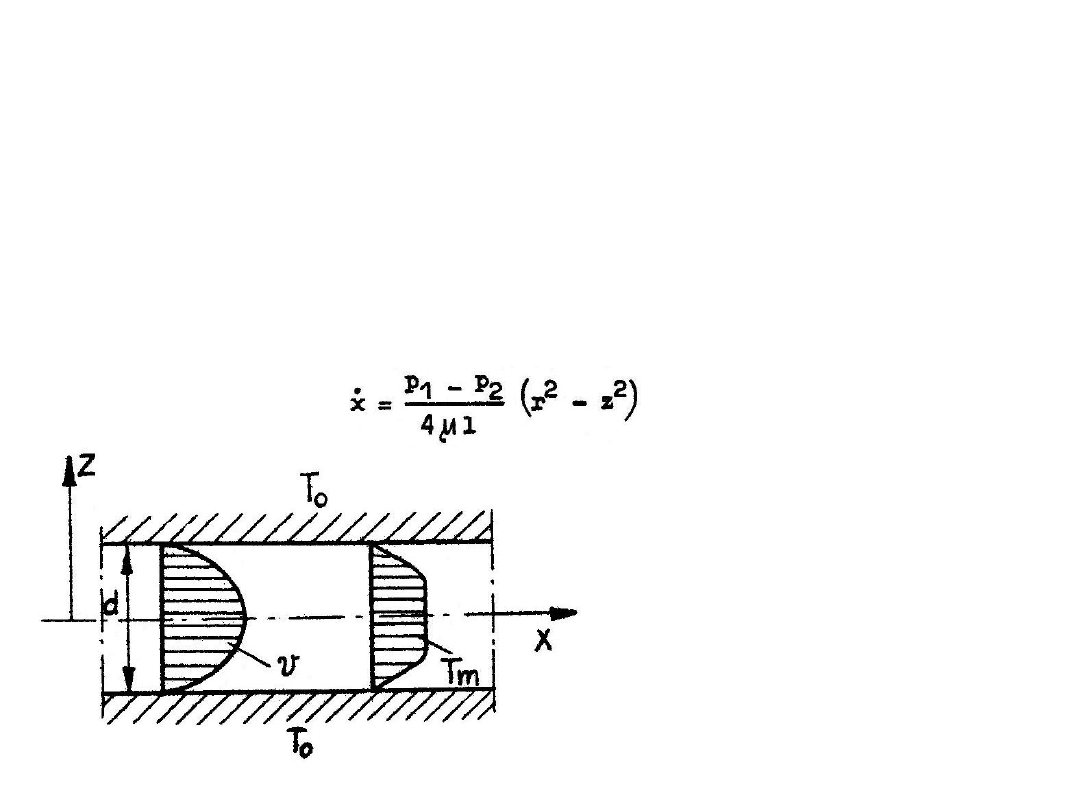
Rozważmy przepływ w kanale utworzonym przez przewód o przekroju kołowym o średnicy d,
utrzymanym w stałej temperaturze T
o
. Oś x przyjmujemy w osi symetrii zaś oś z w kierunki
prostopadłym (rys. 6.9). Profile prędkości i temperatury ze względu na założenia są
niezależne. Rozkład prędkości w tym przypad-ku został przedstawiony w rozdz. 5.2. Z tych
ustaleń prędkość w przekroju przepływu opisana jest związkiem:
Rys. 6.9. Rozkład prędkości i
temperatury w
szczelinie o przekroju
kołowym
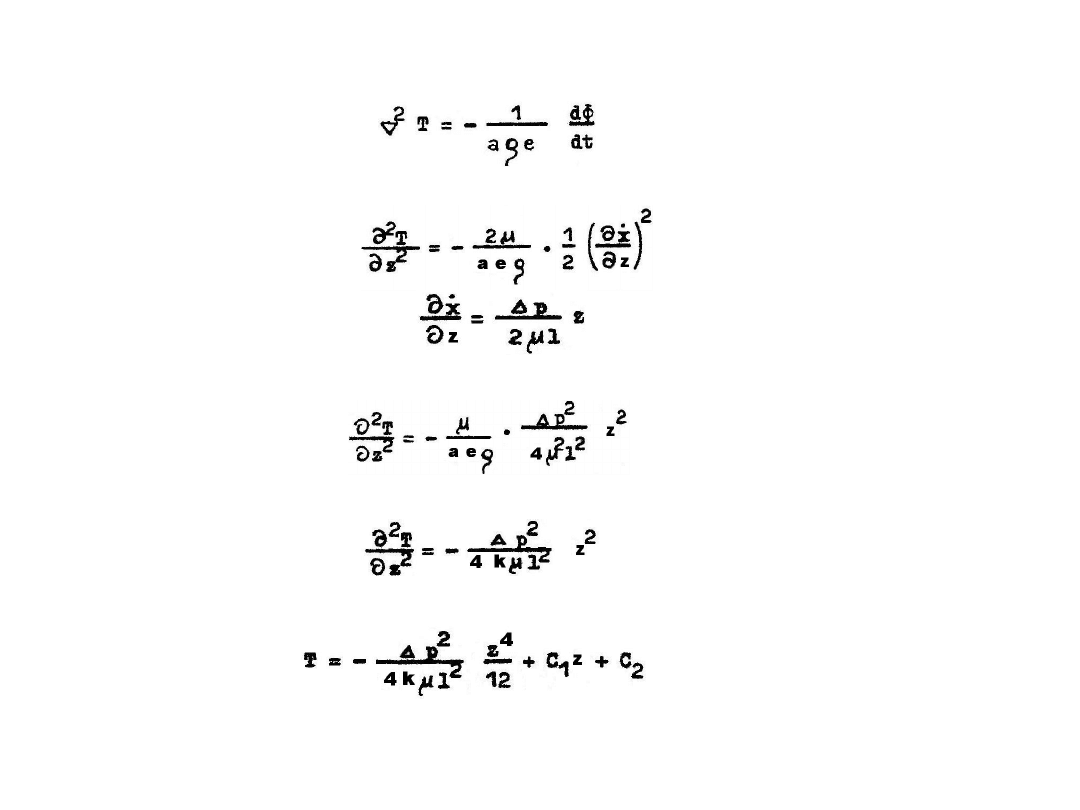
Znając rozkład prędkości w szczelinie można wyznaczyć odpowiadający mu rozkład
temperatury korzystając z równania (4.32) o postaci:
Ponieważ zarówno T jak i prędkość przepływu nie zależy od współrzędnej x otrzymujemy
proste równanie:
(6.67)
(6.68)
x
Wstawiając równanie (6.68) do równania (6.67) otrzymuje się:
Wprowadzając oznaczenia iloczynu a·e· = k i porządkując powyższe równanie uzyska się:
Po scałkowaniu otrzyma się wyrażenie:
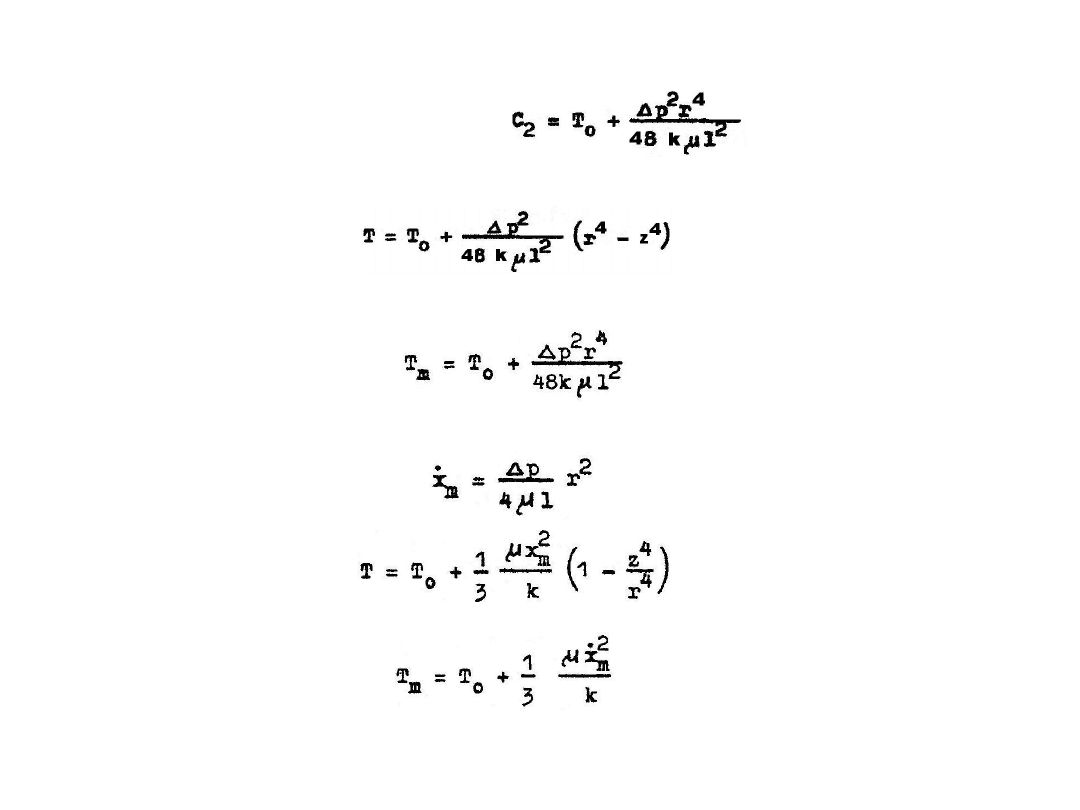
Wprowadzając wyrażenie na prędkość maksymalną do równania (6.70) i (6.71) otrzyma
się:
(6.72)
i
(6.73)
Z równań tych wynika, że przy zerowej lepkości = 0 temperatura T = T
o
= const.
Przyjmując warunki brzegowe zakładające, że dla ścianek ograniczających temperatura jest
stała i równa T
o
, tj. dla z = ± r, T = T
o
, mamy:
C
1
= 0
i
(6.69)
Ostatecznie zależność temperatury cieczy od odległości rozważanego punktu od płaszczyzny
symetrii ma postać:
(6.70)
Temperatura maksymalna występuje w osi symetrii, tj. dla z = 0 i wynosi:
(6.71)
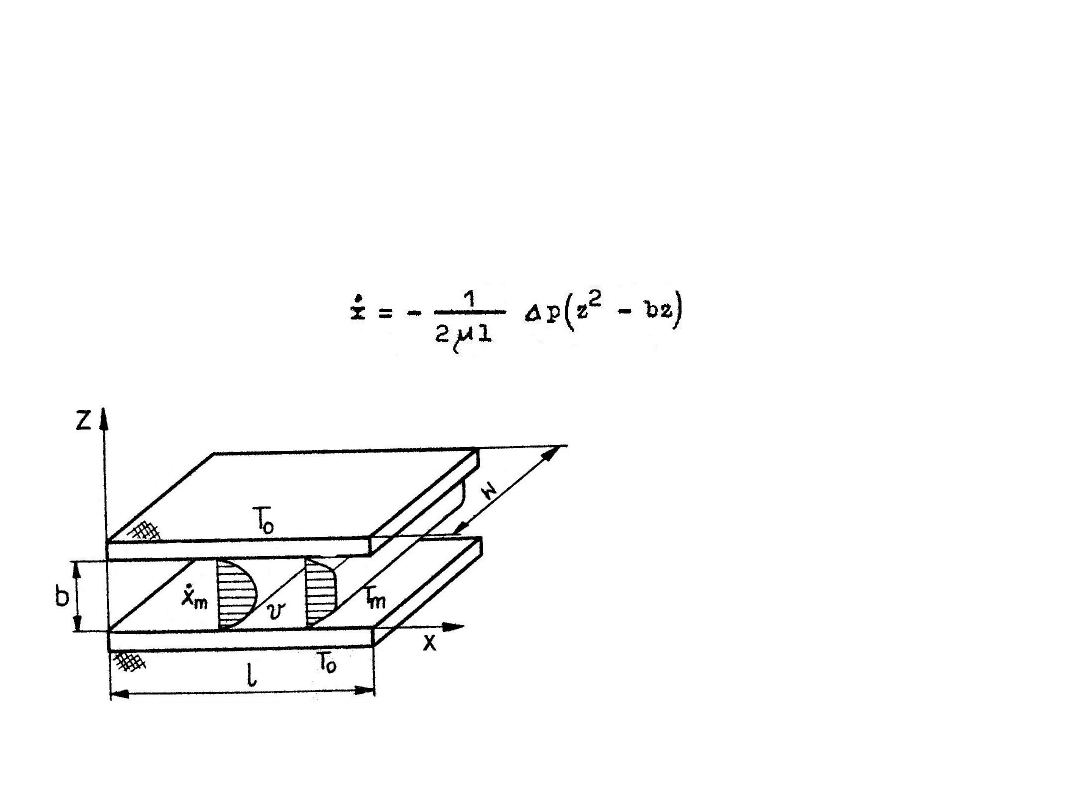
Działanie nagrzewające lepkości opisane jest więc wielkością dodaną do temperatury T
o
,
przy czym maksimum nagrzewania przypada na płaszczyznę symetrii. Profil rozkładu
temperatury w przekroju przedstawionym na rys. 6.9 jest bardziej płaski niż profil rozkładu
prędkości.
6.3.2. Rozkład temperatury w szczelinie płaskiej o nieruchomych ściankach
Rozpatrzmy przepływ cieczy w szczelinie płaskiej o nieruchomych ściankach, przy założeniu
stałej temperatury obu ścianek T
o
. Prędkość przepływu w funkcji wysokości szczeliny
określono według związku:
Rys. 6.10. Rozkład prędkości i
temperatury
w szczelinie płaskiej
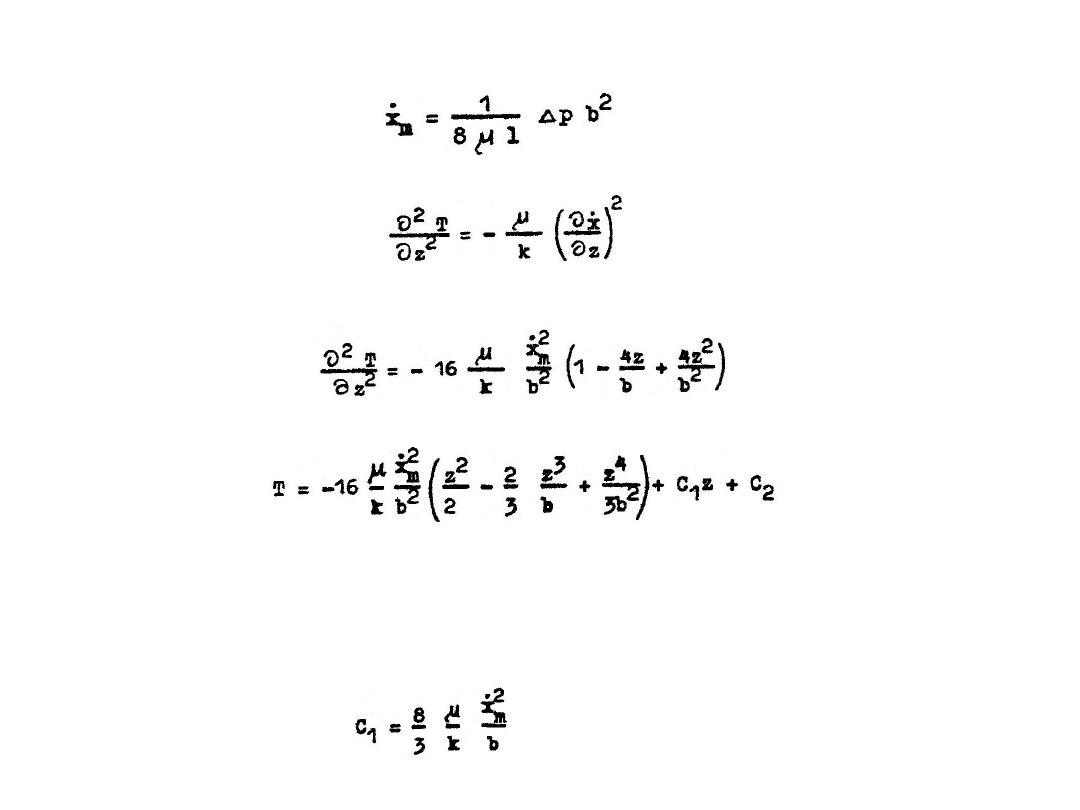
Maksymalna prędkość występuje w płaszczyźnie symetrii szczeliny i wynosi:
Analogicznie rozkład temperatury w szczelinie określi się wychodząc z równania (4.32) o
postaci:
(6.74)
Wprowadzając wyrażenia na prędkość przepływu w szczelinie i jej wartość maksymalną do
równania (6.74) otrzymuje się:
(6.75)
Po scałkowaniu równania (6.75) otrzyma się wyrażenie (6.76):
(6.76)
Dla tego typu szczeliny przyjmuje się następujące warunki brzegowe:
z = 0 , T = T
0
z = b , T = T
0
i otrzymuje się stałe całkowania:
,
C
2
= T
o

Porównując maksymalne temperatury w szczelinie o przekroju kołowym i w szczelinie
płaskiej można stwierdzić, że są zdefiniowane analogicznymi związkami. Prędkości
maksymalne dla obu przypadków są określone odmiennymi związkami wynikającymi z
konstrukcji szczeliny. Charakter rozkładu temperatury w rozważanych, szczelinach jest
ogólnie stwierdzając funkcją stopnia czwartego.
Ostatecznie równanie (6.76) przybiera postać:
bz
6
1
b
3
z
b
z
3
2
2
z
b
x
k
16
T
T
2
4
3
2
2
2
m
o
Maksymalna temperatura występuje w osi symetrii szczeliny, czyli dla z =+(b/2), i wynosi:
(6.78)
2
m
o
m
x
k
3
1
T
T
(6.77)
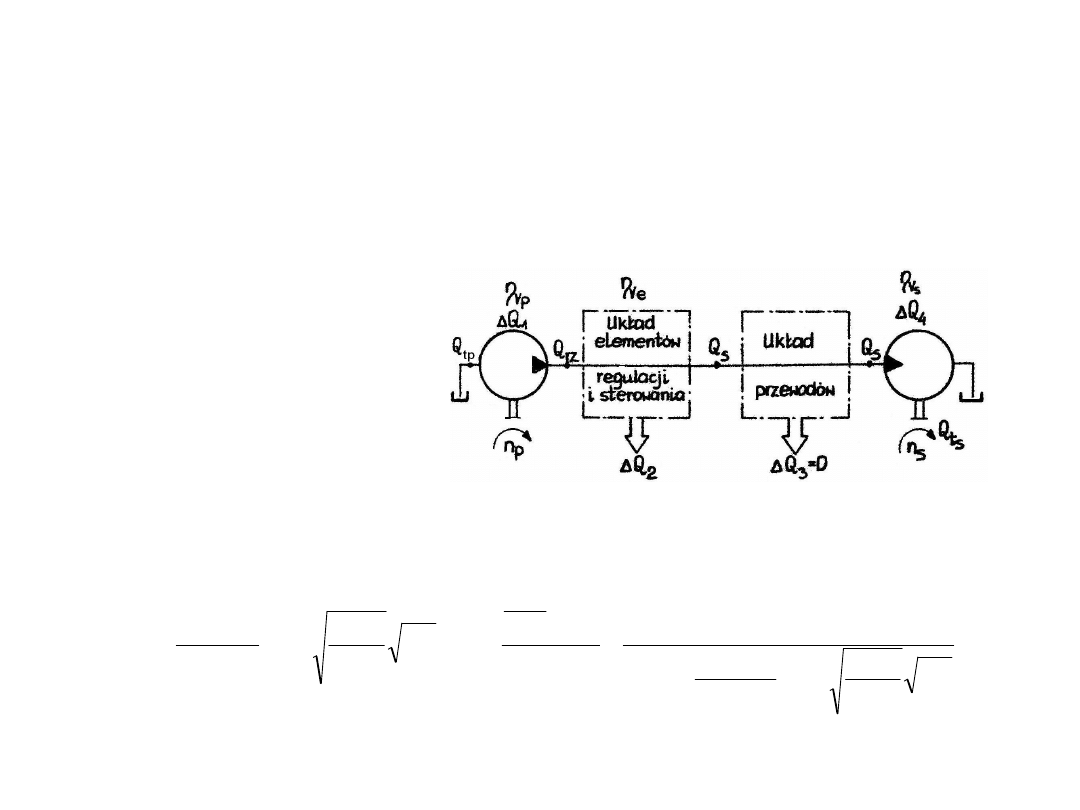
Sprawność objętościowa układu hydraulicznego zgodnie z oznaczeniami rys. 6.15 może
zostać określona jako iloczyn sprawności objętościowych pompy, układu elementów i silnika
hydraulicznego. Przewody w instalacji hydraulicznej nie wnoszą strat objętościowych w
układzie Q
3
= O, a więc natężenie wypływu z układu elementów regulacji i sterowania
równe jest natężeniu doprowadzonej cieczy do silnika hydraulicznego. Wobec powyższych
ustaleń sprawność całkowita wynosi:
vc
=
vp
+
ve
+
vs
(6.114)
6.8. Sprawność objętościowa układu
hydraulicznego
Rys. 6.13.
Zredukowany układ hydrauliczny
z oznaczeniem wielkości do
obliczenia
strat objętościowych
Wprowadzając do równania (6.114) równania (6.106), (6.111) i (6.115) otrzymuje się ogólną
postać na sprawność całkowitą objętościową układu hydraulicznego:
(6.115)
3
1
s
2
s
s
1
s
rs
s
s
1
s
s
rz
n
1
i
i
e
e
3
1
p
2
p
p
1
p
rp
p
1
p
p
p
vc
q
n
p
2
c
n
2
p
c
1
1
Q
X
p
1
q
n
p
2
c
n
2
p
c
1

Zgodnie z wzorami (6.114) i (6.115) wzrost całkowitej sprawności objętościowej układu możliwy
jest poprzez wzrost sprawności objętościowej każdego z elementów układu hydraulicznego.
Wzrost zatem całkowitej sprawności objętościowej układu nożna zapewnić na drodze wzrostu
lepkości, gęstości cieczy roboczej, zwiększenia wydajności (chłonności) właściwej pompy
(silnika hydraulicznego). O wartości sprawności objętościowej elementu hydraulicznego jak i
układu hydraulicznego istotnie decyduje technologia wykonania elementów, a więc wymiary i
liczba szczelin prowadzących do występowania strat objętościowych.
Sprawność objętościowa elementów w układzie hydraulicznym w przepływie szeregowym
należy określić
według wzoru (6.116):
(6.116)
gdzie: Q
1
…. Q
k
- straty objętościowe w poszczególnych elementach hydraulicznych układu
Wprowadzając do równania (6.116) zależność na stratę objętościową elementu hydraulicznego
zdefiniowaną według wzoru (6.105) otrzyma się:
(6.117)
rz
k
2
1
ve
Q
Q
Q
Q
1
...
rz
n
1
i
n
1
n
i
k
k
i
2
2
n
1
i
i
1
1
vc
Q
X
p
X
p
X
p
1
...
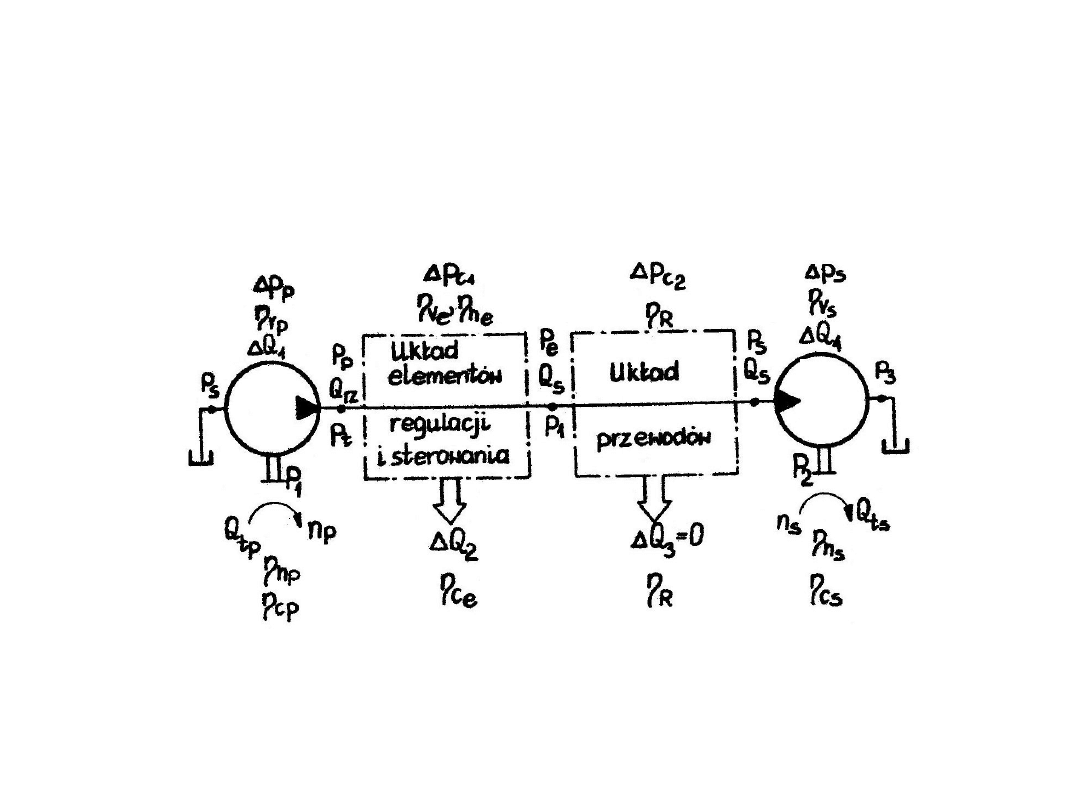
Sprawność całkowita układu hydraulicznego przedstawionego w postaci zredukowanej do
czterech podstawowych grup funkcjonalnych, jak generator, układ elementów
hydraulicznych, układ przewodów i odbiornik (silnik hydrauliczny) może zostać zdefiniowana
ogólnie jako stosunek mocy oddanej przez silnik hydrauliczny P
2
do mocy włożonej w
generator P
1
(rys. 7.1).
7. SPRAWNOŚĆ CAŁKOWITA UKŁADU
HYDRAULICZNEGO
Rys. 7.1. Zredukowany układ hydrauliczny z oznaczeniem wielkości do
określenia
sprawności całkowitej

Zgodnie więc z oznaczeniami (rys. 7.1) można sprawność całkowitą układu hydraulicznego
przedstawić jako iloczyn całkowitych sprawności objętościowych i całkowitych sprawności
hydraulicznych układu:
(7.3)
(7.1)
Z ustaleń przedstawionych w poprzednio moc w układzie hydraulicznym jest iloczynem
natężenia przepływu i ciśnienia, a więc w konsekwencji powyższego sprawność całkowita
określona jest iloczynem sprawności objętościowej i sprawności hydraulicznej (7.2).
(7.2)
1
2
c
P
P
h
v
c
hc
vc
c
vs
ve
vp
hs
R
he
hp
c
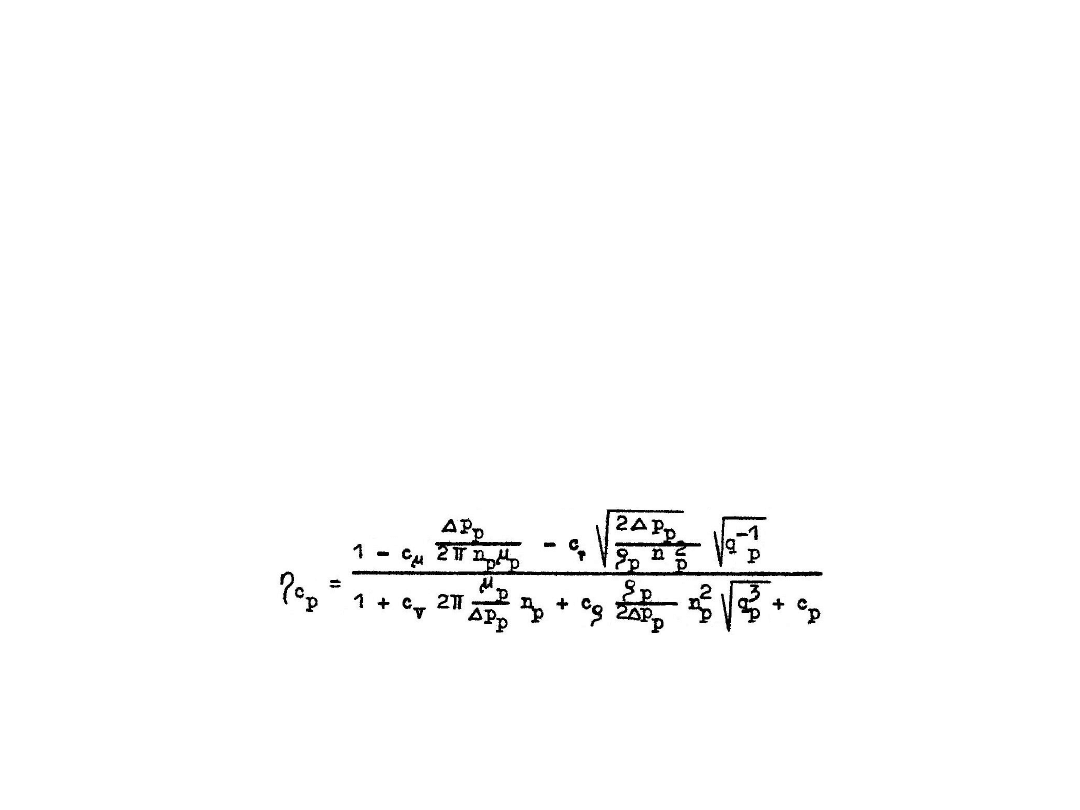
Wprowadzając do równania ogólnego (7.3) wyprowadzone związki na całkowitą sprawność
objętościową i hydrauliczną układu hydraulicznego (5.64) i (6.105) otrzymuje się wyrażenie
ogólne o postaci:
(7.4)
W związku z powyższym wyodrębnić można sprawności całkowite poszczególnych grup
funkcjonalnych, jak generator, układ elementów, przewody i silnik, a mianowicie:
- generator pompa
- układ elementów hydraulicznych
- przewody
- odbiornik (silnik hydrauliczny).
Korzystając z zależności wyprowadzonych w rozdz. 5.8 i 6.7 można ustalić sprawności
całkowite dla podstawowych elementów układu hydraulicznego.
Sprawność całkowita pompy (generatora) określona jest zależnością:
(7.6)
Wartości współczynników strat objętościowych i strat hydraulicznych dla wybranych pomp
wyporowych zostały przedstawione w tabeli.
cp
vp
hp
ce
ve
he
R
cs
vs
hs
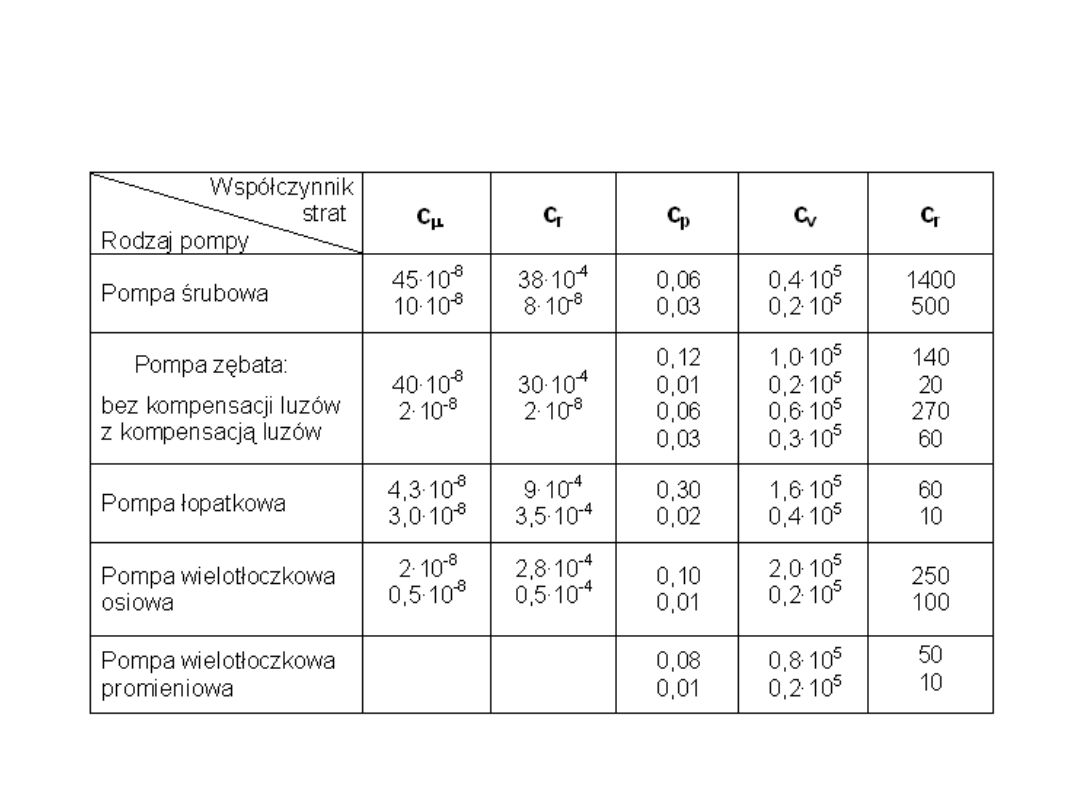
Tabela 7.1
Wartości współczynników strat objętościowych i strat hydraulicznych pomp
wyporowych
o wydajnościach właściwych (10 ÷ 50)·10
-6
m
3
/obr
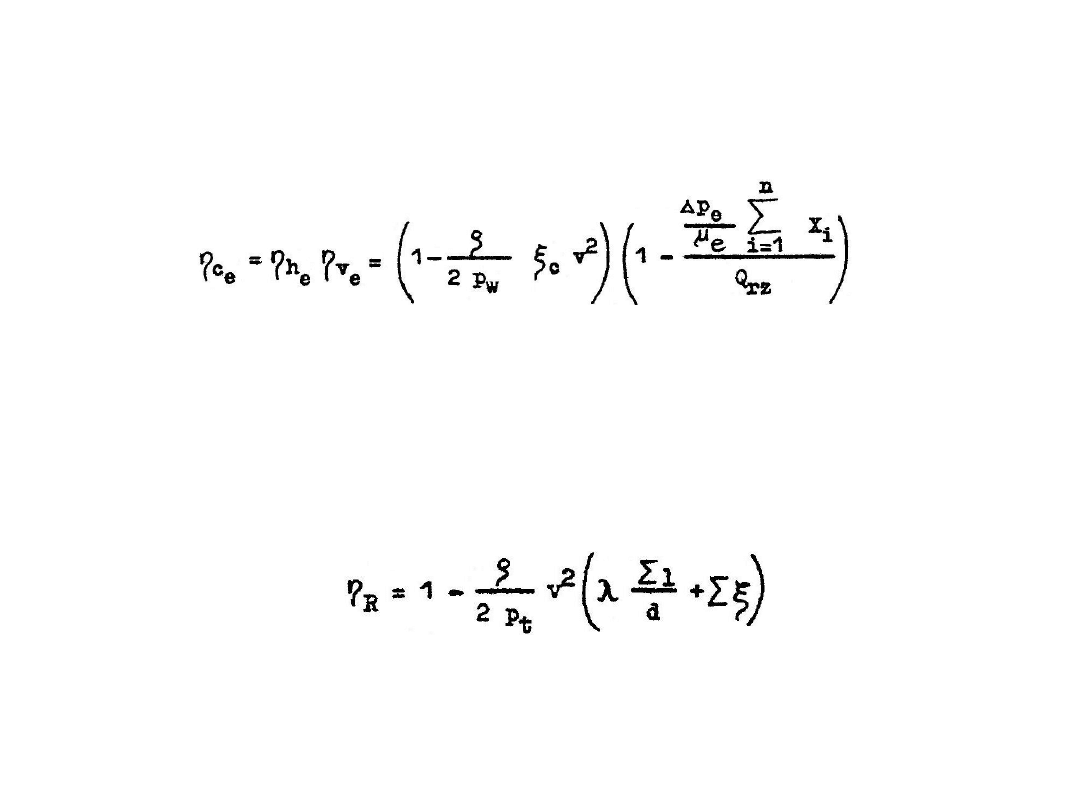
Zależność (7.6) na sprawność całkowitą pompy wyporowej daje możliwość przeprowadzenia
optymalizacji zarówno parametrów eksploatacyjnych jak i parametrów konstrukcyjnych pod
kątem otrzymania maksymalnej wartości sprawności.
Sprawność całkowitą układu elementów hydraulicznych wyznaczyć można zgodnie ze wzorem
(7.5) z wykorzystaniem ustalonych związków rozdziałach 5.8 i 6.7, a mianowicie:
(7.7)
Sprawność całkowita elementów hydraulicznych w układzie hydraulicznym jest tym większa
im większy jest człon sprawności hydraulicznej i sprawności objętościowej. Ogólnie można
stwierdzić, że zmniejszanie różnicy ciśnień p
e
w elementach hydraulicznych oraz
zmniejszenie prędkości przepływu w elementach prowadzi do podwyższenia sprawności
całkowitej elementów.
Przewody hydrauliczne nie powodują strat objętościowych w układzie, lecz jedynie straty
hydrauliczne. Sprawność zatem całkowita przewodów równa jest sprawności hydraulicznej
R
zdefiniowanej w rozdziale 5.7, a więc:
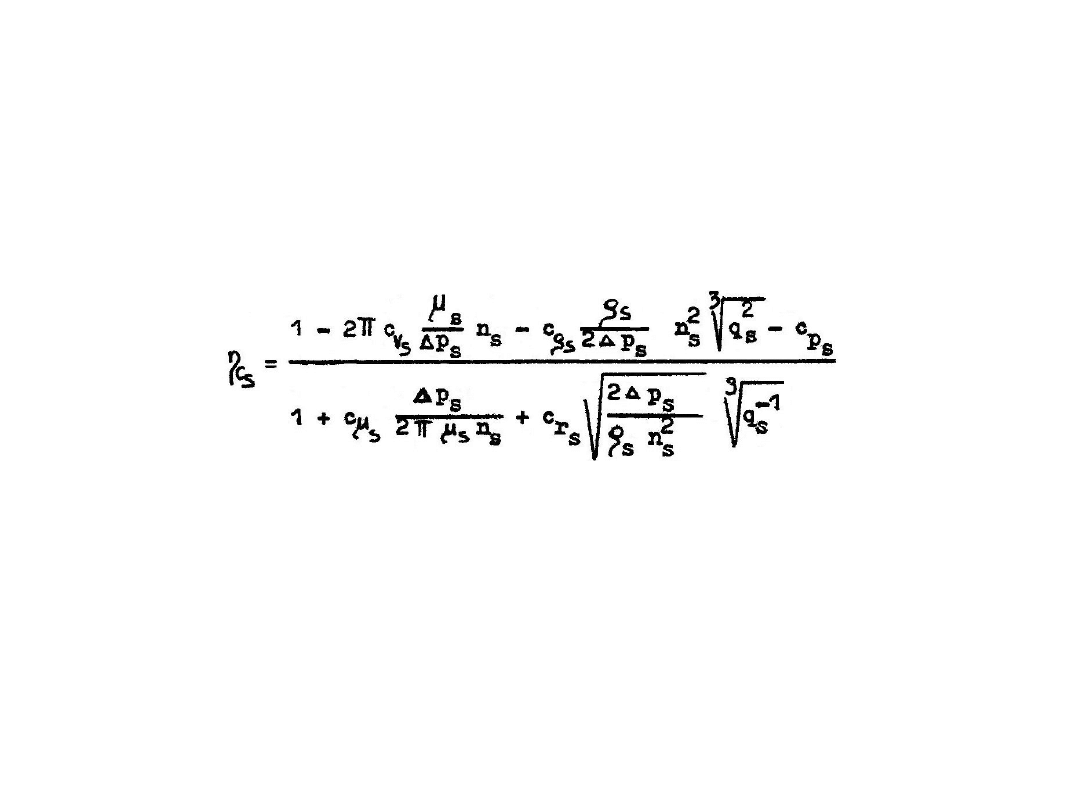
Ostatnim członem funkcjonalnym w układzie hydraulicznym jest odbiornik, czyli silnik
hydrauliczny. Sprawność całkowita silnika hydraulicznego zgodnie ze wzorem (7.5) równa
jest również iloczynowi sprawności hydrauliczno-mechanicznej i objętościowej:
Wprowadzając ustalone związki na sprawność hydrauliczną i objętościową silnika
hydraulicznego otrzyma się wyrażenie:
(7.8)
Porównując związek (7.4) z (7.5) można określić sprawność całkowitą układu
hydraulicznego jako:
(7.9)
vs
hs
cs
cs
R
ce
cp
c
Wprowadzając do równania (7.9) wyprowadzone zależności na sprawności całkowite
poszczególnych grup funkcjonalnych układu uzyska się związek ogólny na sprawność
całkowitą układu (7.10):

Na podstawie zależności ogólnej na sprawność całkowitą układu (7.10) możliwe staje się
określenie stopnia prawidłowości doboru elementów hydraulicznych do układu, jak i
wyznaczenie wpływu poszczególnych członów sprawności na jej wartość ostateczną. Istnieje
więc możliwość głębokiej analizy układu hydraulicznego pod kątem maksymalnej wartości i
jego sprawności całkowitej.
(7.10
)
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34
- Slide 35
- Slide 36
- Slide 37
- Slide 38
- Slide 39
- Slide 40
- Slide 41
- Slide 42
- Slide 43
- Slide 44
- Slide 45
- Slide 46
- Slide 47
- Slide 48
Wyszukiwarka
Podobne podstrony:
Edukacja a stratyfikacja
Mobilność i straty składników nawozowych
Straty ciepla pomieszczen k
P w5 5.11, Studia (Geologia,GZMIW UAM), I rok, Paleontologia ze Stratygrafią, 1. PALEONTOLOGIA WYKŁA
straty lokalne, STUDIA BUDOWNICTWO WBLIW, hydraulika i hydrologia
Zyski i straty ciepla w miesiacach
Rozliczanie straty podatkowej przez podatników CIT
straty lokalne
Kilowaty nie na straty
Ogolny przeglad Obj
09 Monopol straty i korzysci społeczne Ustawodawstwo antymonopolowe
SYSTEMATYKA paleo 2013, Studia (Geologia,GZMIW UAM), I rok, Paleontologia ze Stratygrafią
Tabela stratygraficzna, Nauka, Geografia
Straty na długości
żywienie człowieka straty składników odżywczych
Znaczne straty biznesu szczepionkowego i wirus AH1N1 w Polsce
czastk obj mol 5 03 (2)
Verb Klassifikation nach Subj & Obj
więcej podobnych podstron