Efektywność systemów

informatycznych

Wykład 5

TEMAT:Markowskie systemy

kolejkowe

2

Notacja Kendalla

gdzie:

gdzie:



A

A

– oznacza typ strumienia wejściowego:

– oznacza typ strumienia wejściowego:



M –

M –

strumień Poissona,

strumień Poissona,



E

E

k

k

– strumień Erlanga k-tego rzędu,

– strumień Erlanga k-tego rzędu,



D

D

– strumień deterministyczny,

– strumień deterministyczny,



GI –

GI –

(general input) opóżniony strumień

(general input) opóżniony strumień

rekurencyjny,

rekurencyjny,



A

A

X

X

- strumień niepojedynczy,

- strumień niepojedynczy,



- wiele niezależnych strumieni

- wiele niezależnych strumieni

wejściowych,

wejściowych,



SM

SM

– strumień semimarkowski,

– strumień semimarkowski,

obsł

reg

N

n

B

A

.

|

|

|

|

A



3

Notacja Kenadalla - 2



B

B

– oznacza typ rozkładu czasu obsługi

– oznacza typ rozkładu czasu obsługi

pojedynczego zgłoszenia:

pojedynczego zgłoszenia:



M –

M –

rozkład wykładniczy,

rozkład wykładniczy,



E

E

k

k

– rozkład Erlanga k-tego rzędu,

– rozkład Erlanga k-tego rzędu,



D

D

– czas deterministyczny,

– czas deterministyczny,



G –

G –

rozkład dowolny,

rozkład dowolny,



n

n

– liczba kanałów obsługi (1

– liczba kanałów obsługi (1





n

n





+

+





),

),



N

N

– liczba miejsc w kolejce ( 0

– liczba miejsc w kolejce ( 0





N

N





+

+





),

),



Regulamin obsługi

Regulamin obsługi

– sposób wyboru z kolejki

– sposób wyboru z kolejki

zgłoszenia do obsługi:

zgłoszenia do obsługi:



FIFO

FIFO

– first input first output

– first input first output



LIFO -

LIFO -

last input first output,

last input first output,



LIFO-PR -

LIFO-PR -

last input first output preemptive,

last input first output preemptive,



SIRO –

SIRO –

service in random order

service in random order



PS – processor sharing.

PS – processor sharing.

4

Procesy urodzin i śmierci



Przed omówieniem markowskich modeli

Przed omówieniem markowskich modeli

systemów kolejkowych (markowskich

systemów kolejkowych (markowskich

systemów masowej obsługi – SMO),

systemów masowej obsługi – SMO),

zaprezentowane zostaną procesy urodzin i

zaprezentowane zostaną procesy urodzin i

śmierci. Stanowią one podstawowy aparat do

śmierci. Stanowią one podstawowy aparat do

analizy markowskich SMO.

analizy markowskich SMO.



Niech

Niech

będzie jednorodnym procesem

będzie jednorodnym procesem

Markowa klasy DC

Markowa klasy DC

i

i

X

X

=

=

{0,1,....,n,.....} o

{0,1,....,n,.....} o

następującej macierzy intensywności przejść:

następującej macierzy intensywności przejść:

)

(t

































































































































































0

0

0

0

0

0

0

0

0

2

1

0

2

2

2

2

1

1

1

1

0

0

i

i

i

i

i







































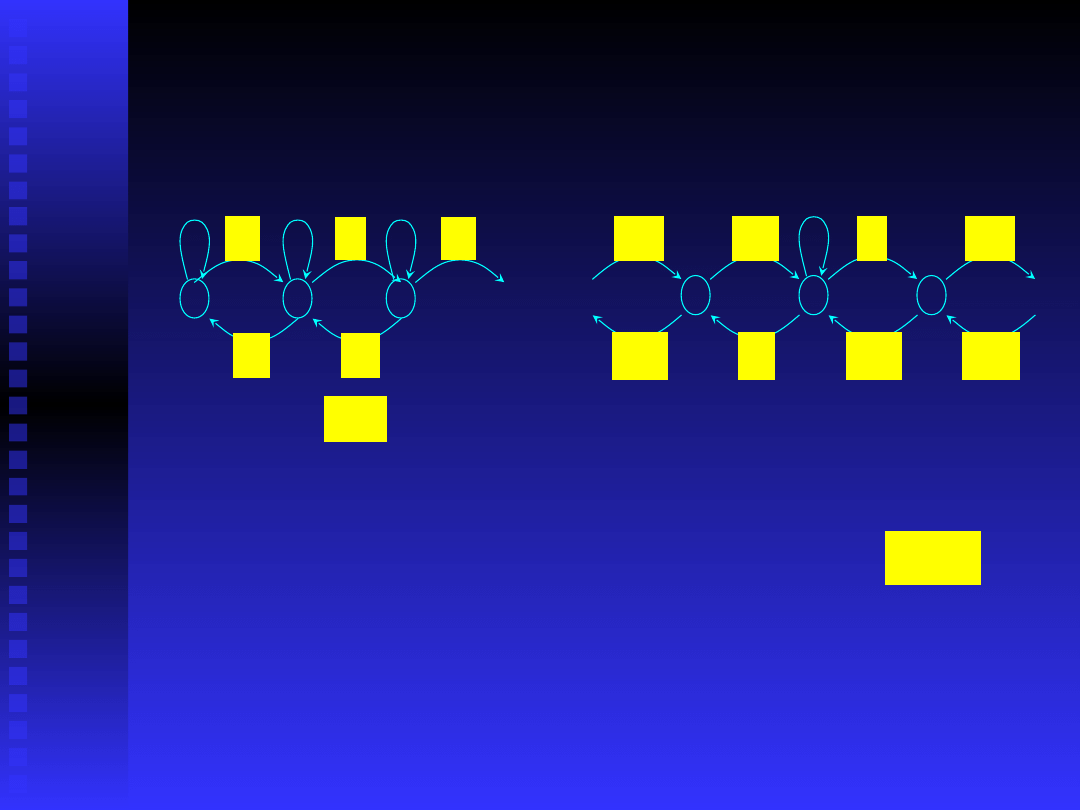
5

Procesy urodzin i śmierci - 2



Graficznie można to przedstawić następująco:

Graficznie można to przedstawić następująco:



Proces

Proces

można

można

opisać

opisać

inaczej przyjmując, że

inaczej przyjmując, że

jest to proces stochastyczny spełniający

jest to proces stochastyczny spełniający

następujące założenia:

następujące założenia:



1.     

1.     

Czas przebywania procesu w stanie

Czas przebywania procesu w stanie

i

i





X

X

jest

jest

zmienną losową o rozkładzie wykładniczym z

zmienną losową o rozkładzie wykładniczym z

parametrem

parametrem

i jest niezależny od trajektorii

i jest niezależny od trajektorii

(przebiegu) procesu do chwili osiągnięcia tego stanu;

(przebiegu) procesu do chwili osiągnięcia tego stanu;



2.      Ze stanu

2.      Ze stanu

i

i





X

X

proces przechodzi do stanu

proces przechodzi do stanu

i+1

i+1

lub

lub



(i-1)

(i-1)

+

+

=max{0, i-1}

=max{0, i-1}

z prawdopodobieństwem

z prawdopodobieństwem

odpowiednio

odpowiednio

p

p

i

i

oraz

oraz

q

q

i

i

=1-p

=1-p

i

i

,

,

p

p

0

0

=1, q

=1, q

0

0

=0.

=0.

 

0



1



2



2



i



1



i



i



1



i



0

1

2

i-1

i

i+
1

1



2



2



i



1



i



i



1



i



)

(t



0



i



6

Procesy urodzin i śmierci - 3



Wobec tego, proces

Wobec tego, proces

jest również procesem

jest również procesem

SM, dla którego:

SM, dla którego:



Przejście między jedna, a druga definicją

Przejście między jedna, a druga definicją

procesu określają następujące zależności:

procesu określają następujące zależności:

 

)

(t



 

 







































h

przypadkac

pozostaych

w

i

j

p

q

i

j

p

q

i

e

t

G

i

i

i

ij

t

i

i

0

1

1

1

,

1





X

X

i

q

III

X

i

p

II

i

I

i

i

i

i

i

i

i

i

i

i

i

ii























,

)

,

)

,

)

1

,

1

,

















X

7

Procesy urodzin i śmierci - 4

 

X

X

X



















i

q

III

i

p

II

i

I

i

i

i

i

i

i

i

i

i

i

i

,

)

'

,

)

'

,

)

'



















8

Własności procesów urodzin i śmierci

 

Dla procesu

Dla procesu

urodzin i śmierci zachodzą dwa

urodzin i śmierci zachodzą dwa

następujące twierdzenia

następujące twierdzenia

:

:

Twierdzenie 5.1.

Twierdzenie 5.1.

Niech

Niech

Wtedy:

Wtedy:

1

1

0

0

Układ

Układ

przy zadanym

przy zadanym

P(0)

P(0)

posiada jednoznaczne

posiada jednoznaczne

rozwiązanie, jeśli spełniony jest warunek:

rozwiązanie, jeśli spełniony jest warunek:

)

(t











0

0

,

1

0

0

1

0

0













i

dla

p

oraz

p

i

i

i







 

 

 

 

  

  

 

1

,

;

1

1

1

1

1

1

0

0

0





























k

t

P

t

P

t

P

t

P

t

P

t

P

t

P

k

k

k

k

k

k

k

k













0

,

1

gdzie

,

1

1

1

0

0

0

0



















 

k

dla

k

k

k

n

n

k

k

k

n























9

Własności procesów urodzin i śmierci -2

2

2

0

0

Niezależnie od stanu początkowego procesu,

Niezależnie od stanu początkowego procesu,

istnieją granice:

istnieją granice:

3

3

0

0

Zbieżność szeregu

Zbieżność szeregu

jest równoważna

jest równoważna

temu, że:

temu, że:

4

4

0

0

Rozbieżność szeregu

Rozbieżność szeregu

jest równoważna

jest równoważna

temu, że:

temu, że:

 

 

0

,

lim









k

t

P

k

k

t









0

k

k



























0

0

1

0

,

0

,

0

k

k

k

k

k

k

k

















0

k

k



0

,

0





k

dla

k



10

Własności procesów urodzin i śmierci -2

Twierdzenie 5.1.A

Twierdzenie 5.1.A

Niech

Niech

Wtedy

Wtedy

1

1

0

0

Układ

Układ

Dla danego

Dla danego

P(0)

P(0)

posiada jednoznaczne

posiada jednoznaczne

rozwiązanie.

rozwiązanie.

2

2

0

0

Istnieją granice:

Istnieją granice:

,

,

przy czym

przy czym

 

 

n

k

t

P

k

k

t











0

,

lim



















0

0

1

..,

,

1

,

0

,

k

k

k

k

n

k













1

0

,

0

1

0

,

1

0















n

n

i

q

p

n

i

dla

p

p

 

 

 

 

  

  

 

 

 

 

t

P

t

P

t

P

n

k

t

P

t

P

t

P

t

P

t

P

t

P

t

P

n

n

n

n

n

k

k

k

k

k

k

k

k

























































1

1

1

1

1

1

1

1

0

0

0

0

,



11

Markowskie systemy kolejkowe



Omówione zostaną następujące klasy

Omówione zostaną następujące klasy

systemów markowskich:

systemów markowskich:



Systemy z oczekiwaniem:

Systemy z oczekiwaniem:



M|M|1|

M|M|1|





= M|M|1

= M|M|1



M|M|n

M|M|n



Systemy ze stratami:

Systemy ze stratami:



M|M|n|N

M|M|n|N

 

12

System M|M|1| |FIFO



Przyjmijmy następujące oznaczenia i założenia:

Przyjmijmy następujące oznaczenia i założenia:



Ciąg

Ciąg

jest ciągiem niezależnych zmiennych

jest ciągiem niezależnych zmiennych

losowych oznaczających odstępy czasu między

losowych oznaczających odstępy czasu między

kolejnymi zgłoszeniami przybywającymi do

kolejnymi zgłoszeniami przybywającymi do

systemu,

systemu,



Ciąg

Ciąg

jest ciągiem niezależnych zmiennych

jest ciągiem niezależnych zmiennych

losowych oznaczających czasy obsługi kolejnych

losowych oznaczających czasy obsługi kolejnych

zgłoszeń,

zgłoszeń,



Ciągi

Ciągi

i

i

są niezależne stochastyczne,

są niezależne stochastyczne,



Z opisu systemu wynika, że:

Z opisu systemu wynika, że:



Niech

Niech

będzie procesem stochastycznym,

będzie procesem stochastycznym,

którego wartość w chwili oznacza liczbę

którego wartość w chwili oznacza liczbę

zgłoszeń w systemie w chwili

zgłoszeń w systemie w chwili

t.

t.

 

 

1



n

n



 

1



n

n



 

1



n

n



 

1



n

n



,...

2

,

1

,

0

,

1

}

{

)

(

,...

2

,

1

,

0

,

1

}

{

)

(





























n

t

e

t

P

t

G

n

t

e

t

P

t

F

t

n

t

n









)

(t



13

System M|M|1| |FIFO c.d.2



Z przyjętych założeń i oznaczeń wynika, że

Z przyjętych założeń i oznaczeń wynika, że

proces

proces

jest jednorodnym procesem Markowa

jest jednorodnym procesem Markowa

klasy DC tzn.:

klasy DC tzn.:



Wobec tego, pełny opis probabilistyczny będą

Wobec tego, pełny opis probabilistyczny będą

stanowić:

stanowić:



macierz intensywności przejść,

macierz intensywności przejść,



rozkład początkowy.

rozkład początkowy.



W pierwszej kolejności wyznaczymy parametry

W pierwszej kolejności wyznaczymy parametry

Zgodnie z twierdzeniem 3.1:

Zgodnie z twierdzeniem 3.1:

Wyznaczmy oszacowanie

Wyznaczmy oszacowanie

. Zauważmy, że:

. Zauważmy, że:

 

)

(t



..}

,

2

,

1

,

0

{

oraz

)

,

0

[









X

T

,..

2

,

1

,

0

, 

i

i









)

(

1

lim

0

ii

t

i

p









)

(



ii

p





}

,

{

)

(

0













k

ii

k

M

k

N

P

p







14

System M|M|1| |FIFO c.d.3

gdzie N

gdzie N

τ

τ

- liczba zgłoszeń, które przybyły w

- liczba zgłoszeń, które przybyły w

czasie (t, t+

czasie (t, t+

τ

τ

)

)

M

M

τ

τ

- liczba zgłoszeń obsłużonych w

- liczba zgłoszeń obsłużonych w

przedziale (t, t+

przedziale (t, t+

τ

τ

).

).

Biorąc pod uwagę, że zdarzenia

Biorąc pod uwagę, że zdarzenia

są rozłączne

są rozłączne

dla k

dla k





l

l

, otrzymujemy, że:

, otrzymujemy, że:

Można pokazać, że:

Można pokazać, że:

(*)

(*)

Z tego wynika natomiast, że:

Z tego wynika natomiast, że:



 



l

M

l

N

i

k

M

k

N

















,

,

 

















0

,

k

ii

k

M

k

N

P

p











 







o

k

M

k

N

P

k











,

1

 





































































1

0

,

0

,

0

1

,

1

1

k

k

ii

k

M

k

N

P

M

N

P

k

M

k

N

P

p

15

System M|M|1| |FIFO c.d.4

A stąd, biorąc pod uwagę (*) można stwierdzić, że:

A stąd, biorąc pod uwagę (*) można stwierdzić, że:

UWAGA

UWAGA

W dalszym ciągu będziemy przyjmować, że

W dalszym ciągu będziemy przyjmować, że

prawdopodobieństwo zdarzenia polegającego na

prawdopodobieństwo zdarzenia polegającego na

tym, że w

tym, że w

krótkim czasie wystąpi więcej niż jedna sytuacja

krótkim czasie wystąpi więcej niż jedna sytuacja

typu:

typu:

napłynęło nowe zgłoszenie, zakończyła się obsługa

napłynęło nowe zgłoszenie, zakończyła się obsługa

zgłoszenia, jest funkcją rzędu

zgłoszenia, jest funkcją rzędu

o(t).

o(t).

 















































0

,

0

1

lim

,

lim

0

,

0

1

lim

1

lim

1

















































M

N

P

k

M

k

N

P

M

N

P

p

o

i

k

o

o

ii

o

i

16

System M|M|1| |FIFO c.d.5

Zatem, dla małych

Zatem, dla małych





mamy:

mamy:

Stąd:

Stąd:

 



























0

,...

2

,

1

,

i

P

i

P

p

ii















 

























































































































































e

e

i

Dla

i

dla

e

e

e

P

P

p

H

H

ii

i

0

0

0

0

0

0

0

lim

1

lim

0

1

lim

1

lim

1

lim

1

lim

17

System M|M|1| |FIFO c.d.6

Obecnie wyznaczymy

Obecnie wyznaczymy

λ

λ

i,i+1

i,i+1

, i ≥ 0

, i ≥ 0

:

:

Zatem:

Zatem:

 





























0

1

,

1

,

i

P

i

P

p

i

i











































































































































































e

e

e

e

e

e

P

P

p

H

H

i

i

i

i

0

0

1

,

0

0

0

0

1

,

0

1

,

lim

1

lim

lim

1

lim

lim

lim

18

System M|M|1| |FIFO c.d.7

Wyznaczymy teraz

Wyznaczymy teraz

λ

λ

i,i

i,i

-

-

1

1

, i ≥

, i ≥

1

1

:

:

Zauważmy, że:

Zauważmy, że:

Wynika stąd, biorąc pod uwagę twierdzenie 3.1,

Wynika stąd, biorąc pod uwagę twierdzenie 3.1,

że pozostałe intensywności przejść są równe

że pozostałe intensywności przejść są równe

zeru. Zatem graficznie proces można

zeru. Zatem graficznie proces można

przedstawić następująco:

przedstawić następująco:

 





 















































































































e

e

e

e

p

P

p

H

i

i

i

i

i

i

0

0

1

,

0

1

,

1

,

lim

1

lim

lim

,

0

1

,

0

1

,

1

,

,...

2

,

1



































oraz

i

i

i

i

i

i

19

System M|M|1| |FIFO c.d.8

Zaś macierz intensywności przejść ma postać:

Zaś macierz intensywności przejść ma postać:

-

-





































0

0

1

1

i

i



































































































0

0

0

0

0

0

0

0

0

0

2

1

0

2

1

0















i

i

20

System M|M|1| |FIFO c.d.9

Z postaci macierzy intensywności wynika, że

Z postaci macierzy intensywności wynika, że

proces

proces

jest procesem urodzin i śmierci , w

jest procesem urodzin i śmierci , w

którym:

którym:

Wobec tego, że spełnione są założenia twierdzenia

Wobec tego, że spełnione są założenia twierdzenia

3.4, to rozwiązanie układu równań:

3.4, to rozwiązanie układu równań:

jest rozkładem chwilowym procesu

jest rozkładem chwilowym procesu

dla

dla

dowolnego

dowolnego

t>0.

t>0.

Rozkład graniczny rozpatrywanego procesu

Rozkład graniczny rozpatrywanego procesu

istnieje, jeśli

istnieje, jeśli

(Tw. 5.1):

(Tw. 5.1):

)

(t























0

,...

2

,

1

,

oraz

i

i

i







)

(

)

(

'

t

P

t

P

)

(t









0

k

k



21

System M|M|1| |FIFO c.d.10



Z określenia wynika, że:

Z określenia wynika, że:

Wobec tego:

Wobec tego:

jeśli

jeśli

Jeżeli natomiast

Jeżeli natomiast

k



1

1

,

0

1

1

0















































i

k

k

k

k

k

















































0

k

k

0

k

k

1

1













1











0

,

k

k

to







22

System M|M|1| |FIFO c.d.11

Zatem, dla przypadku

Zatem, dla przypadku

λ

λ

<

<

μ

μ

otrzymujemy

otrzymujemy

:

:

Wartość

Wartość

π

π

0

0

wyznaczamy wykorzystując warunek

wyznaczamy wykorzystując warunek

normalizacyjny:

normalizacyjny:

a stąd:

a stąd:

Wobec tego, rozkład graniczny ma postać:

Wobec tego, rozkład graniczny ma postać:

0

k

,

0

k

k

k

























































































0

k

0

k

0

k

0

0

k

0

k

k

1

1

1

czyli

1



















dla

0







































warunku

przy

0

k

,

k

k

23

System M|M|1| |FIFO c.d.12

Jeśli natomiast

Jeśli natomiast

λ

λ

≥

≥

μ

μ

,

,

to

to

α

α

k

k

=

=

π

π

k

k

=0 dla k ≥

=0 dla k ≥

0

0

.

.

Wobec tego nie istnieje w tym przypadku rozkład

Wobec tego nie istnieje w tym przypadku rozkład

graniczny w sensie definicji 3.5.

graniczny w sensie definicji 3.5.



Rozkład czasu oczekiwania na obsługę

Rozkład czasu oczekiwania na obsługę



Przyjmijmy oznaczenia:

Przyjmijmy oznaczenia:



V

V

t

t

-

-

oznacza czas pobytu w systemie zgłoszenia,

oznacza czas pobytu w systemie zgłoszenia,

które przybyło do systemu w chwili

które przybyło do systemu w chwili

t

t

,

,



W

W

t

t

-

-

oznacza czas oczekiwania na obsługę

oznacza czas oczekiwania na obsługę

zgłoszenia, które przybyło do systemu w chwili

zgłoszenia, które przybyło do systemu w chwili

t

t

,

,



V – graniczny czas pobytu w systemie zgłoszenia,

V – graniczny czas pobytu w systemie zgłoszenia,



W – graniczny czas oczekiwania na obsługę

W – graniczny czas oczekiwania na obsługę

zgłoszenia

zgłoszenia

.

.

24

System M|M|1| |FIFO c.d.13

Można zauważyć, że

Można zauważyć, że

gdzie:

gdzie:

.

.

Wobec tego, oznaczając przez

Wobec tego, oznaczając przez

H

H

t

t

(

(

τ

τ

)

)

dystrybuantę

dystrybuantę

zmiennej losowej

zmiennej losowej

W

W

t

t

dla ustalonego

dla ustalonego

t

t

otrzymujemy, że

otrzymujemy, że

:

:

Jeśli

Jeśli

to:

to:







t

i

i

D

t

W





0

0

0





 









  





 



























































0

*

0

0

0

k

t

k

k

t

k

i

i

i

i

t

t

k

P

G

k

P

P

P

W

P

H

t





















 

 

 





t

t

D

t

t

W

W

gdzie

W

P

H

a

e

H

H





























lim

,

0

,

1

lim

)

(



























25

System M|M|1| |FIFO c.d.14

Warto zauważyć, że:

Warto zauważyć, że:

czyli

czyli

,

,

co oznacza, że

co oznacza, że

graniczny czas oczekiwania jest równy zeru

graniczny czas oczekiwania jest równy zeru

jeśli zgłoszenie zastanie pusty system

jeśli zgłoszenie zastanie pusty system

.

.

Spełnienie warunku

Spełnienie warunku

powoduje również:

powoduje również:

a rozkład

a rozkład

V

V

czasu pobytu zgłoszenia w systemie

czasu pobytu zgłoszenia w systemie

można wyznaczyć z zależności:

można wyznaczyć z zależności:

 























1

t

H

lim

0

t









0

0

0













P

W

P







V

V

D

t



















t

V

x

dG

x

t

H

t

G

H

t

V

P

t

F

0

)

(

)

(

)

(

}

{

)

(

26

System M|M|n| |FIFO = M|M|n



Podobnie jak w przypadku M | M | 1 proces

Podobnie jak w przypadku M | M | 1 proces

, którego wartość w ustalonej chwili oznacza

, którego wartość w ustalonej chwili oznacza

liczbę zgłoszeń w systemie, jest procesem

liczbę zgłoszeń w systemie, jest procesem

urodzin i śmierci. Jego macierz intensywności

urodzin i śmierci. Jego macierz intensywności

przejść określają zależności:

przejść określają zależności:

Z twierdzenia 5.1 wiadomo, że rozkład graniczny

Z twierdzenia 5.1 wiadomo, że rozkład graniczny

istnieje, jeśli

istnieje, jeśli

. W tym przypadku

. W tym przypadku

ρ

ρ

k

k

jest określone

jest określone

zależnościami:

zależnościami:

 

t











































,....

1

n

i

,

n

n

,

1

i

,

i

,....

2

,

1

,

0

i

,

i

i

i











0

k

k



















































n

k

n

n

n

k

k

n

k

k

k

k

!

1

0

!

1











27

System M|M|n| |FIFO = M|M|n

c.d.2

Łatwo sprawdzić, że warunek zbieżności szeregu

Łatwo sprawdzić, że warunek zbieżności szeregu

jest spełniony, jeśli

jest spełniony, jeśli

. Rozkład graniczny

. Rozkład graniczny

procesu

procesu

określają zależności:

określają zależności:

Przyjmując oznaczenie

Przyjmując oznaczenie

, otrzymujemy:

, otrzymujemy:







 n

 

t





























































n

k

n

n

n

k

k

n

k

k

k

k

k

0

0

!

1

0

!

1





























































n

k

n

!

n

n

k

0

!

k

0

n

k

k

0

k

k

28

System M|M|n| |FIFO = M|M|n

c.d.3



Jeśli

Jeśli

, to nie istnieje rozkład

, to nie istnieje rozkład

graniczny oraz

graniczny oraz



Wartość

Wartość

π

π

0

0

wyznaczamy z warunku

wyznaczamy z warunku

normalizacyjnego i ma ona postać:

normalizacyjnego i ma ona postać:



Analogicznie jak dla M | M | 1 można

Analogicznie jak dla M | M | 1 można

wyznaczyć postać

wyznaczyć postać

. Jeśli

. Jeśli

to:

to:







n

 

0

k

,

0

t

P

lim

k

t

k

















1

1

n

n

0

k

k

0

n

!

n

!

k



































 

 











t

t

H

lim

H







 n

  



































0

t

e

p

1

0

t

0

t

W

P

t

H

t

W

29

System M|M|n| |FIFO = M|M|n

c.d.4

gdzie:

gdzie:

i

i

p

p

W

W

jest

jest

prawdopodobieństwem tego, że zgłoszenie

prawdopodobieństwem tego, że zgłoszenie

przybywając do systemu, po nieskończenie

przybywając do systemu, po nieskończenie

długim okresie jego funkcjonowania, będzie

długim okresie jego funkcjonowania, będzie

musiało oczekiwać na obsługę.

musiało oczekiwać na obsługę.



Strumień wyjściowy systemu M|M|n

Strumień wyjściowy systemu M|M|n

Twierdzenie 5.2

Twierdzenie 5.2

(Tw.Burke’a)

(Tw.Burke’a)

W systemie M | M | n jeśli spełniony jest warunek

W systemie M | M | n jeśli spełniony jest warunek

, to w trybie stacjonarnym strumień

, to w trybie stacjonarnym strumień

wyjściowy jest strumieniem Poissona o

wyjściowy jest strumieniem Poissona o

parametrze

parametrze

λ

λ

.

.







 



0

0

0

0

!

1

1

!

!

!



























































n

n

n

n

n

n

n

n

n

n

n

n

P

p

n

n

n

n

n

k

k

k

n

n

k

n

k

k

W







 n

30

System ze stratami M|M|n|N|FIFO



Proces

Proces

jest procesem urodzi i śmierci o

jest procesem urodzi i śmierci o

następującej macierzy intensywności przejść:

następującej macierzy intensywności przejść:



Z twierdzenia 5.1.A wynika, że rozkład

Z twierdzenia 5.1.A wynika, że rozkład

graniczny istnieje zawsze i posiada postać:

graniczny istnieje zawsze i posiada postać:

gdzie:

gdzie:

 

t























































N

n

,

1

n

i

,

n

n

,

1

i

,

i

1

N

n

,

0

i

,

i

i







































N

n

,

1

n

k

n

!

n

n

,

0

k

!

k

0

n

k

k

0

k

k

1

N

1

r

r

n

n

0

k

k

0

n

!

n

!

k































 













