1

1





klienci pojawiają się w systemie rzadziej niż
są obsługiwani.

Stan równowagi – kiedy sprawność obsługi klientów
w systemie jest nie mniejsza niż częstość napływania
nowych klientów







Analiza funkcjonowania urządzeń

obsługujących

2



Z punktu widzenia ekonomicznego

dążymy do minimalizacji kosztów lub

maksymalizacji przychodów

Koszt oczekiwania

Koszt obsługi

Koszty razem

Liczba stanowisk

K

o

s
z

t

na

j

e

d

n.

cz
as

u

Analiza funkcjonowania urządzeń

obsługujących

3

Zapis Kendalla

Zapis Kendalla

x/y/z/p/n

x/y/z/p/n

x

x

–

charakterystyka przybywania nowych

klientów do systemu

y

y

–

charakterystyka obsługi w

stanowiskach obsługi

z

z

–

liczba stanowisk

p

p

–

dopuszczalna wielkość kolejki

n

n

–

wielkość populacji, z której pochodzą

klienci

Analiza funkcjonowania urządzeń

obsługujących

4

SYMBOLE ZAPISU KENDALLA

SYMBOLE ZAPISU KENDALLA

W KLASYFIKACJI MODELI

W KLASYFIKACJI MODELI

SYSTEMÓW KOLEJKOWYCH

SYSTEMÓW KOLEJKOWYCH

SYMBO

SYMBO

L

L

ZNACZENIE

ZNACZENIE

M

M

Wykładniczy rozkład
prawdopodobieństwa długości odstępu
czasu między kolejnymi zgłoszeniami do

systemu/czasu obsługi

D

D

Wielkość deterministyczna lub o stałym
rozkładzie zgłoszeń klientów/czasu

obsługi

G

G

Dowolny rozkład prawdopodobieństwa o
znanej wartości oczekiwanej i
wariancji zgłoszeń do systemu/czasu

obsługi klientów

E

E

k

k

Rozkład Erlanga rzędu

k

opisujący

rozkład prawdopodobieństwa długości
odstępu czasu między kolejnymi
zgłoszeniami do systemu/czasu obsługi

5

SYSTEM

SYSTEM

M/M/1

M/M/1

(

(

x/y/z)

x/y/z)

Z

Z

NIESKOŃCZONĄ POPULACJĄ

NIESKOŃCZONĄ POPULACJĄ

mamy z nim do czynienia wtedy gdy:

1. czas obsługi klientów w systemie,

2. długość odstępu czasu między

zgłoszeniami napływającymi do
systemu

mają

wykładniczy rozkład

prawdopodobieństwa

, a w systemie

występuje

jedno stanowisko obsługi

6

SYSTEM M/M/S

SYSTEM M/M/S

(

(

x/y/z)

x/y/z)

Z

Z

NIESKOŃCZONĄ POPULACJĄ

NIESKOŃCZONĄ POPULACJĄ

1. czas obsługi klientów w systemie, oraz

czas między zgłoszeniami do systemu
mają

wykładniczy rozkład

wykładniczy rozkład

prawdopodobieństwa

prawdopodobieństwa

,

2. w systemie jest

S

S

równoległych

równoległych

stanowisk obsługi

stanowisk obsługi

ze wspólną kolejką.

7

SYSTEM

M/M/S

M/M/S

ZE SKOŃCZONĄ POPULACJĄ

1. czas między zgłoszeniami do systemu oraz

czas obsługi mają wykładniczy rozkład

wykładniczy rozkład

p

p

rawdopodobieństwa

rawdopodobieństwa,

2. istnieje

S

S

kanałów obsługi,

3. populacja klientów jest skończona, o

liczebności

Nu.

Nu.

4. ogólna budowa formuły

(lambda;mi;n;S;Nu

(lambda;mi;n;S;Nu

)

)

W systemie ze skończoną liczbą klientów

wielkość populacji nie będącej w systemie

zależy w istotny sposób od liczby klientów

obsługiwanych i oczekujących na obsługę w

systemie.

8

Problem 1.

(system

jednokanałowy)*

W ciągu jednej godziny do sali
egzaminacyjnej gdzie odbywa się
egzamin z MAP, przychodzi
średnio 4 studentów. Czas, jaki
egzaminator przeznacza na
pytanie jednego studenta wynosi
około 12 minut.

•Wybrane metody badań operacyjnych w zarządzaniu.
Problemy i zadania., pr. zb. pod red. D.Kopańskiej-Bródki,
AE Katowice 2006

9



Wyznacz stopę przybyć, stopę obsługi i
parametr intensywności ruchu.

Stopa przybyć
W ciągu godziny można przeegzaminować
(stopa obsługi)

studentów.

Parametr intensywności ruchu

Ponieważ
układ jest stabilny (zmierza do stanu

równowagi), tzn. prawdopodobieństwo tego, że
kolejka ma określoną długość jest stałe w każdej
jednostce czasu.

4





5

12

/

60







8

,

0

5

4













1

czyli

5

4















10



Podaj przeciętną liczbę studentów
czekających w kolejce na egzamin
oraz przeciętną liczbę studentów
znajdujących się w sali egzaminacyjnej.

osoby

2

,

3

)

4

5

(

5

4

)

(

1

2

2

2



























q

L

11



Średnia liczba zgłoszeń
przebywających w systemie (łączna
liczba zgłoszeń czekających w kolejce i
obsługiwanych)

osoby

4

4

5

4

















q

L

Średnia liczba studentów przebywających
na sali wynosi 4 studentów (łączna liczba
studentów czekających na egzamin i
egzaminowanych)

12



Podaj przeciętny czas oczekiwania
przez studenta w kolejce na egzamin
oraz średni czas, jaki spędza student w
sali egzaminacyjnej.



Przeciętny czas oczekiwania



Średni czas egzaminu (średni czas
spędzany w systemie)

godziny

8

,

0

)

4

5

(

5

4

)

(



















q

W

godzina

1

4

5

1

1















W

13



Wyznacz prawdopodobieństwo braku
studentów oczekujących na egzamin.

2

,

0

8

,

0

1

1

0













P

14



Wyznacz prawdopodobieństwo, że w
kolejce czeka więcej niż dwóch
studentów.

1

0

0



















k

k

k

P





512

,

0

125

64

5

4

1

2

2























k

P

15



Jeśli liczba studentów przybywających do Sali
egzaminacyjnej zwiększy się do 6 osób,
wówczas podstawowe parametry układu
wynoszą:

Układ jest niestabilny, co spowoduje, że z
upływem czasu kolejka studentów
oczekujących na egzamin będzie coraz dłuższa.

1,2

osób/godz.

5

60/12

osób/godz.

6















16

Pracownicy nowoczesnego biurowca
wpuszczani są na teren budynku przez
specjalne bramki. Przejście przez bramkę
jednego pracownika trwa ok.. 10 sek., w
czasie których komputer zainstalowany
przy bramce odczytuje kartę wejścia
pracownika, zapisuje czas jego przybycia i
zezwala na wejście do budynku. W ciągu
jednej minuty przychodzi 16
pracowników, którzy mogą skorzystać z
jednej z trzech bramek wejściowych.

Problem 2. (system
wielokanałowy)

17

a)

Określ podstawowe parametry

systemu kolejkowego

b)

Wyznacz prawdopodobieństwo tego,

że pracownicy nie będą czekali w

kolejce

c)

Oblicz średnią liczbę pracowników

oczekujących w kolejce

d)

Ile wynosi średni czas oczekiwania w

kolejce oraz przebywania w systemie?

e)

Jakie jest prawdopodobieństwo, że w

kolejce czeka dokładnie dwóch

pracowników?

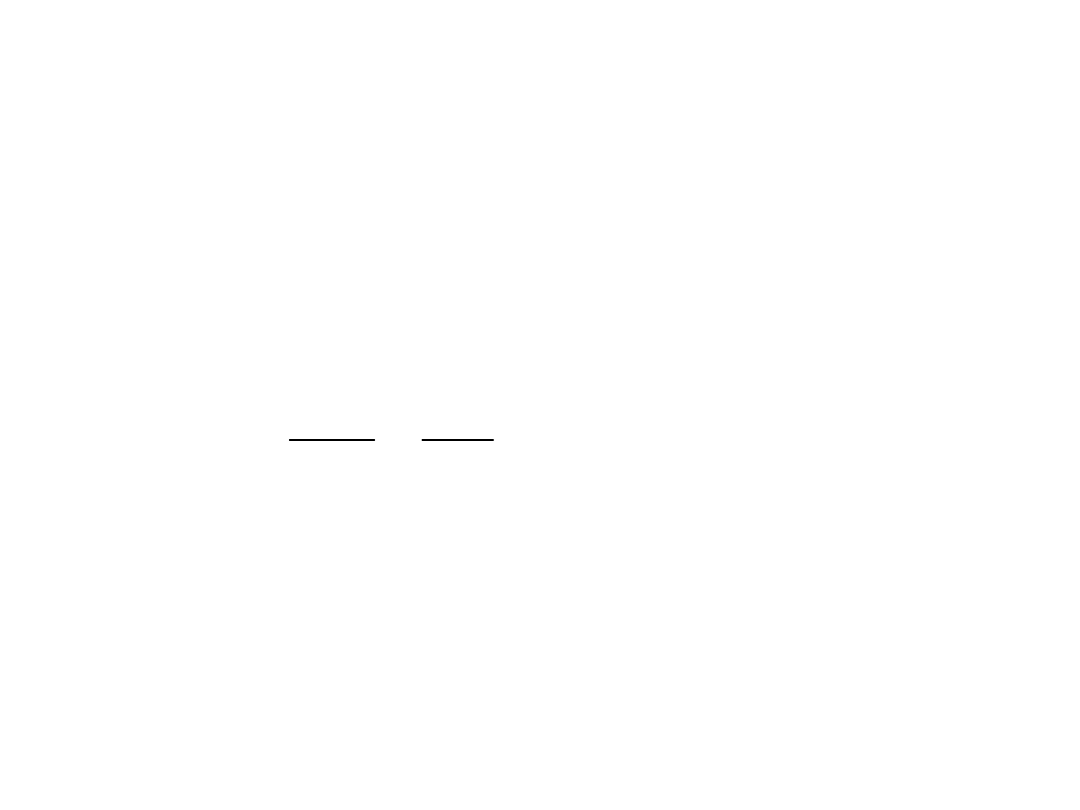
n

stabilny

układ

n

:

ruchu

sci

intensywno

parametr

3

n

obsługi

kanały

6prac./min

10

:

60

obsługi

stopa

przybyć

stopa





































89

0

6

3

16

16

,

min

/

.

prac

a)

19

35

0

85

2

1

3

89

0

2

89

0

1

89

0

0

89

0

1

1

1

3

2

1

0

1

0

0

,

,

!

,

!

,

!

,

!

,

)!

(

)

(

!





























n

i

n

i

n

n

i

P







b)

Prawdopodobieństwo, że przebywający nie będą
oczekiwać w kolejce wynosi 0,35

20

025

0

35

0

1

3

89

0

3

89

0

1

2

1

3

0

2

1

,

,

)!

(

)

,

(

,

)!

(

)

(



























P

n

n

L

n

q





c)

Liczba pracowników oczekujących w kolejce

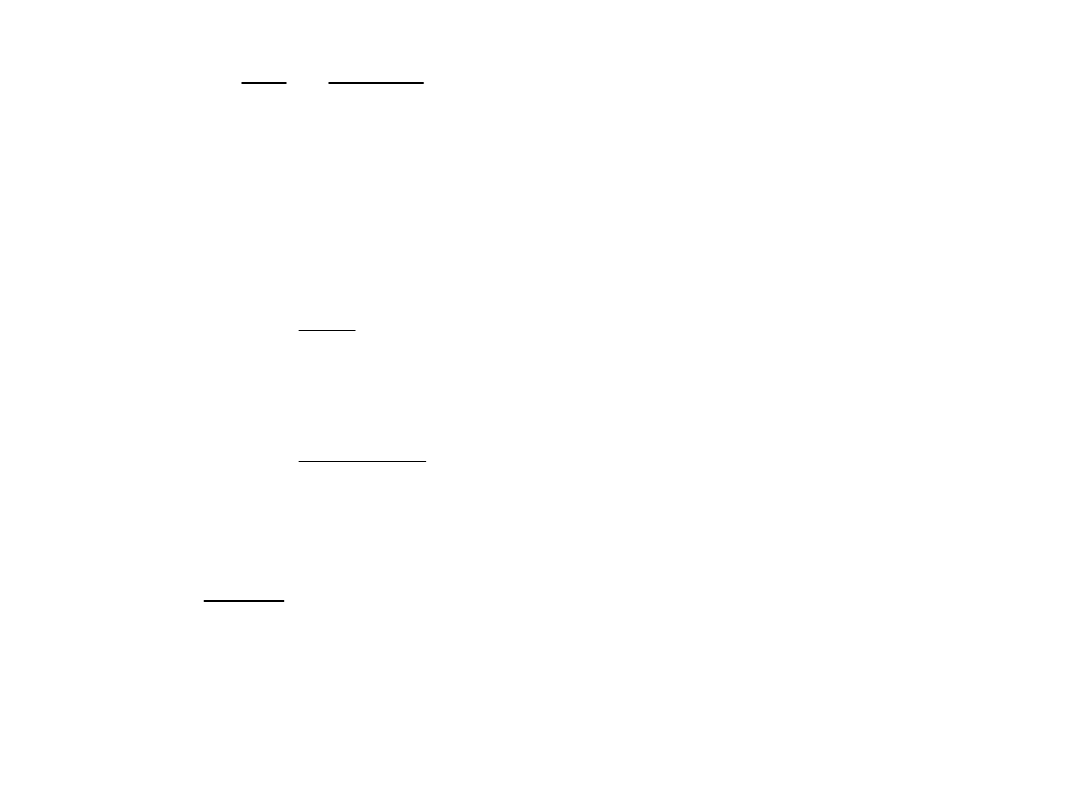
0016

0

16

025

0

,

,









q

q

L

W























n

k

dla

n

n

k

dla

k

-

n

0

0

P

n

P

k

P

k

k

k

!

!





d)

Średni czas oczekiwania w kolejce.

e)

14

0

35

0

2

89

0

2

,

,

!

,







2

P

Prawdopodobieństwo, że w kolejce będzie

oczekiwało 2 klientów

wynosi 0,14.

22

Miłego dnia

Miłego dnia