Prawa Kirchhoffa i ich

zastosowanie

Prawa Kirchhoffa i ich zastosowanie

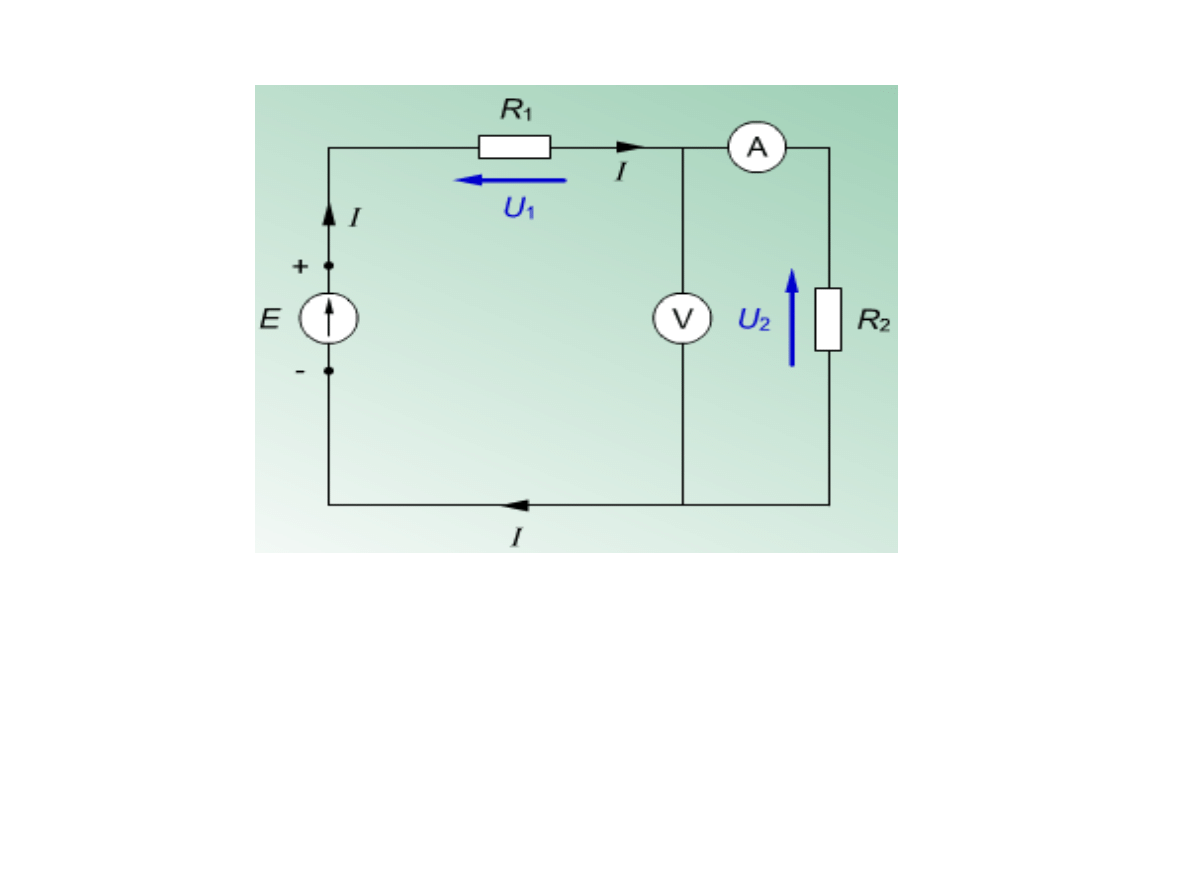
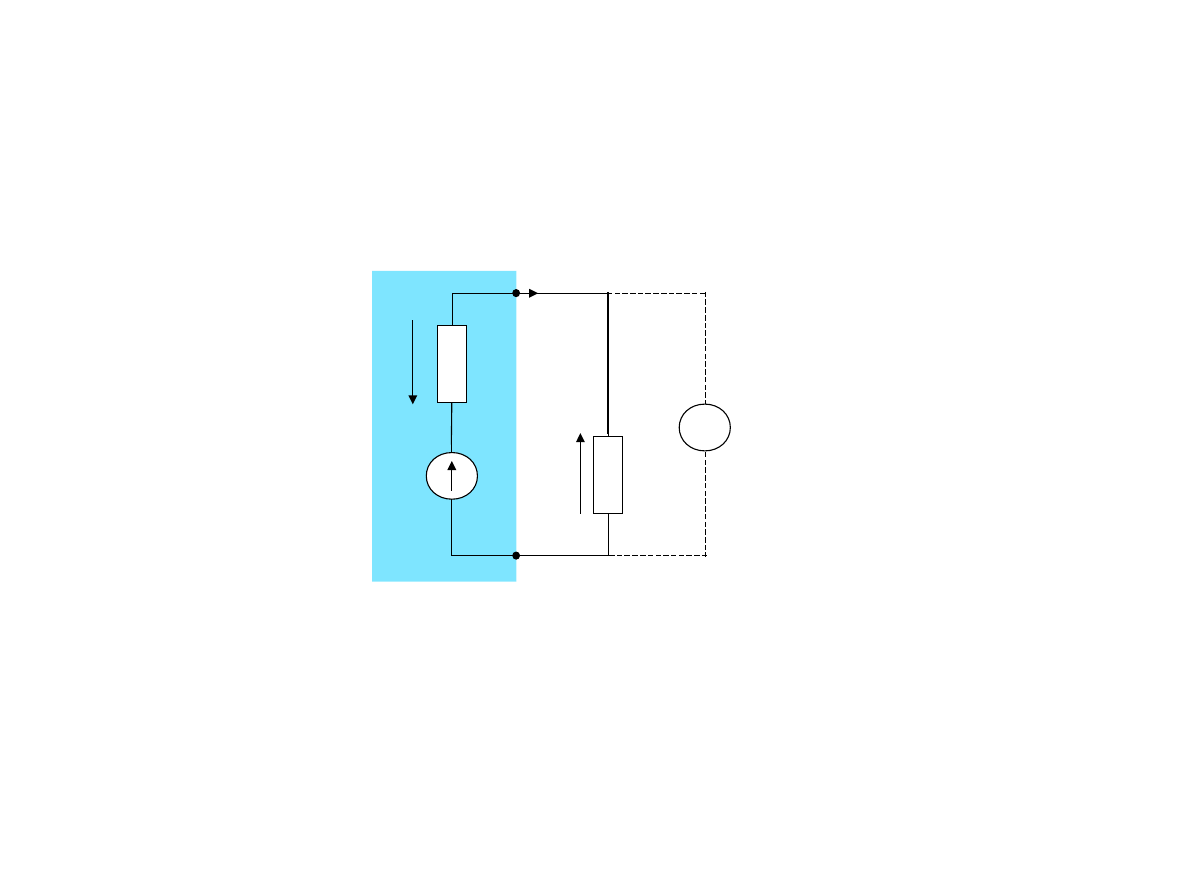
Kierunek przepływu prądu i jego natężenie na schematach

elektrycznych oznaczamy strzałką skierowaną od punktu obwodu

o potencjale wyższym do punktu o potencjale niższym.

Kierunki spadków napięć U1 i U2 są zależne od kierunku prądu,

strzałka źródła wskazuje zacisk dodatni, strzałka napięcia

rezystora wskazuje punkt o wyższym potencjale.

Prawa Kirchhoffa i ich zastosowanie

Do pomiaru

podstawowych wielkości

elektrycznych

(napięcia i natężenia

prądu) służą odpowiednie

mierniki:

woltomierz i

amperomierz.

Woltomierz - przyrząd

pomiarowy służący do pomiaru

napięcia elektrycznego. Idealny

woltomierz posiada nieskończenie

dużą rezystancję wewnętrzną -

następuje wtedy pomijalnie mały

przepływ prądu przez przyrząd.

Woltomierz podłączamy do

obwodu równolegle.

Amperomierz - przyrząd

pomiarowy służący do pomiaru

natężenia prądu elektrycznego.

Idealny amperomierz posiada

nieskończenie małą rezystancję

wewnętrzną - następuje wtedy

pomijalnie mały spadek napięcia

na mierniku.

Amperomierz podłączamy do

obwodu szeregowo.

Uniwersalnym przyrządem

pomiarowym jest multimetr

cyfrowy.

W zależności od ustawienia

pokrętła można mierzyć natężenie

prądu lub napięcie.

Multimetr cyfrowy służy także do

pomiaru innych wielkości

elektrycznych, wartości pomiaru

odczytujemy na wyświetlaczu.

Prawa Kirchhoffa i ich zastosowanie

Odcinek obwodu składa się

z trzech rezystorów: R1, R2, R3

połączonych kolejno tak, że

koniec pierwszego rezystora

połączono z początkiem

drugiego, natomiast koniec

drugiego połączono

z początkiem trzeciego.

Takie połączenie nazywamy

szeregowym. Początek

pierwszego rezystora i koniec

trzeciego muszą być dołączone

do źródła napięcia U.

Prąd I przepływający przez

wszystkie rezystory przy

połączeniu szeregowym ma

taką samą wartość. Prąd

przepływający przez szeregowe

połączenie rezystorów

wywołuje na każdym z nich

spadek napięcia, suma

spadków napięć na

poszczególnych rezystorach

jest równa wartości napięcia

przyłożonego na zaciskach

układu.

Prawa Kirchhoffa i ich zastosowanie

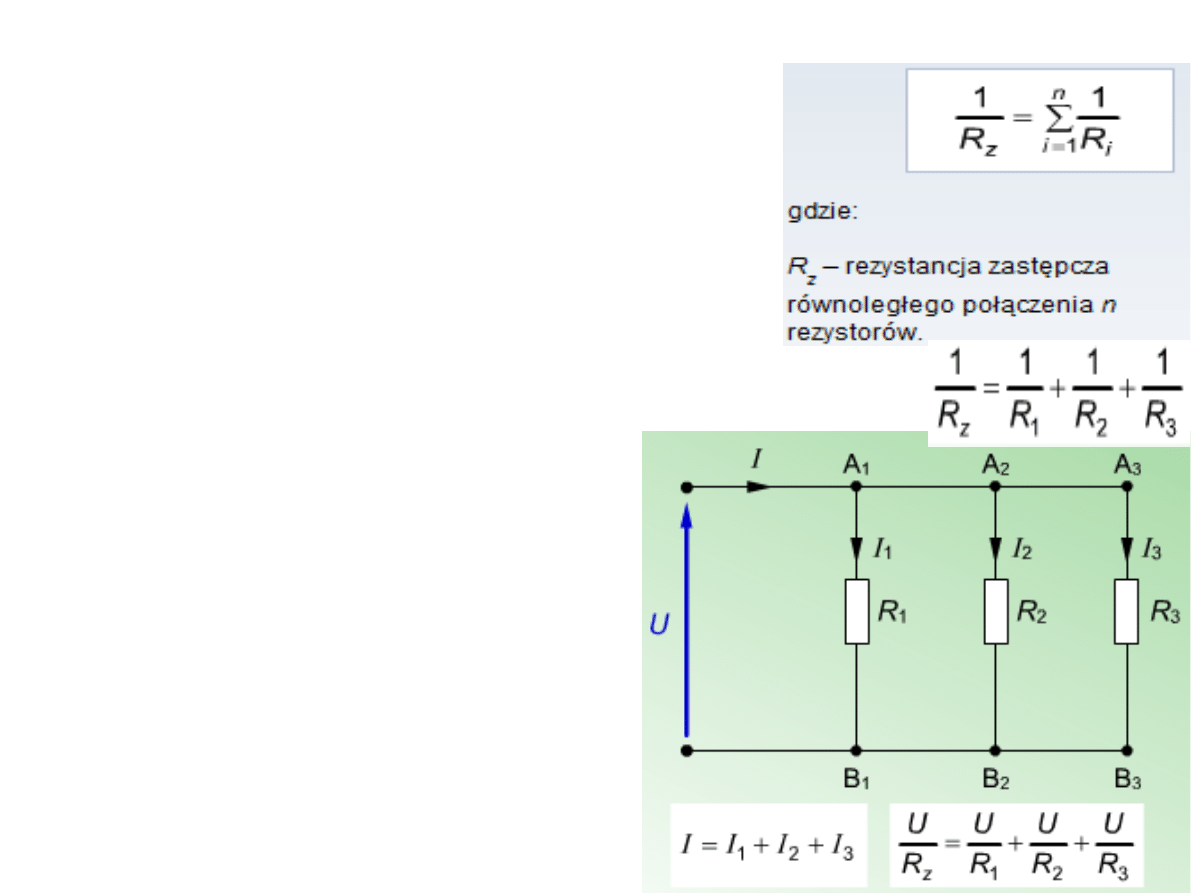
Odcinek obwodu składa się z trzech

rezystorów R1, R2, R3 połączonych

tak, że początek pierwszego rezystora

łączy się z początkiem drugiego i z

początkiem trzeciego. Koniec

pierwszego rezystora łączy się z

końcem drugiego rezystora i końcem

trzeciego.

Takie połączenie nazywamy

równoległym. Początek i koniec

odbiornika jest punktem wspólnym

wszystkich odbiorników połączenia.

Do pierwszego rezystora dołącza się

źródło napięcia U i pod wpływem

przyłożonego napięcia prąd I,

przepływa przez obwód i rozpływa się

na poszczególne gałęzie połączenia

Suma wartości prądów płynących

przez poszczególne gałęzie jest równa

wartości prądu całkowitego I. Spadki

napięć na poszczególnych rezystorach

są równe wartości napięcia U

przyłożonego do układu.

Prawa Kirchhoffa i ich zastosowanie

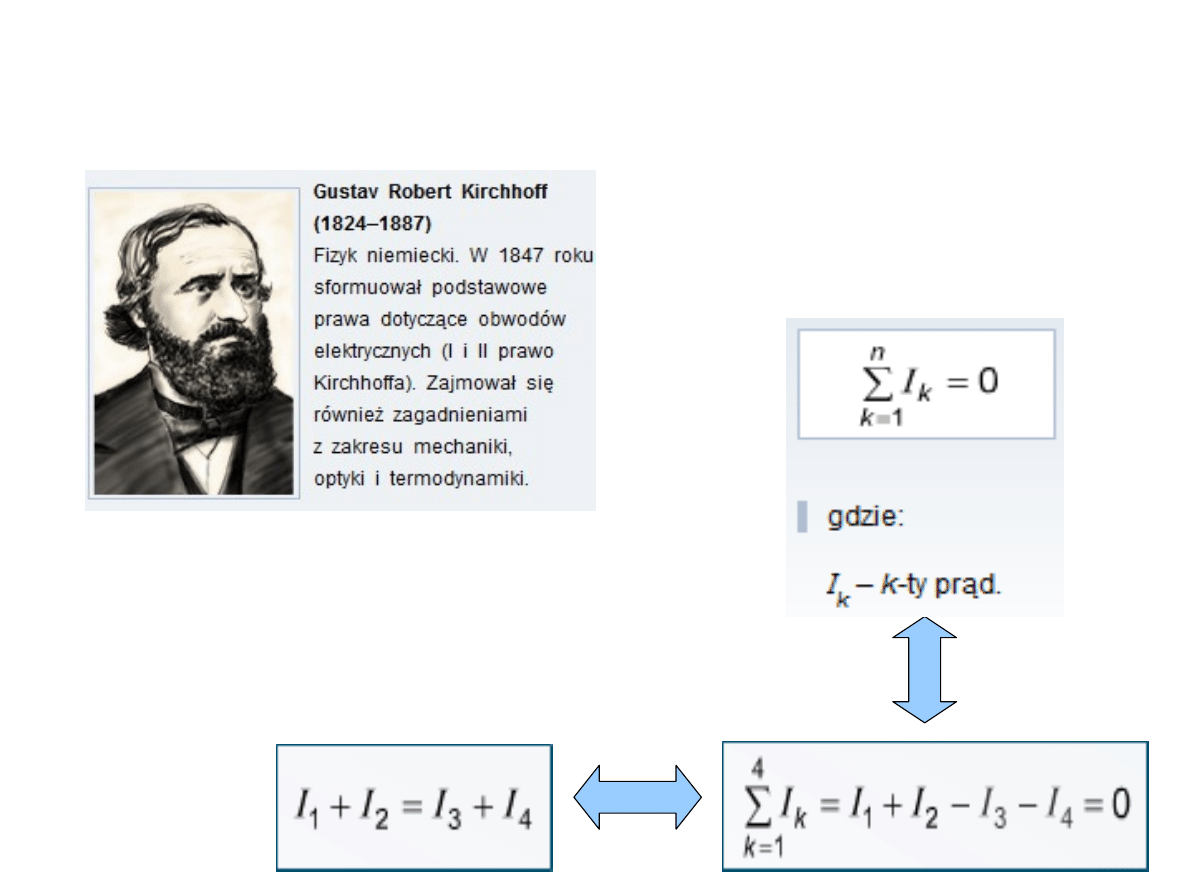
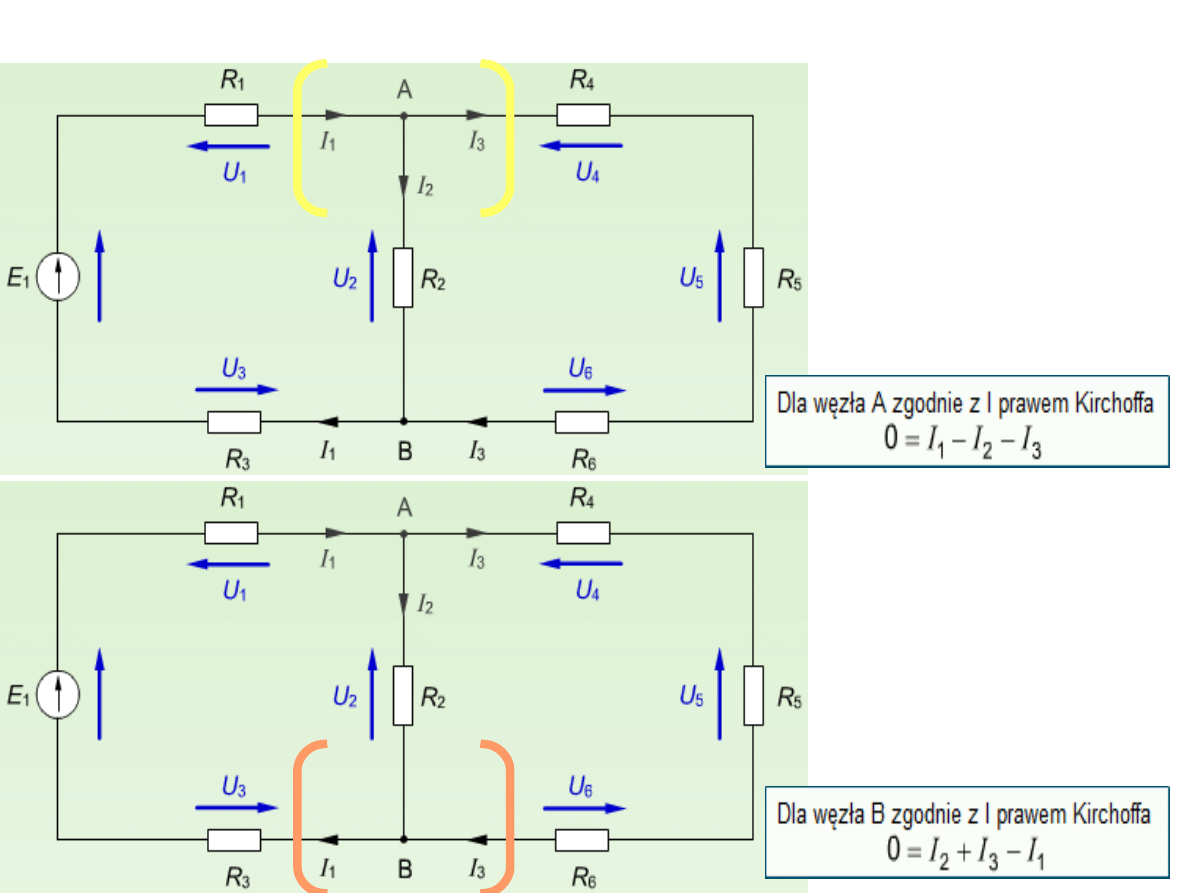
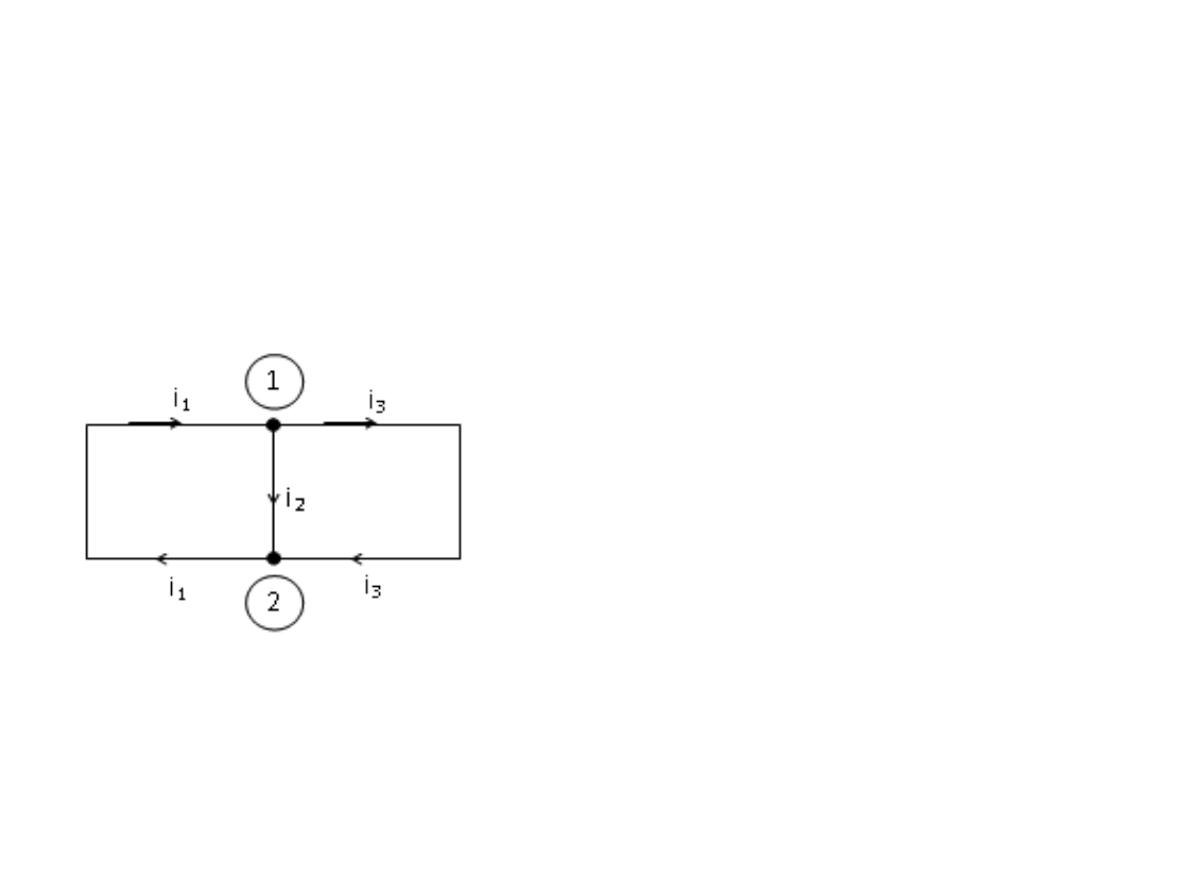
Suma natężeń prądów

dopływających do węzła

obwodu

jest w każdej chwili równa

sumie natężeń prądów

wypływających

z tego węzła.

Prądy dopływające do punktu węzłowego

i wypływające z niego mają znaki przeciwne.

W punkcie węzłowym sieci suma

algebraiczna prądów równa się zero.

Prądom dopływającym do węzła dajemy

znak (+), a prądom odpływającym znak (-).

Zależność między natężeniem prądów

płynących przez węzeł obwodu określa I

Prawo Kirchhoffa:

Prawa Kirchhoffa i ich zastosowanie

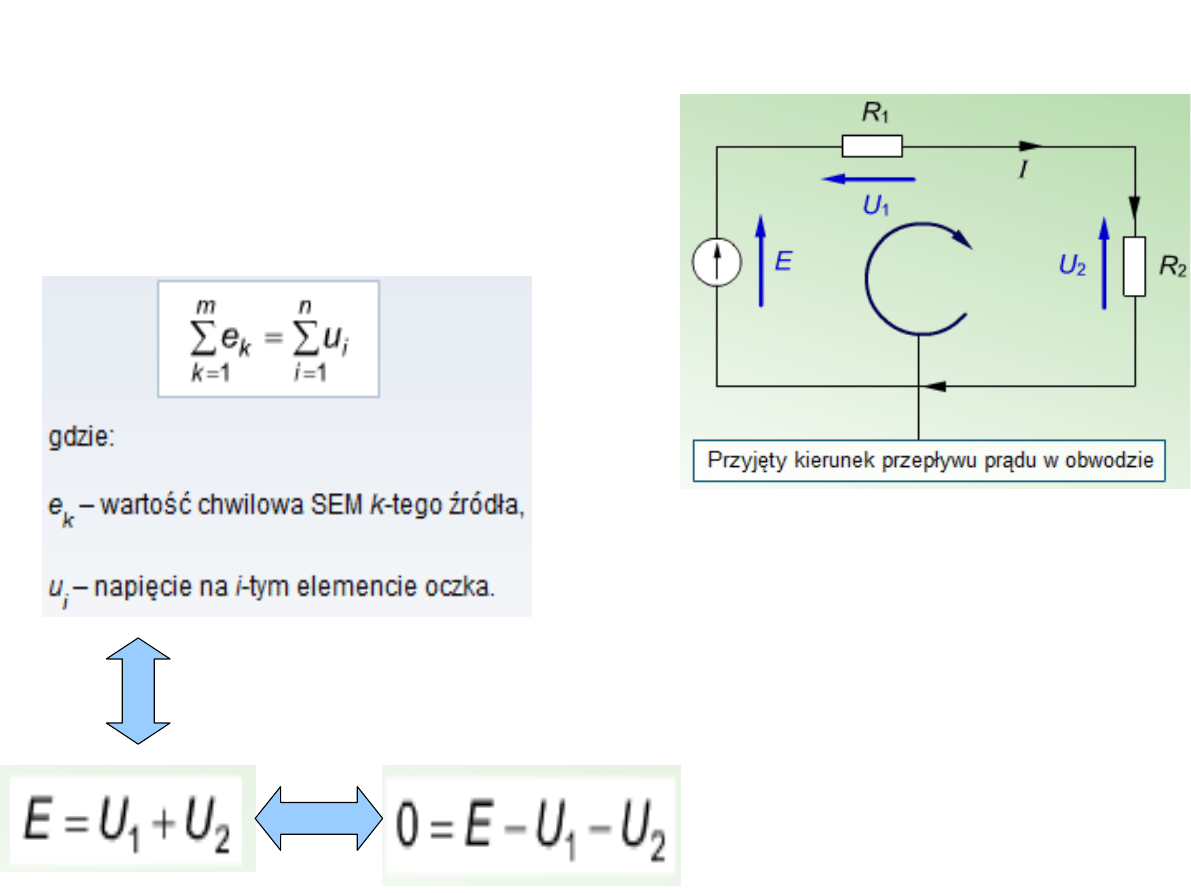
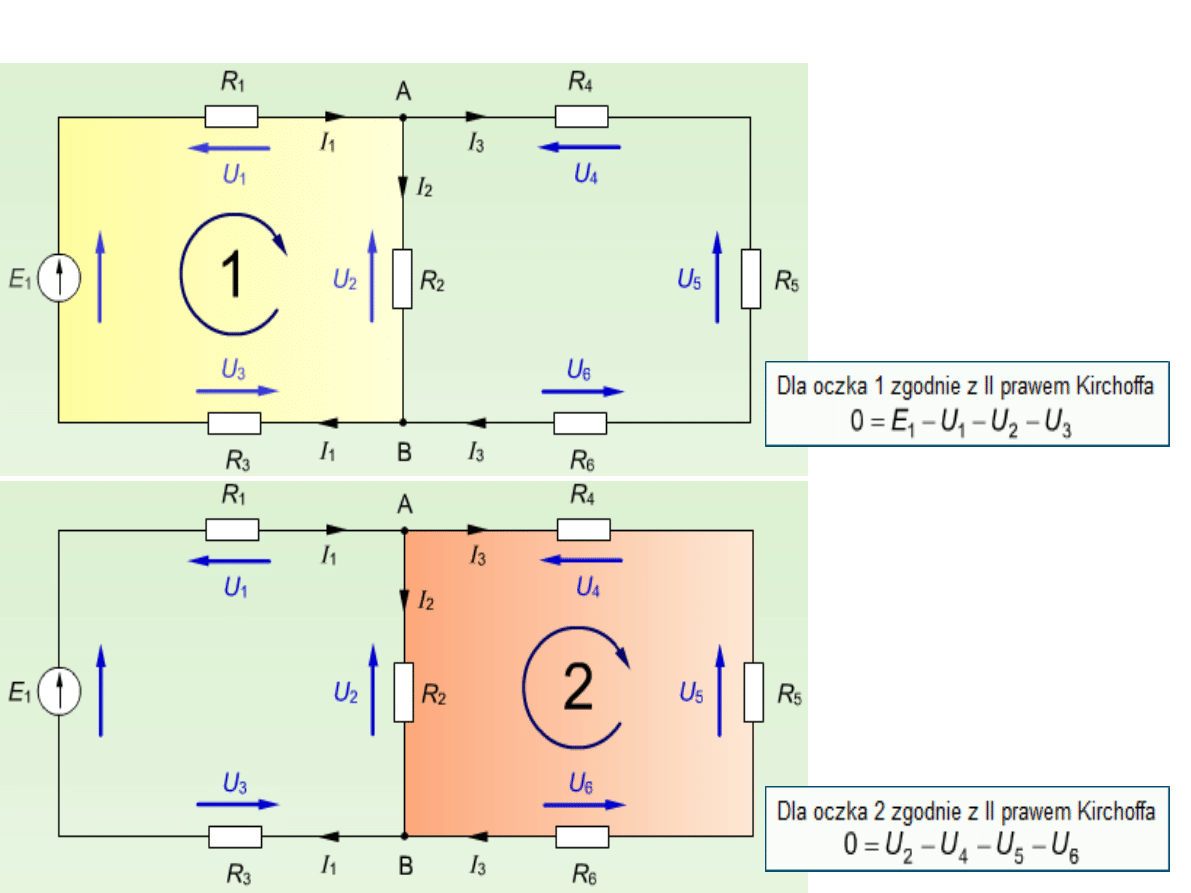
Algebraiczna suma wartości

chwilowych

sił elektromotorycznych

występujących

w obwodzie zamkniętym równa jest

sumie wartości chwilowych napięć

elektrycznych na elementach

pasywnych tego obwodu.

Siła elektromotoryczna (SEM,

E) to różnica potencjałów

(napięcie elektryczne)

powstająca w źródle prądu

elektrycznego.

Jednostką SEM jest 1 wolt

[V].

Prawa Kirchhoffa i ich zastosowanie

Prawa Kirchhoffa i ich zastosowanie

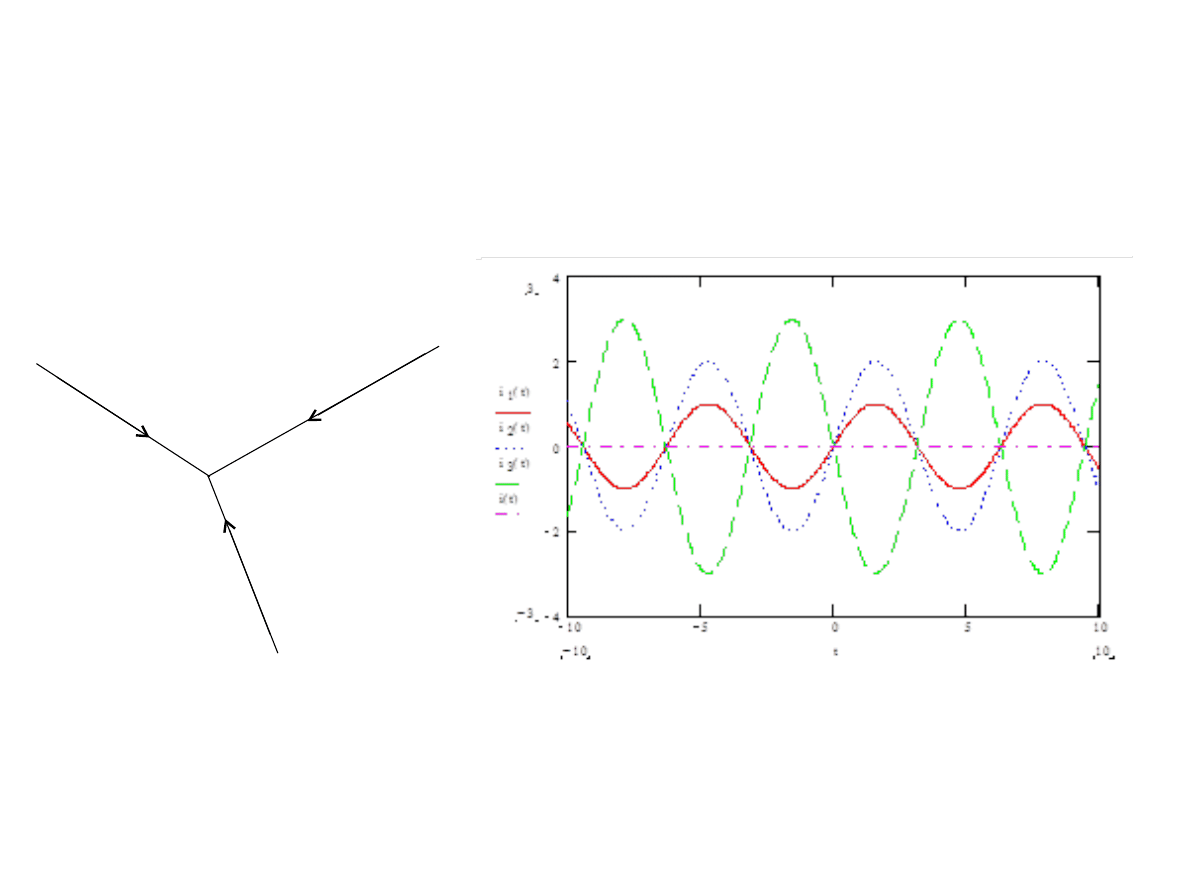
i

1

(t)+ i

2

(t)+ i

3

(t)=i(t)=0

Prawo Kirchhofa musi być spełnione w każdej chwili czasowej bez względu na to czy prądy

płynące w gałęziach są stałe czy zmienne.

i

1

i

2

i

3

Suma wartości chwilowch tych prądów w każdej chwili jest równa zero.

Prawa Kirchhoffa i ich

zastosowanie

Prawa Kirchhoffa i ich

zastosowanie

Jeżeli obwód ma „w” węzłów to można napisać „w”- równań z I

prawa Kirchhoffa:

i

1

-i

2

-i

3

=0

-i

1

+i

2

+i

3

=0

0=0 równania

zależne

Twierdzenie: Obwód zawierający „w” węzłów ma „w-1” węzłów

niezależnych.

Liczba węzłów niezależnych

Dla g – gałęzi oraz „w” węzłów istnieje: o=g-w+1 niezależnych równań napięciowych z II Prawa Kirchhoffa.

Wniosek:
w-1 niezależnych równań z I Prawa Kirchhoffa
g-w+1 niezależnych równań z II Prawa Kirchhoffa





g

równań = liczbie niewiadmych prądów w gałęziach.

W przypadku SPM liczba niewiadomych prądów zamienia się na niewiadome U

I

źródeł SPM

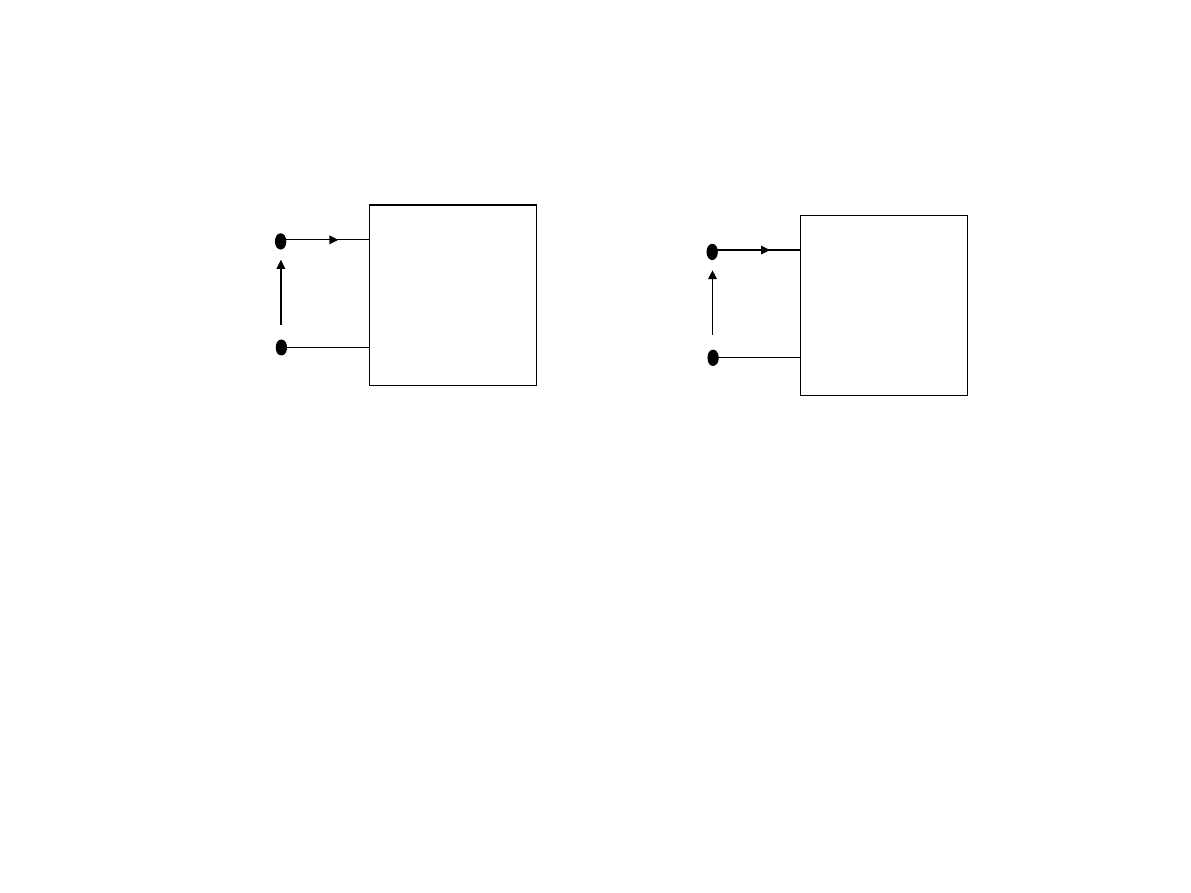
A

I

B

I

i

1

(t

U

U

Równoważne dwójniki

pasywne

Rys.3.11 Dwa równoważne dwójniki

 

Definicja:

Dwa dwójniki uważamy za równoważne jeżeli przy jednakowym wymuszeniu

powstaje jednakowa odpowiedź.

Inaczej dwójniki będą równoważne jeżeli przy jednakowym napięciu zasilania

U popłynie przez dwójniki jednakowy prąd I. Równość napięć i prądów dotyczy

zarówno wymuszenia napięciowego jak i prądowego.

1

R

1

R

2

R

3

2

3



1

R

12

R

23

R

31

1

2

3



2

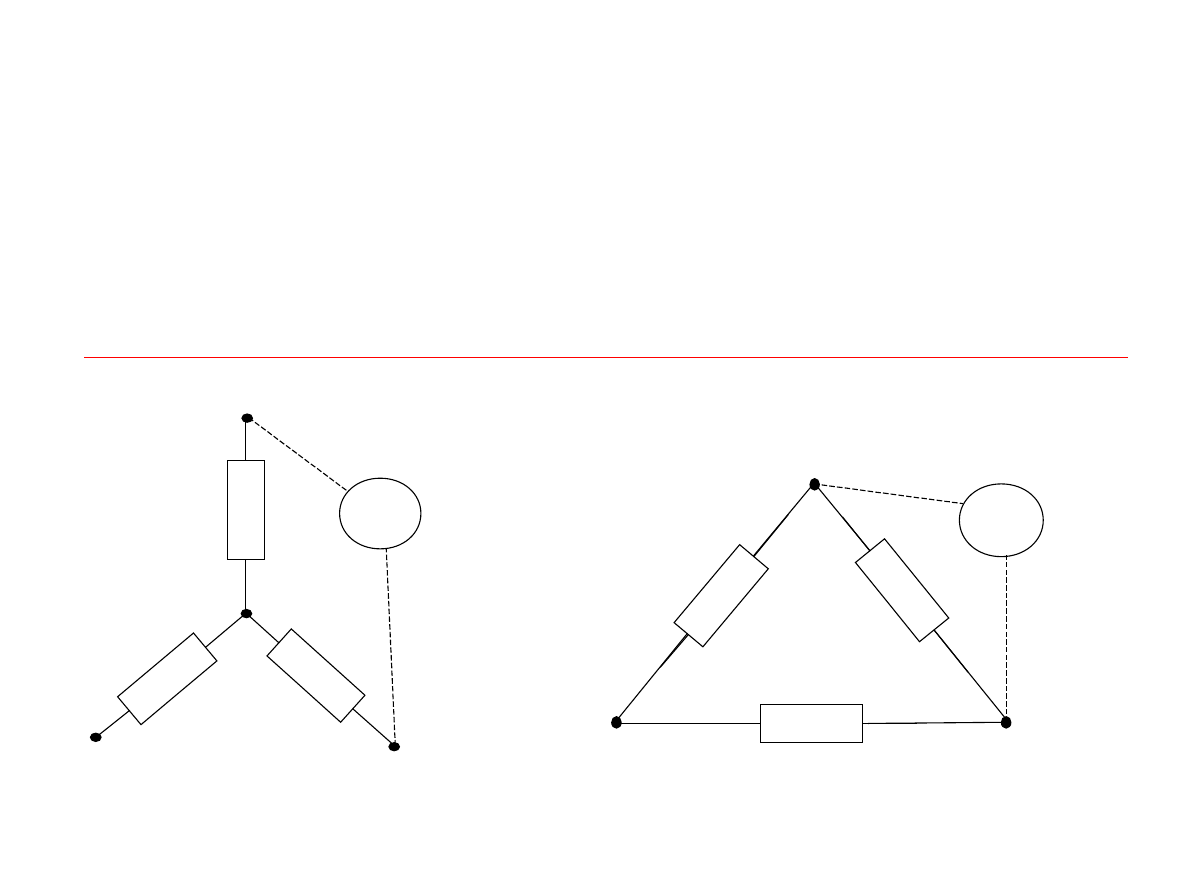
Transfiguracja gwiazda

trójkąt

Równoważność n-wrotników zachodzi, gdy:

 

1). Mają jednakową liczbę zacisków.

2). Ich rezystancje wypadkowe mierzone między dwoma dowolnymi parami odpowiadających sobie

zacisków są jednakowe.

3).Napięcia w stanie jałowym odpowiadającym sobie parom zacisków są równe.

Równoważność trójników pasywnych- transfiguracja gwiazda-trójkąt

Dla wyprowadzenia wzorów transfiguracji gwiazda-trójkąt wystarczy zbadać

punkt 1 i 2.

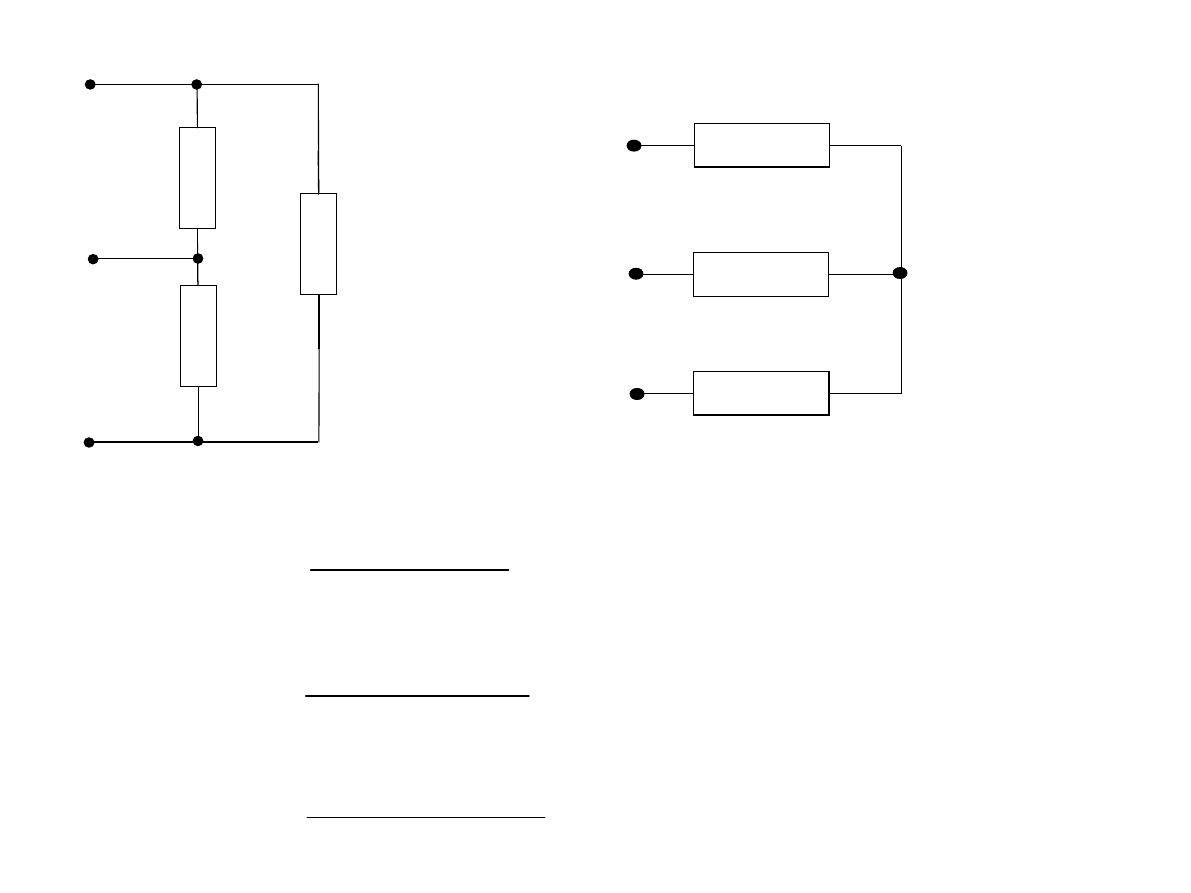
R

12

R

23

R

31

1

2

3

R

1

R

2

R

3

1

2

3

Inny sposób rysowania gwiazdy i trójkąta





2

1

12

23

31

23

31

12

R

R

R

R

R

R



















12

23

31

12

31

23

R

R

R

R

R

R











12

23

31

23

12

31

R

R

R

R

R

R







Wyprowadzenie wzorów na transfigurację gwiazda-trójkąt

Dla zacisków 2-

3.
R

2

+R

3

=

Dla zacisków 1-3.
R

3

+R

1

=

Dla zacisków 1-2.
R

1

+R

2

=

Określając rezystancje widziane z punktu

widzenia wybranej pary zacisków dla

gwiazdy oraz rezystancje

odpowiadającym zaciskom dla trójkąta

otrzymamy układ trzech równań, z

których możemy obliczyć rezystancje

trójkąta względem gwiazdy lub odwrotnie.

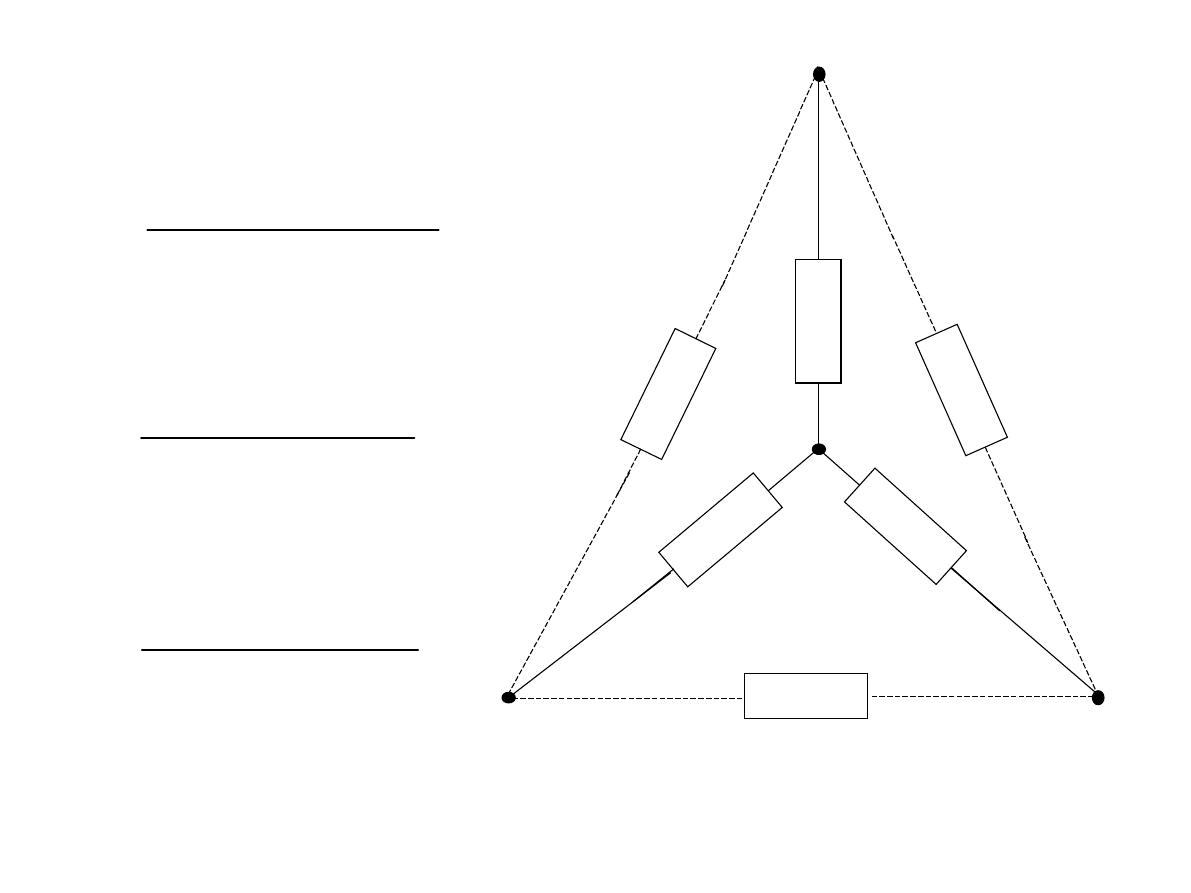
2

1

R

1

R

2

R

3

3

R

12

R

23

R

31

Transfiguracja gwiazda trójkąt

31

23

12

31

12

1

R

R

R

R

R

R









31

23

12

23

12

2

R

R

R

R

R

R









31

23

12

31

23

3

R

R

R

R

R

R









3

R

R

3

R

R

2

















 R

3

R

Transfiguracja trójkąt-gwiazda

 

Rozwiązując powyższy układ ze względu na zmienne R

1

,R

2

,R

3

otrzymamy:

W przypadku, gdy R

1

=R

2

=R

3

=R

otrzymamy

3

2

1

2

1

12

R

R

R

R

R

R









1

3

2

3

2

23

R

R

R

R

R

R









2

1

3

1

3

31

R

R

R

R

R

R









Uzyskane wzory noszą nazwę transfiguracji gwiazda-trójkąt i pozwalają na

obliczenie rezystancji zastępczej dowolnie połączonych dwójników. Wzory te

okażą się prawdziwe również dla obwodów prądu zmiennego.



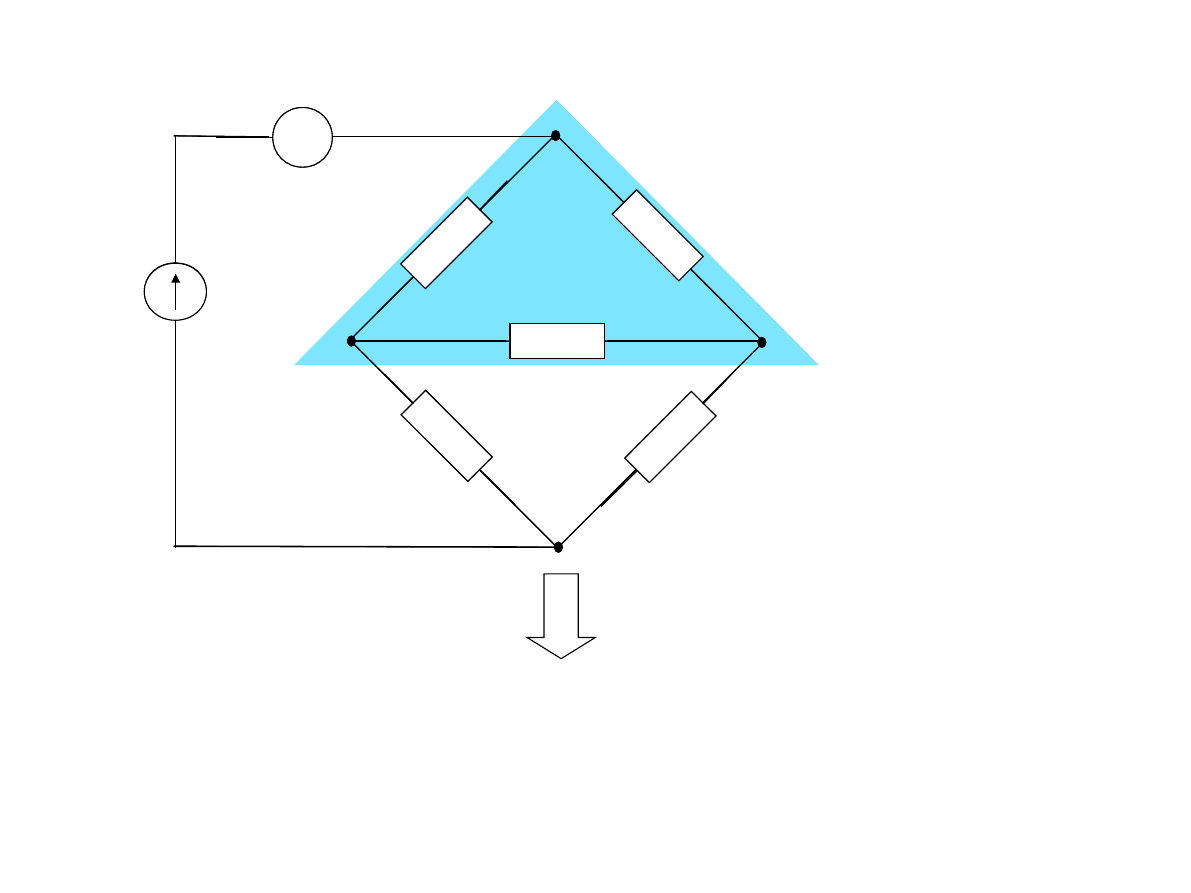
1



2







3

A











A

Przykład 3.4 Obliczyć wskazanie amperomierza.

Zaznaczony trójkąt zostanie zamieniony na gwiazdę zgodnie z

wyprowadzonymi wzorami na transfigurację.



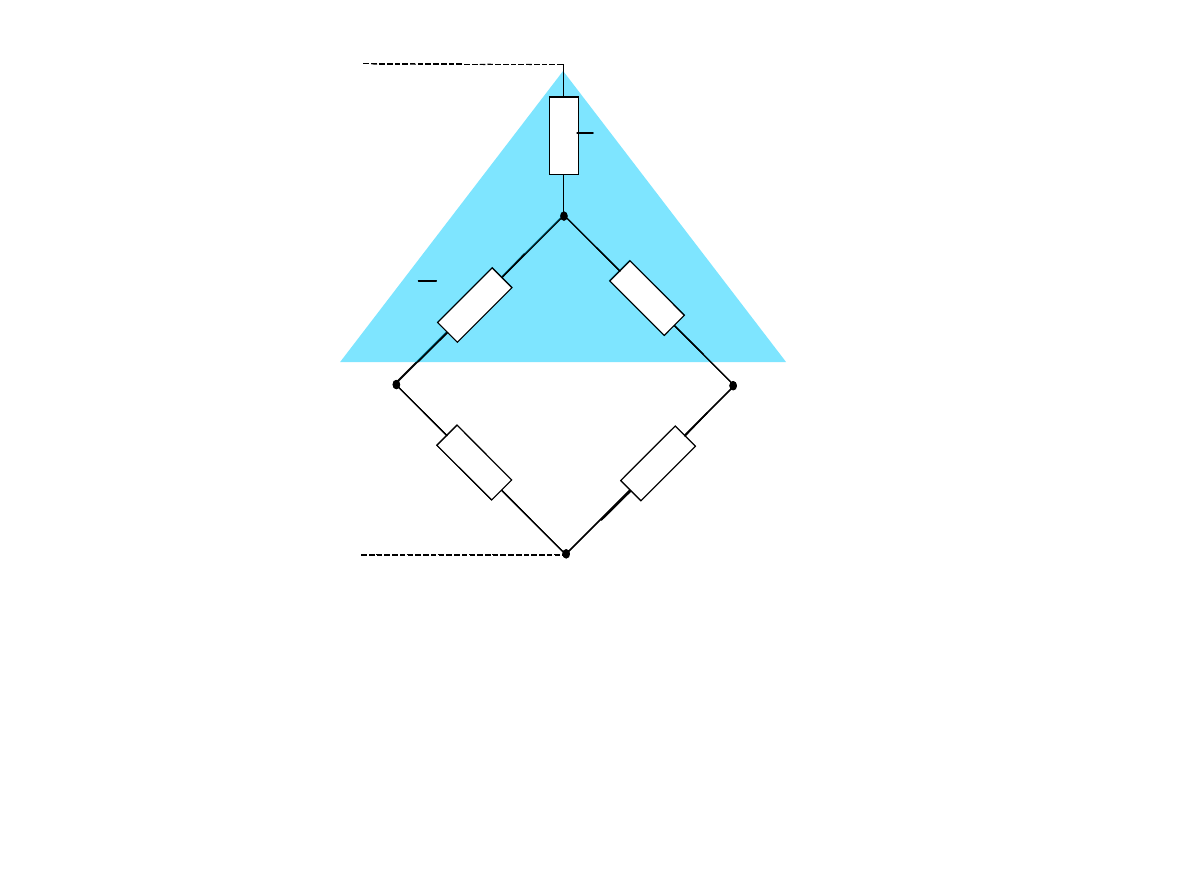
2

1









3

1



2

1









3

1

Dzięki transfiguracji możemy dokonać zwinięcia obwodu stosując

odpowiednio połączenia szeregowe i równoległe.

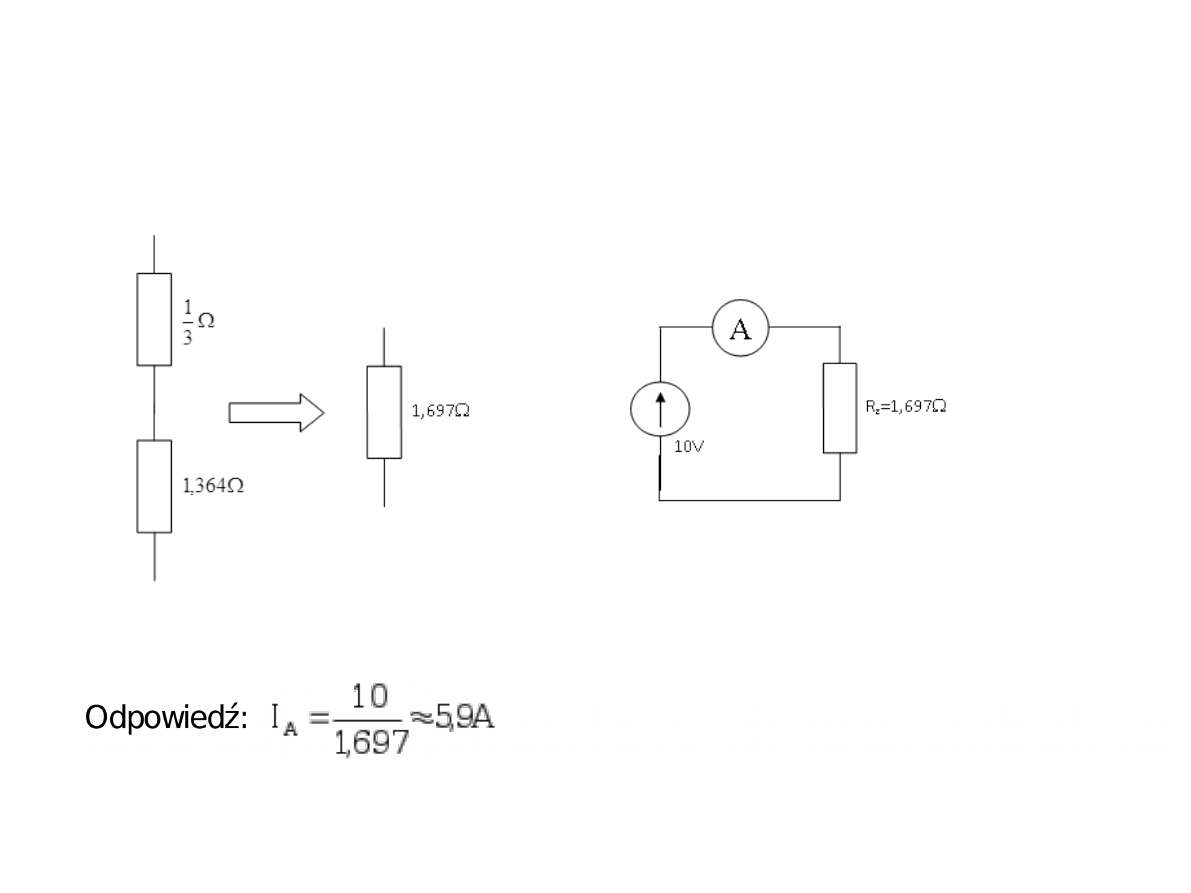
Zatem wskazanie amperomierza obliczamy na podstawie poniższego

schematu:

E

R

R

w

U

I

V

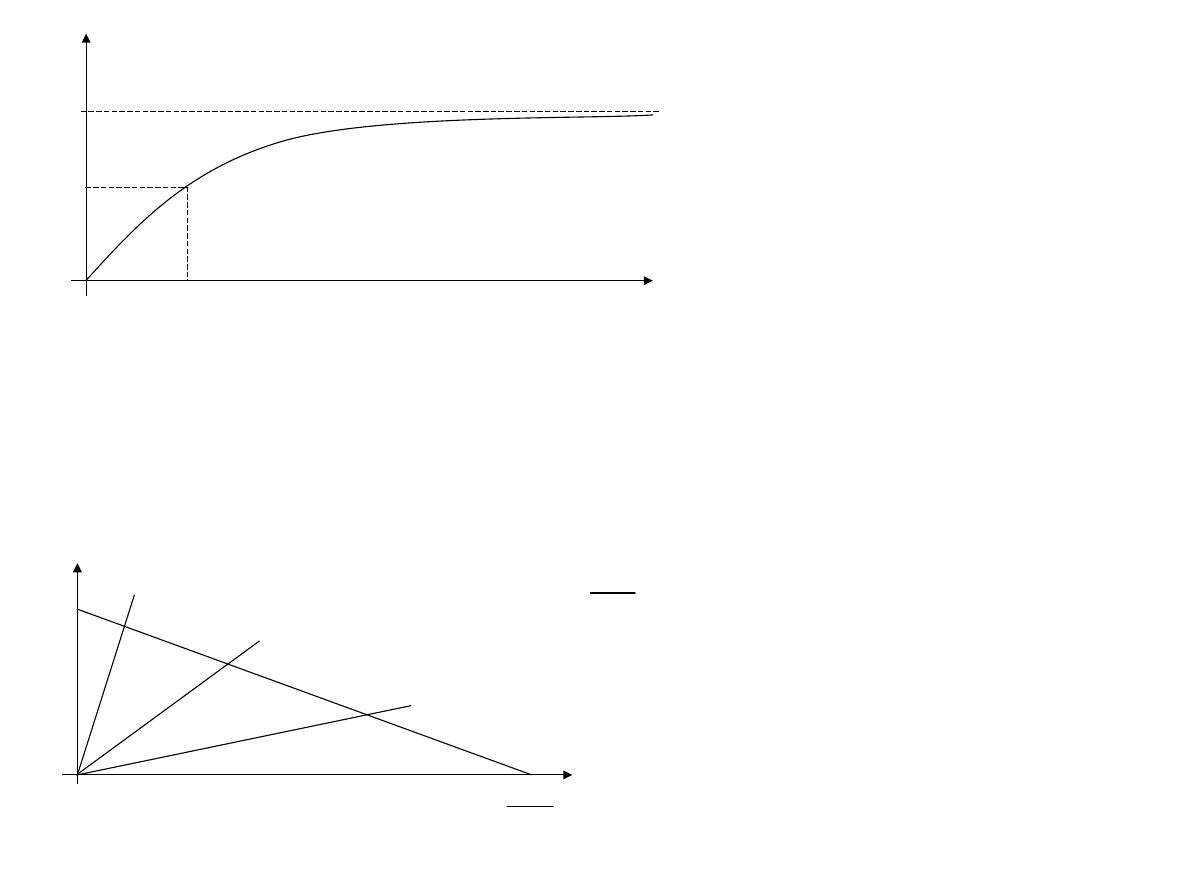
Źródła rzeczywiste

W przykładzie 3.3 zastosowano już źródło rzeczywiste zasilające żarówki.

Zwróć uwagę że woltomierz pokaże niższe napięcie w przypadku włączonej

rezystancji w porównaniu z napięciem jakie wskazuje (E) przy jej braku

(stan jałowy).

Źródła rzeczywiste

Napięcie na zaciskach źródła rzeczewistego w funkcji obciążenia R:









0

R

R

R

E

}

R

R

R

R

R

{

E

dR

)

R

(

dU

2

W

W

2

W

W















E

)

R

(

U

lim

R





0

R

R

E

R

lim

W

0

R











R

R

E

R

)

R

(

U

W







R

R

E

I

0

R

I

R

I

E

W

W

















Zbadanie granicy i pochodnej funkcji U(R) pozwoli na jej wyznaczenie

R

W

E

0,5E

U(R

)

R

E

U(I)

I

W

R

E

R

1

R

2

R

3

R

1

>R

2

>

R

3

Warto zapamiętać, że jeżeli rezystancja obciążenia jest równa rezystancji wewnętrznej

źródła rzeczywistego to spadek napięcia na nim wynosi aż 50%. Okaże się, że

rezystancja R

w

ma jeszcze inną własność.

Przebieg napięcia na zaciskach rzeczywistego źródła napięciowego w funkcji rezystancji

obciążenia.

Charakterystyka zewnętrzna U=f(I)

U(I)=E-IR

W

U(0)=E - stan jałowy

W

R

E

I

0

U







- stn zwarcia

Charakterystyka zewnętrzna i charakterystyki

obciążenia

Charakterystyka zewnętrzna źródła rzeczywistego jest

malejącą linią prostą.

G

I

0

U

G

W

I

G

Z

W

W

W

Z

Z

R

R

R

R

I

G

G

I

G

I

U

I

G

U























R

1

R

R

R

R

I

I

W

W

0









I

0

(R)

I

0,5I

R

W

R

 

R

R

R

I

R

I

W

W

0







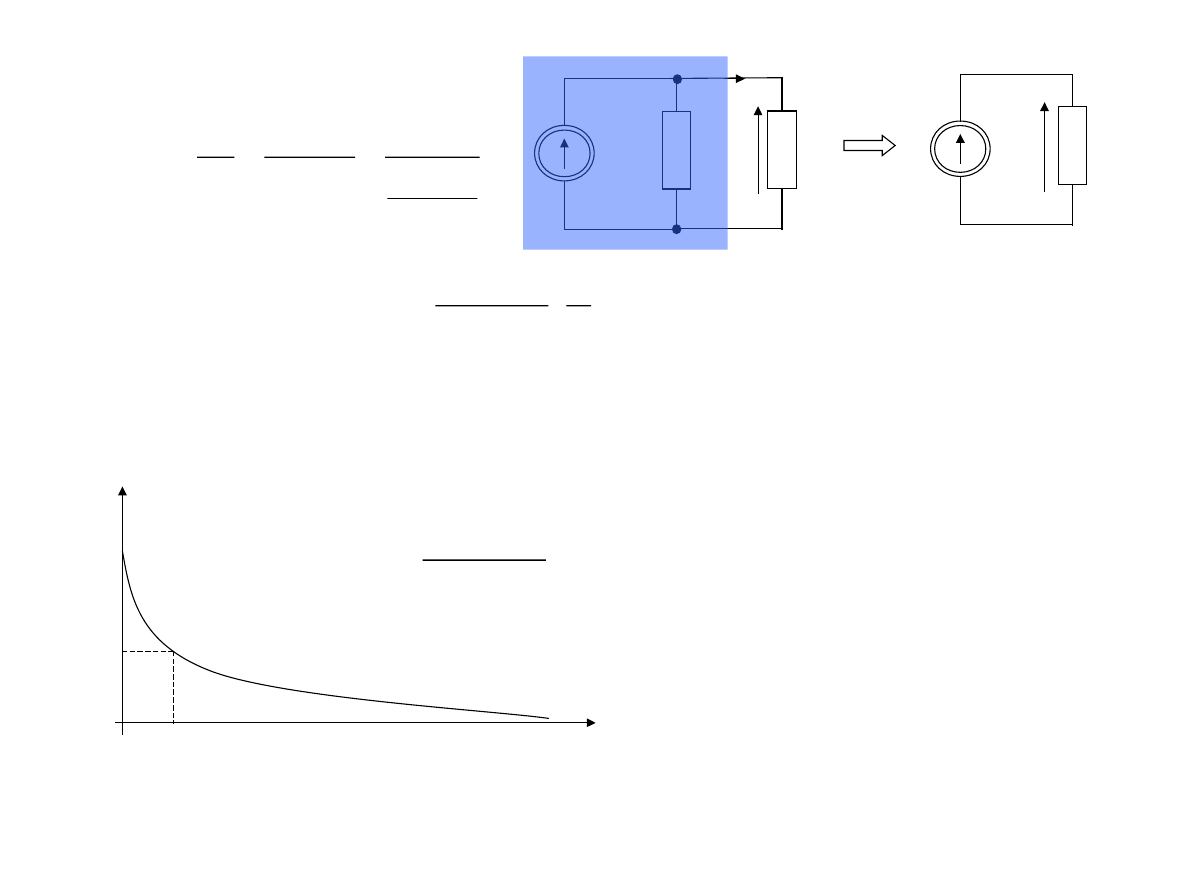
Źródła prądowe rzeczywiste

G

U

I

0





ponieważ

stąd

Przebieg prądu rzeczywistego źródła prądowego w funkcji obciążenia

rezystancją R

Analogicznie jak dla źródła napięciowego można wyznaczyć funkcję prądu od obciążenia.

G

z

=G

W

+G

Porównując otrzymaną charakterystykę obciążenia dla źródła prądowego z analogiczną

charakterystyką dla źródła napięciowego można powiedzieć, że to pierwsze ma lepsze własności dla

małych rezystancji R<R

w

tzn. że szybciej rzeczywiste źródło prądowe można przybliżyć idealną siła

prądomotoryczną SPM. Z kolei dla rezystancji R>Rw rzeczywiste źródło napięciowe szybciej można

aproksymować idealną siłą elektromotoryczą SEM.

I=5A

G

W

=0,5s

V

I

0

=0

I=5A

G

W

=0,5S

V

I=5A

G

W

=0,5s

A

I=5A

G

W

=0,5S

A

Zadanie

a) Obliczyć dla jakich rezystancji napięcie na zaciskach źródła napięciowego nie zmniejszy się poniżej

95% napięcia stanu jałowego (E).

b) Z kolei dla jakich rezystancji, prąd źródła nie zmniejszy się poniżej 95% prądu zwarcia.

Ad.a) R>19R

w

Ad.b) R<

w

1

R

19

Należy zwrócić uwagę, że w pierwszym przypadku rzeczywiste źródło napięciowe można

przybliżyć idealną siłą elektromotoryczną, natomiast w rugim idealną siła prądomotoryczną.

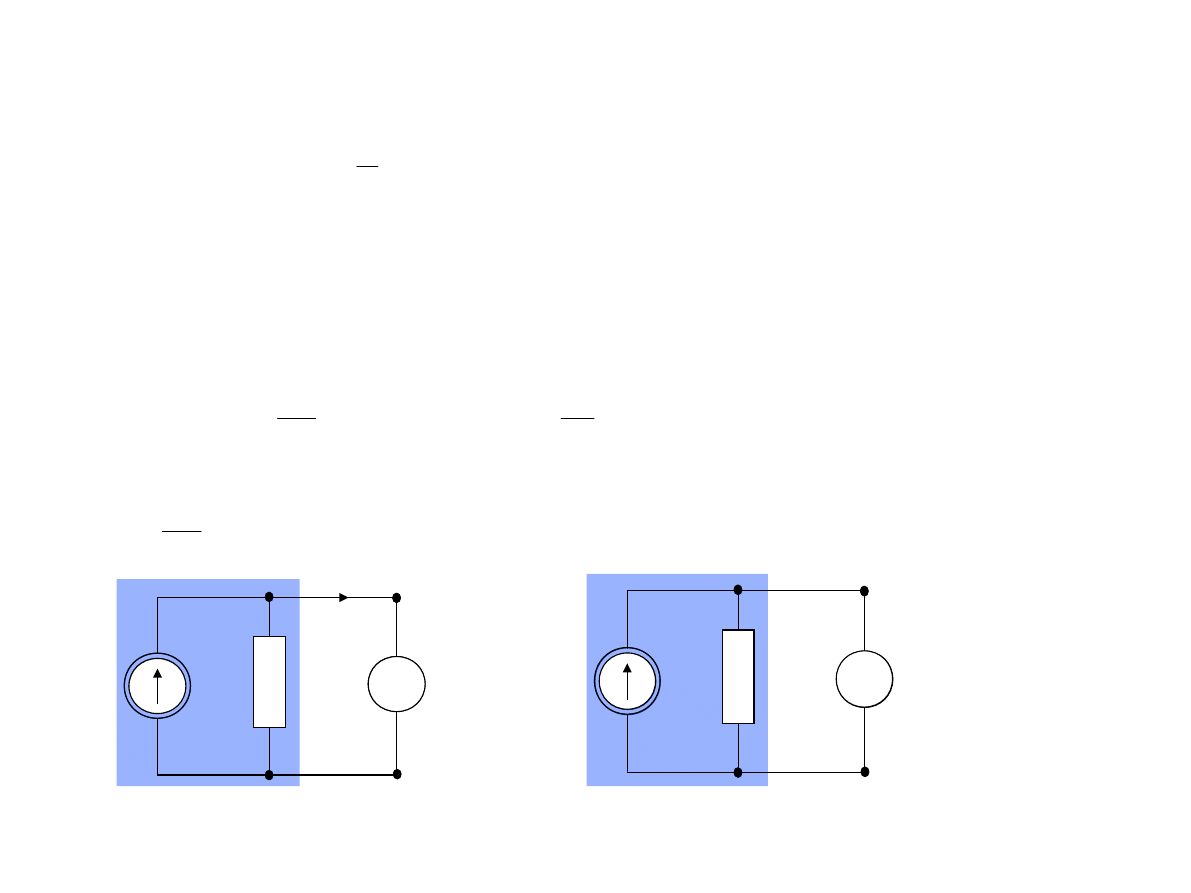
Równoważność źródła napięciowego i prądowego

Badamy źródło prądowe o parametrach:

A

5

R

E

I

W







S

R

G

W

W

5

,

0

1





V

10

G

I

U

W

V





-Stan jałowy

I

A

=I=5A – Stan zwarcia

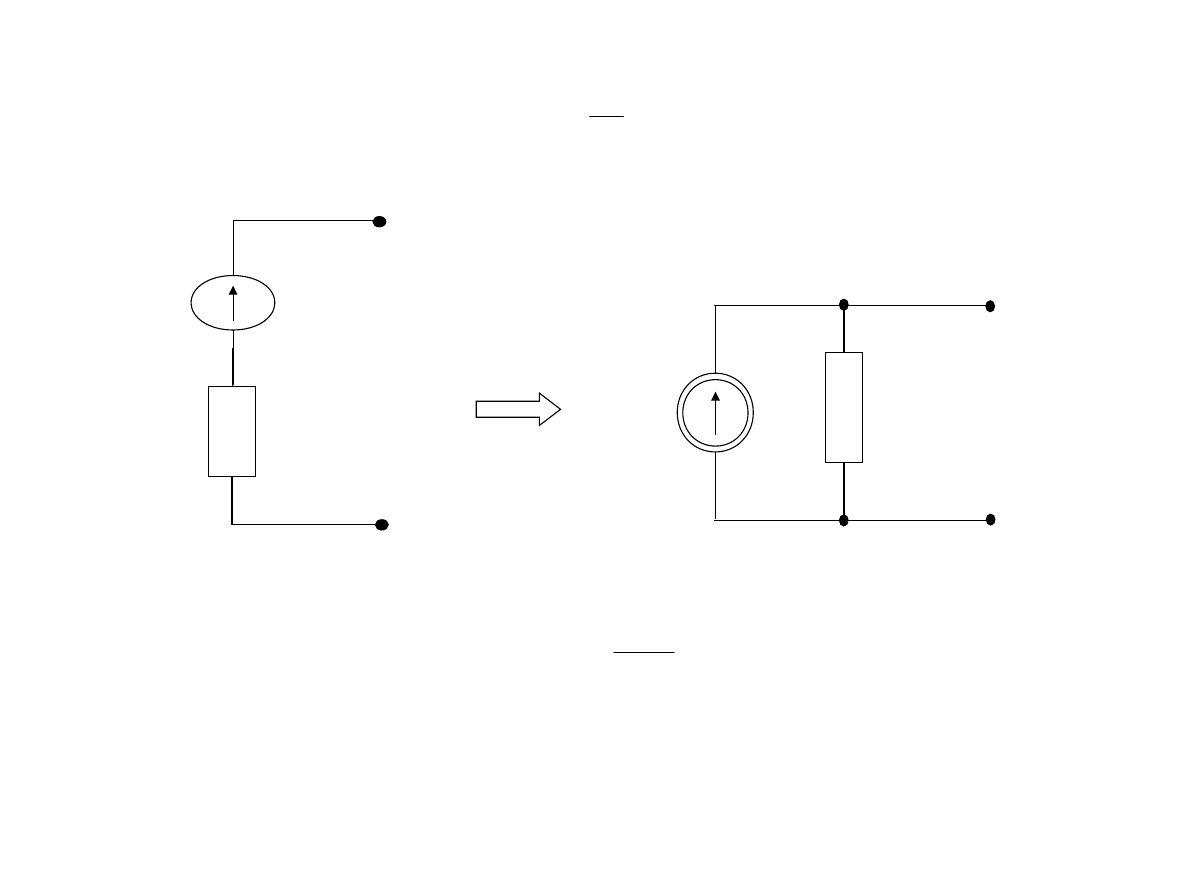
E

R

W

I

G

W

W

R

I

E







W

W

R

G

1



Jeżeli dokonamy analogicznych pomiarów zwarcia i stanu jałowego dla źródła napięciowego o

parametrach spełniającego warunki:

to otrzymamy identyczne wyniki, zatem poniżze źródła będą wówczas równoważne.

W

R

I

E





W

W

R

1

G 

Zatem

są to warunki równowaności źródeł napięciowego i prądowego (tylko rzeczywistych)!

5

2

5

2

5

1

V

A

5

2

5

2

5

1

V

A

U

V

=10

V

I

A

=5A

Jak widać wskazania mierników są identyczne jak w przykładach z

równoważnymi źródłami rzeczywistymi.

 

Wniosek: Każdy fragment obwodu, w którym wyodrębniono dwa zaciski

można potraktować jak dwójnik aktywny stanowiący rzeczywiste źródło

napięciowe.

 

Powyższy wniosek jest znany pod nazwą Twierdzenia Thevenina.

Niech dany będzie następujący obwód. Obliczmy wskazania woltomierza, a

później amperomierza.

V

V

E

T





R

T

E

R

T

Twierdzenie Thevenina:

 

Każdy dwójnik aktywny można zastąpić źródłem rzeczywistym napięciowym o elementach E

T

i

R

T

.

E

T

- zwane napięciem Thevenina, jest to napięcie stanu jałowego na zaciskach dwójnika.

R

T

- rezystancja Thevenina, jest to rezystancja jaką zmierzyłby omomierz przy zwarciu

wszystkich SEM i rozwarciu SPM.

Twierdzenie Thevenina to zastąpienie dwójnika

aktywnego napięciowym źródłem rzeczywistym. Rezystancję R

T

obliczamy jako rezystancję zastępczą dwójnika pasywnego

powstałego po usunięciu źródeł przy czym po SEM gałąź zwie-

ramy a po SPM zostaje przerwana.

Biorąc pod uwagę równoważność rzeczywistych źródeł prądo-

wego i napięciowego każdy dwójnik aktywny można

zatem zastąpić także rzeczywistym źródłem prądowym.

Takie postępowanie nazywamy Twierdzeniem Nortona .

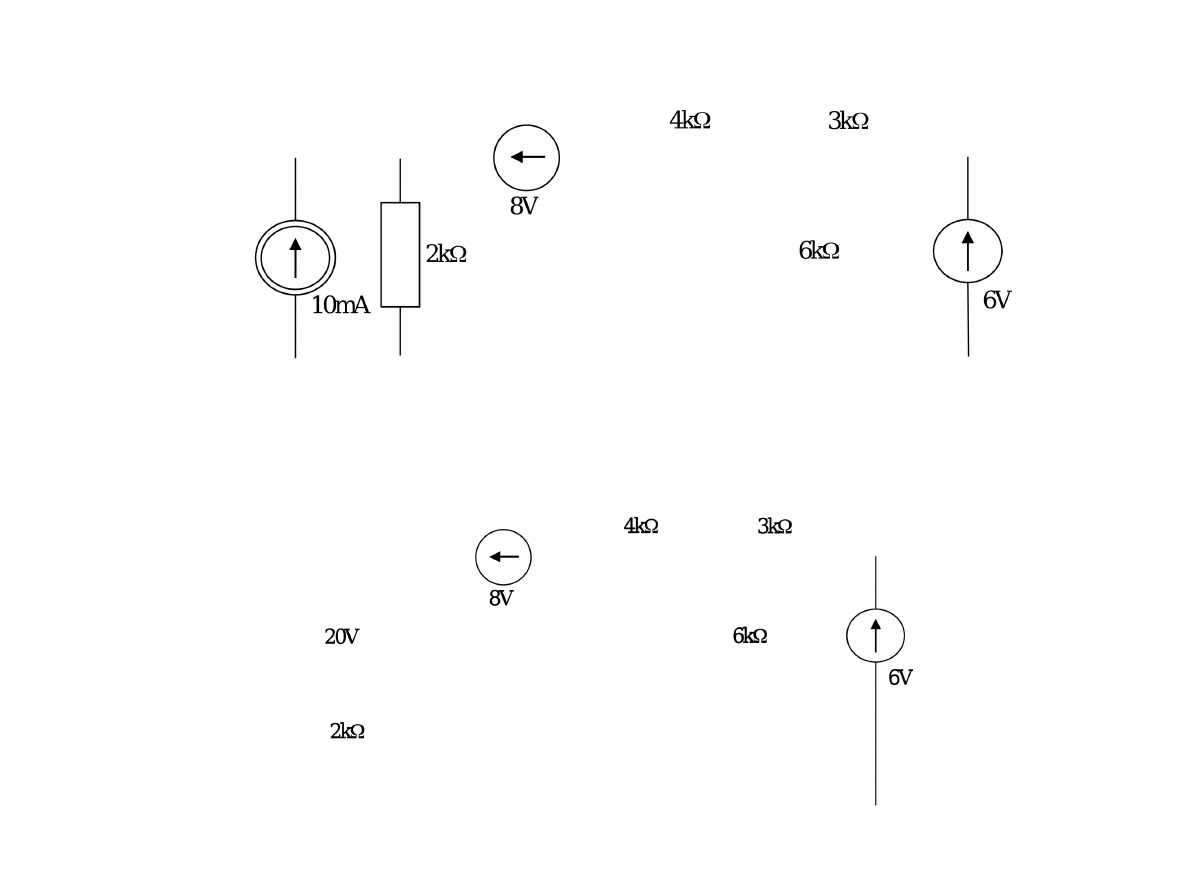
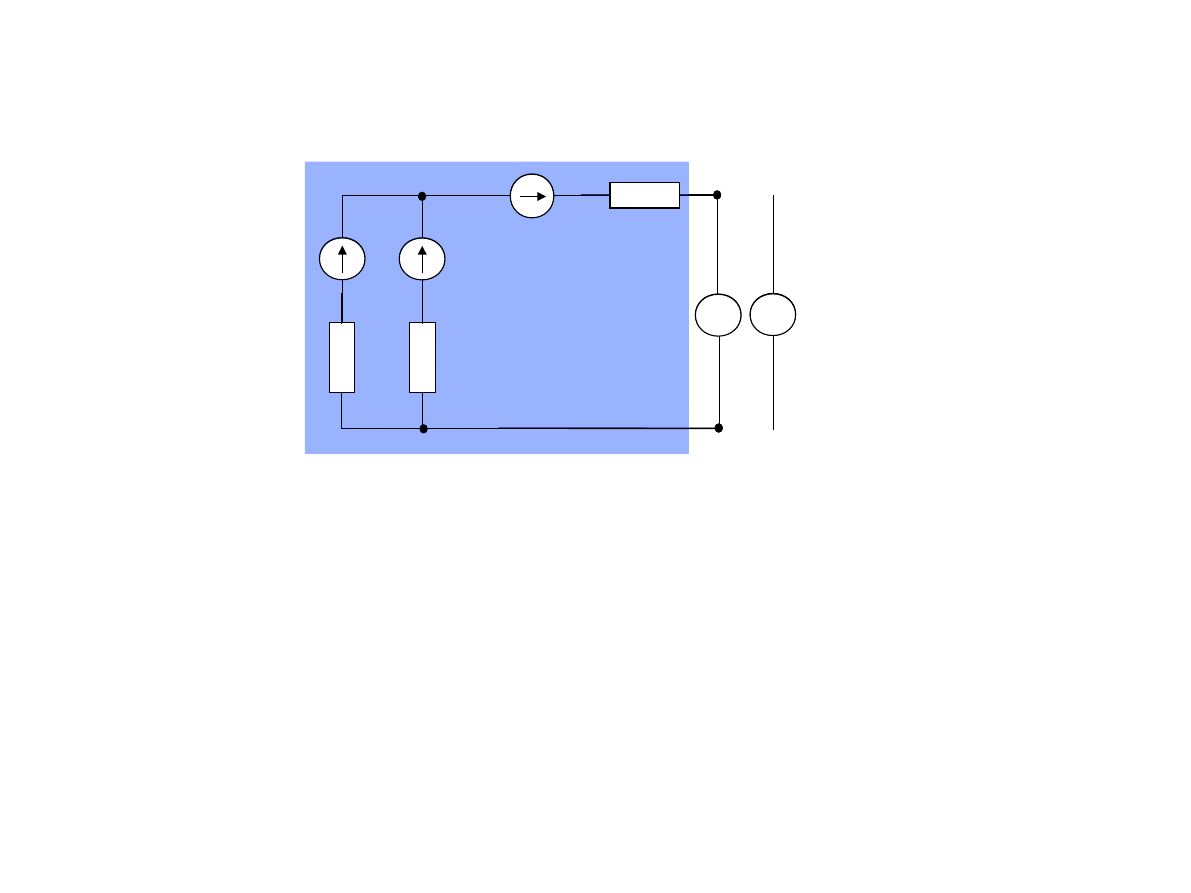
Przykład 3.5

Obliczyć prąd płynący przez rezystor 6k Ω stosując metodę zamiany źródeł i

twierdzenie Thevenina.

Najpierw rzeczywiste źródło prądowe zostanie zamienione na rzeczywiste źródło

napięciowe

zgodnie z formułą zawartą na ekranie 71 tj. E=IR . Rezystancja pozostaje ta sama.

Obwód po zastąpieniu źródła prądowego

napięciowym

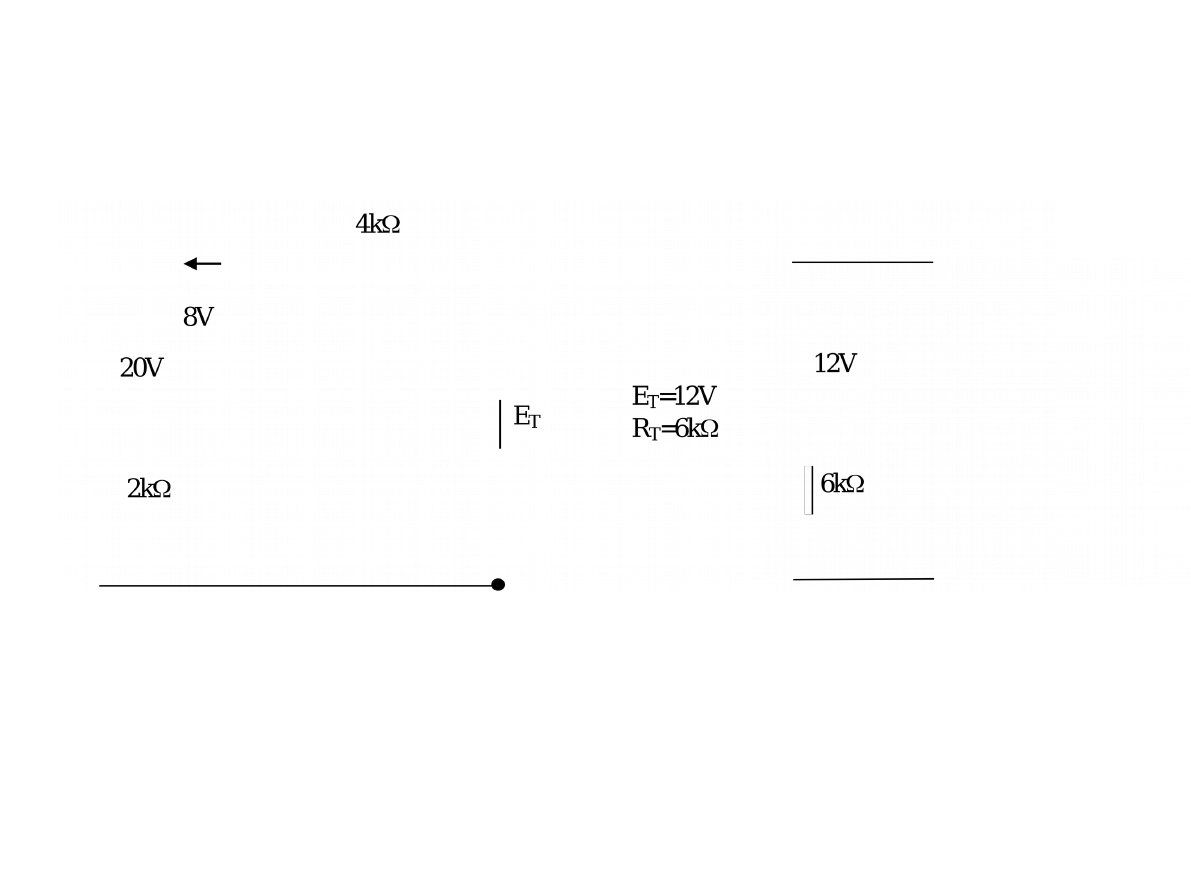
Następnie wytniemy z obwodu lewą (w stosunku do rezystancji 6kΩ

jego część.

Wycięty fragment obwodu zastępujemy źródłem napięciowym zgodnie z Tw.

Thevenina.

 

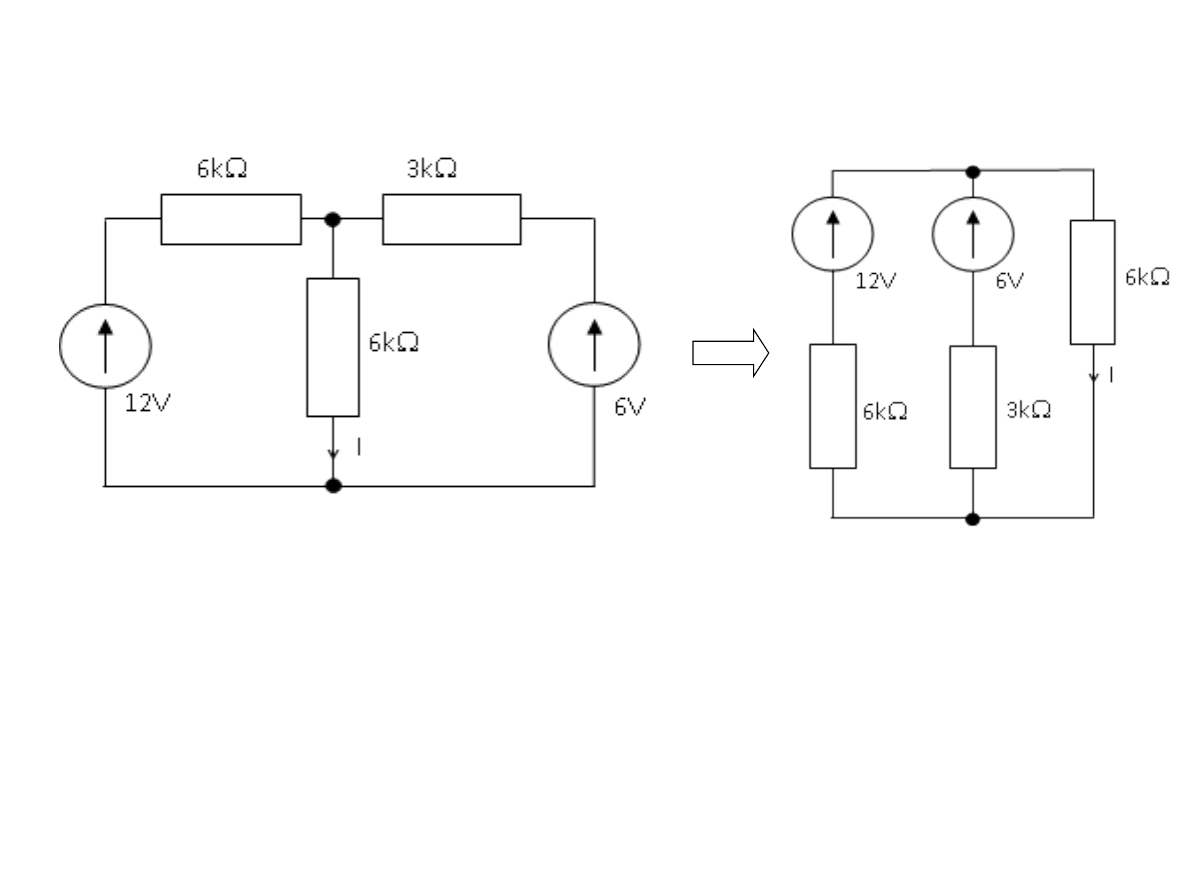
Oba obwody na ekranie są równoważne. Można powiedzieć, że gałąź 6V, 3kΩ

została przerzucona do środka.

Otrzymamy w ten sposób dwa źródła połączone równolegle i obciążone

rezystancją 6kΩ

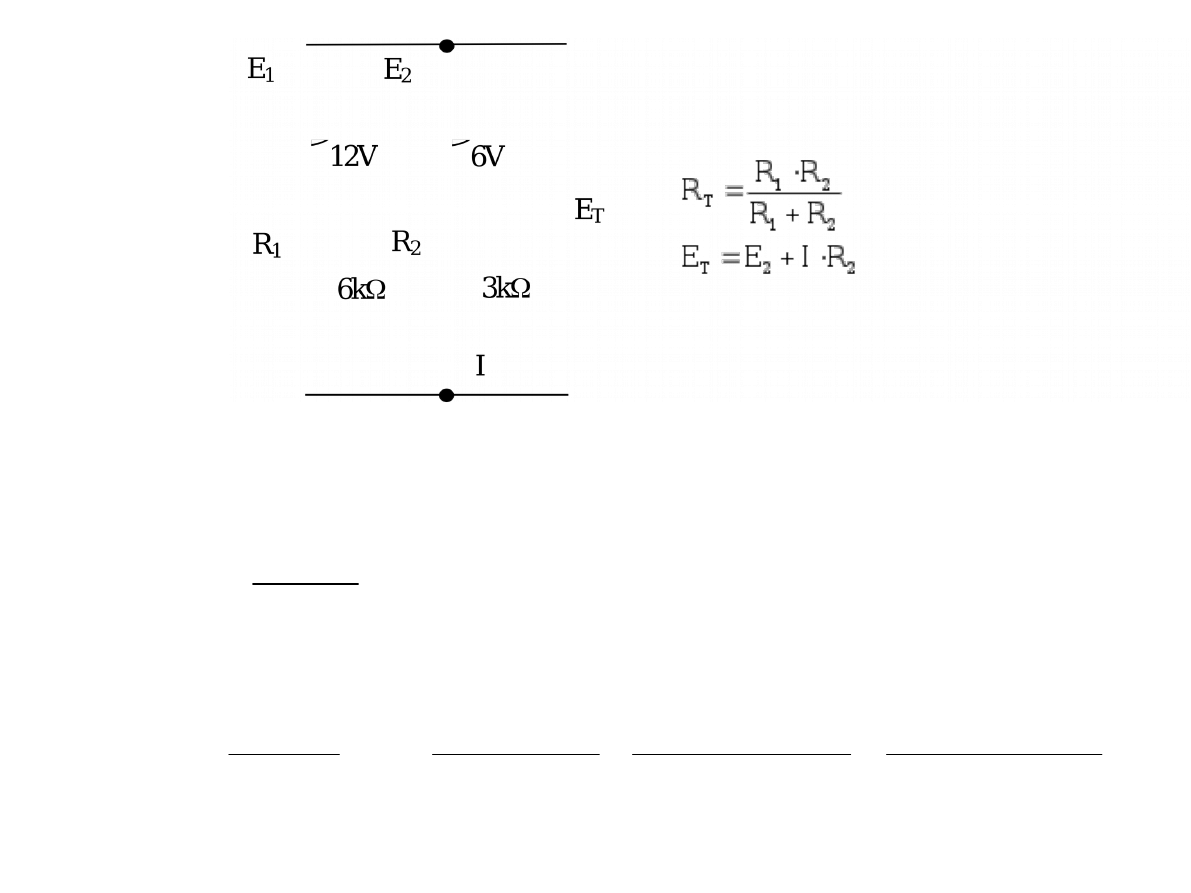
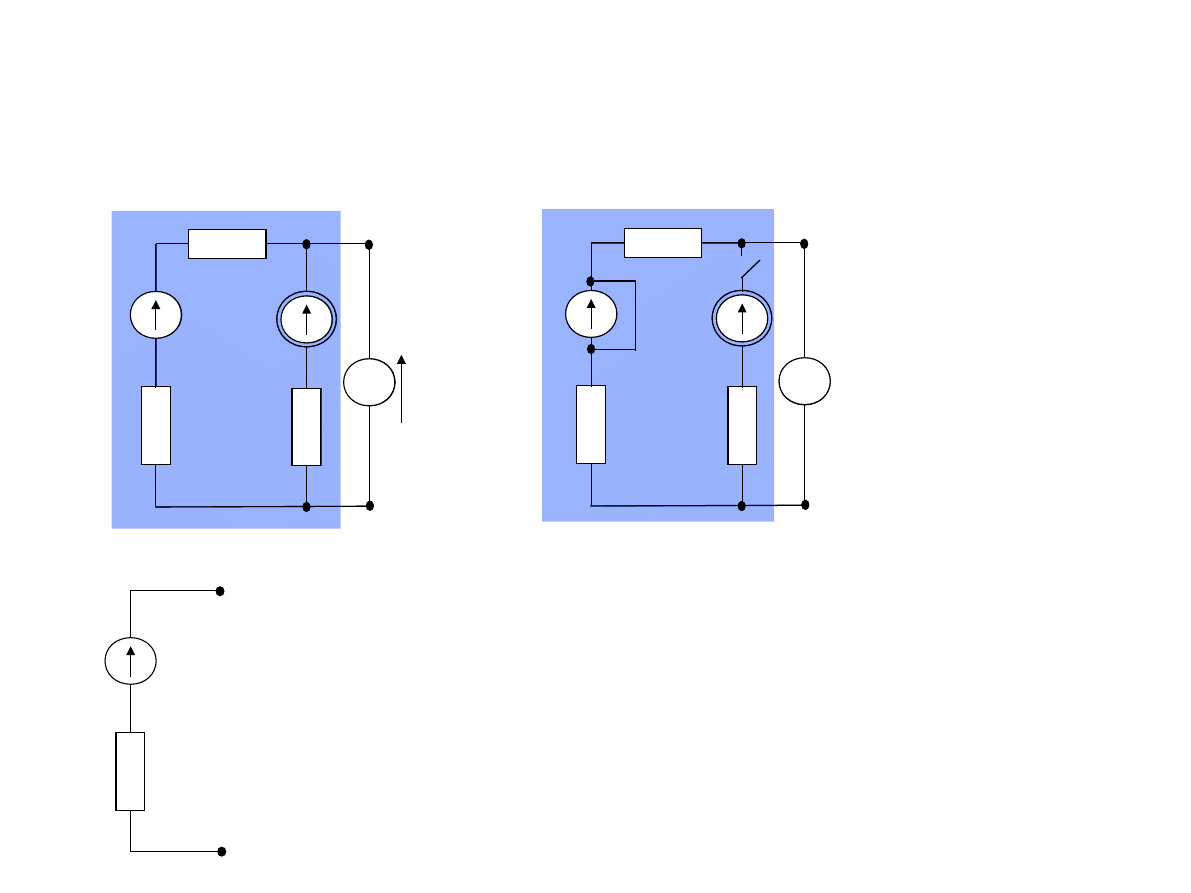
Układ równolegle połączonych żródeł znowu zastępujemy jednym

źródłem Thevenina. Napięcie E

T

można wyznaczyć następująco:

Ponieważ

2

1

2

1

R

R

E

E

I







Stąd





2

1

2

1

1

2

2

1

2

2

2

1

2

1

2

1

2

2

2

1

2

1

2

T

R

R

R

E

R

E

R

R

R

E

R

E

R

R

R

R

E

R

R

R

E

E

E

E





































Stąd

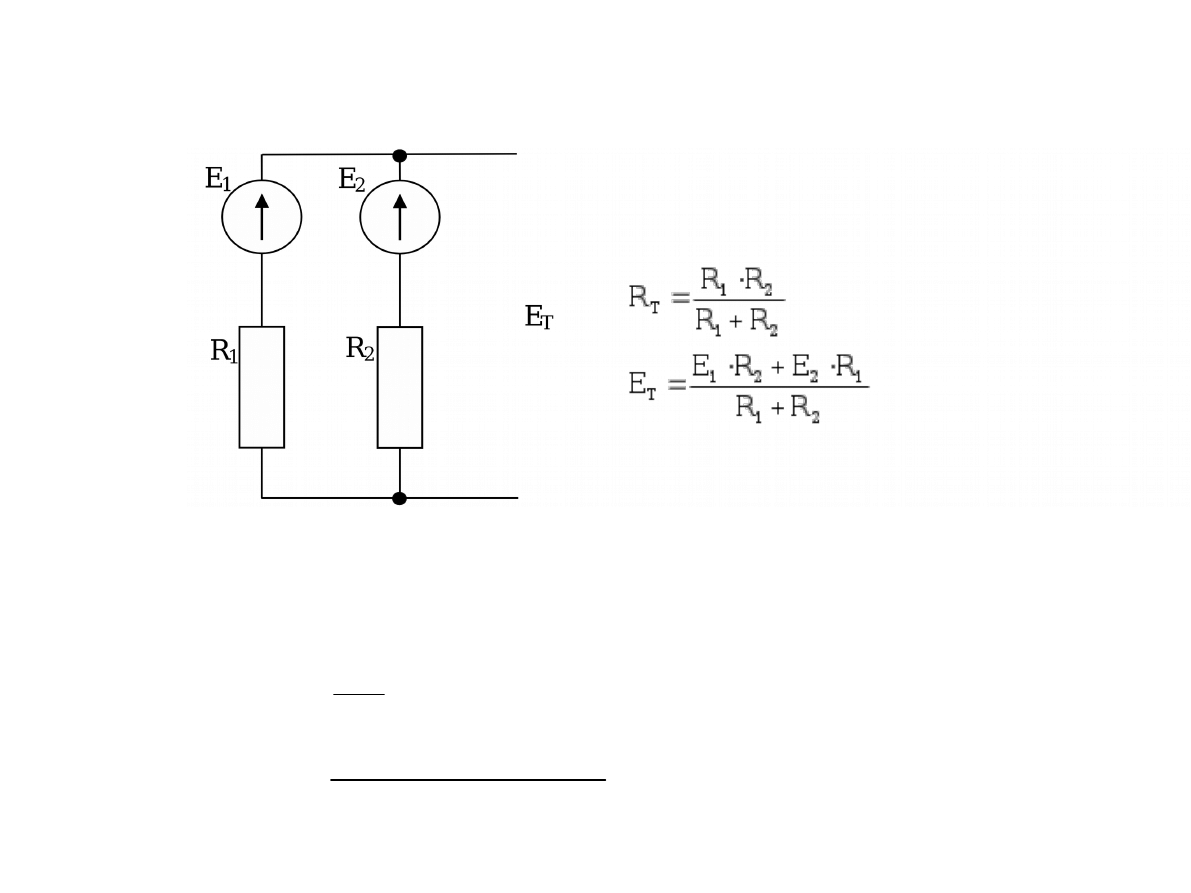
Wzory obok rysunku stanowią uniwersalną formułę na połączenie równoległe

dwóch źródeł napięciowych.

Formułę na E

T

łatwo zapamiętać, zwracając uwagę, że w liczniku wpisujemy sumę

iloczynów sił elektromotorycznych razy rezystancje w przeciwnych gałęziach.

Wstawiając dane zadania otrzymamy:

V

8

k

3

k

6

k

6

V

6

k

3

V

12

E

k

2

k

9

6

3

R

T

T































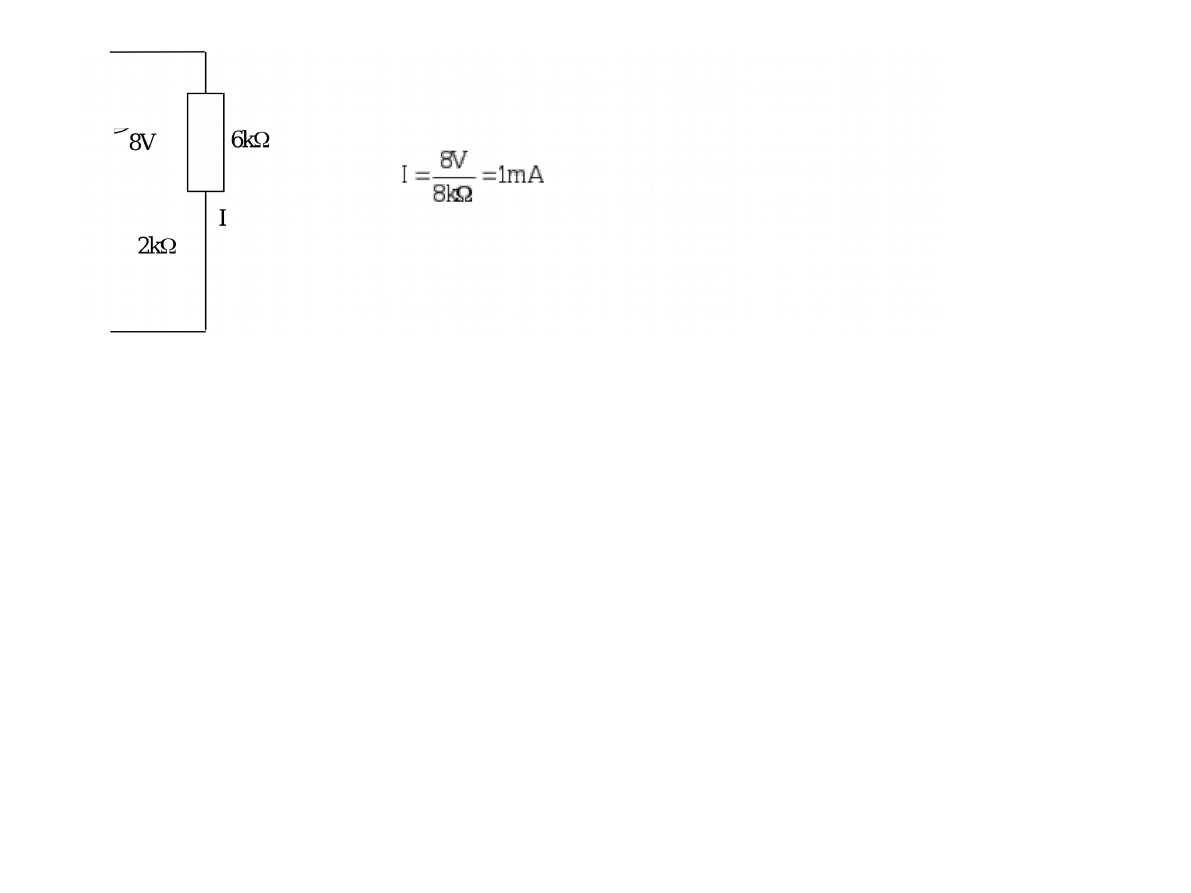
Odpowiedź:

Ostatecznie cały obwód względem

rezystancji 6kΩ został sprowadzony do

jednego źródła o parametrach 8V,2kΩ.

Stąd szukany prąd wynosi 1mA.

To zadanie można było rozwiązać zastępując od razu cały obwód ( po wycięciu

rezystancji 6kΩ) generatorem Thevenina. Przekonaj się, że otrzymasz identyczne

rozwiązanie.

Podsumowanie

 

Należy podkreślić, że większość powyższych metod można stosować tylko w

wypadku obwodów liniowych. Nie da się np. zwinąć obwodu z elementem

nieliniowym gdyż nie będziemy znali jej rezystancji.

Również w przypadku zamiany źródeł prądowego na napięciowe trzeba pamiętać,

że dotyczy to tylko źródeł rzeczywistych. Nie da się zamienić idealnej SPM na

idealną SEM.

Istnieje pojęcie równoważności dwójników aktywnych z elementami sterowanymi.

Niestety nie można analogicznie eliminować sterowanych SPM i SEM jak

dotychczas dla obliczenia np. rezystancji Thevenina.