„Signal Theory” Zdzisław
Papir
•Dirichlet’s convergence
conditions
•Fourier series behaviour
at discontinuity points
•Peter G. L. Dirichlet
•Mean square convergence
•Parseval theorem
•Fractional power
•Gibbs effect
•Fejer, Lanczos windows...
•Summary
Fourier Series
Convergence
„Signal Theory” Zdzisław Papir
Fourier series of signal
x(t)
Exponential form
,
2
,
1
,
0
1
o
o
o
n
dt
e
t
x
T
X
e
X
t
x
T
t
x
t
x
T
t
jn
n
n
t
jn
n
m
n
T
m
n
dt
e
e
e
e
n
e
T
t
m
j
t
jn
t
jm
t
jn
t
jn
,
,
0
,
2
,
1
,
0
,
o
o
o
o
o
o
If the signal x(t) in the interval [0, T]:
Class A signals:
A1)
has a finite number of 1st order discontinuities,
A2)
has a finite number of extrema,
A3)
is bounded
Class B signals:
B1)
has a finite number of 2nd order discontinuities,
B2)
except to
B1
points fits
A1
,
A2
, and
A3
conditions,
B3)
is absolutely integrable
then the exponential Fourier series is
uniformly convergent to the signal x(t) in
its each continuity point.
„Signal Theory” Zdzisław Papir
Dirichlet’s convergence
conditions (I)
T
dt
t
x
Dirichlet’s conditions are sufficient conditions.
t
x
Dirichlet’s conditions
(I)
„Signal Theory” Zdzisław Papir
time
x(t)
0
T
class A signal
I
I
„Signal Theory” Zdzisław Papir
time
x(t)
0
T
class B signal
I
II
Dirichlet’s conditions
(I)
„Signal Theory” Zdzisław Papir
t
x
t
x
t
x
t
x
2
1
lim
lim
2
1
o
o
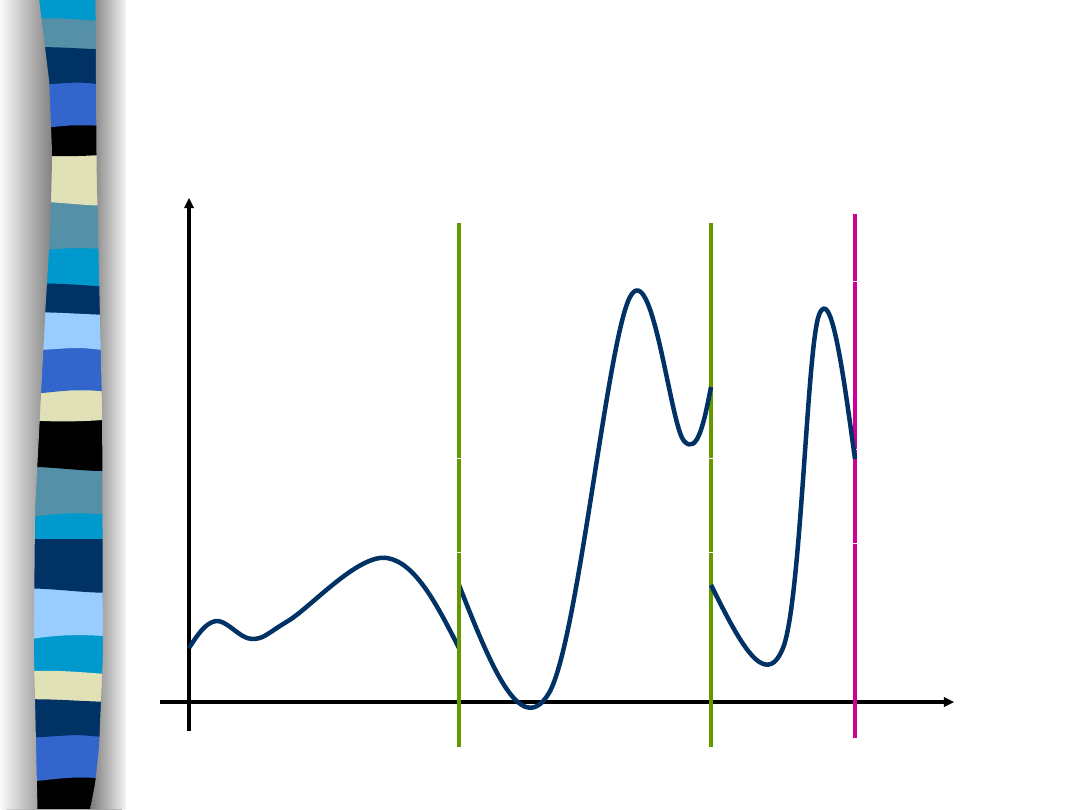
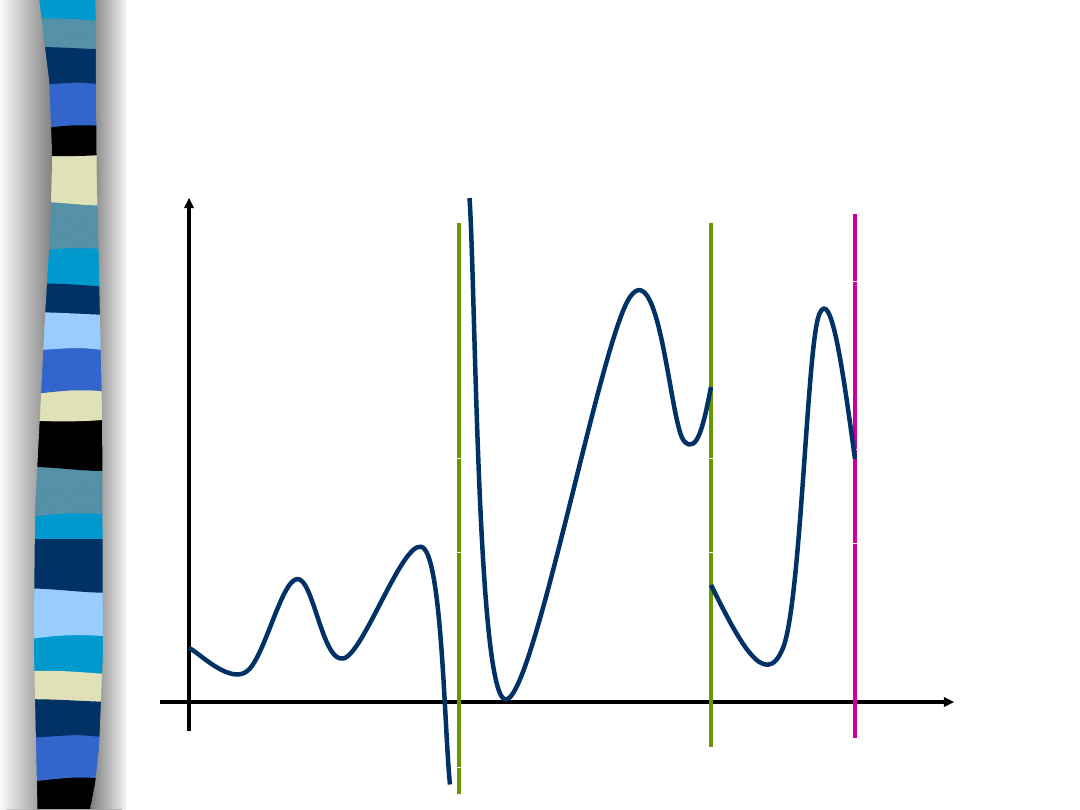
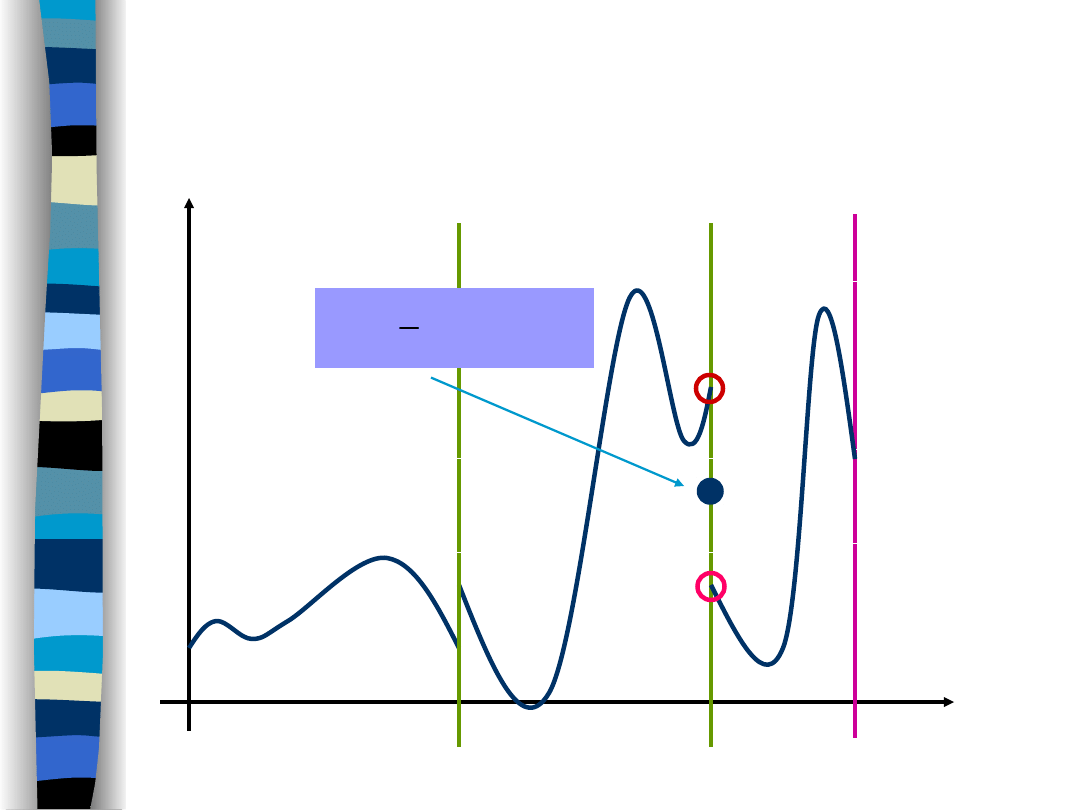
The value of Fourier series in
1st order discontinuity points
equals:
The theorem suggests that the value of the signal in its
discontinuity points should be equal by definition to
an
arithmetic mean of right and left limit values
(at the discontinuity point).
This definition guarantees the Fourier series convergence
to the signal at each time point (a uniform convergence in
continuity points only)
Dirichlet’s conditions
(I)
„Signal Theory” Zdzisław Papir
Fourier series
behaviour
at discontinuity points
time
x(t)
0
T
t
x(t-)
x(t+)
t
x
t
x
t
x
2
1
„Signal Theory” Zdzisław Papir
Discontinuity point
-0.2
0
0.2
0.4
0.6
0.8
1
1.2
0
2
4
6
8
10
12
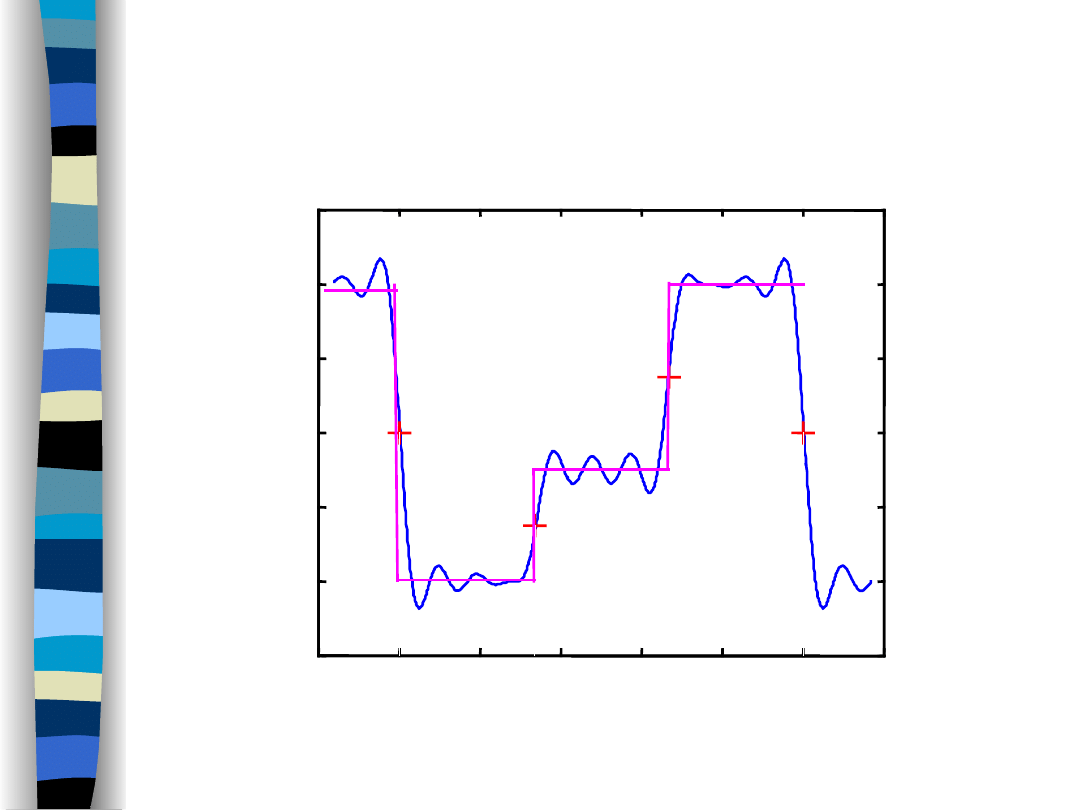
Fourier series behaviour at discontinuity points
czas
(10 components)
time
„Signal Theory” Zdzisław Papir
Discontinuity point
-0.2
0
0.2
0.4
0.6
0.8
1
1.2
0
2
4
6
8
10
12
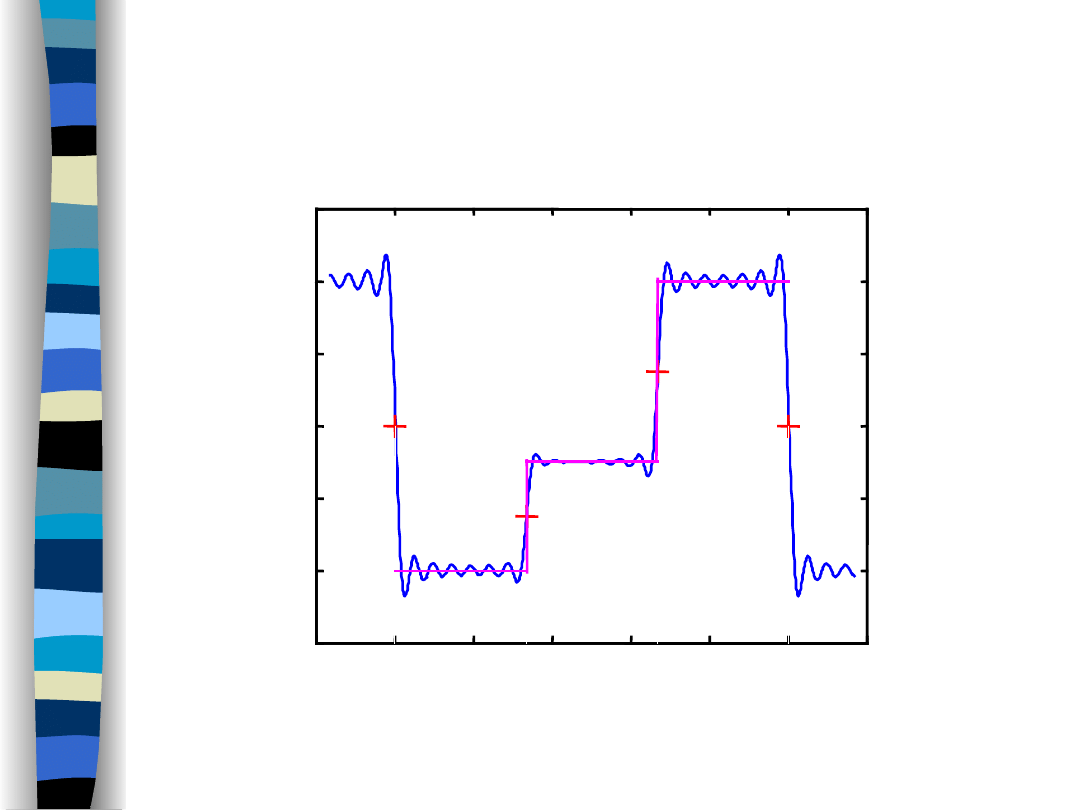
Fourier series behaviour at discontinuity points
czas
(20 components)
time
If the signal x(t) in the interval [0, T]:
class A signals:
A1)
is of bounded variation
class B signals:
B1)
has a finite number of 2nd order discontinuities,
B2)
except for
B1
points fits the condition
A1
,
B3)
is absolutely integrable
then the exponential Fourier series is
uniformly convergent to the signal x(t) in
its each continuity point.
„Signal Theory” Zdzisław Papir
T
dt
t
x
1
0
1
1
2
1
o
0
n
i
i
i
n
i
i
t
x
t
x
T
t
t
t
t
t
t
VARIATION
BOUNDED
conditions II
conditions I
Dirichlet’s convergence
conditions (II)
„Signal Theory”
Zdzisław Papir
Dirichlet’s conditions
(II)
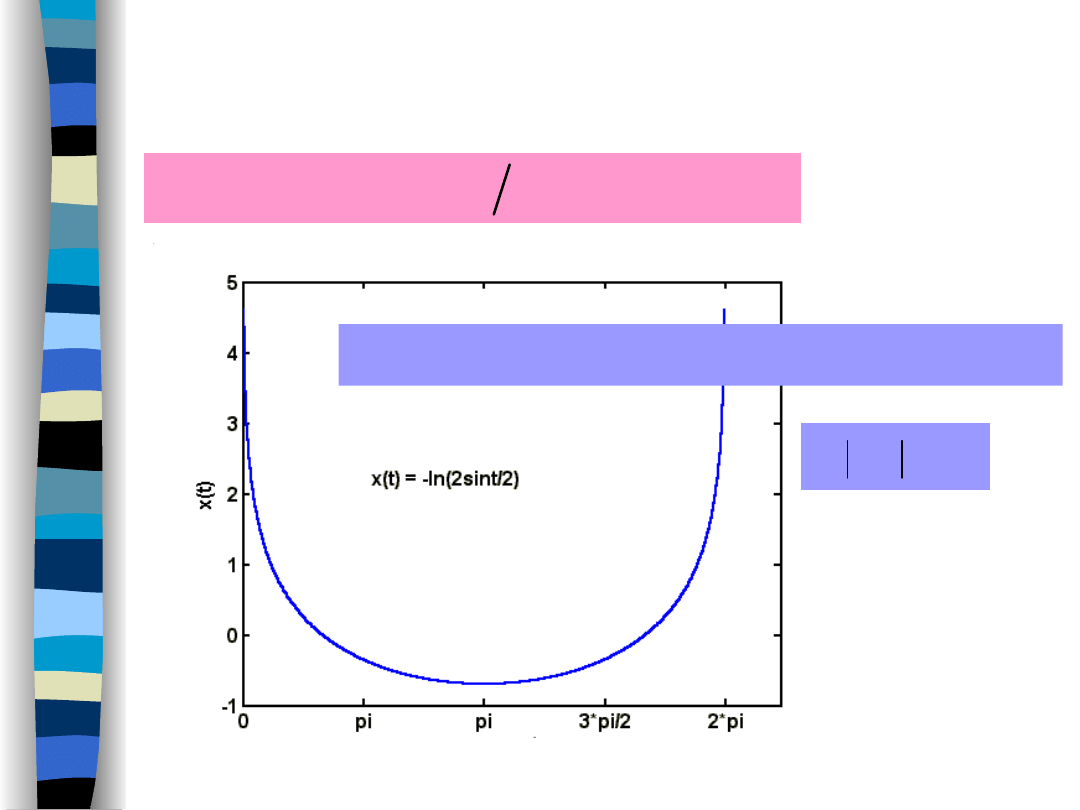
2
0
,
2
sin
2
ln
t
t
t
x
Absolutely integrable signal according to G. M. Fichtenholz
„Rachunek różniczkowy i całkowy”, vol. II, p. 507
2
o
dt
t
x
time
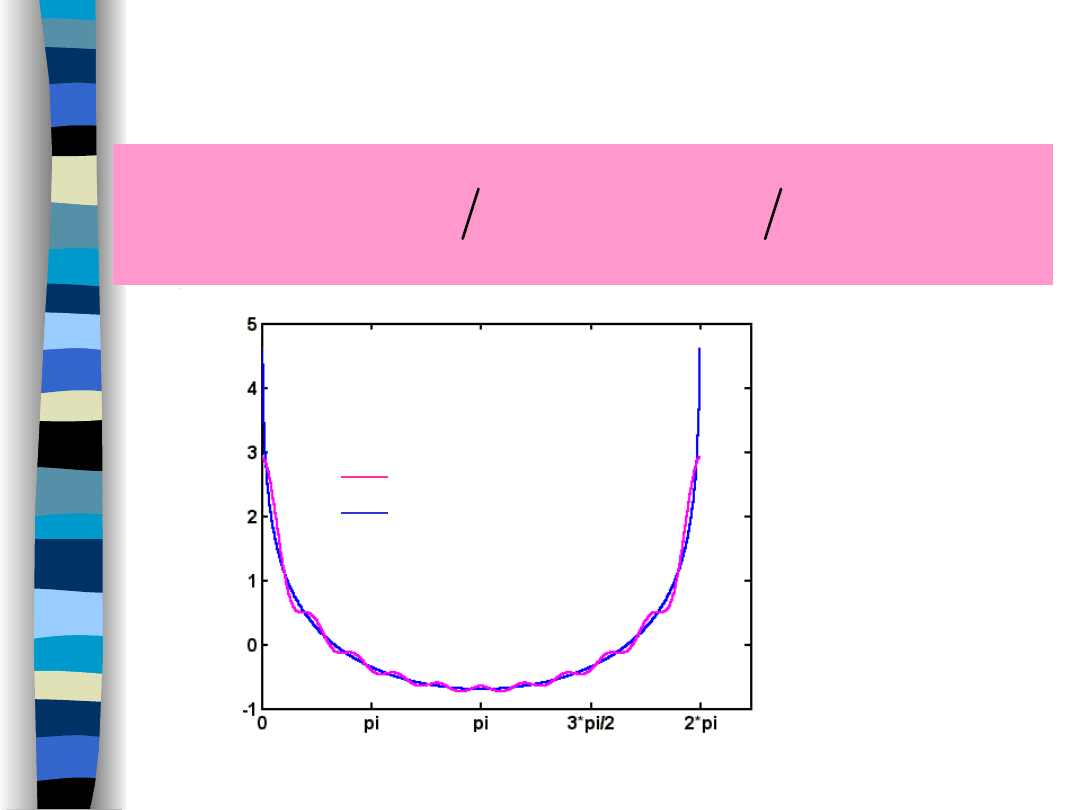
„Signal Theory” Zdzisław Papir
2
0
,
cos
2
sin
2
ln
1
t
n
nt
t
t
x
n
Dirichlet’s conditions
(II)
time
number of components -10
signal x(t)
Fourier series
„Signal Theory” Zdzisław Papir
Peter Gustav Lejeune
Dirichlet
•
German mathematician, I half XIX century
• Most important achievements:
• number theory
– dzeta function
• set theory
– pigeon hole principle
• series theory
– series convergence
„Signal Theory” Zdzisław Papir
Peter Gustav Lejeune
Dirichlet
Riemann’s dzeta function:
(specific case of the Dirichlet’s function)
1
Re
,
1
1
s
n
s
n
s
Euler’s identity:
set
number
prime
,
1
Re
,
1
1
1
p
s
p
s
p
s
„Signal Theory” Zdzisław Papir
Peter Gustav Lejeune
Dirichlet
Riemann hypothesis:
(unproven till today)
1
Re
0
,
0
1
1
s
n
s
n
s
jb
s
2
1
The dzeta function has infinite number of roots given by
the formula:
Proof of the Riemann hypothesis would
change the number theory; computer
calculations verify that more than 1,5 x 10
9
figures satisfy the Riemann hypothesis.
„Signal Theory” Zdzisław Papir
Peter Gustav Lejeune
Dirichlet
Number of prime numbers:
(proof based on dzeta function)
x
x
x
x
x
x
x
x
x
x
x
for
ln
1
ln
lim
2
,
numbers
prime
of
number
-
Estimation error:
x = 10
10
4,5%
x = 10
14
3,0%
x = 10
18
2,5%
„Signal Theory” Zdzisław Papir
Peter Gustav Lejeune
Dirichlet
Pigeon hole principle:
If N objects is placed in K < N containers,
then at least one container contains at least 2 objects.
N = 4
K = 3
Application:
Two Cracow inhabitants have the same number
of hairs on their heads (
N 800.000
).
Maximum number of hairs on a head -
K = 500 000
.
„Signal Theory” Zdzisław Papir
Mean square
convergence
Truncated Fourier series
approximation
Fourier series
Mean square approximation error
k
k
n
t
jn
n
n
t
jn
n
e
X
t
x
e
X
t
x
o
o
a
0
1
o
2
a
2
T
dt
t
x
t
x
T
e
„Signal Theory” Zdzisław Papir
Truncated Fourier series is a mean square approximation
of a signal. Mean square convergence requests a square-
integrable signals:
T
dt
t
x
T
o
2
1
so it is valid for signals of limited energy (power).
Mean square
convergence
0
1
2
o
2
2
k
k
k
n
n
T
X
dt
t
x
T
e
„Signal Theory” Zdzisław Papir
Parseval theorem
n
n
T
X
dt
t
x
T
2
o
2
1
Using Parseval theorem we can determine a signal power:
T
dt
t
x
T
P
o
2
1
in the frequency domain:
n
n
X
P
2
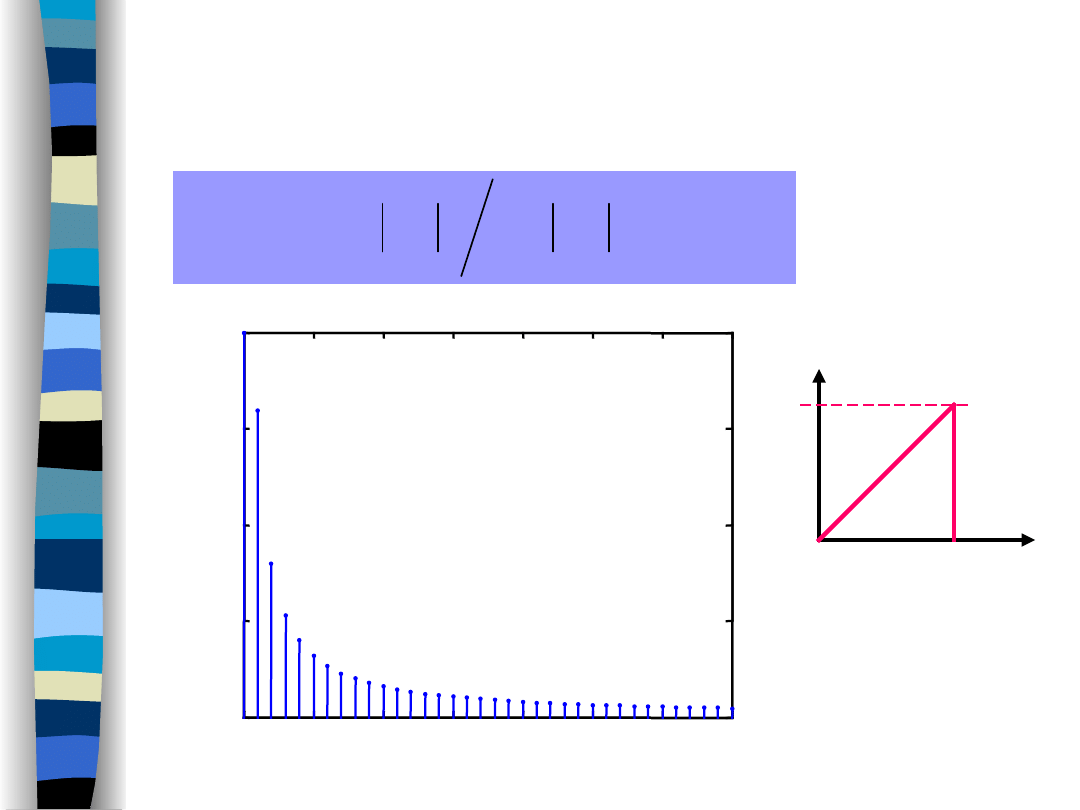
„Signal Theory” Zdzisław Papir
Fractional Power
1
2
2
o
f
k
n
n
k
k
n
n
X
X
kf
P
0
5
10
15
20
25
30
35
0
0.05
0.1
0.15
0.2
kf
o
|X
k
|
Sawtooth signal – Fourier coefficients
T = 1
t
1
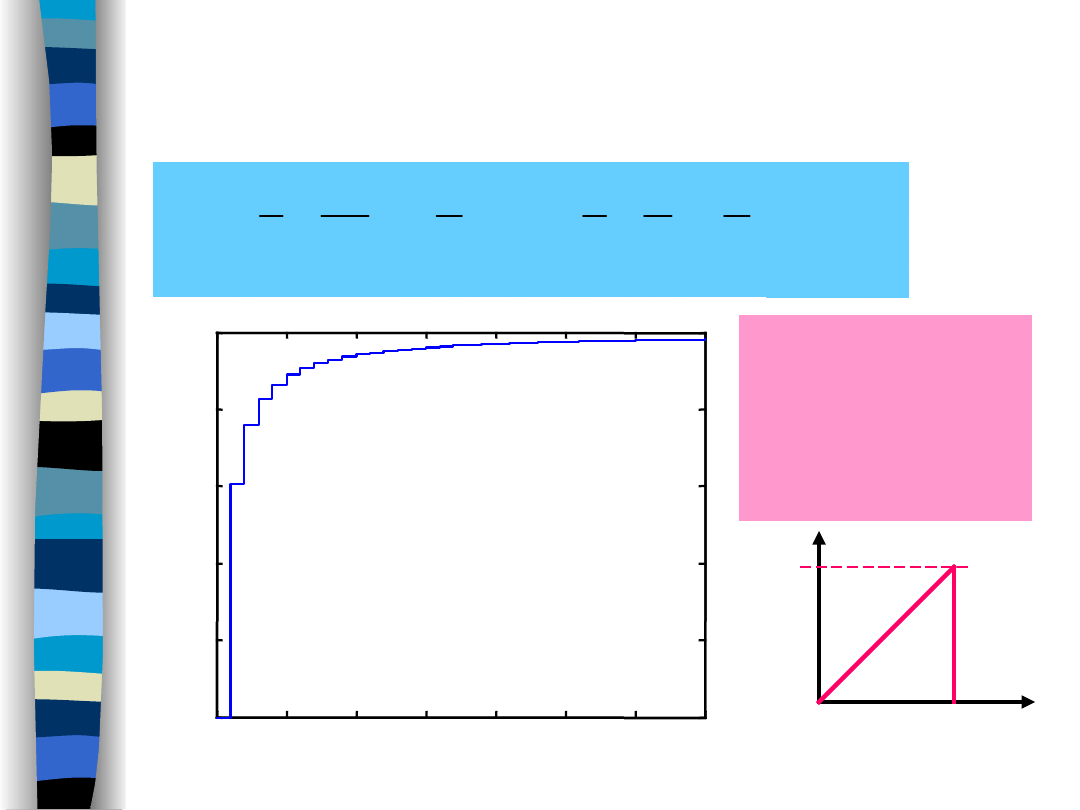
„Signal Theory” Zdzisław Papir
Fractional power
t
n
n
e
n
j
t
x
n
t
jn
n
n
o
1
2
o
sin
1
1
2
1
1
2
2
1
0
5
10
15
20
25
30
35
75
80
85
90
95
100
kfo
P
f
(k
fo
)
[%
]
Sawtooth signal – fractional power
%
99
16
%
95
4
%
90
2
o
f
o
f
o
f
f
P
f
P
f
P
T = 1
t
1
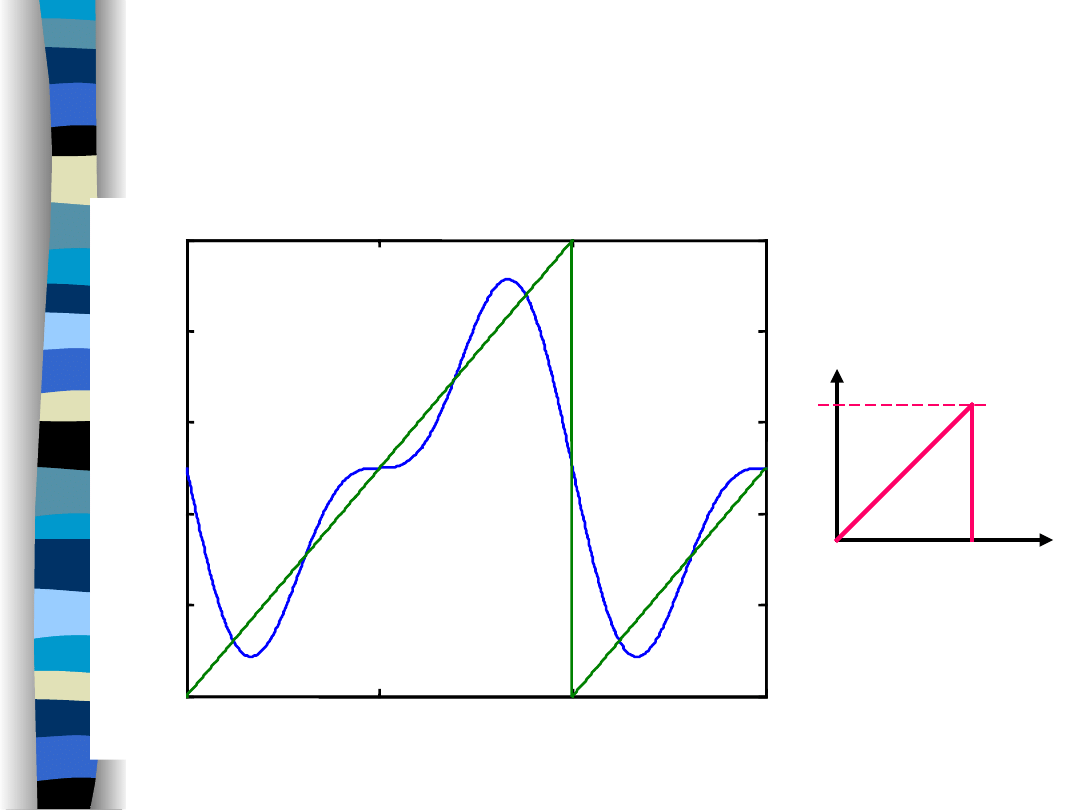
„Signal theory” Zdzisław Papir
Fractional power
(sawtooth signal - 90%)
0
0.5
1
1.5
0
0.2
0.4
0.6
0.8
1
Sawtooth signal approximation
2 harmonics
90% of total signal power
T = 1
t
1
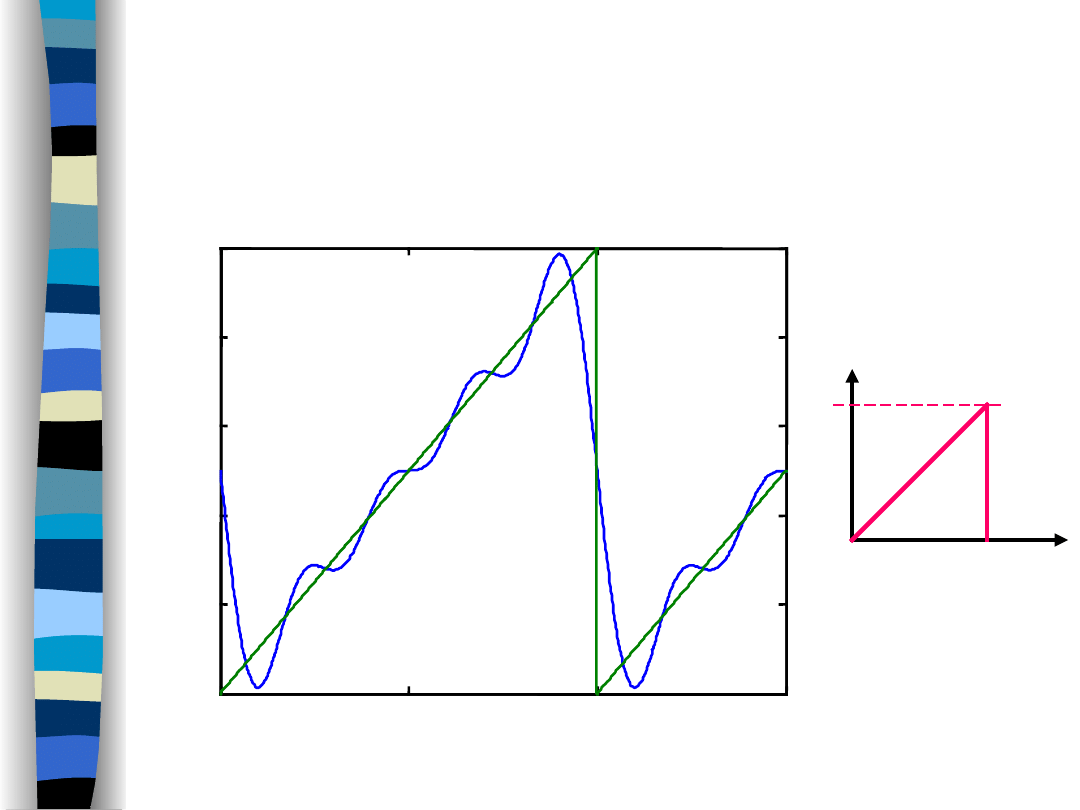
„Signal Theory” Zdzisław Papir
0
0.5
1
1.5
0
0.2
0.4
0.6
0.8
1
Sawtooth signal approximation
4 harmonics
95% of total signal power
T = 1
t
1
Fractional power
(sawtooth signal - 95%)
„Signal Theory” Zdzisław Papir
0
0.5
1
1.5
-0.2
0
0.2
0.4
0.6
0.8
1
1.2
Sawtooth signal approximation
16 harmonics
99% of total signal power
T = 1
t
1
Fractional power
(sawtooth signal - 99%)
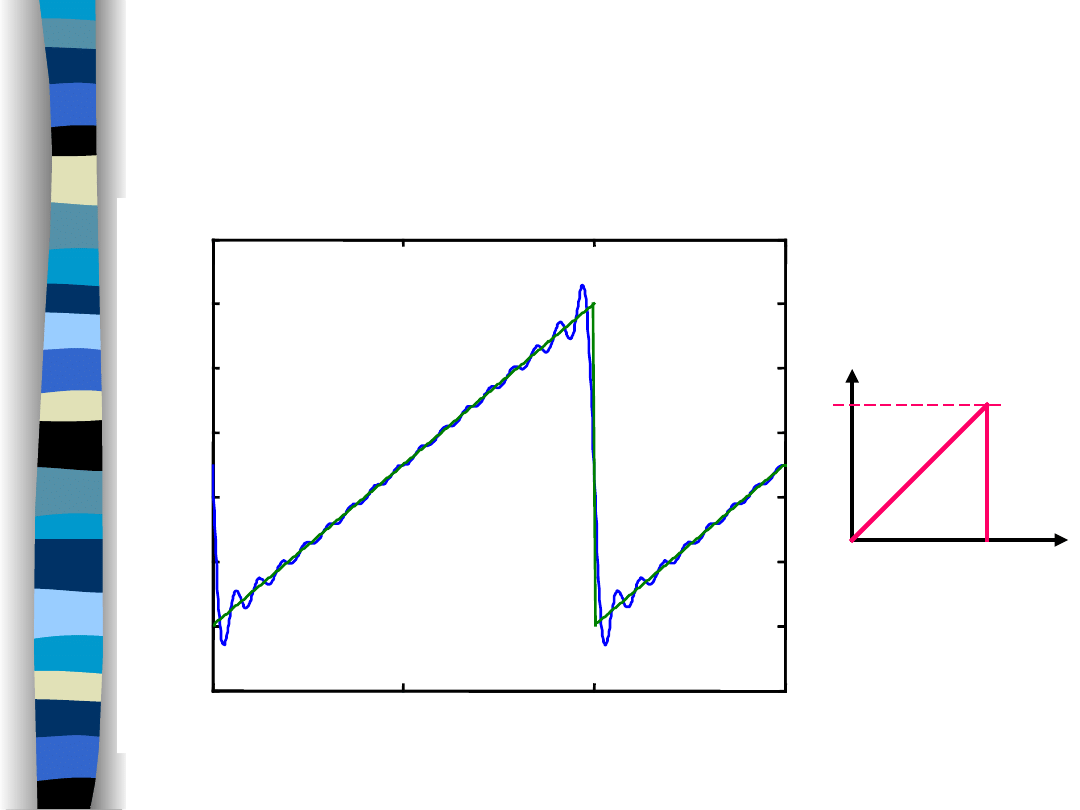
„Signal Theory” Zdzisław Papir
Gibbs effect
-0.5
0
0.5
0
0.2
0.4
0.6
0.8
1
1.2
1.4
Gibbs effect
Rectangular pulse
11 harmonics
„Signal Theory” Zdzisław Papir
Gibbs effect
-0.5
0
0.5
0
0.2
0.4
0.6
0.8
1
1.2
1.4
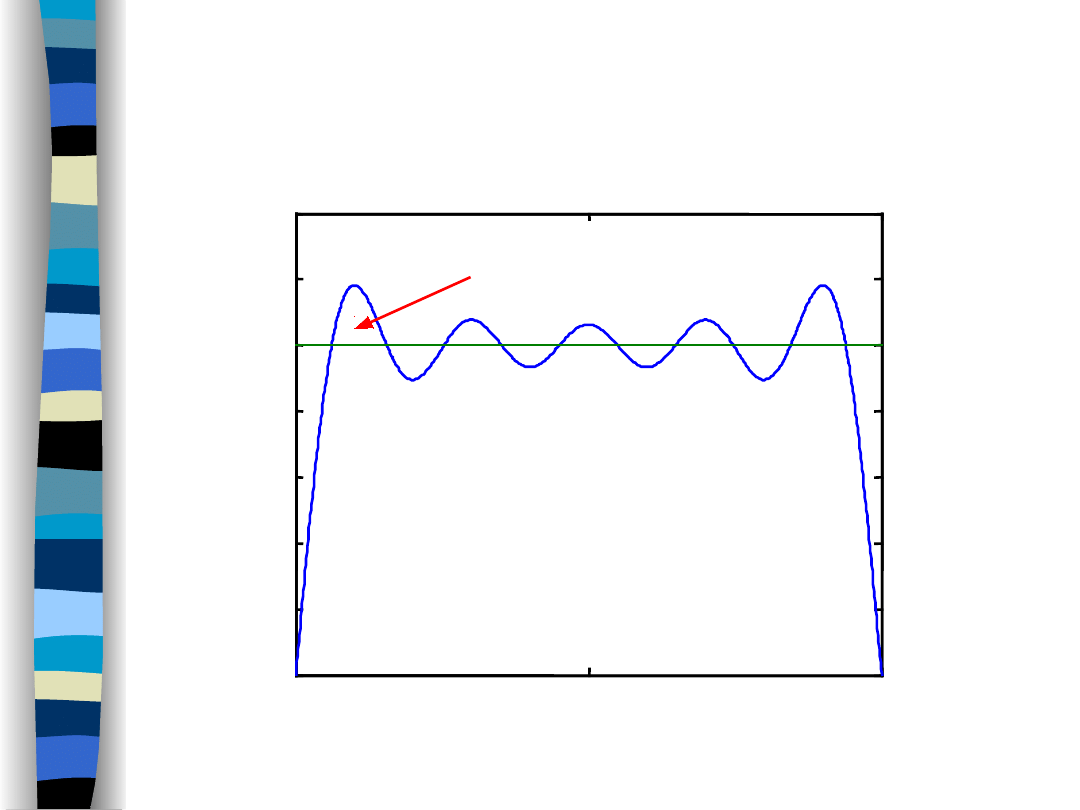
Gibbs effect
Rectangular pulse
39 harmonics
„Signal Theory” Zdzisław Papir
Gibbs effect
-0.5
0
0.5
0
0.2
0.4
0.6
0.8
1
1.2
1.4
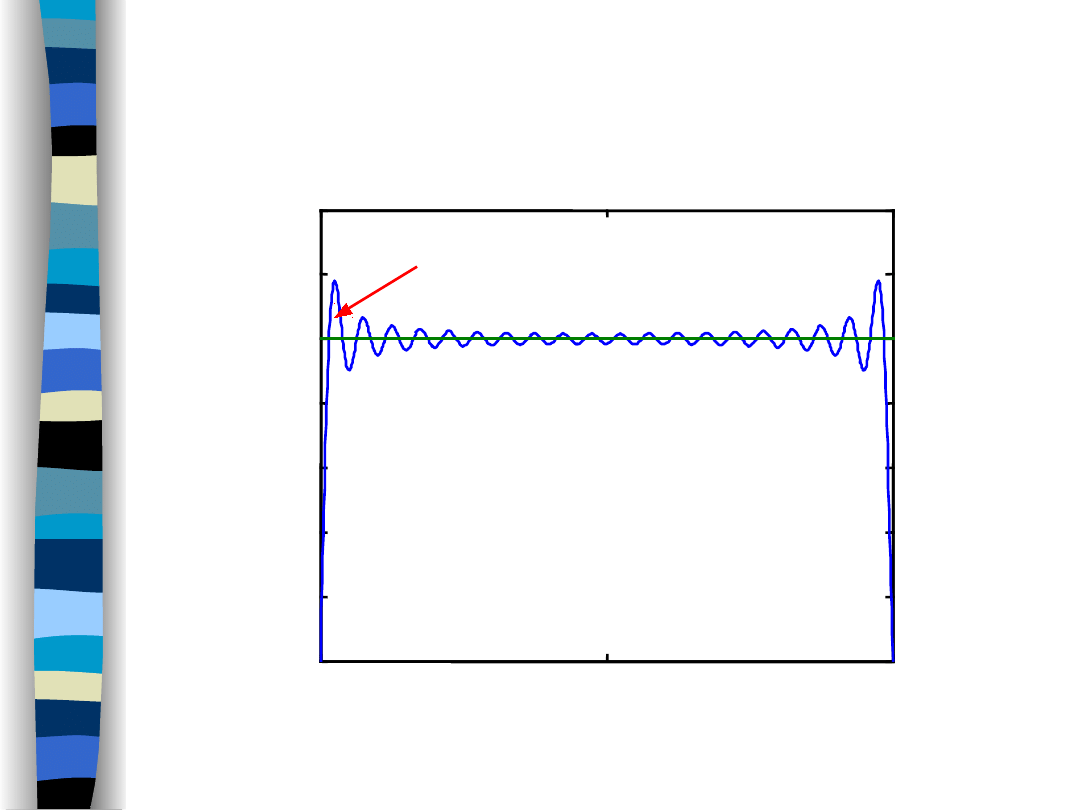
Gibbs effect
Rectangular pulse
79 harmonics
„Signal Theory” Zdzisław Papir
Gibbs effect
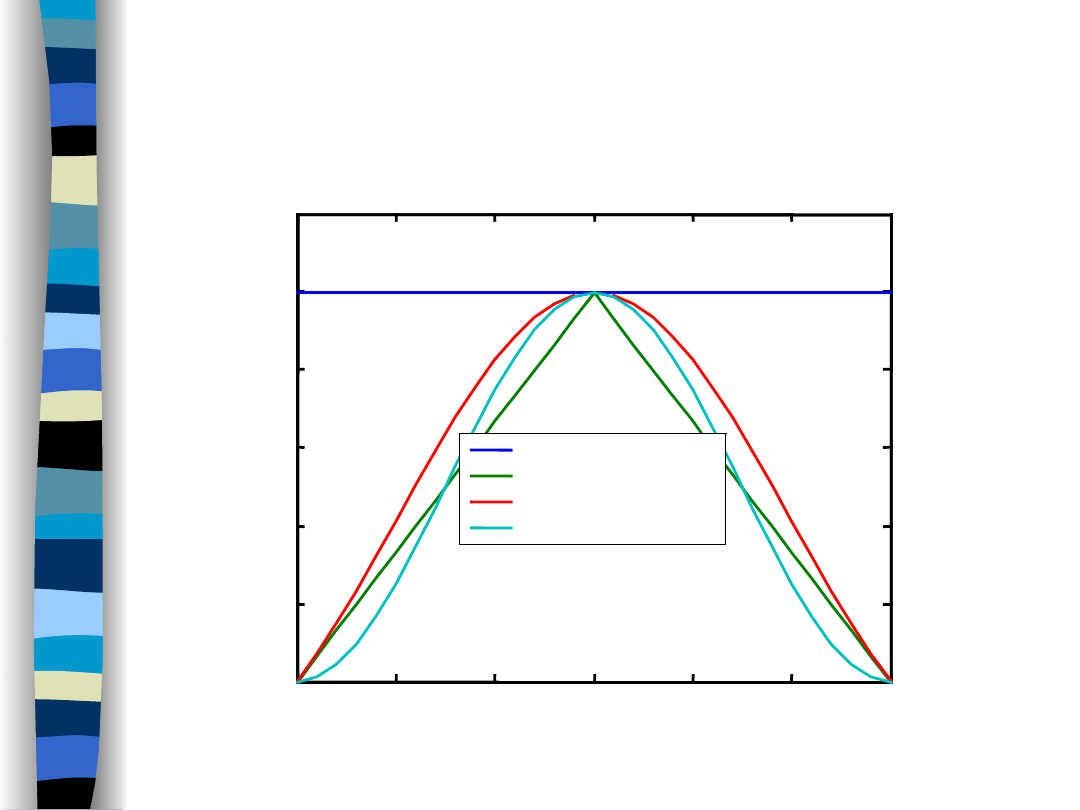
Gibbs effect appears at signal discontinuity
points when
approximating the signal by a truncated
Fourier series.
Gibbs effect is visible as excessive
osscilations close to
discontinuity points.
Gibbs effect does not depend on the how
the truncated
Fourier series is long.
„Signal Theory” Zdzisław Papir
Fejer, Lanczos...
windows
k
k
n
t
jn
n
n
n
t
jn
n
e
X
w
t
s
e
X
t
x
o
o
Window function (a set of different weights)
k
n
w
n
,
0
is tuned to minimize the Gibbs effect.
In a classical case a rectangular window is used:
k
n
w
n
,
1
„Signal Theory” Zdzisław Papir
Rectangular windowFejer window
k
n
w
n
,
1
k
n
k
n
w
n
,
/
1
Lanczos window
von Hann, Hamming, Kaiser... windows
x
x
x
Sa
k
n
k
n
Sa
w
n
/
sin
,
/
Fejer, Lanczos...
windows
„Signal Theory” Zdzisław Papir
-15
-10
-5
0
5
10
15
0
0.2
0.4
0.6
0.8
1
Fourier coefficients
w
e
ig
h
t
w
n
Rectangular window
Fejer window
Lanczos window
von Hann window
Fejer, Lanczos...
windows
„Signal Theory” Zdzisław Papir
-0.5
0
0.5
0
0.2
0.4
0.6
0.8
1
1.2
1.4
Rectangular window
Rectangular pulse
Fejer window
Lanczos window
Impuls prostokątny
11 harmonicznych
Rectangular pulse
7 harmonics
Fejer, Lanczos...
windows
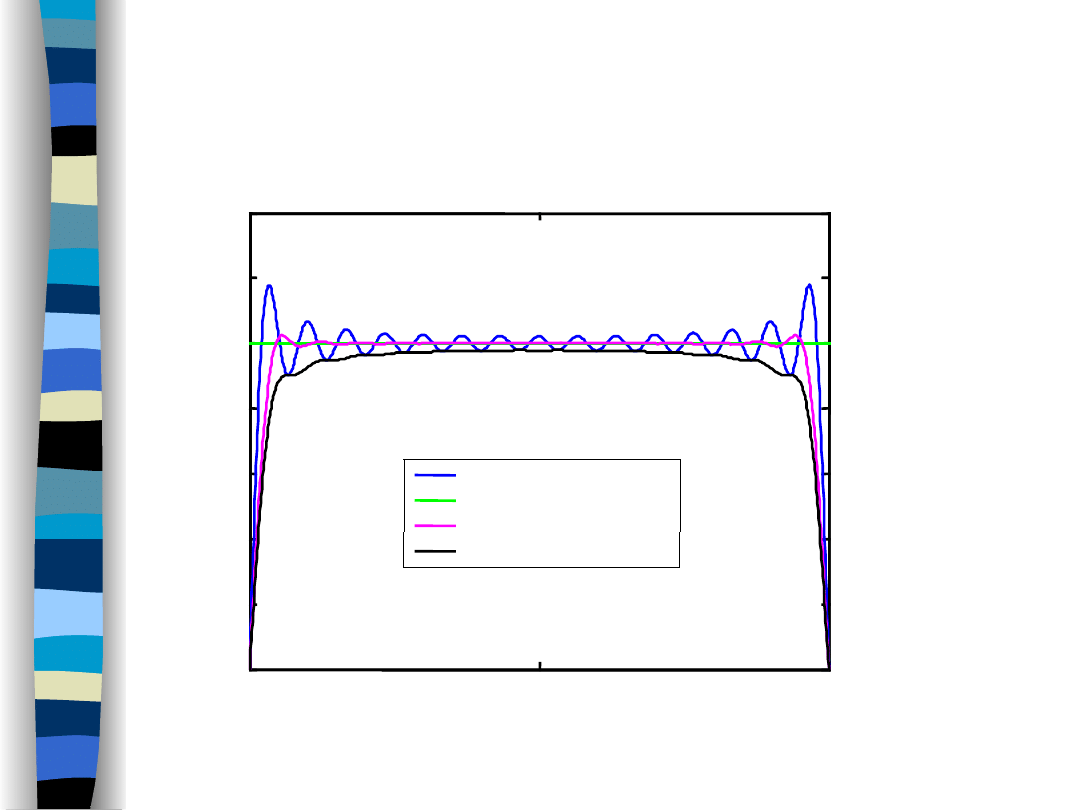
„Signal Theory” Zdzisław Papir
-0.5
0
0.5
0
0.2
0.4
0.6
0.8
1
1.2
1.4
Rectangular window
Rectangular pulse
Fejer window
Lanczos window
Rectangular pulse
15 harmonics
Fejer, Lanczos...
windows
„Signal Theory” Zdzisław Papir
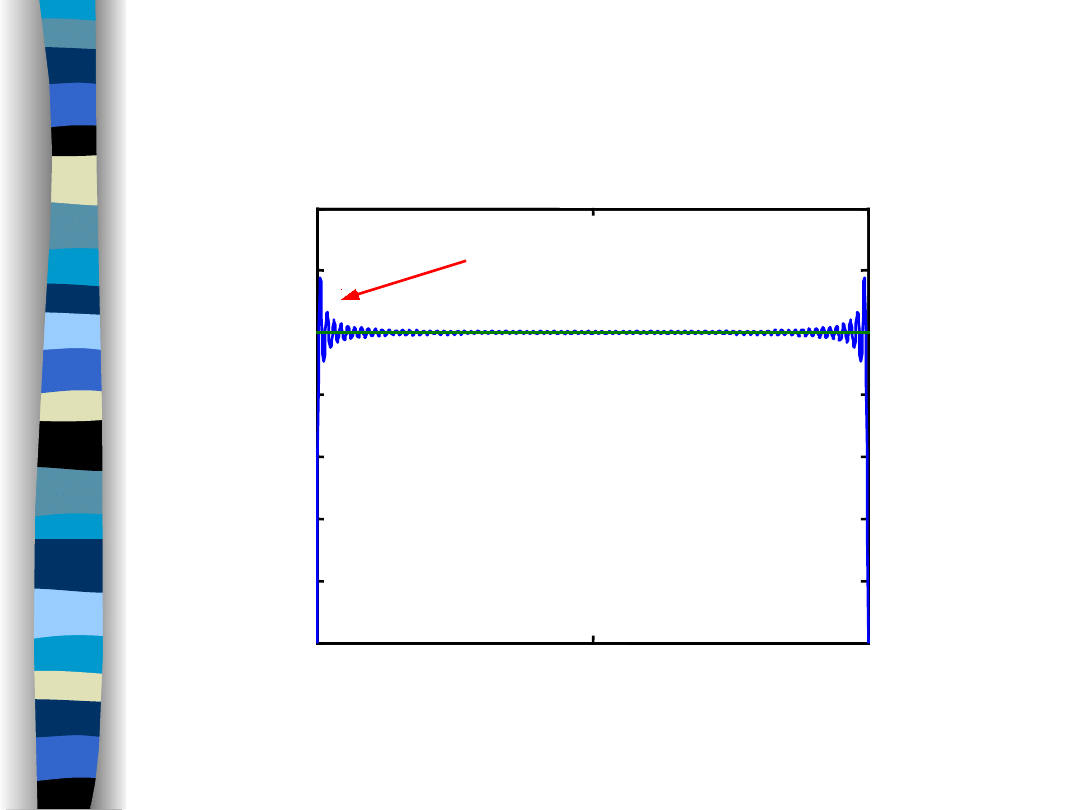
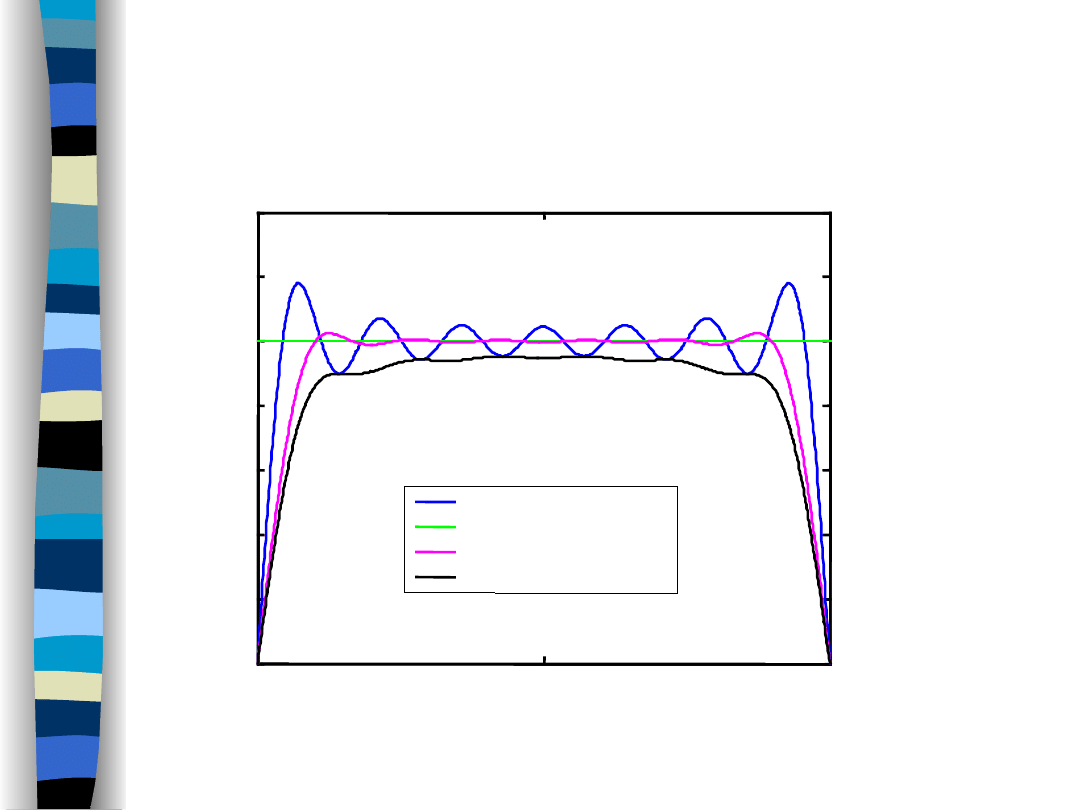
Windows, Gibbs effect
approximation error...
Fejer, Lanczos etc. windows
decrease the Gibbs effect
, however,
at the cost of
increasing of the approximation error
.
The Fourier series (
rectangular window
) is the best signal approximation
in a mean-square sense.
„Signal Theory” Zdzisław Papir
Summary
•
Dirichlet conditions are sufficient conditions for Fourier series
being convergent to a signal; at signal discontinuities they generate
an arithmetic mean of left and right signal limits.
•
The practical condition for Fourier series convergence is limited power
of a signal (mean-square convergence).
•
Mean-square convergence results in the Parseval theorem that splits
total signal power over its harmonics.
•
Fractional power is a tool for evaluating a signal bandwidth.
•
Truncated Fourier series approximation reveals the Gibbs effect being
excessive oscillations close to signal discontinuity points.
•
Fejer, Lanczos etc. windows decrease the Gibbs effect, however,
at the cost of increasing of the approximation error.