„Signal Theory” Zdzisław Papir
•Idea of signal decompostion into
components
•Optimal approximation of the signal
•Orthogonal signals
•Orthogonality and the exponential signal
•Orthogonal system of complex functions
•Orthogonal system of complex exponential
signals
•Exponential Fourier series
•Trigonometric Fourier series
•Frequency characteristics
•Joseph Fourier
•Summary
Decompostion of
signals
Fourier series
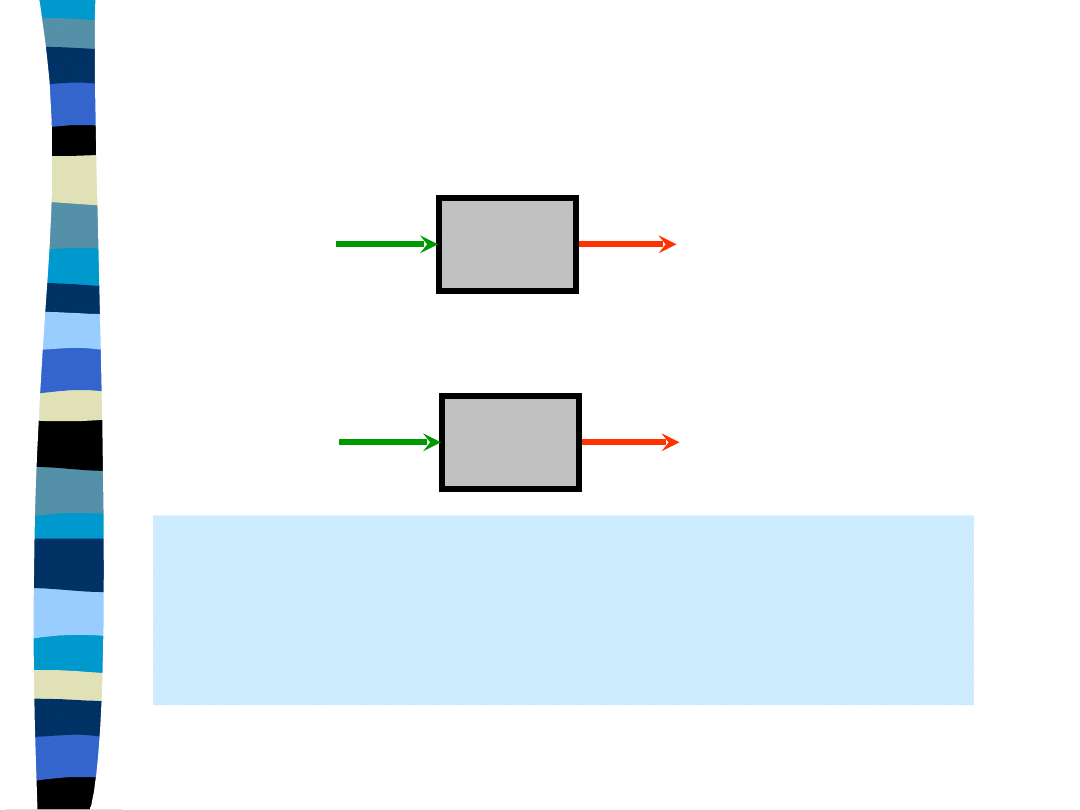
Idea of signal
decompostion
into components
„Signal Theory” Zdzisław Papir
TILS
st
e
st
e
s
H
t
y
TILS
n
t
s
n
n
e
X
t
x
t
s
n
n
n
n
e
s
H
X
t
y
The decompostion of a signal x(t) into
exponential components X
n
exp(s
n
t) let
us to calculate a TILS response for any
input signal.
Optimal approximation
of the signal
„Signal Theory” Zdzisław Papir
t
cx
t
x
a
2
1
t
t
t
t
cx
t
x
t
x
a
e
• Given: a signal x(t) and its approximating
signal x
a
(t).
• We search for an amplitude cx
a
(t) of the
signal to
provide the best possible approximation:
2
1
2
1
2
2
1
min
min
t
t
a
c
c
dt
t
cx
t
x
t
t
e
Solution
2
1
2
1
2
2
1
min
min
t
t
a
c
c
dt
t
cx
t
x
t
t
e
0
2
2
0
2
2
1
1
2
2
1
1
2
2
1
2
2
2
2
1
2
t
t
a
a
t
t
t
t
a
a
dc
d
t
t
dt
t
cx
t
x
t
x
dc
e
d
dt
t
x
c
t
x
t
cx
t
x
dc
e
d
2
1
2
1
)
(
)
(
)
(
2
t
t
a
t
t
a
dt
t
x
dt
t
x
t
x
c
„Signal Theory”
Zdzisław
Papir
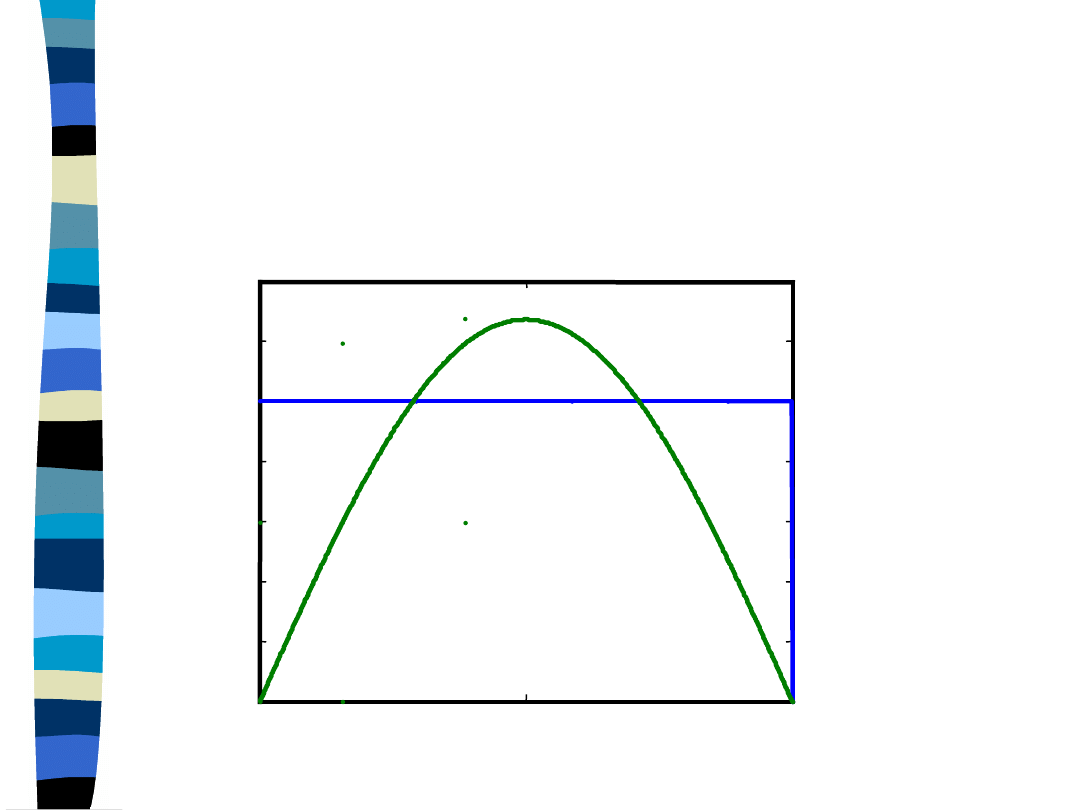
Approximation of the
rectangular signal with the first
harmonic
-0.5
0
0.5
0
0.2
0.4
0.6
0.8
1
1.2
1.4
time
y(t) = (4/pi) *
cos(pi*t)
„Signal Theory” Zdzisław Papir
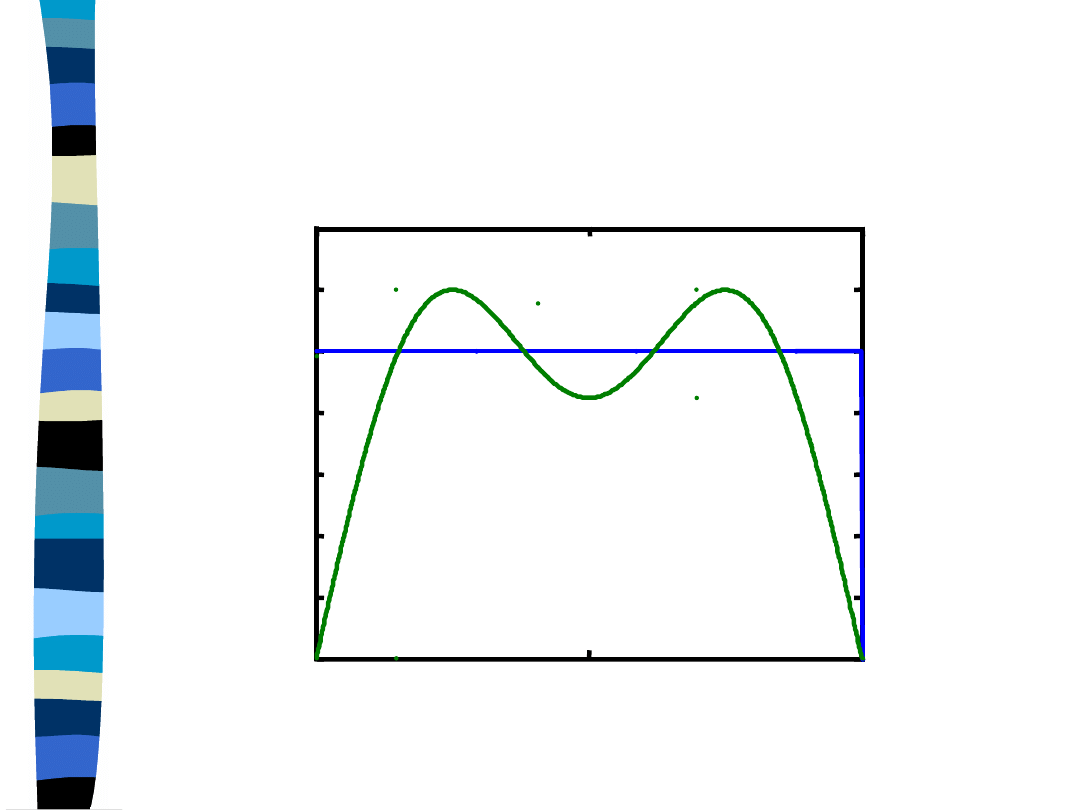
Approximation of the
rectangular signal with the first
and third harmonic
-0.5
0
0.5
0
0.2
0.4
0.6
0.8
1
1.2
1.4
time
y=(4/pi) * cos(pi*t) - (4/3pi) * cos(3*pi*t)
„Signal Theory” Zdzisław Papir
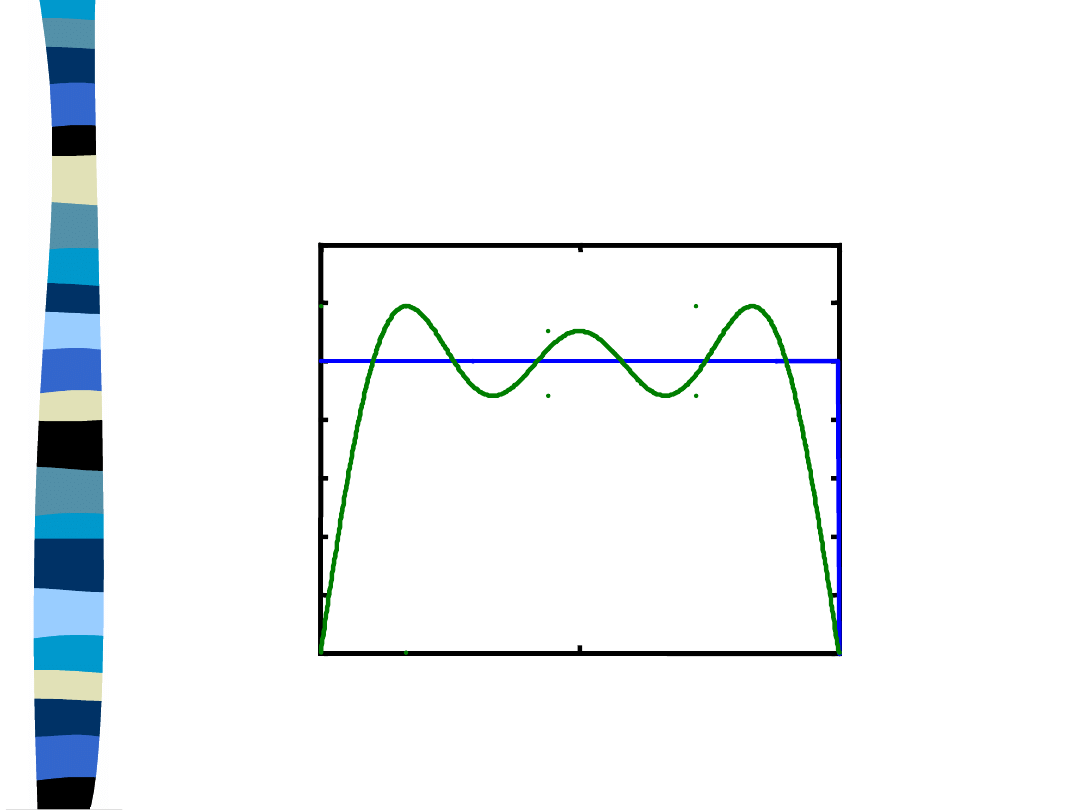
Approximation of the rectangular
signal with the first, third and
fifth harmonic
-0.5
0
0.5
0
0.2
0.4
0.6
0.8
1
1.2
1.4
time
y = (4/pi) * cos(pi*t) - (4/3pi) * cos(3*pi*t) +
+ (4/5pi) * cos(5*pi*t)
„Signal Theory” Zdzisław
Papir
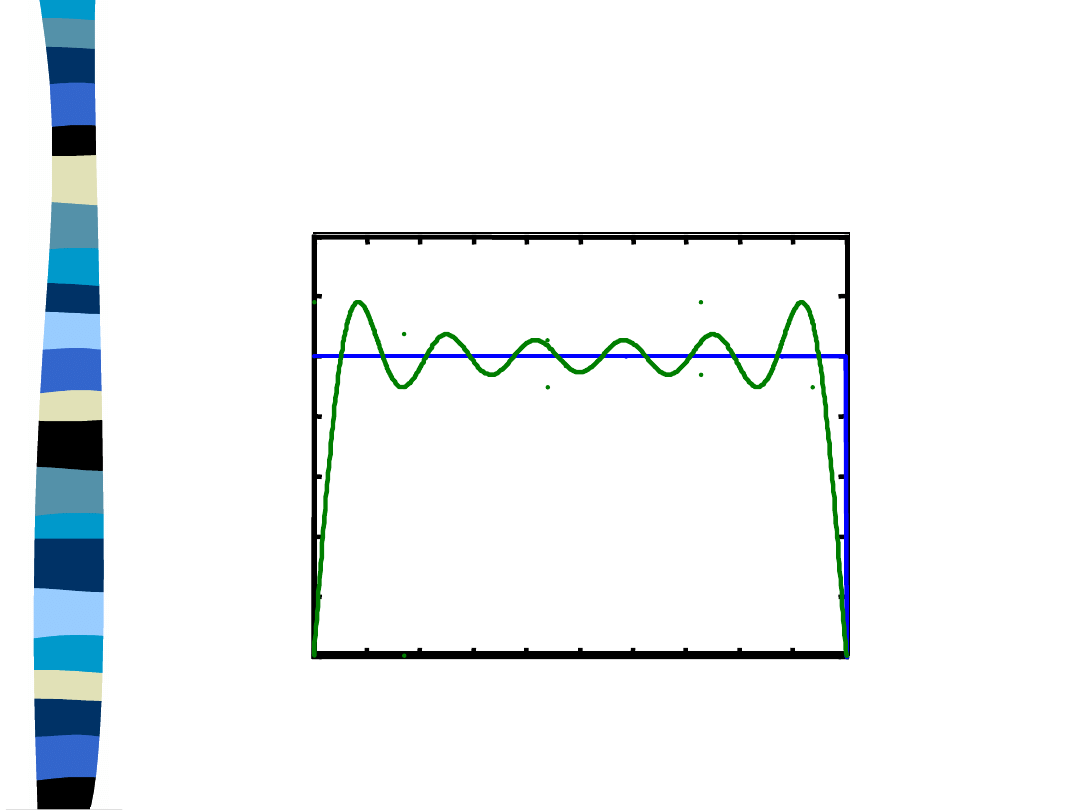
Approximation of the
rectangular signal with the first
eleven harmonics
-0.5 -0.4 -0.3 -0.2 -0.1
0
0.1
0.2
0.3
0.4
0.5
0
0.2
0.4
0.6
0.8
1
1.2
1.4
time
Approximation with first 11 harmonics
„Signal Theory” Zdzisław Papir
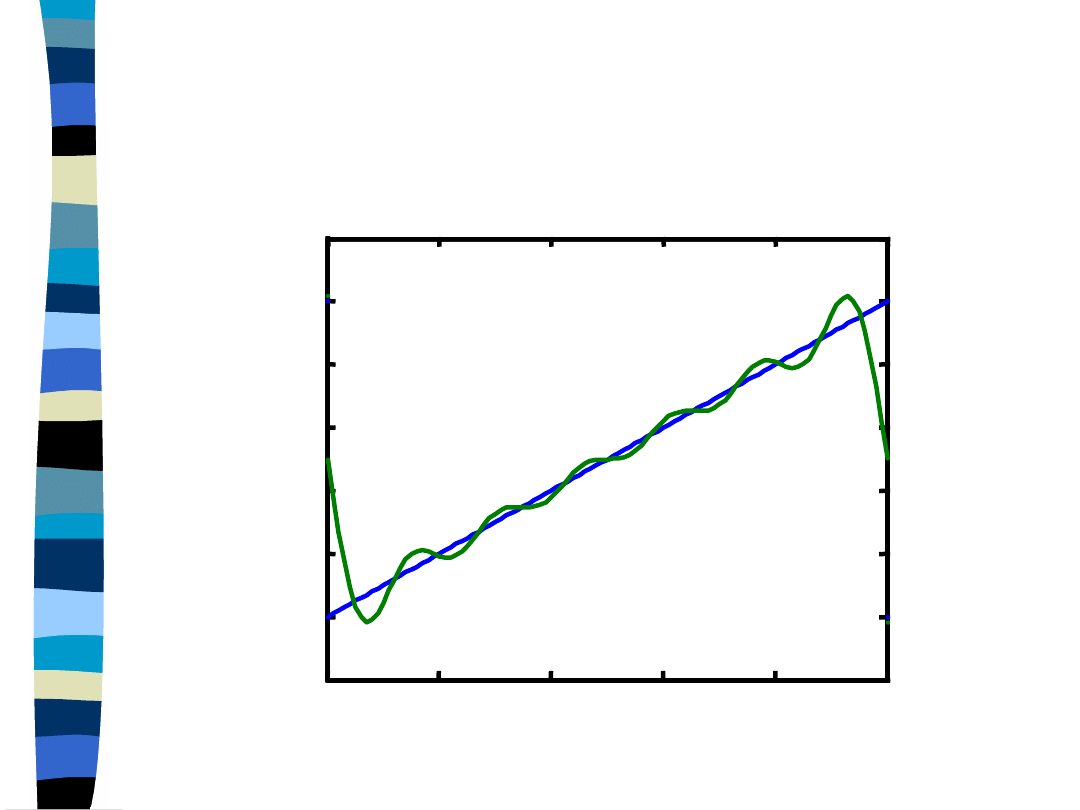
Approximation of the triangular
pulse with the first six
harmonics
0
0.2
0.4
0.6
0.8
1
-0.2
0
0.2
0.4
0.6
0.8
1
1.2
czas t
„Signal Theory” Zdzisław Papir
Orthogonal signals
)
(
),.....,
(
),
(
2
1
t
g
t
g
t
g
K
)
(
0
)
(
,
2
1
t
g
t
g
dt
t
g
t
g
n
m
t
t
n
m
n
m
2
1
,
t
t
t
t
g
n
n
R
2
1
2
2
,
t
t
n
n
n
G
dt
t
g
„Signal Theory” Zdzisław Papir
Orthogonal signals
)
(
.....
)
(
)
(
)
(
2
2
1
1
t
g
c
t
g
c
t
g
c
t
x
K
K
K
n
n
n
a
t
g
c
t
x
1
)
(
)
(
2
1
1
2
1
1
2
1
)
,....
(
2
)
,....
(
min
min
t
t
a
t
t
c
c
c
c
dt
t
x
t
x
e
n
n
„Signal Theory” Zdzisław Papir
Optimal
approximation
2
1
1
2
1
1
2
1
)
,....
(
2
)
,....
(
min
min
t
t
a
t
t
c
c
c
c
dt
t
x
t
x
e
K
K
0
....
2
2
2
1
2
K
dc
e
d
dc
e
d
dc
e
d
K
n
G
dt
t
g
t
x
dt
t
g
dt
t
g
t
x
c
n
t
t
n
t
t
n
t
t
n
n
,
2
,
1
)
(
)
(
)
(
)
(
)
(
2
2
2
1
2
1
2
1
„Signal Theory” Zdzisław Papir
Minimum approximation
error
0
lim
0
1
0
1
2
,
1
2
2
,
2
1
2
2
2
1
1
2
2
2
1
2
1
e
G
c
dt
t
x
t
t
e
dt
t
g
c
t
x
t
t
e
K
K
K
n
n
n
K
const
t
t
t
t
K
n
n
n
1
n
n
n
t
g
c
t
x
Extending the lenght of the orthogonal
approximation makes the
approximation error decreasing.
Infinite long orthogonal approximation
provides the exact orthogonal
reperesentation of a signal.
„Signal Theory” Zdzisław Papir
Orthogonality and the exponential
signal
TILS
n
t
s
n
n
e
X
t
x
t
s
n
n
n
n
e
s
H
X
t
y
Is it possible to calculate an orthogonal
exponential representation of a given
signal?
• simple calculation of the representation
coefficients;
• simple description of the signal transfer in
the TILS.
1
2
0
0
1
2
2
,
2
0
,
,
,
,
0
2
1
2
1
2
1
2
1
t
t
n
t
t
dt
e
dt
e
j
s
j
s
s
s
dt
e
dt
e
e
e
e
n
n
m
t
t
t
j
t
t
t
s
s
n
n
m
m
n
m
t
t
t
s
s
t
s
t
t
t
s
t
s
t
s
n
m
n
m
n
m
n
m
n
m
R
„Signal Theory” Zdzisław Papir
Orthogonal system of complex
functions
2
1
2
1
*
1
2
2
1
2
2
1
1
t
t
a
a
t
t
a
dt
t
x
t
x
t
x
t
x
t
t
dt
t
x
t
x
t
t
e
)
(
),.....,
(
),
(
2
1
t
g
t
g
t
g
K
)
(
0
)
(
,
2
1
*
t
g
t
g
dt
t
g
t
g
n
m
t
t
n
m
n
m
2
1
,
t
t
t
t
g
n
n
C
2
1
2
1
2
*
2
,
t
t
t
t
n
n
n
n
n
G
dt
t
g
t
g
dt
t
g
K
n
G
dt
t
g
t
x
c
n
t
t
n
n
,
2
,
1
)
(
)
(
2
*
2
1
K
n
n
n
a
t
g
c
t
x
1
„Signal Theory” Zdzisław Papir
Orthogonal system of
complex exponential
signals
m
n
T
m
n
dt
e
e
e
e
T
t
t
t
t
n
e
T
t
t
t
jm
t
jn
t
jm
t
jn
t
jn
,
,
0
2
,
,
2
,
1
,
0
,
0
0
o
o
o
o
o
*
0
0
0
0
„Signal Theory” Zdzisław Papir
Orthogonal system of
complex exponential
signals
T
t
t
T
t
t
T
t
t
t
m
n
j
T
t
t
t
jm
t
jn
tdt
m
n
j
tdt
m
n
dt
e
dt
e
e
m
n
0
0
0
0
0
0
0
0
0
0
0
0
sin
cos
:
0
0
)
(
*
T
t
t
T
t
t
t
n
n
j
T
t
t
t
jn
t
jn
T
dt
dt
e
dt
e
e
m
n
0
0
0
0
0
0
0
0
0
)
(
*
:
„Signal Theory” Zdzisław Papir
Exponential Fourier
series
T
T
t
t
t
e
X
t
x
n
t
jn
n
2
,
)
(
0
0
0
0
T
t
t
t
jn
n
dt
e
t
X
T
X
0
0
0
)
(
1
The exponential Fourier series represents a signal as
a composition of complex harmonic signals with
different amplitudes.
„Signal Theory” Zdzisław Papir
Trigonometric Fourier
series
Fourier series coefficients of a real
signal meet the property:
*
n
n
X
X
Exponential form of the Fourier
series coefficent:
n
j
n
n
e
X
X
n
n
n
t
n
X
X
t
x
0
1
0
cos
2
The trigonometric Fourier series represents a signal as a
compostion of real harmonic signals with different
amplitudes and initial phases.
„Signal Theory” Zdzisław Papir
Trigonometric Fourier
series
1
0
0
0
0
1
0
sin
sin
2
cos
cos
2
cos
2
n
n
n
n
n
n
n
n
t
n
X
t
n
X
X
t
x
t
n
X
X
t
x
n
a
n
b
2
0
a
1
0
0
0
sin
cos
2
n
n
n
t
b
t
n
a
a
t
x
T
T
n
n
T
tdt
t
x
T
b
tdt
t
x
T
a
dt
t
x
T
a
0
0
0
0
0
0
sin
2
cos
2
1
„Signal Theory” Zdzisław Papir
Periodicity of the Fourier
series
t
x
e
e
X
e
X
T
t
x
T
t
t
t
e
X
t
x
jn
n
t
jn
n
n
T
t
jn
n
n
t
jn
n
2
0
0
0
0
0
,
)
(
A periodicity of the Fourier series generates a
periodic extension of the x(t) signal in the t
0
< t < t
0
+ T interval.
„Signal Theory” Zdzisław Papir
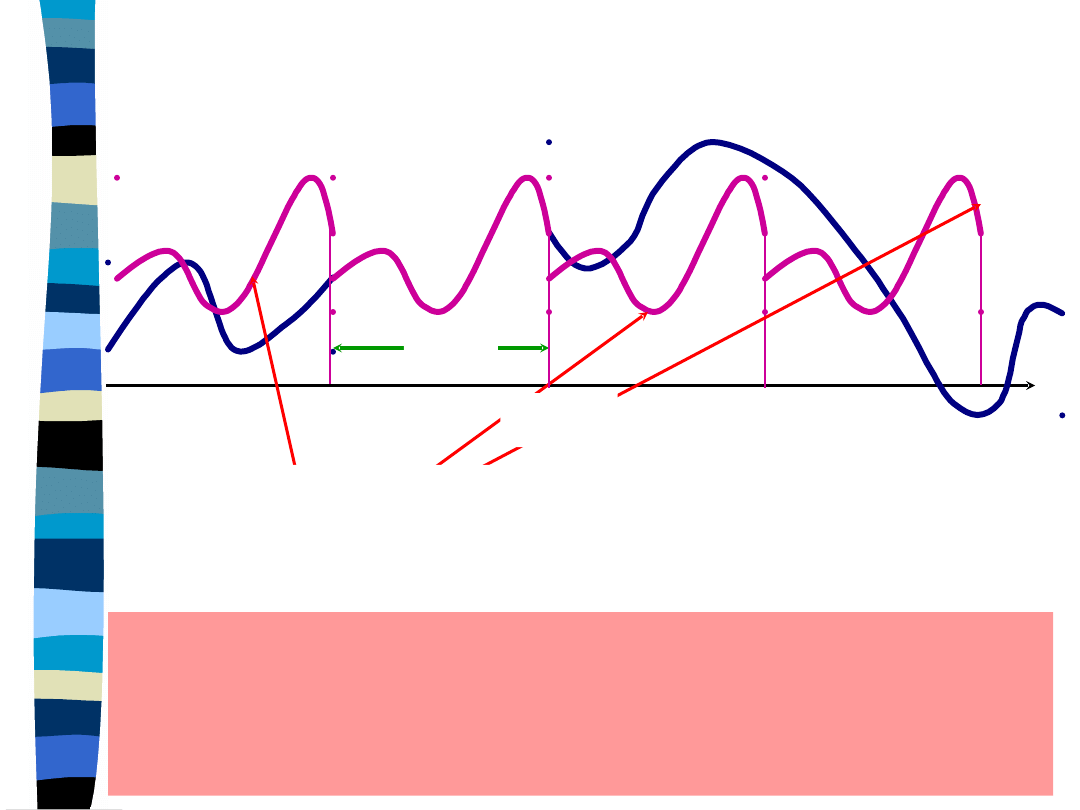
Periodicity of the Fourier
series
t
-T/2
x(t)
Periodical extension of a signal
by the Fourier series
+T/2
The trigonometric Fourier series exactly fits
a signal provided the signal is periodic and
an expansion interval and a period are
equal.
„Signal Theory” Zdzisław Papir
Frequency
characteristics
n
n
n
n
t
jn
n
t
n
j
X
e
X
t
x
0
exp
)
(
0
Amplitude-frequency characteritics:
Phase-frequency characteristics:
2
,
1
,
0
,
0
n
n
n
n
2
,
1
,
0
,
0
n
n
X
X
n
n
„Signal Theory” Zdzisław Papir
Frequency characteristics
Amplitude-frequency characteristics is an
even function:
0
0
n
X
n
X
n
n
Phase-frequency characteristics is an
odd function:
0
0
n
n
n
n
Fourier series coefficients of a real
signal meet the property:
*
n
n
X
X
Exponential form of the Fourier
series coefficent:
n
j
n
n
e
X
X
„Signal Theory” Zdzisław Papir
Frequency characteristics
2
2
T
t
0
,
1
0
,
0
2
sgn
0
2
n
n
n
n
X
e
n
e
e
n
e
t
x
n
n
jnt
n
j
n
n
jnt
j
0
,
2
0
,
2
n
n
n
2
8
6
4
„Signal Theory” Zdzisław Papir
Joseph Fourier
French physicist and mathematician
1768 - 1830
1798 – journey to Egypt with
Napoleon
1807 – French Science Academy
meeting; J. Fourier presents a
trigonometric series
The works on Fourier series led to many
mathematic discoveries - Riemann i
Lebesgue integrals, power of a set, different
kinds of functional series convergence and
generalization of a function and
differentiation definitions.
„Signal Theory” Zdzisław Papir
Summary
•
Decomposition of a given x(t) signal into exponential components
X
n
exp(s
n
t) let us to calculate the TILS response for any input signal.
•
Minimization of a mean-square error (in the integral sense)
let us to calculate the optimal approximation of a signal.
• Approximation gets enhanced along with the growing number
of approximating signals.
•
Orthogonality (in the integral sense) of the approximating signals
significantly simplifies calculation of an optimal approximation.
• Extending the orthogonal approximation makes an approximation
error decreasing. The infinite long orthogonal approximation leads
to the exact orthogonal representation of a signal.
• The orthogonal system of the exponential signals may be designed
using the imaginary exponent values.
• The trigonometric Fourier series represents a signal as a
compostion of harmonic signals with different
amplitudes and initial phases
.
•
The exponential Fourier series represents the spectral distribution
only for the periodical signals.
„Signal Theory” Zdzisław Papir