C 04
1
Zadanie 4.1
W linii współosiowej o promieniach a > b i wypełnieniu
dielektrykiem bezstratnym o ε
r
= 4 rozchodzi się fala
bieżąca. Amplituda prądu w przewodzie wewnętrznym
wynosi I
0
.
Obliczyć amplitudę natężenia pola elektrycznego przy
przewodzie
zewnętrznym.
Zapisać pełne wyrażenia na rzeczywiste wektory pól
w tej
linii dla częstotliwości f = 10 GHz.
Uwaga: pozostaje dowolność wyboru kierunku propagacji
fali oraz
fazy.
E i H
r r
C 04
2
Zadanie 4.2
Zapisać rzeczywiste wektory pól
dla
bezstratnej linii współosiowej o promieniach a i 3a, zwartej
w płaszczyźnie z = a. Amplituda pola całkowitego
wynosi a, a częstotliwość fali .
Uwaga: parametr a wyrażony jest w jednostkach SI,
odpowiednich
dla każdej z powyższych wielkości.
E i H( , , , , , , , )
z
t a
r j
w
e m
r r
E
r
6
c
f
a
=
C 04
3
Zadanie 4.3
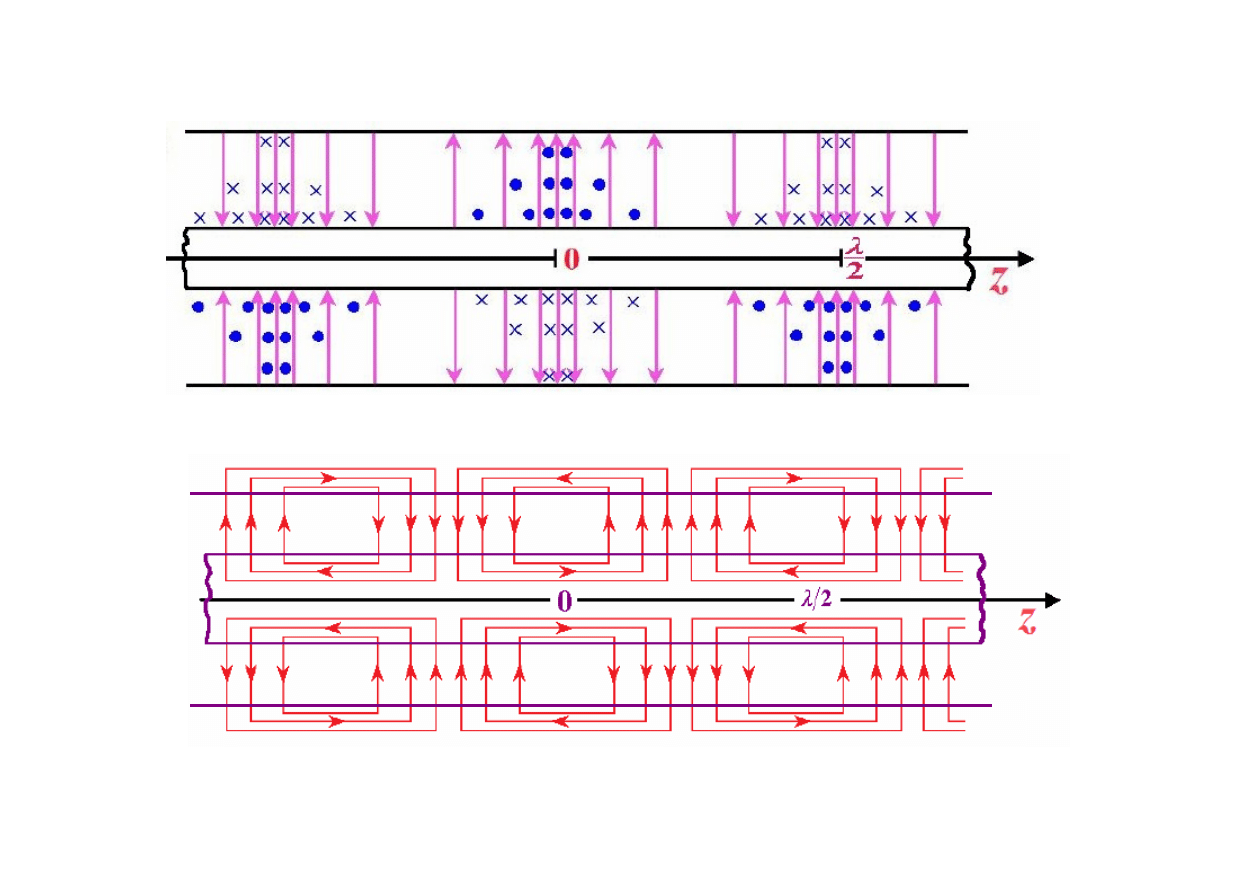
Naszkicować rozkłady linii pola elektromagnetycznego oraz
prądów przewodzenia i przesunięcia w przekroju wzdłużnym
linii współosiowej dla:
A) fali bieżącej rozchodzącej się w kierunku +z
B) fali stojącej.
Szkice sporządzić dla chwili t = 0, zakładając że w tej chwili w
płaszczyźnie z = 0, pole E
ρ
osiąga swoją wartość maksymalną.
Uwaga: Prawidłowe szkice dla przypadku A są pokazane na
rysunkach.
Pełna odpowiedź wymaga jeszcze nazwania
poszczególnych
linii. Następnie należy wykonać szkice dla punktu B.
C 04
4
Zadanie 4.3 (2)
C 04
5
Zadanie 4.4
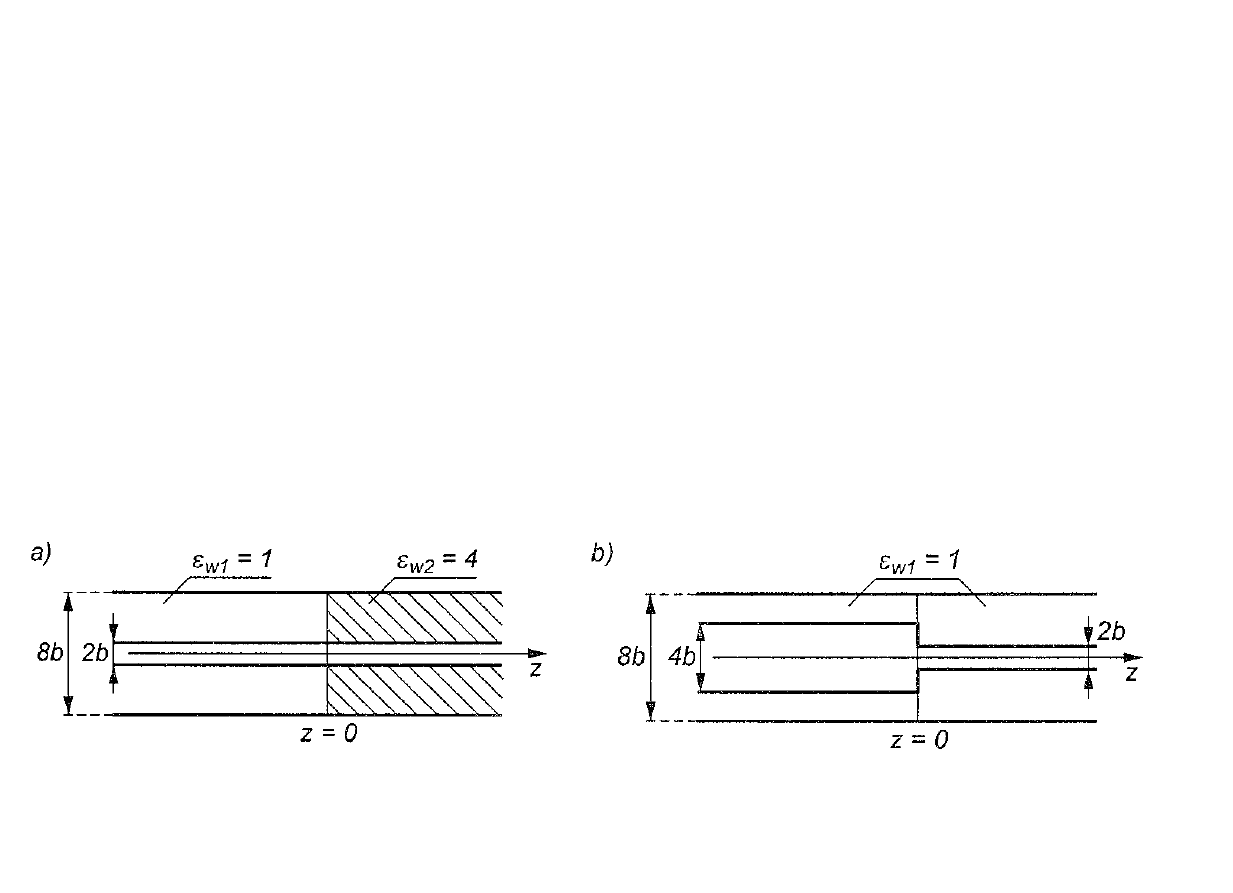
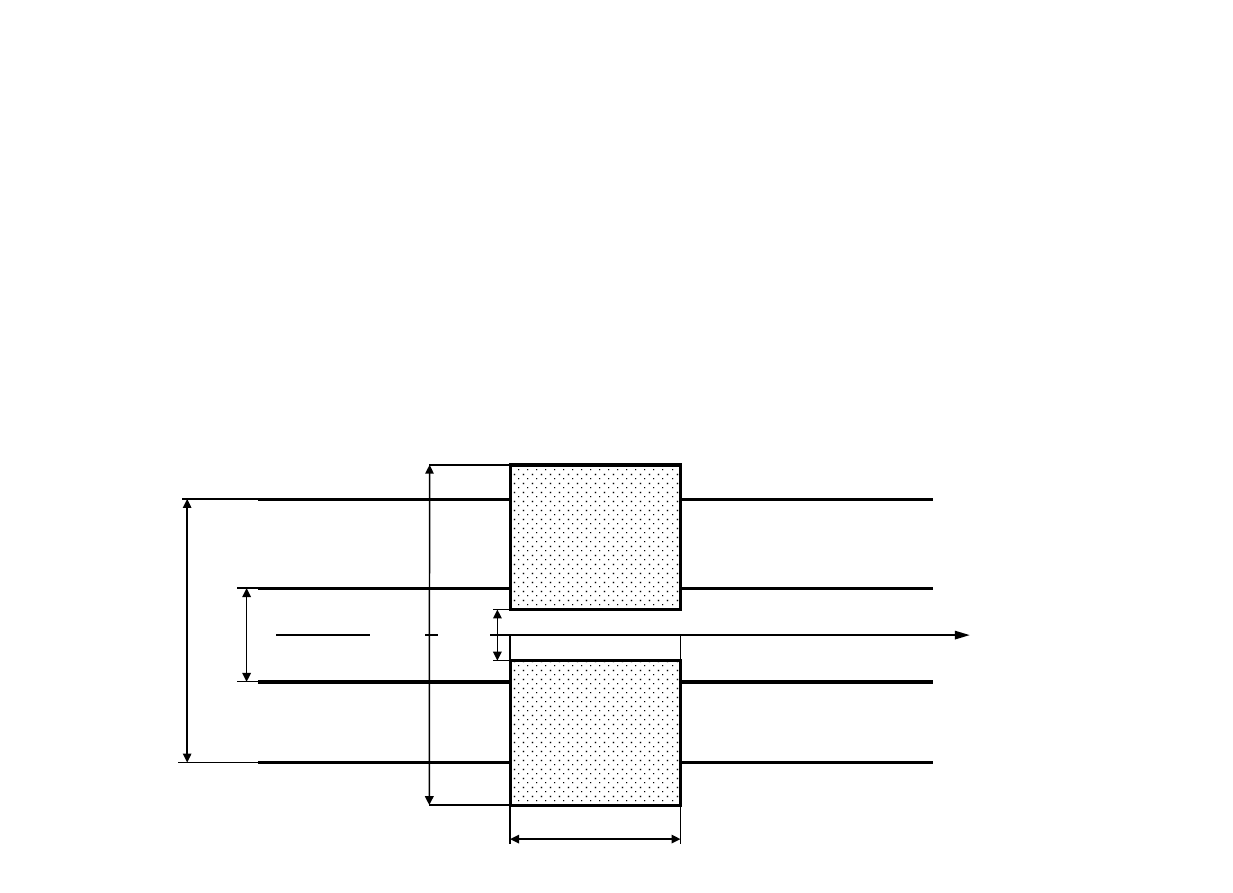
Na rysunku 1 przedstawiono linie współosiowe w przekroju
wzdłużnym.
Obliczyć współczynnik odbicia w płaszczyźnie z = 0.
Pomijamy niejednorodności powstałe w pobliżu płaszczyzny z = 0
wskutek skokowej zmiany wymiarów przewodów (rys. 1b).
Podać przykładowe wzory opisujące fale napięcia i prądu
(w postaci zespolonej i rzeczywistej).
Narysować rozkłady amplitud napięcia i prądu.
Rys. 1. Linie współosiowe w przekroju wzdłużnym
C 04
6
Zadanie 4.4 (2)
• Struktura:
• Fala padająca rozchodzi się w kierunku +0z
linia współosiowa 1 dla z < 0 :
wypełniona próżnią
• Dane:
współczynnik odbicia dla z = 0:
linia współosiowa 2 dla z > 0:
wypełniona dielektrykiem o
ε
w2
= 4
2
4
w
e =
• Obliczyć:
b
promień przewodu wewnętrznego linii współosiowych 1 i 2:
12
?
G =
promień przewodu zewnętrznego linii współosiowych 1 i 2:
4
a
b
=
względna przenikalność dielektryka w linii współosiowej 2:
względna przenikalność dielektryka w linii współosiowej 1:
1
1
w
e =
C 04
7
Zadanie 4.4 (3)
Współczynniki fazy w liniach:
1
0
b
b
=
2
2 0
0
2
w
b
e b
b
=
=
1
0
Z
Z
=
0
0
2
2
2
w
Z
Z
Z
e
=
=
Impedancje właściwe ośrodków:
Impedancje charakterystyczne linii współosiowych:
1
C1
ln
60ln4
2
Z
a
Z
b
p
=
=
dla linii współosiowej 1:
dla linii współosiowej 2:
2
C2
ln
30ln4
2
Z
a
Z
b
p
=
=
C2
C1
2
1
12
C2
C1
2
1
1
3
Z
Z
Z
Z
Z
Z
Z
Z
-
-
G =
=
=-
+
+
Współczynnik odbicia dla z = 0:
1
12
1
(0)
(0)
U
U
-
+
G =
C 04
8
Zadanie 4.4 (4)
fala padająca napięcia w linii współosiowej 1:
1
1
0
j z
U
U e
b
-
+
=
1
1
12
0
j z
U
U e
b
-
=G
fala odbita napięcia w linii współosiowej 1:
fala napięcia w linii współosiowej 1:
Fale napięcia w postaci zespolonej:
(
)
1
1
2
1
0
12
1
j z
j
z
U
U e
e
b
b
-
=
+G
fala napięcia w linii współosiowej 2:
(
)
2
2
0
12
1
j z
U
U
e
b
-
=
+G
fala padająca napięcia w linii współosiowej 1:
(
)
1
0
12
1
12
U
cos
arg
U
t
z
w
b
-
=
G
+
+
G
fala odbita napięcia w linii współosiowej 1:
fala napięcia w linii współosiowej 1:
Fale napięcia w postaci rzeczywistej, przyjmując, że U
0
jest rzeczywiste:
fala napięcia w linii współosiowej 2:
[
]
2
0
12
2
12
U
1
cos
arg(1
)
U
t
z
w b
=
+G
-
+
+G
(
)
1
0
1
U
cos
U
t
z
w b
+
=
-
(
)
(
)
[
]
1
0
1
12
1
12
U
cos
cos
arg
U
t
z
t
z
w b
w
b
=
-
+G
+
+
G
C 04
9
Zadanie 4.4 (5)
• Struktura:
• Fala padająca rozchodzi się w kierunku +0z
linia współosiowa 1 dla z < 0 : promienie przewodów a
1
, b
1
• Dane:
współczynnik odbicia dla z = 0:
• Obliczyć:
1
2
b
b
=
promień przewodu wewnętrznego linii współosiowej 1:
12
?
G =
promień przewodu zewnętrznego linii współosiowej 1:
1
4
a
b
=
linia współosiowa 2 dla z > 0 : promienie przewodów a
2
, b
2
obie linie współosiowe wypełnione próżnią
2
b
b
=
promień przewodu wewnętrznego linii współosiowej 2:
promień przewodu zewnętrznego linii współosiowej 2:
2
4
a
b
=
C 04
10
Zadanie 4.4 (6)
Współczynnik fazy w liniach:
1
2
0
b
b
b
=
=
1
2
0
Z
Z
Z
=
=
Impedancja właściwa ośrodka w liniach:
Impedancje charakterystyczne linii współosiowych:
0
1
C1
1
ln
60ln2
2
Z
a
Z
b
p
=
=
dla linii współosiowej 1:
dla linii współosiowej 2:
C2
C1
12
C2
C1
ln2
1
3ln2 3
Z
Z
Z
Z
-
G =
=
=
+
Współczynnik odbicia dla z = 0:
1
12
1
(0)
(0)
U
U
-
+
G =
0
2
C2
2
ln
60ln4
2
Z
a
Z
b
p
=
=
C 04
11
Zadanie 4.5
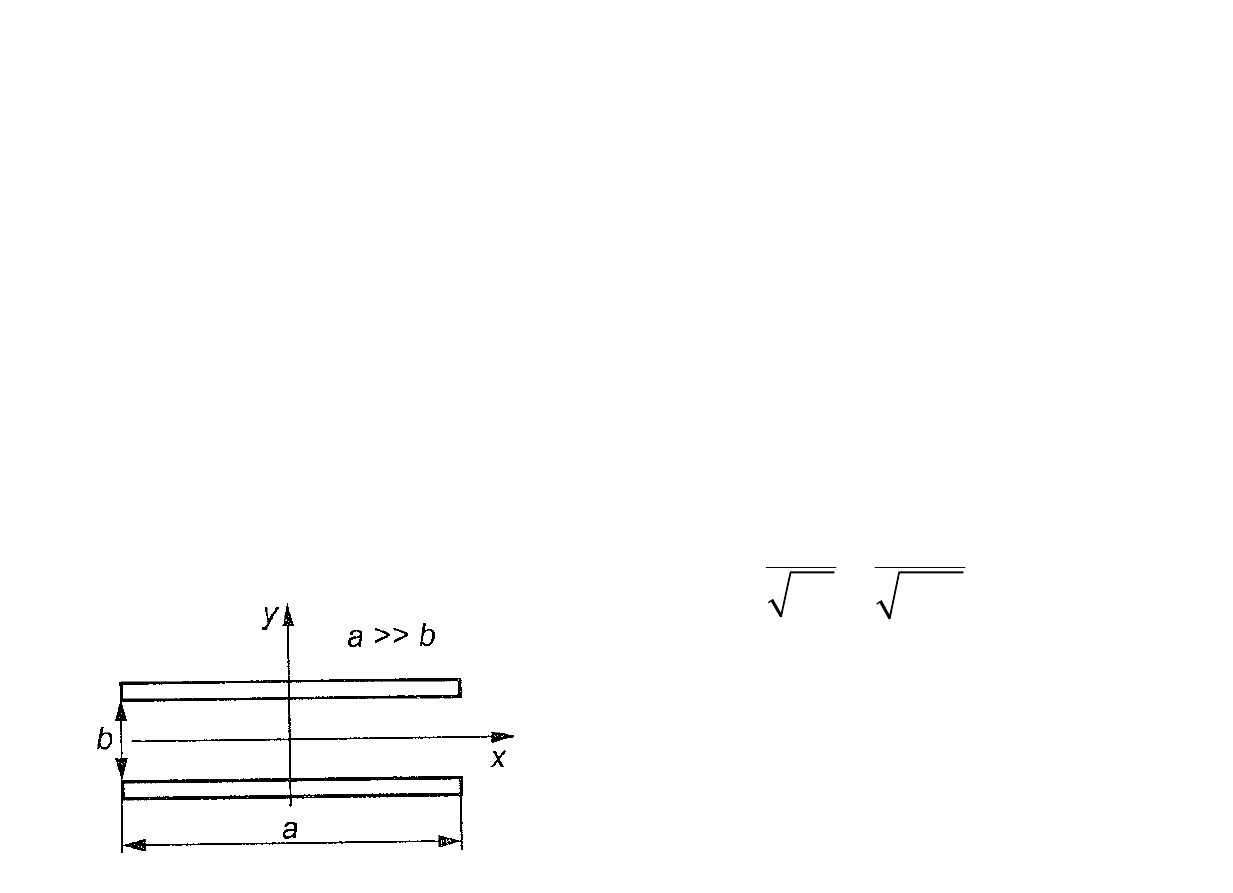
Rozważana jest bezstratna linia płasko-równoległa o przekroju
pokazanym na rys. 2, która wypełniona jest dielektrykiem
o parametrach ε, μ.
Zakładając, że całkowite pole elektromagnetyczne jest jednorodne
i mieści się w prostokącie o bokach a i b między przewodami
linii (tzn. że pola poza tym obszarem pomijamy), wyprowadzić wzory
na indukcyjność jednostkową L
1
oraz pojemność jednostkową C
1
tej prowadnicy falowej.
Sprawdzić, że jest spełniona zależność:
1 1
1
1
v
LC
me
=
=
Rys. 2. Linia płasko-równoległa
w przekroju poprzecznym.
C 04
12
Zadanie 4.6
Na rysunku przedstawiono przekrój wzdłużny struktury zawierającej
powietrzną linię współosiową o promieniach a = 4 mm , b = 2 mm oraz
podporę dielektryczną o względnej przenikalności elektrycznej ε
wd
= 4,
grubości d i promieniach a
d
, b
d
.
Wyznaczyć promienie i grubość podpory, dla których współczynnik
odbicia w płaszczyźnie z = - d wynosi zero dla dowolnej częstotliwości.
Pomijamy niejednorodności powstałe w strukturze wskutek skokowych
zmian wymiarów przewodów.
Narysować rozkłady amplitud napięcia i prądu w strukrurze.
2a
0
z =
z
2b
2
d
a 2
d
b
d
1
w
e =
4
wd
e =