Twierdzenie o próbkowaniu

H. Nyquist 1928, V.A. Kotielnikow 1933, J.M. Whittaker

1935, C.E. Shannon 1949

Próbkowanie sygnałów ciągłych

Ewa Hermanowicz













n

nT

x

n

x

c

)

(

]

[

Próbkowanie okresowe (równomierne) sygnału

)

(t

x

c

– okres próbkowania w sekundach
– częstotliwoś

ć

próbkowania w Hz

T

F

p

/

1



T

)

(t

x

c

T

)

(

]

[

nT

x

n

x

c



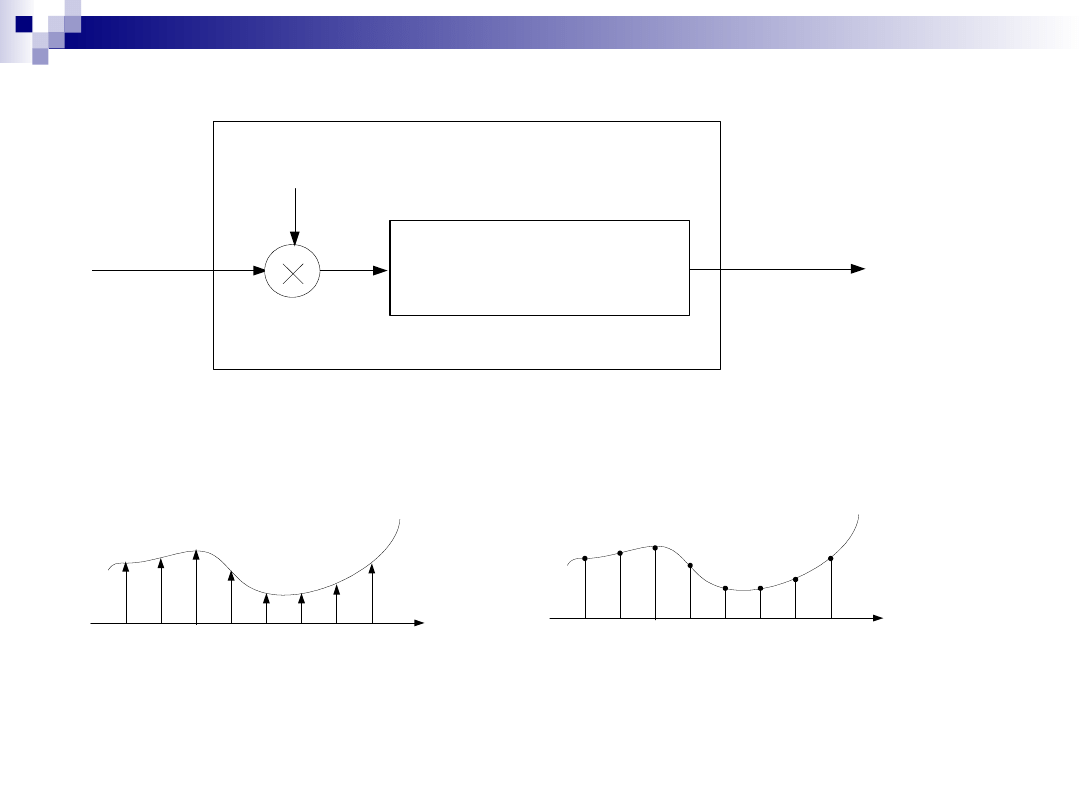
C/D

Schemat blokowy reprezentujący idealny
przetwornik (konwerter) czasu ciągłego na czas
dyskretny – jest to idealny system próbkujący.

Układ fizyczny może by

ć

zrealizowany na różne sposoby.

W ogólności operacja próbkowania nie jest odwracalna, tzn. nie
zawsze można odtworzy

ć

na podstawie .

Aby zapewni

ć

odwracalnoś

ć

, sygnał próbkowany musi

spełnia

ć

twierdzenie o próbkowaniu.

)

(t

x

c

]

[n

x

)

(t

x

c

Twierdzenie Nyquista o próbkowaniu

Niech będzie sygnałem o ograniczonym widmie, tzn.

Wówczas sygnał jest jednoznacznie określony przez ciąg swoich
próbek

jeżeli

lub inaczej (częstotliwości w Hz): ,

czyli jeżeli częstotliwoś

ć

próbkowania jest co najmniej dwukrotnie

większa od maksymalnej częstotliwości w widmie sygnału .
Wówczas mówimy o próbkowaniu prawidłowym.

)

(t

x

c



















s

rad

dla

0

)

(

M

c

j

X

)

(t

x

c



,

1

,

0

),

(

]

[







n

nT

x

n

x

c

M

p

p

F

T











2

2

2





M

p

F

F

2



)

(t

x

c

Minimalna częstotliwoś

ć

próbkowania, przy której można jeszcze

odtworzy

ć

sygnał bez zniekształceń, tzn. częstotliwoś

ć

, nazywa się szybkością Nyquista. Odpowiadający jej

maksymalny okres próbkowania

nazywa się przedziałem Nyquista. Częstotliwoś

ć

Nyquista to

maksymalna częstotliwoś

ć – –

w widmie sygnału .

Terminologia USA

–

Nyquist frequency

–

Nyquist rate

–

Nyquist interval

)

(t

x

c

)

(t

x

c

M

F

M

F

M

F

2

M

F

2

1

M

p

F

F

2



p

F

T

/

1



)

(t

x

c

Konwersja sekwencji

impulsów na ciąg dyskretny

)

(

]

[

nT

x

n

x

c



C/D

k

przetworni

-

e

Próbkowani

)

(t

T



)

(t

x

c



T



C/D

k

przetworni

-

e

Próbkowani



)

(t

x

p



czas



t



0 T T

2 T

3

T

3



T

2



)

(t

x

c



1





]

[n

x



próbki

numer



n



0 1 2 3

3



2



4



Reprezentacja operacji

próbkowania jako procesu

dwustopniowego

Reprezentacja operacji

próbkowania jako procesu dwustopniowego

(dla potrzeb czytelnego opisu analitycznego)

• mnożenie przez ciąg (sekwencję) impulsów Diraca,

• zamiana sekwencji impulsów na ciąg dyskretny.

Dziedzina czasu

a z właściwości próbkującej delty Diraca (
)

Dziedzina częstotliwości

wówczas















n

c

T

c

p

nT

t

t

x

t

t

x

t

x

)

(

)

(

)

(

)

(

)

(





)

(

)

(

)

(

)

(

0

0

0

t

t

t

x

t

t

t

x























n

c

p

nT

t

nT

x

t

x

)

(

)

(

)

(























dt

e

t

x

t

x

j

X

t

j

c

c

c

)

(

)]

(

[

)

(

F



























k

p

p

T

k

j

t

p

)

(

)

(

)]

(

[







F





























k

p

c

c

p

k

j

X

T

j

j

X

j

X

p

)]

(

[

1

)

(

)

(

2

1

)

(





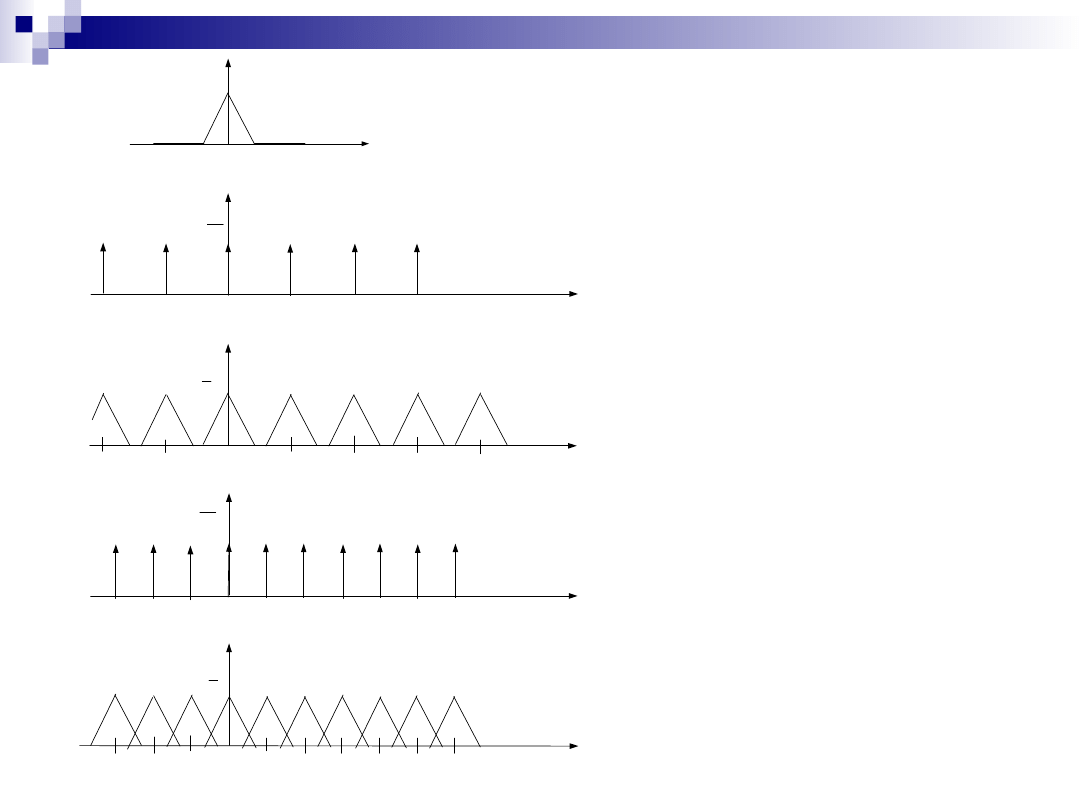
Wniosek: widmo sygnału jest superpozycją

okresowo powtarzających się widm sygnału ciągłego . Kolejne

składniki są poprzesuwane o całkowitą wielokrotnoś

ć

pulsacji próbkowania .

Przyjmijmy, że tak, jak w twierdzeniu

Nyquista, tzn. największą składową w widmie jest

składowa o pulsacji .

)

( 

j

X

p

)

(t

x

p

)

(t

x

c

)

( 

j

X

p

p



M

c

j

X











dla

0

)

(

)

( 

j

X

c

M



)

( 

j

X

p

M







)

( 

j

X

c



0

1

M





0



)

( 



j

p



T



2





0

0

p



p





p



 2

p



2

p



3





T

1

T

1

)

( 

j

X

p

p



p



2

p



p



2

p



3

p



3

p





p





p



 2

p



 2



0

)

( 



j

p



T



2

p



 3

p



4

p



5









p



M

M

p











M

M

p











p





p



2

p



 2

p



3

A. Rozłączne
widma składowe

B. Widma
składowe nie są
rozłączne, ale
nakładają się

M

p







2

M

p







2

Zastosujemy 2 różne
pulsacje próbkowania: A i
B

Rekonstrukcja na podstawie ;

system idealny odtwarzający sygnał ciągły

)

(t

x

c

]

[n

x

)

(

0

t

x

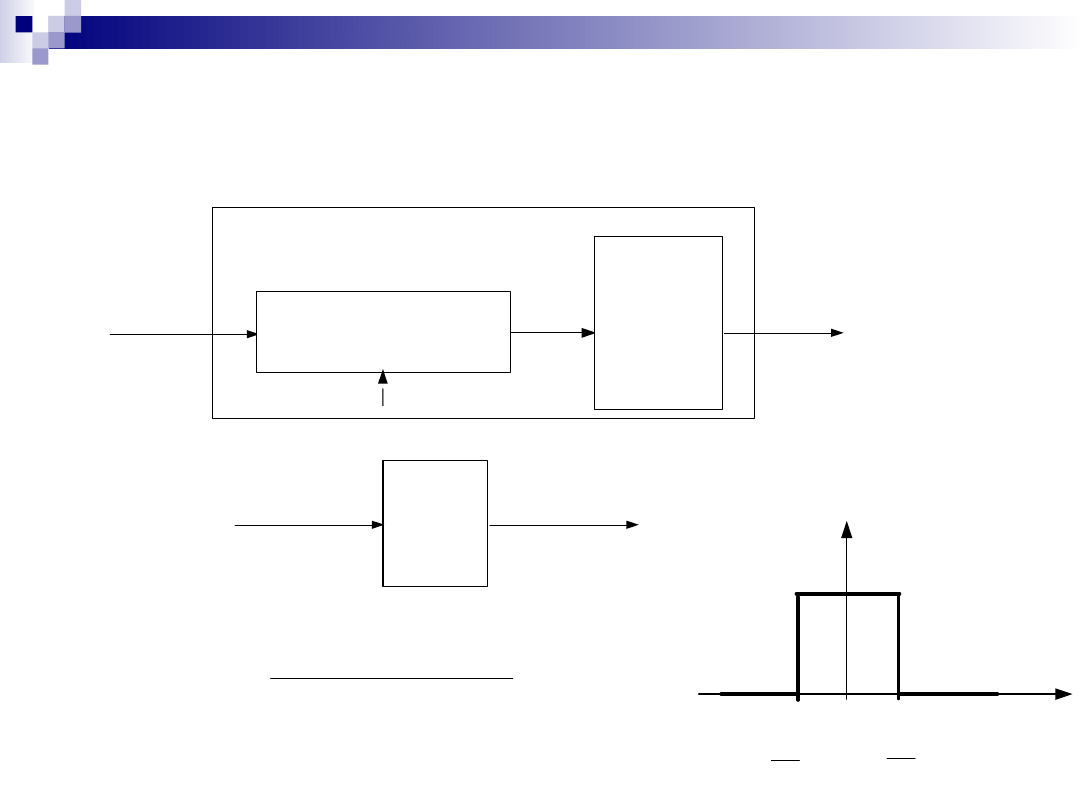
Zamiana ciągu dyskretnego

na sekwencję impulsów

Diraca

]

[n

x

D/C

k

przetworni

-

e

Odtwarzani

)

(t

x

p

Filtr idealny

dolno-

przepustowy

T

)

( 

j

H

d

D/C

]

[n

x

)

(

0

t

x

W systemie idealnym .

)

(

)

(

0

t

x

t

x

c



)

( 

j

H

d

T

T





T



0

















n

T

nT

t

T

nT

t

n

x

t

x

/

)

(

]

/

)

(

sin[

]

[

)

(

0





wzór

interpolacyj

ny

Shannona

Wyprowadzenie wzoru interpolacyjnego Shannona































n

d

n

d

T

nT

t

T

nT

t

n

x

nT

t

h

n

x

t

h

n

x

t

x

/

)

(

]

/

)

(

sin[

]

[

)

(

]

[

)

(

]

[

)

(

0



























T

t

tT

tT

j

H

t

h

d

d

sinc

)

sin(

)]

(

[

)

(

1





F

gdzie

Wówczas

i cały przebieg jest rekonstruowany na
bazie funkcji sinc( ).

 

















0

,

1

0

,

)

sin(

sinc

x

x

x

x

x





)

(

)

(

0

t

x

t

x

c



Twierdzenie o próbkowaniu sygnałów

pasmowych

Jeżeli sygnał analogowy zajmuje pasmo w
Hz, to można go bezbłędnie odtworzy

ć

na podstawie ciągu jego

równoodległych próbek

pod warunkiem, że szybkoś

ć

próbkowania jest co

najmniej dwukrotnie większa od szerokości pasma czyli, gdy
a inaczej , gdzie to odstęp (okres
próbkowania równomiernego) w sekundach, jak poprzednio.

)

,

(

),

(







t

t

x

c

B













n

nT

x

n

x

c

)

(

]

[

T

F

p

/

1



B

B

F

p

2



)

2

/(

1 B

T 

T

)

( 

j

X

c



0

L



U



L





U





B



2

Program wykładu. (około 1 godziny lekcyjnej – 45 min – na

każdy punkt; uwaga – kolejnoś

ć

realizacji poszczególnych

punktów może by

ć

zmieniona celem synchronizacji z

programem

ć

wiczeń).

1. Klasyfikacja sygnałów.

2. Analiza widmowa sygnałów deterministycznych.

Przekształcenie całkowe Fouriera.

3. Właściwości przekształcenia całkowego. Widmo sygnału

analogowego. Twierdzenie o próbkowaniu.

4. Dyskretno-czasowe przekształcenie Fouriera (DTFT).

5. Właściwości przekształcenia DTFT. Widmo sygnału

dyskretnego.

6. Kształtowanie widma przez system liniowy.

7. Dyskretny sygnał zespolony – amplituda, faza i pulsacja

chwilowa.

8. Przekształcenie Hilberta sygnału dyskretnego –

zastosowania.

9. Obwiednia zespolona rzeczywistego dyskretnego sygnału

pasmowego.

10. Konwersja analogowo-cyfrowa.

11. Konwersja cyfrowo-analogowa.

12. Szum kwantyzacji. Model addytywny.

13. Obliczanie stosunku mocy sygnału do szumu kwantyzacji.

14. Równania różnicowe systemów dyskretnych o skończonej

(FIR) i o nieskończonej (IIR) odpowiedzi impulsowej.

15. Schematy strukturalne systemów dyskretnych.

16. Przekształcenie Z.

17. Transmitancja systemu dyskretnego.

18. Systemy dyskretne o skończonej odpowiedzi impulsowej

(FIR).

19. Systemy dyskretne o nieskończonej odpowiedzi impulsowej

(IIR).

20. Realizowalnoś

ć

systemu dyskretnego w czasie rzeczywistym,

a przyczynowoś

ć

.

21. Stabilnoś

ć

. Minimalnofazowoś

ć

systemu dyskretnego.

22. Podstawy filtracji cyfrowej. Filtr FIR – algorytm, struktura.

23. Filtr IIR – algorytmy, struktury. Przykłady projektowania

elementarnych filtrów.

24. Dyskretna transformacja Fouriera – DFT.

25. Szybka transformacja Fouriera – FFT. Zastosowania.

26. Powiązania transformat.

27. Splot dyskretny liniowy.

28. Splot cykliczny (kołowy). Zastosowania.

29. Wprowadzenie do interpolacji i decymacji.

30. Zastosowania interpolacji i decymacji.

Program

ć

wiczeń.

1. Przekształcenie całkowe Fouriera. Widmo sygnału analogowego.

Przykłady.

2. Przekształcenie dyskretno-czasowe Fouriera (DTFT). Widmo

sygnału dyskretnego. Przykłady.

3. Sygnał zespolony – amplituda, faza i pulsacja chwilowa.

Transformator i filtr Hilberta. Obwiednia zespolona rzeczywistego
dyskretnego sygnału pasmowego. Kształtowanie widma przez
system liniowy. Przykład.

4. Próbkowanie, kwantowanie i kodowanie – przykłady. Konwersja

analogowo-cyfrowa i konwersja cyfrowo-analogowa.

5. Szum kwantyzacji. Obliczanie stosunku mocy sygnału do szumu

kwantyzacji.

6. Przekształcenie Z proste i odwrotne. Przykłady.

7. Systemy dyskretne o skończonej (FIR) i o nieskończonej (IIR)

odpowiedzi impulsowej – porównanie właściwości. Równania
różnicowe – algorytmy. Schematy strukturalne. Transmitancje.

8. Kolokwium.

9. Realizowalnoś

ć

systemu dyskretnego w czasie rzeczywistym, a

przyczynowoś

ć

. Stabilnoś

ć

. Minimalnofazowoś

ć

systemu

dyskretnego. Przykłady.

10. Podstawy filtracji cyfrowej.

11. Dyskretno-czasowa (DTFT), dyskretna (DFT) i szybka (FFT)

transformacja Fouriera – porównanie na przykładzie.

12. Powiązania transformat DTFT, DFT i Z. Przykład.

13. Splot dyskretny liniowy i splot cykliczny (kołowy). Przykłady

zastosowań.

14. Wprowadzenie do interpolacji i decymacji. Zasady i przykład

projektowania interpolatora i decymatora.

15. Kolokwium.

Literatura

[1] T.P. Zieliński: Cyfrowe przetwarzanie sygnałów. Od teorii do
zastosowań. WKŁ Warszawa 2005.

[2] J. Szabatin: Podstawy teorii sygnałów. WKŁ Warszawa 1982 i

następne wydania.

[3] J. Osiowski i J. Szabatin: Podstawy teorii obwodów. WNT
Warszawa,

tom I – 1992, tom II – 1993, tom III – 1995 i dalsze

wydania.

[4] A.V. Oppenheim, R.W. Schafer with J.R. Buck: Discrete-Time
Signal Processing. Prentice Hall 1999 – czytelnia WETI.

[5] J.G. Proakis and P.G. Manolakis: Digital Signal Processing.
Principles,

Algorithms and Applications. Prentice-Hall 1996 –

czytelnia WETI.

[6] S.W. Smith: Cyfrowe przetwarzanie sygnałów. Praktyczny
podręcznik

dla inżynierów i naukowców. Wydawnictwo BTC,

Warszawa 2007.

Oryginał – po angielsku – jest dostępny w

Internecie.

Wykład 1/1. Klasyfikacja
sygnałów

[1] Rozdz. 1 str. 1-13.

[2] Rozdz. 1 (4,5 strony).

Wykład 1/2. Analiza widmowa
sygnałów
deterministycznych.
Przekształcenie całkowe
Fouriera.

[1] Rozdz. 3 – Szereg Fouriera. Rozdz. 4 – Całkowe przekształcenie
Fouriera,

p. 4.1 i 4.3.

[2] Rozdz. 6, p. 6.1, 6.2, 6.3, 6.4, 6.6 i p. 6.7.1.

[3] Tom II, p. 5.1. Tom III, p. 9.1.3 A i B.

[6] str. 144 i str. 244-250.

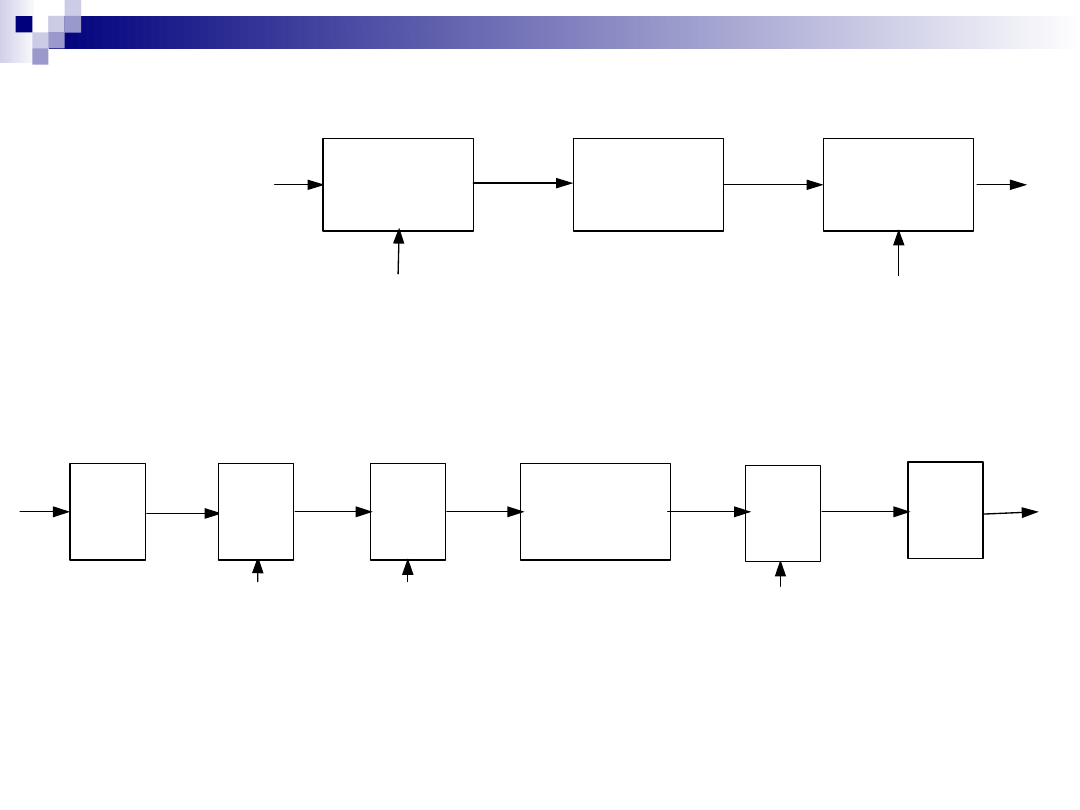
Dalej na tym wykładzie zmierzam do omówienia następujących systemów.

Dyskretno-czasowe przetwarzanie sygnałów
analogowych. System idealny.

C/D – konwerter czasu ciągłego na dyskretny (ang. continuous-to-discrete)
D/C – konwerter czasu dyskretnego na ciągły (ang. discrete-to-continuous)
T – takt zegara

Cyfrowe przetwarzanie sygnałów analogowych. System
praktyczny.

AAF

A/D

System

cyfrowy

)

(t

x

c

)

(

ˆ t

y

r

T

T

)

(

0

t

x

]

[

ˆ n

y

S&H

RF

D/A

T

)

(t

x

a

]

[

ˆ n

x

)

(t

y

DA

C/D

System

dyskretno-

czasowy

D/C

)

(t

x

c

)

(t

y

r

T

T

]

[n

x

]

[n

y

AAF – filtr antyaliasingowy (ang. anti-aliasing filter)
S&H – próbkowanie i podtrzymywanie (ang. sample-and-hold)
A/D – przetwornik (konwerter) analogowo-cyfrowy (ang. analog-to-digital

converter)
D/A – przetwornik (konwerter) cyfrowo-analogowy (ang. digital-to-analog

converter)
RF – filtr rekonstrukcyjny (ang. reconstruction filter)